Atmospheric and Climate Sciences
Vol.3 No.3(2013), Article ID:33895,11 pages DOI:10.4236/acs.2013.33035
Shortwave Cloud and Aerosol Radiative Forcings and Their Effects on the Vertical Local Heating/Cooling Rates
1Department of Electrical and Electronic Engineering, University of Buea, Buea, Cameroun.
2Environmental Energy Technologies Laboratory (EETL), Faculty of Sciences, University of Yaoundé 1, Yaoundé, Cameroon
Email: *languimdo@yahoo.fr
Copyright © 2013 L. Akana Nguimdo, D. Njomo. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received March 29, 2013; revised May 1, 2013; accepted May 10, 2013
Keywords: Planetary Boundary Layer; Upper Layer; Clear Sky Flux; All-Sky Flux; Net Downward Flux; Radiative Forcing; Heating/Cooling Rates
ABSTRACT
An analysis of atmospheric SW-radiative forcing and local heating/cooling rate is made using a one year temporal and vertical profiles of aerosol and cloud over Yaoundé (11.51˚E, 3.83˚N). It appears that the direct influence of aerosols on the surface compared to the TOA can be 3 times larger. Annual mean value obtained at 559 mb altitude is +27.74 W/m2 with range from 0 to +43 W/m2. At 904 mb, we obtained an annual mean of −46.22 W/m2 with range from −65 to −9 W/m2. Frequency distribution indicates that more than 95% of ARF are between +10 and +70 W/m2 at 559 mb (upper limit of UL), and more than 85% of ARF are between −70 and −10 W/m2 at 904 mb (upper limit of PBL). This sign change is explained by the fact that the backscattering peaks at the upper limit of the aerosol PBL layer. The maximum CRF is noted at TOA where it reaches −600 W/m2 based on the time interval and the structure of clouds. The highest values occur between 11.50 and 13.50 LST. Clouds lead to a general heating of the entire atmospheric column with a much greater effect near the surface. Aerosols effect on the heating rate profile show strong cooling during the day for the lower atmosphere, with slight heating at the upper atmosphere. This cooling contribution generally increases from the surface and peacks at the upper boundary of aerosol layer where reflectivity is the most important. Depending on the moment of the day, average heating effect of clouds peacks at surface or within the middle troposphere due to the absorption by clouds particles. Vertical profiles deeply evolve exhibiting differences that exceed −3 K/day according to altitude from one hour to another during a given mean solar day.
1. Introduction
Understanding the role of clouds and aerosols on the atmospheric radiative budget is an immense and painstaking endeavour as it requires the knowledge of their spatial distribution, temporal evolution and the processes controlling their changes and interactions with other components of the earth’s climate [1-3]. The treatment of clouds and the associate feedback in General Circulation Models constitute the largest uncertainty in climate modelling [4,5] and still up to now a debated issue unless decades of in situ and over century of ground-based cloud monitoring. In fact, the mechanisms by which the interaction between clouds and radiation budget take place are extremely complex and involve multiple independent cloud variables acting on a hierarchy of spatial and temporal scales [6]. The way this complexity is taken into account in radiative and satellite models leads to uncertainties in determining the cloud radiative forcing at the surface and at the top of the atmosphere which ultimately alter the accuracy of the cloud radiative forcing ratio that has been employed in many recent studies [2,7]. Aerosols also can significantly modify the earth raditive budget and planetary boundary layer meteorology by reflecting sunlight to space and absorbing solar radiation in the atmosphere [8,9]. Despite limited success achieved, a complete characterization of aerosol optical properties is difficult as it requires information about among others, particle size distribution, chemical composition, both of which are extremely difficult to obtain on large scale on a routine basis. Numerous projects have been far studying different types of clouds [10-13] according to their origin and chemical constitution for global characterization of their basic properties such as optical thickness. However, although the debate on the accurate assessment of the atmospheric radiative budget is maintained by adequate consideration of clouds and aerosols in radiative models, it remains a fact that the lack of trustworthy input data contributes to maintain the already considerable differences about flux values obtained from different models [14]. Therefore, credible estimation of atmospheric radiative budget and hence the heating rate profile need local or regional data on cloud and aerosol microphysical and optical properties.
This study describes the vertical profiles of cloud and aerosol radiative forcings in a standard tropical atmosphere and the resulting heating rate profiles using local data on cloud and aerosol properties deduced from groundbased solar radiation measurements [15,16].
2. Details of Model Simulations
The vertical distribution of shortwave radiative heating in the atmosphere is an important driver of atmospheric circulation, especially in tropics. Aside from the horizontal variability of the atmospheric major components such as clouds, aerosol, water vapour etc, radiative heating associated with vertical variability is also important and may affect the development of convection. Although the vertical redistribution of energy by clouds and aerosols have important feedback to model dynamics, evaluation of model simulations of the Earth radiative budget typically focus on performance at the TOA and surface [17,18] neglecting details of the distribution of radiation within the vertical column [19]. In fact, evaluation of vertical profiles of model fluxes or heating rate is difficult because of the lack of direct observations of heating rate profiles in the atmosphere. This problem is much more important in tropical regions where data sets for calculating all-sky heating rate profiles with high vertical and temporal resolution cover only a very limited area. This is for instance the case of long time series of observations taken at the US Department of Energy’s ARM program [19]. In this study, we combine cloud fraction, water content data and aerosol optical properties previously deduced from ground-based solar radiation measurements to determine the upward and downward solar fluxes within the atmosphere. From these fluxes we evaluate the simulated vertical profiles of clouds and aerosols radiative forcings considered as the change in the balance between radiation coming into the atmosphere and the radiation going out due to the presence of specific atmospheric constituents under investigation. We then use this forcing to assess the effects of these atmospheric constituents on the local heating/cooling rate.
Atmospheric radiative forcing and heating rate are derived using plane parallel atmosphere approximation. At a given time, input to our calculations are the derived vertical profiles of cloud and aerosol measurements [15, 16] and other atmospheric constituents as described in the AFGL tropical standard atmosphere profile [20]. In this study, we define cloud (aerosol) forcing as the difference between the all-sky and the clear sky net downward radiation fluxes. Clear sky denotes the atmosphere without cloud (aerosol) or cloud (aerosol) having been removed. Let us denote the net flux at a given atmospheric level k as
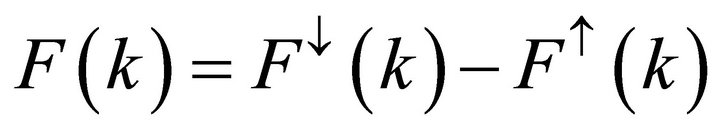 (1)
(1)
and define cloud (aerosol) radiative forcing as
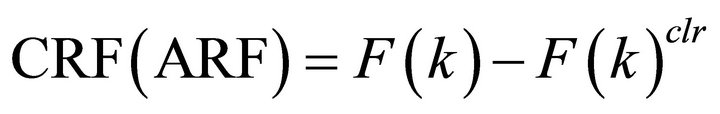 (2)
(2)
where  is downward (upward) SW radiation flux. CRF and ARF respectively denote Cloud and Aerosol Radiative Forcings. The superscript
is downward (upward) SW radiation flux. CRF and ARF respectively denote Cloud and Aerosol Radiative Forcings. The superscript 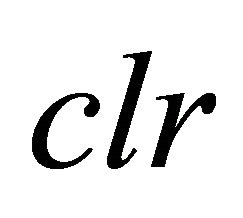 refers to clear sky. This definition makes explicit the verticallyresolved contribution of cloud (aerosol) to radiative heating defined for a given atmospheric layer k as
refers to clear sky. This definition makes explicit the verticallyresolved contribution of cloud (aerosol) to radiative heating defined for a given atmospheric layer k as
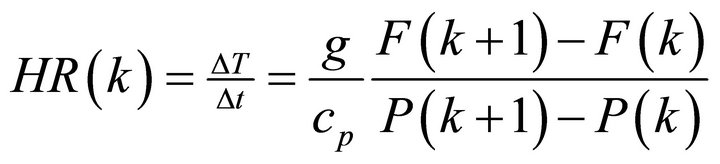 (3)
(3)
From this forcing perspective, we derive average vertical profiles of CRF (ARF) and the effects of clouds and aerosols on the atmospheric Heating Rate for a one year period at Yaoundé (11.51˚E, 3.83˚N). These profiles are presented at hourly time steps of average solar days previously defined using geographical considerations [20]. Figure 1 below presents the schematic representation of the aerosol-cloud vertical distribution for calculations of atmospheric solar fluxes and the heating/cooling rates.
3. Results
3.1. Aerosol Radiative Forcing (ARF)
Current aerosol profile data are far from adequate for quantifying the ARF and the atmospheric response to the
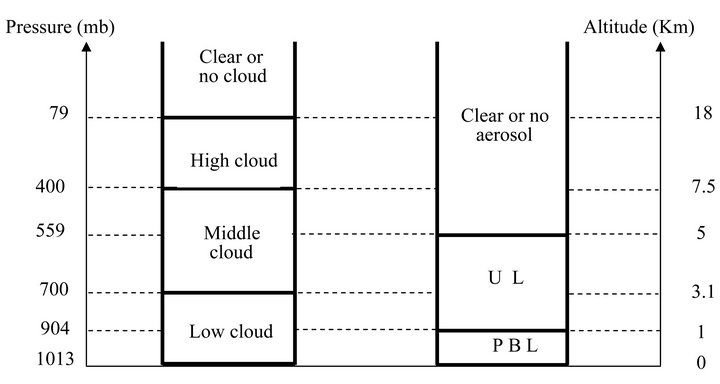
Figure 1. Schematic representation of the aerosol-cloud vertical distribution for calculation of atmospheric solar fluxes and the heating/cooling rates.
forcing [21] at global scale. The data have limited spatial and temporal coverage, even for current space-borne Lidar measurements. Retrieving aerosol extinction profile from lidar measured attenuated back-scatter is subject to large uncertainties resulting from aerosol type characterization. Because of the lack of aerosol vertical distribution observations, the estimates of Direct Radiation Forcing (DRF) remain highly uncertain [22]. It also remains challenging to constrain the aerosol-induced atmospheric heating rate increment that is essential for assessing atmospheric responses to the aerosol forcing.
Progress in the foreseeable future is likely to come from a better use of existing global space-based backscatter Lidar to constrain model simulations and the deployment of new instruments capable of retrieving both extinction and back-scatter from space. In fact, diurnal variability of aerosols can be large, depending on location and aerosol type [23] especially in regions where boundary layer changes during the day. Geostationary satellites provide adequate time resolution but lack information required to characterize aerosol types that can help improve the accuracy of geostationary aerosol retrievals. Adequate estimation of the diurnal aerosol DRF also needs additional efforts such as the characterization of daytime variation of clouds. Due to all these reasons and given the fact that quantifying long-term trends of aerosol requires the construction of consistent multi-decadal records of climate quality data, aerosol trend analysis to be meaningful must be performed on a regional basis. Figure 2 addresses the diurnal vertical profile of ARF at Yaoundé for a one year period.
According to Equation (2), positive value of radiative forcing indicates increased net downward solar radiation due to aerosols consecutive to a decreased back scattered or absorbed shortwave radiation. In contrast, negative forcing indicates decreased net downward solar radiation consecutive to an increased back scattered or absorbed shortwave radiation. It appears from the graphs in Figure 2 that aerosols contribute to a positive forcing in the upper layers of the atmosphere and a negative forcing near the surface. The transition takes place at the upper limit of the aerosol layer (~560 mb) where in all cases studied, forcing passes through its zero value. The change of sign observed reinforces the dependence of ARF on the aerosol profile. In fact, the direct radiative effect of the aerosol in the atmosphere is controlled by parameters such as single scattering albedo, optical thickness and surface albedo. Therefore, combinations of these parameters can lead to a changing sign of ARF with time over the same location. This forcing is very significant at surface with values exceeding −100 W/m2 indicating that aerosols can have strong radiative impacts. The direct influence of aerosols on the surface compared to TOA can be 3 times larger at the Yaoundé local scale, demonstrating the dominance of the surface ARF to that at TOA. Indeed we noticed for some months an Aerosol Radiative Forcing (ARF) exceeding −60 W/m2 for the first hour of the day, which represents over 33% of incident solar flux at TOA. This result is in general agreement with Hatzianastassiou et al., [24] who obtained for many areas of the globe that the direct effect of aerosol on SW radiation can be up to 3 - 4 times larger than at TOA.
The mean hourly ARFs from the SW model at TOA, 559mb (upper limit of the aerosol Upper Layer), 904 mb (upper limit of the Planetary Boundary Layer) and at the surface are shown in Figure 3 for the corresponding period of one year. We note that small values of ARF at TOA do not exclude important aerosol effects taking place within the Earth-atmosphere system. Comparing the ARF at 11.50 LST, we obtained a cooling effect of −92.22 W/m2 at surface (Figure 3(d) and a heating effect of +42.24 W/m2 at TAO (Figure 3(a)). Within the atmosphere, the SW ARF under all sky conditions is very important. Annual mean value obtained at 559 mb is +27.74 W/m2 with range from 0 to +43 W/m2. At 904 mb, we obtained an annual mean of −46.22 W/m2 with range from −65 to −9 W/m2. Frequency distribution graphs describing the probability of occurrence of positive change (heating) or the negative change (cooling) in the flux balance at indicated altitudes in the atmosphere are presented in Figure 4(a). These curves indicate that more than 95% of ARF are between +10 and +70 W/m2 at 559 mb (upper limit of UL), and more than 85% of ARF are between −70 and −10 W/m2 at 904 mb (upper limit of PBL). This sign change is explained by the fact that the backscattering peaks at the upper limit of the aerosol PBL layer. The peak value for each transition level indicated on the graph represents the probability of the most recurrent flux difference class and therefore the corresponding value of radiative forcing can be seen as the image of aerosols activity at the considered altitude.
3.2. Cloud Radiative Forcing
It has long been noted that clouds significantly influence the global climate system [25,26]. There is a general agreement that the effect of clouds on radiative fluxes often defined by the difference in the flux between cloudy and clear sky atmosphere tends to reduce the SW radiation entering the earth atmosphere. Also, recent studies have shown strong variability of CRF with latitude [26, 27] due to cloud amount and various variables such as solar zenith angle and surface albedo that seriously impact the incident solar radiation. Despite this overall agreement, there are significant differences in magnitude among cloud radiation forcing estimates. Sohn and Robertson [27] pointed out the use of various satellite sensors with different spatial and temporal resolution, substantially different estimation methods and different ana-
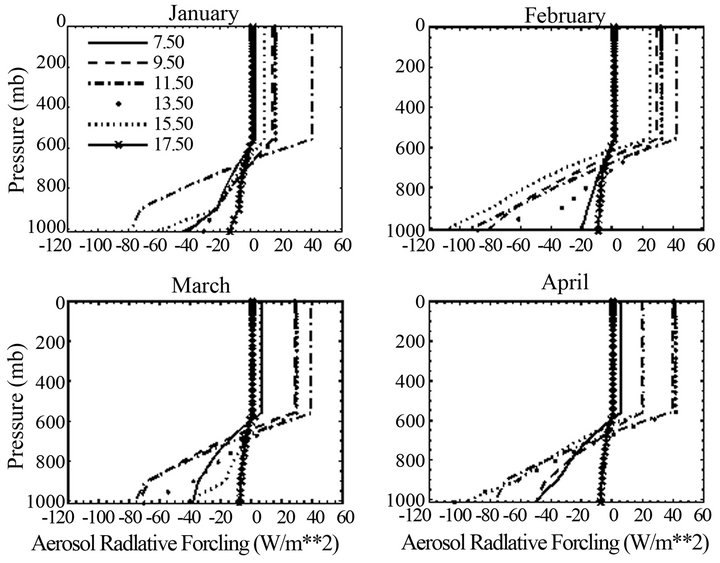

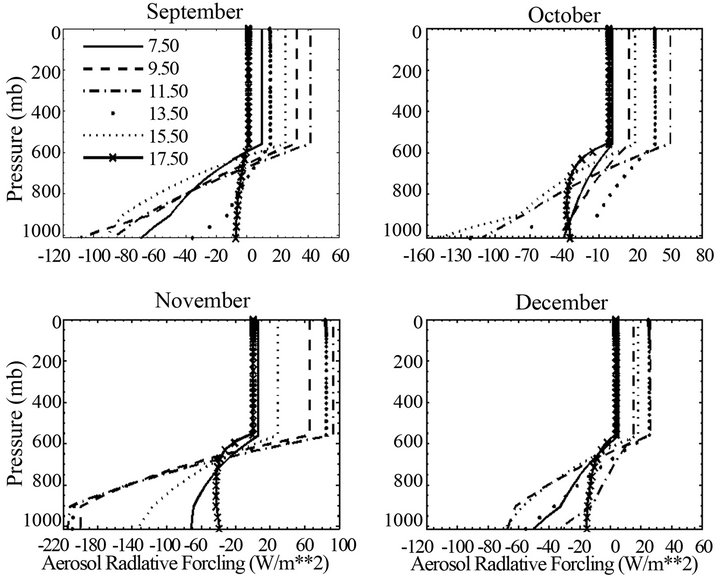
Figure 2. Vertical distribution of average aerosol radiative forcing simulated for given local times (LST) within monthly average solar days of the different months.

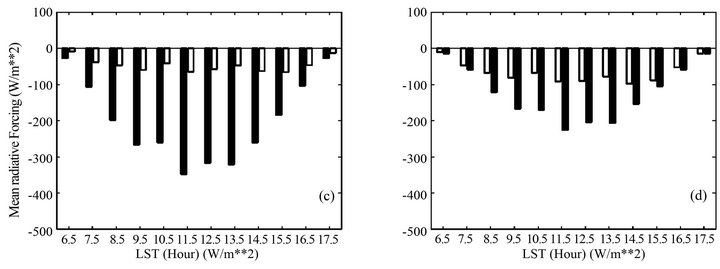
Figure 3. Annual hourly averaged radiative forcing (a) at TOA, (b) and (c) at different levels within the atmosphere and (d) at surface. Note: The abscises shown represent the central values of each time interval. In figure (b) the CRF is calculated at the upper limit of the middle cloud layer and the ARF at the upper limit of the Upper Layer. In figure (c) the CRF is calculated at the upper limit of low cloud layer and the ARF at the upper limit of the Planetary Boundary Layer.
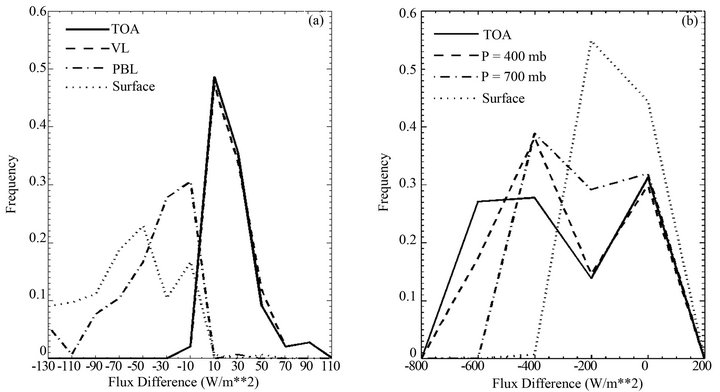
Figure 4. Frequency distributions of (a) aerosols and (b) clouds SW radiative forcings.
lysis periods. Terasova and Cavalcanti [26] suggested the need of improving cloud cover schemes employed by the methods as well as radiation transfer codes. However, these differences might be due to long-wave (LW) radiation. Sohn and Robertson [27] intercomparing five sets of shortwave (SW) CRF obtained using the same dataset for the same analysis period discovered uniformly smaller zonal mean differences between calculations. On contrary large differences were obtained in the case of LW CRF. With this in mind, we analysed numerically the diurnal vertical profile of SW CRF within the atmosphere and at surface. Indeed, although recent studies have focused on the influence of solar zenith angle on the CRF, the information currently available on the radiative impact of clouds do not inform enough about evolution hour after hour, but rather on (local or global) monthly or yearly averages.
Cloud radiative forcing is a parameter that has been extensively used to study cloud radiation interaction. Here, we used the net downward SW radiation (Equation (2)) in the atmosphere, at TOA and at surface to examine the cloud radiative forcing (CRF). Figure 5 presents the diurnal vertical profile of CRF at hourly time scale. We obtained that the SW CRF is negative everywhere indicating the important role of clouds in reducing the downward solar radiation. Also, the importance of this forcing indicates the great capacity of clouds in absorbing or backscattering the solar radiation. Unlike aerosols, the maximum CRF is noted at TOA where it reaches −600 W/m2 based on the time interval and the structure of clouds. The highest values occur between 11.50 and 13.50 LST. This could foreshadow the influence of the insoletion at TOA in that it is at this time interval that the incident solar flux at TOA is the most important. These values compared to those obtained in previous studies [7] seem very large. This is understandable since these studies provide information only on the monthly, annual averages or averages extended to a given time period but does not take into account the variability hour after hour. Histograms of mean hourly CRF at surface, at TOA and within the atmosphere (Figure 3(b)) over the period of study show a significant increase with the cosine of solar zenith angle during the day whatever the level of interest. This observation reveals once again the influence of Cos (Z) suggested by Shupe et al. [28] although here one could not be formal because the vertical configuration of the cloud evolves with time interval. Annual average values obtained are −303 W/m2, −272.23 W/m2, −201.68 W/m2 and −125 W/m2 respectively for TOA, 400 mb, 700 mb and the surface. The ratio CRF (TOA)/CRF (surface) equal to 2.4 is slightly higher than that obtained by Ramanathan et al. [7]. This difference is due to the particular situation of Yaoundé near the equator with a very important sunshine and mostly the quasi-permanent clouds above the station during the year that enhances radiative forcing at TOA. Frequency distribution (Figure 5(b)) shows the surface concentration around small values of CRF with a spread between 0 and −300 W/m2 depending on the time interval and a shift towards larger values at high altitudes where there is great similarity between the profiles at TOA and 400 mb altitude.
3.3. Effect of Clouds and Aerosols on the Atmospheric Heating
Specification of the correct vertical distribution of clouds and aerosols properties is important to climate simulation. Clouds for instance redistribute energy vertically within the atmospheric column and this energy redistribution affects local and large scale dynamics. Aerosol in particular can lead to both cooling by reflecting sunlight back to the space and warming by absorbing solar radiation. In this section, differences in all-sky and clear sky fluxes are examined to isolate the effects of these atmospheric components on the tropospheric vertical heating rate profile. As in radiative forcing calculations, heating rates are calculated on an hourly basis using the vertical profile of the atmosphere pre-calculated at that time step [15,16]. Incident solar radiation at the TOA is calculated using geographical considerations [29] and diurnal variations of solar radiation are considered using the solar zenith angle at the middle of the considered time step (Table 1). In order to avoid computational expenses of re-running clear sky heating rates (case of no cloud or no aerosol), input data are introduced in a common file and are called sequentially in our routine. Outputs are then kept in specific files allowing to easily performing the differences calculations. Figures 6 and 7 present respectively the effects of aerosols and clouds on the vertical heating rate profile at Yaoundé for the 12 months involved in this study.
According to Equation (3), SW heating/cooling depends directly on the sign of the solar flux divergence defined as 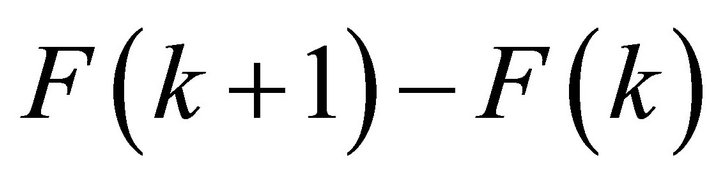 where F is the net SW downward flux. A positive flux divergence corresponds to the atmospheric heating. On the contrary, negative flux divergence induces atmospheric cooling. Therefore, although the clouds lead to overall a negative forcing, their net radiative flux divergence is positive for most of the cases studied. We found (Figure 7) a general heating of the entire atmospheric column with a much greater effect near the surface. From Figure 6, one can note that aerosols effect on the heating rate profile [30] shows strong cooling during the day for the lower atmosphere, with slight heating at the upper atmosphere. This SW cooling in aerosol layer is caused by the reflection of solar radiation from the aerosols, which reduces the amount of solar radiation available for absorption. This cooling contribution generally increases from the surface and peacks at the upper boundary of aerosol layer where reflectivity is the most important. Depending on the moment of the day, average heating effect of clouds peacks at surface or within the middle troposphere due to the absorption by
where F is the net SW downward flux. A positive flux divergence corresponds to the atmospheric heating. On the contrary, negative flux divergence induces atmospheric cooling. Therefore, although the clouds lead to overall a negative forcing, their net radiative flux divergence is positive for most of the cases studied. We found (Figure 7) a general heating of the entire atmospheric column with a much greater effect near the surface. From Figure 6, one can note that aerosols effect on the heating rate profile [30] shows strong cooling during the day for the lower atmosphere, with slight heating at the upper atmosphere. This SW cooling in aerosol layer is caused by the reflection of solar radiation from the aerosols, which reduces the amount of solar radiation available for absorption. This cooling contribution generally increases from the surface and peacks at the upper boundary of aerosol layer where reflectivity is the most important. Depending on the moment of the day, average heating effect of clouds peacks at surface or within the middle troposphere due to the absorption by

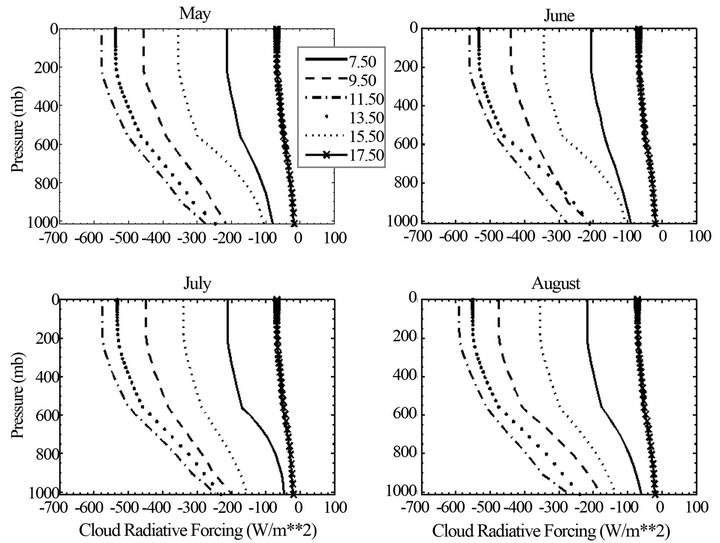
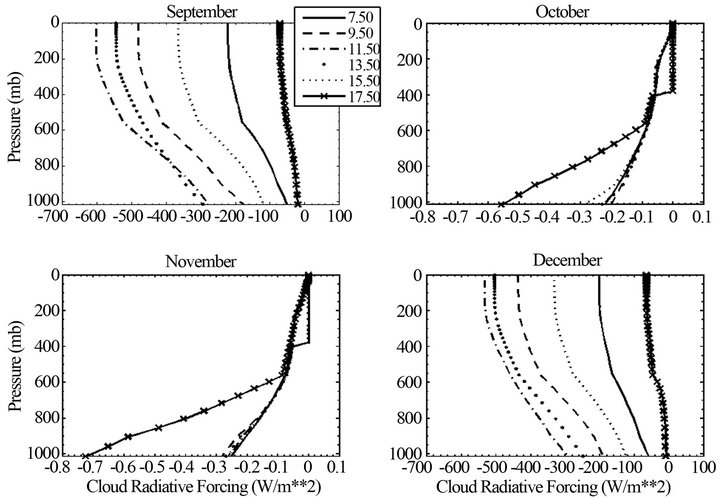
Figure 5. Vertical distribution of average cloud radiative forcing simulated for given local times (LST) within average solar days of the different months.
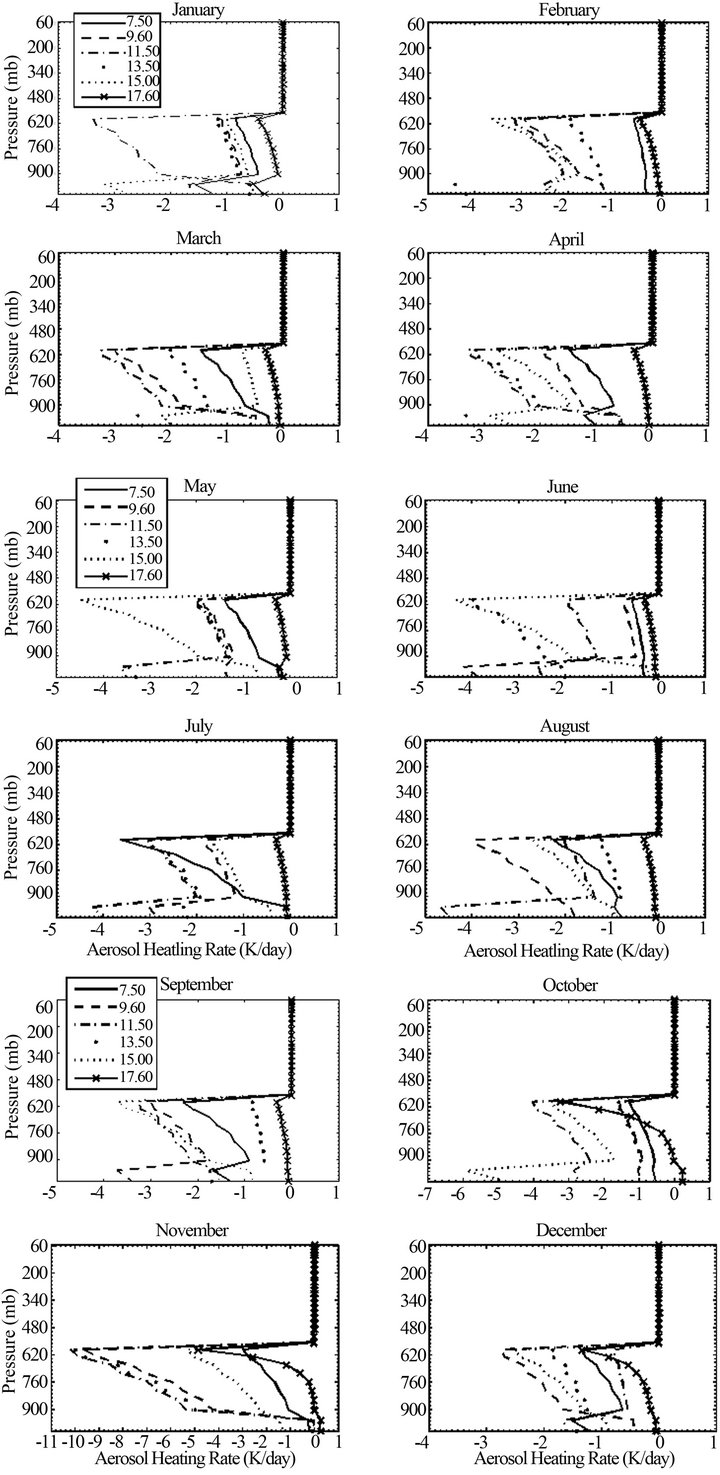
Figure 6. Average impact of aerosols on the SW net heating rate (all-sky minus clear sky) during average solar days of the different months.

Figure 7. As figure 6 but for clouds.
clouds particles. It is of importance to point out the light cloud cooling effect that occurred during the months of October and November. These months correspond to a maximum of aerosol cooling effect with an impact exceeding −5 K/day and −10 K/day respectively. This cooling may be the result of the indirect effect of aerosols on clouds of which the conesquence is to annihilate their heating tendency.
Models need to predict not only correct average atmospheric radiation profiles but also the correct variability. There are large variations in the effects of clouds (aerosols) on the local vertical heating/cooling rate profiles of the atmosphere. These are due both to time variability of the cloud amount, cloud water content, the aerosol optical thickness and to their vertical location in the atmosphere given the fact that the data cited above are essentially dynamic. These fluctuations introduce the diurnal variability of radiation heating which is an important factor to dynamic in the tropics. Besides this very changing vertical profile of atmospheric constituents involved in this study [16], the diurnal variability of the incoming solar radiation may be considered as an additional reason to the strong variability in the diurnal cycle of the SW heating/cooling rates. Our calculations show vertical profiles deeply evolving with differences exceeding −3 K/ day according to altitude from one hour to another during a given mean solar day. By comparing the results obtained at the same time (same cosine of solar zenith angle) but for two different months, there are also significant differences of up to −8 K/day. These differences become negligible above the aerosol layer where their impact on the local heating is also very low. This result is explained by the fact that whatever the moment of the day, not only the aerosol backscattering at this altitude is maximum but also the completely clear state of the atmosphere helps reduce significantly the divergence of the solar radiation flux.
4. Conclusion
In this study, we quantified the aerosols and clouds radiative forcings and infered their direct effects on the vertical atmospheric heating at the Yaoundé meteorological station for a one year period. The results globally demonstrate the aerosols cooling effect near the surface and the light heating effect of the upper atmospheric layers. Clouds on contrary lead to the heating of the Earthatmosphere system during almost all the period of study (unless during October and November). On an hourly basis, clouds are found to decrease the net downward solar radiation within the entire atmospheric column with more intensified activity at the TOA where CRF exceeds −480 W/m2. This effect of clouds decreases with altitude and is approximately 225 W/m2 at its hourly maximum at surface. As a result, the cloud effect on the flux divergence increases with decreasing altitude and leads to more pronounced atmospheric heating near the surface. On the other hand, aerosols contribute to increase the net downward (atmospheric heating) solar radiation at upper atmospheric layers and to decrease it near the surface (atmospheric cooling). According to our computations, the magnitude of aerosols reduction in downward SW radiation is very important near the surface. More specifically, the ARF translates to an estimated cooling ranges at its hourly maximum from −1 K/day to −8 K/day near the surface.
REFERENCES
- J. Hansen, W. Rossow, B. Carlson, A. Lacis, L. Travis, A. Del Genio, I. Fung, B. Cairns, M. Mishchenko and M. Sato, “Low-Cost Long-Term Monitoring of Global Climate Forcing and Feedbacks,” Climate Change, Vol. 31, No. 2-4, 1995, pp. 247-271. doi:10.1007/BF01095149
- Z. Li, “Influence of Absorbing Aerosols on the Inference of Solar Surface Radiation Budget and Cloud Absorption,” Journal of Climate, Vol. 11, 1998, pp. 5-15. doi:10.1175/1520-0442(1998)011<0005:IOAAOT>2.0.CO;2
- Z. Li and A. P. Trishcenko, “Quantifying Uncertainties in Determining SW Radiative Forcing and Cloud Absorption Due to Variability in Atmospheric Conditions,” Journal of the Atmospheric Sciences, Vol. 58, 2000, pp. 376- 379. doi:10.1175/1520-0469(2001)058<0376:QUIDSC>2.0.CO;2
- R. D. Cess, G. L. Potter, J. P. Blanchet, G. J. Boer, S. J. Ghan, J. T. Kiehl, H. Le Treut, Z.-X. Li, X.-Z. Liang, J. F. B. Mitchell, J.-J. Morcrette, D. A. Randall, M. R. Riches, E. Roeckner, U. Schlese, A. Slingo, K. E. Taylor, W. M. Washington, R. T. Wetherald and I. Yagai, “Interpretation of Cloud-Climate Feedbacks as Produced by 14 Atmospheric General Circulation Models,” Science, Vol. 245, No. 4917, 1989, pp. 513-516. doi:10.1126/science.245.4917.513
- IPCC, “Climate Change, the IPCC Scientific Assessment,” Cambridge University Press, Cambridge, 1995.
- M.-D. Chou and M. J. Suarez, “A Solar Radiation Parameterization for Atmospheric Studies (CLIRAD-SW),” In: NASA Technical Memorandum, 1999, pp. 1-38.
- V. Ramanathan, B. Subasilar, G. J. Zhang, W. Conant, R. D. Cess, J. T. Kiehl, H. Grassl and L. Shi, “Warm Pool Heat Budget and Shortwave Cloud Forcing: A Missing Physics,” Science, Vol. 267, No. 5197, 1995, pp. 499- 503. doi:10.1126/science.267.5197.499
- J. A. Coakley, R. D. Cess and F. B. Yurevich, “The Effect of Tropospheric Aerosols on the Earth’s Radiation Budget: A Parameterization for Climate Models,” Journal of Atmospheric Sciences, Vol. 40, No. 1, 1983, pp. 116-138. doi:10.1175/1520-0469(1983)040<0116:TEOTAO>2.0.CO;2
- O. E. Garcia, A. M. Diaz, F. J. Exposito and J. P. Diaz, “Aerosol Radiative Forcing and Forcing Efficiency in the UVB Regions Affected by Saharan and Asian Mineral dust,” Journal of the Atmospheric Sciences, Vol. 66, No. 4, 2009, pp. 1033-1040. doi:10.1175/2008JAS2816.1
- NASA, “Report of the Aerosol Interdisplinary Research Program Workshop, October 30-November 1,” NASA, Washington DC, 1996.
- M. D. King, Y. J. Kaufman, W. P. Menzel and D. Tanre, “Remote Sensing of Cloud, Aerosol, and Water Vapour Properties from the Moderate Resolution Imaging Spectrometer (MODIS),” IEEE Transactions on Geoscience and Remote Sensing, Vol. 30, 1992, pp. 2-27. doi:10.1109/36.124212
- G. M. McFarquhar and A. J. Heymsfield, “Parameterization of Tropical Cirrus Ice Crystal Size Distribution and Implications for Radiative Transfer: Results from CEPEX,” Journal of Atmospheric Sciences, Vol. 54, No. 17, 1997, pp. 2187-2200. doi:10.1175/1520-0469(1997)054<2187:POTCIC>2.0.CO;2
- G. M. McFarquhar and S. G. Cober, “Single Scattering Properties of Mixed Phased Artic Clouds at Solar Wavelengths: Impacts on Radiative Transfer,” Journal of Climate, Vol. 17, No. 19, 2004, pp. 3799-3813. doi:10.1175/1520-0442(2004)017<3799:SPOMAC>2.0.CO;2
- Y. Liu, W. Wu, M. P. Jensen and T. Toto, “Relationship between Cloud Radiative Forcing, Cloud Fraction and Cloud Albedo, and New Surface—Based Approach for Determining Cloud Albedo,” Atmospheric Chemistry and Physics, Vol. 11, No. 14, 2011, pp. 7155-7170. doi:10.5194/acp-11-7155-2011
- N. L. Akana and D. Njomo, “Assessing the Aerosol Optical Thickness in Cameroon Using Ground-Based Solar radiation Measurements,” Advanced Science Letters, Vol. 3, 2010, pp. 1-7.
- N. L. Akana and D. Njomo, “Profiles of Cloud Fraction and Water Content Deduced from Ground-Based Solar Radiation Measurements,” Asian Pacific Journal of Atmospheric Science, Vol. 46, No. 4, 2010, pp. 483-496.
- J. T. Kiehl, J. J. Hack, G. B. Bonan, B. A. Boville, D. L. Williamson and P. J. Rasch, “The National Center for Atmospheric Research Community Climate Model: CCM3,” American Meteorological Society, Vol. 11, 1998, pp. 1131- 1149.
- O. E. Garcia, A. M. Diaz, F. J. Exposito and J. P. Diaz, “Shortwave Radiative Forcing and Efficiency of Key Aerosol Type Using AERONET Data,” Atmospheric Chemistry and Physics Discussions, Vol. 11, No. 12, 2011, pp. 32647-32684.
- S. A. McFarlane, J. H. Mather and T. P. Ackerman, “Analysis of Tropical Radiative Heating Profile: A Comparison of Models and Observations,” Journal of Geophysical Research, Vol. 112, 2007, Article ID: D14218. doi:10.1029/2006JD008290
- G. P. Anderson, J. H. Chetwynd, S. A. Clough, E. P. She1tle and F. X. Kneizys, “AFGL Atmospheric Constituent Profiles (0 - 120 km),” Environmental Research Paper, Vol. 954, 1986, pp. 1-46.
- US Climate Change Science Program, “Atmospheric Aerosol Properties and Climate IMPACT,” Synthesis and Assessment Product 2.3.
- I. N. Sokolik and O. B. Toon, “Incorporation of Mineralogical Composition into Models of the Radiative Properties of Mineral Aerosol from UV to IR Wavelengths,” Journal of Geophysical Research, Vol. 104, No. D8, 1999, pp. 9423-9444. doi:10.1029/1998JD200048
- A. Smirnov, N. B. Holben, N. T. O’Neill, T. F. Eck, D. L. Westphal, A. K. Goroch, C. Pietras, O. Dubovik and I. Slutsker, “Atmospheric Aerosol Optical Properties in the Persian Gulf,” Journal of Atmospheric Sciences, Vol. 59, No. 3, 2002, pp. 620-634. doi:10.1175/1520-0469(2002)059<0620:AAOPIT>2.0.CO;2
- N. Hatzianastassiou, C. Matsoukas, E. Drakakis, P. W. Stackhouse Jr., P. Koepke, A. Fotiadi, K. G. Pavlakis and I. Vardavas, “The Direct Effect of Aerosol on Solar Radiation Based on Satellite Observations, Reanalysis Datasets, and Spectral Aerosol Optical Properties from Global Aerosol Data Set (DADS),” Atmospheric Chemistry and Physics Discussions, Vol. 7, 2007, pp. 753-783. doi:10.5194/acpd-7-753-2007
- L. Zhou, R. T. Pinker and I. Laszlo, “Shortwave Radiative Cloud Forcing in the Tropical Pacific Including the 1982-1983 and 1987 EL NINOs,” International Journal of Climatology, Vol. 16, No. 1, 1996, pp. 1-13. doi:10.1002/(SICI)1097-0088(199601)16:1<1::AID-JOC990>3.0.CO;2-5
- T. A. Terasova and I. F. A. Cavalcanty, “Annual Cycle of Cloud Radiative Forcing over South America Simulations with CPTEC/COLA AGCM and SRB Data,” Preprints of Sixth International Conference on Southern Hemisphere Meteorology and Oceanography, AMS, Boston, 2000.
- B.-J. Sohn and F. R. Robertson, “Intercomparison of Observed Cloud Radiative Forcing: A Zonal and Global Perspective,” Bulletin of the American Meteorology Society, Vol.74, No. 6, 1993, pp. 997-1006. doi:10.1175/1520-0477(1993)074<0997:IOOCRF>2.0.CO;2
- D. M. Shupe, P. Zuidema and T. Uttal, “Cloud Radiative Heating Rate Forcing from Profiles of Retrieved Artic Cloud Microphysics,” Proceedings for the Twelfth ARM Science Team Meeting, St. Petersburg, 8-12 April 2002.
- N. L. Akana and D. Njomo, “Spatial and Temporal Distributions of Downwelling Solar Radiation in Cameroon as Derived Using a Parameterized Solar Radiative Transfer Model in a Molecular Atmosphere,” JP Journal of Heat and Mass Transfer, Vol. 3, No. 2, 2009, pp. 73-93.
- J. Su, J. Huang, Q. Fu, P. Minnis, J. Ge and J. Bi, “Estimation of Asian Dust Aerosol Effect on Cloud Radiation Forcing Using Fu-Liou Radiative Model and CERES Measurements,” Atmospheric Chemistry and Physics Discussions, Vol. 8, No. 1, 2008, pp. 2061-2084.
NOTES
*Corresponding author.

