International Journal of Astronomy and Astrophysics
Vol.06 No.03(2016), Article ID:70583,19 pages
10.4236/ijaa.2016.63025
Halo Orbits around Sun-Earth L1 in Photogravitational Restricted Three-Body Problem with Oblateness of Smaller Primary
Prithiviraj Chidambararaj, Ram Krishan Sharma
Department of Aerospace Engineering, Karunya University, Coimbatore, India

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 20 July 2016; accepted 11 September 2016; published 14 September 2016
ABSTRACT
This paper deals with generation of halo orbits in the three-dimensional photogravitational restricted three-body problem, where the more massive primary is considered as the source of radiation and the smaller primary is an oblate spheroid with its equatorial plane coincident with the plane of motion. Both the terms due to oblateness of the smaller primary are considered. Numerical as well as analytical solutions are obtained around the Lagrangian point L1, which lies between the primaries, of the Sun-Earth system. A comparison with the real time flight data of SOHO mission is made. Inclusion of oblateness of the smaller primary can improve the accuracy. Due to the effect of radiation pressure and oblateness, the size and the orbital period of the halo orbit around L1 are found to increase.
Keywords:
Halo Orbits, Photogravitational Restricted Three-Body Problem, Oblateness, Lindstedt-Poincaré Method, Lagrangian Point, SOHO

1. Introduction
The subject of halo orbits in restricted three-body problem (RTBP) has received considerable attention in the last four decades. A halo orbit is a periodic, three-dimensional orbitnear the collinear Lagrangian points in the three-body problem. Analytical solutions to generate the halo orbits around any of the collinear points can be obtained. Farquhar first used the name “halo” in his doctoral thesis [1] and proposed an idea for placing a satellite in an orbit around L2 of the Earth-Moon RTBP. Had this idea been implemented, one could continuously view the Earth and the dark side of the moon at the same time. A communication link satellite is not necessary, if satellites are placed around Lagrangian points of the respective systems. Breakwell & Brown [2] generated halo orbits for the Earth-Moon system. Richardson [3] contributed significantly to obtain the halo orbits, by finding an analytical solution using Lindstedt-Poincaré method. A good amount of research has been carried out till date in this interesting area of halo orbits. Some of the important contributions are by Howell [4] , Howell and Pernicka [5] , Folta and Richon [6] and Howell et al. [7] .
The classical model of the restricted three-body problem are relatively less accurate for studying the motion of any Sun-planet system as they do not account for the effect of the perturbing forces such as oblateness of planets, cosmic rays, magnetic field, radiation pressure etc. Cosmic rays are immensely high-energy radiation, mainly originating outside the solar system. They produce showers of secondary particles that penetrate and impact the Earth’s atmosphere and sometimes even reach the surface. They interact with gaseous and other matter at high altitudes and produce secondary radiation. The combination of both contributes to the space radiation environment. In addition to the particles originating from the Sun are particles from other stars and heavy ion sources such as nova and supernova in our galaxy and beyond. In interplanetary space these ionizing particles constitute the major radiation threat. These particles are influenced by planetary or Earth’s magnetic field to form radiation belts, which in Earth’s case are known as Van Allen Radiation belts, containing trapped electrons in the outer belt and protons in the inner belt. The composition and intensity of the radiation varies significantly with the trajectory of a space vehicle. Anomalies in communication satellite operation have been caused by the unexpected triggering of digital circuits by the cosmic rays. In our present study, we restrict ourselves with the solar radiation and oblateness of the planet.
Radzievskii [8] was the first one to study the effect of solar radiation pressure. He found out that the maximum force due to the radiation pressure acts in the radial direction, given by
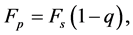
where q is defined in terms of particle radius a, density δ and radiation pressure efficiency factor x as
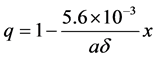 (c.g.s. units)
(c.g.s. units)
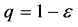 .
.
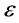 is a variable, depending upon the nature of the third body (satellite). The value of q can be considered as a constant, if the fluctuations in the beam of solar radiation and the effect of planet’s shadow are neglected. Using the model of [1] , Dutt and Sharma [9] studied periodic orbits in the Sun-Mars system using the numerical technique of Poincare surface of sections and found out more than 74 periodic orbits.
is a variable, depending upon the nature of the third body (satellite). The value of q can be considered as a constant, if the fluctuations in the beam of solar radiation and the effect of planet’s shadow are neglected. Using the model of [1] , Dutt and Sharma [9] studied periodic orbits in the Sun-Mars system using the numerical technique of Poincare surface of sections and found out more than 74 periodic orbits.
Sharma and Subba Rao [10] introduced the oblateness of the more massive primary in the three-dimensional restricted three-body problem. It has two terms, one with a z term in the numerator. Sharma [11] studied the periodic orbits around the Lagrangian points in the planar RTBP by considering Sun as source of radiation and smaller primary as an oblate spheroid with its equatorial plane coincident with the plane of motion. Tiwary and Kushvah [12] followed the model of Sharma [11] to study the halo orbits around the Lagrangian points L1 and L2 analytically. However, they did not consider the z term in oblateness in their study. In the present work, we have considered both the terms due to oblateness of the smaller primary in the photogravitational restricted three-body problem to study the halo orbits analytically as well as numerically around L1.
The first satellite placed in the halo orbit at Sun-Earth L1 point was International Sun-Earth Explorer-3 (ISEE-3), launched in 1978. Solar Heliospheric Observatory (SOHO), launched in 1975 by NASA succeeded ISEE-3.We have taken data of the path of the SOHO mission from the mission website over a period of January-June 2008, to validate our analytical and numerical solutions.
2. Circular Restricted Three-Body Problem
The circular RTBP consists of two primary masses revolving in circular orbits around their centre of mass under the influence of their mutual gravity. The third body of infinitesimal mass moves under the gravitational effect of these two primaries (Figure 1). RTBP has five equilibrium points, called Lagrangian or libration points. These points are the points of zero velocities and an object placed in these points remains there. Out of the five Lagrangian points, three are collinear (L1, L2, L3) and the other two points (L4, L5) form equilateral triangles with the primaries. Although the Lagrangian point is just a point in empty space, its peculiar characteristic is that
Figure 1. Three-dimensional restricted three-body problem.
it can be orbited. Halo orbits are three-dimensional orbits around the collinear points.
The equations of motion for the RTBP (Szebehely [13] ) including radiation pressure and oblateness of the smaller primary is written in accordance with Sharma & Subba Rao [10] , Sharma [11] as
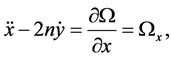 (1)
(1)
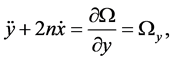 (2)
(2)
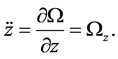 (3)
(3)
where
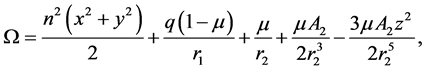
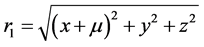 ,
, 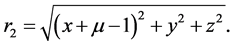
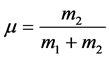 , where m1 and m2 are masses of larger and smaller primary respectively.
, where m1 and m2 are masses of larger and smaller primary respectively.
The perturbed mean motion, n of the primaries due to oblateness is given by
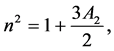
where
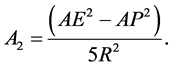
AE, AP being the dimensional equatorial and polar radii of the smaller primary and R is the distance between the primaries. The two terms occurring in Ω due to oblateness of the smaller primary were introduced by Sharma and Subba Rao [10] .
3. Computation of Halo Orbits
For the computation of the halo orbits, the origin is transferred to the Lagrangian points L1 and L2. The transformation is given by
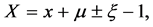
The equation of motion can be written as
where

The upper sign in the above equations depicts the Lagrangian point L1 and the lower sign corresponds to L2. The distance between these Lagrangian points and the smaller primary is considered to be the normalized unit as in Koon et al. [14] and Tiwary and Kushvah [12] .
The usage of Legendre polynomials can result in some computational advantages, when non-linear terms are considered. The non-linear terms are expanded by using the following formula given in Koon et al. [14] :
where
The above formula is used for expanding the non-linear terms in the equations of motion. The equations of motion after substituting the values of the non-linear terms and by some algebraic manipulations by defining a new variable cm after expanding up to m = 2 become



with
Neglecting the higher-order terms in Equations ((4)-(6)), we get



It is clear that the z-axis solution obtained by putting X = Y = 0 does not depend upon X and Y and c2 > 0. Hence we can conclude that the motion in Z-direction is simple harmonic. The motion in XY-plane is coupled.
A fourth degree polynomial is obtained which gives two real and two imaginary roots as eigenvalues:
The solution of the linearized Equations ((7)-(9)), as in Thurman and Worfolk [15] , is
where


Frequency and amplitude terms are introduced to find solution through Lindstedt-Poincaré method. The solution of the linearized equations is written in terms of the amplitudes (Ax and Az) and the phases (In-plane phase, ϕ and out-of-plane phase, ψ) and the frequencies (λ and

3.1. Amplitude Constraint
For halo orbits, the amplitudes 

where l1 and l2 depend upon the roots of the characteristic equation of the linear equation. The correction term 
Hence, any halo orbit can be characterized by specifying a particular out-of-plane amplitude 
3.2. Phase Constraint
For halo orbits, the phases ϕ and ψ are related as
When Ax is greater than certain value, the third-order solution bifurcates. This bifurcation is manifested through the phase-angle constraint. The solution branches are obtained according to the value of m. For m = 1, Az is positive and we have the northern halo (z > 0). For m = 3, Az is negative and we have the southern halo (z < 0).
3.3. Lindstedt-Poincaré Method
Lindstedt-Poincaré method involves successive adjustments of the frequencies to avoid secular terms and provides approximate periodic solution. The equations of motion with non-linear terms up to third-order approximation as in Richardson [3] and Thurman and Worfolk [15] are
A new independent variable τ = ωt is introduced, where 

The values of 
The coefficients 




We continue the perturbation analysis by assuming the solutions of the form



where 
Substituting Equations ((13)-(15)) in Equations ((10)-(12)), and equating the coefficients of the same order of
3.3.1. First-Order Equations
The first-order equations are obtained by taking the coefficients of the term
The periodic solution to the above equations is



where
3.3.2. Second-Order Equations
Coefficients of the term 
where
To remove the secular terms, we set ω1 = 0. The particular solution of the second-order equations are obtained with the help of Maxima software as



The coefficients are given in the Appendix.
3.3.3. Third-Order Equations
By collecting the coefficients of
where
From the above equations, it is not possible to remove the secular terms by setting ω2 = 0.
Hence, the phase relation is used to remove the secular terms.
The solution of the third-order equation is obtained as



The coefficients are given in the Appendix. Thus, the third-order analytical solution is obtained.
3.3.4. Final Approximation
The mapping, 


The coefficients are given in the Appendix.
4. Analytical Construction of Orbit
4.1. Input Parameters
The input parameters to generate a halo orbit include mass ratio (μ), mean distance between the two primaries, radiation pressure (q or ε), oblateness coefficient (A2), amplitude in z-direction (Az). Once all the input parameters are given, the co-ordinates for the halo orbit are computed.
4.2. Halo Orbit for Classical Case
The halo orbits are generated with the following data for Sun-Earth L1:
Mass ratio = 0.000003, mean distance = 149,600,000 km, q = 1, A2 = 0.
The amplitude in z-direction is taken to be Az= 110,000 km (Amplitude of the ISEE-3 mission around the Sun-Earth L1 point). Figures 2-5 show the different views of the halo orbits for the classical case.
4.3. Halo Orbit for Different Values of Radiation Pressure
The halo orbits are generated for different values of radiation pressurein the vicinity of L1. Figure 6 shows the variation in orbit for different values of radiation pressure. The orbital period increases and the orbits increase in size with the increase in the radiation pressure of the more massive primary.
Table 1 shows the change in the distance of the Lagrangian point L1 due to radiation pressure. It is noticed that the Lagrangian point L1 moves towards the more massive primary with increase in radiation pressure. It is also noticed that L1 moves further towards the more massive primary for q < 0.8.
5. Numerical Computation of Halo Orbits
The third-order analytical solution provides a good initial estimate to compute the halo orbits numerically. Analytical approximation must be combined with a suitable numerical method to obtain accurate halo orbits around the Lagrangian points. The method of differential correction is a powerful application of Newton’s method that employs the State Transition Matrix (STM) to solve various kinds of boundary value problems. In order to propagate an orbit in RTBP, the equations of motion are numerically integrated by using adaptive fourth-order Runge-Kutta method, until the desired orbit is obtained.
The initial guess for finding the numerical solution is taken from the analytic solution. Since the halo orbits are symmetric about xz-plane (y = 0), and they intersect this plane perpendicularly i.e.
The final state vector which lies on the same plane, takes the form as given below and crosses the xz-plane perpendicularly:
Figure 2. X vs Y for Sun-Earth system.
Figure 3. Y vs Z for Sun-Earth system.
Then the orbit will be periodic with period 







5.1. Numerically Generated Halo Orbits
The numerically generated orbits which are more accurate, are usually considered for mission purposes. Figure 7
Figure 4. X vs Z for sun-earth system.
Figure 5. 3D view for sun-earth system.
Figure 6. Analytically generated halo orbits [A2 = 0].
Figure 7. Numerically generated halo orbits for different values of q [A2 = 0].
Table 1. Variation in the location of Lagrangian point L1 with radiation pressure q.
shows the numerically generated orbit due to variation in radiation pressure. The numerically generated obits show a close resemblance to the analytically generated orbits. Figure 8 shows the comparison between them.
The analytical solution which includes the radiation pressure of more massive primary and oblateness of the smaller primary can improve the accuracy over the existing solution as given by Tiwary and Kushvah [12] .
The time period of SOHO orbit was around 179 days and its dimensions were approximately 4.3 × 2.7 × 3.7 m. The computed value of radiation pressure is roughly 0.99997. The flight data of SOHO mission from January to June 2008 was taken from the mission website and is plotted. From Figure 9 and Figure 10, it is clear that the addition of the extra term due to oblateness shows improvement in the orbit computation. However, the deviation in the orbit is due to the actual scenario, where the real satellite in space undergoes the effect of various other perturbations.
Figure 8. Comparison of numerically and analytically generated halo orbits.
Figure 9. Comparison of numerically generated halo orbit with SOHO Mission orbit.
Figure 10. Comparison of numerically generated halo orbit with SOHO mission orbit (enlarged view).
Figure 11. Effect of adding the new term on halo orbit at L1 with q = 1, A2 = 0.000001.
5.2. Improvement over the Existing Results
It can be seen from the Figure 11 that the results show improvement in orbit computation due to the addition of the new term due to oblateness.
The time period of the orbit increases by 30 minutes for q = 1 and A2 = 0.000001 as given in Table 2. Thus, it is clear that the addition of the new term in the potential function has helped in predicting the orbit closer to the real time condition.
5.3. Perturbing Effects on the Orbit
The effects due to radiation pressure and oblateness can be seen from Figure 12. It is seen that with increase in radiation pressure as well as oblateness, the orbit moves towards the source of radiation i.e. the more massive primary. The oblateness coefficient are taken as A2 = 0, 0.000001, 0.000002 and the radiation pressure, q = 1, 0.99, 0.98. With increase in perturbing forces, it is seen that the orbit moves towards the more massive primary.
Since the amplitude Az is bounded by amplitude constraint, the variation in it also affects the size and time period of the orbit, which can be seen in Figure 13. The time period of the orbit also changes with the perturbations and the amplitude Az. For the halo around L1, with increase in radiation pressure and oblateness, the time period increases. It can be noticed in Figure 14 and Table 3.
The amplitudes about the z-axis, Az was taken in a range of 80,000 to 140,000 km. There is a minimum Ax for the feasibility of a halo orbit, when we fix the amplitude Az.
6. Conclusion
The analytical solution obtained using Lindstedt-Poincaré method provides good initial estimate to generate halo orbits around the collinear point L1 with numerical integration in the photogravitational restricted three-body
Table 2. Effect of new term on time period of the halo orbit.
Figure 12. Variation in orbit due to perturbations around L1 (μ = 0.000003).
Figure 13. Variation in orbit due to Az (μ = 0.000003).
Figure 14. Time period due to q and Amplitude, Az around L1 (μ = 0.000003).
problem, when the smaller primary is considered as an oblate spheroid with its equatorial plane coincident with the plane of motion. A comparison with the orbital data of SOHO mission is carried out. The radiation pressure and oblateness are found to play significant role in improving the accuracy of halo orbits computation. In the vicinity of L1, it is noticed that with increase in radiation pressure, the size of halo orbit increases with the increase in the orbital period. The results for L1 coincide with the results obtained by Eapen and Sharma [16] . The Lagrangian point L1 moves towards the more massive primary with perturbations and the orbit tends to bend towards the smaller primary with the increase in oblateness. The future aspects of the project involve designing
Table 3. Time period of the halo orbit around L1 (μ = 0.000003).
interplanetary trajectories from Earth to Mars with the help of halo orbits. These trajectories can reduce the cost of the interplanetary and deep space missions.
Cite this paper
Prithiviraj Chidambararaj,Ram Krishan Sharma, (2016) Halo Orbits around Sun-Earth L1 in Photogravitational Restricted Three-Body Problem with Oblateness of Smaller Primary. International Journal of Astronomy and Astrophysics,06,293-311. doi: 10.4236/ijaa.2016.63025
References
- 1. Farquhar, R. (1968) The Control and Use of Libration Point Satellites. Ph.D Thesis, MIT, California.
- 2. Breakwell, J.V. and Brown, J.V. (1979) “Halo” Family of 3-Dimensional Periodic Orbits in the Earth-Moon Restricted 3-Body Problem. Celestial Mechanics, 20, 389-404.
http://dx.doi.org/10.1007/BF01230405 - 3. Richardson, D. (1980) Analytical Construction of Periodic Orbits about the Collinear Points. Celestial Mechanics, 22, 241-253.
http://dx.doi.org/10.1007/BF01229511 - 4. Howell, K.C. (1984) Three-Dimensional, Periodic, “Halo” Orbits. Celestial Mechanics, 32, 53-71.
http://dx.doi.org/10.1007/BF01358403 - 5. Howell, K.C. and Pernicka, H.J. (1988) Numerical Determination of Lissajous Trajectories in the Restricted Three-Body Problem. Celestial Mechanics, 41, 107-124, 1988.
http://dx.doi.org/10.1007/BF01238756 - 6. Folta, D. and Richon, K. (1998) Libration Orbit Mission Design at L2: A MAP and NGST Perspective. AIAA Paper, AIAA 98-4469.
http://dx.doi.org/10.2514/6.1998-4469 - 7. Howell, K.C., Beckman, M., Patterson, C. and Folta, D. (2006) Representations of Invariant Manifolds for Applications in Three-Body Systems. The Journal of the Astronautical Sciences, 54, 25 p.
- 8. Radzievskii, V. (1950) The Restricted Problem of Three Bodies Taking Account of Light Pressure. Astronomicheskii Zhurnal, 27, 250.
- 9. Dutt, P. and Sharma, R.K. (2011) Evolution of Periodic Orbits in the Sun-Mars System. Journal of Guidance, Control and Dynamics, 34, 635-644.
http://dx.doi.org/10.2514/1.51101 - 10. Sharma, R.K. and Subba Rao, P.V. (1976) Stationary Solutions and Their Characteristic Exponents in the Restricted Three-Body Problem When the More Massive Primary Is an Oblate Spheroid. Celestial Mechanics, 13, 137-149.
http://dx.doi.org/10.1007/BF01232721 - 11. Sharma, R.K. (1987) The Linear Stability of Libration Points of the Photogravitational Restricted Three-Body Problem When the Smaller Primary Is an oblate Spheroid. Astrophysics and Space Science, 135, 271-281.
http://dx.doi.org/10.1007/BF00641562 - 12. Tiwary, R.D. and Kushvah, B.S. (2015) Computation of Halo Orbits in the Photogravitational Sun-Earth System with Oblateness. Astrophysics and Space Science, 357, 1-16.
http://dx.doi.org/10.1007/s10509-015-2243-5 - 13. Szebehely, V. (1967) Theory of Orbits. Academic Press, New York.
- 14. Koon, W.S., Lo, M.W., Marsden, J.E. and Ross, S. (2008) Dynamical Systems, the Three-Body Problem and Space Mission Design.
http://www.cds.caltech.edu/~marsden/volume/missiondesign/KoLoMaRo_DMissionBk.pdf - 15. Thurman, R. and Worfolk, P.A. (1996) The Geometry of Halo Orbits in the Circular Restricted Three Body Problem. Univ. Minnesota, Minneapolis, MN, Tech. Rep. GCG 95.
- 16. Eapen, R.T. and Sharma, R.K. (2014) A Study of Halo Orbits at the Sun-Mars L1 Lagrangian Point in the Photogravitational Restricted Three-Body Problem. Astrophysics and Space Science, 352, 437-441.
http://dx.doi.org/10.1007/s10509-014-1951-6
Appendix
Coefficients for the second and third-order equations and solution
Submit or recommend next manuscript to SCIRP and we will provide best service for you:
Accepting pre-submission inquiries through Email, Facebook, LinkedIn, Twitter, etc.
A wide selection of journals (inclusive of 9 subjects, more than 200 journals)
Providing 24-hour high-quality service
User-friendly online submission system
Fair and swift peer-review system
Efficient typesetting and proofreading procedure
Display of the result of downloads and visits, as well as the number of cited articles
Maximum dissemination of your research work
Submit your manuscript at: http://papersubmission.scirp.org/































































































