International Journal of Astronomy and Astrophysics
Vol.05 No.01(2015), Article ID:55077,3 pages
10.4236/ijaa.2015.51008
The Efficiency of CP-Violating a2-Dynamos from Primordial Cosmic Axion Oscillation with Torsion
L. C. Garcia de Andrade
Department of Theoretical Physics, State University of Rio de Janeiro (UERJ), Rio de Janeiro, Brazil
Email: garcia@dft.if.uerj.br
Copyright © 2015 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 7 September 2014; accepted 23 March 2015; published 26 March 2015
ABSTRACT
Recently torsion fields were introduced in CP-violating cosmic axion a2-dynamos [Garcia de Andrade, Mod Phys Lett A, (2011)] in order to obtain Lorentz violating bounds for torsion. Here instead, oscillating axion solutions of the dynamo equation with torsion modes [Garcia de Andrade, Phys Lett B (2012)] are obtained taking into account dissipative torsion fields. Magnetic helicity torsion oscillatory contribution is also obtained. Note that the torsion presence guarantees dynamo efficiency when axion dynamo length is much stronger than the torsion length. Primordial axion oscillations due to torsion yield a magnetic field of 109 G at Nucleosynthesis epoch. This is obtained due to a decay of BBN magnetic field of 1015 G induced by torsion. Since torsion is taken as 10?20 s?1, the dynamo efficiency is granted over torsion damping. Of course dynamo efficiency is better in the absence of torsion. In the particular case when the torsion is obtained from anomalies it is given by the gradient of axion scalar [Duncan et al., Nuclear Phys B 87, 215] that a simpler dynamo equation is obtained and dynamo mechanism seems to be efficient when the torsion helicity, is negative while magnetic field decays when the torsion is positive. In this case an extremely huge value for the magnetic field of 1015 Gauss is obtained. This is one order of magnitude greater than the primordial magnetic fields of the domain wall. Actually if one uses tDW ~ 10−4 s one obtains BDW ~ 1022 G which is a more stringent limit to the DW magnetic primordial field.
Keywords:
Torsion Theories, Axion Dynamo, Primordial Magnetic Fields

1. Introduction
Earlier Mielke and Romero [1] have shown that Cartan spacetime torsion [2] in the chiral anomaly induces a dynamical axion coupled with gravitation. This torsion-induced pseudo-scalar is given in such way that its gradient yields the torsion vector. Earlier Campanelli et al. [3] have investigated the primordial oscillation of axions and respective magnetic fields when CP-violating dynamos [4] in QCD are present. In early universe torsion effects are stronger than usual [3] which justifies the introduction of torsion in the dynamo equation [5] . In this work we consider QCD era and we are very far any galaxy formation. Therefore instead of the usual classical Maxwell electrodynamics non-minimally coupled with photon-torsion coupling in the realm of quan- tum electrodynamics (QED) we use early universe electrodynamics. In this paper a FRW universe is given as background for axion dynamo equation with torsion. It is shown that torsion oscillations enhance cosmic axion oscillations computed by Campanelli and Gianotti [4] . Primordial axion oscillations due to torsion yields a magnetic field of 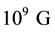 at Nucleosynthesis epoch. This is obtained due to a decay of BBN magnetic field of
at Nucleosynthesis epoch. This is obtained due to a decay of BBN magnetic field of 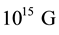 induced by torsion. In the last section of the paper a dynamo equation is obtained from axion scalar torsion string where huge magnetic fields are obtained from
induced by torsion. In the last section of the paper a dynamo equation is obtained from axion scalar torsion string where huge magnetic fields are obtained from 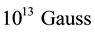 seed fields.
seed fields.
2. Axions, Photons and Torsion
Parity violation in gravity has been investigated recently by B Mukhopadhayaya, S Sen and Sur [6] which conclude that on a torsion-axion duality arising in a string scenario via Kalb-Ramond field leads to parity-
violating interactions for spin- fermions. More recently the author [7] has investigated the role of parity vio-
fermions. More recently the author [7] has investigated the role of parity vio-
lation in torsion has been used to built dynamo equation. By analogy photon-axion coupling may happen giving rise to magnetic fields that eventually may be amplified giving rise to the 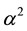 -dynamos addressed in the next section.
-dynamos addressed in the next section.
3. Efficiency of CP-Violating Dynamos
In this section we shall consider the solution the CP-violation dynamos and its efficiency on a torsion back- ground. Let us start by considering the dynamo equation as [1]
 (1)
(1)
where H is the Hubble parameter, a is the expansion of the universe, S represents the torsion vector and 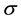 is the conductive. Here
is the conductive. Here 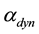
 (2)
(2)
the metric is given by
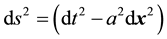 (3)
(3)
Here  represents the axion field primordial field. The Fourier analysis of first equation becomes
represents the axion field primordial field. The Fourier analysis of first equation becomes
 (4)
(4)
From this solution one notes that the torsion oscillating length is complex representing a true oscillation. Here k is the wave coherent scale number. The solution of this equation is
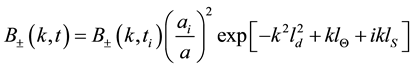 (5)
(5)
where the oscillation lengths are
 (6)
(6)
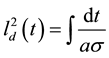 (7)
(7)
 (8)
(8)
Here 


The magnetic helicity contribution of torsion oscillation is

Note that the magnetic helicity generation now has a contribution of the torsion oscillation length. Finally let us compute the torsion oscillation new term to compare it with the dynamo length to see if the torsion dissipative term may damp the dynamo length. Then

when the argument is small this expression reduces to

and for Big Bang Nucleosynthesis (BBN)

where we have used the seed field for


which is able to seed galactic dynamos. Dynamo efficiency is given by

where torsion field 


4. Dynamo Equation from Torsion Axion Anomalies
Earlier Duncan et al. [7] investigated axion hair anomalies in Riemann-Cartan spacetime where torsion was given by the gradient of axion scalar f. In this section instead of using the a dynamo equation of the previous one we shall addopt this approach and obtain a simpler dynamo equation which solution gives rise to stronger magnetic fields starting from the magnetic field of 

where star in front of the Maxwell tensor F means that we are taking the dual of F given by

By taking the scaled version of this equation in Fourier space one obtains

which solution yields

From this expression one sees that the torsion helicity sign 

Here the coupling constant 

high as in the next section 






5. Discussions and Conclusions
Torsion fields introduced in CP-violating cosmic axion 


Acknowledgements
We would like to express my gratitude to D. Sokoloff and A. Brandenburg for helpful discussions on the subject of this paper. I thank Prof. C. Sivaram for initiating me on the problem of dynamos and torsion. Financial support from CNPq. and University of State of Rio de Janeiro (UERJ) are grateful acknowledged.
Cite this paper
L. C. Garcia de Andrade,, (2015) The Efficiency of CP-Violating <i>α</i>2-Dynamos from Primordial Cosmic Axion Oscillation with Torsion. International Journal of Astronomy and Astrophysics, 05, 56-59. doi: 10.4236/ijaa.2015.51008
References
- Campanelli, L. and Gianotti, M. (2005) Magnetic Helicity Generation from the Cosmic Axion Field. Physical Review D, 72, Article ID: 123001.
http://dx.doi.org/10.1103/PhysRevD.72.123001 - Garcia de Andrade, L.C. (2011) Mod Phys Lett A., 26, 2863.
- Garcia de Andrade, L.C. (2012) Primordial Magnetic Fields and Dynamos from Parity Violated Torsion. Physics Letters B, 711, 143-146.
http://dx.doi.org/10.1016/j.physletb.2012.03.075 - Widrow, L. (2001) Rev Mod Phys, 74, 775; Turner, M. and Widrow, L. (1988) Phys Rev D; Prokopec, T., Tornkvist, O. and Woodward, R. (2002) Phys Rev Lett., 89, 101301; Ruzmakin, A., Sokoloff, D.D. and Shukurov, A. (1988) Magnetic Fields in Galaxies, Kluwer; Garcia de Andrade, L.C. (2011) Nuclear Phys B; Garcia de Andrade, L. (2011) Phys Lett B, 468, 28; Ratra, B., Caltech preprint and Garcia de Andrade, L. (2011) Lorentz Violation Bounds from Torsion Trace and Radio Galactic Dynamos. Phys Rev D (Brief Reports).
- Laemmerzahl, C. (1997) Phys Lett A., 228, 223.
- de Sabbata, V., Garcia de Andrade, L.C. and Sivaram, C. (1993) Torsion and Gauge-Invariant Massive Electrodynamics. International Journal of Theoretical Physics, 32, 1523-1530.
http://dx.doi.org/10.1007/BF00672853 - Duncan, M., Kaloper, N. and Olive, K.A. (1992) Nucl Phys B, 87, 215.
- Cea, P. and Tedesco, L. (year) Dynamical Generation of the Primordial Magnetic Field by Ferromagnetic Domain Walls. arXiv:hep-th/9811221v1.
- Kisslinger, L.S. (2003) Magnetic Wall from Chiral Phase Transition and CMPR Correlations. arXiv: hep-ph/0212206v2.

