International Journal of Astronomy and Astrophysics
Vol.3 No.2(2013), Article ID:32735,6 pages DOI:10.4236/ijaa.2013.32015
Gravitational Self Energy Mass and Gravitational Radiation Quantization within the Framework of the Generalized General Relativity
1Physics Department, College of Science, Sudan University of Science & Technology, Khartoum, Sudan
2Physics Department, Faculty of Science, Khartoum University, Khartoum, Sudan
3Physics Department, College of Science, Al Imam Mohammad Ibn Saud Islamic University, Riyadh, KSA
4Science Department, College of Education, Sudan University of Science & Technology, Khartoum, Sudan
Email: *mheisas@hotmail.com
Copyright © 2013 M. D. Abdalla et al. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received February 21, 2013; revised March 22, 2013; accepted March 31, 2013
Keywords: Gravitational; Energy Mass; Radiation; Generalized; General Relativity
ABSTRACT
In this work, the mass resulting from self energy is obtained by utilizing the generalized relativity. The expression for the mass which results from the gravitational field is finite. This expression is found by considering the mass first as small tiny string and second as small sphere. A useful equation for the propagation of graviton waves in space indicates that graviton propagates as travelling wave. By treating gravitation waves as wave packets a plank quantum expression for graviton energy dependent on the frequency is also found. The gravitational constant (parameter) is quantized also in this work.
1. Introduction
Einstein’s Theory of general Relativity (EGR) is one of biggest achievements in physics. This theory describes gravitation in a geometrical language by utilizing curved Riemann geometry [1]. EGR is found to be successful in describing a large number of astronomical observations [2]. Despite these successes, EGR suffers from noticeable setbacks. It is the most disastrous, and is the description of the radiation and pre-radiation eras, where elementary particles are dominant [3]. The elementary particles description is done by using quantum theory. Thus one needs a quantum gravitational theory to describe the early universe [4,5], from the start of the big bang, pre plank and blank quantum era [6], up to radiation era. Quantum gravity theory is also needed to describe the behavior of black holes, neutron stars and pulsars [7]. Many attempts were made to construct a quantum gravity model [8]. Some of them are based on super string or string theory [8]. Others, like the wave function of the universe are proposed by Dwelt [9] and Hawking [10].
These attempts, although they are promising, but they are still done for from giving a complete full consistent quantum gravity theory. This failure stems from the fact that EGR derivation is not inconformity with the conventional method used to derive the field equations. In this conventional method the equation of motion and the energy-momentum equation are different. The first one results from the variation of the field variables, while the second one results from the space-time variation [11]. In EGR the equation of motion and the energy-momentum equation are the same. They stem from the replacements of the potential field term by a geometrical term, and the matter term by the energy-momentum term [12]. This situation makes EGR isolated from other field theories, including quantum field theory. This bizarre situation necessitates searching for a new version of EGR, by keeping its beautiful geometrical language and abandoning Newton Poisson equation. This new version is first proposed by Lanczos [13] and then by Ali Eltahir [14]. It is based on the conventional action approach [14]. This generalized EGGR reduces to EGR thus shares with it all their successes. Moreover, GEGR is proved to be non singular [15] and capable of solving the gravity energy-momentum problem, horizon, entropy and flatness problem, beside galaxy formation problem. This EGGR is introduced in Section 2. Section 3 is devoted to explain how gravity can generate mass. Sections 4 and 5, exhibit the graviton equation of motion and quantization of the gravity field in the form of graviton. In Section 6 the gravitational constant is quantized. The discussion and conclusion are in Sections 7 and 8, respectively.
2. Generalized General Relativity
Since general relativity faces many several problems [16], different attempts were made to go beyond EGR. One of these attempts is based on a more generalized field equation which generalizes EGR. This Generalized General Relativity (GEGR) was first obtained by Lanczos [13] and then Ali El-Tahir [14]. In the later derivation the principle of least action is utilized by taking the field variables to be the metric tensor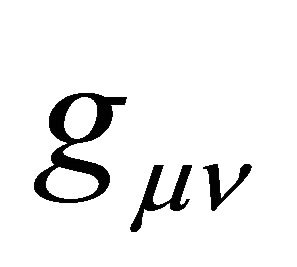 . This conventional approach leads to the EGGR in the form;
. This conventional approach leads to the EGGR in the form;
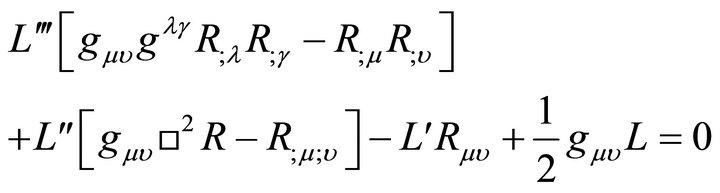 (1)
(1)
where the lagrangian L depends on R This equation reduces to EGR by considering the linear lagrangian;
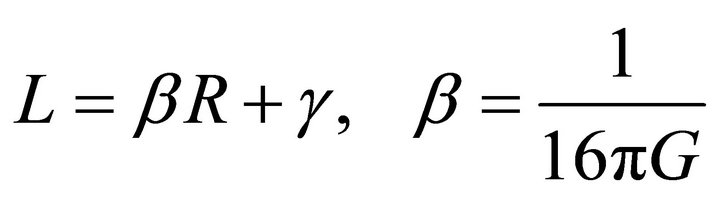 (2)
(2)
Equation (1) then reduces to;
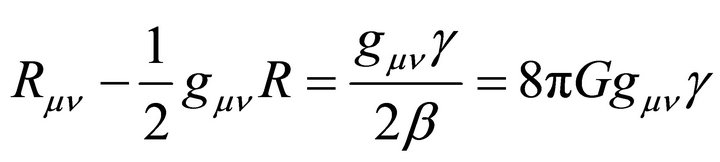 (3)
(3)
One can set;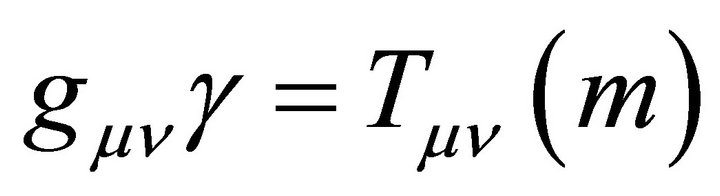 .
.
where, 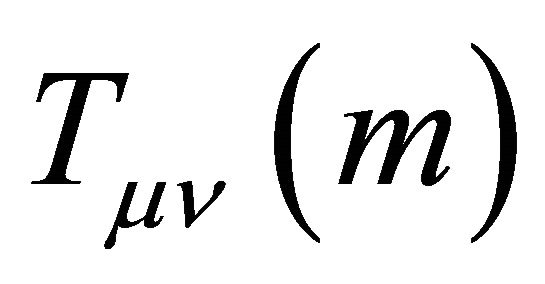 , stands for the matter energy momentum tensor. In this case Equation (1) reduces to GR where;
, stands for the matter energy momentum tensor. In this case Equation (1) reduces to GR where;
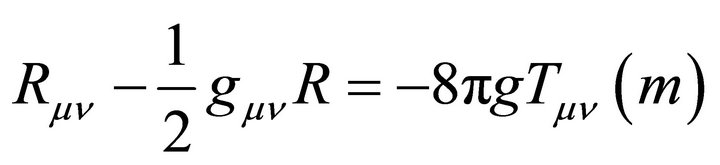 (4)
(4)
The fact that EGGR reduces to EGR indicates that this new Einstein’s version shares with GGR all its successes [16].
Motivated by the quadratic Lagrangian of the electromagnetic field, a Lagrangian quadratic in R was utilized by some authors to construct a useful gravitational equation. This equation is used for static field to obtain non singular solution, and a solution reduced to Schwarzschild solution [15]. The EGGR cosmological model is also constructed and found to share with EGR all its successes. This model is free from the singularity, flatness, entropy and horizon problems [16]. Moreover, this model can also solve the galaxy formation problem [17]. Recently EGGR is utilized to express a quantum model using conventional quantum mechanics. This model is capable to predicting the universe expanding at its early stage [18]. The EGGR model shows that Einstein’s GR can still be capable of rearranging and refurnishing itself to describe physical phenomena.
3. Gravitational Self Energy Mass
Since the mass of anybody generates gravitational field thus one expects the inverse process to take place i.e. the gravitational field frozen out to generate masses. This resembles what happens in the pair production, where a photon generates a pair of a particle and the anti-particle annihilate to form a photon. To see how the gravitational field generates masses one can utilize the contracted form of the GGR, i.e.; Equation (1) to get;
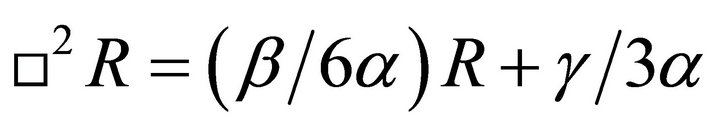 (5)
(5)
where the Lagrangian takes the form;
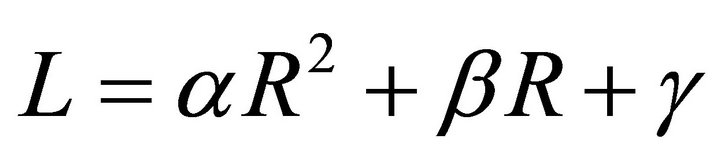
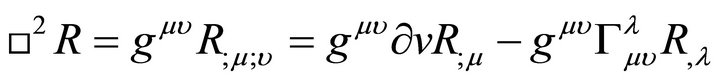 (6)
(6)
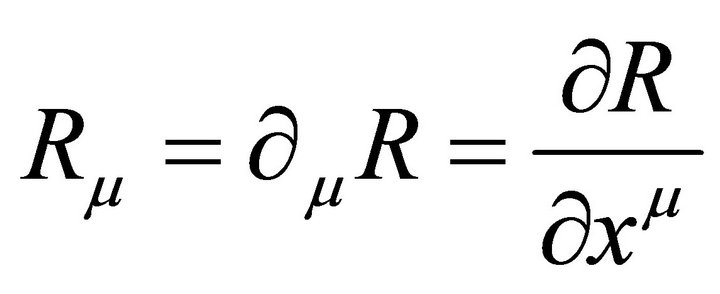 (7)
(7)
Using the coordinate condition;
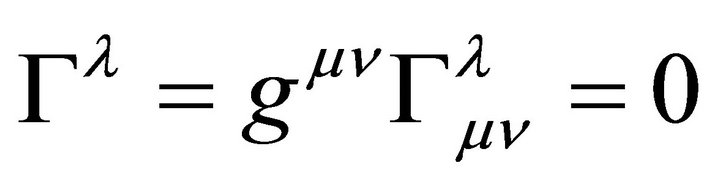 (8)
(8)
Equation (5) reduces to;
 (9)
(9)
To describe the behavior of a certain star it is suitable to use static isotropic metric;
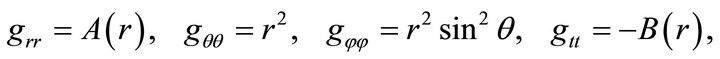 (10)
(10)
The scalar curvature R is a function of r only in this case i.e.;
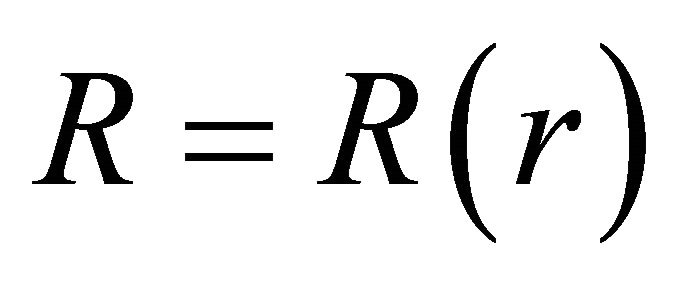 (11)
(11)
Thus the only non vanishing terms in this case are the r-r components.
Thus Equation (9) reduces to;

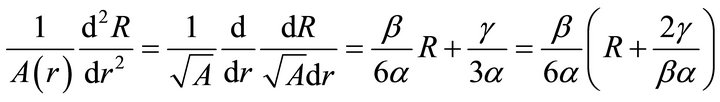 (12)
(12)
To simplify this equation, it is convenient to define the variables;
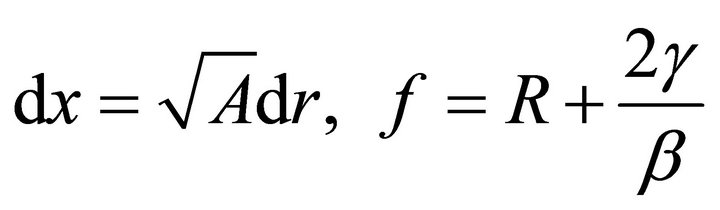 (13)
(13)
To get;
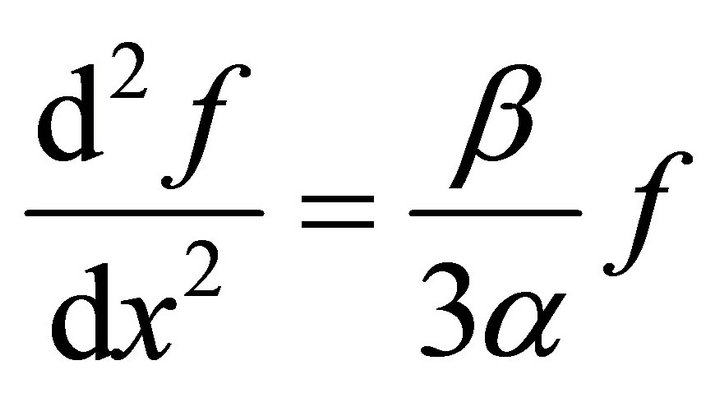 (14)
(14)
One of the possible solutions of this equation is in the form;
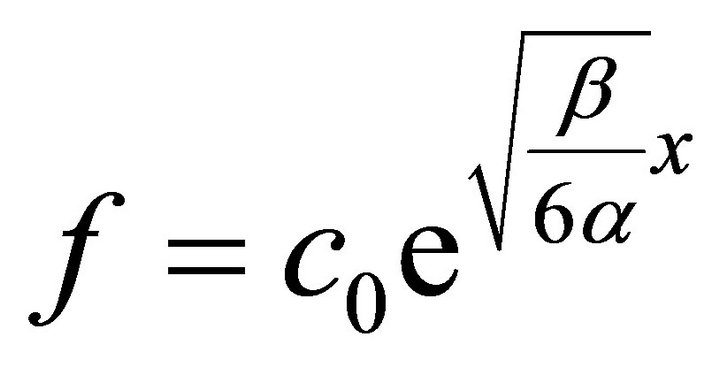 (15)
(15)
In view of Equation (13);
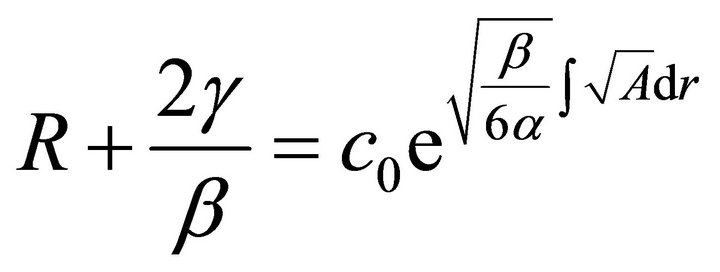 (16)
(16)
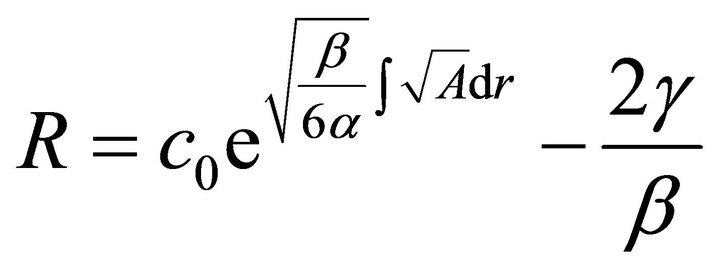 (17)
(17)
The relation between the scalar curvature and the matter density ρ can be found by using the contracted form of GR, i.e., Equation (4) to get;
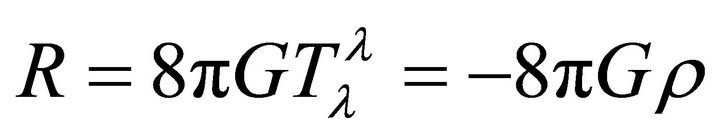 (18)
(18)
Thus (16) reads;
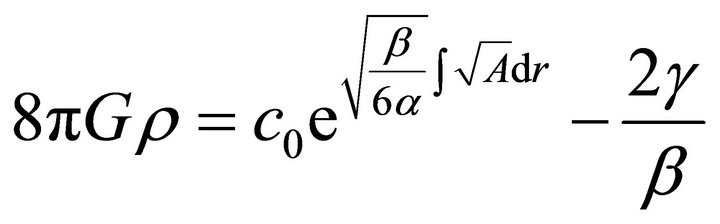 (19)
(19)
When the mass is considered to be generated by gravitational field only, the contribution of non gravitational field via the term γ is ignored i.e. γ = 0 Thus, Equation (19) becomes;
 (20)
(20)
To simplify treatments one can consider flat space or nearly flat space metric, where;
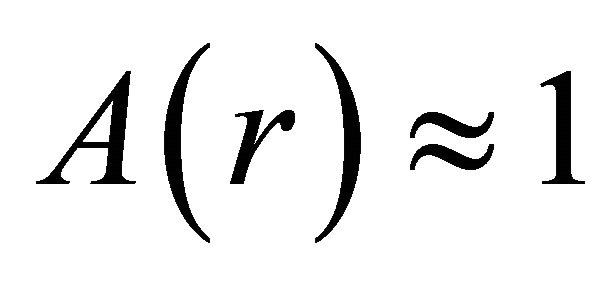 (21)
(21)
In this case Equation (20) becomes;
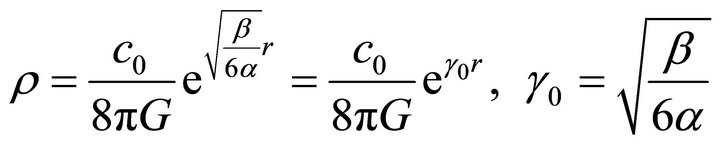 (22)
(22)
The physical meaning of the γ can be understood by resolving Equation (14) i.e.;
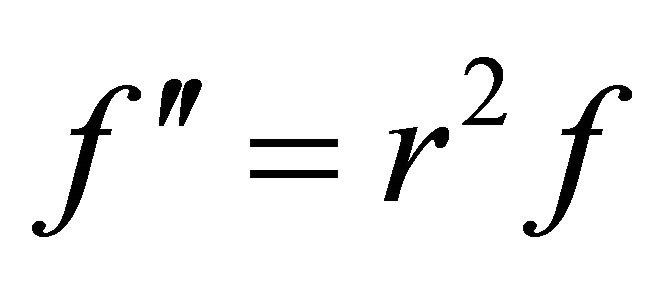 (23)
(23)
In the form;
 (24)
(24)
This represents a wave number;
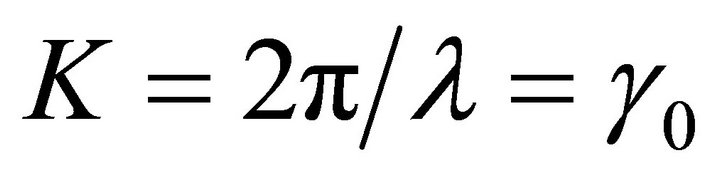 (25)
(25)
Consider now a particle in the form of a small tiny string of the length r0.
The mass of this string can be found from Equation (22) to be.
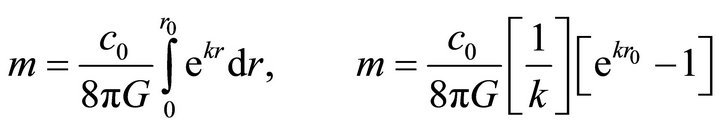 (26)
(26)
For very small r0;
 (27)
(27)
If the particle is in the form of sphere of volume;

The mass then taken the form;

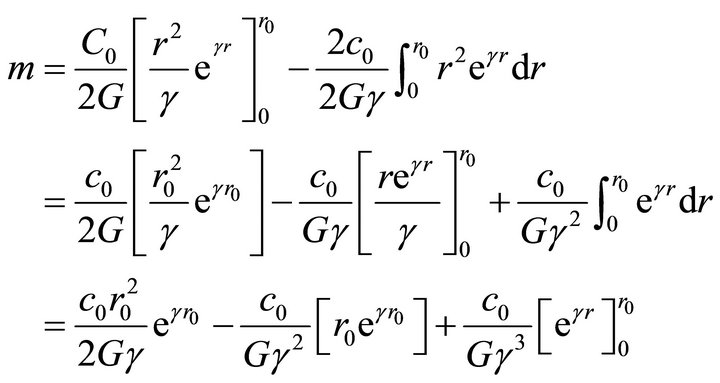
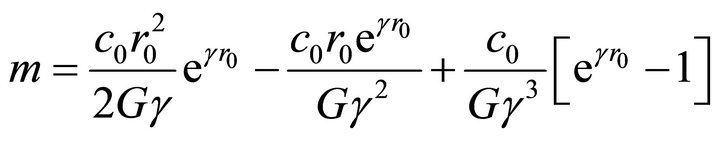
If r0 is very small such that;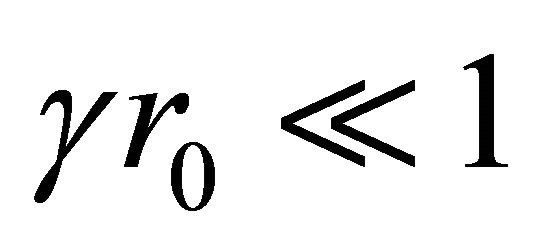 ,
,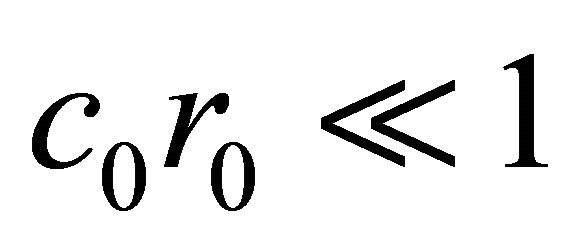 . In this case,
. In this case, 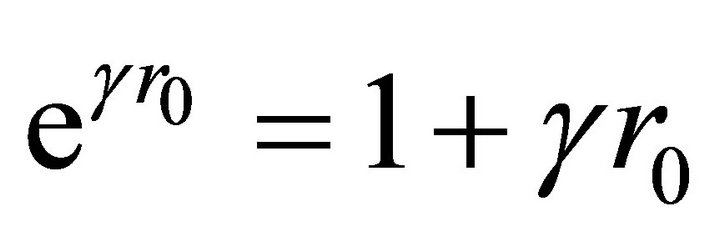
Hence the mass can be given to be;

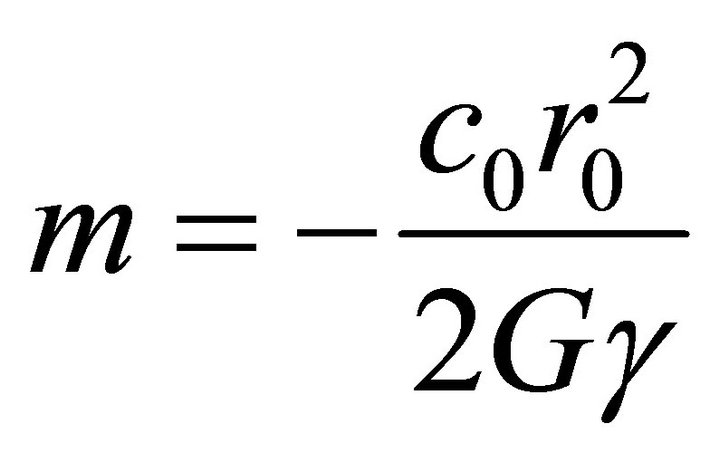 (28)
(28)
where, one neglects the terms r compared to r0. Thus the mass is dependent on the radius r, gravitational coupling constant G, the wave number γ beside the free parameter c.
4. Graviton Equation of Motion
The graviton is the energy quantum which results from gravity quantization, which should be in the form of gravitational waves. Thus, one need to prove that the gravitational field can be propagated in the form of travelling waves. To do this consider the metric and scalar curvature to be dependent on r and t; i.e.
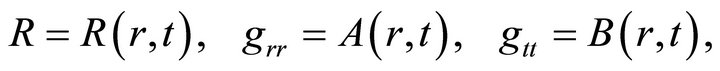 (29)
(29)
In view of Equation (9) one gets;
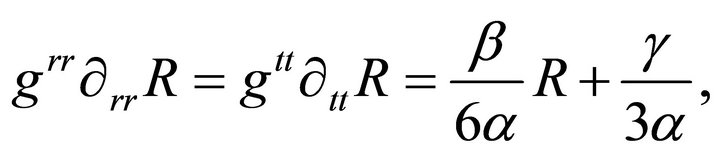 (30)
(30)
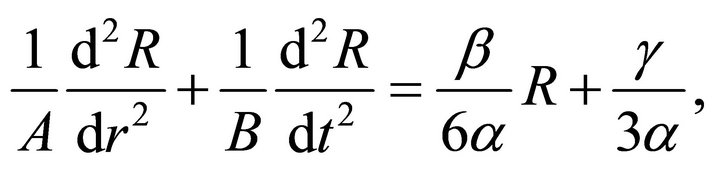
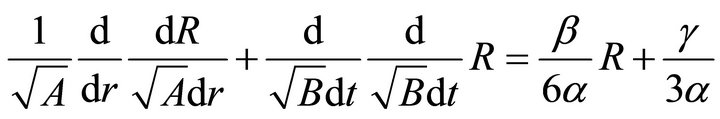 (31)
(31)
Define α and t to satisfy;
 (32)
(32)
Thus, Equation (3) reduces to;
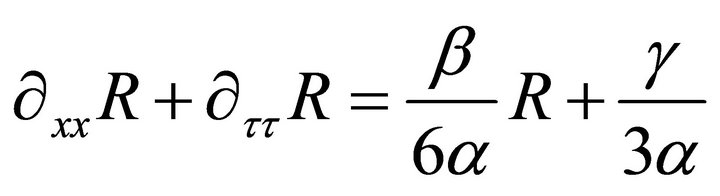 (33)
(33)
Outside a given star, one expects the matter density γ to vanish, hence one can consider the solution;
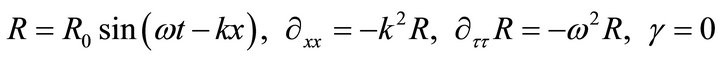 (34)
(34)
A direct substitution of (34) in (33) yields;
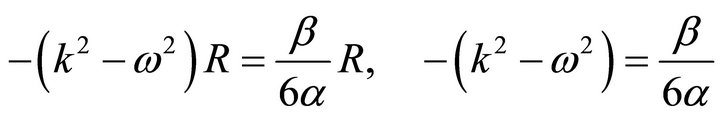 (35)
(35)
In the r, t space the travelling wave equation becomes;
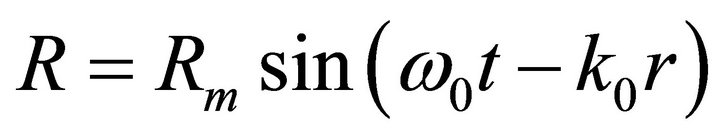 (36)
(36)
In view of Equations (36), (34), (32) the angular frequency ω0, and the wave number k0 are given according to the relations;
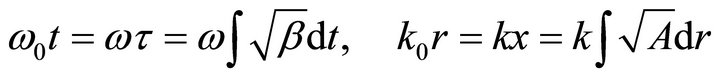 (37)
(37)
It is clear that the frequency and the wave number are dependent on the gravitational field via the metric components B and A. Equation (36) also indicates that the gravitational field can be propagated in the form of a travelling wave.
5. Graviton Energy
In quantum mechanics the particle is thought to be associated with a wave packet (wave group). The graviton can be treated equally as a wave packet by integrating (22) in the k-space to get;
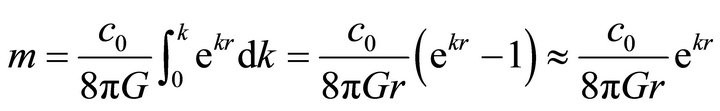 (38)
(38)
where, one can be neglected in Equation (38) compare with exponential term. Therefore, Equation (25) in which, γ = k, is used. The radius at which, m is minimum can be found by differentiating m with respect to r to get;
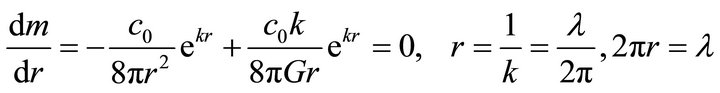 (39)
(39)
Hence the circular circumference is occupied by one complete wave. This relation resembles the Bohr radius. Thus, according to Equations (38) and (39), the mass and the energy of the graviton are given to be;
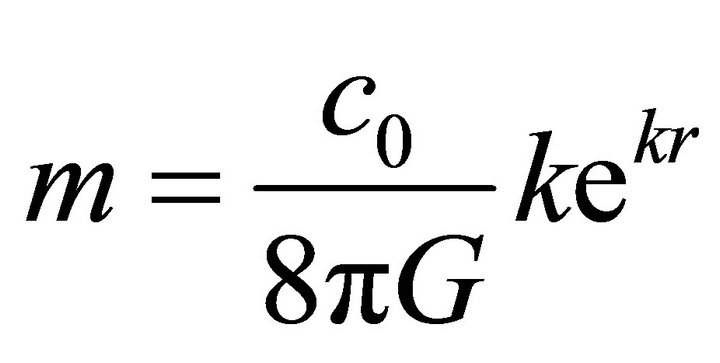 (40)
(40)
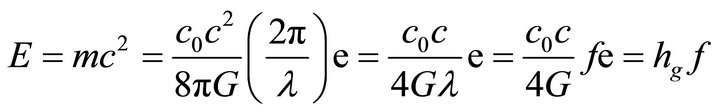 (41)
(41)
This expression resembles plank quantum photon energy. This expression can also be obtained directly from expression (22) for very small radius r→0 where the exponential term can be expanded by using Taylor series to get;
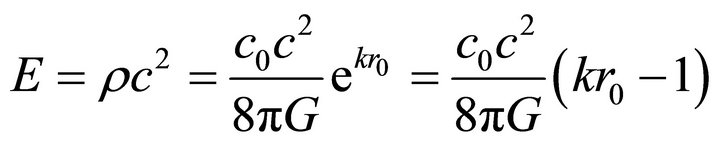
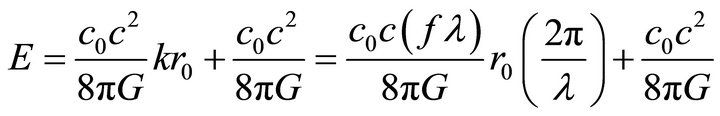
 (42)
(42)
6. Spatial and Time Dependent Scalar Curvature and Gravitational Constant Quantization
In the previous sections one tries to find R with direct suggestion of solution for R as a function of r and t directly. In this section one needs to use the separation of variables to solve (33) without the source term i.e.  to get;
to get;
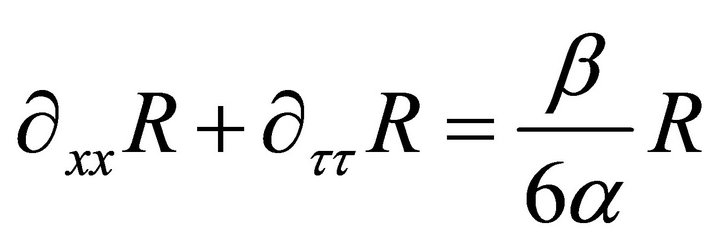 (43)
(43)
Using the method of separation of variables now let R to be a product of two functions, T which depends on time t, beside X which depends on x.
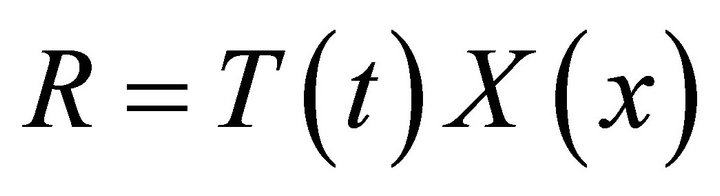 (44)
(44)
Inserting (44) in (43) one gets;
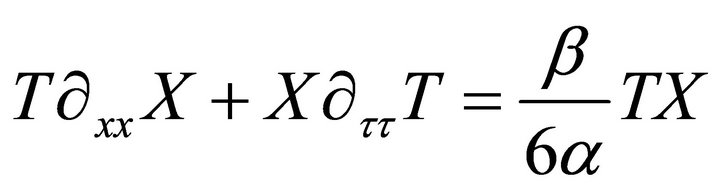
Dividing both sides by TX yields;
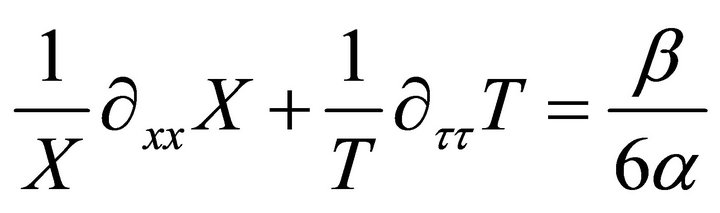 (45)
(45)
This means that the first term and the second term on the left hand side are constants. Hence one can set the time dependent part to be;
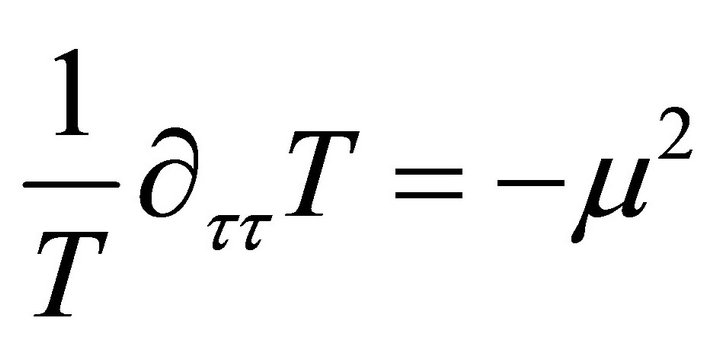 (46)
(46)
This equation can be solved by suggesting T to be;
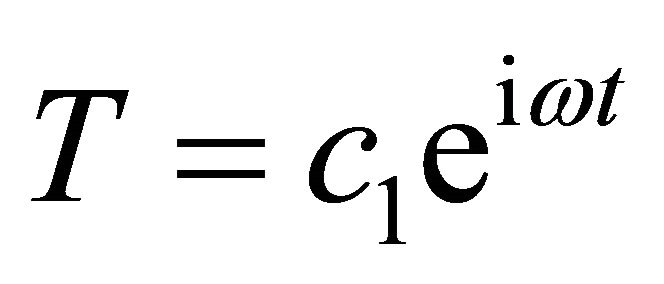
Whereas,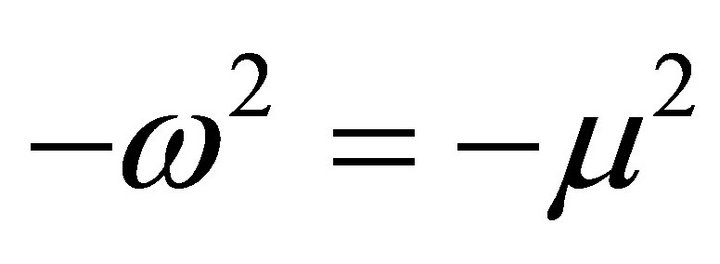 and
and  (47)
(47)
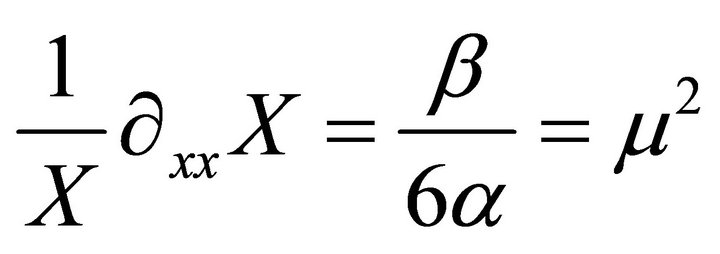 (48)
(48)
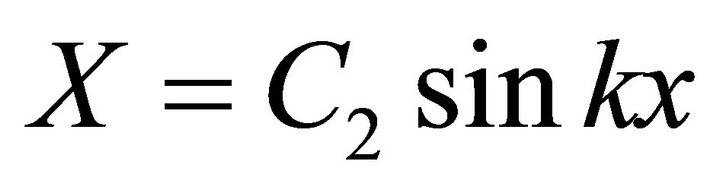 (49)
(49)
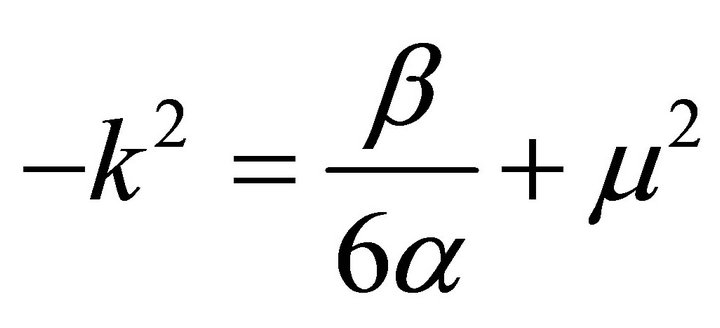
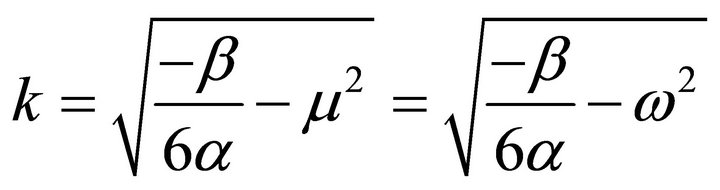 (50)
(50)
The term α is found by some researchers to be negative strictly speaking in the Ph.D. work of Dirar [16] α was found to be;
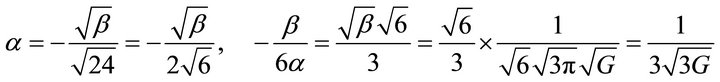
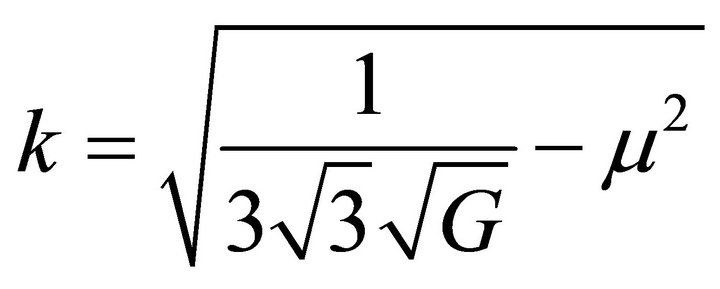 (51)
(51)
To take the source term γ in consideration one can define f as in (13) and substitute it in (33) to get;
 (52)
(52)
By setting;
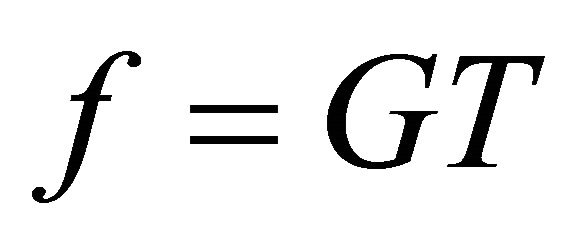 (53)
(53)
And following the same procedures done for R in Equations (43) up to (51) after comparing (52) with (43) to get;
 (54)
(54)
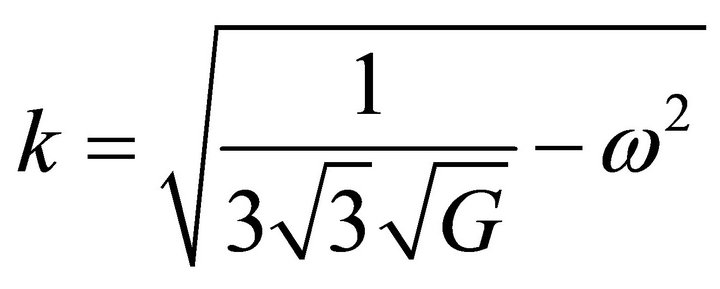 (55)
(55)
Recalling Equations (13) yields;
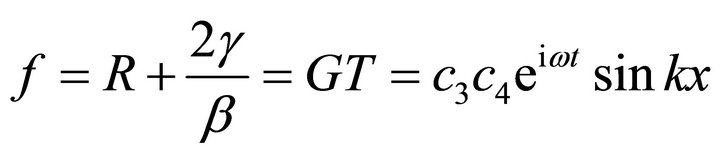
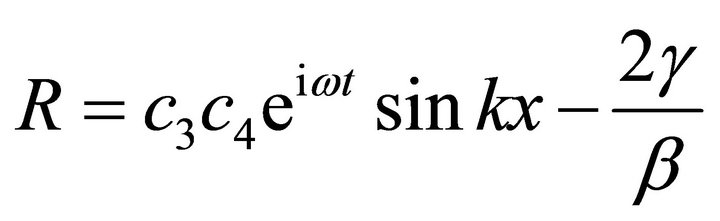 (56)
(56)
In this expression for R, k is real when;
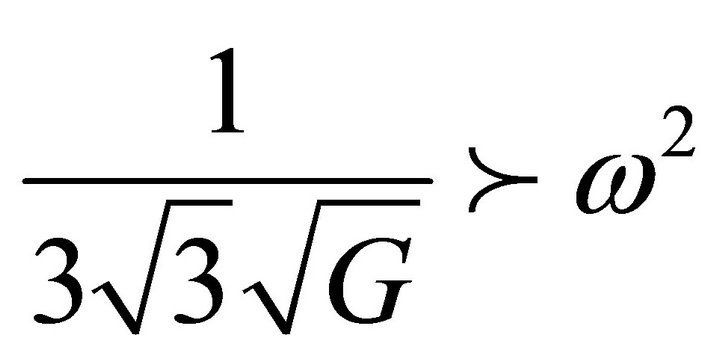 (57)
(57)
One can quantize the gravitational field by bearing in mind that outside the universe both gravity (R) and matter (γ) vanishes outside the universe near the boundaries i.e.;
 (58)
(58)
Hence Equation (56) becomes;
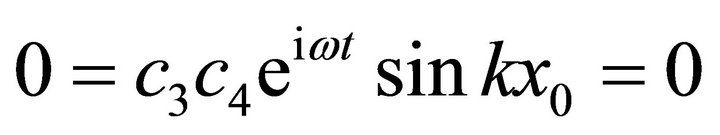 (59)
(59)
This can be satisfied if,
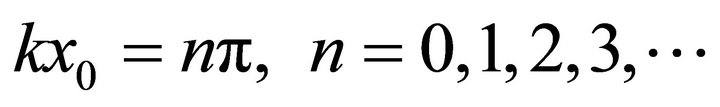
Hence;
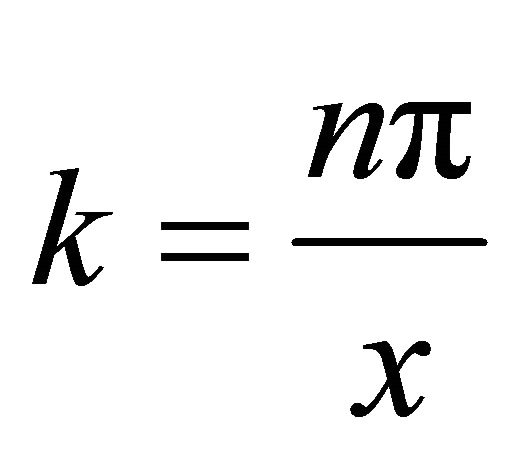
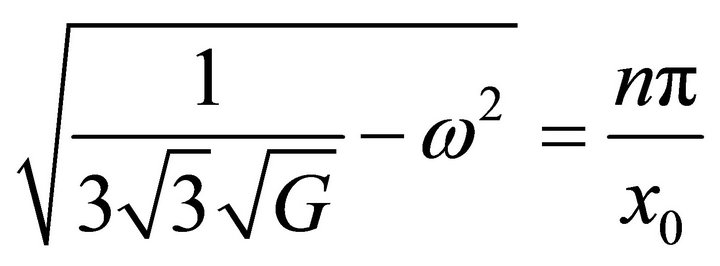
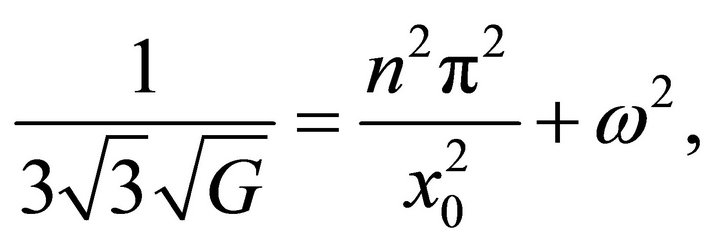
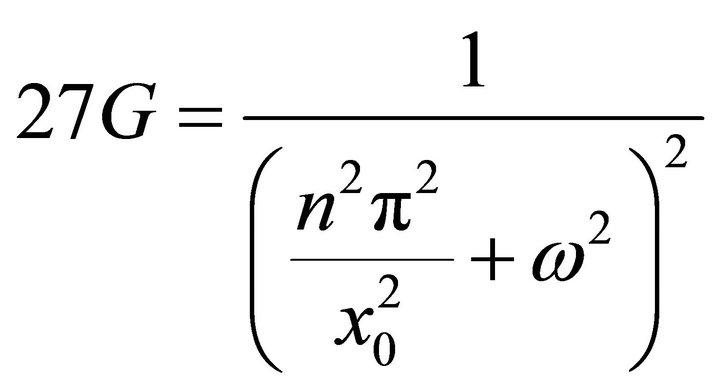
 (60)
(60)
Thus the gravitational coupling is constant is quantized. At the early universe x0 is small thus quantized takes place. However at present x0→∞, hence; 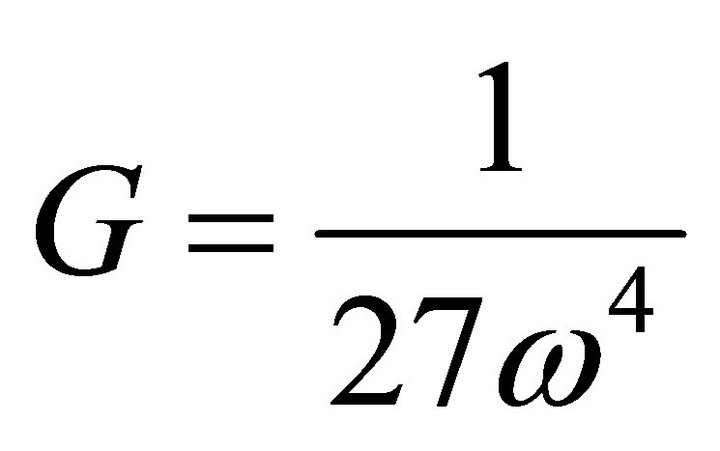
Thus no quantization is observed.
7. Discussion
The mass of the string in Equation (27) is finite for very small radius which is true also for Equation (28) when the particle considered as a sphere. If c0 is positive then one expects the string to represent the particle while the sphere representing an anti-particle. The mass in both versions is directly proportional to the radius, thus increasing with the radius. This in conformity with experiments where the larger the radius the larger the mass as in case of protons and neutrons compared to electrons. The mass is also dependent on the gravitational constant G which is also quite natural as for as the mass general gravitational field and is also affected by it. However, the mass of spherical bodies depends on the wave number γ unlike the string mass which is free from this term. The free parameter c0 provides as with freedom to adjust its value to give as the value of all elementary particles. The gravitational field is shown by Equation (36) to be propagated in form of a travelling wave. The energy of the graviton is determined in Equation (42) by treating the graviton as a wave packet. It is interesting to find that the graviton mass is a function of its frequency in complete agreement with the Plank energy for the photon but with new (Plank) gravitational constant, the graviton expression for the energy can also be obtained by utilizing the expression for the mass density, when the radius r0 is very small [see Equation (42)]. Again one gets Plank quantum gravity expression but with a background zero energy. This means that the vacuum E˳ is a media in which graviton transmit it. It is also amazing to find in Equation (42) and that the gravity plank constant hg is dependent on the gravitational constant G. Equation (60) shows that the gravitational constant G is quantized. At the early universe x0 is small and quantized term including the discrete number n dominates. Thus, the gravitational parameter “constant” G in Equation (60) is quantized and is no longer a constant. But at present x0→∞ and the quantized term is smeared out and G is a constant parameter and is no longer quantized.
8. Conclusion
The capability of EGGR to quantize the gravitational field and gravitational constant indicates that it can secure a good basis for a full quantum gravitational theory. The ability of this model to explain the origin of the mass in relation to the gravitational field, and to be an amenable to quantization, raises a hope of unifying all fundamental forces by bridging the gap between GR and quantum mechanics, beside finding a pathway to unify gravity with other forces by using Riemannian geometry as a common language.
9. Acknowledgements
The authors would like to express their gratitude to all those who gave their help to complete this work, specially, the American Physical Society.
REFERENCES
- A. Einstein, “The Foundation of the General Theory of Relativity,” The Principle of Relativity, Dover Publications, Inc., Dover, 1952, pp. 111-164.
- R. M. Wald, “General Relativity,” University of Chicago Press, Chicago, 1984. doi:10.7208/chicago/9780226870373.001.0001
- C. W. Misner, K. S. Thorne and J. A. Wheeler, “Gravitation,” W. H. Freeman & Co., San Francisco, 1973.
- S. Hawking, “A Brief History of Time,” Time Magazine, 1999.
- M. Carmeli, “Classical Fields: General Relativity and Guage Theory,” John Wiley and Sons, New York, 1992.
- E. Alvares, “Quantum Gravity: An Introduction to Some Recent Results,” Reviews of Modern Physics, Vol. 61, No. 3, 1989, pp. 561-604. doi:10.1103/RevModPhys.61.561
- J. A. Wheeler, “Battelle Rencontres: 1967 Lectures in Mathematics and Physics,” Benjamin, New York, 1968.
- J. M. Maldacena, “The Large N Limit of Super Conformal Field Theories and Super Gravity,” International Journal of Theoretical Physics, Vol. 38, No. 4, 1999, pp. 1113-1133. doi:10.1023/A:1026654312961
- B. S. DeWitt, “Quantum Theory of Gravity: I. The Canonical Theory,” Physical Review, Vol. 160, No. 5, 1967, pp. 1113-1148. doi:10.1103/PhysRev.160.1113
- S. W. Hawking and D. N. Page, “Operator Ordering and the Flatness of the Universe,” Nuclear Physics B, Vol. 264, 1986, pp. 185-196. doi:10.1016/0550-3213(86)90478-5
- M. Dirar, “Applications of the Generalized Field Equations to Energy and Cosmological Problems,” Ph.D. Thesis, Khartoum University, Khartoum, 1998.
- S. Weinberg, “Gravitation and Cosmology,” John Wiley and Sons, Inc., New York, 1972.
- C. Lanczos, “Electricity as a Natural Property of Riemannian Geometry,” Physical Review, Vol. 39, No. 4, 1932, pp. 716-736. doi:10.1103/PhysRev.39.716
- Ali El-Tahir, “A Generalized Variational Principle of Gravitation,” Ph.D. Theses, City University, London, 1982.
- Ali El-Tahir, “A Generalized Metric of Gravitation,” International Journal of Modern Physics, Vol. 7, No. 13, 1992, p. 3133. doi:10.1142/S0217751X9200140X
- M. Dirar, Ali EL-Tahir and M. H. Shaddad, “A Generalized Field Cosmology,” Modern Physics Letters A, Vol. 13, No. 37, 1998, pp. 3025-3031. doi:10.1142/S0217732398003211
- M. Dirar, Ali EL-Tahir and M. H. Shaddad, “Short Range Gravitational Field and the Red Shift of Quasars,” International Journal of Theoretical Physics, Vol. 36, No. 6, 1997, pp. 1395-1400. doi:10.1007/BF02435932
- M. Y. Shargawi, “Derivation of Quantum Cosmological Model,” Ph.D. Thesis, Sudan University of Science & Technology [SUST], Khartoum, 2012.
NOTES
*Corresponding author.

