International Journal of Astronomy and Astrophysics
Vol.4 No.1(2014), Article ID:43529,10 pages DOI:10.4236/ijaa.2014.41008
Canonical Treatments for the Two Bodies Problem with Varying Mass Taking into Consideration the Periastron Effect
M. I. El-Saftawy1,2, Amirah R. Algethami1
1Astronomy Department, Faculty of Science, King Abdu Aziz University, Jeddah, Saudi Arabia
2Space Science Laboratory-NRIAG, Cairo, Egypt
Email: malsaftawy@kau.edu.sa
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 16 January 2014; revised 10 February 2014; accepted 17 February 2014
ABSTRACT
In this work, the Hamiltonian of the two body problem with varying mass was developed in the extended phase space taking into consideration the periastron effects. The short period solution was obtained through constructing a second order canonical transformation using “Hori’s” method developed by “Kamel”. The elements of the transformation as well as the inverse transformation were obtained too. The final solution of the problem was derived using “Delva-Hanslmeier” method.
Keywords:Two Body with Varying Mass; Perturbation; Hori’s Method

1. Introduction
The problem of the two bodies with varying mass has roots going back in the history since the middle of the 19th century. Since F. Mestschersky’s initial study a great many researchers have dedicated much of their time to this problem, telling it became one of the classics of celestial mechanics, which has become known as the Gylden-Mestschersky.
An ample bibliography can be found in the published works of E. N. Polyakova [1] and C. Prieto [2] . The specific case which results in a slow isotropic mass loss has also been the focus of exhaustive studies carried out by researchers, for instance, J. D. Hadjidemetriou [3] [4] , to name but a few. The vast majority of these, in search of the stellar application, have taken the so-called Eddington-Jeans law [5] [6] , as a law of the variation of mass,
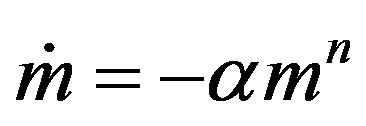 (1)
(1)
where a and n are real numbers, the first of them is positively proximate to zero and the second is varying between 1.4 and 4.4.
Prieto [7] [8] intended to present an approximate analytic solution of the two-body problem with slowly decreasing mass which is obtained through the integration of the Hamilton equations using Deprit’s method of perturbations. The solution, obtained through the Eddington-Jeans law, is put into practice in a specific case and compared with F. Mestschersky’s exact equation; n = 2; and with that which results from numerically integrating the equations.
In the framework of celestial mechanics, this problem has been exhaustively addressed by Docobo [9] , Andrade [10] , among others.
In 2002, M. Andrade [11] analyzed the dynamics of binary systems with time-dependent mass loss and periastron effect i.e., a supposed enhanced mass loss during periastron passage by means of analytical and numerical techniques.
M. Andrade and J. A. Docobo [12] studied the dynamics of binary systems with small parameter perturbation model, the time-dependence of the whole set of orbital elements, concluded, could be calculated over long timescales and even for high eccentricities. In these models, they studied the following timeand distance-dependent mass-loss law:
 (2)
(2)
where the first term represent time-dependent mass loss, and the last one introduces the periastron effect, where “r” is the distance between the two components,  is the total angular momentum and β is another small parameter close to zero.
is the total angular momentum and β is another small parameter close to zero.
W. A. Rahoma et al. [13] were introduction paper concerned with the two-body problem with varying mass in case of isotropic mass loss from both components of the binary systems. The law of mass variation used gives rise to a perturbed Keplerian problem depending on two small parameters. The problem is treated analytically in the Hamiltonian frame-work and the equations of motion are integrated using the Lie series developed and applied, separately by Delva [14] and Hanslmeier [15] . A second order theory of the two bodies eject mass was also constructed, returning the terms of the rate of change of mass up to second order in the small parameters of the problem.
W. A. Rahoma et al. [16] studied the two-body problem with varying mass in case of isotropic mass loss. In that work, the problem was treated analytically in the Hamiltonian frame-work and the equations of motion ware integrated using the Lie operator and Lie series.
Our work is aimed to introduce an analytical solution for the problem of two bodies with varying mass, taking into consideration the periastron effects, using the canonical perturbation technique derived by Hori and developed by Kamel.
2. The Hamiltonian of the Problem
The Hamiltonian is constructed in terms of Delaunay’s variables as described in Deprit [17] :
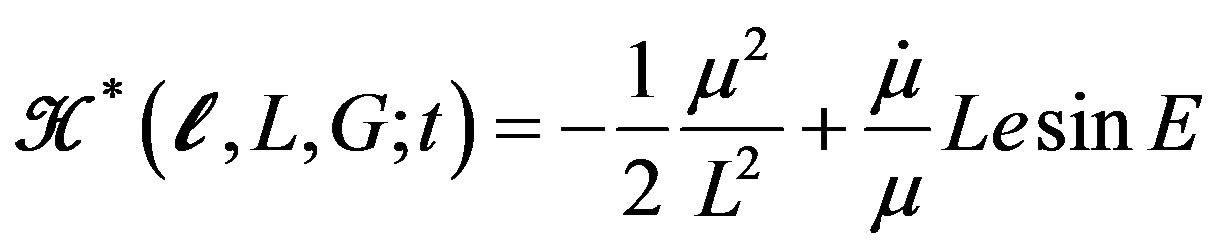 (3)
(3)
The first term in the Hamiltonian function, described by Equation (3), is the Hamiltonian in the Keplerian case (with constant mass)  while the second term represents the varying mass effects. In terms of the Delaunay variable, we can develop the Hamiltonian as:
while the second term represents the varying mass effects. In terms of the Delaunay variable, we can develop the Hamiltonian as:
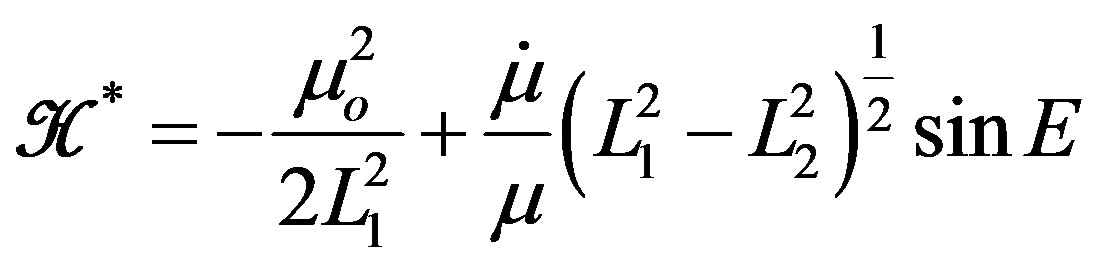 (4)
(4)
That is meant that the Hamiltonian is function of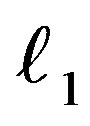 ,
, 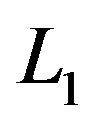 and
and  as:
as:

The variation of 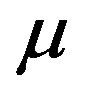 may be retained from one of the two masses
may be retained from one of the two masses 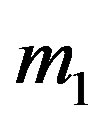 or
or  and this is the case of one body eject mass. Otherwise the case of the two bodies ejects masses. We will concern with the first case. Then;
and this is the case of one body eject mass. Otherwise the case of the two bodies ejects masses. We will concern with the first case. Then;
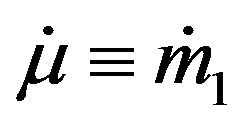 (5)
(5)
The Hamiltonian  represented by Equation (4) is implicit depending on time through the variable mass
represented by Equation (4) is implicit depending on time through the variable mass 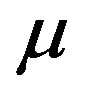 and its time derivative
and its time derivative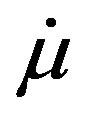 . By modifying Docobo’s law for the rate of change of mass assigned by Equation (2) and use Jeans law described by Equation (1) we get:
. By modifying Docobo’s law for the rate of change of mass assigned by Equation (2) and use Jeans law described by Equation (1) we get:
 (6)
(6)
By applying Equation (6) in the Hamiltonian function (4) which can be written as:
 (7)
(7)
with n positive number varying between 1.4 and 4.4.
Since the variable mass can be expressed as a Taylor series expansion as:
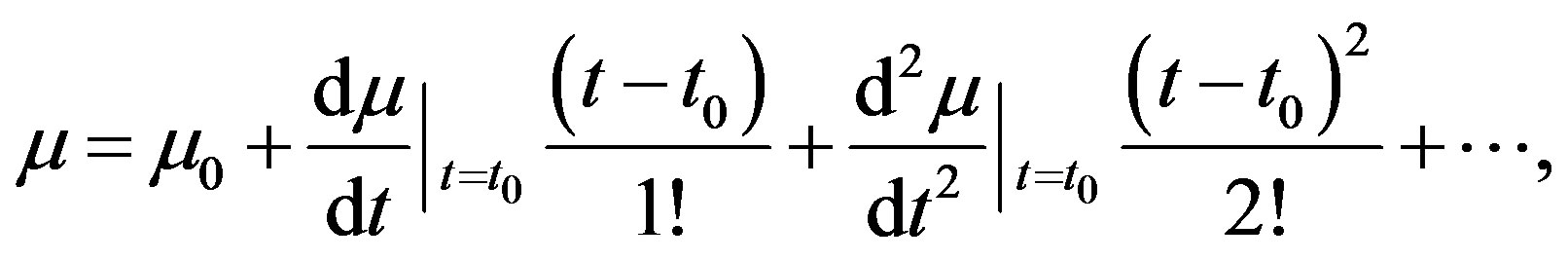
that will lead to a Hamiltonian with explicit dependence of time. So we must extend the phase space by introducing a new pair of variable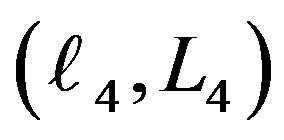 . The first is “
. The first is “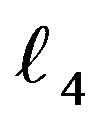 ” assigned as the variable mass and the second its conjugate momentum “
” assigned as the variable mass and the second its conjugate momentum “ ”.
”.
The new systems of canonical equations of motion are:
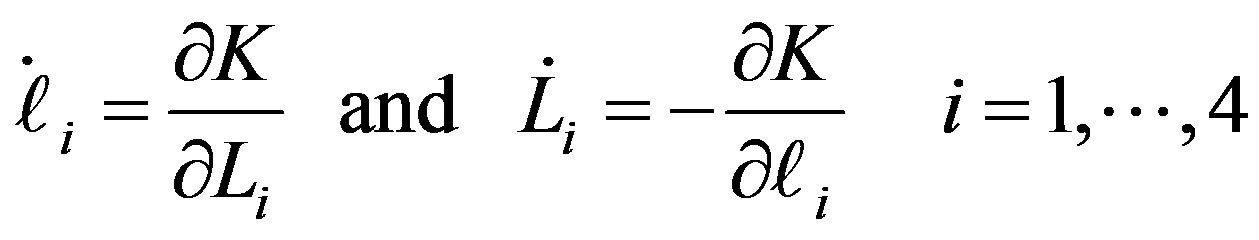 (8)
(8)
where K is the new Hamiltonian in the extended phase space which can be expressed as:
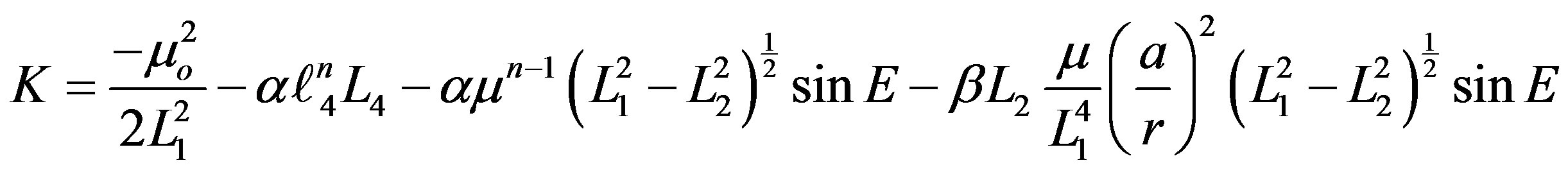 (9)
(9)
The first term in Equation (9) is contribution of the two body with constant mass with 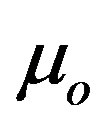 is total mass of the system at specific time
is total mass of the system at specific time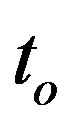 . The small parameter
. The small parameter  is close to zero as well as the small parameter
is close to zero as well as the small parameter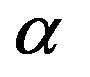 . In this stage, we can handle the problem as two bodies with two small parameters. But, if we assume that the two small parameters
. In this stage, we can handle the problem as two bodies with two small parameters. But, if we assume that the two small parameters 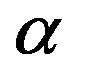 and
and 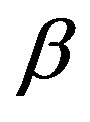 has the same order of magnitude the problem will turn into one small parameter problem.
has the same order of magnitude the problem will turn into one small parameter problem.
The Hamiltonian (9) can be written in the form:
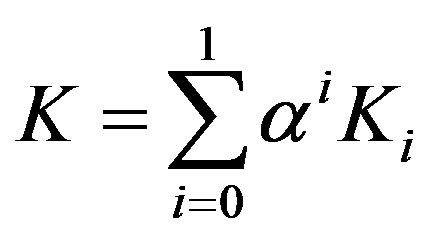 , (10)
, (10)
where,
 (10.1)
(10.1)
with,
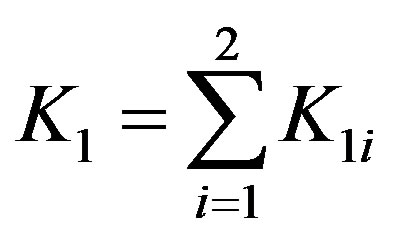 (10.2)
(10.2)
and,

The canonical equations of motion for the Hamiltonian K are:
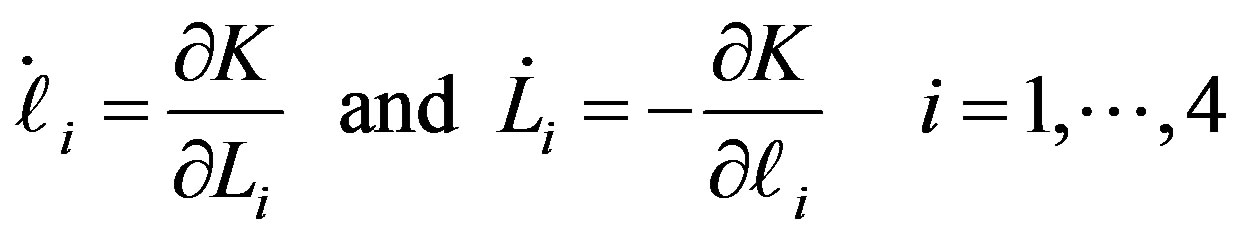 (11)
(11)
Applying the last Equation for the Hamiltonian function represented by Equation (10) yields:
 (11.1)
(11.1)
 (11.2)
(11.2)
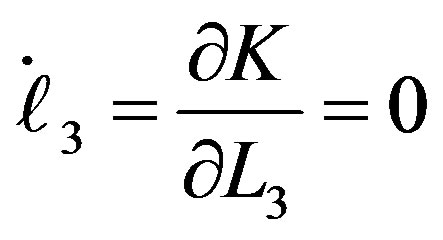 (11.3)
(11.3)
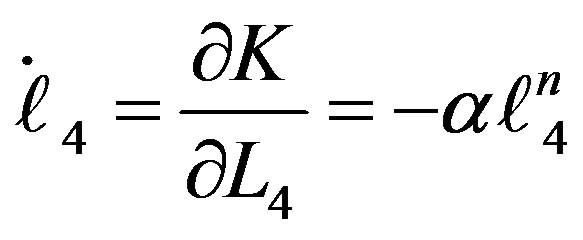 (11.4)
(11.4)
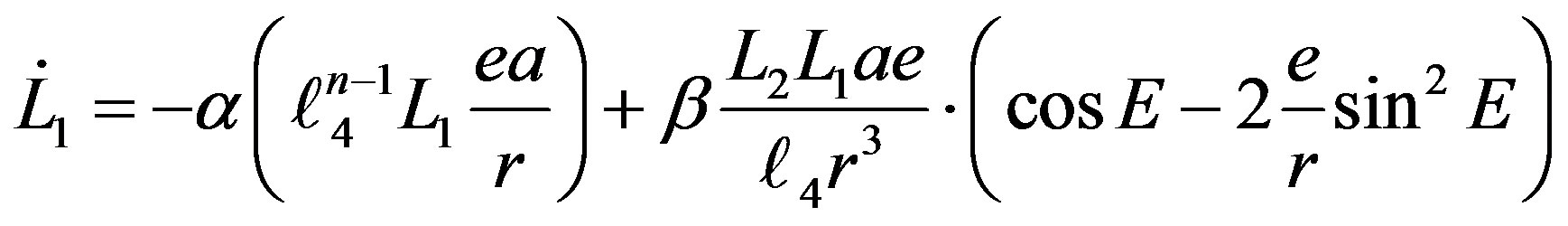 (11.5)
(11.5)
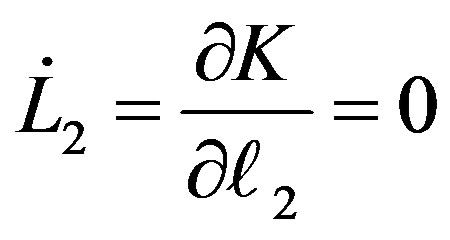 (11.6)
(11.6)
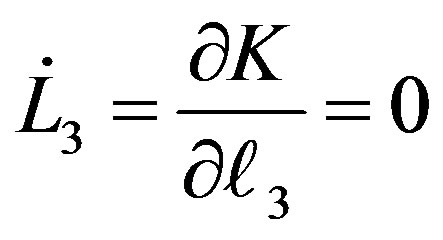 (11.7)
(11.7)
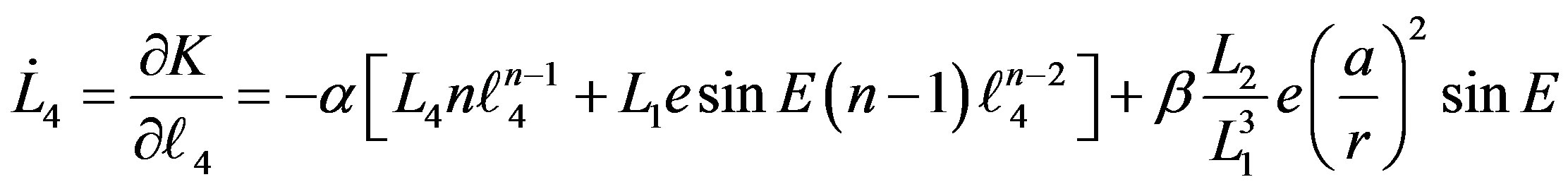 (11.8)
(11.8)
3. Short Period Solution Using Hori Method’s
The Hameltonian function K is function of  and
and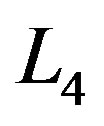 . The integrable part of the Hameltonian, K0, is function of
. The integrable part of the Hameltonian, K0, is function of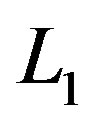 . So the variable
. So the variable 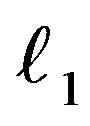 can be consedered as the fast variable.
can be consedered as the fast variable.
In the next stage we will use Hori’s method [18] , developed by Kamel [19] to elemeinate the short period termes from the Hameltonian. And the transformed Hameltonian,  , can be written, up to second orders, as follows:-
, can be written, up to second orders, as follows:-
3.1. Zero Order
By applying the Hori’s Perturbation technique developed by Kamel yields:
 (12)
(12)
3.2. First Order
The first order transformed Hamiltonian derived by Horis’ can be outlined as:
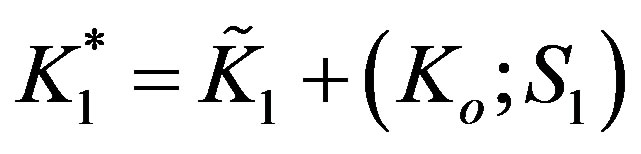 (13.1)
(13.1)
where;
 . (13.2)
. (13.2)
And by choosing;
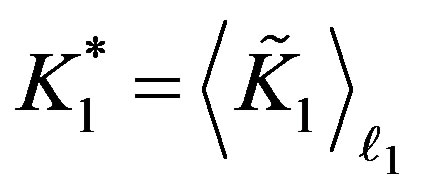 . (13.3)
. (13.3)
then
 (13.4)
(13.4)
So the first order generating function, S1, is therefore obtained by integral:
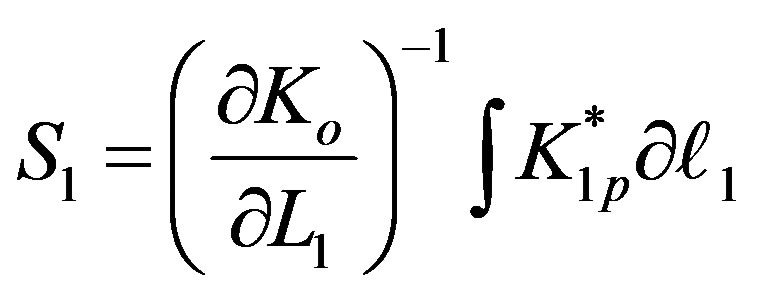 . (13.5)
. (13.5)
By averaging the Hameltonian, 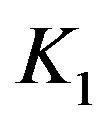 , over the mean anomaly
, over the mean anomaly 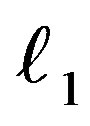 we can determine the transformed first order Hamiltonian,
we can determine the transformed first order Hamiltonian,  , as:-
, as:-
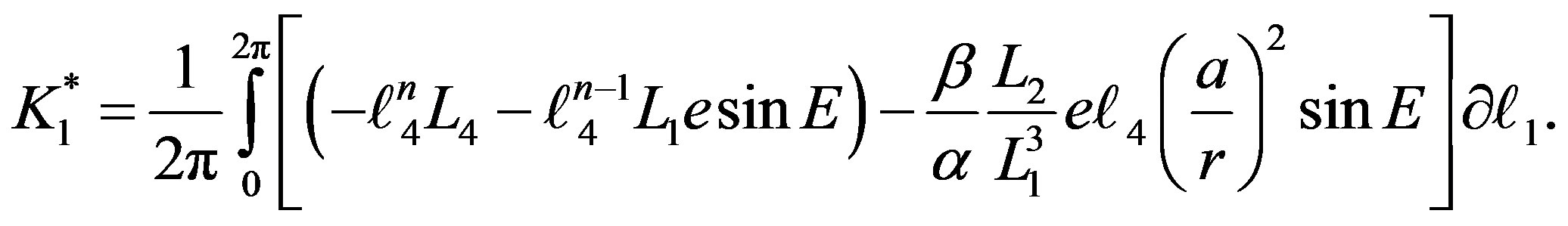
After calculating the required integrals needed in the last equation we get:
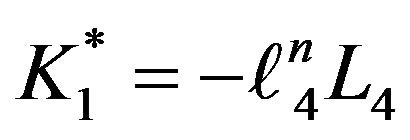 . (14)
. (14)
By applying Equation (13.4) to calculate the periodic part of the Hamiltonian as:
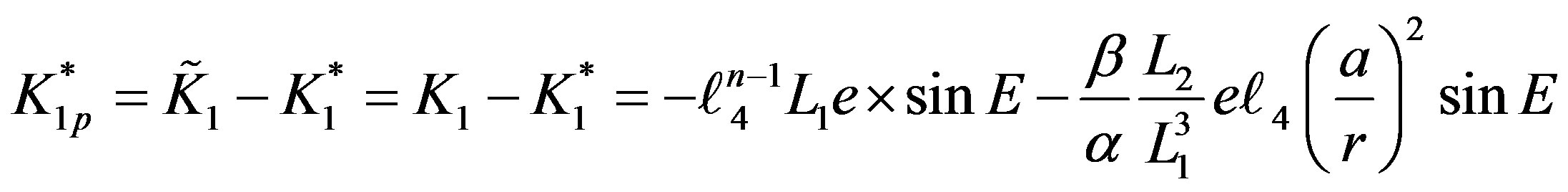 (15)
(15)
To calculate the first order generating function, 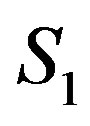 , we must use Equation (13.5) (with the help of Equations (12) and (15)) which lead, after calculate the required derevativs and products, to the results:-
, we must use Equation (13.5) (with the help of Equations (12) and (15)) which lead, after calculate the required derevativs and products, to the results:-
 (16)
(16)
where B’s are function of  and given by:
and given by:
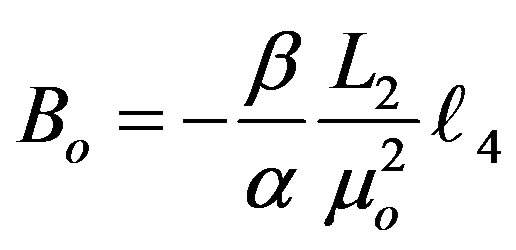 (16.1)
(16.1)
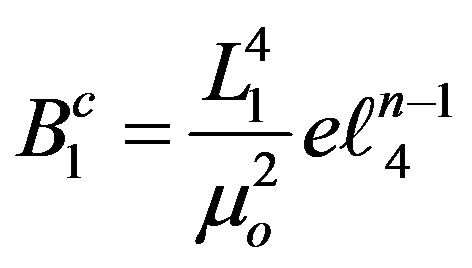 (16.2)
(16.2)
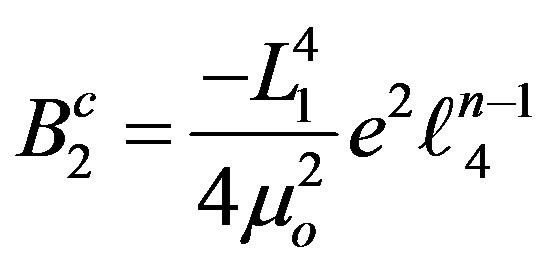 (16.3)
(16.3)
3.3. Second Order
The seconed order transformed Hamiltonian derived by Horis’ can be outlined as:-
 (17)
(17)
where;
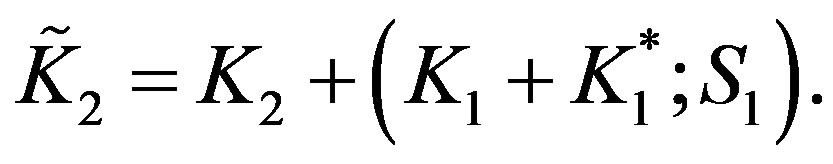 (17.1)
(17.1)
Choosing;
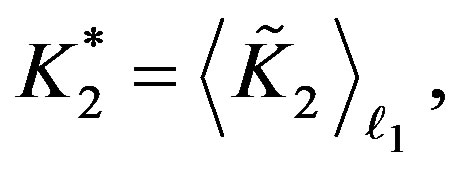 (17.2)
(17.2)
and;
 (17.3)
(17.3)
Hence S2 therefore can be obtained by;
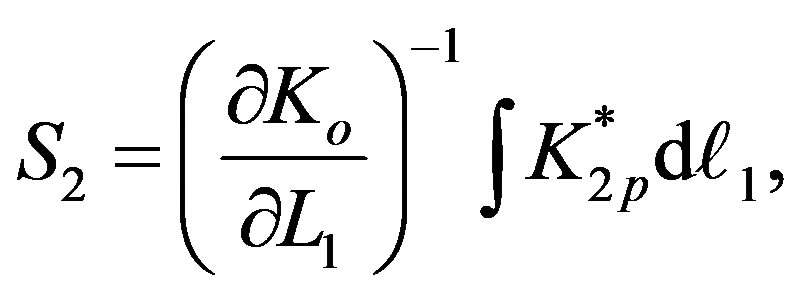 (17.4)
(17.4)
To construct the function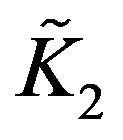 , we need, first, to calculate the Poisson bracket
, we need, first, to calculate the Poisson bracket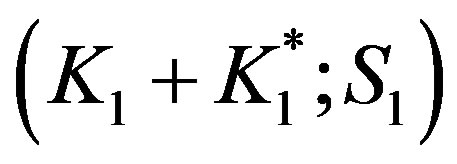 . By the help of Equations (10.2), (14) and (16) with
. By the help of Equations (10.2), (14) and (16) with 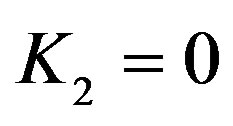 yeilds:
yeilds:
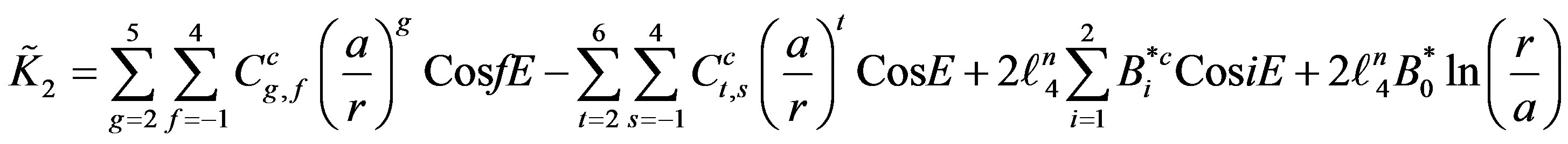 (18)
(18)
where the coeffecients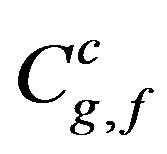 ,
, 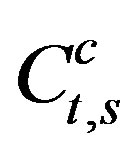 and
and 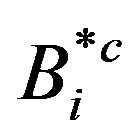 are function of
are function of  defined as:-
defined as:-
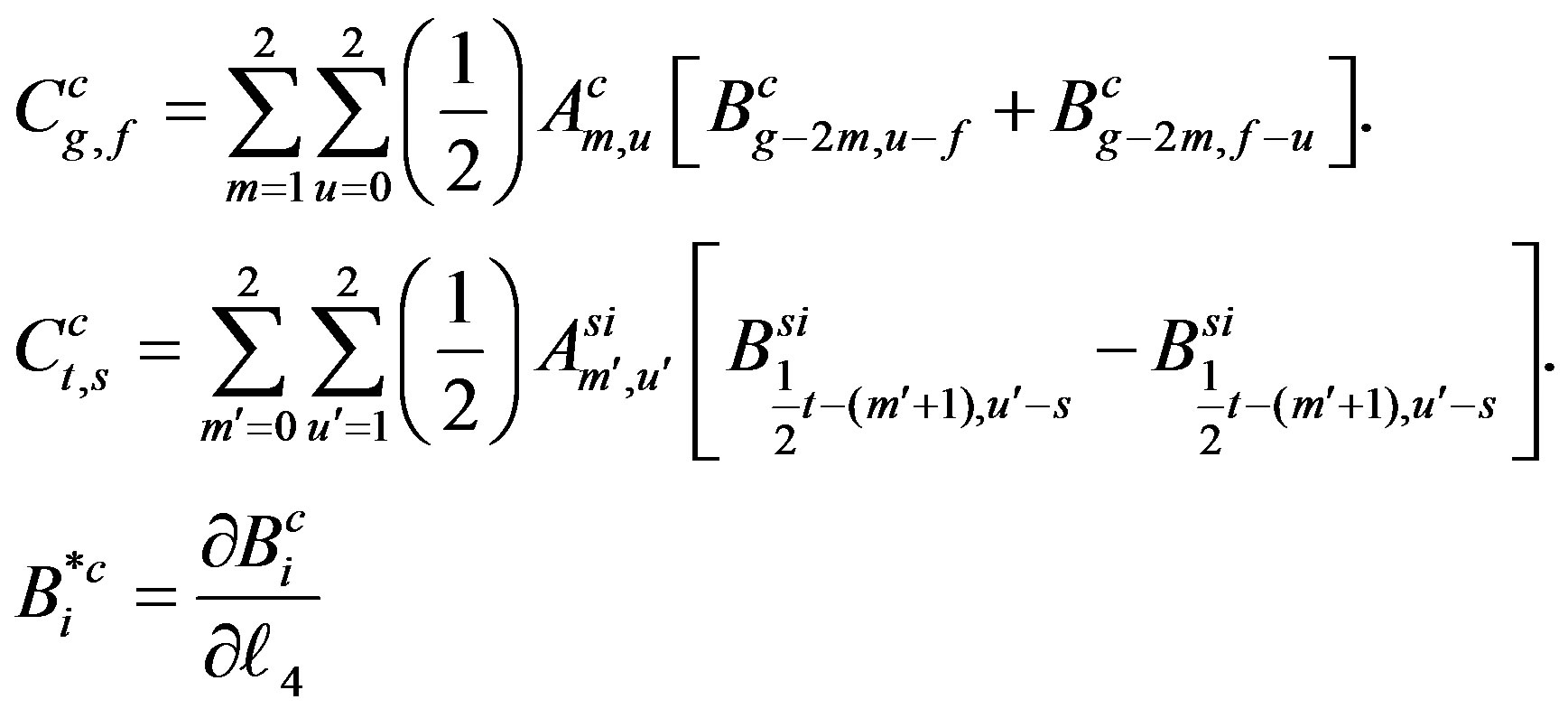
Then, applying Equation (17.2) by averaging over the mean anomaly 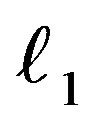 for the last Equation (18), we can determine the transformed second order Hamiltonian,
for the last Equation (18), we can determine the transformed second order Hamiltonian,  , as:-
, as:-
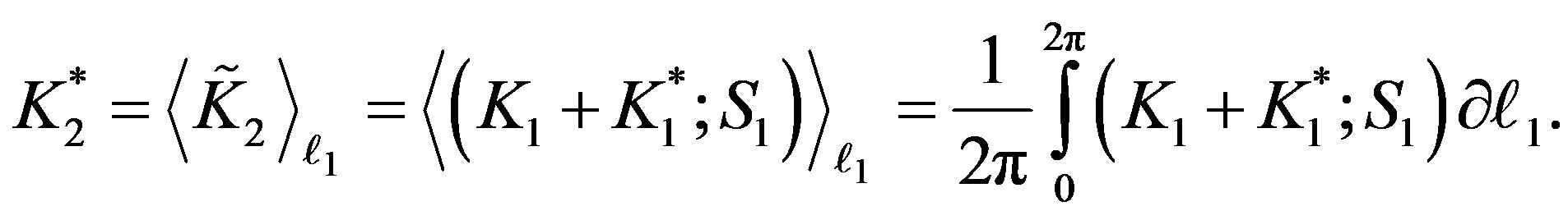 (19)
(19)
Substituting from Equation (18) in the last Equation yeilds:-
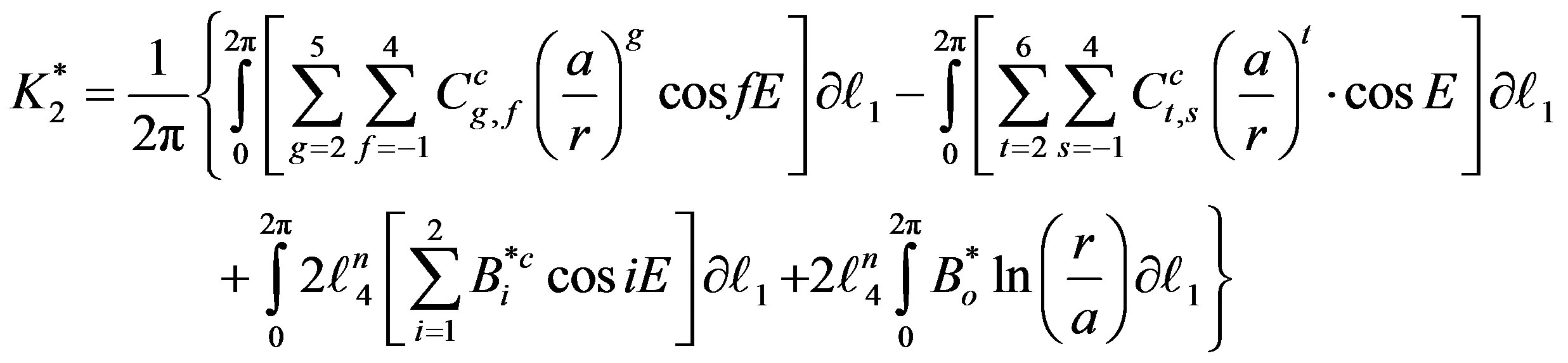 (20)
(20)
A useful paper for Ahmed (1994) [20] , was used to calculate the required integral. While the last integral was solved except for the case of hyperbolic orbits.

where 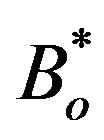 and
and  are coefficients, ware derived during the calculation of the Poisson brackets
are coefficients, ware derived during the calculation of the Poisson brackets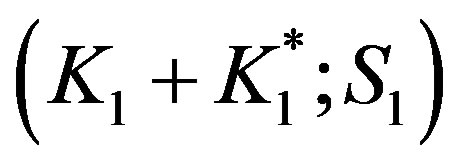 , defined as:
, defined as:
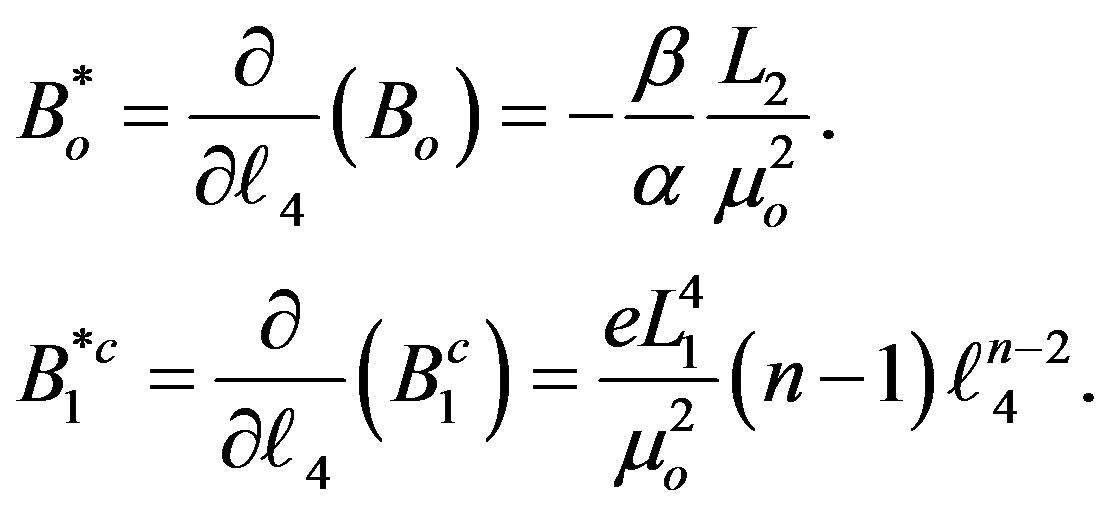
Finally, the required transformed second order Hamiltonian can be written as: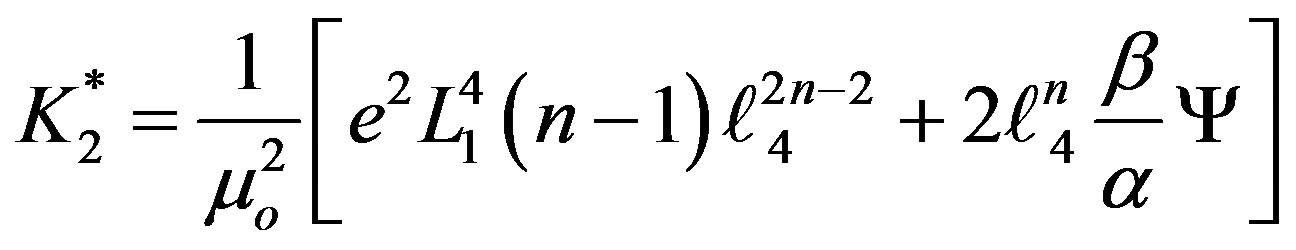 (21)
(21)
where Y is function of L1 and L2 and defined by:
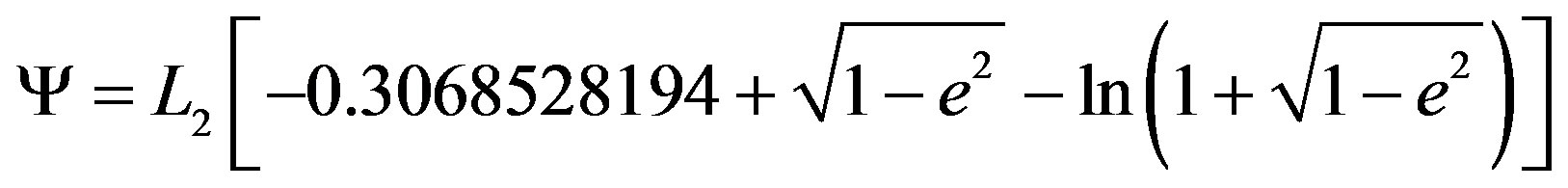
The last, second orders Hamiltonian, is valid in all cases of orbits except in the case of hyperbolic orbits (e > 1).
3.4. The Transformed Hamiltonian
The second order transformed Hamiltonian;  can be constructed in the form:
can be constructed in the form:
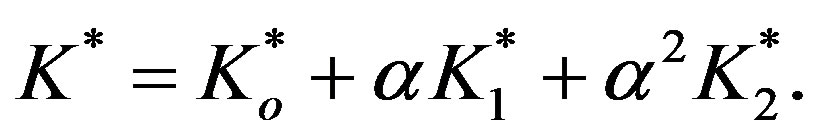
Which can be written by using Equations (12), (14) and (21) as:
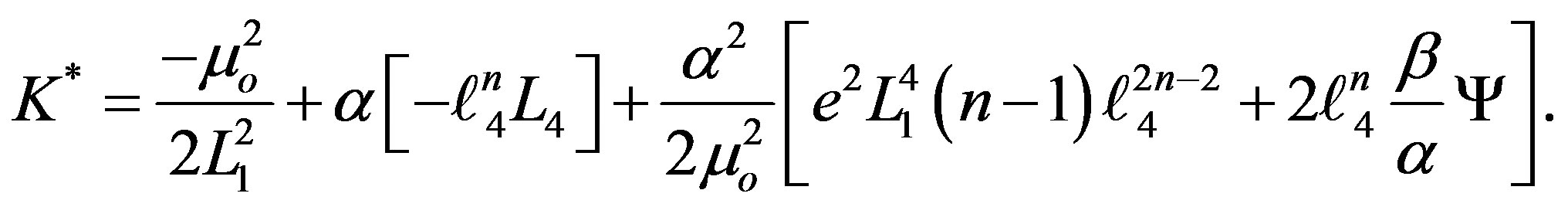 (22)
(22)
The equations of motion in the transformed augmented phase space can be derived as follows:
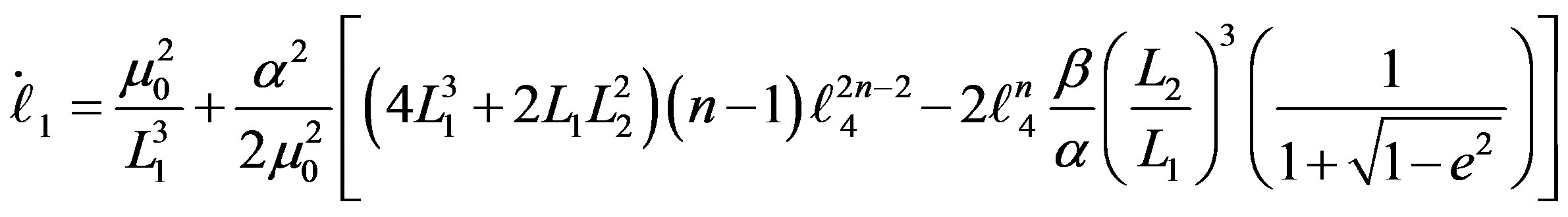 (23-1)
(23-1)
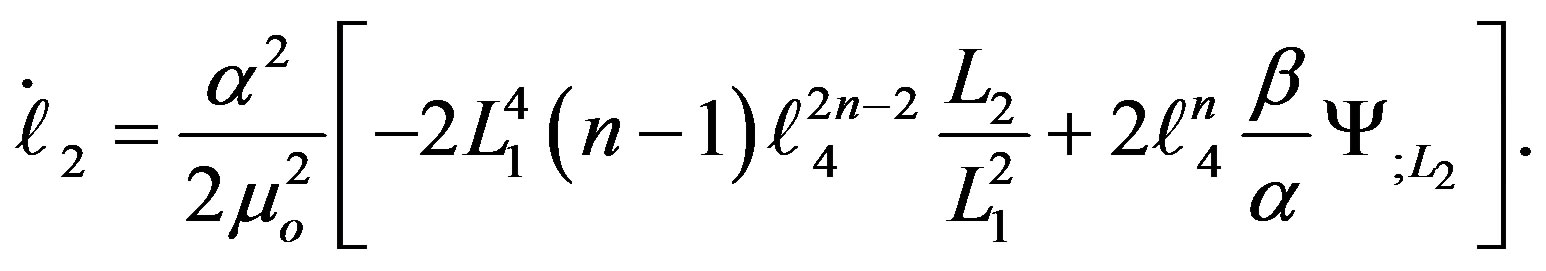 (23-2)
(23-2)
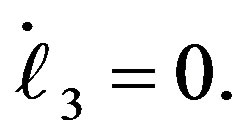 (23-3)
(23-3)
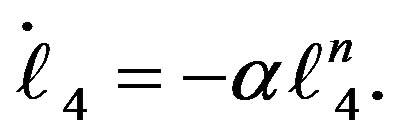 (23-4)
(23-4)
 (23-5)
(23-5)
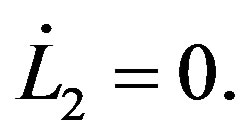 (23-6)
(23-6)
 (23-7)
(23-7)
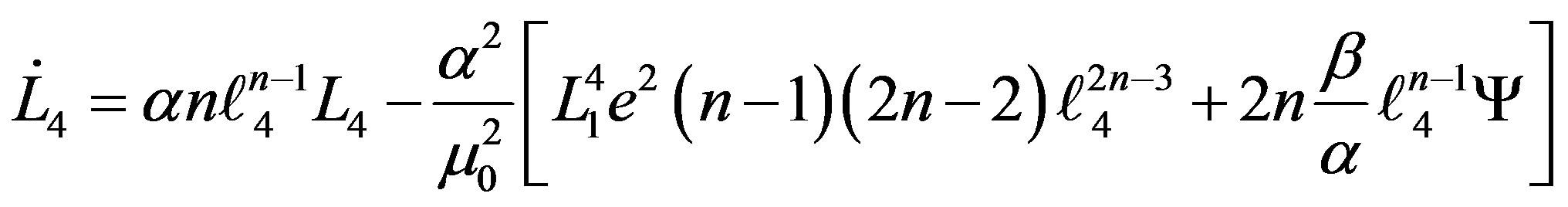 (23-8)
(23-8)
where 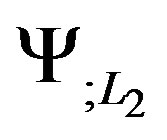 is the partial differentiation for the function Ψ with respect to the momentum L2 and given by:
is the partial differentiation for the function Ψ with respect to the momentum L2 and given by:
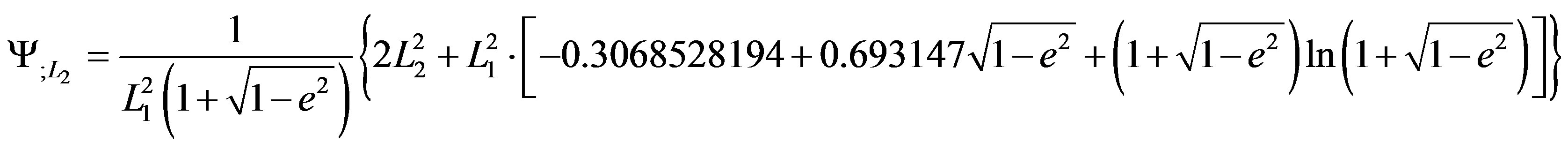
The Hamiltonian and the system of differential equation, described by Equations (23), has one degree of freedom since the variable 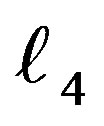 is explicitly appears in them.
is explicitly appears in them.
3.5. The Element of Short Period Transformation and Its Inverse
The elements of short period transformation can be calculated using equations:
 (24.1)
(24.1)
 (24.2)
(24.2)
The inverse transformation equations can be calculated as follows:
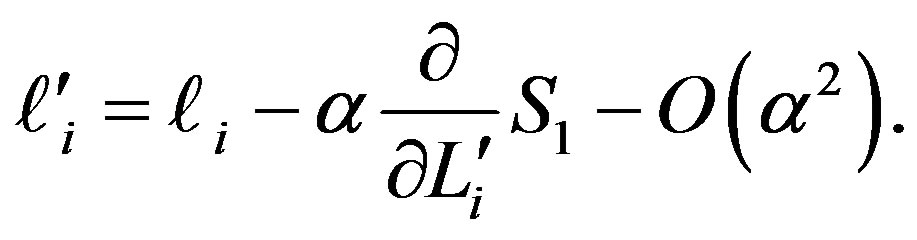 (25.1)
(25.1)
 (25.2)
(25.2)
where ,
,  ,
,  and
and  can be calculated using Equation (13.5).
can be calculated using Equation (13.5).
The prime over the variables means that variables in the transformed phase space which will be omitted for the sake of simplicity.
The variable mass 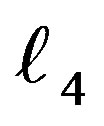 is implicitly function of time through the relation (7’), so we will complete the solution using the method which was introduced by Delva [14] and Hanslmeier [15] , separately.
is implicitly function of time through the relation (7’), so we will complete the solution using the method which was introduced by Delva [14] and Hanslmeier [15] , separately.
4. The Final Solution
A special linear differential operator, the Lie operator, produces a Lie series to construct an approximate solution. The convergence of the Lie series is similar to that of Taylor series, since the Lie is only another analytic form of the Taylor series. The algorithm for the method was outlined in Delva [14] and Hanslmeier [15] .
The Lie operator, D, can be defined as:
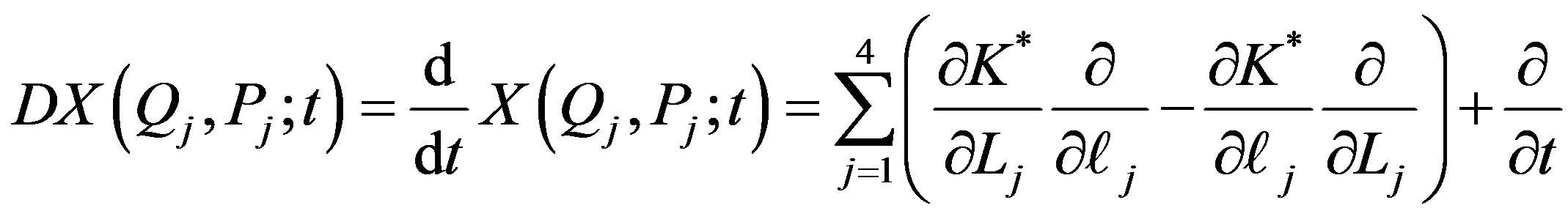 (26.1)
(26.1)
and the second order “D” operator, which can be noted as D2, constructed as:
 (26.2)
(26.2)
The coefficients of the operator D, 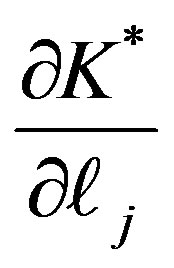 and
and , can be replaced by the canonical equations of motion represented by Equations (23). Then, Lie operator for our case can be written as:
, can be replaced by the canonical equations of motion represented by Equations (23). Then, Lie operator for our case can be written as:
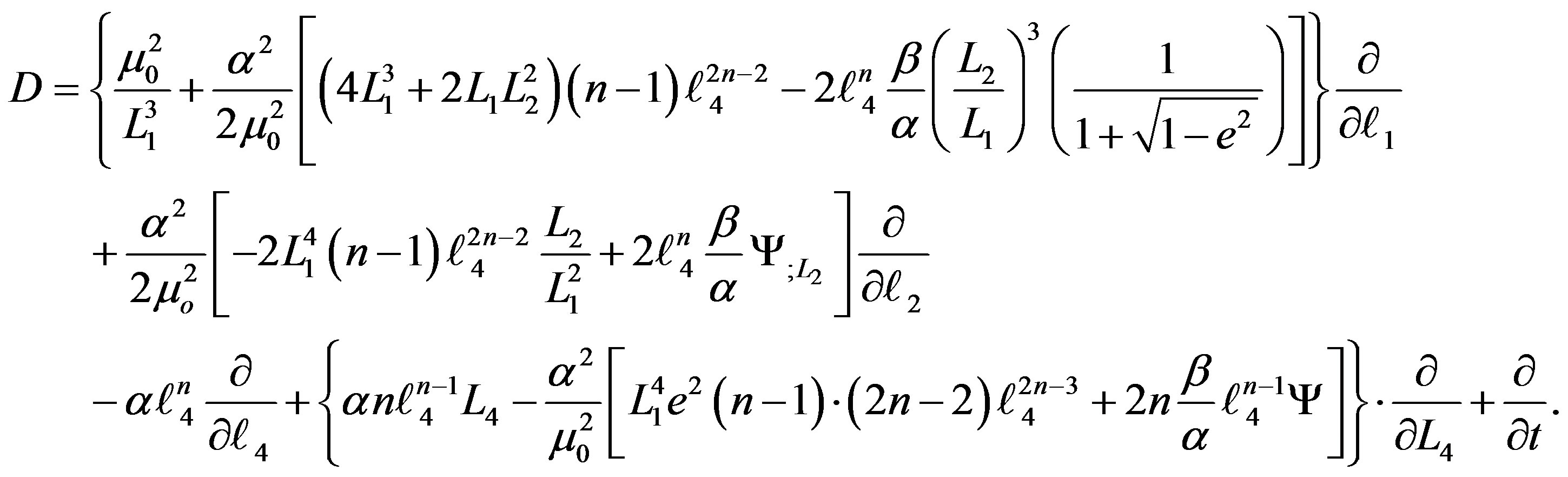 (27)
(27)
Now, we can calculate the solution by applying the D operator, represented by Equation (27), up to second orders, to the variables 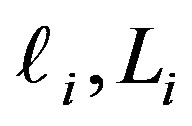 and the results are as follows:
and the results are as follows:
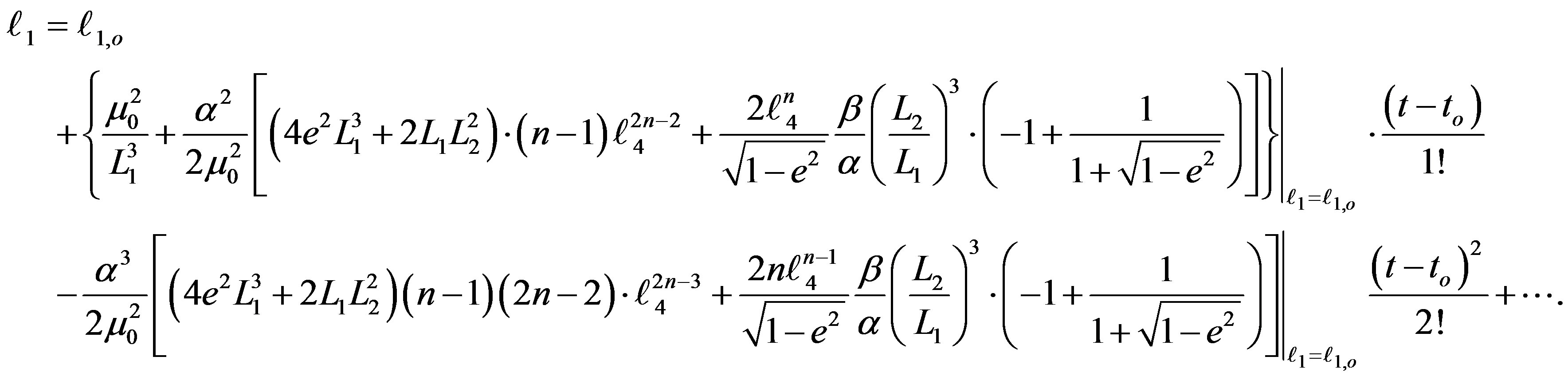 (28)
(28)
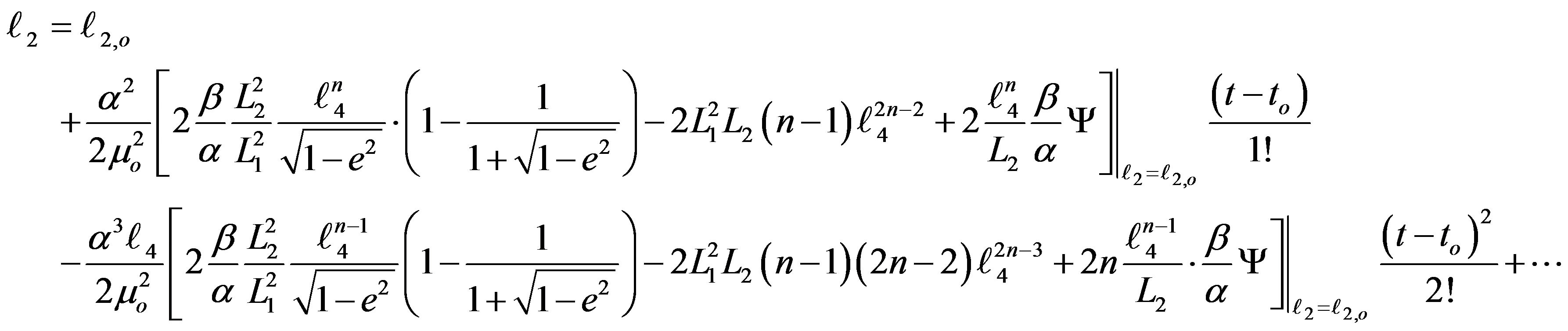 (29)
(29)
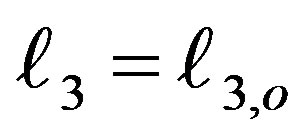 (30)
(30)
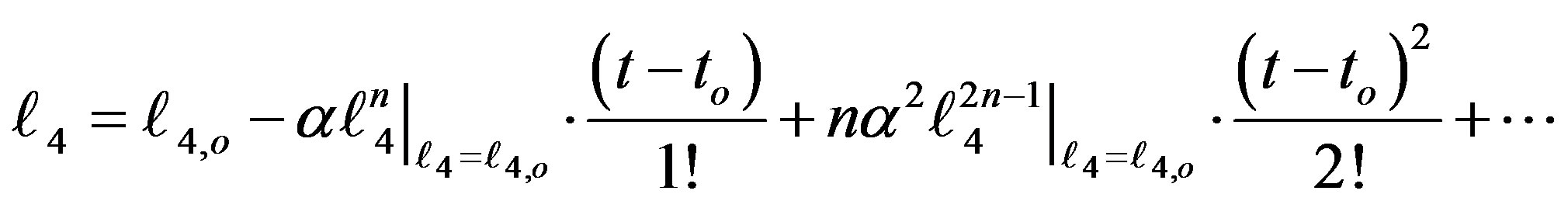 (31)
(31)
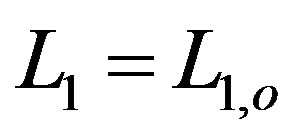 (32)
(32)
 (33)
(33)
 (34)
(34)
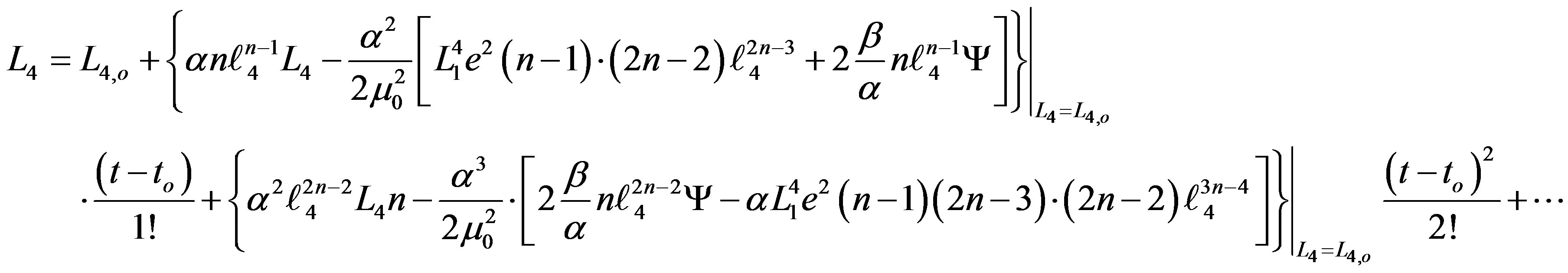 (35)
(35)
where the quantities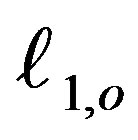 ,
, 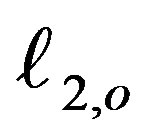 ,
, 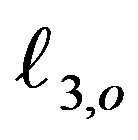 ,
, 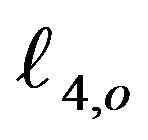 ,
, 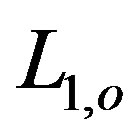 ,
, 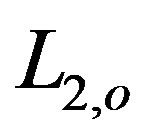 ,
,  and
and 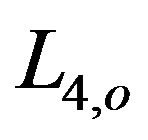 are the orbital elements at time
are the orbital elements at time  Using the initial values for the orbital elements, with the help of Equations (28) - (35), we can calculate the new perturbed orbital elements due to the varying mass.
Using the initial values for the orbital elements, with the help of Equations (28) - (35), we can calculate the new perturbed orbital elements due to the varying mass.
5. Discussion and Conclusions
The last group of equations is a second order solution for the two body problem with m1 varying mass. In those equations, the following results are included.
1. The varying mass gives rise to the change of mean anomaly  and the argument of preside
and the argument of preside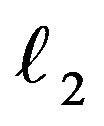 . That rises influenced by both the varying mass and the periastron effect.
. That rises influenced by both the varying mass and the periastron effect.
2. A new varying, second order, mass formula was derived and represented by Equation (31).
3. The varying mass, as well as the periastron effects, does not affect the argument of ascending node 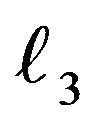 and the momenta
and the momenta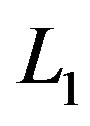 ,
, 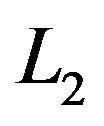 and
and 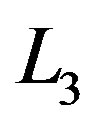 in the extended transformed phase space.
in the extended transformed phase space.
4. A second order equation for calculation of the momentum associated to the varying mass,  , as well as the periastron effect, was derived and represented by Equation (35).
, as well as the periastron effect, was derived and represented by Equation (35).
Future work: We plane to apply these equations for deferent systems as well as comparing the results with others and with observations.
References
- Polyakhova, E.N. (1994) A Two-Body Variable-Mass Problem in Celestial Mechanics: The Current State. Astronomy Reports, 38, 283-291.
- Prieto, C. (1995) Publicaciones del Departamento de Matematica Aplicada, Universidade de Santiago de CompostelaSpain.
- Hadjidemetriou, J. (1963) Two-Body Problem with Variable Mass: A New Approach. Icarus, 2, 440-451. http://dx.doi.org/10.1016/0019-1035(63)90072-1
- Hadjidemetriou, J. (1966) Analytic Solutions of the Two-Body Problem with Variable Mass. Icarus, 5, 34-46. http://dx.doi.org/10.1016/0019-1035(66)90006-6
- Jeans, J.H. (1924) Cosmogonic Problems Associated with a Secular Decrease of Mass. MNRAS, 85, 2-11.
- Jeans, J.H. (1925) The Effect of Varying Mass on a Binary System. MNRAS, 85, 912-925.
- Prieto C. and Docobo, J.A. (1997) Analytic Solution of the Two-Body Problem with Slowly Decreasing Mass. Astronomy & Astrophysics, 318, 657-661.
- Prieto, C. and Docobo, J.A. (1997) On the Two-Body Problem with Slowly Decreasing Mass. Celestial Mechanics and Dynamical Astronomy, 68, 53-62. http://dx.doi.org/10.1023/A:1008235630740
- Docobo, J.A., Blanco, J. and Abelleira, P. (1999) Monografias de la Academiade Ciencias de Zaragoza, 14, II Jornadas de Mecanica Celeste, Academia de Ciencias de Zaragoza, Zaragoza, 33. (in Spanish)
- Andrade, M. and Docobo, J.A. (2000) The Influence of Decreasing Mass on the Orbits of Wide Binaries: An Approach to the Problem. Proceedings of the 4th Scientific Meeting of the Spanish Astronomical Society (SEA), Santiago de Compostela, 11-14 September 2000, 273.
- Andrade, M. and Docobo, J.A. (2002) The Influence of Mass Loss on Orbital Elements of Binary Systems by Periastron Effect. International Conference on Classical Nova Explosions, AIP Conference Proceedings, Santiago de Compostela, 82-85.
- Andrade, M. and Docobo, J.A. (2003) Orbital Dynamics Analysis of Binary Systems in Mass-Loss Scenarios. Conference to Honor John Dyson, Pátzcuaro, Michoacán, México, Santiago de Compostela, 223-225.
- Rahoma, W.A., et al. (2009) Analytical Treatment of the Two-Body Problem with Slowly Varying Mass. Journal of Astrophysics and Astronomy, 30, 187-205. http://dx.doi.org/10.1007/s12036-009-0012-y
- Delva, M. (1984) Integration of the Elliptic Restricted Three-Body Problem with Lie Series. Celestial Mechanics, 34, 145-154. http://dx.doi.org/10.1007/BF01235797
- Hanslmeier, A. (1984) Application of Lie-Series to Regularized Problems in Celestial Mechanics. Celestial Mechanics, 34, 135-143. http://dx.doi.org/10.1007/BF01235796
- Rahoma, W.A., et al. (2011) Two-Body Problem with Varying Mass in Case of Isotropic Mass Loss. Advances in Theoretical and Applied Mechanics, 4, 69-80.
- Deprit, A. (1983) The Secular Accelerations in Gylden’s Problem. Celestial Mechanics, 31, 1-22. http://dx.doi.org/10.1007/BF01272557
- Hori, G. (1966) Theory of General Perturbation with Unspecified Canonical Variable. Astronomical Society of Japan, 18, 287.
- Kamel, A.A. (1969) Expansion Formulae in Canonical Transformations Depending on a Small Parameter. Celestial Mechanics, 1, 190-199. http://dx.doi.org/10.1007/BF01228838
- Ahmed, M.K.M. (1994) On the Normalization of Perturbed Keplerian Systems. The Astronomical Journal, 107, 1900- 1903. http://dx.doi.org/10.1086/117001

