World Journal of Nano Science and Engineering
Vol.4 No.2(2014), Article
ID:47171,7
pages
DOI:10.4236/wjnse.2014.42013
First-Principles Calculations of the Structural, Mechanical and Thermodynamics Properties of Cubic Zirconia
Ibrahim D. Muhammad1*, Mokhtar Awang1, Othman Mamat1, Zilati Bt Shaari2
1Mechanical Engineering Department, Universiti Teknologi Petronas, Seri Iskandar, Malaysia
2Chemical Engineering Department, Universiti Teknologi Petronas, Seri Iskandar, Malaysia
Email: *ibrahimuhd@gmail.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 20 April 2014; revised 20 May 2014; accepted 20 June 2014
ABSTRACT
The structural, mechanical and thermodynamics properties of cubic zirconium oxide (cZrO2) were investigated in this study using ab initio or first-principles calculations. Density functional theory was used to optimize the crystal structure of cZrO2 and thereafter, simulations were conducted to predict the lattice parameters and elastic constants. The Zr-O bond distance was calculated as 2.1763 Å with unit cell density of 6.4179 g/cm3. The data obtained were used to determine Young’s modulus, bulk modulus, Poisson’s ratio and hardness of cZrO2 as 545.12 GPa, 136.464 GPa, 0.1898 and 12.663(Hv) respectively. The result indicates that cZrO2 is mechanically stable with thermodynamics properties of a refractory material having potential for structural and catalytic applications in various forms as a nanomaterial.
Keywords:Cubic Zirconium Oxide, First-Principles Calculation, CASTEP, Elastic Constants

1. Introduction
Recently, zirconium oxide in cubic polymorph has attracted interest due to its mechanical and thermal properties. These interests have resulted in the use of cZrO2 to various applications such as catalysts, fuel cells, oxygen sensors and others [1] -[4] . Thus cZrO2 has been synthesized at nanoscale in various forms. The sol-gel method was used to produce ZrO2 nanoparticles with fairly uniform dimension ranging from 50 nm to 90 nm [5] . ZrO2 nanosheets with thickness in the range of 3.2 - 4.2 nm were produced through bottom-up synthesis by impregnation of graphene oxide in cyclohexane containing Zr-based alkoxides [6] . Also, ZrO2 nanotubes have been prepared via several methods such as direct anodization, template-assisted depositions and hydrothermal treatments [2] ; the nanotubes obtained have different inner and outer diameters, thicknesses and lengths.
For efficient and cost-effective applications of cZrO2, its structural and mechanical properties are required at molecular and atomic scale. But due to complexity and high cost of equipment, only limited experiments have been conducted to characterize required properties of cZrO2 at nanoscale and/or atomic level [2] [4] . This led to computational modeling and simulation of various properties of cZrO2 based on atomistic and continuum approaches [1] [2] . However, most of the simulations already conducted are limited to properties such as electronic structures, phonon dispersion, surface adsorption and diffusion [7] -[13] with limited emphasis on structural and mechanical properties.
Therefore, in this study the first-principles calculations are utilized to numerically predict the structural characteristics, mechanical properties and thermodynamic properties of cZrO2. The values obtained are used to analyze the structural stability of cZrO2 and compared available data for further simulation(s).
2. Computational Methods
The 3D structure of cZrO2 was modeled from available data [2] using the surface builder tools of the Material Studio software [14] . The crystal structure ofcZrO2 was optimized geometrically in order to obtain initial lattice parameters and density based on density function theory (DFT) as implemented in Cambridge Sequential Total Energy Package (CASTEP) code [15] . In this calculation, the Generalized Gradient Approximation (GGA) having Burke-ErnZerhof Potential (PBE) for solids was used [13] . To obtain accurate structures, the calculations were conducted in the irreducible Brillouin zone with 8 × 8 × 8 k point mesh Monk horst-Pack scheme [16] . In order to obtain plane wave expansions, a kinetic energy cut-off value of 380 eV was used. Thereafter the BroydenFletcher-Goldfarb-Shannon (BFGS) optimization method was used with fixed basis quality to obtain the symmetric crystal structure of cZrO2. During the optimization process, the total energy was designed to converge to 5 × 10−6 eV and the force per atom diminished to 0.002 eV/Å. The optimized structure of cZrO2 was then simulated to obtain required mechanical and thermodynamics properties.
3. Results and Discussion
3.1. Crystal Structure
The bulk crystal structure of cZrO2 belongs to the Fm-3m space [4] [9] and is modeled in various forms as seen in Figure 1. The geometric structure has influence on the properties of the material even at nanoscale [2] . After optimization, all the lattice parameters were recorded and compared with values obtained from other simulations and experiments as summarized in Table1 It was observed that the deviation of the lattice parameters is less than 3% from the experimental values, which may be due to the approximation method used during optimization.
 (a)
(a) (b)
(b) (c)
(c)
Figure 1. Crystal structure of cZrO2 in various forms: (a) Unit Cell; (b) Primitive Cell; (c) Zr-O Bond (O2 and Zr atoms are represented by red and light blue balls respectively).
3.2. Mechanical Properties
The mechanical properties of cZrO2 are based on the elastic constants of the crystal which indicates response to external forces. There are six components of stress and a corresponding six components of strain for the general 3-D case. Thus, Hooke’s law may be expressed as:
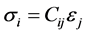 (1)
(1)
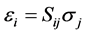 (2)
(2)
where C = stiffness or elastic constant, S = compliance, σ = stress and ε = strain. In matrix format, the stressstrain relation showing the 36 (6 × 6) independent components of stiffness can be represented as [3] :
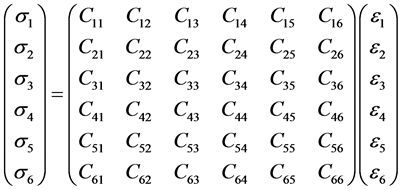 (3)
(3)
The number of independent elastic constants in cZrO2is three (3), i.e. C11, C12 and C44 which are computed as 596.33, 137.04 and 74.34 GPa respectively. Also the bulk modulus (B) was calculated as 290.134 GPa using the Voigt model, which is comparable to experimental value [17] .
With reference to Born-Huang’s lattice dynamic theory [19] , the mechanical stability of a cubic system is based on the conditions expressed in Equations (4) and (5).
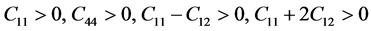 (4)
(4)
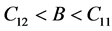 (5)
(5)
Based on conditions outlined in Equations (4) and (5), the structure is mechanically stable due to lattice parameters and orientation of the crystal. The stability will make polycrystalline cZrO2 less vulnerable to generating micro cracks [19] .
For cZrO2, computed Young’s modulus (E) is 545.12 GPa, shear modulus (G) based on Voigh model is 136.464 GPa and the Lame modulus based on Reus model is 222.195 GPa. The G/B ratio indicates the ductility or brittleness of a material [19] and was found out to be 0.469, which indicates that cZrO2 ionic and brittle. This is becausefor covalent and ionic materials, the typical relations between bulk modulus and shear modulus are as G ≈ 1.1B and G ≈ 0.6B, respectively [20] . The Poisson’s ratio (υ) of cZrO2 vary from 0.14 to 0.189, which indicates less metallic and ionic character in the Zr-O bond.
In crystals, hardness quantifies the resistance to deformation and may be predicted using microscopic models [17] . The hardness (Hv) of cZrO2 is determined using a semi-empirical equation defined as follows [21] [22] :
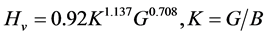 (6)
(6)
The obtained hardness (Vickers number) for cZrO2 is 12.663, which is consistent with the chemical bonding and elastic modulus as analyzed above and in similar other studies [19] -[22] .
3.3. Thermodynamic Properties
The thermodynamic properties of a solid have direct relevance to its phonon characteristics as it indicates the quantum of elastic strain energy [19] . Hence, the phonon dispersion curve of a material elucidates the thermal properties based on the concept of lattice vibrations and interpretation of lattice dynamics [15] . Using the method of linear response with 0.05 1/Å q-vector grid spacing, the phonon dispersion curves (PDC) for cZrO2 was generated as shown in Figure 2. The lower section of G-X direction indicates higher longitudinal energy while most of the branches in the X-K direction converge as non-degenerate, thus leading to the expected nine branches for a typical cubic structure [19] .
With the aid of data from the phonon dispersion curves (PDC), quasi-harmonic approximation was used to evaluate some temperature dependent properties of cZrO2 such as entropy, enthalpy, free energy and Debye temperature as illustrated in Figure 3 and Figure 4. From Figure 3, the zero-point energy was computed to be 0.20385 eV and the heat capacity per unit cell had a maximum value of 16.8957 cal/K (0.07069 kJ/K) at 992.25 K. Debye temperature gives an approximation for the low temperature heat capacity of insulating crystalline solids. The maximum Debye temperature for cZrO2 was found to be 946 K which is similar to 963 K for Y2O3 stabilized cZrO2 determined experimentally using neutron powder diffraction [23] . All the computed thermodynamics properties of cZrO2 indicates it has less thermal conductivity despite having high ionic conductivity thus confirming its major characteristic as a refractory material.
4. Conclusion
Using the first principles calculations, the properties of cZrO2 were investigated. The calculated lattice parameters showed conformity with available experimental data. The computed properties based on elastic constants
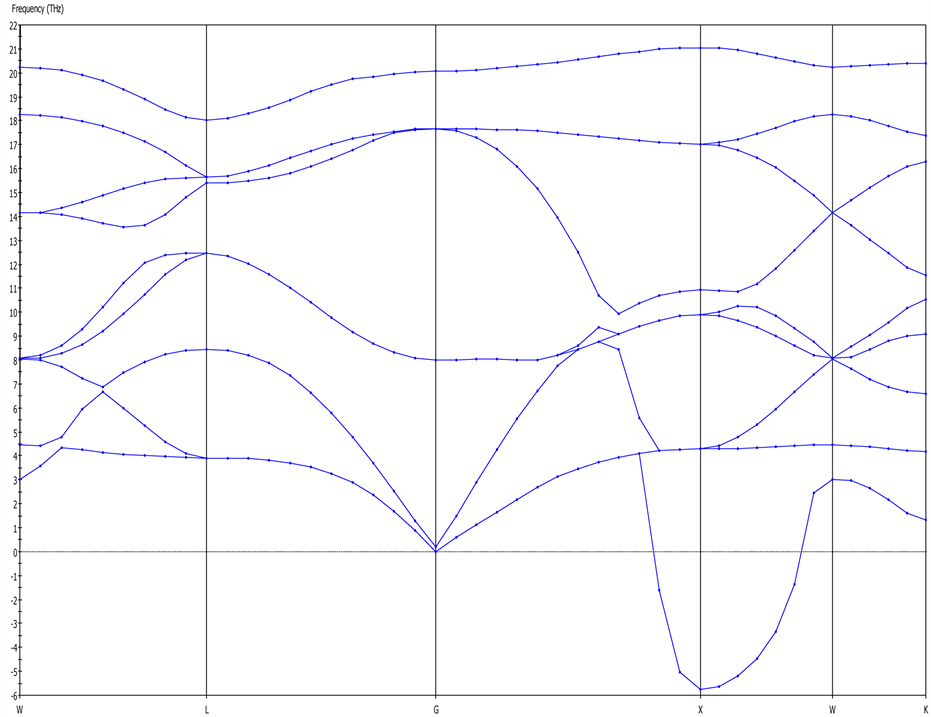
Figure 2. Phonon dispersion curves of cZrO2.
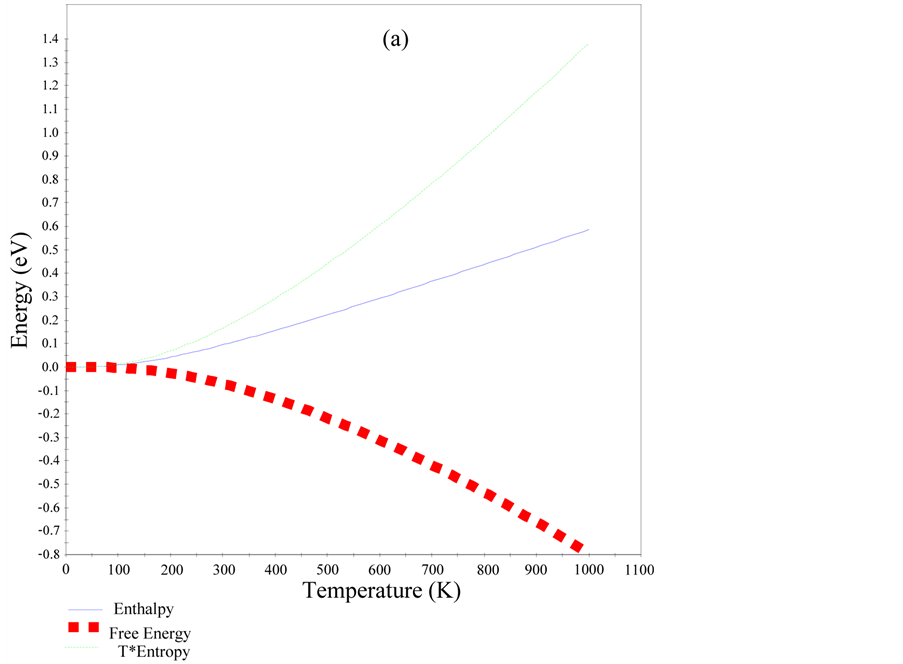

Figure 3. Enthalpy, free energy and entropy (a) and heat capacity of cZrO2.
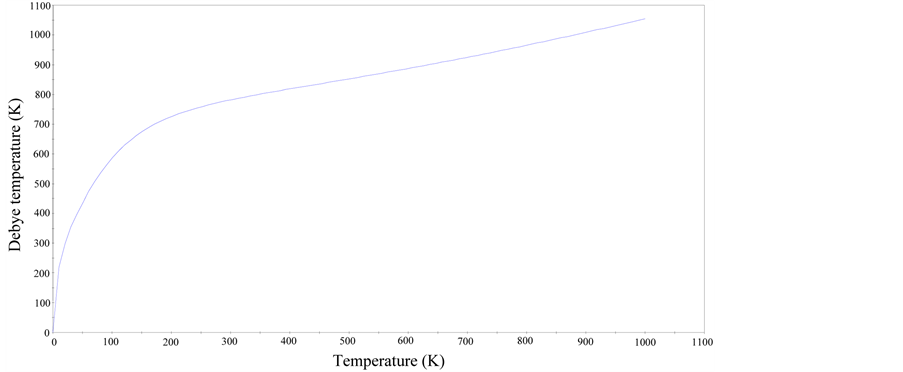
Figure 4. Debye temperature graph of cZrO2.
indicate that cZrO2 has satisfied the mechanical stability requirements; however, the young’s modulus and hardness are high when compared to similar material such as cerium oxide. As expected, the thermodynamic properties obtained confirmed the ceramic characteristics of cZrO2. The data obtained may further be used to predict properties in relation to defects and/or dopants and setting parameters for processing nanocomposites related to cZrO2.
Acknowledgements
The authors are grateful for the supports provided by Universiti Teknologi Petronas and Malaysian Ministry of Higher Education (MOHE) through the Long Term Research Grant Scheme (LRGS) for One Baja Research Programme (Project 6).
References
- Xia, X., Oldman, R. and Catlow, R. (2009) Computational Modeling Study of Bulk and Surface of Yttria-Stabilized Cubic Zirconia. Chemistry of Materials, 21, 3576-3585. http://dx.doi.org/10.1021/cm900417g
- Bandura, A.V. and Evarestov, R.A. (2012) Ab Initio Structure Modeling of ZrO2 Nanosheets and Single-Wall Nanotubes. Computational Materials Science, 65, 395-405. http://dx.doi.org/10.1016/j.commatsci.2012.08.001
- Wang, C. (2009) Multiscale Modeling and Simulation of Nanocrystalline Zirconium Oxide. Ph.D. Thesis, University of Nebraska at Lincoln.
- Muhammad, I.D. and Awang, M. (2013) Modelling the Interatomic Potential of Cubic Zirconia. Applied Mechanics and Materials, 446-447, 151-157. http://dx.doi.org/10.4028/www.scientific.net/AMM.446-447.151
- Suciu, C., Gagea, L., Hoffmann, A.C. and Mocean, M. (2006) Sol-Gel Production of Zirconia Nanoparticles with a New Organic Precursor. Chemical Engineering Science, 61, 7831-7835. http://dx.doi.org/10.1016/j.ces.2006.09.006
- Takenaka, S., Uwai, S., Ida, S., Matsune, H. and Kishida, M. (2013) Bottom-Up Synthesis of Titania and Zirconia Nanosheets and Their Composites with Graphene. Chemistry Letters, 42, 1188-1190. http://dx.doi.org/10.1246/cl.130587
- Kulkova, S., Bakulin, A., Hocker, S. and Schmauder, S. (2012) Ab-Initio Study of Metal-Zirconia Interfaces. Materials Science and Engineering, 38, 012004. http://dx.doi.org/10.1088/1757-899X/38/1/012004
- Lamperti, A., Cianci, E., Ciprian, R., Sangalli, D. and Debernardi, A. (2013) Stabilization of Tetragonal/Cubic Phase in Fe Doped Zirconia Grown by Atomic Layer Deposition. Thin Solid Films, 533, 83-87. http://dx.doi.org/10.1016/j.tsf.2012.11.127
- Welberry, T.R., Withers, R.L., Thompson, J.G. and Butler, B.D. (1992) Diffuse Scattering in Yttria-Stabilized Cubic Zirconia. Journal of Solid State Chemistry, 100, 71-89. http://dx.doi.org/10.1016/0022-4596(92)90157-Q
- Hou, Z.F. (2008) Ab Initio Calculations of Elastic Modulus and Electronic Structures of Cubic CaZrO3. Physical B: Condensed Matter, 403, 2624-2628. http://dx.doi.org/10.1016/j.physb.2008.01.025
- Zhang, P., Lu, Y., He, C. and Zhang, P. (2011) First-Principles Study of the Incorporation and Diffusion of Helium in Cubic Zirconia. Journal of Nuclear Materials, 418, 143-151. http://dx.doi.org/10.1016/j.jnucmat.2011.06.025
- Zhao, X., Shang, S., Liu, Z. and Shen, J. (2011) Elastic Properties of Cubic, Tetragonal and Monoclinic ZrO2 from First-Principle’s Calculations. Journal of Nuclear Materials, 415, 13-17. http://dx.doi.org/10.1016/j.jnucmat.2011.05.016
- Miller, S.P., Dunlap, B.I. and Fleischer, A.S. (2012) Cation Coordination and Interstitial Oxygen Occupancy in Co-Doped Zirconia from First Principles. Solid State Ionics, 227, 66-72. http://dx.doi.org/10.1016/j.ssi.2012.07.017
- Accelrys Software Inc., San Diego (2012) Materials Studio. http://accelrys.com/products/materials-studio/index.html
- Clark, S.J., Segall, M.D., Pickard, C.J., Hasnip, P.J., Probert, M.J., Refson, K. and Payne, M.C. (2005) First Principles Methods Using CASTEP. Zeitschrift Fuer Kristallographie, 220, 567-570.
- Perdew, J.P., Burke, K. and Ernzerhof, M. (1996) Generalized Gradient Approximation Made Simple. Physical Review Letters, 77, 3865-3868. http://dx.doi.org/10.1103/PhysRevLett.77.3865
- Soo, Y.L., Chen, P.J., Huang, S.H., Shiu, T.J., Tsai, T.Y., Chow, Y.H., et al. (2008) Local Structures Surrounding Zr in Nanostructurally Stabilized Cubic Zirconia: Structural Origin of Phase Stability. Faculty Publications—Chemistry Department, Paper 18. http://digitalcommons.unl.edu/chemfacpub/18
- Chang, Y., Wang, H., Zhu, Q., Luo, P. and Dong, S. (2013) Theoretical Calculation and Analysis of ZrO2 Spherical Nanometer Powders. Journal of Advanced Ceramics, 2, 21-25. http://dx.doi.org/10.1007/s40145-013-0036-2
- Goldsby, J.C. (2013) Basic Elastic Properties Predictions of Cubic Cerium Oxide Using First-Principles Methods. Journal of Ceramics, 2013, Article ID: 323018. http://dx.doi.org/10.1155/2013/323018
- Yang, Z.-J., Guo, Y.-D., Linghu, R.-F. and Yang, X.-D. (2012) First-Principles Calculation of the Lattice, Compressibility, Elastic Anisotropy and Thermodynamic Stability of V2GeC, China Physics B, 21, 036301 http://dx.doi.org/10.1088/1674-1056/21/3/036301
- Tian, Y., Xu, B. and Zhao, Z. (2012) Microscopic Theory of Hardness and Design of Novel Superhard Crystals. International Journal of Refractory Metals and Hard Materials, 33, 93-106. http://dx.doi.org/10.1016/j.ijrmhm.2012.02.021
- Chong, X., Jiang, Y., Zhou, R. and Feng, J. (2014) First Principles Study the Stability, Mechanical and Electronic Properties of Manganese Carbides. Computational Materials Science, 87, 19-25. http://dx.doi.org/10.1016/j.commatsci.2014.01.054
- Kisi, E. and Yuxiang, M. (2003) Debye Temperature, Anharmonic Thermal Motion and Oxygen Non-Stoichiometry in Yttria Stabilized Cubic Zirconia. Journal of Physics: Condensed Matter, 10, 3823-3832. http://dx.doi.org/10.1088/0953-8984/10/17/013
NOTES

*Corresponding author.


