Received 26 December 2014; accepted 9 January 2015; published 15 January 2015

ABSTRACT

Industrially produced sodium water glasses were dried in climates with controlled temperature and humidity to transparent amorphous water containing sodium silicate materials. The water glasses had molar SiO₂:Na₂O ratios of 2.2, 3.3 and 3.9 and were dried up to 84 days at temperatures between 40˚C and 95˚C and water vapour pressures between 5 and 40 kPa. The materials approached final water concentrations which are equilibrium values and are controlled by the water vapour pressure of the atmosphere and the microstructure of the solids. The microstructure of the dried water glasses was characterized by atomic force microscopy. It has a nanosized substructure built up by the silicate colloids of the educts but deformed by capillary forces. In the final drying equilibrium, the water vapour pressure of the atmosphere in the drying cabinet is equal to the reduced vapour pressure of the capillary system built up by the silicate colloids. Their size scale can be explained by the deformation of colloidal aggregates due to capillary forces.

Keywords:

Concentrated Sodium Silicate Sol, Silica Colloids, Drying, Atomic Force Microscopy, Capillarity

1. Introduction

Sodium water glasses are commonly produced by dissolving either alkali silicate glasses in water or silica materials in NaOH solutions at hydrothermal conditions [1] [2] . The old literature on water glass was compiled by Vail [1] ; more contemporary reviews were published by Iler [3] and Falcone [4] . The structure of water glasses can be described as colloidal suspensions in aqueous sodium silicate solutions or briefly as sodium silicate sols [2] [3] . The main silicate ingredients of water glasses are colloids and monomeric or oligomeric silicatic anions or molecules. The distinction between anions and molecules on one hand and colloids on the other hand is arbitrary, since the colloids can also be regarded as large molecules. In concentrated water glasses with R_m (=molar SiO₂:Na₂O ratio) > 2, a cut at a diameter of 1 nm seems to be appropriate. Such a diameter corresponds to 10 to 11 SiO₂ formula units.

Colloids in water glass consist mainly of silica [5] . Iler [6] investigated colloids extracted with tetrahydrofurane from sodium silicate solution (R_m = 3.22, 28.7 wt% SiO₂) with static light scattering and found 10% monomers, 15% oligomers and 75% colloids with a diameter of about 1.8 - 1.9 nm. An electric double layer at the surface of the colloids and steric effects [7] are supposed to stabilize the colloidal suspensions at basic pH values. The double layer consists of negatively charged Si-OH groups covered by a layer of hydrated sodium ions. Bahlmann et al. [8] investigated the molecular content of a concentrated water glass (R_m = 4.0, 25 wt% SiO₂) by ²⁹Si NMR spectroscopy and found that nearly 75% of the silicon atoms are present as highly polymerized Q³ or Q⁴ units which are typical of colloidal silica. Own investigations with dynamic light scattering [9] yielded particle size distributions with three or more particle size maxima at diameters between 1 and 200 nm even in diluted solutions with silica contents down to 1 wt%. The smallest particle sizes having a maximum frequency density occur at diameters of 1 nm. Nordström et al. [10] confirmed these findings by dynamic light scattering and small angle X-ray scattering but highlighted the importance of smaller oligomers, small “clusters”, with diameters of approximately 1.4 nm as the main part of the silica. Tognonvi et al. [11] combined ²⁹Si NMR spectroscopy and small angle X-ray scattering to describe solvated silicate ions. They proposed a neutral Si₇O₁₈H₄Na₄ complex as primary building unit with a size of 0.6 to 0.8 nm in concentrated liquid water glasses with R_m = 3.4. Halasz et al. [12] measured osmotic pressures of sodium silicate sols with up to 3 mol/dm³ SiO₂ and concluded that the average silicate unit in a sodium water glass with R_m = 3.3 contains about 10 SiO₂ units. These results on colloid sizes in sodium water glasses can be interpreted by the assumption that small primary particles form larger aggregates [6] [9] .

Commercially available sodium silicate solutions are characterized by a molar SiO₂:Na₂O ratio of 2 - 4 and SiO₂ contents of 25 - 30 wt% [1] . For some applications the materials have to be partially dried e.g. by spray drying for binder applications. Dried water glass is also a component of fire protecting materials e.g. [13] . In the application case it is heated and foams forming porous thermal insulation materials. During drying the viscosity of the solution is raised within a narrow concentration range by a few orders of magnitude as a function of the water content [1] .

Results on thermal analysis of dried water glasses were published by Dent Glasser and Lee [14] . They heated their samples in open crucibles and found at least two endothermic signals in differential thermal analysis which they attributed to structural rearrangements and condensation reactions. In own investigations [15] [16] , transparent, solid and amorphous materials were obtained by drying a sodium silicate solution with R_m = 3.27. During heating thermal reactions occur which were investigated by combined application of simultaneous thermal analysis, electron microscopy and hot stage microscopy. One of these reactions was attributed to a sol-gel or a sol-colloidal glass transition. Based on these structural findings, a model of the structural evolution of the solutions during drying was developed [16] in accordance to structure models developed for amorphous materials with a colloidal microstructure [17] . According to this model, the sol solidifies to a dense gel by reducing the distance between the colloids until their movement is sterically hindered.

The vapour pressure of a solvent in a homogeneous solution is reduced according to Raoult’s law by the dissolved matter itself. The reduction is a colligative property and depends on the number of dispersed or dissolved units. Thermodynamically, the vapour pressure reduction is due to the difference of chemical potential between water dispersed in the sol and pure water. A consequence of that difference is the increase of boiling temperature. However measurements show that this effect is limited [18] . Boiling point elevations up to 1.5˚C for concentrated sodium silicate sols with R_m ~ 1.7 were reported. The boiling point elevations decrease with higher R_m values. These data on boiling point elevations correspond to a vapour pressure reduction of less than 5%. This small effect was explained [1] by the colloidal structure of liquid water glasses: the number of dissolved units is limited because the total number of colloids is small compared to the number of SiO₂ formula units.

Dried colloidal suspensions are heterogeneous on a colloidal scale [17] and are made up of a more or less dense packing of colloids. The voids in this packing build up an interconnected capillary system filled with a solvent or, in the case of dried water glasses, with an aqueous solution. In such a microstructure, the vapour pressure is further reduced by the negative curvatures of the surface of the solvent in the capillary pores system [19] . The influence of capillary geometry on vapour pressure is described by the Thomson-Freundlich [19] equation―also known as Gibbs-Thomson equation [20] . It links the vapour pressure with the capillary diameters of the pore system. The drying process of porous gels was described by Brinker and Scherer [19] . They distinguished three time periods of drying. At first a constant drying rate is observed where the water evaporates directly from the surface. Later the drying front moves into the drying body with the consequence that the drying rate is decreased and the sample gets translucent due to the formation of interfaces between gas and condensed matter in the interior of the sample. In the constant rate period, the mass loss rate follows the Hertz-Knudsen equation [2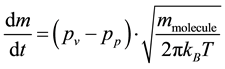1] :

, (1)

with

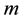: mass of drying body,

: time,

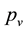: vapour pressure of liquid,

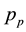: partial pressure of evaporating molecule in gas phase,

: mass of evaporating molecule,

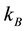: Boltzmann constant, and

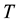: absolute temperature.

As a consequence, the mass loss stops when 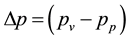becomes zero. As mentioned above some applications of sodium water glasses depend on partially drying the materials. Investigating the drying kinetics will help to choose optimal drying conditions. Knowing the structure of the dried materials contributes to our understanding of the foaming behaviour relevant for intumescent layers in fire protective glazings. Therefore, results on sodium water glasses dried to mass constancy under controlled atmospheres will be presented. Especially the relations among vapour pressure during drying, temperature and residual water content were investigated. The implications of drying conditions on structure will be discussed and compared with results of structural characterizations of dried water glasses by atomic force microscopy. Also differences to normal drying processes will be discussed.

2. Materials and Methods

Three types of technical grade sodium water glasses with different R_m values were used as starting materials. Their compositions and some properties are listed in Table 1. The liquid water glasses were named NaSi (for sodium and silicon) augmented by the R_m value, for instance NaSi2.2 for the sodium water glass with R_m = 2.2. The compositions were analysed by titration with 0.5 M HCl (yields Na₂O content) and by loss on ignition. Impurities were neglected. pH was measured with a glass electrode (pH 330i, WTW, Weilheim, Germany), density by a pycnometer, refractive index by an Abbe Refractometer, and viscosity by the Ubbelohde method. All values were measured at 25˚C. The water glasses were dried in polystyrene or polytetrafluoroethylene beakers in controlled climates established in climate chambers (Hereaus Vötsch VTKR 150 and Vötsch VCL 4010). The applied climate conditions are shown in Table 2. In one test run the samples have been stored above a saturated NaNO₂ solution (Climate A in Table 2) [22] .

The surface area of the samples exposed to the atmosphere stayed constant during the test runs. Volume reduction due to evaporation resulted only in reduction of sample height and not in reduction of the drying surface area. After drying the samples were stored in closed polystyrene containers without gas exchange with atmosphere. Three individual samples of 10 g liquid water glass were dried at each parameter variation of climate and type of water glass. The standard deviation of a single determination of water content was lower than 0.3 wt%. Drying times between 14 and 84 days were applied. Within this time period the samples were weighed in intervals, in the earlier experimental stage daily, later twice a week. The weight loss of the sodium silicate solutions was used to calculate the residual water content. Some of the samples were used for other investigations. Samples for atomic force microscopy (AFM) were cut with a low speed saw (Isomet, Buehler, Düsseldorf, Germany) with water free sawing liquid into appropriate sizes of about 1 × 1 cm². The sawing liquid was removed with

ethanol. AFM measurements were performed with an Extended MultiMode (Digital Instruments, now Bruker, Santa Barbara, CA, USA) in contact mode applying a constant set-point force between the probing tip at a cantilever and the sample. The force acting between the tip and the surface, measured by the deflection of the cantilever, is kept constant by controlling the vertical displacement of the sample by means of a feedback-loop. During the scan the vertical displacements, needed to keep the force constant, are displayed as “height image” while the remaining deflection (error signal of the feedback-loop) is displayed as “deflection image”, which is very sensitive to small topographical changes.

3. Results and Discussion

3.1. Drying Kinetics

After drying the materials were solid, transparent and amorphous, at least at room temperature. Only after very long drying times some materials became opaque. In former experiments e.g. [15] this was attributed to cracking and/or formation of small gas bubbles. The masses of the samples reached nearly weight constancy after about 14 to 28 d, depending on climate. The results were used to calculate the residual H₂O content of the drying materials. Figure 1 shows the development of the residual water content of the three different liquid water glasses in climate D (T = 80˚C and p(H₂O) = 10.01 kPa). The data on water contents have been evaluated by a time law which is typical of a first order reaction:

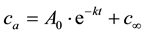, (2)

with:

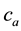: actual water content in wt% (of the dried sample),

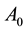: prefactor or fitting parameter,

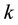: rate constant,

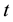: drying time in d, and

: the final water content in wt%.

A least square refinement was used to fit the parameters of the rate law to the experimental data. In the first days of the drying process the fit is not optimal. This is probably due to the transition from the liquid state to the solid state which changes the kinetics. Therefore, the time law is applied for drying times exceeding three days. In later test runs drying times of 14 d were sufficient to calculate. The fitted curves are included in Figure 1. Only at very humid conditions (80˚C and 40.53 kPa p(H₂O)) the water contents of the drying materials did not follow the proposed rate law. At these humidity conditions the water content first rose with drying time and then― after more than 30 d―decreased a bit. In these specific test runs the three water glasses stayed liquid during drying at 80˚C, but NaSi3.3 and NaSi3.9 became solid after cooling to room temperature. In the latter cases the liquid to solid transition could be followed by visible inspection. Samples dried at other climates were solid, transparent and amorphous even at drying temperatures. The fitted end values of of the water contents are reported in Table 3 and have been used for further evaluation. While was quite stable during a single test run, the repeatability of the determination was worse: deviations up to 2.6 wt% were observed, especially in more humid climates. The final H₂O content is related to drying temperature at a constant water vapour pressure, e.g. of 5.07 kPa as displayed in Figure 2. As expected, the residual water content decreased with increasing temperature (Figure 2) and with decreasing water vapour pressure (data in Table 3). The final water contents depend on R_m and decrease in the order NaSi2.2 > NaSi3.3 > NaSi3.9, when the other conditions remain constant. The rate constants (k) did not clearly depend on H₂O vapour pressure or drying temperature. This is due to differences of geometry, convection and forced flow of atmosphere in the different applied drying chambers.

3.2. Atomic Force Microscopy

Figure 3(a) shows the surface of a dried NaSi2.2 sample imaged by the height signal in contact mode. Circular objects with a diameter of 80 to 200 nm can be seen. The deflection signal of the same sample area is shown in

Figure 3(b). In this mode the interfaces separating the objects can be seen more clearly. As a consequence the deflection signal was used as the main information source. Figure 4 shows the deflection signal of the surface of a dried NaSi3.3 sample. The spherical objects have sizes between 50 and 300 nm. The surface looks more heterogeneous and the lines separating the objects lack definition in comparison to the NaSi2.2 sample. Figure 5 shows the surface area of an NaSi3.9 sample imaged with the height signal (left) and the deflection signal (right). There are objects with sizes up to 1300 nm with a mean value of 790 nm. This image of NaSi3.9 allowed size statistics by measuring the diameters of 100 particles: the particle size distribution is broad and looks like a normal distribution (Figure 6). Therefore, it is supposed that the spheres in the AFM images show the original size of the particles and not sections of the spheres [23] .

3.3. Capillary Forces

The weight constancy after long drying times suggests that a thermodynamic equilibrium between gas phase and dried materials is reached: the vapour pressure of the dried sodium silicate materials is equal to the H₂O vapour pressure of the drying climate.

The Thomson-Freundlich equation [19] [20] relates equilibrium vapour pressure in a capillary system with the capillary radius in the following way:

, (3)

with

: actual water vapour pressure in drying atmosphere,

: vapour pressure of H₂O at the equilibrium temperature T,

: molar volume of liquid H₂O,

: surface tension between liquid H₂O and atmosphere,

: contact angle between liquid and solid,

: ideal gas constant,

: absolute temperature, and

: pore radius.

Values for surface tension were taken from [24] . The molar volume of water was calculated from density data [25] . The applied data and the calculated capillary diameters are listed in Table 4. The contact angle q of water on silica particles depends on the surface density of silanol groups [26] . For colloids in equilibrium with aqueous solution most authors assume the contact angle to be zero e.g. [19] , which is assumed here, too.

If the vapour pressure of the applied climate is equal to the vapour pressure of the sodium silicate materials dried at 80˚C and 5.07 kPa, the vapour pressure of H₂O is reduced from 47.3 kPa to 5.07 kPa which is a reduction by roughly 90%. Figure 7 shows the relation between water content and capillary diameter at constant drying temperature, whereas Figure 8 shows the relation at constant water vapour pressure. Except for climates with high relative humidity (A and F) capillary diameters between 0.5 and 2.0 nm have been calculated. The accuracy of the determination does not affect the particle size, because the Thompson-Freundlich equation does not contain that variable. The accuracy of the capillary diameter depends on the accuracy of the climate camber to control humidity and on the accuracy of the surface energy, which is stated to be better than 0.5% in [24] .

In many cases, structure models for sols and gels are based on the assumption that the colloids are rigid spheres [18] , a model which was also used in own studies published before [16] . By atomic force microscopy particle diameters between 50 and 1300 nm have been detected. These particle diameters are larger than those identified by dynamic light scattering [2] [9] . The conclusion is that larger particles are formed during drying by further aggregation. Capillary diameters between 0.7 and 10 nm were calculated via the Thomson-Freundlich equation. When the microstructure of the dried water glasses is interpreted―in analogy to [18] ―as a random

close packing of particles, the capillaries are the voids between the particles. If the particles are rigid spheres, the size of the voids is between 40% and 70% of the particles diameters, i.e. between 16 and 700 nm. This size range cannot explain the results obtained by the application of the Thomson-Freundlich equation. In earlier measurements ultrafiltration was applied [2] : particles with diameters between 100 and 300 nm passed 25 nm filters nearly quantitatively. This was explained by deformation of the particles which was enabled by the aggregation of small primary colloids to weaker bonded aggregates. This deformation of larger aggregates might explain some of the observations. The capillary pressure again depends on the curvature of the liquid surface in the pore system. The Washburn equation [27] can be used also to calculate capillary pressures [19] :

, (4)

with

: capillary pressure,

: surface tension between liquid H₂O and atmosphere,

: pore radius, and

: contact angle liquid to solid.

The respective capillary pressures are reported in Table 4, too. Again, 0˚ is assumed to be the contact angle. Under these conditions, the capillary pressures contract the liquid pore phase. As a consequence, the volume of the solid is reduced. Pressures up to 460 MPa might be able to press the water out of the pores, compress the capillary system and deform the aggregates. The microstructure shown in the AFM micrographs can be explained by the suggested deformations. The deformation mechanism is illustrated in a two-dimensional sketch in Figure 9. From these suggestions it is concluded that the capillary pressures exceed the stresses necessary for plastic deformation. The differences to the “normal” drying processes of gels as described in [19] can also be explained by deformation. The capillary forces deform the drying water glass in a way that the volume occupied

by water is always equal to the pore volume. Under this assumption, the difference between water vapour pressure of the capillary system and the water vapour pressure of the drying atmosphere controls the drying rate at constant temperature, surface area of drying materials and atmospheric flow conditions. The water vapour pressure of the capillary system is reduced during drying so that a first order reaction rate is observed, although the drying morphology of the water glass is typical of the constant rate period of the drying process described in [19] .

4. Conclusions

The later stages of the drying of water glasses can be explained by a first order rate law. Driving force of the drying process is the difference between water vapour pressure of the drying solid and the water vapour pressure of the atmosphere surrounding the drying solid. Drying stops when both vapour pressures become equal. The colloidal microstructure of the dried materials was confirmed by atomic force microscopy. The microstructure is transformed during drying first to an amorphous solid made up by spherical colloids which―upon further drying―are deformed due to capillary forces. Therefore, the observed microstructures fit to a drying process based on the following transitions:

sol « aggregate/colloid gel « capillary solid with deformed aggregates.

The capillary pores have sizes between 0.7 and 10 nm. The deformed microstructure can be visualized by atomic force microscopy and reveals aggregate sizes between 50 and 1300 nm. The drying in controlled climates enhances the accuracy of the measurements.

Acknowledgements

The experimental assistance of S. Brinke is gratefully acknowledged. Thanks are also due to the state Saxony- Anhalt for funding a new climate chamber.

References

NOTES

^*Corresponding author.