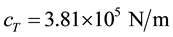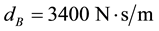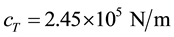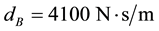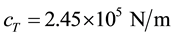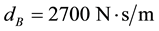Journal of Transportation Technologies
Vol.04 No.03(2014), Article ID:48420,11 pages
10.4236/jtts.2014.43025
Optimized Parameter Combinations of Hydraulic Damper Modules
R. Sonnenburg
ZF Friedrichshafen AG, Schweinfurt, German
Email: reinhard.sonnenburg@t-online.de
Copyright © 2014 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 7 April 2014; revised 3 May 2014; accepted 27 May 2014
ABSTRACT
This paper is devoted to the problem of finding optimized parameter combinations of automotive damper modules. Different cost functions using the amplitude spectrum of the excitation and the frequency response function of the car model will be investigated and it is shown that for three different arbitrary road excitations there exists a parameter combination of top mount stiffness, piston rod mass and damping constant that provides an optimum for the dynamic wheel load fluctuation. The achieved advantage of the optimized damper module regarding the dynamic wheel load fluctuation compared to a simple damper in a two mass vibration system can reach up to 20 percent.
Keywords:
Viscous Damping, Shock Absorber, Top Mount, Ride Comfort, Ride Safety, Vehicle Dynamic, Parameter Optimization

1. Introduction
The problem of finding an optimal damping characteristic for a two mass quarter car model regarding comfort and safety has been solved for synthetic white noise excitations [1] . Comfort and driving safety are measured by the variances of body acceleration and dynamic wheel load fluctuation. Another method to describe the problem of tuning a spring damper combination in a two mass oscillating system is the so-called conflict diagram. The Root Mean Square (RMS) values of the body acceleration are plotted as a function of the RMS-values of the dynamic wheel load fluctuation when the spring stiffness is constant while the damping constant varies and vice versa. The result is a Pareto optimum that indicates that there is no optimal parameter combination for both comfort and safety at the same time [2] .
But there are obviously some problems concerning these characteristics. Firstly white noise similar road excitation is an idealization. There are a lot of different and very special road excitation types that have to be successfully completed by a new vehicle before the tuning process is ended. During the test rides over different road types, different velocity ranges of the characteristic will be examined. The result of the test rides is a usually nonlinear damping characteristic. Secondly in all cases analyzed in literature known to the author never has a damper module been optimized but only a damper in a two-mass quarter-car model. Even actual scientific works regarding the controller design of adaptive suspension systems do not include top mount stiffness and piston rod mass [3] . In reality in absolutely all cases the damper is connected to the vehicle body via the piston rod and spring stiffness, called top mount, which changes the effective damping force a lot [4] [5] . The combination of the damping force element, the piston rod mass and the spring stiffness is called a damper module throughout this paper. It is a generally accepted opinion that the use of a top mount is necessary for comfort reasons, because frequency excitations arising from the damper beyond the resonance frequency of the piston rod mass will be isolated from the body. Excitations of smaller frequency however will be passed to the body. The theory and methods given by [1] [2] do neither consider the top mount nor the piston rod mass. Hence, in everyday practice, no one uses an optimization procedure based on white noise excitation and a simple damper to find a damping characteristic.
The aim of this paper is to find optimal damper module parameter combinations that may serve as a basis for designing realistic nonlinear damping characteristics
2. The Quarter Car Model
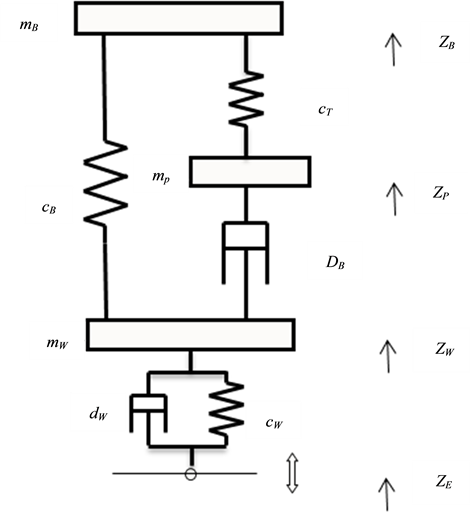
The used car model consists of three masses, the body mass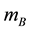 , the wheel mass
, the wheel mass 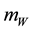 and the piston rod mass
and the piston rod mass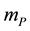 . The complete schema of the model is shown in Figure 1.
. The complete schema of the model is shown in Figure 1.
The damper module comprises the piston rod mass which is connected to the wheel by the body damping force element with the damping constant 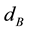 and to the body by the top mount stiffness
and to the body by the top mount stiffness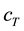 . The system of equations describing the model is:
. The system of equations describing the model is:
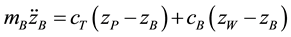 (1)
(1)
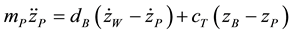 (2)
(2)
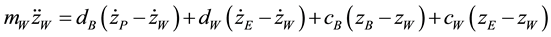 (3)
(3)
Figure 1. Schematic quarter car model.
Using the matrix notation this set of equations can be written as:
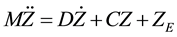 (4)
(4)
where the mass, damping and stiffness matrixes are given by:
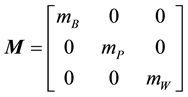
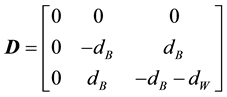
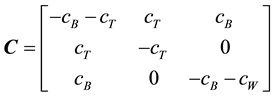
The displacement vectors are of the form:
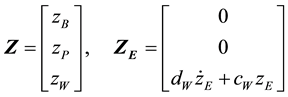
For the calculations the following values have been taken:
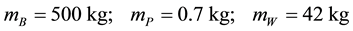
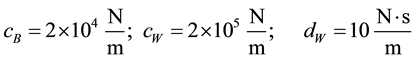
Since the system (1) - (3) is linear Equation (4) can be transformed from the time domain into the frequency domain:
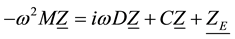
with the corresponding displacement vectors:
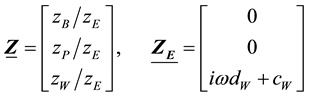
The components of the displacement vector 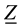
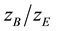
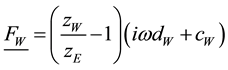
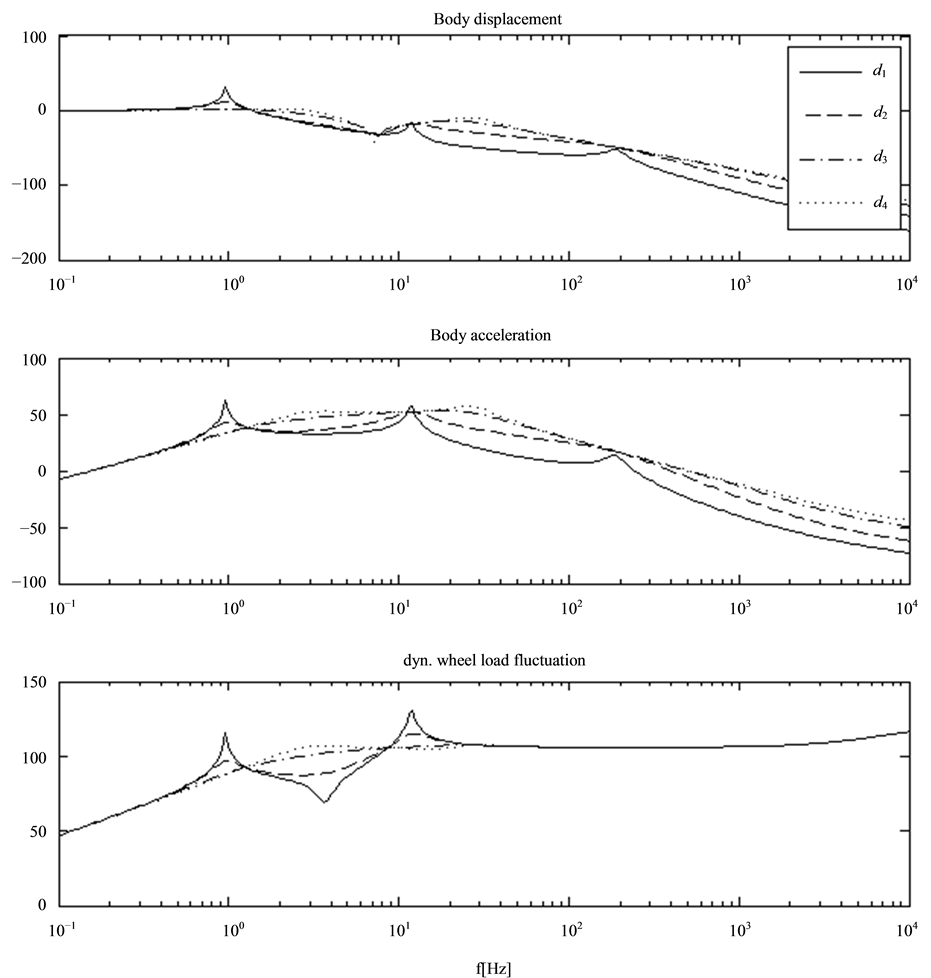
Figure 2 shows frequency response functions for the body displacement, the body acceleration and the dynamic wheel load fluctuation of the system (1) - (3) for different damping constants 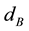
Obviously and well established the dynamic properties of the three mass vibration system are depending strongly on the body damping constant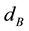
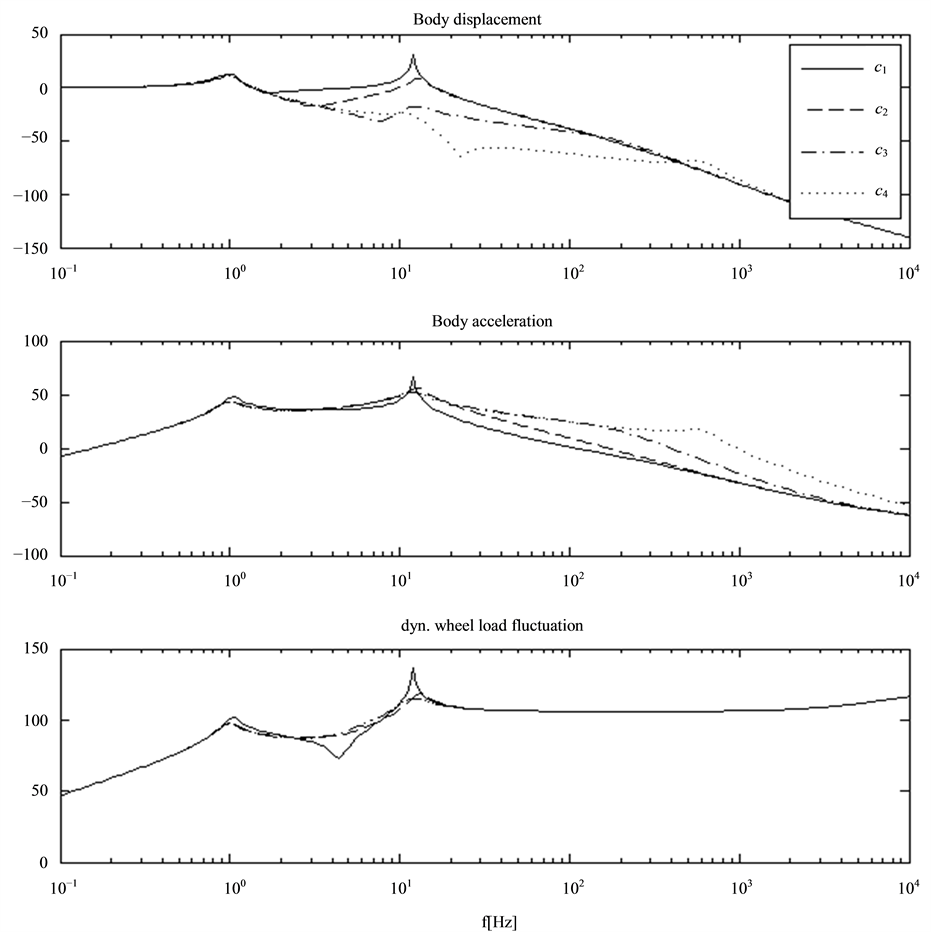
Figure 3 gives the same frequency response functions as in Figure 2 but for different top mount stiffness values 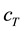
Figure 2. Frequency response function of body displacement (upper graph), body acceleration (center graph) and dynamic wheel load fluctuation (lower graph) for different damping constants dB.
As to expect the top mount stiffness affects the dynamics of the system (1) - (3) remarkably. Even the dynamic wheel load fluctuation depends on the top mount stiffness.
At first sight it seems that the frequency response function of the dynamic wheel load fluctuation is less sensitive to changes of the module parameters than the other displayed functions.
3. The Cost Function
In the automotive industry a common measure for driving comfort and safety are the Root Mean Square (RMS) values of the body acceleration and the dynamic wheel load fluctuation. So called conflict diagrams show the RMS values of the body acceleration over the RMS values of the dynamic wheel load fluctuation for a specific excitation. Hence, the excitation of the system, the body acceleration and the dynamic wheel load fluctuation
Figure 3. Frequency response function of body displacement (upper graph), body acceleration (center graph) and dynamic wheel load fluctuation (lower graph) for different top mount values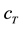
should be somehow combined to a cost function for an optimization procedure.
Another way of defining a cost function may the introduction of the energy of the vibration system (Figure 1) [6] . Depending on the spectral distribution of the excitation amplitude there should be a parameter combination 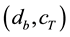
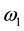
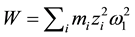
where 
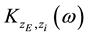
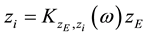
can be seen as a weighting function for the excitation spectrum. To minimize, as an example, the displacements of all masses of a vibrating system it is necessary to sum up all products of the excitation amplitude times the frequency response function of all masses at all frequencies for defined damping constant and top mount stiffness. Doing this for varying damping constants and top mount stiffness values a function of the sum of all displacements in dependence of the damping constant and top mount stiffness is generated. This function will have a minimum. Hence, the minimum condition can be written:
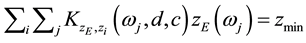
where 
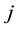
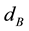
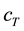
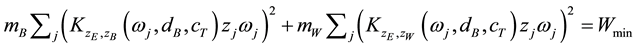
In an analog way the cost functions for the body acceleration:
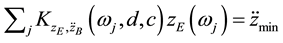
and the dynamic wheel load fluctuation:
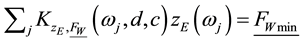
can be defined.
The task than is to find out which of these functions may serve in general to find the best possible parameter combinations of the damper module.
4. The Excitation Functions
Since the defined cost functions contain the amplitude spectrums of the excitation suitable excitation functions have to be found. From the character of the cost function it is clear that optimal parameter combination of the damper module depends on the excitation. In every day practice during the tuning process of a car the responsible tuning personnel chooses roads of different quality on their test sites and change the setting of the damper module until they feel good with the result.
For the optimization in this paper for different road excitations have been chosen, three roads of different kinds and one single event excitation.
The amplitude spectrums of the excitations will be given in the next figures.
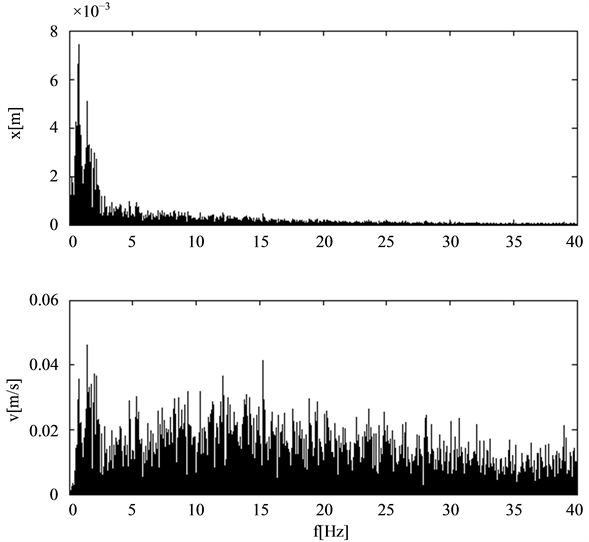
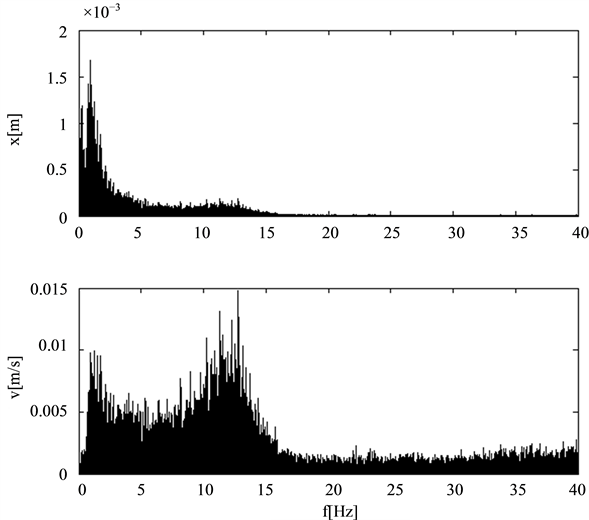
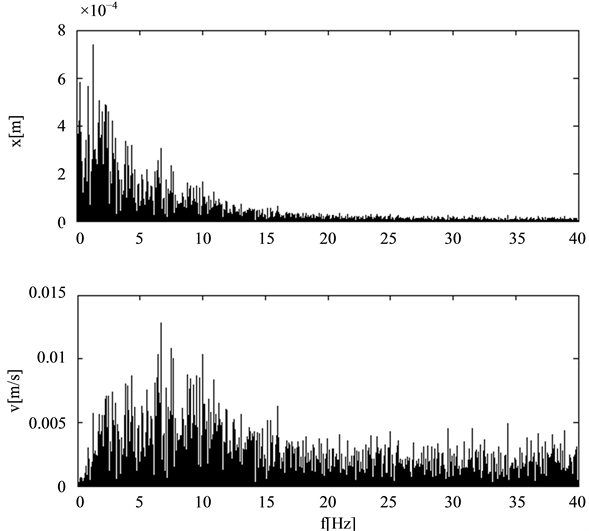
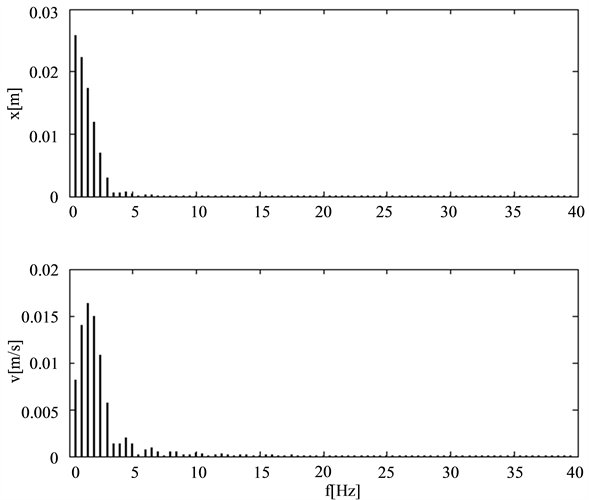
The Figures 4-7 show both the amplitude spectrums of the excitation displacement and velocity since damping forces are velocity dependent. Roads 1 and 2 are rather rough while Road 3 has very good quality.
In the next chapter the cost functions will be analyzed using these excitations.
5. Parameter Optimization
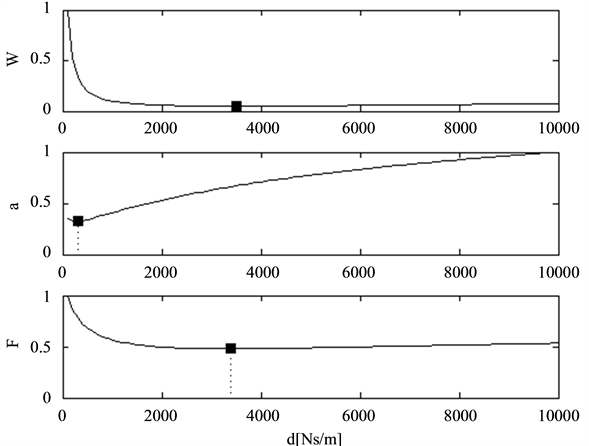
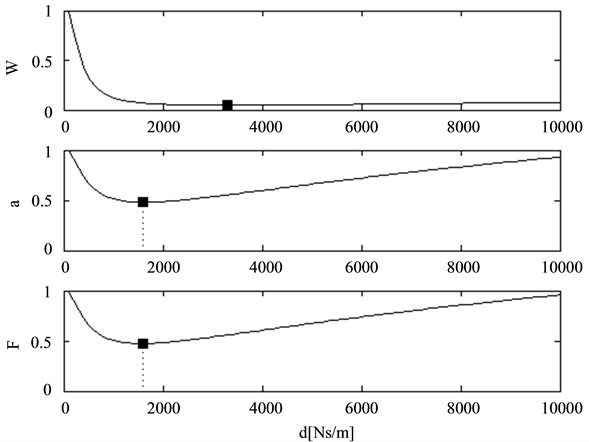
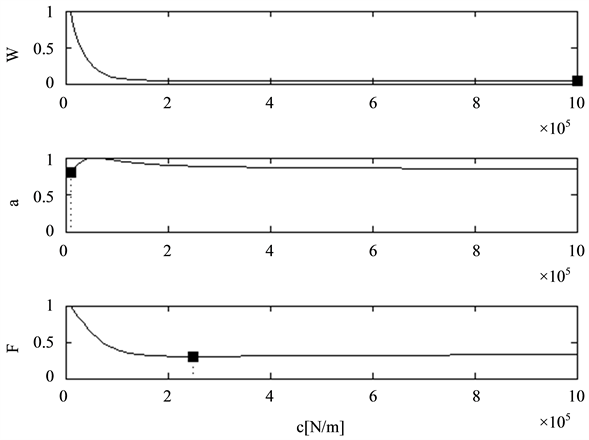
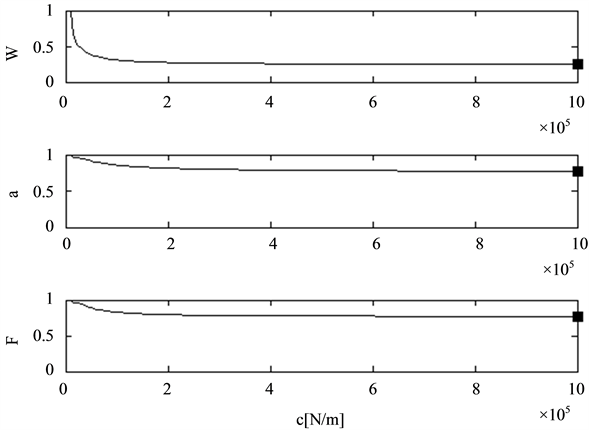
The goal of this chapter is to find a procedure that gives the optimal parameter combination of a damper module in quarter car models. Before applying the two dimensional search for a minimum of the above defined cost functions a preliminary selection will be carried out to show, which of the three targets, system energy, body acceleration or dynamic wheel load fluctuation, may deliver good results. To do this the borders of reasonable values for the body damping constant and the top mount stiffness have to be defined. In Figure 8 the three cost functions are displayed at constant top mount stiffness as a function only of the damping constant
Obviously the body acceleration may not serve as criteria for an optimal damping constant because the body damping constant at the minimum of the cost function is much too small to provide sufficient driving safety, as can be seen from the lower chart of Figure 6. It has to be said that comfort is good, but safety is more important. The damping constant values at the minimum of the cost functions for energy and dynamic wheel load fluctuation are reasonable (by experience) and promising.
Figure 4. Amplitude spectrum Road 1.
Figure 5. Amplitude spectrum Road 2.
The results for the roads 2 and 3 are similar. In case of the speed bump excitation (Figure 9) the minimum values of the damping constants of the body acceleration and the dynamic wheel load fluctuation are close to each other but much smaller than for the energy function.
Next the cost functions dependence on the top mount stiffness will be analyzed. The results for Road 1 are shown in Figure 10.
By experience top mount stiffness values beyond 106 N/m are not realistic. Hence, the energy cost function is
Figure 6. Amplitude spectrum Road 3.
Figure 7. Amplitude spectrum speed bump.
not a suitable candidate for search for optimal damper module parameters. Again, the results for the other road excitation are similar to Road 1 and the speed bump results do not fit in this picture as can be seen from Figure 11.
In case of the speed bump excitation all defined cost functions do not have a minimum value within borders of reasonable top mount stiffness values. Since this excitation may be real, it is not the normal excitation for which chassis are designed. So the speed bump excitation will not be included in the further calculations of this paper.
Figure 8. Normalized cost functions of energy (upper graph), body acceleration (center graph) and dynamic wheel load fluctuation for Road 1 over the body damping constant 
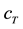
Figure 9. Normalized cost functions of energy (upper graph), body acceleration (center graph) and dynamic wheel load fluctuation for the speed bump over the body damping constant 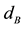
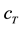
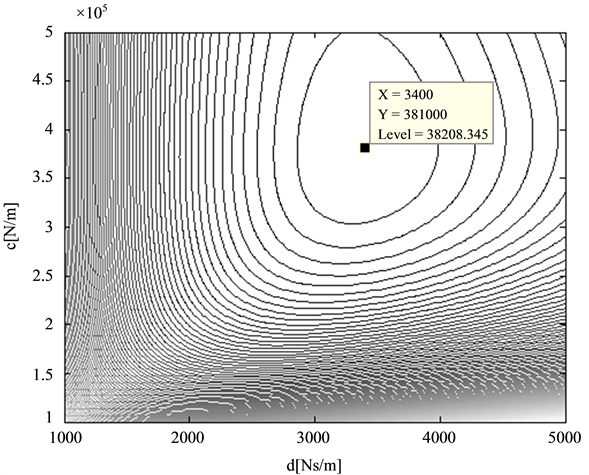
After choosing the dynamic wheel load fluctuation cost function the two dimensional search for a minimum of that function is carried out for all three road excitations. Figure 12 illustrates the two dimensional cost function using Road 1.
The optimal parameter combinations for the three roads are:
Road 1:
Road 2:
Road 3:
Figure 10. Cost functions of energy (upper graph), body acceleration (center graph) and dynamic wheel load fluctuation for Road 1 over the top mount stiffness 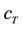
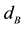
Figure 11. Cost functions of energy (upper graph), body acceleration (center graph) and dynamic wheel load fluctuation for the speed bump over the top mount stiffness 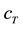
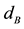
Such top mount stiffness values are typical in passenger cars and the damping constants are normal in the bleed area of the force-velocity characteristic (at small velocities)
It is worth to mention the fact, that the classical so call damping ratio of a vibration system, here:
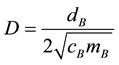
does not include the top mount stiffness. The system behavior depends not only on the damping constant of the
damper but also on the top mount characteristics and the masses of the piston rod. Due to the effects of these additional spring and inertia force elements of the damper module the damping characteristics of the damper itself and the damper module are quite different. The damper as a pure, ideal, viscous force element is a one-to-one function in both linear and nonlinear cases. In contrast the force-velocity characteristic of the damper module shows hysteresis effects which are frequency dependent. The higher the frequency, the larger the hysteresis and smaller the maximum force. In this situation is the force-velocity characteristic different for different frequencies. As a consequence vibrating systems including damper modules are showing dynamic (frequency dependent or frequency selective) behavior and need to be characterized by new dynamic parameters. An example of such a parameter could be the power number of the damper module. Analog to the power number of the damper it is defined by the ratio of the spring power to the damping power of the module (see [4] ).
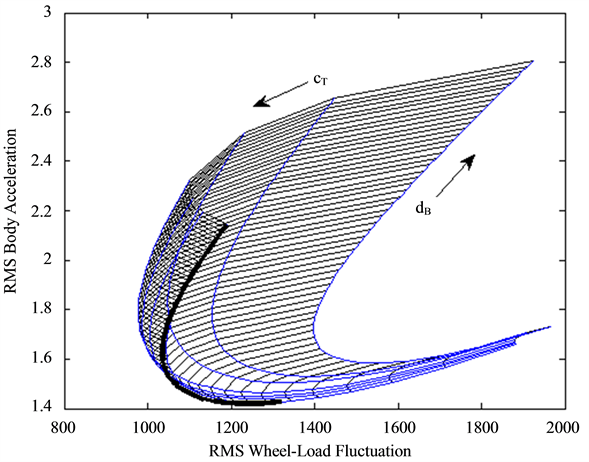
The conflict diagrams in Figure 13, which are widely accepted in the automotive industry, show that the minimum of the RMS values of the dynamic wheel load fluctuation can be found exactly at the calculated optimal parameter combinations.
Interesting to point out, that compared to the pure damper design the comfort level is getting worse when reducing the top mount stiffness. The dynamic wheel load fluctuation in contrast passes an optimum value.
Finally, the damping coefficients calculated by the cost functions may be used to design a nonlinear force- velocity characteristic (if preferred) using the method described in [6] .
6. Conclusions
There are two main conclusions of this paper. Firstly, the inclusion of a conservative force element in the damper module leads to better driving safety and worsens the driving comfort (at least in terms of RMS values). This result is surprising because in the general opinion, the top mount is needed for comfort only. Depending on the excitation, up to 20 percent reduction of the dynamic wheel load fluctuation is possible compared to the use of a pure damper instead of a damper module. In other words the damper module delivers more driving safety at the same comfort level.
Secondly there is a very simple procedure to find the optimum parameter combination of the damper module compared to existing methods. The main problem for the chassis designer is to choose the relevant excitation that meets his expectations how the future car is exploited. But since in today’s tuning process, this problem is solved by test side roads. These roads have to be analyzed regarding their amplitude spectrums and then put into the proposed cost function.
Figure 12. Contour plot of the cost function of the dynamic wheel load fluctuation and Road 1.
Figure 13. Conflict diagram of the RMS values of body acceleration versus dynamic wheel load fluctuation (Road 1). The thick line indicates the use of a pure damper.(The arrows indicate raising values).
The case of the speed bump excitation underlines the problem of the excitation dependence of the best module setting. Not for all excitation, the proposed procedure may deliver satisfying results. It seems however, that these kinds of excitations are not the typical cases. The three investigated arbitrary road excitations are measured roads and may be therefore called typical roads.
References
- Popp, K. and Schielen, W. (1993) Fahrzeugdynamik. Teubner, Stuttgart
- Mitschke, M. And Wallentowitz, H. (2004) Dynamik der Kraftfahrzeuge, VDI Buch. http://dx.doi.org/10.1007/978-3-662-06802-1
- Koch, G.P.A. (2011) Adaptive Control of Mechatronic Vehicle Suspension Systems. Dissertation, Technische Universität München, Munich.
- Sonnenburg, R. and Stretz, A. (2010) Damper Modules with Adapted Stiffness Ratio. Archive of Applied Mechanics, 81, 853-862. http://dx.doi.org/10.1007/s00419-010-0455-2
- Sonnenburg, R. and Stretz, A. (2012) Dynamic Properties of Automotive Damper Modules. Archive of Applied Mechanics, 82, 1795-1804. http://dx.doi.org/10.1007/s00419-012-0627-3
- Sonnenburg, R. (2006) Verfahren zur Dämpfkrafteinstellung bei einem Schwingungsdämpfer. Patentschrift DE 10 2004 021 132 B4, 2006.04.27.