Journal of Signal and Information Processing
Vol. 4 No. 1 (2013) , Article ID: 28296 , 8 pages DOI:10.4236/jsip.2013.41008
Two Blind Adaptive Equalizers Connected in Series for Equalization Performance Improvement
![]()
Department of Electrical and Electronic Engineering, Ariel University of Samaria, Ariel, Israel.
Email: monika.pinchas@gmail.com
Received November 5th, 2012; revised December 6th, 2012; accepted January 4th, 2013
Keywords: Blind Adaptive Equalizers; Blind Adaptive Deconvolution; Equalization Performance; Variable Step-Size
ABSTRACT
A variable step-size parameter is usually used to accelerate the convergence speed of a blind adaptive equalizer with N1 + N2 − 1 coefficients where N1 and N2 are odd values. In this paper we show that improved equalization performance is achieved when using two blind adaptive equalizers connected in series where the first and second blind adaptive equalizer have N1 and N2 coefficients respectively compared with the case where a single blind adaptive equalizer is applied with N1 + N2 − 1 coefficients. It should be pointed out that the same algorithm (cost function) is used for updating the filter taps for the different equalizers and that a fixed step-size parameter is used. Simulation results show that for the low signal to noise ratio (SNR) environment and for the case where the convergence speed is slow due to the channel characteristics, the new method has a faster convergence speed with a factor of approximately two while leaving the system with approximately the same or lower residual intersymbol interference (ISI).
1. Introduction
We consider a blind deconvolution problem in which we observe the output of an unknown, possibly nonminimum phase, linear system (SISO-FIR system) from which we want to recover its input (source) using an adjustable linear filter (equalizer). The problem of blind deconvolution arises comprehensively in various applications such as digital communications, seismic signal processing, speech modeling and synthesis, ultrasonic nondestructive evaluation and image restoration [1]. Blind deconvolution algorithms are essentially adaptive filtering algorithms designed such that they do not require the external supply (training sequence) of a desired response to generate the error signal in the output of the adaptive equalization filter [2,3]. The algorithm itself generates an estimate of the desired response by applying a nonlinear transformation to sequences involved in the adaptation process [2,3]. Let us consider for a moment the digital communication case. During transmission, a source signal undergoes a convolutive distortion between its symbols and the channel impulse response. This distortion is referred to as ISI. Thus, a blind adaptive equalizer is used to remove the convolutive effect of the system to produce the source signal.
In this paper, we consider a blind adaptive equalizer based on a predefined cost function that characterizes the convolutive distortion. Minimizing this cost function with respect to the equalizer parameters will reduce the convolutional error. Minimization is performed with the gradient descent algorithm that searches for an optimal filter tap setting [2]. The equalization performance of such an equalizer depends on the nature of the equalizer (on the predefined cost function), on the system’s filter characteristics, on the added noise, on the step-size parameter used in the adaptation process, on the equalizers tap length (number of coefficients) and on the input signal statistics. Fast convergence speed and reaching a residual ISI where the eye diagram is considered as open (communication case), are the main requirements from a blind adaptive equalizer. Fast convergence speed may be obtained by increasing the step-size parameter. But, increasing the step-size parameter will lead to a higher residual ISI which might not answer anymore on the system’s requirements. In the literature, we may find the variable step-size parameter approach for accelerating the convergence speed, where the step-size parameter is changed during the deconvolution process according to a function involving the equalized output data. The constant modulus algorithm (CMA) or Godard’s algorithm [4] is one of the most widely studied blind equalization algorithm in the literature. Thus, we may find in the literature many variable step-size parameter algorithms ([5-8] to name only few) for the CMA and its variant (Modified Constant Modulus Algorithm (MCMA)).
In this paper, we show another approach for accelerating the convergence speed of a blind adaptive equalizer without using the variable step-size parameter approach and that is applicable not only for the CMA or MCMA algorithm. It should be pointed out, that in the literature we may find other blind adaptive methods such as the WNEW algorithm (derived in [2]) with improved equalization performance compared with the CMA algorithm while having approximately the same computational burden. We show in this paper via simulation results, that two blind adaptive equalizers connected in series where the first and second blind adaptive equalizer have N1 and N2 coefficients respectively and N2 > N1 is much more attractive from the convergence speed point of view than using a single blind adaptive equalizer with N1 + N2 − 1 filter taps. As a matter of fact, simulation results show that the convergence speed of our new proposed system is approximately twice faster compared to a system with a single blind adaptive equalizer while leaving the system with approximately the same residual convolutive distortion level or even with a lower one.
The paper is organized as follows: In Section 2, we describe the system under consideration and present all the relevant details and explanations how to build up efficiently the blind adaptive equalizer with two blind adaptive equalizers connected in series where the first and second blind adaptive equalizer have N1 and N2 coefficients respectively. In Section 3, simulation results are presented and the conclusion is given in Section 4.
2. System Description and Two Blind Adaptive Equalizer Connected in Series
The system under consideration is illustrated in Figure 1, where we make the following assumptions:
1) The input sequence 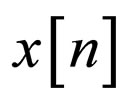 belongs to a constellation input with zero mean.
belongs to a constellation input with zero mean.
2) The unknown SISO system defined as 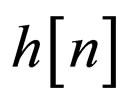 is a possibly nonminimum phase linear time-invariant filter in which the transfer function has no zeros on the unit circle.
is a possibly nonminimum phase linear time-invariant filter in which the transfer function has no zeros on the unit circle.
3) The equalizer  is a tap-delay line.
is a tap-delay line.
4) The noise 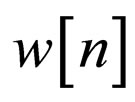 is an additive Gaussian white noise with zero mean and variance
is an additive Gaussian white noise with zero mean and variance  where
where 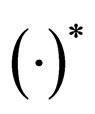 and
and 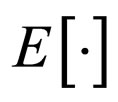 denote the conjugate and expectation operator on
denote the conjugate and expectation operator on  and on
and on 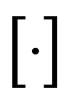 respectively.
respectively.
Comments:
1) In the communication field, the popular constellation inputs, have the property of zero mean. Therefore, many cost functions (and those that are used in this paper) are based on the assumption having a source with zero mean.
2) An adaptive FIR equalizer can be used only if the transfer function of the channel (modeled with a FIR filter) has no zeros on the unit circle.
3) The zeros of the channels' transfer function may be outside the unit circle (nonminimum phase case). Thus, a cost function based on higher order statistics (HOS) is necessary for the equalization process. Second order statistics (SOS) (auto-correlations or power spectra) based methods cannot be used if the channel is nonminimum phase since these methods are blind of the channel, whereas phase information is preserved in statistics of order higher than two. In this paper, we use HOS based cost functions.
4) There are many cases such as the wired case in which the channel is static, namely, does not change in time or almost does not change in time. Thus, the channel may be described as a time-invariant filter. Since we model the channel as a time-invariant FIR filter, the channel coefficients will not vary with time.
5) Assumptions 1 - 4 were also made in many other papers dealing with the blind adaptive equalization problem ([2,9,10] to name a few of them).
The sequence 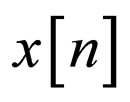 is sent through the system
is sent through the system 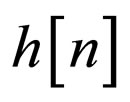 and is corrupted with noise
and is corrupted with noise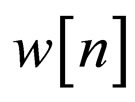 . Therefore, the equalizer’s input sequence
. Therefore, the equalizer’s input sequence 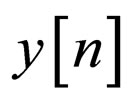 may be written as:
may be written as:
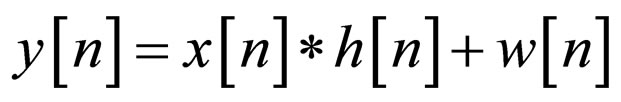 (1)
(1)
where “*” denotes the convolution operation. The equal-

Figure 1. Block diagram of a SISO FIR system with a blind adaptive equalizer.
ized output signal can be written as:
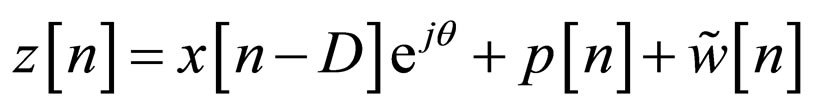 (2)
(2)
where D is a constant delay, 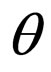 is a constant phase shift,
is a constant phase shift,  is the convolutional noise, namely, the residual convolutive distortion arising from the difference between the ideal equalizer’s coefficients and those chosen in the system and
is the convolutional noise, namely, the residual convolutive distortion arising from the difference between the ideal equalizer’s coefficients and those chosen in the system and . Next we turn to the adaptation mechanism of the equalizer which is based on a predefined cost function
. Next we turn to the adaptation mechanism of the equalizer which is based on a predefined cost function 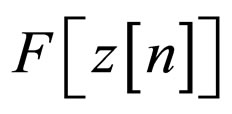 that characterizes the convolutive distortion, see [4,9-12]. Minimizing this
that characterizes the convolutive distortion, see [4,9-12]. Minimizing this  with respect to the equalizer parameters will reduce the convolutional error. Minimization is performed with the gradient descent algorithm that searches for an optimal filter tap setting by moving in the direction of the negative gradient-
with respect to the equalizer parameters will reduce the convolutional error. Minimization is performed with the gradient descent algorithm that searches for an optimal filter tap setting by moving in the direction of the negative gradient- over the surface of the cost function in the equalizer filter tap space [13]. Thus the updated equation is given by [13]:
over the surface of the cost function in the equalizer filter tap space [13]. Thus the updated equation is given by [13]:
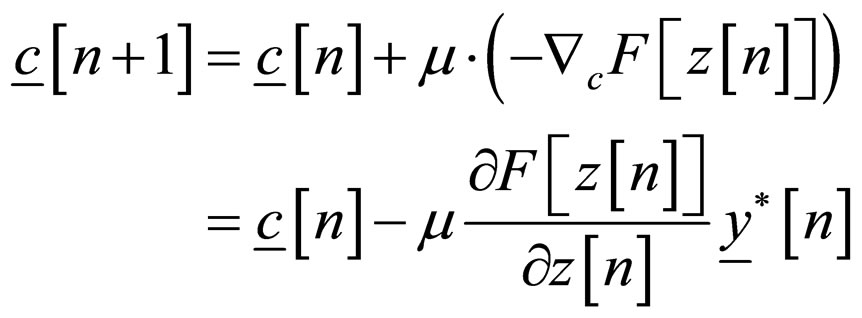 (3)
(3)
where  is the step-size parameter,
is the step-size parameter, 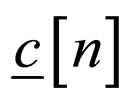 is the equalizer vector where the input vector is
is the equalizer vector where the input vector is  and N is the equalizer's tap length. The operator
and N is the equalizer's tap length. The operator 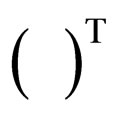 denotes for transpose of the function
denotes for transpose of the function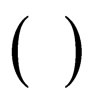 .
.
Next, we turn to describe our new proposed system (Figure 2) with two blind adaptive equalizers connected in series where the first and second blind adaptive equalizer have N1 and N2 coefficients respectively. The input signal to the first blind adaptive equalizer is 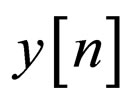 (1). The equalized output from this equalizer, given by
(1). The equalized output from this equalizer, given by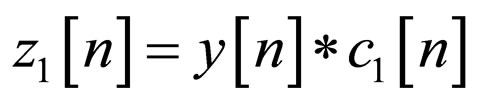 , is then sent to the input of the second blind adaptive equalizer. Thus, the total equalized output signal may be written as:
, is then sent to the input of the second blind adaptive equalizer. Thus, the total equalized output signal may be written as:
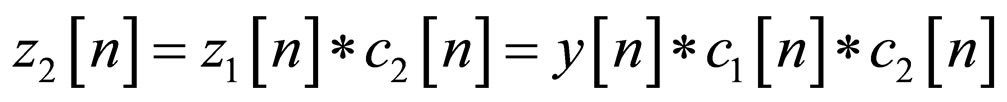 (4)
(4)
The update equations for the first and second blind adaptive equalizer are given by:
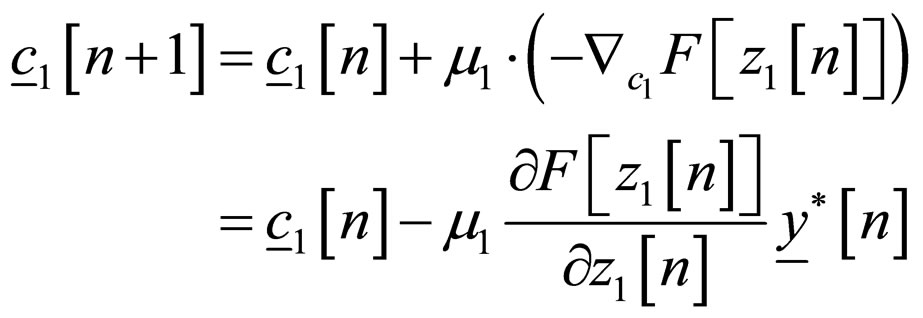 (5)
(5)
 (6)
(6)
where 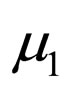 and
and 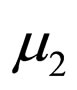 are the step-size parameters. According to [14], the more coefficients in the equalizer, the more “noise” is introduced into the adaptation of each coefficient by the simultaneous adaptation of the other coefficients. Thus, this might be the reason why having a larger convergence speed for higher numbers of coefficients in the equalizer. It should be pointed out, that this was also observed in [15] where higher numbers of coefficients in the equalizer have lead to a longer convergence speed. Obviously, choosing a higher step-size parameter may increase the convergence speed but on the same time it increases also the residual ISI which might not meet any more the system’s requirements. In order to get improved convergence speed, two blind adaptive equalizers connected in series,
are the step-size parameters. According to [14], the more coefficients in the equalizer, the more “noise” is introduced into the adaptation of each coefficient by the simultaneous adaptation of the other coefficients. Thus, this might be the reason why having a larger convergence speed for higher numbers of coefficients in the equalizer. It should be pointed out, that this was also observed in [15] where higher numbers of coefficients in the equalizer have lead to a longer convergence speed. Obviously, choosing a higher step-size parameter may increase the convergence speed but on the same time it increases also the residual ISI which might not meet any more the system’s requirements. In order to get improved convergence speed, two blind adaptive equalizers connected in series, 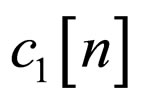 and
and , are used where
, are used where 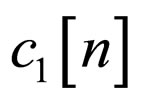 is responsible for getting fast convergence speed (achieved with N1 < N2 < N and
is responsible for getting fast convergence speed (achieved with N1 < N2 < N and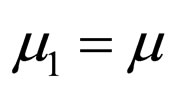 ) and
) and  compensates the high residual ISI left at the output from
compensates the high residual ISI left at the output from  (accomplished by setting
(accomplished by setting ). We may express the two blind adaptive equalizers connected in series as an equivalent filter defined by
). We may express the two blind adaptive equalizers connected in series as an equivalent filter defined by  with N1 + N2 − 1 filter taps. In our proposed system, N = N1 + N2 − 1 where N, N1 and N2 have odd values. In all our cases we have chosen N1 to be approximately half of N,
with N1 + N2 − 1 filter taps. In our proposed system, N = N1 + N2 − 1 where N, N1 and N2 have odd values. In all our cases we have chosen N1 to be approximately half of N, 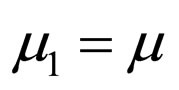 and
and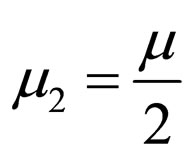 .
.
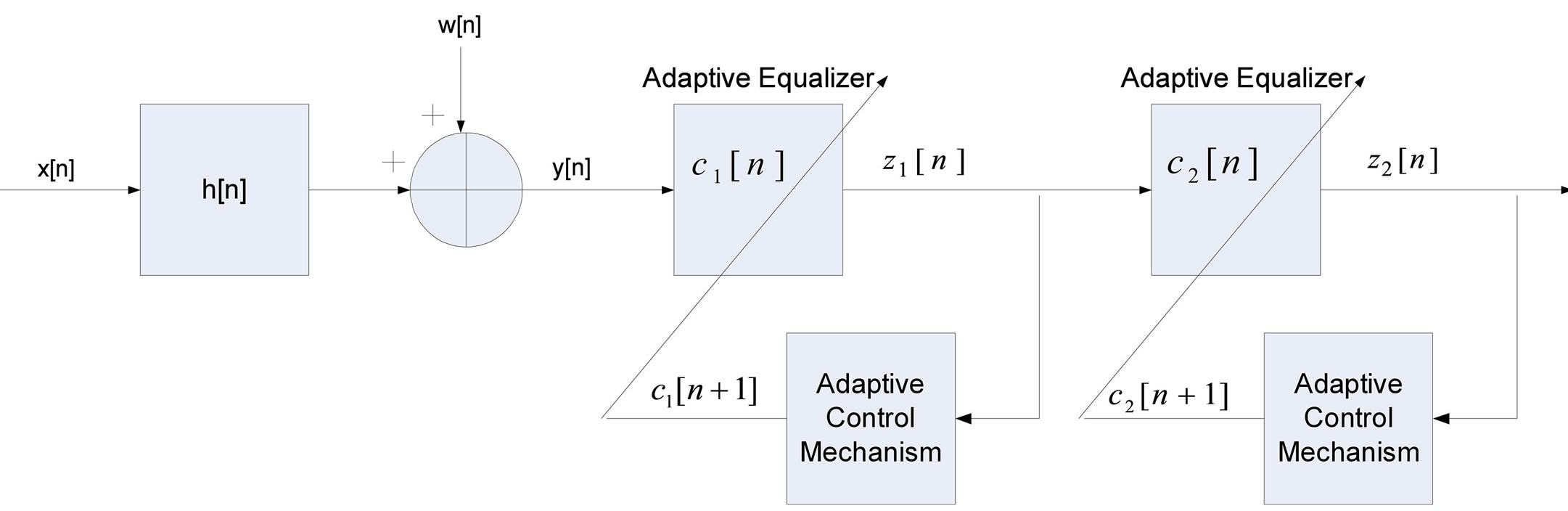
Figure 2. Block diagram of a SISO FIR system with two serial connected blind adaptive equalizers.
3. Simulation
In this section we compare the equalization performance of our new proposed system with two blind adaptive equalizers connected in series with a system using only a single blind adaptive equalizer. For simplicity we used the digital communication case where the the source signal belongs to a 16 QAM (Quadrature Amplitude Modulation-QAM) constellation (a modulation using ±{1, 3} levels for in-phase and quadrature components) and to a 32QAM input (Figure 3). But, in order to show that the new proposed method also works well for other source inputs and not only for those belonging to the digital communication case, we used a third source signal  where the real and imaginary parts of
where the real and imaginary parts of 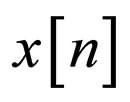 were independently uniformly distributed within
were independently uniformly distributed within . The ISI is often used as a measure of performance in equalizer’s applications, defined by
. The ISI is often used as a measure of performance in equalizer’s applications, defined by
 (7)
(7)
where 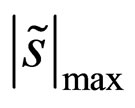 is the component of
is the component of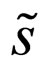 , given in (8), having the maximal absolute value.
, given in (8), having the maximal absolute value.
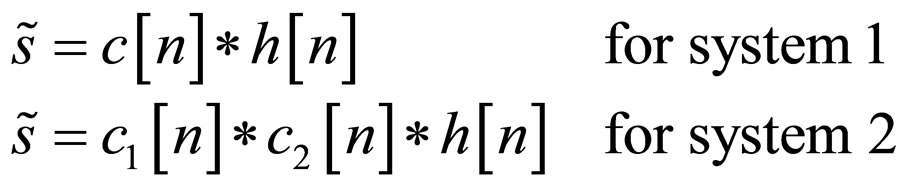 (8)
(8)
where system 1 and system 2 are defined as the system with a single blind adaptive equalizer and the system with two blind adaptive equalizers connected in series respectively. In the following we define  as a channel. Two different channels were considered.
as a channel. Two different channels were considered.
Channel 1 (initial ISI = 0.88): The channel parameters were determined according to:
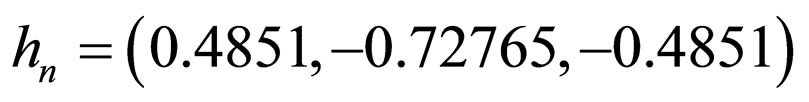 .
.
Channel 2 (initial ISI = 1.402): The channel parameters were determined according to [11]:
 .
.
Figure 3. 32QAM constellation.
As it can be seen, the ISI caused by the chosen channels is very high which means that the initial convolutive distortion level is very high. In our simulation, we used two different predefined cost functions 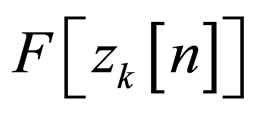 (where
(where 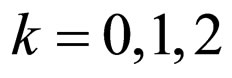 and
and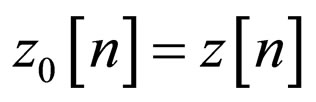 ) in order to show that the new proposed system is not a special case for a specific predefined cost function. Thus, for Godard’s method [4] we have:
) in order to show that the new proposed system is not a special case for a specific predefined cost function. Thus, for Godard’s method [4] we have:
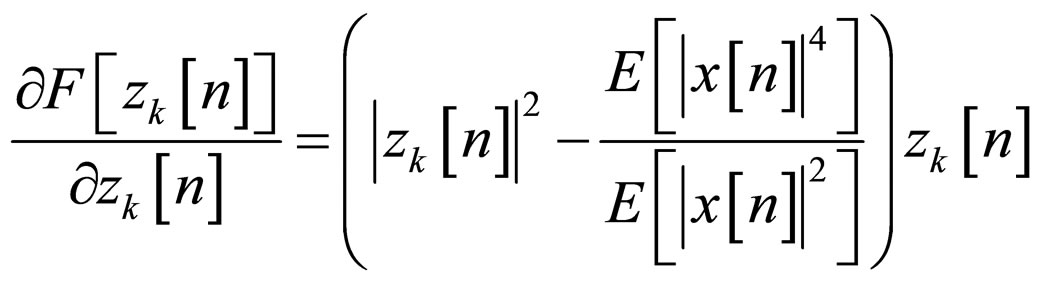 (9)
(9)
while for the WNEW algorithm [2] the function  is defined by:
is defined by:
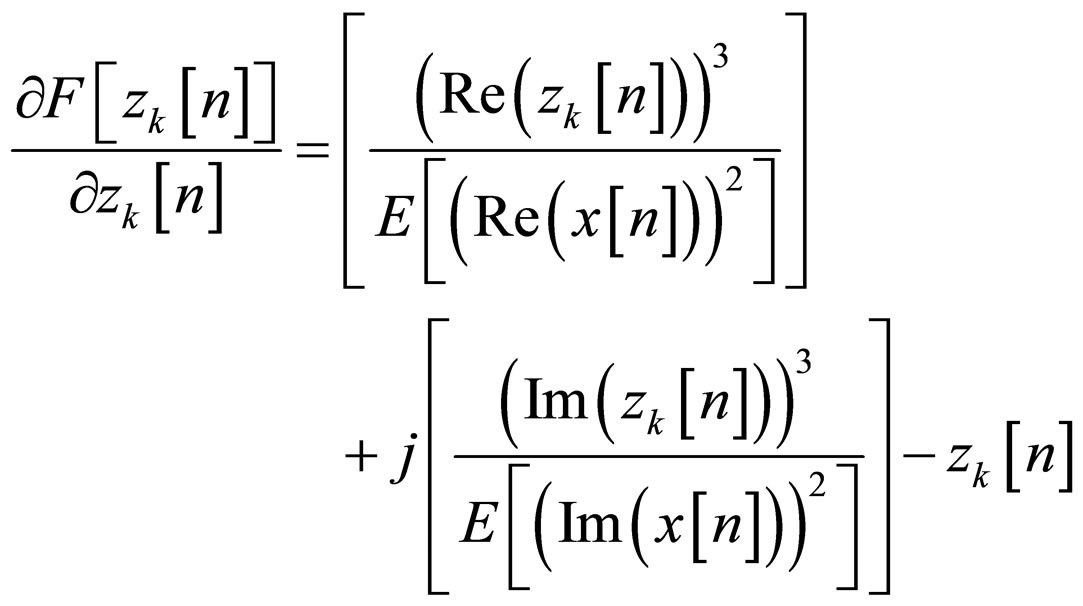 (10)
(10)
where  and
and  are the real and imaginary parts of
are the real and imaginary parts of  respectively. In our simulation, the equalizers were initialized by setting the center tap equal to one and all others to zero. The step-size parameters were chosen for fast convergence with low steady state ISI. The step-size parameters for channel 2 were chosen from [2]. Figures 4-8 show the equalization performance of our new proposed system ( system 2), namely the ISI as a function of iteration number for two different source signals (16QAM and uniformly distributed source) and channels and SNR values of 10 [dB] and 30 [dB], compared with system 1. According to Figures 4 and 8, both obtained with SNR = 10 [dB], the equalization performance improvement is seen in the residual ISI (improvement of approximately 2 [dB]) as well as in the convergence speed (the convergence speed is faster than a factor of two). According to Figures 6 and 7, both obtained with SNR = 30 [dB], the equalization performance improvement is seen in the convergence speed (the convergence speed is approximately faster by a factor of two) while the residual ISI is approximately the same. Please note that the two curves for the ISI as a function of iteration number obtained in Figures 6 and 7 intersect in the long term. This means that in long term, a slightly better residual ISI is obtained with system I over system 2. But, this is of no significance since the main purpose of a blind adaptive equalizer is to reach as fast as possible a residual ISI where the eye diagram is considered as open.
respectively. In our simulation, the equalizers were initialized by setting the center tap equal to one and all others to zero. The step-size parameters were chosen for fast convergence with low steady state ISI. The step-size parameters for channel 2 were chosen from [2]. Figures 4-8 show the equalization performance of our new proposed system ( system 2), namely the ISI as a function of iteration number for two different source signals (16QAM and uniformly distributed source) and channels and SNR values of 10 [dB] and 30 [dB], compared with system 1. According to Figures 4 and 8, both obtained with SNR = 10 [dB], the equalization performance improvement is seen in the residual ISI (improvement of approximately 2 [dB]) as well as in the convergence speed (the convergence speed is faster than a factor of two). According to Figures 6 and 7, both obtained with SNR = 30 [dB], the equalization performance improvement is seen in the convergence speed (the convergence speed is approximately faster by a factor of two) while the residual ISI is approximately the same. Please note that the two curves for the ISI as a function of iteration number obtained in Figures 6 and 7 intersect in the long term. This means that in long term, a slightly better residual ISI is obtained with system I over system 2. But, this is of no significance since the main purpose of a blind adaptive equalizer is to reach as fast as possible a residual ISI where the eye diagram is considered as open.
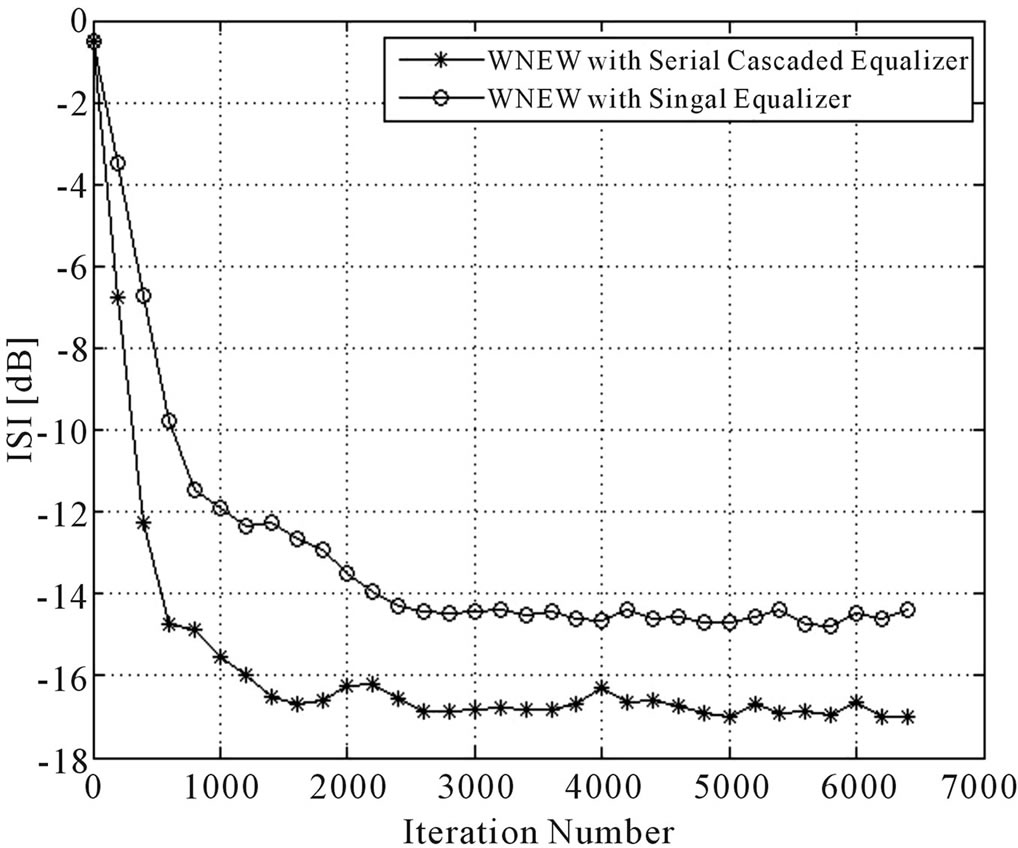
Figure 4. Equalization performance comparison between the system with a single blind adaptive equalizer and the system with two blind adaptive equalizers connected in series. In both cases we used a 16QAM source input going through channel 1 and the WNEW algorithm. The averaged results were obtained in 100 Monte Carlo trials for SNR = 10 dB. We set N = 11, N1 = 5, N2 = 7, μ = μ1 = 0.001 and μ2 = 0.0005.
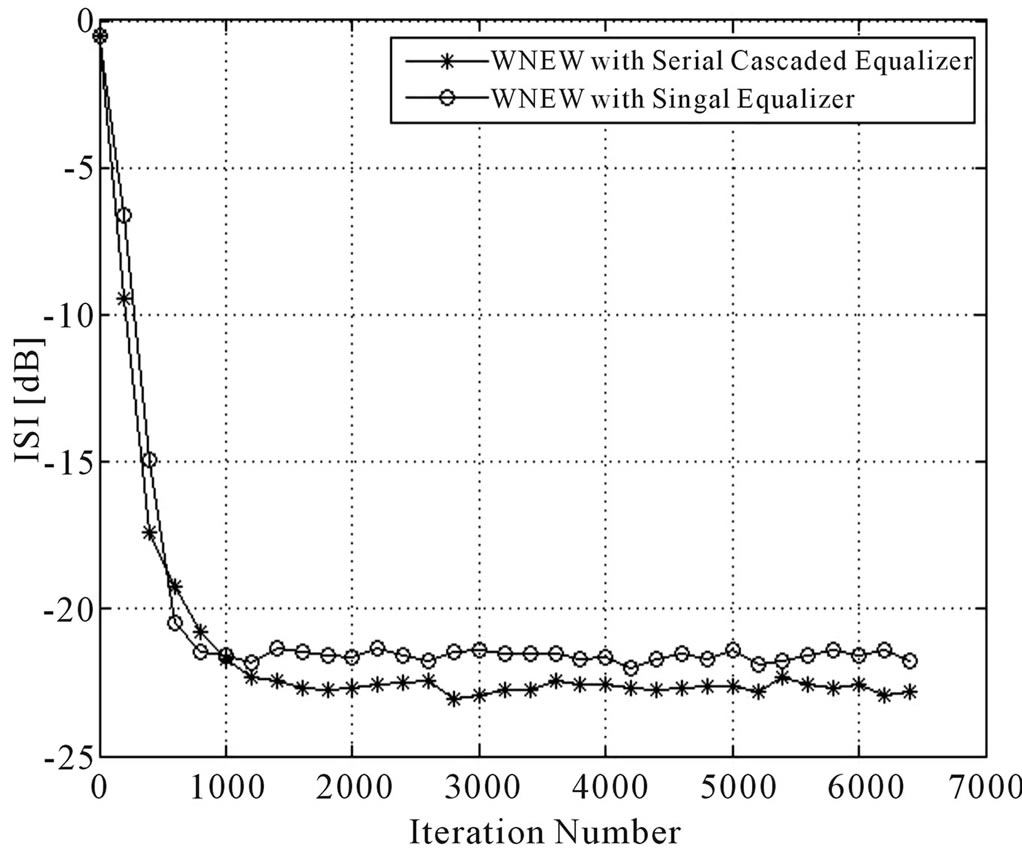
Figure 5. Equalization performance comparison between the system with a single blind adaptive equalizer and the system with two blind adaptive equalizers connected in series. In both cases we used a 16QAM source input going through channel 1 and the WNEW algorithm. The averaged results were obtained in 100 Monte Carlo trials for SNR = 30 dB. We set N = 11, N1 = 5, N2 = 7, μ = μ1 = 0.001 and μ2 = 0.0005.
When this occurs, the equalized output is driven to a DFE (decision feedback equalizer) for further equalization improvement. In our case (Figures 6 and 7), the eye diagram is considered as already open when the residual ISI is less than –15 [dB]. According to Figures 6 - 7 the residual ISI for both systems (1 and 2) is much lower

Figure 6. Equalization performance comparison between the system with a single blind adaptive equalizer and the system with two blind adaptive equalizers connected in series. In both cases we used a 16QAM source input going through channel 2 and the WNEW algorithm. The averaged results were obtained in 100 Monte Carlo trials for SNR = 30 dB. We set N = 21, N1 = 9, N2 = 13, μ = μ1 = 0.0002 andμ2 = 0.0001.

Figure 7. Equalization performance comparison between the system with a single blind adaptive equalizer and the system with two blind adaptive equalizers connected in series. In both cases we used a 16QAM source input going through channel 2 and the Godard algorithm. The averaged results were obtained in 100 Monte Carlo trials for SNR = 30 dB. We set N = 21, N1 = 9, N2 = 13, μ = μ1 = 0.00001 and μ2 = 0.000005.
than –15 [dB] when the equalizer has converged. According to Figure 5, obtained with SNR = 30 [dB], the equalization performance improvement is seen only slightly in the residual ISI. Up to now, we have used a source signal where the x and y-axis of the signal are independent. Next we turn to a source signal (the 32QAM
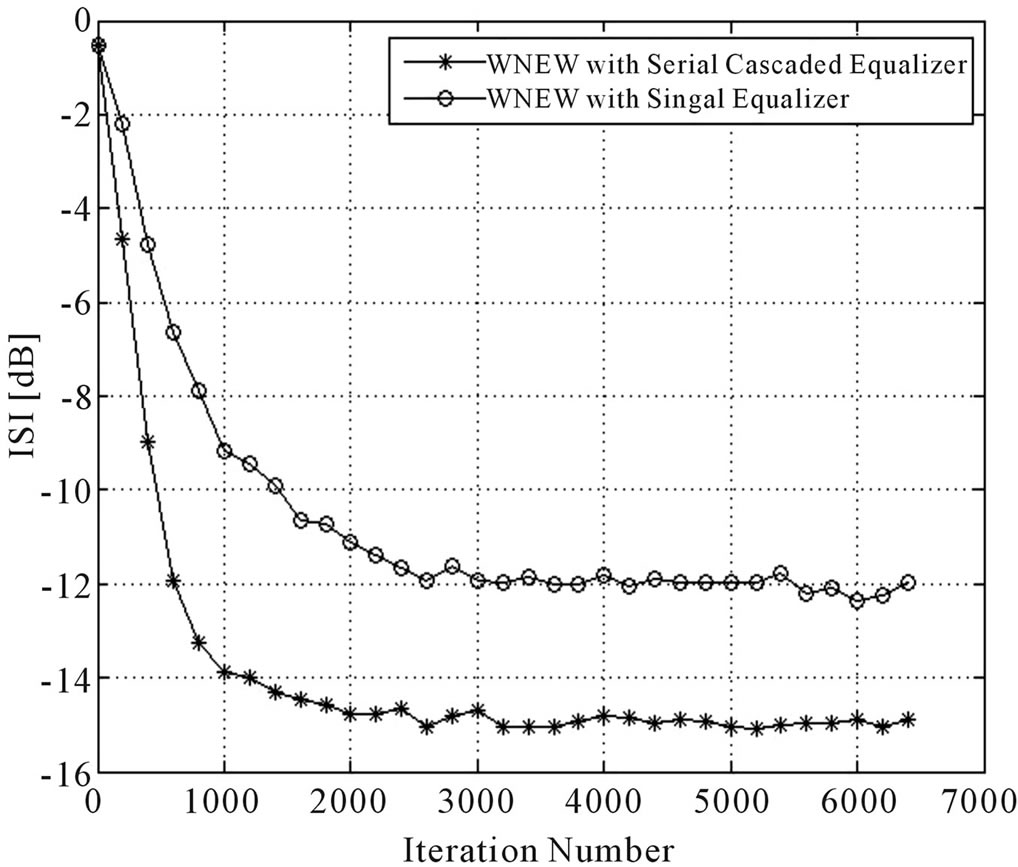
Figure 8. Equalization performance comparison between the system with a single blind adaptive equalizer and the system with two blind adaptive equalizers connected in series. In both cases we used a source signal x[n] where the real and imaginary parts of x[n] were independently uniformly distributed within [−4, +4]. For both cases, the source input was sent through channel 1 and the WNEW algorithm was used. The averaged results were obtained in 200 Monte Carlo trials for SNR = 10 dB. We set N = 11, N1 = 5, N2 = 7, μ = μ1 = 0.001 and μ2 = 0.0005.
case) where the x and y-axis of the signal are dependent. Figure 9 shows the equalization performance of our new proposed system (system 2), namely the ISI as a function of iteration number for the 32QAM input case, channel 1 and SNR = 10 [dB], compared with system 1. According to Figure 9, the equalization performance improvement is seen in the residual ISI as well as in the convergence speed. According to simulation results we may say that the equalization performance improvement is obtained in the low SNR environment as well as in the case where the convergence speed of the deconvolution process of a single blind adaptive equalizer is very long.
The simulation results for the two serial cascaded adaptive equalizers made us wonder whether it is possible to get further equalization performance improvement by using three serial cascaded adaptive equalizers. Figure 10 shows the equalization performance comparison, namely, the ISI as a function of iteration number between a system with two serial cascaded blind adaptive equalizers and a system with three blind adaptive equalizers connected in series for the 16QAM source input, channel 2 and SNR = 30 [dB]. According to Figure 10, improved equalization performance is obtained from the convergence speed point of view with the three serial cascaded blind adaptive equalizers compared with the system with two blind adaptive equalizers connected in series. Next, we compare a system using two serial cascaded blind adaptive equalizers with a system using three blind adap-
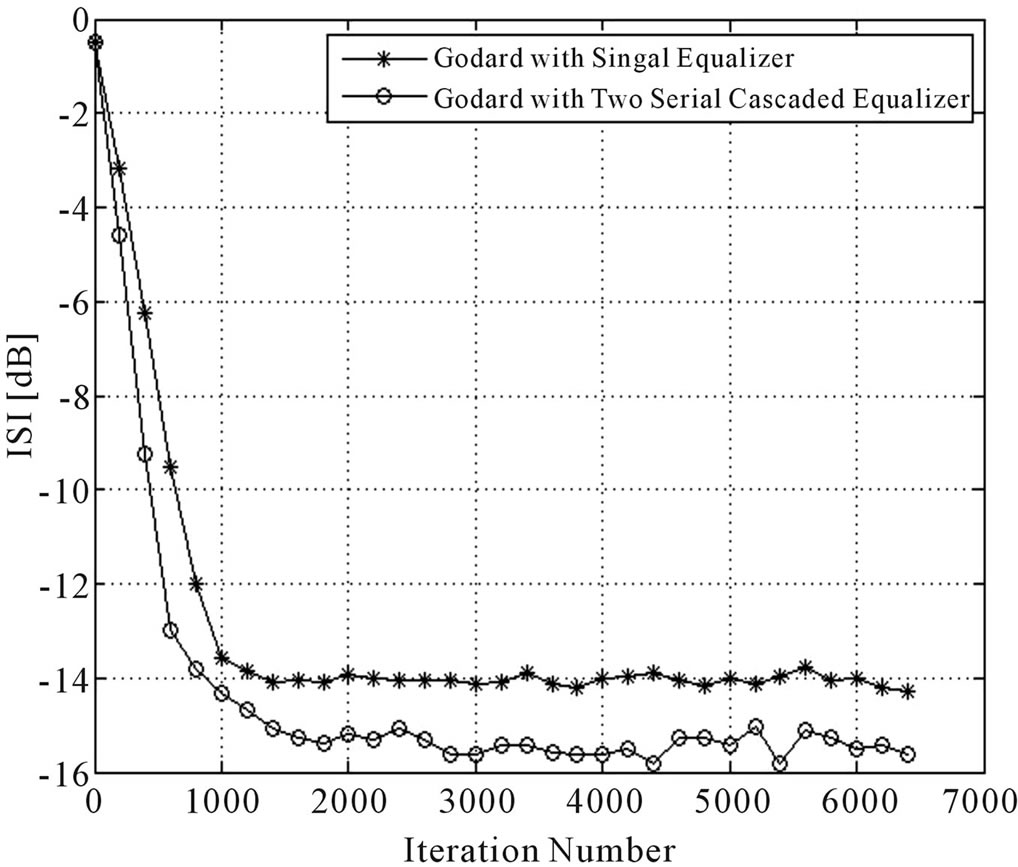
Figure 9. Equalization performance comparison between the system with a single blind adaptive equalizer and the system with two blind adaptive equalizers connected in series. In both cases we used a 32QAM source input going through channel 1 and the Godard algorithm. The averaged results were obtained in 100 Monte Carlo trials for SNR = 10 dB. We set N = 11, N1 = 5, N2 = 7, μ = μ1 = 0.00002 and μ2 = 0.00001.

Figure 10. Equalization performance comparison between the system with two serial cascaded blind adaptive equalizer and the system with three blind adaptive equalizers connected in series. In both cases we used a 16QAM source input going through channel 2 and the WNEW algorithm. The averaged results were obtained in 50 Monte Carlo trials for SNR = 30 dB. We set N1 = 9, N2 = 13, μ1 = 0.0002 and μ2 = 0.0001 for the two serial cascaded equalizer, N1 = 3, N2 = 7, N3 = 13, μ1 = 0.0002,  and
and 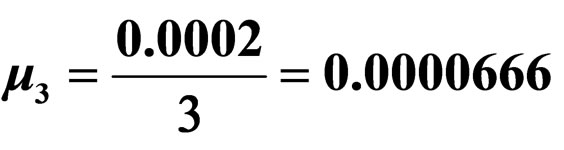 for the three serial cascaded equalizer.
for the three serial cascaded equalizer.
tive equalizers connected in series for the 16QAM source input, channel1 and SNR = 10 [dB]. Let us denote 6 cases:
Case1: A system with three serial cascaded adaptive equalizers with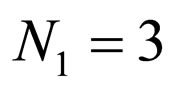 ,
, 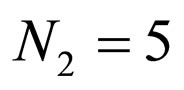 ,
, 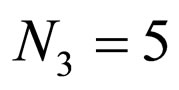 ,
, 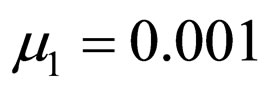 ,
,
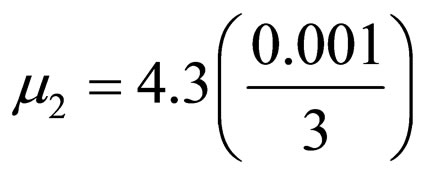 and
and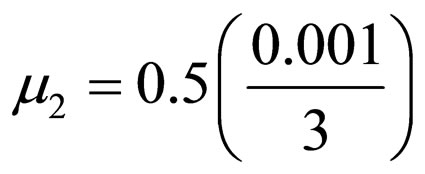 .
.
Case 2: A system with three serial cascaded adaptive equalizers with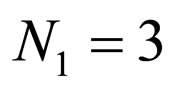 ,
, 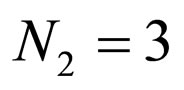 ,
, 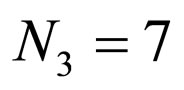 ,
, 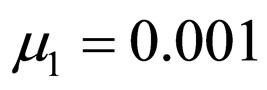 ,
,
 and
and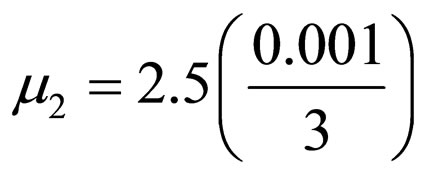 .
.
Case 3: A system with three serial cascaded adaptive equalizers with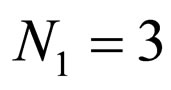 ,
,  ,
, 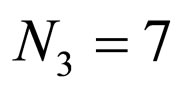 ,
, 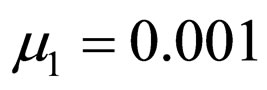 ,
,
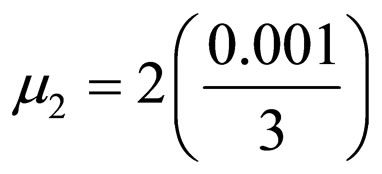 and
and .
.
Case 4: A system with three serial cascaded adaptive equalizers with ,
, 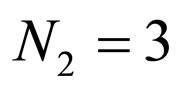 ,
, 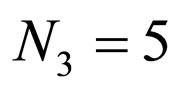 ,
, 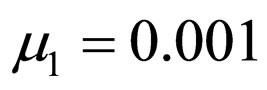 ,
,
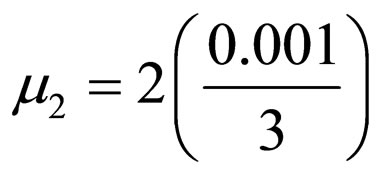 and
and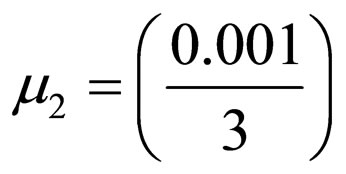 .
.
Case 5: A system with three serial cascaded adaptive equalizers with ,
,  ,
, 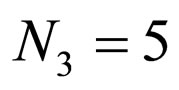 ,
, 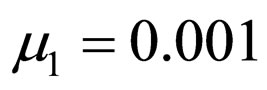 ,
,
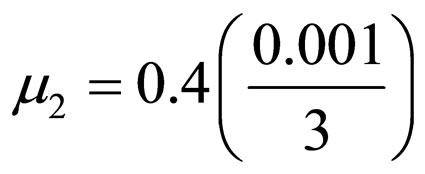 and
and .
.
Case 6: A system with two serial cascaded adaptive equalizers with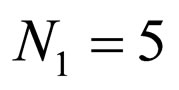 ,
, 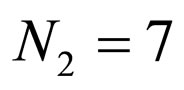 ,
, 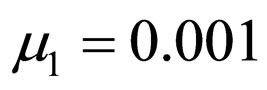 and
and 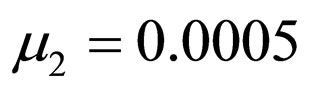 .
.
Figure 11 shows the equalization performance comparison, namely, the ISI as a function of iteration number between the system with two serial cascaded blind adap-

Figure 11. Equalization performance comparison between the system with two serial cascaded blind adaptive equalizer and several systems with three blind adaptive equalizers connected in series. In all cases we used a 16QAM source input going through channel 1 and the WNEW algorithm. The averaged results were obtained in 100 Monte Carlo trials for SNR = 10 dB.
tive equalizers named as Case 6 and a system with three blind adaptive equalizers connected in series (with five different cases named as Cases 1-5) for the 16QAM source input, channel 1 and SNR = 10 [dB]. According to Figure 11, the best equalization performance is obtained for Case 6. In other words, for channel 1, SNR = 10 [dB] and 16QAM source input, the best equalization performance is obtained with two serial cascaded blind adaptive equalizers and not with a system using three blind adaptive equalizers connected in series.
4. Conclusion
In this paper, we have shown another promising approach for accelerating the convergence speed of a blind adaptive equalizer with N1 + N2 − 1 coefficients (where N1 and N2 are odd values) that does not use the variable step-size parameter approach and that is applicable not only for the CMA or MCMA algorithm. We have shown that a system with two blind adaptive equalizers connected in series where the first and second blind adaptive equalizer have N1 and N2 (N1 < N2) coefficients respectively achieves improved equalization performance compared with the case where a single blind adaptive equalizer is applied with N1 + N2 − 1 coefficients. It should be pointed out that the same algorithm (cost function) was used for updating the filter taps for the different equalizers. Thus, the equalization performance improvement of the blind adaptive equalizer was not achieved due to a better cost function. The equalization performance improvement was mainly seen in the convergence speed which was found to be approximately faster by a factor of two for the low SNR environment as well as in the case where the convergence speed of the deconvolution process of a single blind adaptive equalizer is very long. Since the new approach used fixed step-size parameters, it might be possible that further equalization performance improvement may be obtained if instead for the fixed step-size parameter we use the variable step-size parameter approach. But, this is beyond this paper.
5. Acknowledgements
I would like to thank the anonymous reviewers for their helpful comments.
REFERENCES
- C. Feng and C. Chi, “Performance of Cumulant Based Inverse Filters for Blind Deconvolution,” IEEE Transaction on Signal Processing, Vol. 47, No. 7, 1999, pp. 1922-1936. doi:10.1109/78.771041
- M. Pinchas and B. Z. Bobrovsky, “A Maximum Entropy Approach for Blind Deconvolution,” Signal Processing (Eurasip), Vol. 86, No. 10, 2006, pp. 2913-2931. doi:10.1016/j.sigpro.2005.12.009
- C. L. Nikias and A. P. Petropulu, “Higher-Order Spectra Analysis a Nonlinear Signal Processing Framework,” Chapter 9, Prentice-Hall, Upper Saddle River, 1993, pp. 419-425.
- D. N. Godard, “Self Recovering Equalization and Carrier Tracking in Two-Dimenional Data Communication System,” IEEE Transactions on Commications, Vol. 28, No. 11, 1980, pp. 1867-1875. doi:10.1109/TCOM.1980.1094608
- M. A. Demir and A. Ozen, “A Novel Variable Step Size Adjustment Method Based on Autocorrelation of Error Signal for the Constant Modulus Blind Equalization Algorithm,” Radioengineering, Vol. 21, No. 1, 2012, pp. 37-45.
- R. Hamzehyan, R. Dianat and N. C. Shirazi, “New Variable Step-Size Blind Equalization Based on Modified Constant Modulus Algorithm,” International Journal of Machine Learning and Computing, Vol. 2, No. 1, 2012, pp. 30-34.
- X. Zhang, L. S. Li, D. F. Zhuo and Z. S. Dong, “A New Adaptive Step-Size Blind Equalization Based on Autocorrelation of Error Signal,” 7th International Conference on Signal Processing, Beijing, 31 August-4 September 2004, pp. 1719-1722.
- L. Y. Zhang, L. Chen and Y. S. Sun, “Variable Step-Size CMA Blind Equalization Based on Non-Linear Function of Error Signal,” International Conference on Communications and Mobile Computing, Kunming, 6-8 January 2009, pp. 396-399.
- M. Lazaro, I. Santamaria, D. Erdogmus, K. E. Hild, C. Pantaleon and J. C. Principe, “Stochastic Blind Equalization Based on pdf Fitting Using Parzen Estimator,” IEEE Trans. on Signal Processing, Vol. 53, No. 2, 2005, pp. 696-704. doi:10.1109/TSP.2004.840767
- O. Shalvi and E. Weinstein, “New Criteria for Blind Deconvolution of Nonminimum Phase Systems (Channels),” IEEE Transactions on Information Theory, Vol. 36, No. 2, 1990, pp. 312-321. doi:10.1109/18.52478
- M. Pinchas, “A MSE Optimized Polynomial Equalizer for 16QAM and 64QAM Constellation,” Signal, Image and Video Processing, Vol. 5, No. 1, 2011, pp. 29-37. doi:10.1007/s11760-009-0138-z
- G.-H. Im, C. J. Park and H. C. Won, “A Blind Equalization with the Sign Algorithm for Broadband Access,” IEEE Communication Letters, Vol. 5, No. 2, 2001, pp. 70-72. doi:10.1109/4234.905939
- A. K. Nandi, “Blind Estimation Using Higher-Order Statistics,” Chapter 2, Kluwer Academic, Boston, 1999, pp. 78-79.
- E. A. Lee and D. G. Messerschmitt, “Adaptive Equalization,” In: E. A. Lee and D. G. Messerschmitt, Eds., Digital Communication, 2nd Edition, Kluwer Academic Publisher, Boston, 1997.
- M. Pinchas, “A Closed Approximated Formed Expression for the Achievable Residual Intersymbol Interference Obtained by Blind Equalizers,” Signal Processing Journal (Eurasip), Vol. 90, No. 6, 2010, pp. 1940-1962. doi:10.1016/j.sigpro.2009.12.014

