Journal of Signal and Information Processing
Vol. 3 No. 3 (2012) , Article ID: 22127 , 8 pages DOI:10.4236/jsip.2012.33044
Design of Sharp 2D Multiplier-Less Circularly Symmetric FIR Filter Using Harmony Search Algorithm and Frequency Transformation
![]()
Department of Electronics and Communication Engineering, National Institute of Technology, Calicut, Kerala, India.
Email: manju.manuel@gmail.com, elizabeth@nitc.a.c.in
Received March 31st, 2012; revised April 29th, 2012; accepted May 11th, 2012
Keywords: Two Dimensional Filter; Frequency Response Masking; Harmony Search Algorithm; T1 and T2 Transformations; Canonic Signed Digit Representation
ABSTRACT
In this paper, we present a novel and efficient method for the design of a sharp, two dimensional (2D) wideband, circularly symmetric, FIR filter. First of all, a sharp one dimensional (1D) infinite precision FIR filter is designed using the Frequency Response Masking (FRM) technique. This filter is converted into a multiplier-less filter by representing it in the Canonic Signed Digit (CSD) space. The design of the FRM filter in the CSD space calls for the use of a discrete optimization technique. To this end, a new optimization approach is proposed using a modified Harmony Search Algorithm (HSA). HSA is modified in such a way that, in every exploitation and exploration phase, the candidate solutions turns out to be integers. The 1D FRM multiplier-less filter, is in turn transformed to the 2D equivalent using the recently proposed multiplier-less transformations namely, T1 and T2. These transformations are successful in generating circular contours even for wideband filters. Since multipliers are the most power consuming elements in a 2D filter, the multiplier-less realization calls for reduced power consumption as well as computation time. Significant reduction in the computational complexity and computation time are the highlights of our proposed design technique. Besides, the proposed discrete optimization using modified HSA can be used to solve optimization problems in other engineering disciplines, where the search space consists of integers.
1. Introduction
Frequency Response Masking (FRM) is a much acclaimed technique to synthesize sharp linear phase 1D FIR filters with sparse coefficients [1]. The prominent feature of this approach is that the sparse filter coefficients results in fewer number of multipliers and better saving of power. This enormous computational saving by this approach compared to the traditional mini-max approach has resulted in the deployment of the FRM technique in a wide variety of applications like software defined radio, array beam-forming, filter-banks, FPGA implementations etc [2]. The computational complexity can be brought down further, if the coefficients of the FRM filter are represented in the SPT space [3]. Regarding the implementation of a digital filter, since multipliers are the most computationally intensive blocks, replacing them by shifters and adders will result in the saving of the computation time as well as chip area. It is also known that if subtractions are also used to carry out multiplication, the number of SPT terms can further be minimized as in the case of the Canonic Signed Digit Representation [4].
Direct rounding of the filter coefficients to the CSD space, causes degradation in the filter performance. This necessitates the use of a suitable optimization technique filter in the discrete space with the required specifications. Since the search space is discrete, the conventional gradient based approaches cannot be employed. In this context, the meta-heuristic optimization algorithm is a good alternative, since it is capable of generating optimal solutions in a multimodal, multidimensional search space. A multiplier-less FRM FIR filter was designed in the CSD space using the Genetic Algorithm (GA) in [3]. Besides, GA was used to design a 2D filter in [5]. The problem associated with GA is the slow convergence speed [6]. Genetic algorithm was modified in [7] and used for the design of 1D FRM FIR filter. But enormous computational time was required for this approach. Therefore, we propose an efficient technique for the design of FRM filter in the CSD space using the modified Harmony Search Algorithm with reduced computation time as well as good performance [8]. Harmony Search algorithm has been modified in such a way that in the course of optimization, the candidate solutions turn out to be integers and efficient exploration and exploitation of the search space are done. This discrete optimization can be used in other engineering fields also for integer programming Yet another contribution of our work is a novel design approach to obtain the 2D sharp circularly symmetric, zero-phase FIR filter which is totally multiplier-less. This is accomplished by extending the FRM based 1D multiplier-less filter to the 2D scenario using the very recently proposed T1 and T2 transformations [9]. T1 and T2 transformations are capable of generating circular contours even for wideband 2D filters which is not possible in traditional McClellan transformation. Since T1 and T2 transformations are fully multiplier-less, the resulting 2D filter synthezised using the proposed approach is also multiplier-less. The computation time of the 2D filter is significantly reduced since the contour mapping problem is avoided. Besides, the efficient implementation of McClellan transformation permits the design of the 2D filter with significant reduction in the computational complexity compared to other 2D filter design methods. The use of FRM for the design of the 1D filter as well as its implementation in the CSD space also adds to the reduction in computational complexity. In short, reduced computation time and reduced complexity are the highlights of our proposed design technique. Since the proposed design approach results in a sharp 2D filter, it can be deployed in applications where a response, which is very close to that of the ideal filter is required.
The paper is organized as follows. Section 2 describes the Frequency Response Masking approach for the design of sharp FIR filter. A brief introduction of the Harmony Search Algorithm is given in Section 3. T1 and T2 transformations are briefed in Section 4. The proposed design of the 1D FRM filter in the CSD space using the modified HSA algorithm is discussed in Section 5. Section 6 describes the proposed design of the 2D circularly symmetric sharp filter. In Section 7, the results are discussed and the conclusions are presented in Section 8.
2. Frequency Response Masking Approach
Frequency Response Masking is a very good technique for the design of an arbitrary bandwidth sharp FIR filter with reduced computational complexity [1]. Efficient hardware implementation of the filter designed using FRM is possible due to the large number of zero-valued coefficients. It consists of a prototype filter Ha(z), complimentary filter Hc(z), masking filter Hma(z) and a complimentary masking filter Hmc(z). The complimentary filter Hc(z) can be realized by subtracting the outputof the low pass filter Ha(z) from the delay block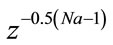 , provided, the model filters are FIR in nature. The block diagram of the FRM filter is shown in Figure 1.
, provided, the model filters are FIR in nature. The block diagram of the FRM filter is shown in Figure 1.
The overall transfer function of the FRM filter can be written as follows.
 (1)
(1)
The prototype filter, also called the band edge shaping filter, is interpolated by a factor M and therefore its transition width is reduced by a factor of M. The masking filters are used to retain the necessary spectrum repetitions for the formation of any arbitrary bandwidth filter under consideration.
3. Harmony Search Algorithm
Inspired by the music improvisation scheme, the Harmony Search Algorithm (HSA) [8] was introduced for the optimization of mathematical problems and was used in various scientific applications [10,11]. A promising aspect of HSA is that it does not demand the objective function to be differentiable, continuous or linear. Here the musicians are identified with the decision variables and the harmonies correspond to the solutions. Analogous to the population initialization in GA, a Harmony Memory (HM) is initialized, where the variables in a solution resemble different musical notes. Similar to the way in which, the musicians improve the harmonies for getting better aesthetics, the HS algorithm explores the search space for finding the candidate solutions with good fitness values. Aesthetics is analogous to the fitness function and the pitch range denotes the range of values of the optimization variable. A new solution is generated in the improvisation process in the HS using any of the three alternatives.
1) Choosing any one value from the Harmony Memory (Memory Consideration);
2) Choosing an adjacent value from the Harmony Memory (Pitch Adjustment);
3) Choosing a totally random value from the possible value range (Random Selection).
The three rules in HS algorithm are effectively directed using two parameters, namely, the harmony memory

Figure 1. Frequency response masking filter.
considering rate (HMCR) and the pitch adjusting rate (PAR). If after the improvisation process, the new harmony is better than the existing worst harmony in the HM, the new harmony is included in the HM and the worst harmony is excluded from the HM. This process is called the updation of harmony memory. The harmony improvisation and updation of the harmony memory are repeated until the termination criteria is satisfied.
4. T1 and T2 Transformations
The frequency response of the 2D filter designed using McClellan transformation [12] is given below.
![]() (2)
(2)
In the above equation, Tn(x) refers to the nth order Chebyshev polynomial in x. a(n) is defined as given below
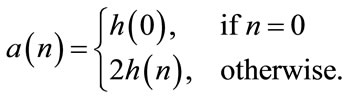 (3)
(3)
Here, h(n) represents the impulse response coefficients of the 1D prototype filter. The first order McClellan transformation for obtaining circular contours is given below.
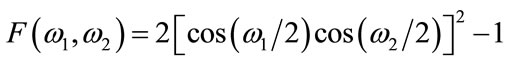 (4)
(4)
T1 and T2 transformations [9] were proposed by Liu and Tai (2011) to design circularly symmetric, 2D wideband filters with an objective to avoid the drawback of the traditional McClellan transformation generating squarish contours at wide cutoff radius of the 2D filter. These multiplier-less transformations were based on the kth order McClellan transformation. The kth order McClellan transformation [12] is given below.
 (5)
(5)
4.1. T1 Transformation
A cascading term was introduced in the kth order McClellan transformation term to improve the circularity of contours at wider cutoff radius. The cascading term 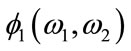 for the T1 transformation [9] is briefed below.
for the T1 transformation [9] is briefed below.
 (6)
(6)
With this modification, the T1 transformation is described below.
 (7)
(7)
Taylor’s Series expansion and binomial series were used to find out the frequency mapping of the T1 transformation. The mapping, i.e., the relationship between the 1D frequency Ω and the 2D radius ω at low frequency is obtained as
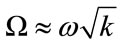 (8)
(8)
Using the above expression it is also shown that the relationship of the transition width of the 1D filter to that of the 2D filter is the same as in Equation (8). The reduced transition width of the 1D filter brings forth lesser order for the 1D prototype filter and hence lesser computational complexity at low frequencies.
4.2. T2 Transformation
Regarding the T2 transformation [9], the cascading term 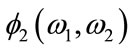 is briefed below.
is briefed below.
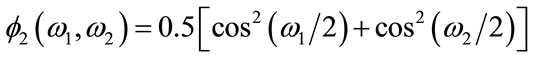 (9)
(9)
With this modification, the T2 transformation is described as
 (10)
(10)
The frequency mapping of the T2 transformation, i.e. the relationship between the 1D frequency and the 2D frequency is obtained as
![]() (11)
(11)
A prominent feature of the T1 and T2 transformations is that they are multiplier-less. Hence the complexity in terms of the number of multipliers of the 2D filter will be only due to that of the 1D prototype filter. However the contour approximation error of these transformations is more at lower radius of the 2D filter compared to the McClellan transformation. In those applications were, the power dissipation and chip area are to be minimum, the complexity of the 1D filter has to be minimized further. Towards this, we propose a multiplier-less design of the 1D filter, which will lead to a 2D filter which is totally multiplier-less.
5. Proposed Design of the 1D Multiplier-Less FRM FIR Filter
The initial part of this work consists of the design of an infinite precision FRM FIR low pass filter. To obtain the 2D filter by using frequency transformation, the 1D prototype filter should have linear phase. The conditions as outlined in [13] have been used in our design to obtain the 1D filter using the FRM approach with linear phase. The various sub-filters have been designed using the Remez Exchange Algorithm. The optimal interpolation factor M was chosen such that the total number of multipliers of the sub-filters and therefore the computational complexity become minimum.
Direct rounding of this continuous filter to the CSD space with restricted SPT terms calls for the degradation in the frequency response. Hence a suitable optimization technique is required to obtain the multiplier-less filter.
5.1. Statement of the Problem
The design of the FRM filter in the CSD space is modelled as a discrete optimization problem as done in [14]. Since the design of the multiplier-less FRM filter is a sort of approximation problem, the objective function is defined as the L2-norm of the error of approximation. The objective function for this optimization problem is given below.
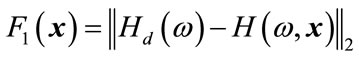 (12)
(12)
where 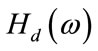 is the zero phase frequency response of the infinite precision FRM filter and
is the zero phase frequency response of the infinite precision FRM filter and  is the zero phase frequency response, of the multiplier-less FRM filter. x is the design vector constituted by concatenating the filter coefficients of the sub-filters of the FRM filter. To reduce the number of SPT terms in the CSD equivalents, a constraint has also been added to the optimization problem as
is the zero phase frequency response, of the multiplier-less FRM filter. x is the design vector constituted by concatenating the filter coefficients of the sub-filters of the FRM filter. To reduce the number of SPT terms in the CSD equivalents, a constraint has also been added to the optimization problem as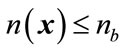 , where
, where  denotes the average number of non-zero SPT coefficients after optimization and nb is the upper bound of
denotes the average number of non-zero SPT coefficients after optimization and nb is the upper bound of . Here the constraint is included in the optimization problem using the penalty method. The constraint is included in the objective function as
. Here the constraint is included in the optimization problem using the penalty method. The constraint is included in the objective function as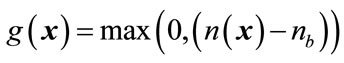 . In this case, variable number of SPT terms have been used for the synthesis of the optimum FRM filter. This allocation has a definite advantage over the CSD approximation using fixed number of SPT terms for each filter coefficient as pointed out in [15]. The implementation cost can be brought down if minimum number of SPT terms is used. Hence for designing the FRM filter, computational complexity has also been included other than the approximation accuracy. In short, the final objective function for the coefficient synthesis of the discrete FRM filter is given below.
. In this case, variable number of SPT terms have been used for the synthesis of the optimum FRM filter. This allocation has a definite advantage over the CSD approximation using fixed number of SPT terms for each filter coefficient as pointed out in [15]. The implementation cost can be brought down if minimum number of SPT terms is used. Hence for designing the FRM filter, computational complexity has also been included other than the approximation accuracy. In short, the final objective function for the coefficient synthesis of the discrete FRM filter is given below.
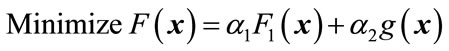
α1 and α2 can be defined according to the relative importance to be attached with each term of the objective function.
5.2. Encoding of the Optimization Variables
An appropriate encoding of the filter coefficients is needed to design the FRM FIR filter in the CSD space. Canonic Signed Digit representation is a typical SPT form where a binary number contains the fewest number of non-zero bits [4]. The features are as follows.
1) It is a minimal representation.
2) It has a unique SPT representation for a given decimal input.
3) It is a ternary system.
4) No two consecutive bits are nonzero.
5) An N bit CSD number cannot have more than 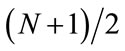 non-zero bits, often fewer.
non-zero bits, often fewer.
We make use of the CSD encoding used in [14]. To this end, first of all, a look up table with four fields are created. The four fields are index, CSD numbers, decimal equivalents and the number of nonzero SPT terms. A 14 bit CSD representation is used for a given decimal number with 12 bits for the fractional part and 2 bits for the integer part. Here also, we adopt the joint optimization of the various sub-filters, i.e., the coefficients of the sub-filters Ha(z), Hma(z) and Hmc(z) are concatenated together to form the candidate vector for the optimization problem. Since the sub-filters are assumed to be linear phase filters, the number of optimization variables can be further reduced by extracting only half of the symmetrical filter coefficients of each sub-filter. In order to represent the filter coefficients in the CSD space, they are encoded as the signed indices of the look up table locations of the nearest decimal number. If the decimal filter coefficient is negative, then it is encoded as the negative of the index of the location of its positive counterpart. Such an encoding is quite useful such that the dimension of the candidate solution has been brought down significantly as compared to that in [7]. Through this procedure, the running time of the optimization is minimized. Classical gradient based optimization techniques cannot be deployed in our problem since the search space consists of integers. So, we adopt an optimization based on meta-heuristic approaches which can be properly tuned to obtain the optimal solutions.
5.3. Proposed Modified HS Algorithm for CSD Based Coefficient Synthesis of FRM Filter
Harmony Search Algorithm uses a random search instead of a gradient search in the exploration phase of the optimization [16]. We have modified the HS algorithm so that it is suitable for the discrete optimization problem. A typical harmony vector is formed by concatenating the CSD encoded coefficients of the sub-filters of FRM filter. Exploiting the symmetry property of the sub-filters which are linear phase, only half the number of the filter coefficients are needed. The various control parameters namely, Harmony Memory Size (HMS), Harmony Memory Considering Rate (HMCR) and Pitch Adjusting Rate (PAR) are initialized. The various steps are briefed below.
5.3.1. Initialization of Harmony Memory
The various solutions are generated by perturbing the initial harmony vector. In order to begin with a wider search space, where the probability of obtaining good quality solutions are more, the initial number of Harmony memory locations are taken to be an integer multiple of the number of memory locations (HMS) being used in the subsequent exploration and exploitation phase of the optimization. A typical harmony vector at the kth location of the harmonic memory can be represented as follows.
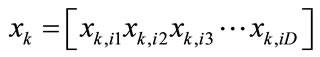
“D” is the dimension of the harmony vector which is equal to the number of optimization variables. In our problem, it corresponds to the total number of filter coefficients of the sub-filters of the FRM filter. xk,i represents a typical CSD encoded filter coefficient.
5.3.2. Prioritized Enlisting of Harmony Memory Locations
Prioritized Enlisting can bring forth promising solutions in the search process. The fitness function of the harmony vectors in the initialization process, are evaluated and the best solutions are passed over to the subsequent stages of optimization. In our problem, since the approximation error is taken as the objective function and the optimization problem is modeled as a minimization one, the candidate solution with less error are selected. The number of these prioritized solutions is taken to be “HMS”.
5.3.3. Harmony Improvisation
A new harmony vector, i.e., a new encoded filter coefficient vector is generated from the HM, based on memory considerations, pitch adjustments, and random selection. These three rules in HS algorithm are effectively directed using two parameters, namely, the harmony memory considering rate (HMCR) and the pitch adjusting rate (PAR) and the procedure works as follows.
for all decision variables  do
do
• Memory Consideration Select the value of the ith parameter of the vector in the harmony memory with probability HMCR

with a probability HMCR.
• Pitch Adjustment Adjust this value slightly with probability PAR. The change is made as follows
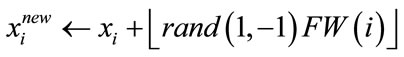
with a probabilityPAR  denotes rounding to the lower value. This modification ensures that the new candidate solutions also turn out to be integers. Thus the encoding of the filter coefficients are not affected. FW(i) is an arbitrary distance bandwidth for the ith design variable, and rand(1, −1) is a uniformly distributed random number between −1 and 1.
denotes rounding to the lower value. This modification ensures that the new candidate solutions also turn out to be integers. Thus the encoding of the filter coefficients are not affected. FW(i) is an arbitrary distance bandwidth for the ith design variable, and rand(1, −1) is a uniformly distributed random number between −1 and 1.
• Random Selection Generate a random value for this filter coefficient with a probability (1-HMCR)
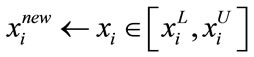
where 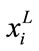 and
and 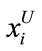 denote the lower bound and upper bound of the variable xi respectively
denote the lower bound and upper bound of the variable xi respectively
• Verification It has to be ensured that any encoded filter coefficient undergoing the modification in the Harmony improvisation phase, confirms to the boundaries of the CSD lookup table(vlb and vub). Hence the following step is performed.
if 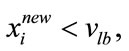 then
then 
if 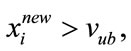 then
then 
end for
Even after harmony improvisation, the candidate solution confirms to legitimate CSD codes, which avoids the use of restoration algorithms.
5.3.4. Memory Update
The fitness function is evaluated for the new harmony vector![]() . If it is better, than the worst harmony in Harmony Memory, in terms of fitness function, then the new harmony is included in HM and the worst harmony is excluded from HM.
. If it is better, than the worst harmony in Harmony Memory, in terms of fitness function, then the new harmony is included in HM and the worst harmony is excluded from HM.
5.3.5. Termination
Termination is achieved either when the approximation error becomes less than the tolerance specified or a prespecified number of iterations are reached. Otherwise, steps 5.3.3 and 5.3.4 are repeated. Once convergence is reached, the best harmony vector is taken from the HM and decoded to get the optimal FRM filter in the CSD space. If the CSD encoding and decoding are avoided and the initial harmony vector is taken to be integers, this modified optimization technique can be used for integer programming in other engineering disciplines also.
6. Proposed Design of the Sharp, Circularly Symmetric, 2D Multiplier-Less Filter
From the design specifications of the 2D filter, the band edges of the 1D filter are obtained. Using these band edges, the infinite precision FRM filter is designed. Then, the 1D multiplier-less FRM filter is designed using the proposed modified HS algorithm briefed in Section 5. Once the 1D multiplier-less filter is obtained, T1 or T2 transformation is applied to obtain the required 2D multiplier-less circularly symmetric filter. The advantage of the above 2D filter design is that without any additional computations, the 2D filter can be directly obtained by applying the transformations to the 1D prototype filter. The efficient realization of the 2D filter using T1 or T2 transformations [12] is shown in Figure 2. In our proposed design, the
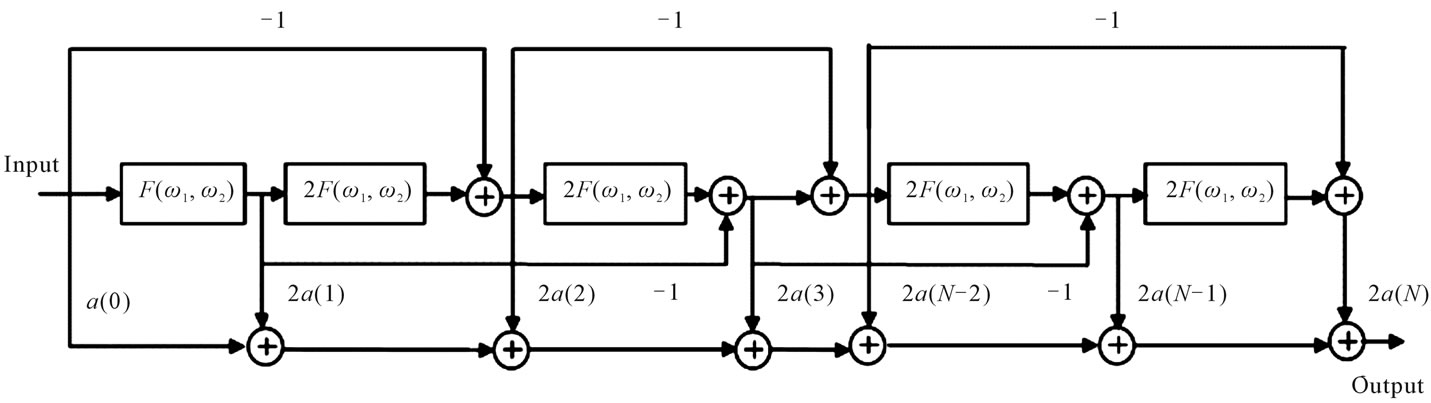
Figure 2. Efficient realization of the 2D filter.
coefficients  of the 1D filter shown in the realization are represented in the CSD space.
of the 1D filter shown in the realization are represented in the CSD space.
The resulting 2D filter is computationally efficient. The reasons for the reduction in the computational complexity are many fold. One of the factors that contributes to the reduction in the complexity is the use of the sparse coefficients obtained using FRM technique. Yet another reason is the multiplier-less realization of the 1D filter. A 2D filter obtained by T1 or T2 transformation require multipliers whose total number is proportional to N while that using direct convolution requires N2 multipliers per output value for an N × N 2D filter. Here, each multiplier is replaced by add and shift operations. The computation time of the resulting 2D filter is also low. This is because, an analytical expression is available for the T1 and T2 transformations and therefore the contour mapping problem is avoided. Yet another reason for reduction in computation time is that the signed integer encoding of the filter coefficients permits the reduction in the running time of optimization of the 1D filter.
7. Results and Discussions
Simulation was performed on a Dual Core AMD Opteron processor operating at 3 GHz using MATLAB 7.10.0. The proposed design technique has been applied to the design of a sharp 2D, circularly symmetric, FIR filter whose specifications are given below.
 (13)
(13)
Here 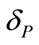 = 0.01 and
= 0.01 and 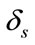 = 0.01. The band edges of the 1D prototype filter were found out from the 2D filter specifications, using T1 transformation. The band edges were found to be [0.7944π 0.8013π]. First of all, the continuous coefficient 1D prototype filter was designed. The length of the various subfilters Ha(z), Hma(z) and Hmc(z) are 89, 37 and 33 respectively.
= 0.01. The band edges of the 1D prototype filter were found out from the 2D filter specifications, using T1 transformation. The band edges were found to be [0.7944π 0.8013π]. First of all, the continuous coefficient 1D prototype filter was designed. The length of the various subfilters Ha(z), Hma(z) and Hmc(z) are 89, 37 and 33 respectively.
The 1D multiplier-less filter was designed using the proposed HS algorithm. The parameters of the HS algorithm used are shown in Table 1. The parameter values have been selected based on the performance of the optimization algorithm. nb was selected to be 3.
The magnitude response of continuous coefficient 1D FRM filter is shown in Figure 3, and that of the discrete 1D filter FRM filter using the proposed optimization using modified HSA is shown in Figure 4.
The performance results of the FRM filter designed using the proposed method has been compared with the infinite precision filter and the CSD rounded filter and is shown in Table 2. This result is the best out of 10 runs of the HS algorithm. The running time of the proposed optimization is very low compared to the novel GA in [7]. The magnitude response and the contour plot of the 2D filter designed with the proposed approach using T1 transformation are shown in Figure 5 and Figure 6 and

Table 1. Parameters of HS algorithm.
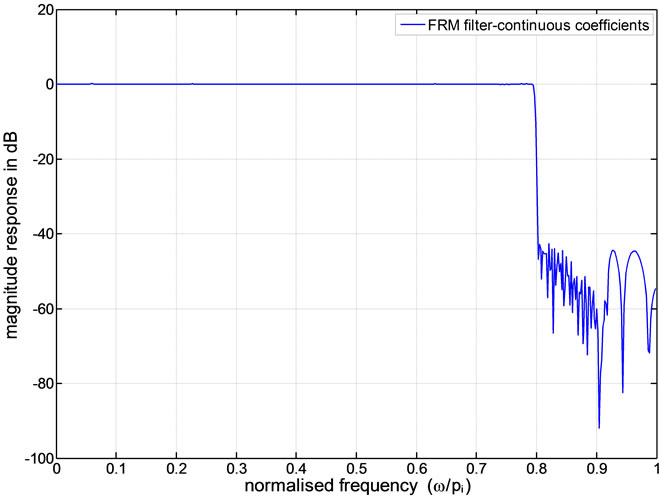
Figure 3. Magnitude response of the continuous co-efficient 1D FRM FIR filter.

Figure 4. Magnitude response of the 1D FRM Filter before and after the proposed optimization using modified HAS.

Figure 5. Magnitude response of the 2D filter designed using the proposed method with T1 transformation.

Figure 6. Contour of the 2D filter designed using the proposed method with T1 transformation.

Table 2. Performance results of the 1D FRM filter.
respectively.
8. Conclusions
A novel approach for the design of a sharp, 2D wideband, circularly symmetric, multiplier-less FIR filter is presented. To this end, a new discrete optimization technique is proposed by modifying the Harmony Search algorithm, which has a simple computational model. The proposed optimization technique was extended to the design of an FRM FIR filter in the CSD space. The 1D multiplier-less filter thus obtained is transformed into the 2D domain using T1 or T2 transformations. This results in a sharp 2D, wideband circularly symmetric filter. The following merits can be claimed by the proposed approach for the design of 2D circularly symmetric multiplier-less filter.
1) Reduced computational complexity due to the use of FRM, CSD representation and the efficient realization of T1 and T2 transformations.
2) Reduced computation time since the contour mapping problem is avoided and the appropriate encoding of candidate solutions in the 1D optimization problem.
Besides, the proposed discrete optimization using HSA can be extended to the solution of integer programming in other engineering disciplines also.
REFERENCES
- Y. C. Lim, “Frequency Response Masking Approach for the Synthesis of Sharp Linear Phase Digital Filters,” IEEE Transactions on Circuits and Systems, Vol. 33, No. 4, 1986, pp. 357-364. doi:10.1109/TCS.1986.1085930
- Y. C. Lim, Y. J. Yu, K. L. Teo and T. Saramaki, “FRMBased FIR Filters with Optimum Finite Word-Length Performance,” IEEE Transactions on Signal Processing, Vol. 55, No. 6, 2007, pp. 2914-2924. doi:10.1109/TSP.2007.893965
- Y. J. Yu and Y. C. Lim, “Genetic Algorithm Approach for the Optimization of Multiplierless Sub-Filters Generated by the Frequency Response Masking Technique,” Proceedings of IEEE International Conference on Electronics, Circuits and Systems, Vol. 3, Croatia, 2002, pp. 1163-1166.
- R. I. Hartley, “Subexpression Sharing in Filters Using Canonic Signed Digit Multipliers,” IEEE Transactions on Circuits and Systems II: Analog and Digital Signal Processing, Vol. 43, No. 10, 1996, pp. 677-688. doi:10.1109/82.539000
- B. Elkarami and M. Ahmadi, “An Efficient Design of 2-D FIR Digital Filters by Using Singular Value Decomposition and Genetic Algorithm with Canonical Signed Digit (CSD) Coefficients,” Proceedings of Midwest Symposium on Circuits and Systems, Seoul, 7-10 August 2011, pp. 1- 4.
- C. Ling, “A Hybrid Genetic Algorithm for the Design of FIR Filters with SPOT Coefficients,” Signal Processing, Vol. 87, No. 3, 2007, pp. 528-540. doi:10.1016/j.sigpro.2006.06.015
- P. Mercier, S. Mohan-Kilambi and B. Nowrouzian, “Optimization of FRM FIR Digital Filters over CSD and DBNS Multiplier Coefficient Spaces Employing a Novel Genetic Algorithm,” Computers, Vol. 2, No. 7, 2007, pp. 20-31.
- Z. W. Geem, J. H. Kim and G. V. Loganathan, “A New Heuristic Optimization Algorithm: Harmony Search,” Simulation, Vol. 76, No. 2, 2001, pp. 60-68. doi:10.1177/003754970107600201
- J. C. Liu and Y. L. Tai, “Design of 2-DWideband Circularly Symmetric FIR Filters by Multiplier-Less HighOrder Transformation,” IEEE Transactions on Circuits Systems I, Vol. 58, No. 4, 2011, pp. 746-754.
- E. M. Kermani, H. Salehinejad and S. Talebi, “PAPR Reduction of OFDM Signals Using Harmony Search Algorithm,” Proceedings of International Conference on Telecommunications, Cyprus, 8-11 May 2011, pp. 90-94.
- W. C. Ming and H. Y. Fu, “Self Adaptive Harmony Search Algorithm for Optimization,” Experts Systems, Application, Vol. 37, No. 4, 2010, pp. 2826-2837. doi:10.1016/j.eswa.2009.09.008
- R. M. Mersereau, W. F. G. Mecklenbrauker and T. F. Quatieri Jr., “McClellan Transformations for Two-Dimensional Digital Filtering: I Design,” IEEE Transactions on Circuits Systems, Vol. 23, No. 7, 1976, pp. 405- 414. doi:10.1109/TCS.1976.1084236
- W. S. Lu and T. Hinamoto, “Optimal Design of Frequency-Response-Masking Filters Using Semidefinite Programming,” IEEE Transactions on Circuits and Systems I: Fundamental Theory and Applications, Vol. 50, No. 4, 2003, pp. 557-568. doi:10.1109/TCSI.2003.809809
- M. Manuel and E. Elias, “Design of Frequency Response Masking FIR Filter in the Canonic Signed Digit Space Using Modified Artificial Bee Colony Algorithm,” Engineering Applications of Artificial Intelligence, 2012, In Press. doi:10.1016/j.engappai.2012.02.010
- Y. C. Lim, R. Yang, D. N. Li and J. J. Song, “Signed Power-of-Two Term Allocation Scheme for the Design of Digital Filters,” IEEE Transactions on Circuits and Systems II, Vol. 46, No. 5, 1999, pp. 577-584. doi:10.1109/82.769806
- K. Lee and Z. Geem, “A New Meta-Heuristic Algorithm for Continuous Engineering Optimization: Harmony Search Theory and Practice,” Computer Methods in Applied Mechanics and Engineering, Vol. 194, No. 36-38, 2005, pp. 3902-3933. doi:10.1016/j.cma.2004.09.007

