Journal of Signal and Information Processing
Vol. 3 No. 2 (2012) , Article ID: 19563 , 7 pages DOI:10.4236/jsip.2012.32025
Low Complexity Precoded Greedy Power Allocation Algorithms for OFDM Communication Systems
![]()
Department of Electronics and Electrical Communications, Faculty of Electronic Engineering, Menoufia University, Menouf, Egypt.
Email: {najib_odhah, dr_moawad, waleed_alhanafy, fathi_sayed}@yahoo.com
Received July 2nd, 2011; revised January 10th, 2012; accepted February 29th, 2012
Keywords: OFDM; Uniform Power Allocation; Greedy Algorithm; Throughput Enhancement; MRC Precoding
ABSTRACT
In this paper, an enhanced greedy bit and power allocation algorithms for orthogonal frequency division multiplexing (OFDM) communication systems are introduced. These algorithms combine low complexity greedy power allocation algorithms with a simplified maximum ratio combining (MRC) precoding technique at the transmitter for maximizing the average data throughput of OFDM communication systems. Results of computer simulations show that precoding is an effective technique for improving the throughput performance of the proposed bit and power allocation algorithms.
1. Introduction
Multicarrier modulation (MCM) is a powerful transmission technique that provides improved performance in various communication fields; it introduces important benefits as efficient bandwidth optimization, enhanced spectrum utilization, low equalization complexity, and multiuser potentiality. Moreover, it is widely used in new application fields, such as power line communications (PLC) [1-3], and wireless local area networks (WLANs) [4-6] due to its recognized value to confront various channel impairments, including frequency selectivity, intersymbol interference (ISI), and impulse noise.
Two important MCM techniques that have wide spread use are OFDM [6] mainly employed in wireless applications, and discrete multitone (DMT) [7] used in wireline systems. In conventional wireless OFDM systems, all subcarriers employ the same signal constellation. However, the overall error probability is dominated by the subcarriers with the worst performance. To improve system performance and throughput, adaptive bit and power allocation algorithms can be employed, where the signal constellation size and power distribution vary according to the measured signal-to-noise ratio (SNR) values across the subcarriers [8].
The bit and power allocation is a constraint optimization problem, and generally two cases are of practical interest; rate maximization (RM) and margin maximization (MM), where the objective is the maximization of the achievable data rate or the achievable system margin, respectively. A rate-optimal algorithm known as the greedy power allocation (GPA) algorithm [9,10], of which a number of different variations have emerged constraining either the average bit error rate (BER) [8] or the total power [11]. For a good review of greedy algorithms, please refer to [1]. Suboptimal GPA algorithms, whereby the bit and power re-allocation are performed in groups of subcarriers are proposed in [12], resulting in low complexity algorithms compared with the GPA algorithm.
An MRC precoding technique is proposed to enhance the low complexity GPA algorithms proposed in [12] for OFDM signal transmission in hostile environments and to simplify receiver complexity by transferring the signal processing to the transmitter. For high speed communications, the channel is changing faster than it can be estimated and fed back to the transmitter. So adaptive bit and power allocation algorithms perform poorly. Other means for mitigating the effect of fading should be used [13]. In this paper, enhanced adaptive bit and power allocation algorithms for OFDM communication systems are introduced. These algorithms combine low complexity bit and power allocation algorithms and a simplified precoding technique at the OFDM transmitter for data throughput enhancement. The proposed system operates in time division duplex (TDD) mode in which the channel reciprocity between alterative uplink and downlink transmissions is exploited to feed the channel state information (CSI) back to the transmitter side.
The rest of this paper is organized as follows. In Section 2, the problem of bit and power allocation for OFDM system is overviewed. The proposed bit and power allocation algorithms are described in Section 3. Simulation results are given in Section 4. Finally, conclusions are given in Section 5.
2. Bit and Power Allocation for OFDM System
OFDM is a promising technique for achieving the high data rate transmission required for wireless multimedia services over time dispersive multipath channels [14]. To improve the OFDM system throughput, adaptive bit and power allocations are employed.
2.1. Problem Definition
The problem of the maximization of the transmission rate over the OFDM wireless system is considered, where the multipath channel characterized by a finite impulse response (FIR) vector 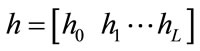 of order L is converted to an N-subcarriers system with different gains
of order L is converted to an N-subcarriers system with different gains . The nth subcarrier experiencing the gain
. The nth subcarrier experiencing the gain  will be used to transmit
will be used to transmit  bits per symbol. The following constrained optimization problem must be solved to determine the optimum bit and power allocations to maximize the OFDM system throughput
bits per symbol. The following constrained optimization problem must be solved to determine the optimum bit and power allocations to maximize the OFDM system throughput
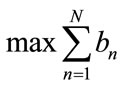 subject to
subject to
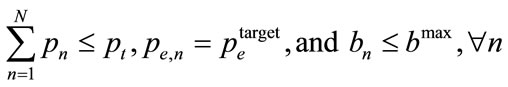 (1)
(1)
where  and
and 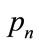 are the bit and power allocated to the nth subcarrier to achieve a bit error rate (BER) of
are the bit and power allocated to the nth subcarrier to achieve a bit error rate (BER) of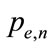 ,
,  is the total power budget, and
is the total power budget, and  is the maximum number of permissible allocated bits per subcarrier .
is the maximum number of permissible allocated bits per subcarrier .
The nth subcarrier power to noise ratio can be defined as follows:
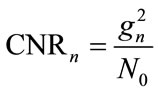 (2)
(2)
where 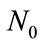 is the noise power at the receiver, and the SNR of this subcarrier is
is the noise power at the receiver, and the SNR of this subcarrier is
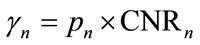 (3)
(3)
Symbols of 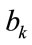 -bits,
-bits, 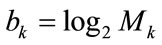 can be loaded to the subcarrier with the minimum required SNR
can be loaded to the subcarrier with the minimum required SNR 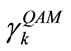 [12,15] of
[12,15] of
 (4)
(4)
where 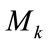 is the maximum permissible QAM constellation by the transmission system and
is the maximum permissible QAM constellation by the transmission system and 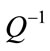 is the inverse of a well-known Q function that is the tail probability of the standard normal distribution [15]. The solution of the constrained optimization problem in (1) can be divided into two steps, uniform power allocation (UPA) initialization step and the GPA algorithm. Both of them are described below.
is the inverse of a well-known Q function that is the tail probability of the standard normal distribution [15]. The solution of the constrained optimization problem in (1) can be divided into two steps, uniform power allocation (UPA) initialization step and the GPA algorithm. Both of them are described below.
2.2. Uniform Power Allocation (UPA) Algorithm
The steps of UPA algorithm can be summarized as follows [12]:
1) Calculate 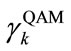 for all
for all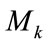 ,
, 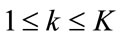 and the target BER
and the target BER 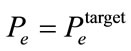 using (4).
using (4).
2) Allocate the total power budget 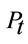 between all subcarriers, equally, as follows
between all subcarriers, equally, as follows
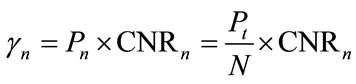 (5)
(5)
3) Redistribute subcarriers according to their SNRs  into QAM groups Gk,
into QAM groups Gk, 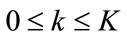 bounded by QAM levels
bounded by QAM levels 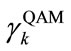 and
and  with
with 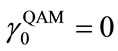 and
and
 i.e.
i.e. 
4) Load subcarriers within each Gk group with QAM constellation Mk such that the total allocated bits of this group is
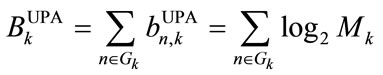 (6)
(6)
with 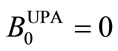 and the total excess power for this group
and the total excess power for this group
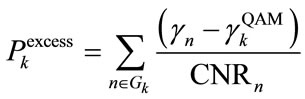 (7)
(7)
5) The total number of the system allocated bits and the used power for the UPA algorithm are
 (8)
(8)
 (9)
(9)
The total excess power produced by the UPA algorithm is well exploited by a number of algorithms, and this represents a useful indication about the efficient utilization of the total transmit power .
.
2.3. Full Greedy Power Allocation (GPA) Algorithm
The GPA algorithm [1,9,10,12] is based on the initialization step described above. This algorithm performs an iterative re-distribution of the excess power of the UPA algorithm. Applying the steps described in Table 1, resulting in an overall system allocated bits and used power given, respectively, by
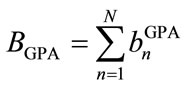 (10)
(10)
and


Table 1. Full GPA algorithm.
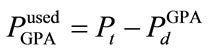 (11)
(11)
3. The Proposed Pre-Coded Bit and Power Allocation Algorithms
Bit and power allocation algorithms for OFDM systems with equalization at the receiver have been studied in the literature. However, applying bit and power allocation algorithms with pre-coding techniques is still new, and there are a lot of open issues. In this paper, hybrid algorithms comprising the low complexity bit and power allocation algorithms in [12] and a pre-coding technique [16] will be proposed and studied.
3.1. MRC Pre-Coding Technique
A MRC pre-coding is proposed for enhancing the bit and power allocation of OFDM system as shown in Figure 1, where it is based on correcting the phase and weighting the amplitude of each subcarrier [16]. The signal model of MRC Pre-coded OFDM system is described as follows
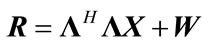 (12)
(12)
where R is the 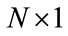 received signal vector,
received signal vector,  is an
is an 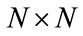 diagonal channel matrix containing the frequency domain channel coefficient of each subcarrier,
diagonal channel matrix containing the frequency domain channel coefficient of each subcarrier,  is
is 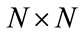 complex conjugate transpose of
complex conjugate transpose of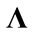 , X is an
, X is an 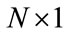 transmitted signal vector, and W is an
transmitted signal vector, and W is an  additive white Gaussian noise (AWGN) vector. The
additive white Gaussian noise (AWGN) vector. The 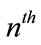 subcarrier gain
subcarrier gain  in (2) is replaced by MRC pre-coded
in (2) is replaced by MRC pre-coded 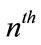 subcarrier gain
subcarrier gain 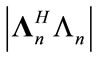 . Based on the new pre-coded channel coefficients described above, UPA algorithm is re-applied to determine new subcarriers bit allocation
. Based on the new pre-coded channel coefficients described above, UPA algorithm is re-applied to determine new subcarriers bit allocation 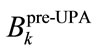 and new total excess power
and new total excess power  for each QAM level group as defined in (6) and (7), respectively. Three enhanced low-complexity greedy algorithms are proposed and studied to efficiently utilize the new total excess power of the Pre-UPA algorithm. These algorithms are Pre-coded QAM-Level GPA (Pre-LGPA) algorithm, Pre-coded Power Moving up GPA (Pre-MuGPA) algorithm, and Precoded Power Moving down GPA (Pre-MdGPA) algorithm.
for each QAM level group as defined in (6) and (7), respectively. Three enhanced low-complexity greedy algorithms are proposed and studied to efficiently utilize the new total excess power of the Pre-UPA algorithm. These algorithms are Pre-coded QAM-Level GPA (Pre-LGPA) algorithm, Pre-coded Power Moving up GPA (Pre-MuGPA) algorithm, and Precoded Power Moving down GPA (Pre-MdGPA) algorithm.
3.2. Pre-LGPA Algorithm
The direct application of the GPA algorithm is computationally very complex, because at each iteration, exhaustive sorting and searching algorithms of all subcarriers are required as shown in Table 1. A simplified technique of the GPA algorithm can be obtained if the subcarriers are firstly divided into QAM  groups
groups 
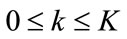 according to their SNRs.
according to their SNRs.
The GPA algorithm is therefore independently applied to each group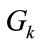 . The Pre-LGPA algorithm is well described in Table 2 where it permits upgrading to the next QAM level only and therefore may leave some left-over power
. The Pre-LGPA algorithm is well described in Table 2 where it permits upgrading to the next QAM level only and therefore may leave some left-over power 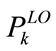 for each QAM group
for each QAM group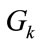 , resulting in a total left-over power of
, resulting in a total left-over power of
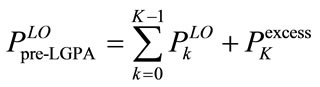 (13)
(13)
The Pre-LGPA algorithm has to be executed K times, once for each QAM group resulting in an overall system that allocates bits and power according to
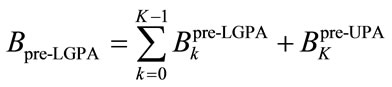 (14)
(14)
and
 (15)
(15)
3.3. Pre-MuGPA Algorithm
The Pre-LGPA algorithm results in an unused  for
for
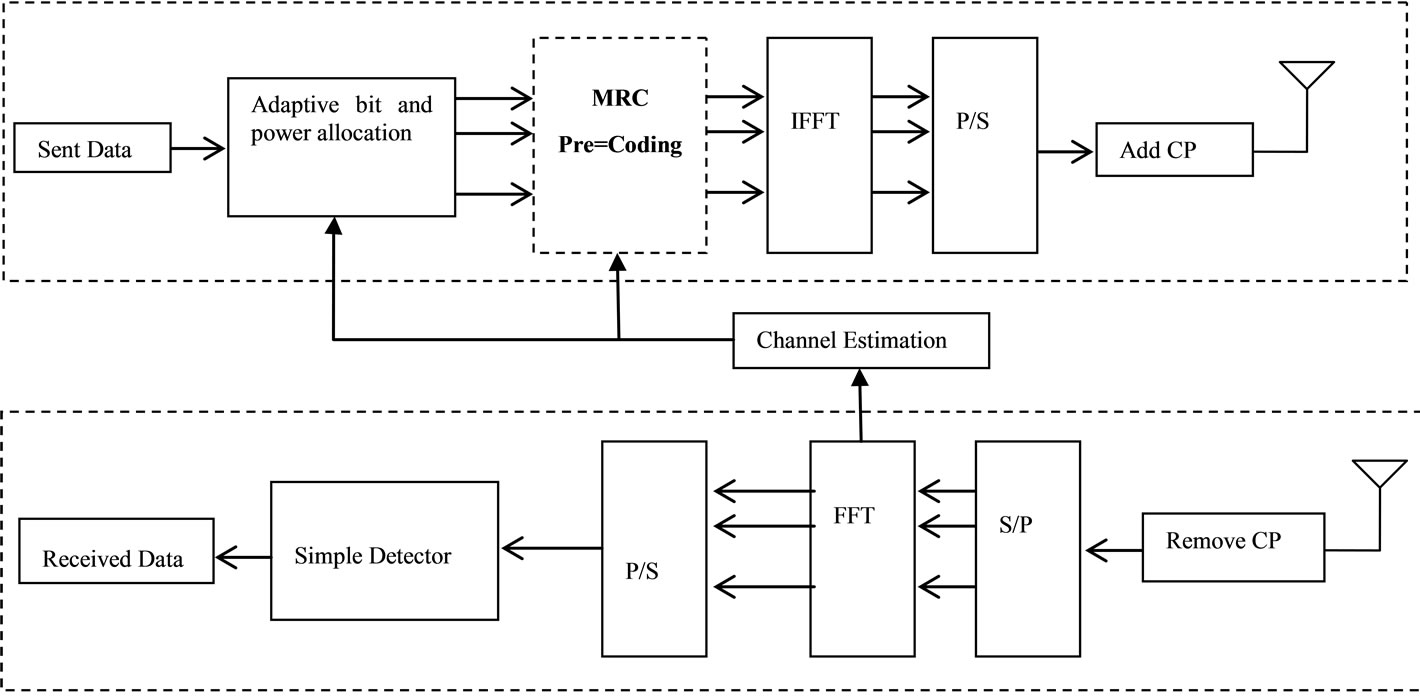
Figure 1. The architecture of the proposed scheme for OFDM system.

Table 2. Pre-LGPA algorithm.
each QAM group. This residual power can be exploited by a second stage, whereby it is proposed to move this power upwards starting from the lowest QAM group. This modifies the Pre-LGPA algorithm by considering the left-over power 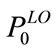 of the QAM group
of the QAM group 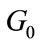 after running the Pre-LGPA algorithm on that group, and assigning this power for redistribution to group
after running the Pre-LGPA algorithm on that group, and assigning this power for redistribution to group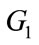 . Any left-over power after running Pre-LGPA algorithm on
. Any left-over power after running Pre-LGPA algorithm on  is then passed further upwards to
is then passed further upwards to , and so forth. At the
, and so forth. At the 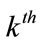 algorithmic iteration, the Pre-MuGPA algorithm is working with
algorithmic iteration, the Pre-MuGPA algorithm is working with 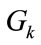 and tries to allocate the sum of the excess power missed by the Pre-UPA algorithm of that group as well as the left-over power resulting from the application of the Pre-LGPA algorithm to the previous group
and tries to allocate the sum of the excess power missed by the Pre-UPA algorithm of that group as well as the left-over power resulting from the application of the Pre-LGPA algorithm to the previous group  i.e.
i.e. 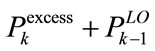 . Finally, the left-over power resulting from the QAM group
. Finally, the left-over power resulting from the QAM group 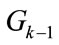 is added to the excess power of the
is added to the excess power of the 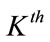 QAM group
QAM group 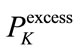 to end up with a final left-over power given by:
to end up with a final left-over power given by:
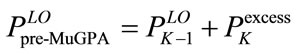 (16)
(16)
The overall number of the system allocated bits and the used power of this algorithm are, respectively, given by:
 (17)
(17)
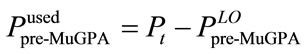 (18)
(18)
3.4. Pre-Md GPA Algorithm
The residual power  resulting from the Pre-LGPA algorithm can be exploited by a second algorithm called pre-coded moving down GPA (Pre-MdGPA) algorithm, whereby it is proposed to move the residual power downwards starting from the highest QAM group
resulting from the Pre-LGPA algorithm can be exploited by a second algorithm called pre-coded moving down GPA (Pre-MdGPA) algorithm, whereby it is proposed to move the residual power downwards starting from the highest QAM group  to the lowest QAM group
to the lowest QAM group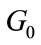 , at the kth stage this algorithm applies the Pre-LGPA algorithm for the available power that comprises both the excess power missed by the Pre-UPA algorithm of the previous QAM group
, at the kth stage this algorithm applies the Pre-LGPA algorithm for the available power that comprises both the excess power missed by the Pre-UPA algorithm of the previous QAM group 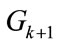 and the left-over power of the previous stage. This will finally result in a left-over power of
and the left-over power of the previous stage. This will finally result in a left-over power of
 (19)
(19)
The overall system allocated data bits and the used power of this algorithm are, respectively, given by:
 (20)
(20)
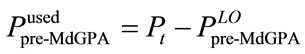 (21)
(21)
4. Simulation and Discussions
In this section, computer simulations are carried out to evaluate the performance of the proposed pre-coded bit and power allocation algorithms. For comparison purpose, the non precoded bit and power allocation algorithms are also simulated. Simulation parameters are listed in Table 3. Channel coefficients are obtained from complex Gaussian process with zero mean and unit variance through ensemble averages across 1000 channel realizations for various levels of SNRs using QAM modulation schemes, 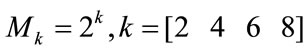 with the maximum permissible QAM level of constellation size
with the maximum permissible QAM level of constellation size 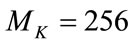 which is equivalent to 8 bits per data symbol The total average system throughput is studied and shown in Figures 2 and 3 for the recent (non pre-coded) [12] and proposed (precoded) bit and power allocation algorithms with 6 and 12-tabs FIR filters, respectively.
which is equivalent to 8 bits per data symbol The total average system throughput is studied and shown in Figures 2 and 3 for the recent (non pre-coded) [12] and proposed (precoded) bit and power allocation algorithms with 6 and 12-tabs FIR filters, respectively.
Figure 2 shows that the optimum throughput is achieved by the GPA algorithm in each of the recent and proposed algorithms. However, because of its very large computational complexity, low complexity algorithms are proposed to efficiently use the power budget. These are pre-LGPA, Pre-MuGPA and Pre-MdGPA algorithms. The two proposed MuGPA and MdGPA with and without the MRC pre-coding approach the optimum power allocation GPA algorithm in two distinct SNR regions. MuGPA performs better at low SNRs, while MdGPA performs better at higher SNRs. The proposed precoded algorithms satisfy about 250 bits per symbol throughput enhancement over the non precoded algorithms. Figure 3 shows that the throughput is improved by about 50 bits per symbol for 12-taps FIR over 6-taps FIR filters due to the multipath diversity of the MRC precoding.
Figure 4 shows the average system throughput versus target BER at SNR = 30 dB. Intuitively, throughput is
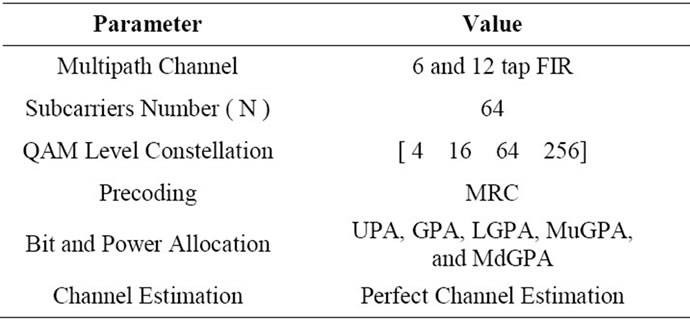
Table 3. Simulation parameters.

Figure 2. Average system throughput for 64-subcarrier OFDM system with target BER = 10–3 and 6-tap FIR.
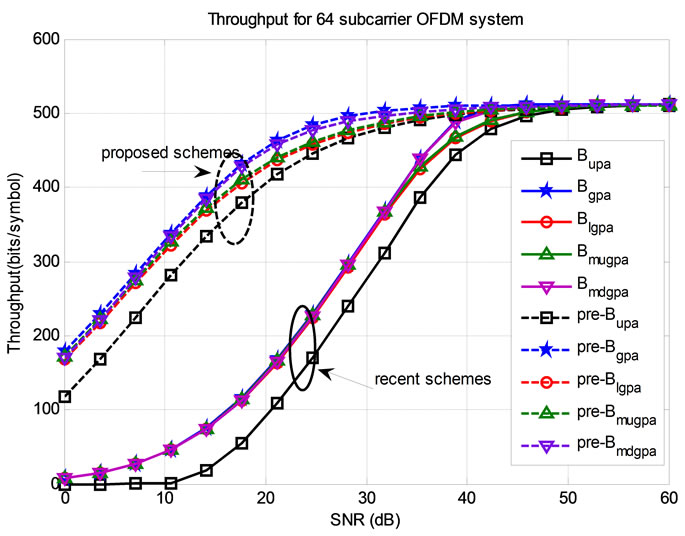
Figure 3. Average system throughput for 64-subcarrier OFDM system with target BER = 10–3 and 12-tap FIR.
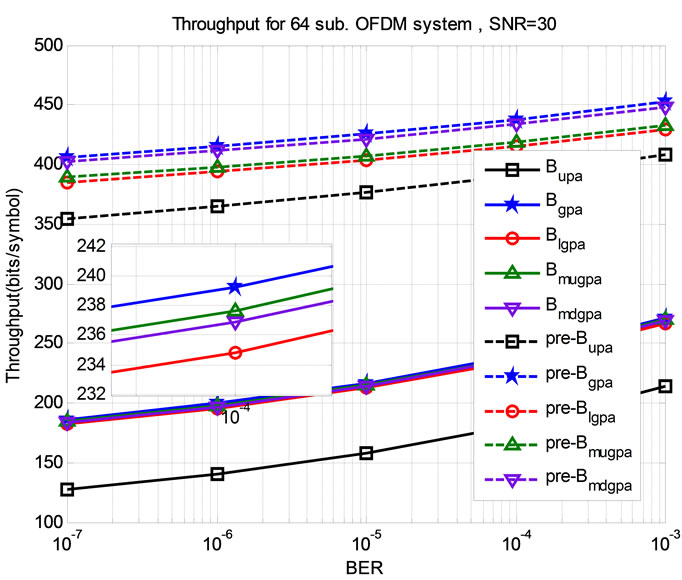
Figure 4. Average system throughput for 64-subcarrier OFDM system with SNR = 30.
increasing with the increase of target BER. The pre-coded algorithms outperform the non precoded algorithms. The pre-MdGPA achieves about 210 bits/symbol throughput enhancement over pre-MuGPA at target BER = 10–7 and 180 bits/symbol at BER = 10–3. This can be attributed to low variation with target BER for pre-coded algorithms compared with the non pre-coded algorithms. Also the pre-MdGPA is better than pre-MuGPA at all target BERs.
Figure 5 shows the used power by all algorithms as a function of the power budget at target BER 10–3. The UPA with and without precoding exhibits the worst performance. The other algorithms are better than UPA in utilizing the transmit power. At low SNRs, all algorithms use approximately all power budget for bit and power allocations with different throughput performance as shown in Figure 2. At high SNRs, LGPA and MuGPA algorithms with and without pre-coding approaches the UPA algorithm due to the increase of highest QAM level excess power, which is missed by both of them, and therefore deteriorates their performances. Since Figure 5 is crowded; it is subdivided into two figures; Figures 6 and 7 for the recent and the proposed algorithms, respectively.
5. Conclusions
The optimum solution of the discrete bit and power allocation problem is provided by the greedy algorithm, which operates across all subcarriers but it is computationally very expensive. Therefore, in this paper suboptimal low complexity alternatives have been explored in a manner in which the greedy algorithm is applied through subsets of subcarriers, which are grouped according to the QAM levels assigned to them in the uniform power allocation stage. MRC precoding is proposed to enhance the throughput performance of these low complexity
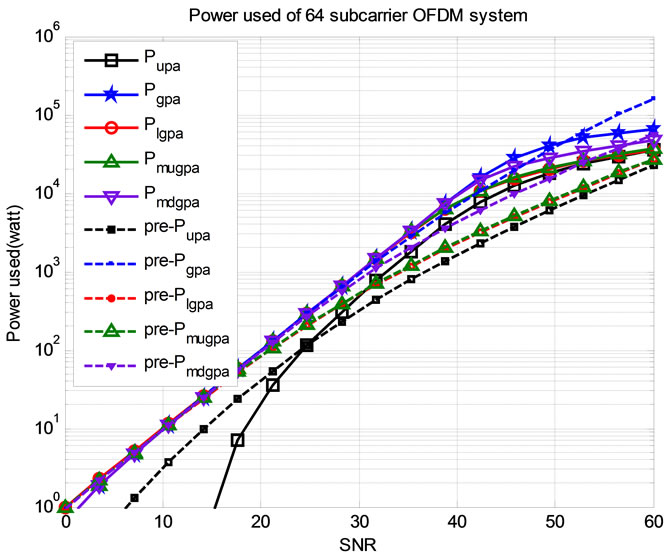
Figure 5. The power used (watt) with target SNR (dB) variation at target BER = 10–3 for all algorithms.

Figure 6. The power used (watt) with target SNR (dB) variation at target BER = 10–3 for the recent algorithms.
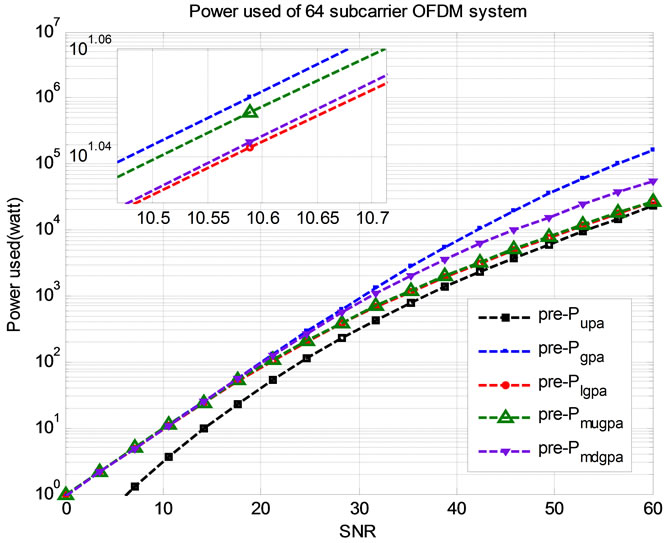
Figure 7. The Power used (watt) with target SNR (dB) variation at target BER = 10–3 for the proposed algorithms.
algorithms, the proposed precoded bit and power allocation algorithms outperform the non-pre-equalized algorithms and introduce less variation with target BER. PreMuGPA approaches GPA algorithm at low SNRs whereas Pre-MdGPA approaches GPA algorithm and outperforms Pre-MuGPA at high SNRs.
REFERENCES
- N. Papandreou and T. Antonakopoulos, “Bit and Power Allocation in Constrained Multicarrier Systems: The Single-User Case,” EURASIP Journal on Advances in Signal Processing, Vol. 2008, 2008, pp. 1-14. doi:10.1155/2008/643081
- E. Biglieri, “Coding and Modulation for a Horrible Channel,” IEEE Communication Magazine, Vol. 41, No. 5, 2003, pp. 92-98. doi:10.1109/MCOM.2003.1200107
- S. Baig and N. D. Gohar, “A Discrete Multitone Transceiver at the Heart of the PHY Layer of an in-Home Power Line Communication Local Area Network,” IEEE Communication Magazine, Vol. 41, No. 4, 2003, pp. 48- 53. doi:10.1109/MCOM.2003.1193974
- R. van Nee and R. Prasad, “OFDM for Wireless Multimedia Communications,” Artech House, Boston, 2000.
- R. van Nee, G. Awater, M. Morikura, H. Takanashi, M. Webster and K. W. Halford, “New High-Rate Wireless LAN Standards,” IEEE Communication Magazine, Vol. 37, No. 12, 1999, pp. 82-88. doi:10.1109/35.809389
- J. Heiskala and J. Terry, “OFDM Wireless LANs: A Theoretical and Practical Guide,” Sams, Indianapolis, 2002.
- J. M. Cioffi, “A Multicarrier Primer,” ANSI Contribution T1E1.4/91-157, Clearfield, FLA, 1991.
- A. M. Wyglinski, F. Labeau and P. Kabal, “Bit Loading with BER Constraint for Multicarrier Systems,” IEEE Transactions on Wireless Communication, Vol. 4, No. 4, 2005, pp. 1383-1387. doi:10.1109/TWC.2005.850313
- J. Campello, “Optimal Discrete Bit Loading for Multicarrier Modulation Systems,” IEEE International Symposium on Information Theory, Stanford, 16-21 August 1998, p. 193.
- J. Campello, “Practical Bit Loading for DMT,” IEEE International Conference on Communications, Vol. 2, 1999, pp. 801-805.
- L. Zeng, S. McGrath and E. Cano, “Rate Maximization for Multiband OFDM Ultra Wideband Systems Using Adaptive Power and Bit Loading Algorithm,” IEEE Fifth Advanced International Conference Telecommunication, Venice/Mestre, May 2009, pp. 369-374.
- W. Al-Hanafy and S. Weiss, “Greedy Power Allocation for Multicarrier Systems with Reduced Complexity,” URSI National Radio Science Conference, Menofia University, 16-18 March 2010, Article ID 27156.
- A. J. Goldsmith and S.-G. Chua, “Variable-Rate VariablePower MQAM for Fading Channels,” IEEE Transactions on Communication, Vol. 45, No. 10, 1997, pp. 1218-1230. doi:10.1109/26.634685
- A. Ghosh and R. Muhamed, “Fundamentals of WiMAX: Understanding Broadband Wireless Networking,” Prentice Hall, New York, 2007.
- A. Goldsmith, “Wireless Communications,” Cambridge University Press, Cambridge, 2005.
- P. Bisaglia, N. Benvenuto and S. Quitadamo, “Performance Comparison of Single-User Pre-Equalization Techniques for Uplink MC-CDMA Systems,” Proceeding of GLOBECOM, San Francisco, December 2003, pp. 3402- 3406.

