Journal of Biomaterials and Nanobiotechnology
Vol.3 No.1(2012), Article ID:17002,9 pages DOI:10.4236/jbnb.2012.31008
A Thermo-Mechanical Behavior Simulation of a NiTi Staple Used for the Correction of Idiopathic Scoliosis
![]()
1Institut National des Sciences Appliquées et de Technologie (INSAT), Université de Carthage, Tunis, Tunisia; 2Tunisian group of spine and spinal cord study and research, Tunis, Tunisia; 3René-Lévesque Ouest, Montréal, Canada.
Email: fafa.benhatira@insat.rnu.tn
Received October 16th, 2011; revised November 29th, 2011; accepted December 20th, 2011
Keywords: shape memory alloy; constitutive law; finite element modeling; idiopathic scoliosis; staple
ABSTRACT
In order to treat scoliosis, a thermo-mechanical behavior study of shape memory alloy bone staple has been proposed. A pre-stretched shape-memory-alloy bone staple, which has been heated above the transition temperature, provides greater compressive force upon insertion between two vertebrae and allows the control of idiopathic scoliosis development. Until now, the optimal design has not been reached due to the lack of appropriate design tools for shape memory alloy devices. In this paper, a shape memory alloy bone staple model is proposed by developing a user subroutine UMAT based on Boyd et al. [1] unified thermodynamic shape memory alloy constitutive law using the finite element analysis software, ABAQUS. The numerical results for superelastic and shape memory effect under the tensile and three-point bending tests are presented. Simulations of the shape memory effects and force generation of the shape memory alloy staple are also shown.
1. Introduction
Shape memory alloys (SMAs) show unusual but intelligent material behavior such as superelaticity (ability to recover large elastic strain) and shape memory effect (ability of a deformed SMA element to recover its initial shape when it is heated) [2]. These effects are, in general, interpreted as martensitic transformations between a more ordered crystal phase, called austenite, and a less ordered crystallographic phase, called martensite [3,4]. These inherent and induced characteristics of SMA have given rise to their usage in a wide array of applications. Among several other applications, SMA are used to produce shrink fit rings, actuators in the form of torque beams or wires (Bo et al., [5], Trochu et al. [6,7]), orthodontic wires and other medical devices (Auricchio et al. [8-10]). SMA also are useful as dampers, due to the energy dissipated in the pseudo-elastic hysteresis (Qidwai et al. [11] and Boyd et al. [1,12]).
Despite several successful applications of SMA devices, SMA is currently not of large industrial use [13]. Traditionally, new products were developed by prototyping and evaluation. However, this process is very time consuming and often does not fully reveal the potential failures. Finite element analysis (FEA) can greatly reduce testing and marketing time by allowing the designer to develop and simulate products prior to prototype fabrication. Research on modeling shape memory alloys originates from the interest expressed by several companies for new medical applications as vascular stents, osteosynthesis staples, Harrington wires for scoliosis correction, [14] and orthodontic wires [15]. Current commercially available software do not support shape memory effect material properties in 3D, and have limited support on superelasticity effect.
Models that were developed to represent SMA behaveior mostly are based on experimental data [16]. Constitutive laws are classified under three families: thermodynamical, micromechanical, and mesomechanical models.
The thermodynamical models are based on macroscopic experimentation and identification of the principal thermomechanical parameters. The advantages of these models are simplicity, appropriateness for numerical computing, and practicality for industrial applications. However, the validation is difficult due to the lack of the multiaxial experimental data. The differences between published thermodynamical models are the variation in the internal state variables and the kinetics equation. Liang and Rogers [17] have proposed a multi dimensional constitutive model using the marten-site volume fraction as internal state variable. Lagoudas et al. [18]. Auricchio et al. [10,19-22] and Qidwai [11] have developed a unified thermodynamic constitutive law and have demonstrated the unification of models by optimizing the function of the elastic strain energy.
Micromechanical models are based on researchers following a micromechanics approach, Tanaka [16], Patoor [23]; Brinson et al. [24], Lexcellent et al. [25,26]; Huang et al. [27]; Gao et al. [28], and Sun et al. [29] have attempted to closely follow the crystallographic phenomena within the material, using thermodynamics laws to describe the transformation. These models consider the martensitic variant as a transforming inclusion and use micromechanics to calculate the interaction energy due to the phase transformation in the material. Stresses and strains are obtained as volume averages calculated over a volume in which many inclusions are considered, representing the possible variants. Models based on this approach are much more complicated than thermodynamic models and are usually computationally demanding. On the other hand, being based on an accurate definition of the material properties, these models seem to offer the most rational method to derive a highly accurate three-dimensional constitutive law.
Mesomechanical model, as proposed by Kafka [30-32] represent an approach, that combines the two proceedings. While taking advantage from the accuracy that offers a description of the is adopted maintaining its appropriateness for numerical computing. In this model the shape memory alloys are considered heterogeneous material, where heterogeneous implies that the material is composed of different atomic components.
The goal of this present paper is not to propose a new constitutive model for shape memory alloy but to focus on the development of a robust and efficient integration algorithm for Boyd et al. [12] unified thermodynamic model, and the integration of 3D model to simulate and to invetigate the superelasticity and the shape memory effect as proven under the tensile and three point bending test of the orthopaedic staple.
2. Materials and Methods
2.1. Description of the Model
The model used here consists of a mechanical law, governing the stress-strain behavior, and a kinetic law governing the crystallographic transformation. These two relationships are coupled (stress necessarily feeds into the kinetic laws and the evolving phase fraction affects the stressstrain behavior.
Total strain (1) is the sum of the elastic and plastic strain due to martensite transformation
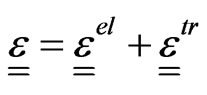 (1)
(1)
A mechanical law relates the strain to the stress, temperature, and transformation strain (2) as
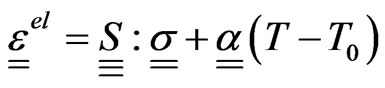 (2)
(2)
The effective compliance tensor is defined as being the inverse of elastic rigidity tensor 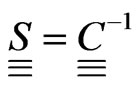 where
where 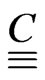 and the thermal expansion coefficient tensor,
and the thermal expansion coefficient tensor, 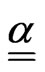 are given according to the martensitic volume fraction
are given according to the martensitic volume fraction 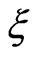 as follows:
as follows:
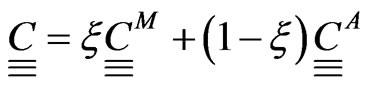 (3)
(3)
 (4)
(4)
Based on this assumption, the following relations are induced to relate the evolution of transformation strain tensor to the evolution of the martensitic volume fraction (5)
 (5)
(5)
where the transformation tensor 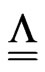 is given by the following formulae:
is given by the following formulae:
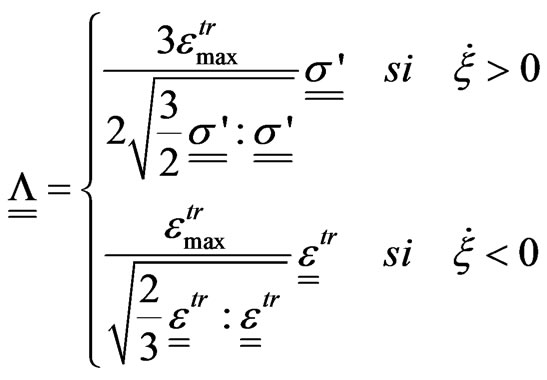 (6)
(6)
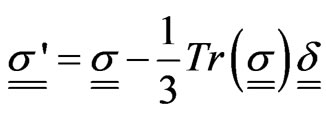 (7)
(7)
 is the maximum uniaxial transformation.
is the maximum uniaxial transformation.
The activation of the transformation phase from austenite to martensite and vice versa is verified by the thermodynamic conjugate force,  to x:
to x:
 (8)
(8)
s0 and u0 are effective specific entropy at reference condition and effective specific internal energy at the reference condition, respectively.
The value of the volume fraction , is given by the condition
, is given by the condition  = 0 through direct or inverse transformations.
= 0 through direct or inverse transformations.
The hardening function , is responsible for the transformation induced strain hardening in the SMA material and given by
, is responsible for the transformation induced strain hardening in the SMA material and given by
 (9)
(9)
2.2. Implementation of the Theoretical Model into a Nonlinear Finite Element Model
SMA finite element model takes into account geometric and material nonlinearities. The Newton Raphson method was used by transfoming the material and geometrical non-linear equations into a sequence of linear equations solved numerically. The return mapping algorithm for the elastic prediction and transformation correction has already been adopted by many researchers [1,11,12,18, 33]. The implementation of the SMA constitutive equations proposed in the framework of this project was done as a user defined material. Numerical simulations was carried out using the commercially available nonlinear finite element code ABAQUS [10,11,34] on a parallel computer. The incremental (discretized) SMA constitutive model based algorithm was implemented in the user supplied subroutine UMAT [7]. This algorithm was divided into two steps:
1) A thermo elastic predictor step to preview the direction of a strain and stress variation:
 and
and 
 and
and 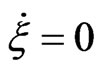
2) A transformation corrector step to compute transformation strain, correct stress value, and deduce tangent stiffness tensor:
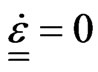 and
and 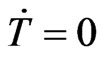
 and
and 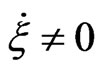
The material properties described were used to simulate and validate the SMA behavior.
We have considered several examples to assess the performance of the proposed model, simulating the behavior of SMA structure. In the following, all tests were simulated starting from an initial temperature T0 = 294 K (where the temperature is greater than the temperature from the finish of austenite transformation Af).
3. Results and Discussion
3.1. Uniaxial Response: Tension Test
An uniaxial simulation was used to show the ability of the constitutive model to properly reproduce the superelastic and shape memory effect. A three-dimensional beam with 5 mm sides and a length of 100 mm was simulated where a finite element mesh has been constructed with 80 quadratic hexahedral elements each having 20 nodes. The first extremity of the beam was fixed and a simple tensile was applied on the opposing extremity (Figure 1).
3.1.1. Supereleasticiy Effect
The SMA beami s subjected to a simple tensile loading-unloading with a constant temperature (T = 294 K, T < As). The sample has developed a recoverable deformation higher than 6% as shown in the stress-strain response in Figure 2. The result obtained from a uniaxial test induced a full transformation. It is important to note the ability of the model to reproduce the superelastic effect in a uniaxial state of stress.
3.1.2. Shape Memory Effect
Keeping the temperature fixed at T = 294 K (T < As), a complete loading and unloading cycle in terms of axial strain is achieved. Holding the axial deformation constant (ε = 0%), we initially cool the sample from T = 297 K to T = 291 K. Keeping the temperature fixed (T = 320 K), a complete loading-unloading cycle is also carried
Figure 1. Three-dimensional beam mesh for tensile test.

Figure 2. Superelastic effect for the tensile load.
out. Finally, keeping the curvature fixed, specimen is heated to back up to 320 K. The beam had remained permanently deformed due martensite’s presence. With heating at T = 320 K (T > Af), the beam recovered its initial form and the permanent deformation had disappeared. Figure 3 shows the material response in terms of stress, strain, temperature, and the capacity simulation to model the unidirectional shape memory effect. We can observe the ability of the specimen to recover its initial state during the final heating process, that is, its ability to reproduce the shape-memory effect during bending, and reaching a temperature at above T = 320 K.
3.2. Three-Point Bending Test
The second series of tests were to investigate the response of a SMA beam undergoing pure bending. The geometry of the beam is chosen to be of 2 mm by 1 mm sides having a length of 50 mm. A finite element mesh has been constructed using quadratic hexahedral elements with 5 elements for thickness, 4 elements for width, and 30 elements for length. The extremities of the beam were supported and a force of 250 N was applied in the middle (figure 4(a)).
An investigation of the structural response of the superelastic and the shape memory effect has been once again carried out, (figure 4(b)).
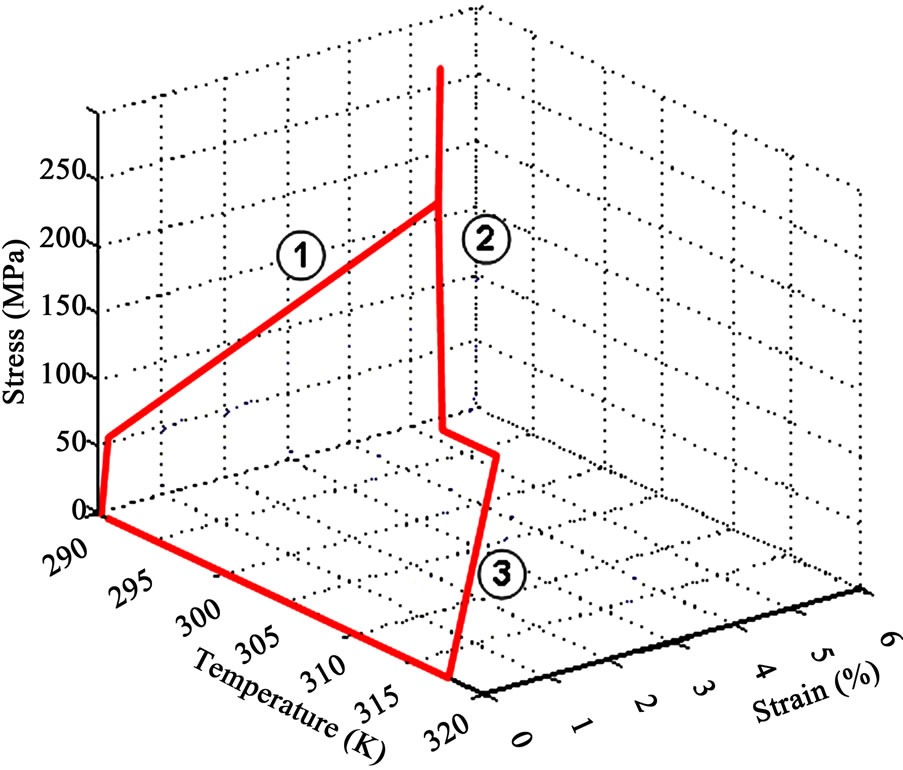
Figure 3. Tensile test shape memory effect, Strain-temperature curve.
 (a)
(a) (b)
(b)
Figure 4. (a) Three-dimensional beam mesh for three-point bending; (b) The structural response of the superelastic and the shape memory effect.
3.2.1. Supereleasticiy Effect
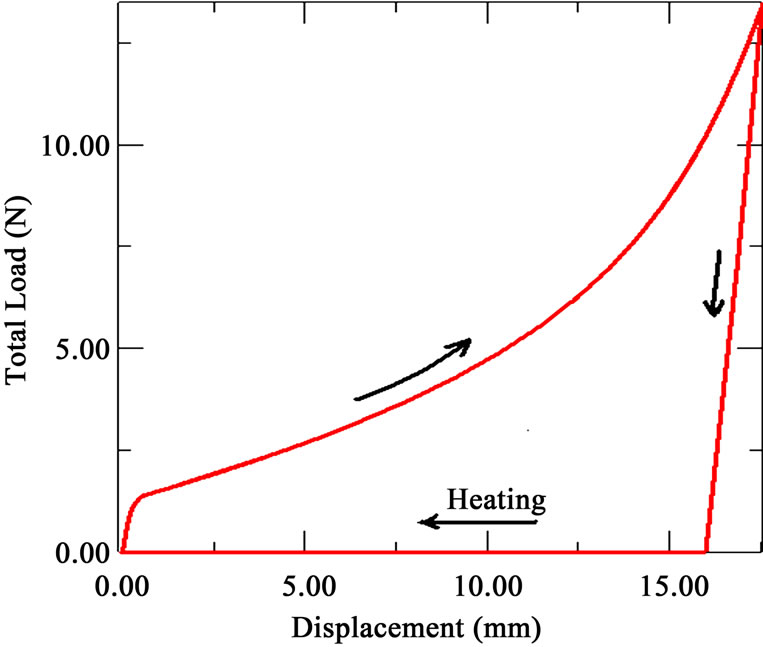
Keeping the temperature constant (T = 294 K), the beam was subjected to a loading and unloading solicitation which is equivalent to apply a bending force. Figure 5 shows the superelastic behavior for applied force versus displacement of numerical model. The ability of the model to recover completely from the deformation during unloading at a temperature above T (As), is remarkable as well as its ability to reproduce the superelastic effect under bending tests.
3.2.2. Shape Memory Effect
Keeping the curvature fixed, the beam has been initially cooled from T = 295 K to T = 271 K. We later kept the temperature fixed (T = 271 K) to perform a complete loading-unloading cycle. Finally, keeping the curvature fixed, the specimen was heated back up to 320 K.
Figures 6(a)-(d) show the total load-curvature-temperature, loading-unloading, and heating response.
3.3. Three-Dimensional Orthopaedic Staple
In order to take advantage of the SMA staples’ superelestic and shape memory behavior for the orthopedic scoliosis correction, it is important to perform a finite element modeling in order to determine the limitation of the staple before its validation. For this task, a mesh consisting of 4620 hexahedral elements and 516 tetrahedral elements (Figure 7) was build up. The properties of the materials used were the same as those used in previous tests (Table 1) and Figure 8.

Figure 5. Three point bending test: superelastic behavior.
 (a)
(a)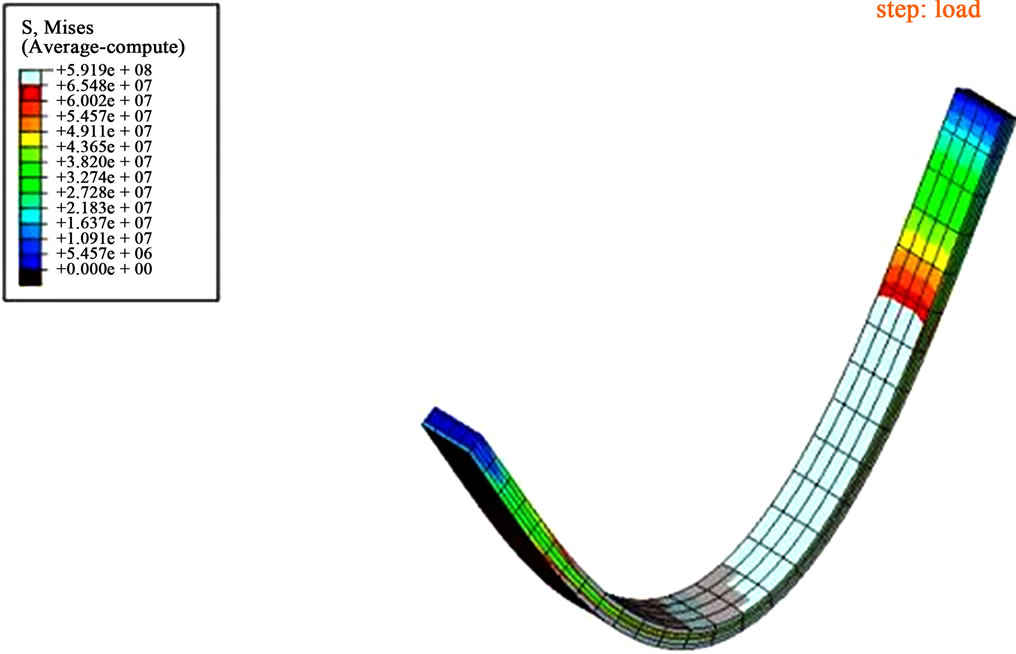 (b)
(b)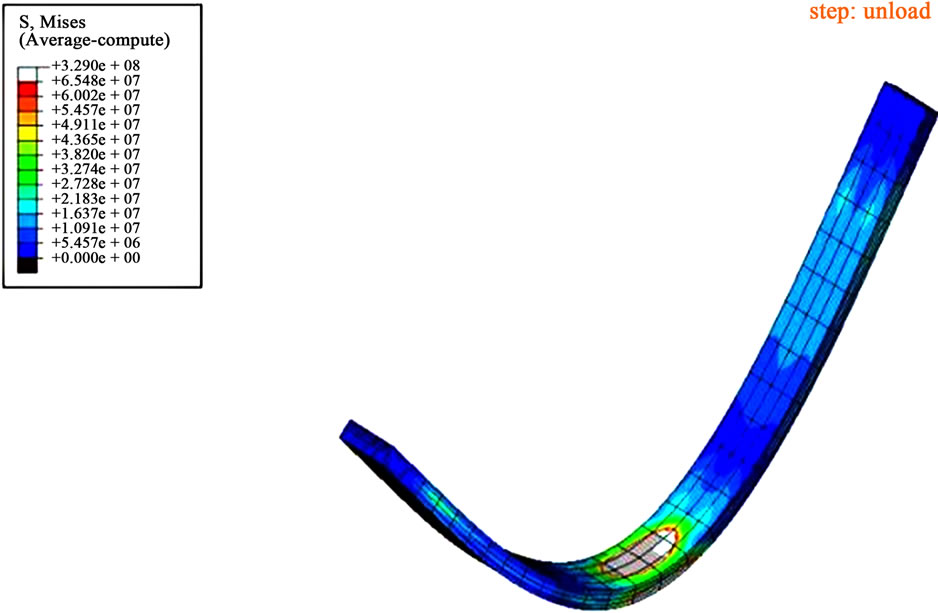 (c)
(c)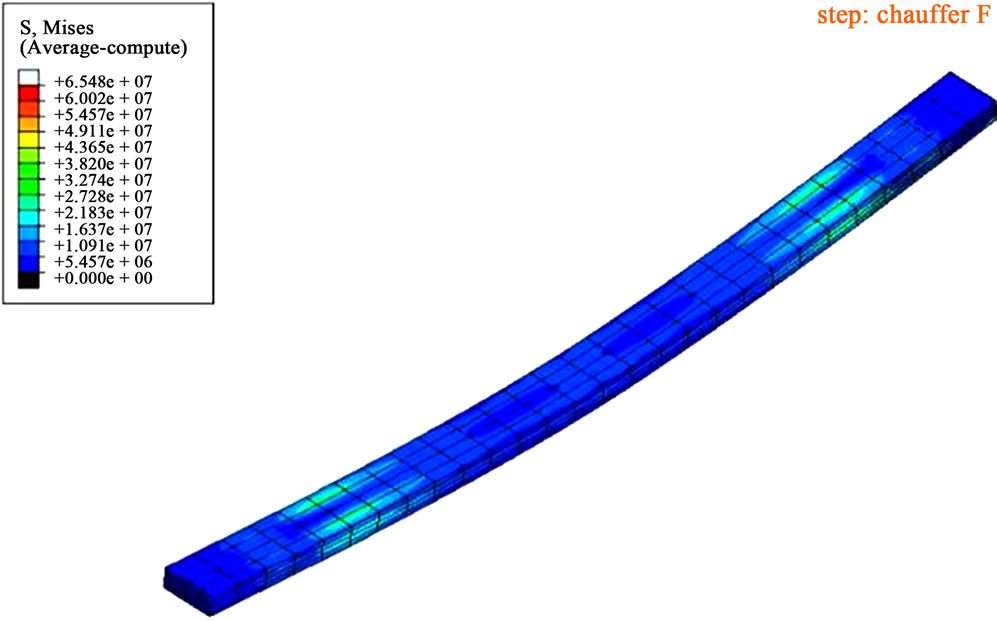 (d)
(d)
Figure 6. (a) Three-point bending for shape memory effect in single way; (b) Loading; (c) Unloading and (d) Heating.
 (a)
(a) (b)
(b)
Figure 7. (a) Three-dimensional staple mesh and (b) Boundary conditions and load.
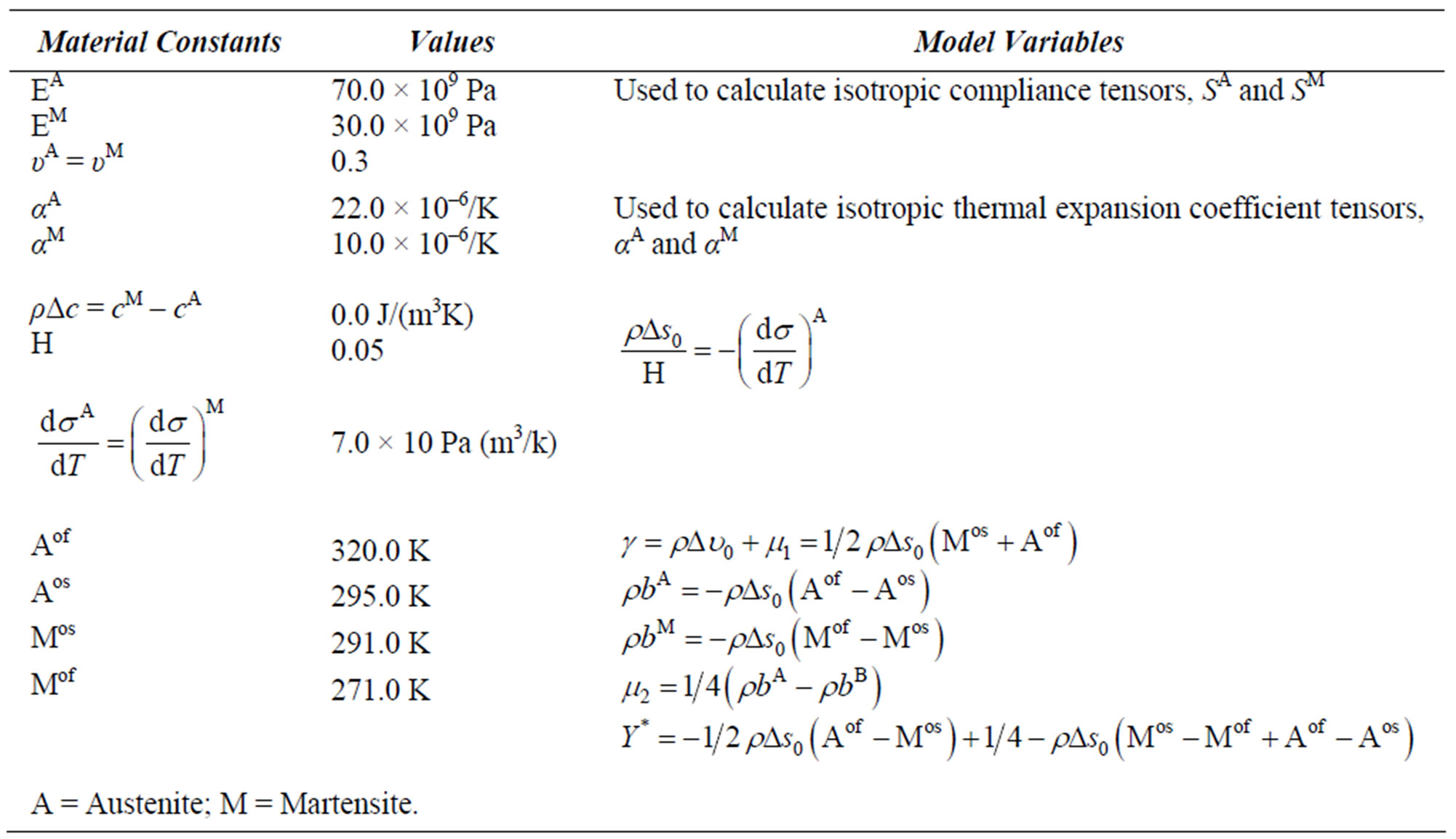
Table 1. Shape memory alloy materials parameters [11].
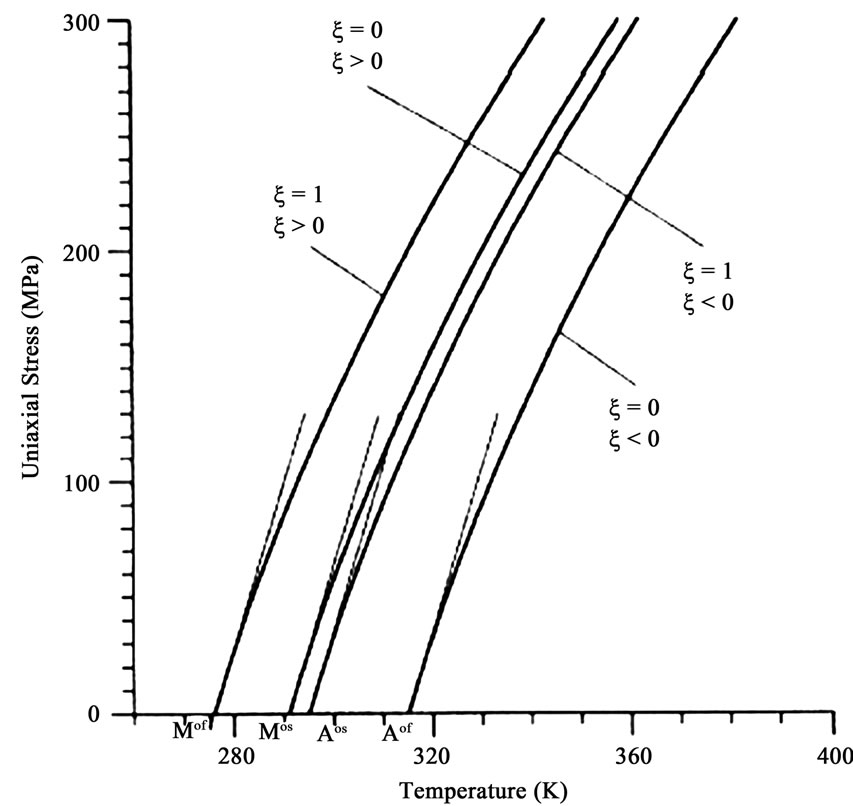
Figure 8. Shape memory alloy uniaxial stress-temperature phase diagram [10].
The thermomechanical loading history applied to the staple is as follows and consists of three steps:
1) Keeping the temperature fixed, T = 294 K (T < As), to open the prongs of the staple and applying a pressure on the extremities of the staple.
2) Unloading or removing the two previous forces.
3) Heating the staple heated up to T = 320 K (T > Af).
Shape Memory Effect
During the first test, the thermomechanic behavior of the free staple is observed. Figure 9 shows that the model
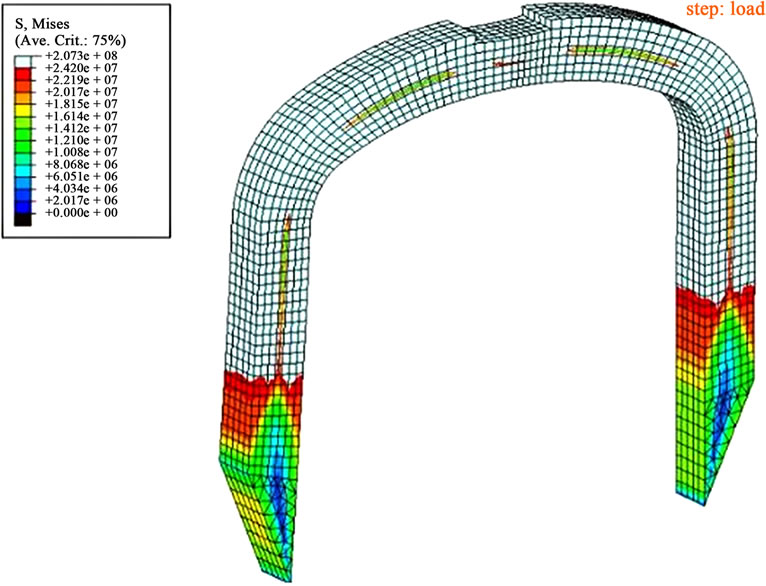 (a)
(a)  (b)
(b)  (c)
(c)
Figure 9. Shape memory effect of the staple with a free legs loading. (a) Loading; (b) Unloading; and (c) Heating.
has succeeded in reproducing the staple’s shape memory effect. After rendering the two prongs normal to the staple body and removing, the applied load the martensite production is noticed due to exceeding the constraint limits at the initial transformation. The staple undergoes a permanent deformation transformation which prevented the legs from returning to its initial shape. This shape can only be recovered from heating.
Notice that the presence of residual constraints after unloading will shift the final transformation temperature to austenite. This indicates that increasing the temperature to Af is insufficient to recover the initial form, and therefore, must be heated to a temperature much greater until the all the martensite vanishes.
We tried to model the obstacle caused by the bone using planar supports, which prevent the recovery of the staple legs, and are able to observe the force produced by the staple legs, where Figure 10(a) shows the load distribution on the legs. The curve shown in Figure 10(b) illustrates the variation of the load as a function of the temperature.
 (a)
(a) 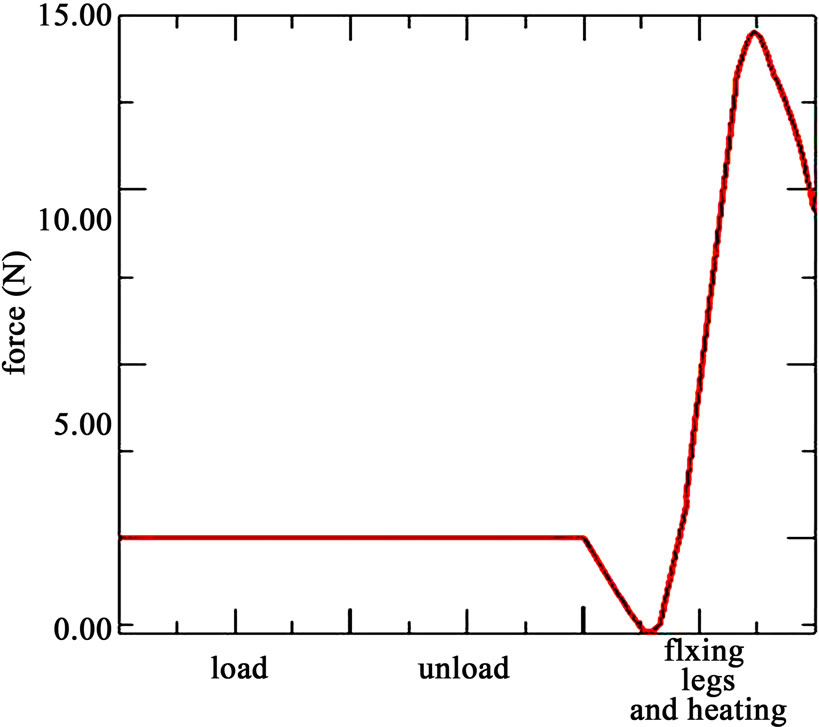 (b)
(b)
Figure 10. Stress generated after binding the legs and heating. (a) Stress distribution on the legs; (b) Variation of the total stress applied by the legs.
4. Conclusions
The template is designed so that author affiliations are we have proposed a computation tool for the design of SMA-based devices. The tool is based on two main compounds:
1) A three dimensional constitutive model able to reproduce the basic macroscopic features of shape memory material, such as the superelasticity, the shape memory behaviour, and different response under tension (and compression);
2) The development of a robust algorithm solution and the integration into a 3D model.
Another aspect of crucial importance, is that the complex thermomechanical loading history should be taken into account, as for the case of the SMA structure.
To establish the viability of the proposed approach we have simulated the superelasticity and the shape memory effect under the tensile and three point bending test of the orthopedic staple.
The numerical investigations demonstrated that the developed formulation is a powerful tool to study the 3D model of the shape memory alloy devices in biomedical application.
5. Acknowledgements
The authors would like to acknowledge the financial support of the Biomedical Science and Technologies Research Group (GRSTB), Fonds de la Recherche en Santé du Québec (FRSQ), the Natural Science and Engineering Research Council of Canada (NSERC—Strategic grant program), and Medtronic Sofamor Danek.
REFERENCES
- J. G. Boyd and D. C. Lagoudas, “A Thermodynamical Constitutive Model for Shape Memory Materials. Part 1. The Monolithic Shape Memory Alloy,” International Journal of Plasticity, vol. 2, No. 6, 1996, pp. 805-842. doi:10.1016/S0749-6419(96)00030-7
- E. Patoor, “Les alliages a mémoire de forme, ” HermesParis, Paris, 1990.
- X. D. Zhang, C. A. Rogers and C. Liang, “Modeling of the two way shape Memory Effect,” Journal of intelligent Material System and structures, vol. 80, No. 4, 1997, pp. 353-362.
- C.-Y. Chang, D. Vokoun and C.-T. Hu, “Two-Way Shape Memory Effect of NiTi Alloy Induced by Constraint Aging Treatment at Room Temperature,” Metallurgical and Materials Transactions A, Vol. 32, No. 7, 2001, pp. 1629- 1634. doi:10.1007/s11661-001-0141-7
- Z. Bo, D.C. Lagoudas and D. Miller, “Material Characterization of SMA actuators under Non proportional thermomechanical loading,” Journal of Engineering Material & Technology, Vol. 31, No. 1, 1998, pp. 75-85.
- F. Trochu and Y. Y. Qian, “Non linear finite element simulation of superelastic shape memory alloy parts I,” Computer & Structures, Vol. 62, No. 5, 1997, pp. 799- 810. doi:10.1016/S0045-7949(96)00288-X
- F. Trochu and P. Therriaul, “Non linear modeling of hysteretic laws by dual kriging and application,” Computer methods in applied mechanics and engineering, Vol. 151, No. 3-4, 1998, pp. 545-558. doi:10.1016/S0045-7825(97)00165-5
- F. Auricchio and E. Sacco, “One dimensional model for superelastic shape memory alloys with different elastic properties between austenite and martensite,” International Journal of non-linear Mechanics, Vol. 32, No. 6, 1997, pp. 1101-1114. doi:10.1016/S0020-7462(96)00130-8
- F. Auricchio and E. Sacco, “A SMA thermomechanical finite element beam model,” The International Organization on Shape Memory and Superelastic Technologies, Materials Park, 1997.
- F. Auricchio, “A robust integration algorithm for a finite strain shape memory alloy superelastic model,” Journal of Plasticity, Vol. 17, No. 7, 2001, pp. 971-990. doi:10.1016/S0749-6419(00)00050-4
- M. A. Qidwai, P. B. Entchev, D. C. Lagoudas and V. G. DeGiorgi, “Modeling of the Thermomechanical Behavior of Porous Shape Memory Alloys,” International Journal of Solids and Structures, Vol. 38, No. 48-49, 2001, pp. 8653-8671. doi:10.1016/S0020-7683(01)00118-4
- J. G. Boyd and D. C. Lagoudas, “A Thermodynamical Constitutive Model for Shape Memory Materials. Part 2. The Sma Composite Material,” International Journal of Plasticity, Vol. 12, No. 7, 1996, pp. 843-873. doi:10.1016/S0749-6419(96)00031-9
- D. A. Hodgson, “Using Shape Memory Alloys,” Shape Memory Applications, Sunnyvale, 1988.
- M. A. Schmerling, M. A.Wilkov and M. D. Sanders, “Proposed medical application of shape memory effect,” In: A NiTi Harrington Rod for the treatment of scoliosis, Shape Memory Effects in Alloy, Plenum Press, New York, 1975, pp. 563-574.
- V. Birman, “Review of mechanics of shape memory alloy structures,” Applied Mechanics Reviews, Vol. 50, No. 11, 1997, pp. 629-645. doi:10.1115/1.3101674
- K. Tanaka, “A Thermomechanical Sketch of Shape Memory Effect: One-Dimensional Tensile Behavior,” Res Mechanica, Vol. 2, No. 3, 1986, pp. 59-72.
- C. Liang and C. Rogers, “A multi dimensional constitutive model for shape memory alloys,” Journal of Engineering Mathematics, Vol. 26, No. 3, 1992, pp. 429-443. doi:10.1007/BF00042744
- D. C. Lagoudas, Z. Bo and M. A. Qidwai, “A Unified Thermodynamic Constitutive Model for Sma and Finite Element Analysis of Active Metal Matrix Composites,” Mechanics of Composite Materials and Structures, Vol. 3, No. 2, 1996, pp. 153-179. doi:10.1002/(SICI)1234-986X(199606)3:2<153::AID-MCM36>3.3.CO;2-J
- F. Auricchio and E. Sacco, “A temperature depend beam for shape memory alloys: constitutive modeling, finite element implementation and numerical simulation,” Computational Methods in Applied Mechanics & Engineering, Vol. 174, No. 1-2, 1999, pp. 171-190.
- F. Auricchio and E. Sacco, “Thermo-Mechanical modeling of a superelastic shape-memory wire under cyclic strenching-bending loading,” International Journal of Solids and Structures, Vol. 38, No. 34-35, 2001, pp. 6123- 6145.
- F. Auricchio, R. L. Taylor and J. Lubliner, “Shape memory alloys macromodeling and numerical simulations of the finite strain superelastic behaviour,” Computer Methods in Applied Mechanics and Engineering, Vol. 146, No. 3-4, 1997, pp. 281-312. doi:10.1016/S0045-7825(96)01232-7
- F. Auricchio and R. L. Taylor, “A Return-Map Algorithm for General Associative Isotropic Elasto-Plastic Materials in Large Deformation Regime,” International Journal of Plasticity, Vol. 15, No. 12, 1999, pp. 1359-1378. doi:10.1016/S0749-6419(99)00044-3
- E. Patoor and M. Berveiller, “Technologie Des Alliages A Mémoire De Forme,” Hermes-Paris, Paris, 1994.
- L. C. Brinson and M. S. Huang, “Simplifications and Comparisons of Shape Memory Alloy Constitutive Models,” Journal of Intelligent Material Systems and Structures, Vol. 7, No. 1, 1996, pp. 108-114. doi:10.1177/1045389X9600700112
- C. Lexcellent, B. C. Goo, Q. P. Sun and J. Bernardini, “Characterization thermomechanical behavior and micromechanical based constitutive model of shape memory Cu Zn Ni single crystal,” Acta Materialia, Vol. 44, No. 9, 1996, pp. 3773-3780. doi:10.1016/1359-6454(95)00452-1
- C. Lexcellent and J. Rejzner, “Modeling of the strain rate effect, creep and relaxation of a Ni-Ti shape memory alloy under tension (compression)-torsional proportional loading in the pseudoelastic range,” Smart Materials and Structure, Vol. 9, No. 5, 2000, pp. 613-621.
- M. Huang, X. Gao and C. Brinson, “A multi variant micromechanical model for SMAs Part 2. crystallographic issues for single crystal model,” International Journal of Plasticity, Vol. 16, No. 10-11, 2000, pp. 1371-1399. doi:10.1016/S0749-6419(00)00014-0
- X. Gao, M. Huang and C. Brinson, “A multivariant micromechanical model for SMAs Part 1. Crystallographic issues for single crystal model,” International Journal of Plasticity, Vol. 16, No. 10-11, 2000, pp. 1345-1369. doi:10.1016/S0749-6419(00)00013-9
- Q. P. Sun and K. C. Hwang, “Micromechanics modelling for the constitutive behavior of polycristalline shape memory Alloy (Part I and II),” Journal of the Mechanics and Physics of Solids, Vol. 41, No. 1, 1993, pp. 1-33. doi:10.1016/0022-5096(93)90060-S
- V. Kafka, “Mesomechanical constitutive modeling, Series on advances in Mathematics for Applied Sciences,” Institute of technology and applied Academy of Sciences, Czech Republic World Scientific, 2001.
- V. Kafka, “Shape memory under complex loading: mesomechanical modeling,” Acta Technica, Vol. 44, 1999, pp. 17-33.
- V. Kafka, “Two way shape memory its nature and modeling,” Acta Technica, Vol. 43, 1998, pp. 375-391.
- D. C. Lagoudas and S. G. Shu, “Residual deformation of active structures with SMA actuators,” International Journal of Mechaical Sciences, Vol. 41, No. 6, 1999, pp. 595- 619. doi:10.1016/S0020-7403(98)00035-6
- P. Terriault, F. Viens and V. Brailovski, “Non-isothermal finite element modeling of a shape memory alloy actuator using ANSY,” Computational Materials Science, Vol. 36, No. 4, 2006, pp. 397-410. doi:10.1016/j.commatsci.2005.05.010

