Agricultural Sciences
Vol.3 No.1(2012), Article ID:16853,9 pages DOI:10.4236/as.2012.31008
Evaluation of pan coefficient equations in a semi-arid Mediterranean environment using the ASCE-standardized Penman-Monteith method
![]()
Department of Hydraulics, Soil Science and Agricultural Engineering, School of Agriculture, Aristotle University of Thessaloniki, Thessaloniki, Greece; *Corresponding Author: vasanton@agro.auth.gr
Received 10 September 2011; revised 22 November 2011; accepted 6 December 2011
Keywords: Pan evaporation; reference evapotranspiration; ASCE-standardized Penman-Monteith
ABSTRACT
Reference crop evapotranspiration (ETo) is essential for irrigation, water resources management and environmental assessment. The indirect estimation of ETo is based a) on energy budget approach using meteorological data and b) pan evaporation measurements (Epan) multiplied by pan coefficients (kp) adapted to the surrounding environmental conditions. Significant interest is shown for the kp equations, which have to be tested before their use. The purpose of this study is to evaluate six different kp equations, such as those of Cuenca, Allen and Puitt, Snyder, Pereira et al., Orang, Raghuwanshi and Wallender for the summer growing season (April to October) of Thessaloniki plain in Greece, which is characterized by a semi-arid Mediterranean environment. The evaluation of the kp equations is performed by two years Epan measurements, using as reference the daily ETo values estimated by the ASCE-standardized Penman-Monteith equation (ASCE-PM) in hourly time step. The results of this study showed that Cuenca’s equation provided more accurate daily estimations. Additional analysis is performed in other methods such as those of FAO-56 and Hargreaves based on the calculation time step (hourly or daily) and their correspondence to the ASCE-PM.
1. INTRODUCTION
The reference crop evapotranspiration (ETo) constitutes the major factor for the accurate estimation of the crop water requirements, which are essential in irrigation planning, scheduling, hydrologic balance studies and watershed hydrology. Many methods have been proposed for the estimation of ETo, based on the energy budget approach, such as the corrected FAO-24 Blaney-Criddle method [1], the Priestley-Taylor method [2], the corrected FAO-24 Penman method [3], the Shuttleworth and Wallace method [4], the Hargreaves method [5], the FAO-56 Penman-Monteith method [6] and the ASCEstandardized Penman-Monteith method [7]. Numerous of empirical linear and non-linear equations have also been developed but with restricted validity at regional scale. The FAO-56 Penman-Monteith constitutes the most popular methodology in agricultural studies and the ASCEstandardized Penman-Monteith method was recently presented as an improvement of this by the ASCE-EWRI Task Committee [7].
Significant efforts for the correct estimation of ETo under the Greek environmental-meteorological conditions have been carried out by several researchers, which they focused on comparisons and sensitivity analysis between the aforementioned methods, their parameters and their calculation time step [8-11]. Additional studies have been performed for the development of new methodologies for the estimation of ETo using empirical equations such as the “Copais model” [12] or equations based on Penman formula with reduced parameters [13].
A different approach for ETo estimation is the use of pan evaporation measurements (Epan) and pan coefficients (kp). The kp is obtained as a constant value adjusted to specific environmental conditions [6] or as equations [14,15]. The use of Epan measurements and kp coefficients has the advantage of the low cost equipment, while it has the disadvantage of the kp calibration and the frequent visits for the preservation of water level and clarity versus the agro-meteorological stations.
The objective of this study is to compare and evaluate different equations for the pan coefficient kp using ClassA pan evaporimeter measurements for the estimation of ETo during the summer crop growing season (April to October). Measurements were obtained in Thessaloniki region, which is under a semi-arid Mediterranean environment and constitutes one of the major plains for agricultural production in Greece. Due to the lack of equipment for the direct measurement of the reference crop evapotranspiration (e.g. weighted lysimeters), the method of ASCE-standardized Penman-Monteith method (ASCE-PM) calculated in hourly time step, was selected to be used as reference for the comparisons between the different kp equations. The comparison between the ASCE-PM and other popular methods such as those of FAO-56 Penman-Monteith and Hargreaves was also performed.
2. METHODOLOGY AND DATA
2.1. Estimation of the Reference Crop Evapotranspiration
2.1.1. The Methods of ASCE and FAO-56 Penman-Monteith
ASCE-EWRI (2005) have proposed two reference crops, a short crop similar to a clipped-grass (0.12 m height) and a tall crop similar to a full cover alfa-alfa (0.5 m height) [7]. Considering the two reference crops, the ASCE-EWRI Task Committee revised and improved the FAO-56 Penman-Monteith (FAO56-PM) equation, presenting the new ASCE Penman-Monteith (ASCE-PM) method. The equation of ASCE-PM using daily or hourly time step for the two different cases of reference crop is given by [7]:
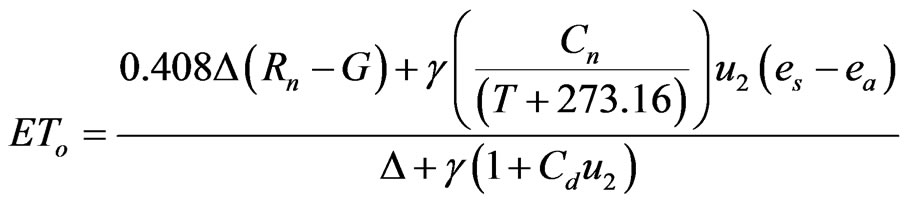 (1)
(1)
where ΕΤο is the reference crop evapotranspiration for short (ETos) or tall (ETrs) reference crops (mm·d−1 for daily time step or mm·h−1 for hourly time step), Rn is the net radiation at the crop surface (MJ·m−2·d−1 for daily time step or MJ·m−2·h−1 for hourly time step), u2 is the mean daily or hourly wind speed at 2 m height (m·s−1), T is the mean daily or hourly air temperature at 2 m height (˚C), G is the soil heat flux density at the soil surface (MJ·m−2·d−1 for daily time step or MJ·m−2·h−1 for hourly time step), es is the daily or hourly saturation vapor pressure (kPa), ea is the daily or hourly mean actual vapor pressure (kPa), Δ is the slope of the saturation vapor pressure-temperature curve (kPa·˚C−1), γ is the psychrometric constant (kPa·˚C−1), Cn and Cd are constants, which vary according to the time step, the reference crop type (bulk surface resistance, and aerodynamic roughness of the surface) and daytime/nighttime ratio.
According to the time step and the type of the reference crop, the values of Cn, Cd and G are modified and the eq.1 is referred to different methods (Table 1):
• Two cases for daily time step a) the ΑSCE-PMos(d) which is the same with the FAO56-PM(d) for short reference crop and b) the ASCE-PMrs(d) for tall reference crop.
• Three cases for hourly time step calculations a) the ΑSCE-PMos(h) for short reference crop, b) the ASCE-PMrs(h) for tall reference crop and c) the FAO56-PM(h) for short reference crop.
The calculation of saturation vapour pressure es, actual vapour pressure ea, net longwave radiation Rnl and soil heat flux G is carried out by different equations accordingly to the time step [6,7]. The selected equations of es, ea and Rnl, that concern the daily calculations, were chosen after comparisons with the respective ones that concern the hourly time step calculations (Table 1 and Appendix).
2.1.2. Hargreaves Method
The Hargreaves equation HG(d) [5] is calculated in a daily step and is given by:
 (2)
(2)
where ΕΤο is the reference crop evapotranspiration (mm·d−1), Tmean is the mean daily air temperature (˚C),

Table 1. Characteristics of the selected reference crop evapotranspiration methods.
Tmin is the minimum daily air temperature (˚C), Tmax is the maximum daily air temperature (˚C), Ra is the total extraterrestrial solar radiation (mm·d−1), αh, bh and ch are Hargreaves’ equation coefficients (Table 1).
2.2. Epan and Pan Coefficient Equations
One of the most popular methods for the indirect ΕΤο estimation is through Εpan measurements and kp coefficients adjusted to the surrounding environment and conditions (e.g. relative humidity, wind speed and windward side distance of green crop or a dry fallow).
The relationship between ΕΤο and Εpan is given by the following equation [6]:
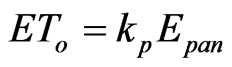 (3)
(3)
where Epan is the pan evaporation (mm·d−1) and kp is the pan coefficient.
Based on literature review, the values of kp cover a range between 0.3 and 1.1, and are proportional to relative humidity and inverse proportional to wind speed [6,14,15]. Significant efforts have been performed for the indirect estimation of kp by equations, that use meteorological data and the characteristics of the surrounding environment, such as those of Cuenca [16], Allen and Puitt [3], Snyder [17], Pereira et al. [18], Orang [19], Raghuwanshi and Wallender [20] for the case of Class-A pan evaporimeter. The above equations are used for the estimation of ETo for the short reference crop and are given, respectively, by:
 (4)
(4)
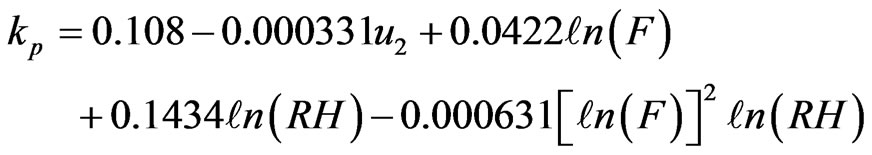 (5)
(5)
 (6)
(6)
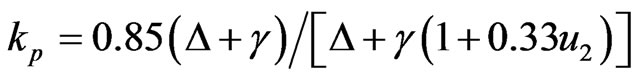 (7)
(7)
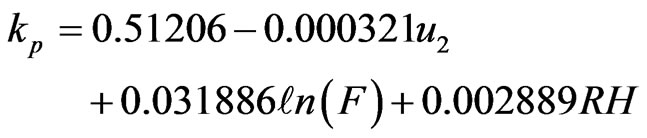 (8)
(8)
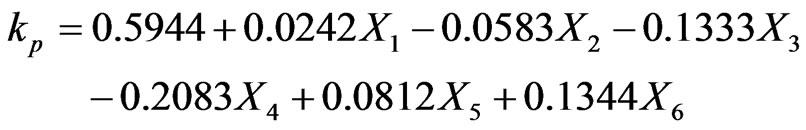 (9)
(9)
where RH is the mean daily relative humidity (%), u2 is the mean daily wind speed at 2 m above the soil surface (in km·d−1 for the Eqs.4, 5, 6, 8 and in m·s−1 for the eq.7) and F is the windward side distance of green crop or a dry fallow (m). For the eq.9, X1 = ln(F), X2, X3 and X4 are wind speed categories of 175 - 425, 425 - 700, and >700 km·d−1, respectively, and are assigned values of one or zero depending upon their presence. A zero value for these variables represents a wind speed of <175 km·d−1. Similarly, X5 and X6 are relative humidity categories of 40% - 70% and ≥70%, respectively. Again the values of one or zero were assigned depending on their presence and a zero value for these variables represents a relative humidity of ≤40%.
2.3. Study Site and Measurements
Hourly meteorological data of temperature, relative humidity, solar radiation, wind speed and precipitation obtained by the meteorological station of the Aristotle University of Thessaloniki farm (40˚32'08''Ν, 22˚59'18''Ε), covering the summer growing season (April to October) for three years (2008-2010) were used for the ETo estimations. The mean monthly values of the meteorological data for the period 2008-2010 are presented in Table 2.
Daily Epan measurements were colected using Class-A pan evaporimeter for two years (2008-2009). The data describe adequately the meteorological conditions of the Thessaloniki plain, where the climate is considered as a semi-arid Mediterranean environment.
3. RESULTS AND DISCUSSION
3.1. Estimation and Evaluation of ETo Methods
The daily ETo for the summer growing season (April to October) was estimated using the methods presented in Table 1. The daily ΕΤο values of ASCE-PM method, calculated for hourly time-step, were used as reference for the comparisons among the methods presented in Table 1. The mean daily values of ΕΤο (mm·d−1) for each method and the transition coefficients for each one in order to be converted in ASCE-PMos(h) are given in Table 3.
The comparisons among the methods for the short reference crop are given in Figures 1(a)-(c), while for the tall reference crop in Figure 1(d). The statistical tests of the coefficient of determination (R2), the root mean square error (RMSE) and the mean bias error (MBE) were used for the comparison analysis [12,21] and are given by:
 (10)
(10)
 (11)
(11)

Table 2. Mean monthly values of the meteorological parameters during the period of April-October for 2008-2010.
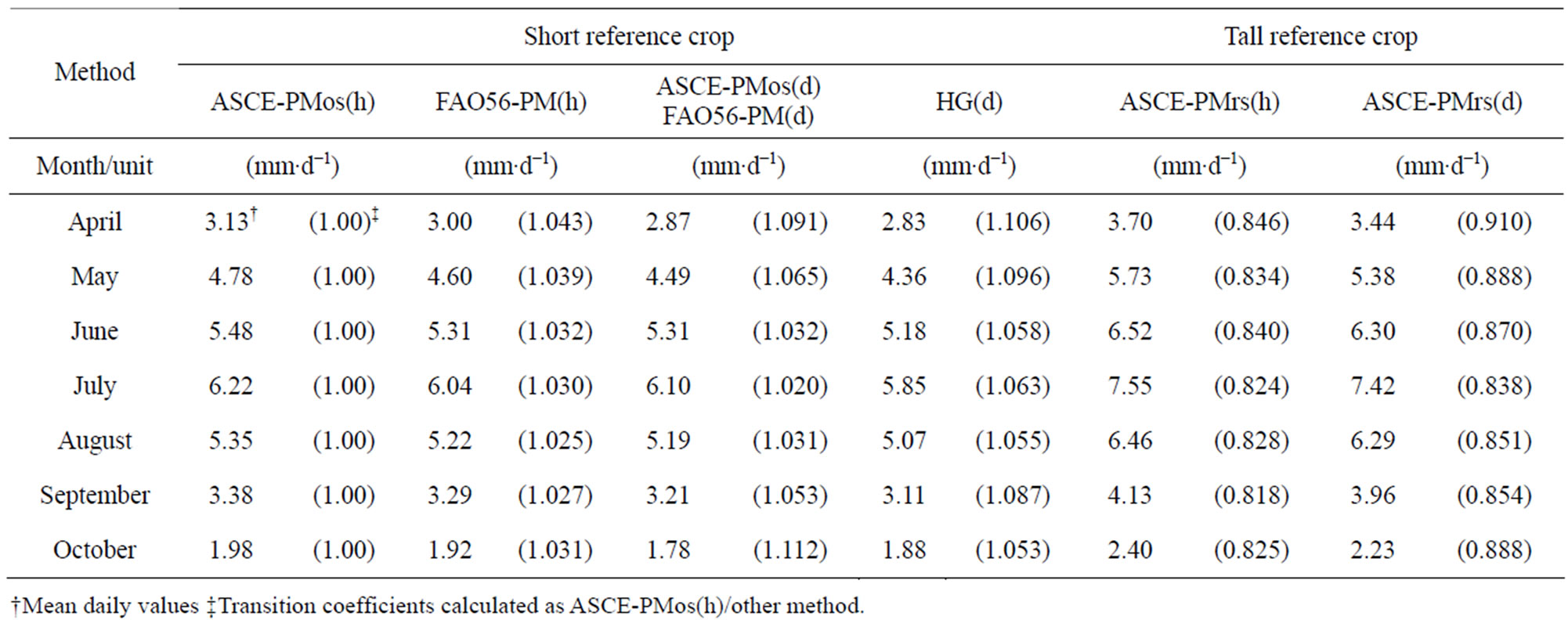
Table 3. Mean daily values of ΕΤο (mm·d−1) for each method and transition coefficients for each method using the daily ΕΤο values of ASCE-PMos(h) as reference.
 (12)
(12)
where O are the observed values (the reference values of ASCE-PM in hourly time step), C are the computed values by the other methods and Om and Cm are the mean observed and computed values, respectively.
The results showed a relative underestimation of the calculated ΕΤο (relatively small values of RMSE and negative values of MBE) for all the methods compared to the daily ΕΤο values of ASCE-PM method in hourly time-step, for both cases of the reference crop. Considering the simplicity of the Hargreaves model, it was found a very good correspondence with the ASCEPMos(h), but it deflects for the days where the wind speed override the values of 1.5 - 2.0 m·s−1. In order to correct the results of each method using the ASCE-PM(h) as reference for the summer growing season, either the transition coefficients for each month or the regression equations from Figure 1 can be used. The ETo values of the ASCE-PM(h) for the tall reference crop were found about 10% - 20% higher of those for short reference crop. The transition coefficients also allow the conversion from tall to short ETo values and the opposite.
3.2. Evaluation of Pan Coefficients Equations
The evaluation of kp selected equations (Eqs.4 to 9) was performed using as reference the ASCE-PMos(h) and the daily Epan measurements of a Class-A pan evaporimeter, which was established at F = 0.25 m from active growing crop (Figures 2(a)-(f)). The mean monthly observed values of kp derived by the ratio ASCEPMos(h)/Epan, for the total period of April to October, were 0.7 and 0.71 for 2008 and 2009, respectively. The mean monthly kp values for the 2-years study period using the eqs.3 up to 9 are given in Table 4. Using the ASCE-PMos(h) for the estimation of the daily ETo and the statistical criteria of R2, RMSE and MBE (Figure 2) from the comparison analysis between the different kp equations, resulted the following order in prediction ac-
 (a)
(a) (b)
(b) (c)
(c)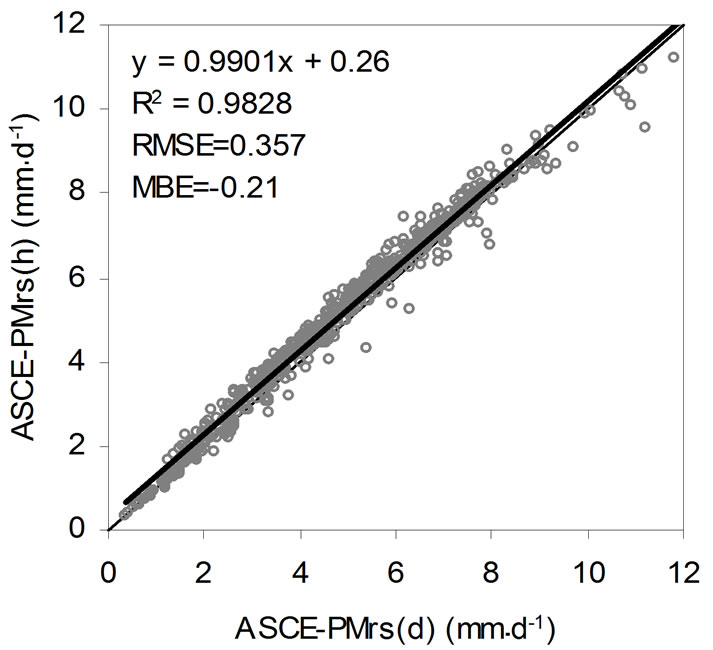 (d)
(d)
Figure 1. Comparison of the daily ETo estimated by the methods of ASCE-PMos(h) against (a) FAO56-PMos(h); (b) FAO56-PMos(d); (c) HG(d) for short reference crop and (d) by ASCEPMrs(d) for tall reference crop.

Table 4. Mean monthly values of the observed kp (ETo/Epan) and mean monthly values using the different kp equations.
curacy: Cuenca (eq.4) > Raghuwanshi & Wallender (eq. 9) > Allen & Pruit (eq.5) > Pereira et al. (eq.7) > Orang (eq.8) > Snyder (eq.6). The equation of Cuenca indicated the best adaptation to the ASCE-PMos(h) method compared to the other equations and adequate performance for the estimation of ETo under the climatologicalenvironmental conditions of the study area.
Taking into account the results of other similar studies
 (a)
(a) (b)
(b)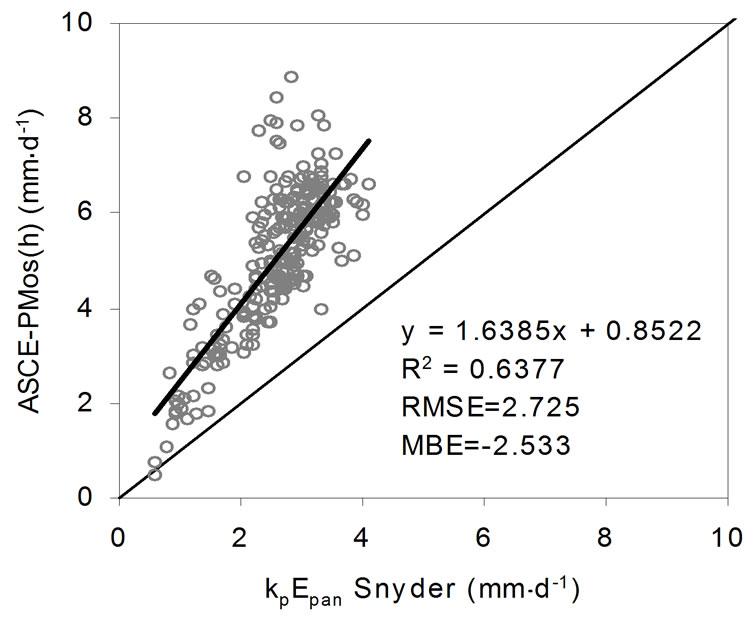 (c)
(c)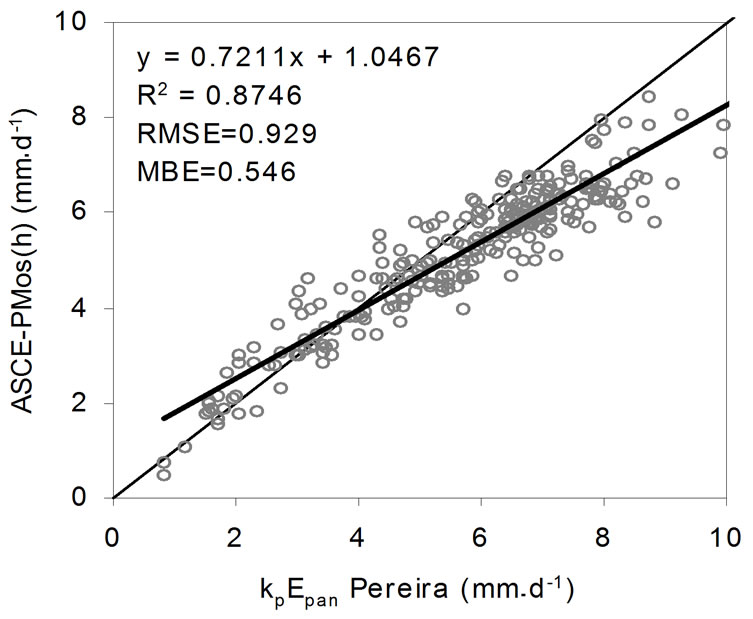 (d)
(d) (e)
(e) (f)
(f)
Figure 2. Comparison of the daily ETo estimated by ASCE-PMos(h) method and by eq.3 using the different kp equations (a) Cuenca; (b) Allen & Pruitt; (c) Snyder; (d) Pereira et al.; (e) Orang and (f) Raghuwanshi & Wallender.
[14,15], different predictive accuracy is observed among the aforementioned kp equations, which can be ascribed a) mainly to the different reference evapotranspiration method, which is used for the comparisons and b) secondly to the different climatic-environmental conditions. This indicates the necessity to validate these equations before their use.
4. CONCLUSIONS
Reference crop evapotranspiration was calculated for the irrigation period and three succeeding years using the proposed by ASCE, FAO and Hargreaves methods. Meteorological data from Thessaloniki in Northern Greece were used. ASCE-standardized Penman-Monteith method considered the reference method to evaluate the performance of the other methods.
Evaluation of the FAO-56 and Hargreaves methods was based on the calculation time step (hourly or daily) and their correspondence to the ASCE-PM. From the comparison between the different ETo methods a relative underestimation of the calculated ΕΤο was found for all the methods compared to the daily values of ASCEPM(h), calculated in hourly time step, for both cases of the reference crop. Considering the simplicity of the Hargreaves model, it was found a very good correspondence with the ASCE-PMos(h), but it deflects for the days where the wind speed override the values of 1.5 - 2.0 m·s−1.
ETo was also calculated using measurements of pan evaporation and six equations for pan coefficient (kp) estimation. These values evaluated in relation of ASCEPM method. The comparison analysis between the different kp equations resulted the following order in prediction accuracy: Cuenca > Raghuwanshi & Wallender> Allen & Pruit > Pereira et al. > Orang > Snyder. The Cuenca’s equation indicated the best adaptation to the ASCE-PM method compared to the other equations and adequate performance for the estimation of ETo under the climatological-environmental conditions of the study area.
REFERENCES
- Doorenbos, J. and Pruitt, W.O. (1977) Guidelines for predicting crop water requirements. Irrigation and Drainage Paper No. 24, (1st and 2nd Edition). Food and Agriculture Organization of the United Nations, Rome, 179 and 156 pp.
- Priestley, C.H.B. and Taylor R.J. (1972) On the assessment of surface heat flux and evaporation using largescale parameters. Monthly Weather Review, 100, 81-92. doi:10.1175/1520-0493(1972)100<0081:OTAOSH>2.3.CO;2
- Allen, R.G. and Pruitt, W.O. (1991) FAO-24 reference evapotranspiration factors. Journal of Irrigation and Drainage Engineering, 117, 758-773. doi:10.1061/(ASCE)0733-9437(1991)117:5(758)
- Shuttleworth, W.J. and Wallace, J.S. (1985) Evaporation from sparse crops—An energy combination theory. Quarterly Journal of the Royal Meteorological Society, 111, 839-855. doi:10.1256/smsqj.46909
- Hargreaves, G.H. and Samani, Z.A. (1985) Reference crop evapotranspiration from temperature. Transactions of ASAE, 1, 96-99.
- Allen, R.G., Pereira, L.S., Raes, D. and Smith, M. (1998) Crop Evapotranspiration: Guidelines for computing crop water requirements. Irrigation and Drainage Paper No. 56, Food and Agriculture Organization of the United Nations, Rome, 300 pp.
- ASCE-EWRI (2005) The ASCE standardized reference evapotranspiration equation. Technical Committee Report to the Environmental and Water Resources Institute of the American Society of Civil Engineers from the Task Committee on Standardization of Reference Evapotranspiration. ASCE-EWRI, 1801 Alexander Bell Drive, Reston, VA 20191-4400, 173 Pages.
- Papamichail, D.M. and Terzidis, G.A. (1996) Assessment of the Meteorological Parameters—Effects on the Daily Penman Reference Evapotranspiration. 2nd International Symposium on Irrigation of Horticultural Crops, Chania, Acta Horticulturae, 449, 281-288.
- Papamichail, D.Μ. and Georgiou, P.Ε. (1999) Comparative analysis of hourly and daily estimates of reference evapotranspiration by using FAO Penman-Monteith equation. Proceedings of the 4th National Conference of the Greek Committee for Water Resources Management, Volos, 183-189 (in Greek).
- Ampas, V., Baltas, E. and Papamichail, D. (2006) Comparison of different methods for the estimation of the reference crop evapotranspiration in the Florida region. WSEAS Transactions on Environment and Development, 12, 1449-1454.
- Anadranistakis, M., Liakatas, A., Kerkides, P., Rizos, S., Gavanosis, J. and Poulovassilis, A. (2000) Crop water requirements model tested for crops grown in Greece. Agricultural Water Management, 45, 297-316. doi:10.1016/S0378-3774(99)00106-7
- Alexandris, S., Kerkides, P. and Liakatas, A. (2006) Daily reference evapotranspiration estimates by the “Copais” approach. Agricultural Water Management, 82, 371-386.
- Valiantzas, J.D. (2006) Simplified versions for the Penman evaporation equation using routine weather data. Journal of Hydrology, 331, 690-702. doi:10.1016/j.jhydrol.2006.06.012
- Gundekar H.G., Khodke, U.M., Sarkar, S. and Rai, R.K. (2008) Evaluation of pan coefficient for reference crop evapotranspiration for semi-arid region. Irrigation Science, 26, 169-175. doi:10.1007/s00271-007-0083-y
- Rahimikhoob, A. (2009) An evaluation of common pan coefficient equations to estimate reference evapotranspiration in a subtropical climate (north of Iran). Irrigation Science, 27, 289-296. doi:10.1007/s00271-009-0145-4
- Cuenca, R.H. (1989) Irrigation system design: An engineering approach. Prentice Hall, Englewood Cliffs, 552.
- Snyder, R.L. (1992) Equation for evaporation pan to evapotranspiration conversions. Journal of Irrigation and Drainage Engineering, 118, 977-980. doi:10.1061/(ASCE)0733-9437(1992)118:6(977)
- Pereira, A.R., Villanova, N., Pereira, A.S. and Baebieri, V.A. (1995) A model for the class—A pan coefficient. Agricultural Water Management, 76, 75-82.
- Orang, M. (1998) Potential accuracy of the popular nonlinear regression equations for estimating pan coefficient values in the original and FAO-24 tables. Unpublished rep. California Department of Water Resources, Sacramento.
- Raghuwanshi, N.S. and Wallender, W.W. (1998) Converting from pan evaporation to evapotranspiration. Journal of Irrigation and Drainage Engineering, 118, 977- 980.
- Antonopoulos, V. and Wyseure, G. (1998). Modeling of water and nitrogen dynamics on an undisturbed soil and a restored soil after open-cast mining. Agricultural Water Management, 37, 21-40. doi:10.1016/S0378-3774(98)00040-7
APPENDIX. EQUATIONS FOR INTER-CALCULATIONS (ASCE-EWRI, 2005)
For hourly time step calculations:
 (A1)
(A1)
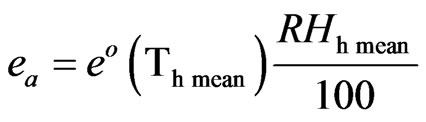 (A2)
(A2)
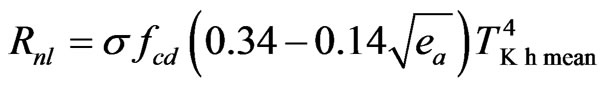 (A3)
(A3)
For daily time step calculations:
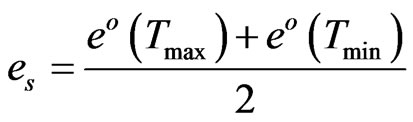 (A4)
(A4)
 (A5)
(A5)
 (A6)
(A6)
where RHhmean: mean hourly relative humidity (%), Thmean and TKhmean: mean hourly air temperature in (˚C) and in (K), respectively, Rnl: mean hourly or daily net longwave radiation (MJ·m−2·h−1 or MJ·m−2·d−1), σ: StefanBoltzman constant, es: daily or hourly saturation vapor pressure (kPa), ea: daily or hourly mean actual vapor pressure (kPa), fcd: factor of relative cloudiness 0.05 ≤ fcd ≤ 1.0, Τmean, Τmax, Τmin: mean, maximum and minimum daily temperature, respectively in (˚C), ΤKmean, ΤKmax, ΤKmin: mean, maximum and minimum daily temperature, respectively in (K), and RHmean, RHmax, RHmin: mean, maximum and minimum daily relative humidity (%).

