Journal of Data Analysis and Information Processing
Vol.03 No.04(2015), Article ID:61409,9 pages
10.4236/jdaip.2015.34018
Role of Feature Selection on Leaf Image Classification
Arun Kumar1*, Vinod Patidar2, Deepak Khazanchi3, Poonam Saini1
1Department of Computer Science and Engineering, Sir Padampat Singhania University, Udaipur, India
2Department of Physics, Sir Padampat Singhania University, Udaipur, India
3College of Information Sciences and Technology, University of Nebraska, Omaha, NE, USA

Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).


Received 30 October 2015; accepted 21 November 2015; published 24 November 2015

ABSTRACT
The digital images have been studied for image classification, enhancement, image compression and image segmentation purposes. In the present work, it is proposed to study the effects of feature selection algorithm on the predictive classification accuracy of algorithms used for discriminating the different plant leaf images. The process involves extracting the important texture features from the digital images and then subjecting them to feature selection and further classification process. The leaf image features have been extracted by using Gabor texture features and these Gabor features are subjected to Random Forest feature selection algorithm for extracting important texture features. The four classification algorithms like K-Nearest Neighbour, J48, Classification and Regression Trees and Random Forest have been used for classification purpose. This study shows that there is a net improvement in the predictive classification accuracy values, when classification algorithms have been applied on selected features over the complete set of features.
Keywords:
Leaf Image, Feature Selection Algorithm, Random Forest, Gabor Texture Features

1. Introduction
With the increase in human population, human beings are building their abode in the areas on earth inhabited by trees, herbs and shrubs. In this process, the vegetation is losing its existence and even some of the plant species are on the verge of extinction. Therefore, it has become quite imperative that different plant species must be preserved for future. But the biggest hurdle in preserving the different plant species lies in first knowing them and then taxonomically classifying them according to their species. There are millions of plant species on this planet earth. A considerable number are still unknown or have regional or geographical variants untouched by the biologists, and very soon will be wiped out of this planet, due to negligence or due to the human needs for homes, roads and bridges etc. For classifying the plants, the different parts of the plants roots, shoots, seeds and flowers have been studied either independently or in groups.
The biologist is doing commendable work in taxonomically classifying and preserving the different plant species for future use. With the advancement in the technology, computer scientists and technologists are playing a crucial role by providing newer tools for understanding such species. The computer scientists are trying to understand the different plant species in a different way by applying image processing and machine learning techniques. These techniques involve fetching the features from the image data through different devices, sensors, statistical observations and analyzing these characteristic features for a meaningful plant classification. The concept of plant classification using image processing techniques involves studying the images of the leaves, flowers and their placement on the plant. The classification of plants leaf needs the study of its geometrical shape, venation pattern, color and texture through their digital images.
According to [1] , the size of the dataset can be measured in two dimensions and they are: number of features (N) and number of instances (P). In the present scenario, both N and P are enormously large. This leads to the fact that there is a need to identify the subset of features according to a certain criterion and this can be used as tool to study the datasets. When N (i.e. the number of features) is reduced, the value of P (i.e. the number of instances) gets automatically reduced, and the size of the overall dataset shrinks and a small unique dataset is formed which is devoid of unwanted, irrelevant and duplicate features and is ready for further analysis. Therefore, it can be stated that the basic motto of feature selection techniques is to find and learn some unique functions from the patterns available from the dataset undertaken for study and then makes the new pattern recognized by these learning functions.
According to [2] [3] , the process of feature selection helps in improving the predictive classification accuracy and reduces the time required for computation, thereby making the dataset comprehensible. The feature selec- tion methods have been grouped into three major categories. Firstly, in the case of embedded methods for fea- ture selection, such methods are part of the predictors as in the case of decision trees and neural networks. In the case of filtering methods, they are independent of predictors and base themselves on the ranking of the features and measures the indices of the relevance of the feature quality from the subset of features selected. In the case of filtering techniques, correlation, chi-square and probability of distribution are often used as methods to find the relevant features. The third category is called wrappers which wrap around certain predictors and check the performance on them. The dataset is divided into training set and testing set to test the predictor’s performance.
The concept of feature selection algorithms is very popular in machine learning problems involving digital images. The digital images have been studied for image classification, enhancement, image compression and image segmentation purposes. Each digital image is made up of pixels of different intensity values and is placed in a pattern. The human beings can detect or distinguish different objects through their eyes using certain peculiar characteristic features of the objects like color, shape, geometry or texture features. When the new subset of the object is presented to the human beings, the object becomes discernible as the brain makes a comparative analysis of the new subset with that of the existing feature set in the brain. In the case of machine learning as well, there is a need for a feature set containing different characteristic features of the object of interest, may be digital images or any measurable object. The characteristic feature set of such objects is studied and subjected to feature selection and further classification process.
In this work, it is proposed to study the effect of feature selection algorithm on the predicative classification accuracy of algorithms used for discriminating the different plant leaf images. The process involves extracting the important texture features from the digital images and then subjecting them to feature selection and further classification process. Section 2 describes about the methodology adopted to find the features from the leaf images of different plant species and preparation of the feature set. Section 3 describes about the application of feature selection algorithm in extracting useful features. Section 4 describes about the application of classification algorithms like KNN, J48, CART and RF on two different sets of data one representing all the features extracted from the leaf images and the second one representing the chosen few features. Section 5 represents the result analysis and comparative study with other works of similar nature.
2. Gabor Texture Feature Extraction
The present work involves studying the effect of feature selection algorithm on the predictive accuracy of the classifiers working with digital leaf image datasets. In this work, 250 images of 10 plant species have been ta- ken for the experimental purpose and a sample of the leaf image dataset is shown in Figure 1. The colored leaf images were converted to gray scale and the size of all the images was reduced to 256 × 256. Each gray scaled slice of a leaf image was preprocessed and background was removed and its contrast and intensity values were enhanced [4] as shown in Figure 2. Figure 2 shows the Slice-1 in gray scale and its enhanced image has been shown as Slice-1E, the next part of Figure 2 shows the histogram of the Slice-1 and that of the Slice-1E. The histogram of Slice-1 shows that the distribution of the pixels concentrated in a region whereas the histogram of Slice-1E shows that the pixel intensities have been distributed over a wider region.
To pursue, work in the area of digital images, there is a need to extract important features. Texture is a basic characteristic visual feature, which helps the human visual system in segmentation and recognition based processes, performed by human brain. Texture based features in computer vision science have been playing its role for the last couple of years. Textures can be divided into two categories, namely, tactile and visual textures. Tactile textures refer to the immediate tangible feel of a surface. Visual textures refer to the visual impression that textures produce to human observer, which are related to local spatial variations of simple stimuli like color, orientation and intensity in an image [5] .
In this study, Gabor features have been extracted from the enhanced images. The term Gabor filter has been coined after the name of Dennis Gabor, who in the year 1946 experimented and subsequently proposed the representation of the signals. In image processing tasks, Gabor filters have been extensively been used for feature extraction for the digital leaf images. The frequency and orientation representation as used in Gabor filters, are useful for texture representation and discrimination and the same concept is used in human visual system. The Gabor features are invariant to illumination, rotation, scale and translation. The Gabor filters have several advantages in feature extraction process over other techniques such as Gray Level Co-occurrence Matrix (GLCM). The Gabor feature vectors can be used directly, as input to a classification or segmentation operator or they can first be transformed into feature vectors which are then used as input to another stage. The Gabor features have been successfully used in face recognition, character recognition, browsing and retrieving of image data, to name a few areas where Gabor features have created a niche for themselves. The Equations (1), (2) and (3) re- present Gabor Theory [5] .
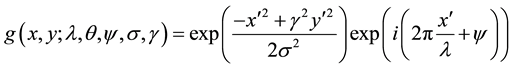 (1)
(1)
Figure 1. A sample of dataset of colored leaf images.
Figure 2. Leaf image for Slice-1 and its enhanced leaf image Slice-1E with their respective histograms.
The Equation (1) represents the complex form of the Gabor representation
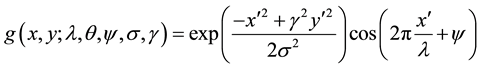 (2)
(2)
The Equation (2) represents the real part of the Gabor representation
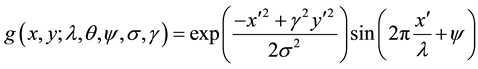 (3)
(3)
The Equation (3) represents the imaginary part, where
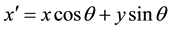 and
and
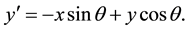
In these equations,
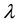 represents the wavelength of the sinusoidal factor,
represents the wavelength of the sinusoidal factor,
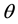 represents the orientation of the normal to the parallel stripes of a Gabor function,
represents the orientation of the normal to the parallel stripes of a Gabor function,
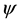 is the phase offset,
is the phase offset,
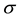 is the sigma or the standard deviation of the Gaussian envelop and
is the sigma or the standard deviation of the Gaussian envelop and
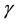 is the spatial aspect ratio and specifies the ellipticity of the support of the Gabor function. A single Gabor filter will detect patterns in the leaf images with a certain fixed frequency and an orientation value. To capture the entire texture features available in the digital image, the Gabor filter bank is tuned at different frequency and orientation values. For each image in the dataset, the Gabor filter generates 32 real images for 4 different values of Scale (2, 4, 8, 16) and 8 different orientation values (22˚, 44˚, 66˚, 88˚, 110˚, 132˚, 154˚, 176˚).
is the spatial aspect ratio and specifies the ellipticity of the support of the Gabor function. A single Gabor filter will detect patterns in the leaf images with a certain fixed frequency and an orientation value. To capture the entire texture features available in the digital image, the Gabor filter bank is tuned at different frequency and orientation values. For each image in the dataset, the Gabor filter generates 32 real images for 4 different values of Scale (2, 4, 8, 16) and 8 different orientation values (22˚, 44˚, 66˚, 88˚, 110˚, 132˚, 154˚, 176˚).
Figure 3 shows the 32 images obtained by convolving the enhanced image Slice-1 with Gabor Filter and Figure 4 shows the details of the 32 images at different scale and orientation values.
After the images had undergone the process of image enhancement, a stack of enhanced images was prepared. This stack was subjected to the process of feature extraction using Gabor filters [5] and six texture features namely Mean, Energy, Standard Deviation, Skewness, Contrast and Kurtosis were derived and the measured values were stored in separate CSV file, for classification purpose as mentioned in next sections.
・ Mean (GTF1): It is denoted as mentioned in Equation (4).
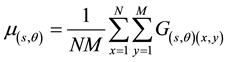 (4)
(4)
・ Energy (GTF2): The texture energy is expressed as
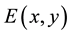 and is mentioned in Equation (5).
and is mentioned in Equation (5).
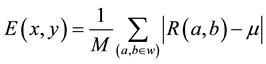 (5)
(5)
・ Standard Deviation (GTF3): The standard deviation has been calculated as mentioned in Equation (6).
Figure 3. Slice-1 convolved with Gabor filter, generates 32 images at different scales and orientation values.
Figure 4. Image details for Slice-1 convolved with Gabor filter, generates 32 images at different scales and orientation values.

・ Skewness (GTF4): Skewnessis the measure of asymmetry and is denoted by

・ Contrast (GTF5) and Kurtosis(GTF6): Contrast is expressed as


where

The Gabor Texture Feature Dataset (GTFD) has been prepared using all the six Gabor features extracted and has been shown in Equation (9).

Here

3. Application of Random Forest Algorithm for Feature Selection
A two copies of CSV file of data with six features has been prepared using Equation (9). One copy of the file has been preserved for classification purpose and the other copy has been subjected to feature selection algo- rithm.
Automatic feature selection methods can be used to build many models with different subsets of a dataset and identify those attributes that are not required to build an accurate model [1] [5] .
In this algorithm, dataset is divided into training and test sets. The training set is trained over all the predica- tors. The predictive accuracy of the unknown sample is calculated and then the variable importance is calculated. Now the training set is again trained over the few important variable having higher ranking than others and the predictive accuracy of the unknown sample is again calculated. The appropriate number of predictors are identi- fied and the model is prepared over the new set of predictors. The variable importance depends upon the interac- tion of the variables with each other. The Random Forest algorithm estimates the importance of variables by looking at how the prediction error increases, when the out of bag (OOB) data are permuted while others are left unchanged.
In this present study, there are six predictor variables as mentioned in Section 2, they are subjected to random feature elimination algorithm to find the best features, avoiding correlated variables as far as possible. Figure 5 shows the resampling performance over a subset size using 10-fold cross-validation technique. Figure 5 shows the use of number of variables on the x-axis plotted against predictive accuracy values (10-fold cross validated). From Figure 5, it is clear that out of six features, it is appropriate to choose five features which shall provide comparable accuracy results as are provided by using six features.
Figure 6 shows the plot for variable importance (VIMP). The left part of Figure 6 shows mean decrease in the accuracy values plotted against the features of the dataset and it has been observed that GTF3 has the highest value of 158.024 which makes it the most important variable and GTF2 has the lowest value of 109.50 making it the least important variable in the dataset.
The mean decrease in accuracy a variable causes is determined during the out of bag error calculation phase. The more the accuracy of the random forest decreases due to the exclusion (or permutation) of a single variable, the more important that variable is deemed, and therefore variables with a large mean decrease in accuracy are
Figure 5. Resampling performance over subset size.
Figure 6. The visualization of variable importance.
more important for classification of the data. The mean decrease in Gini coefficient is a measure of how each variable contributes to the homogeneity of the nodes and leaves in the resulting random forest. Each time a par- ticular variable is used to split a node, the Gini coefficient for the child nodes are calculated and compared to that of the original node. The Gini coefficient is a measure of homogeneity from 0 (homogeneous) to 1 (heterogene- ous). The changes in Gini are summed for each variable and normalized at the end of the calculation. Variables that result in nodes with higher purity have a higher decrease in Gini coefficient.
A type 1 variable importance plot shows the mean decrease in accuracy, while a type 2 plot shows the mean decrease in Gini [6] .
The five best predictor variables found by using random forest algorithm are GTF3, GTF5, GTF6, GTF1 and GTF2 placed in highest to the lowest variable importance order.
These five features were subjected to find the predictive classification accuracy.
4. Application of Classification Algorithms
The following four classification algorithms have been used: K-Nearest Neighbor (KNN), J48, Classification and Regression Trees (CART), Random Forest (RF) using [7] [8] .
・ K-Nearest Neighbour (KNN): KNN is a non-parametric technique, as it does not take into consideration the data distribution. KNN is a lazy learning technique as it takes up all the data, and training period is near minimal. This algorithm is able to deal with continuous and categorical dataset.
・ J48: This algorithm is a Java language based implementation of the C4.5 algorithm of Weka data mining tool. It was developed by Ross Quinlan. This algorithm creates decision trees based on the labelled input da- ta.
・ Classification and Regression Trees (CART): Classification and regression trees algorithm was given by Breiman Friedman Olsen and Stone. It’s a greedy, top-down binary, recursive partitioning, that divides feature space into sets of disjoint rectangular regions.
・ Random Forest (RF): RF is an ensemble classifier that consists of many decision trees and outputs the class that is the mode of the class’s output by individual trees. Random Forests are often used when we have very large training datasets and a very large number of input variables (hundreds or even thousands of input vari- ables). A Random Forest model is typically made up of tens or hundreds of decision trees.
Each data set was split into two groups (Training and Test sets) in the ratio 75:25. The training data set con- tains the class labels, whereas the testing dataset does not contain the class labels. The pre-processing of the data involved centring and the scaling of the data matrix. In the classification procedure, a 10-fold cross validation technique has been applied which is repeated three times for validating any predictive model. Predictive accu- racy and kappa values have been adopted as a measurable parameter for the classification process. Kappa is de- fined as the degree of right predictions of a model. This is originally a measure of agreement between two clas- sifiers and is calculated with Equation (10).

In broad terms a kappa below 0.2 indicates poor agreement and a kappa above 0.8 indicates very good agree- ment beyond chance [9] .
5. Result Analysis
The predictive accuracy values calculated for the feature set containing all the six features show that, RF algo- rithm gives the highest predictive accuracy value of 89.72%, closely followed by J48 algorithm at 86.09%, as shown in Figure 7.
In the case of model where the features have been chosen through RF technique and then the percentage ac- curacy value has been calculated, again the RF classification algorithm gives the highest predictive accuracy value of 90.51% and closely followed by J48 algorithm at 86.68%, as shown in Figure 8.
Figure 7. Predictive accuracy chart for the complete feature set.
Figure 8. Predictive accuracy value chart for five feature set.
A margin is a measure of the certainty of classification. This method calculates the difference between the support of a correct class and the maximum support of an incorrect class. A margin is the measurement of certainty of the classification; it is computed by the support of the correct class and the maximum support of the incorrect class. The formula of margins is represented in Equation (11).

In the Random Forest classifier the margin [6] [10] for the data points was also calculated and has been shown in Figure 9. The margin of a data point is defined as the proportion of votes for the correct class minus maximum proportion of votes for the other classes.
Here, the margin of the xi sample equals the support of a correctly classified sample (c denotes the correct class) minus the maximum support of a sample that is classified to class j (where j ≠ c and j = 1 ∙∙∙ k). Therefore, correctly classified examples will have positive margins and misclassified examples will have negative margins. If the margin value is close to one, it means that correctly classified examples have a high degree of confidence. On the other hand, examples of uncertain classifications will have small margins.
Thus under majority votes, positive margin means correct classification, and vice versa as shown in Figure 9. In the dataset there are eight thousand tuples shown on x-axis and y-axis show the proportion of correct votes for the class minus the maximum votes for other classes.
Figure 10 shows the error rate over the trees. In the case of Random Forest classification method, the number of trees prepared were 500 (ntree). The curve shows the number of trees constructed on the x-axis and corresponding errors on y-axis per leaf image class in different colors. The Out Of Bag (OOB) error has been shown in black color. The OOB data is used to get a running unbiased estimate of the classifier errors as trees are added to the forest per leaf image class.
The Kappa values shown in Table 1 also prove that the models prepared are appropriate. The values of Kappa for the J48 and RF model are having values beyond 0.8. The predictive accuracy results show that Random Forest algorithm fares the best amongst all the discrimination algorithms used for testing purpose, due to the fact that it applies resampling technique and avoids the correlated variables, thereby increasing the value of predictive accuracy.
6. Conclusion
The predictive accuracy value in case of selected features is higher as compared to prediction values calculated
Figure 9. Number of records plotted against predicted margin values for each leaf image class.
Figure 10. The number of trees constructed corresponding to the error rate generated per class.
Table 1. Kappa values for the two different feature sets.
upon all the features of the leaf image dataset as discussed in Section 4. The higher performance has also been expressed through the kappa values mentioned in Table 1 and further through the margin values represented in Figure 9. The results discussed in Section 4, have proved the assumption of this study that feature selection has an incremental effect on predictive accuracy values for leaf image classification. The size of the dataset has also been reduced due to selected features. The future scope of the leaf image classification lies in studying genetic algorithms and optimization techniques.
Cite this paper
ArunKumar,VinodPatidar,DeepakKhazanchi,PoonamSaini, (2015) Role of Feature Selection on Leaf Image Classification. Journal of Data Analysis and Information Processing,03,175-183. doi: 10.4236/jdaip.2015.34018
References
- 1. Liu, H. and Motoda, H. (1998) Feature Selection for Knowledge Discovery and Data Mining. 1st Edition, Kluwer Academic Publishers, New York.
http://dx.doi.org/10.1007/978-1-4615-5689-3 - 2. Blachnik, M., Duch, W., Kachel, A. and Biesiada, J. (2009) Feature Selection for Supervised Classification: A Kolmogorov-Smirnov Class Correlation-Based Filter. Proceedings of Methods of Artificial Intelligence, Gliwice, 10-19 November 2009, 33-40.
- 3. Hall, M.A. (1999) Correlation-Based Feature Selection for Machine Learning. PhD Thesis, University of Waikato, Hamilton.
- 4. Gonzalez, R.C. and Woods, R.E. (2001) Digital Image Processing. 2nd Edition, Prentice Hall, New Jersey.
- 5. Gabor Filters. https://en.wikipedia.org
- 6. Dins Lab, Random Forest. https://dinsdalelab.sdsu.edu/metag.stats/code/randomforest.html
- 7. R Development Core Team (2008) R: A language and Environment for Statistical Computing. R Foundation for Statistical Computing, Vienna.
- 8. Rasband, W.S. (1997-2014) ImageJ. U. S. National Institutes of Health, Bethesda.
- 9. Sim, J. and Wright, C.C. (2005) The Kappa Statistic in Reliability Studies: Use, Interpretation, and Sample Size Requi- rements. Physical Therapy, 85, 257-268.
- 10. Yu, W. and Chiu, D. (2015) Machine Learning with R Cookbook. 1st Edition, Packt Publishing Ltd., Birmingham.
NOTES
*Corresponding author.













