Received 19 March 2016; accepted 24 April 2016; published 27 April 2016

ABSTRACT

The location of gold veins, due to a slanting magma dike intrusion in a cold rock, considering earth surface effects is determined. The 400˚C and 500˚C isotherm evolution resulting from this magma intrusion are studied considering a 2-D model. In this analysis, it is shown that the isotherm envelopes are the most important surfaces. Analytic solutions have been found as a function of the angle a between the dike and the vertical planes. The present results are more general than previous ones in the contest of vertical dikes. Magma convection has been considered in a simplified way. The agreement found that the results in the work the actual vein sites at the gold mine, called Colombia, in the auriferous area of El Callao, located 180 Km south of Ciudad Guayana in Bolivar state, Venezuela, are much better than in previous works.

Keywords:

Gold Veins, Magma Intrusion, Heat Flux, Gold Mines, Geothermal

1. Introduction

Intrusion related gold systems is a term that reflects a tendency common to all magmatic hydrothermal environ- ments to form gold ores in spatial associations with intrusive centres. The global distribution and the large number of these types of gold deposits have produced an increasing interest in the investigation and exploration of intrusion related gold systems. Excellent references of our previous statements can be found in the work of Lang and Baker (2001) [1] , where there are 77 references on this matter, and where there are also a lot of deposit examples in USA, Europe (Spain, ...), Asia and Australia. In this paper, our attention will be concentrated in the Colombia gold veins in El Callao, Venezuela. The exploitation of this mine is carried out by the government company Minerven, which is part of the Corporacion Venezolana de Guayana holding. Thus it is left open that anyone interested in the application of our analysis to other mines, could study the ample group of examples of the above referred references.

As it was pointed out in a previous paper [2] , most of the analysis of gold veins and temperature calculations in and around intrusive dikes were performed at the beginning considering vertical walls and magma heat propagating in the direction normal to the plane of separation between magma and rock [3] [4] . In this case, the mathematical analysis can be considered as 1-D diffusion problem. This kind of treatment does not give results according with actual location of the gold veins in the deposits, and there was no interest for a theoretical treatment of dike intrusion-related gold systems. More elaborated treatments, taken in account the fact that the surface of the earth act as an isothermal surface lead to better results between theory and actual gold veins location [2] . They gave a new impetus to the theoretical analysis. In these case, the mathematical problem be- comes a 2-D heat propagation analysis. The agreement now between the theoretical predictions on the gold veins in the Colombia mines was now much better, but the acual gold veins were out of the prediction angles, though not very far away. The main limitation in the previous works [2] was that the dike intrusion was con- sidered as vertical, and the real one was inclined 15˚ with respect to the vertical plane. In this paper, this limitation was removed and the dike was taken to form in general an angle a with the vertical plane, instead of zero degrees as before. All of the equations are now more difficult to be solved, but a set of transformations have been found, which allows, to get variable separation and analytic results. The agreement of the new theoretical results and the actual gold veins in Colombia mines is now better.

2. Theoretical Treatment: Basic Considerations

As in previous work [2] , the present analysis is carried out for the isotherm evolution due to of the magma intrusion of a hot dike in a cold rock. the temperature of the igneous dike is 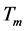at the moment of the intrusion,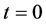. At this time, the surface separating the dike and the nearby rock is considered a plane forming an angle a with the vertical plane. The temperature of the plasma rock is, and uniform at. 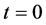The earth surface is considered to be at temperature at any time. Dike magma and country rock are brought suddenly into contact at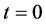. It is also assumed that latent heat fusion L of the magma is constant, and well defined. Specific heat c, thermal conductivity k and density 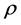of the country rock and magma are also uniform and equal for both elements. A unique melting point temperature 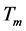for the magma will be considered here. The main source of heat for our mathematical treatment is due to for the magma latent heat of fusion L, this solidification heat source is more important than the heat due to the cooling of the plasma. This last effect is not taken into account here, though could be also considered in future papers. The effect of magma superheating is usually small [5] , and it can be also taken in a more precise way in future works. Hydrothermal currents and other fluid transports, which could be very important for some gold deposits, are not so important in the kind of deposits here considered, because of the high value of the fusion latent heat L, compared with the heat propagation due to fluid currents. It seems that the heat source due to magma convection can produce some modifications in our results, and since this is an additional heat source, the simple way of taken account this phenomena is to consider

a higher melting point temperature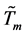. To introduce this effect in a more precise way seems to be very complicated, and this kind of treatment will be left for future works.

In the present treatment the magma intrusion is considered to fill up the half-space on the left of the axis. Taken account of the thickness of the dike does not produce important changes in the analysis [6] , and this is also left for future works. The evolution of the 400˚C and 500˚C isotherms is the most relevant ones [7] , because the oxidation of the gold salts occurs above 500˚C and reduction above 400˚C. The locations of the gold veins is in between the highest temperature at each point above or below of the gold deposition temperature range. In previous treatment the gold veins location were considering also to be in between the 400˚C and the 500˚C isotherms. However in our previous papers [2] [6] , it was shown that the actual gold veins are determined by the envelopes of the isotherms, instead of the isotherms itself, that means, that you have to look for the singular solutions of the heat transport equations, instead of the usual solutions. This is important, because this concept could be generalized to other mineral depositions.

The heat flux q is due to temperature gradient, that is

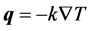(1)

where k is the thermal conductivity coefficient and T the temperature.

The heat diverging from the system is compensated by the heat changes in the country rocks, that is,

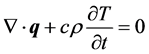(2)

where c is the specific heat, 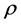the density of the country rock and t the time.

From this two equations, the time dependent heat conduction equation is obtained

(3)

where is thermal diffusivity defined by

(4)

Now it is useful to use the dimensionless variable in the following way

(5)

where the dimensionless temperature is defined as

(6)

here is the uniform temperature of the host country rock at t = 0 and is the unique melting point temperature of the magma. The geometry of the country rock and magma intrusion here considered is shown below in Figure 1.

3. Matematical Analisis

For the matematical treatment, it is convenient to define dimensionless and similarity variables and, instead of the linear variables x and y as follows

(7)

As in previous paper, x is measured along the horizontal right line at the earth surface, and perpendicular to the intersection line between dike and earth surface. The vertical line corresponds to the coordinate y. Now it is convenient to introduce a new coordinate-axis, which is a line separating magma and country rock at time, and therefore forming an angle with the y-axis, and the coordinate forming a angle with the x-axis.

The surface separating magma and country rock at any time is not a plane, and this surface will be determined at any time t with our equations. The usual orthogonal coordinates x and y are now related with the new coordinates and by

(8)

The new dimensionless coordinates and are also related to the previous ones as follows

(9)

Using these new similarity variables, the heat diffusion equation [5] takes the form

(10)

where

(11)

In this way the diffusion Equation (10) is transformed in the equation

(12)

Now, we can follow the same procedure as in previous paper [2] , that is

(13)

where and are given by

(14)

and is a constant to be determined. Here as in our previous paper is zero, because this is the only value compatible with all the boundary conditions [2] . The proof in detail of this, was done in Appendix B of previous work [2] , and the value of is obtained, when the asymptotic behaviour of the equation is analyzed. The

equation for at, is an irregular singular point of rank two [8] [9] . Changing variables from to, such that, then the irregular singular point will become of rank one. Comparing the asymptotic solution for this kind of singularities with the results of Carslaw and Jaeger [4] , it is concluded that the only solution in this case is. Thus, the solution of the partial differential equation is reduced to solve two ordinary differential equations

(15)

(16)

The solutions of these equations are the error functions and complementary error functions , which are defined by [10] [11]

(17)

and

(18)

Any linear combination of both functions is a solution. The boundary conditions will determine the right combination. Let us analyse first when x tend to infinite, also tends to ¥ for any value of including the case of. On the other hand, when, the influence of the dike is null and T is therefore we obtain and. This is accomplished by.

The analysis for the earth, now it is a little different than in our previous paper [2] . the solution now for Equation (16) will be. At the surface of the earth, , and; but now only if. If, the points where will be zero, are where

(19)

Then the surface with, will be a straight line forming an angle with the horizontal. In order to keep this analysis simple, it is convenient to assume that the earth surface form an angle with the horizontal plane. This assumption will keep our analysis simple, and it is very close with the reality, since in our assumptions, is small (in El Callao, Venezuela). It is also important to point out, that the main influence on the gold vein locations are due to the dike temperature. The effect of the earth surface have been modified in several ways, as for instance, sedimentation, which in the case of El Callao mines is several tenth of meters, thus how was the actual form of the earth is not so important. In the case of, the earth surface

will be horizontal. As in previous papers [2] [6] , it is convenient to introduce parameters and, instead of the usual constant factors. In this way the solutions for will be

(20)

where now and are defined by the equations

(21)

(22)

We know also that the parameters and are given by Equation (44) and Equation (45) in Ref. [2]

(23)

(24)

where L is the latent heat of the magma.

One very important isotherm is the contact surface between the magma and the country rock defined by the dimensionless equation

(25)

where the points of the isotherms are denoted by. In previous paper [2] , there was only a dimen- sionless contact curve, however now, there are several dimensionless contact curves depending of the coordi- nates to be used. The most important of these curves are those defined by the coordinates , as well as, those defined by the coordinates,

(26)

where

(27)

and

(28)

These equations are shown in Figure 2 and Figure 3.

In Figure 2, the magma isotherms in dimensionless variables are shown for several values of (and 20˚). Each isotherm has two asymtotas, one paralled to the -axis, and the other parallel to the -axis. Each asymptote is characterized by a value or given by

(29)

(30)

where it has been used that

(31)

Another important characteristic in Figure 2 is that all of this curves go through the point denoted with P at the figures. This point correspond to the polar angle already defined in the previous paper [2] . The values for and were also given on this reference (and). These values correspond to the energy balance between the solidification heat (L) and the diffusion heat through the rock.

In Figure 3, the magma isotherms are shown using (x, y) variables for two different times (and) and for the angles and. The corresponding value of is also determinated.

4. Isotherm Envelope

The determination of the gold vein location, is performed looking to the envelopes of the 400˚C and 500˚C isotherm families. The procedure to obtain the envelope is performing the partial derivatives with respect the parameter t of Equation (20) obtaining

(32)

where

(33)

Considering now a particular isotherm for the temperature, then the equation for the envelope at this temperature will be

(34)

(35)

From this system of equations with two unknowns and, two particular values of and will be obtained for each. Now the equation in terms of the coordinates x and y will be given by

(36)

Equation (36) can also be written down in a more convenient way as

(37)

where

(38)

In the case of, Equation (67) in Ref. [2] , is recovered. Now considering the angle this equation is also an straight line through the origin, as it is shown in the Figure 4 and Figure 5 for

and. The 400˚C and 500˚C isotherms are the most relevant isotherms in this case. The envelopes are shown in Figure 4 for with some isotherms at times 10², 10³, 10⁴ and 10⁵ days, and similarly for in Figure 5.

5. Case Study

We want now to compare our results with those of the gold mine Colombia selected in previous paper [2] . This mine is sited in the auriferous area of El Callao located 100 Km South of Ciudad Guayana in Bolivar State of Venezuela. Minerven is the government Company exploiting the mine, which is part of Corporacion Venezolana de Guayana holding.

In Figure 6, the straight line trough the actual galleries in the mine are shown, as well as the envelopes for and Here we are also including the envelopes obtained in Reference [2] for this mine, which were obtained considering a vertical dike treatment and rotation in 15˚. The diabase dike is also shown. The depth and horizontal distances of galleries,isotherms, envelopes and dike are shown in Table 1.

It is clear now, that our results are good since the actual galleries are almost inside the angle formed by the 400˚C and the 500˚C isotherms envelopes. The differences between our results and the actual site of the galleries, seems to be due to the magma convection which has not been taken in account until now. However in the introduction, we discuss that a simple way to include this effect in the calculations, it is to consider that the heat coming out due to convection is equivalent to heat source overheating the magma. If this analisys is

performed and a 20% overheating is considered, that is, the new is taken as 1600˚C instead of 1300˚C, then a complete agreement with the actual vein location is reached.

This is shown in Figure 7, where the envelopes of the 400˚C and 500˚C are shown for, and now the galleries are exactely in the center of the angle formed for those straight lines.

6. Conclusion

The gold vein location around magma intrusive dikes have been analyzed considering a 2-D isotherm problem, that is, including the earth surface effects. The present analysis differs from the most common previous studies in that the boundary conditions is now 2-D instead of 1-D. Previous treatments considering 2-D boundary conditions were performed considering that the magma dike was vertical. A more general analysis has been realized in the present work, where the boundary conditions have been applied to a general dike, inclined an angle a with respect to vertical plane. In this work, it is shown that the isotherm envelopes are the most important surface to find out the location of the gold veins. Analytic solutions have been obtained for this general case, using error functions. Accurate calculations have also been performed in the case of El Callao gold mines, and the present results agree much better with the actual situation of galleries in these mines, than any previous ones. Two main lines of analysis have been performed. In the first one, the convention effects were not considered, and in this case the calculations predicting the gold galleries location agree only a litle better with the actual sites than previous ones. However, when the heat convection effect was included in a simple way, a total agreement was found.

Acknowledgements

This work was partially supported by FONACIT, Programa de Estimulo a la Investigación, PEI, Grant Project N˚3125, Venezuela; Universidad de Antofagasta, Programa Mecesup, Grant Project ANT128, and Decanatura de Ciencias Básicas, Chile.

Cite this paper

P. Martin,F. Maass,J. Puerta,L. Cortes, (2016) Gold Veins Location in Deposits Originated by a Slanting Magma Intrusion Dike. International Journal of Geosciences,07,548-557. doi: 10.4236/ijg.2016.74042

References