International Journal of Geosciences
Vol.05 No.11(2014), Article ID:50876,20 pages
10.4236/ijg.2014.511109
Two-Edge-Corner Image Features for Registration of Geospatial Images with Large View Variations
Parvaneh Saeedi, Mao Mao
School of Engineering Science, Simon Fraser University, Burnaby, Canada
Email: psaeedi@sfu.ca, maom@sfu.ca
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 6 August 2014; revised 2 September 2014; accepted 27 September 2014
ABSTRACT
This paper presents a robust image feature that can be used to automatically establish match correspondences between aerial images of suburban areas with large view variations. Unlike most commonly used invariant image features, this feature is view variant. The geometrical structure of the feature allows predicting its visual appearance according to the observer’s view. This feature is named 2EC (2 Edges and a Corner) as it utilizes two line segments or edges and their intersection or corner. These lines are constrained to correspond to the boundaries of rooftops. The description of each feature includes the two edges’ length, their intersection, orientation, and the image patch surrounded by a parallelogram that is constructed with the two edges. Potential match candidates are obtained by comparing features, while accounting for the geometrical changes that are expected due to large view variation. Once the putative matches are obtained, the outliers are filtered out using a projective matrix optimization method. Based on the results of the optimization process, a second round of matching is conducted within a more confined search space that leads to a more accurate match establishment. We demonstrate how establishing match correspondences using these features lead to computing more accurate camera parameters and fundamental matrix and therefore more accurate image registration and 3D reconstruction.
Keywords:
Image Variant Features, Geometrical Image Features, Feature Grouping, Large View Variation, Match Correspondences

1. Introduction
Establishing match correspondences between two or more images are one of the most common tasks in applications of image processing in computer vision. This is a challenging task especially under conditions such as oblique view, illumination change, and large view variation where the viewing camera undergoes a large transformation. Most cutting-edge matching approaches extract affine-invariant regions and assess their similarities using intensity-based image properties. These methods perform well for images with shorter baselines or small affine transformations. However, they easily fail when it comes to images of wider baselines or those with larger view variation. When establishing match correspondences in aerial images of suburban regions, the difficulties of the matching lie in several factors. Firstly, these images could be visually significantly dissimilar if the viewing direction or angle (pitch angle in specific) is not at nadir. In such situations, the projective transformations between the two views cannot be simply ignored. Secondly, due to changes in the background (originating from perspective projection) identical physical regions of the scene, at best, contain only partial similarities. Finally, the existence of many repetitive shapes with similar sizes, colors and, patterns in the construction of suburban areas (originating from similar design plans and identical construction materials) makes the identification based on simple features an erroneous one. Therefore, recognition of identical features cannot be accurately and robustly achieved via traditional matching techniques [1] .
This paper presents a novel approach to creating unique features in complex suburban environments that can be identified even when they undergo large viewpoint variation. The paper is structured in the following order. Related works are reviewed next followed by the contributions of the proposed approach. Section 2 describes the characteristics of the input images and their accompanying auxiliary data. Section 3 introduces the proposed 2EC features and describes how they are constructed. Section 4 presents our proposed method for establishing 2EC match correspondences in two or more images. Experimental results and comparison with the state of the art are provided in Section 5. Finally, Section 6 summarizes the conclusions of this work.
1.1. Related Work
During several last decades, the problem of wide baseline matching has been addressed in numerous ways. A wide variety of approaches involve detection of distinct features and viewpoint invariant descriptors. Discrete points are among the most popular features used in the applications of computer vision. Lowe [2] proposed to detect Scale-Invariant Feature Transform (SIFT) using DoG filter. He used a 64 dimension descriptor based on image gradients to describe each feature. These features are scale and partially rotationally invariant. Mikolajc- zyk [3] described a scale-adapted Harris measure that located interest points at different scales using a Laplace function that selected points at local measure maxima. Compared with Lowe’s SIFT features, this method tolerated higher scale variation. The Harris-Affine [4] and Hessian-Affine [5] methods were also developed by Mi- kolajczyk to achieve higher repeatability under larger affine transformations. The interest points were extracted by multi-scale Harris detector. Using an iterative procedure, each point’s location would converge to the most stable affine invariant region. Tuytelaars et al. [6] extracted Parallelogram-shaped regions around Harris corner points and considered them as affine invariant regions. They established affine invariant regions based on local intensity extrema. By checking the intensity profiles along each ray radiating from the extrema, a maximum point on each ray was then selected. These points were then joined together to form a region which was fitted to an ellipse. In [7] , Matas’ detection of maximally stable extremal regions (MSER) was introduced based on intensity thresholding. A voting strategy along with the correlation was utilized to identify tentative matching correspondences. According to [8] , MSER provides the best result when dealing with planar projective transformations, followed by Hessian-Affine, while [9] reported that SIFT is the best descriptor for the MSER detector.
One common trait of all the above features is the drop in the features’ repeatability as the viewpoint differences increase. Moreover, all of these methods assume that the local areas associated with features are planar. This, however, is not a valid assumption when working with aerial imagery of suburban regions. These regions include buildings at variable heights. Naturally these methods have less success in handling the registration of aerial imageries under larger view variation.
Corners, as rotationally and scale invariant features, have been used for image registrations for many years. To add to the consistency of the features’ locations, some methods have suggested incorporating edges into the detection procedure. Xiao et al. [1] reported a novel feature called edge-corner that announced corners as the intersection of two or more edges. The initial matching method was done by comparing patches around the edge- corners, using Sum of Squared Differences (SSD) and followed up by an optimization process that modeled a more precise affine model for the matching. Similar to all the other affine invariant approaches, the method assumed that the local areas around the edge-corners were flat plane and had no depth differences or occlusion. Xie et al. [10] solved this problem by creating corner-edge-regions around the proposed edge-corner features in [1] . The corner-edge-region was separated into several sub-regions by edges emanating from the center corner as its intensity was used for determining the match correspondences. This method performed better than the other methods when local neighboring regions had certain depths, since comparison was only applied within each sub-region, which were more likely to be planar surfaces. A disadvantage of this method was that the local corner-edge-region may not be distinctive enough in images with repetitive patterns.
Beside points and their invariant regions, lines are also commonly used as features when it comes to image registration. Schmid et al. [11] developed an approach using intensity values on the two sides of line segments. Bay et al. [12] introduced an algorithm using color information along line segments. Wang et al. [13] developed a segment grouping method based on spatial proximity and relative saliency, and a new descriptor based on configuration of line segment pairs. Generally, since there are plenty of straight lines in man-made environments, methods that rely on lines as features are more robust for urban and indoor scenes. Using line segments as features has some drawback of its own. For example, the end points of line segments may not be very stable and change locations as the viewing angle changes. Moreover, pixels’ intensity and color values vary as the illumination or viewing direction change.
There are also some works that utilize combination of interest points and lines or edges. Tell et al. [14] created line segments between two Harris points. Affine invariant Fourier coefficients were then computed from intensity profiles along the line segments. Cyclically order constraint was added to achieve more accurate results. This method, however, required textured objects that were locally planar. Kingsbury [15] proposed a matching system that took both appearance and spatial constraints into consideration. SIFT descriptor and a pair-wise relationship descriptor was used to measure the similarity between them. Eric [16] presented a descriptor which disambiguate locally similar features by combining SIFT descriptor with a global context vector. This method was a time consuming one, specially for larger images, since it took every pixel into account when creating and updating global shape context for each SIFT feature.
Some methods take advantage of the characteristics of man-made objects, such as straight lines and planar surfaces. In order to establish correspondences between images of building facades, Lee [17] proposed to detect quadrilateral shapes formed by four line segments and their intersections. This method achieved true correspondences between two images of building facades even over 50˚ view angle differences. It, however, required a dominant plane that limited its application domain. Ding [18] proposed a method to map oblique aerial images onto 3D LiDAR data using 2DOC feature, created based on orthogonal vanishing point pairs. A real 2DOC feature was supposed to represent the orthogonal corner of a building profile. The number of true 2DOC was significantly influenced by the type of buildings and environment. For large and simple building shapes, such as those in downtown district, the method worked well. However, for complex building structures like those on campus and residential areas, it failed up to 50% of the times due to the lack of real 2DOC features. Wang [19] reported a novel feature called 3CS to map oblique aerial images onto 3D LiDAR data. Each 3CS feature contained three line segments, which were connected to each other based on their endpoints proximity. Six attributes including length ratios, and orientation were used to describe 3CS features. The distinctiveness of 3CS features increased the number of correct correspondences among candidates. However, when registering two aerial images, 3CS feature could not be used directly, since the repeatability of such features in both images was too low.
In this paper, we introduce a novel feature and a unique matching technique for automatic establishing match correspondences between two oblique aerial images of the suburban regions under a large projective transformation. The proposed feature utilizes two straight lines and their intersections, which could correspond to a vertex and two connected edges of a building’s rooftop. We refer to our proposed features as 2 Edges and a Corner or 2EC features. Similar to [19] , our method takes advantage of typical structures on man-made environments. However, [19] intersects lines merely based on their spatial proximity and therefore it could lead to fake features that do not correspond to true outlines of building rooftops. Our feature detection algorithm utilizes the image edge map as a reference to extend/complete line segments that may have been detected partially. In addition, the stability of the endpoints of each line segment is strengthened using Harris corners. Unstable features, usually arising from unstable or very small lines, are identified and eliminated to accelerate the performance and the robustness of the matching process. The description of our features involves both geometrical and visual information. [19] uses length and orientation of line segments as feature descriptors. Even though it performs very well on 3D LiDAR models, it fails for aerial images due to numerous similar patterns that naturally exist in the construction of cities and suburban areas. During the matching process, we assume that a rough estimation of the camera parameters (i.e. yaw, pitch, roll angles, and xyz coordinates) are provided. For every feature in the first image, its candidate correspondences in the second image are searched within a narrow belt along the corresponding epipolar line (estimated using the rough camera parameters). To predict the shape of a feature in the second image, the line segments and intersections are transformed using a rough estimate of the acquisition geometry. The descriptors are computed for the converted features and all the candidate matches in the search space. Matches are obtained by comparing descriptors. The epipolar geometry is utilized to refine match correspondences and improve the final registration parameters.
1.2. Contributions
The main contributions of this paper are as following:
1) We propose 2EC features that hold geometrical traits of straight edges and their intersections with each other and are especially designed to represent typical configurations in man-made structures. Since 2EC features hold geometrical relationships between structures’ lines and corners, they can be tracked and associated even when they are viewed from a completely different viewing direction.
2) A new matching algorithm is developed that utilizes both visual and geometrical properties in a hierarchical approach to robustly and accurately 2EC match correspondences between two or more images of a scene.
2. Input Data
The oblique aerial images from Pictometry International Corp. dataset are used as the input of the proposed algorithm. All the aerial images in our dataset are 2672 × 4008 pixels covering a ground area of 420 × 640 m2 with a sample distance of 0.15 meter/pixel. These images are captured at a slant angle from an elevated position. The image acquisition system includes four cameras, each obliquely downward pointing to North, West, South and East. The input images are captured via an airplane flying over the region of interest in a zigzag way. Considering the way these images are acquired, usually several images cover each particular scene. These images are taken at an average of 50˚ pitch angle, and therefore any two images of the same scene, captured by different cameras, undergo large projective variation. An example of an oblique aerial image pair, taken under such condition, is shown in Figure 1.
A file called metadata is accompanied with each image that includes the flight information, the internal and external parameters of the camera at the time of image capture. A sample metadata file is presented in Figure 2. The camera orientation and location provided in the metadata file have limited accuracy and relying on them solely to establish correspondences between image pairs is not practical. However, they can be still used to reduce the search space in finding match correspondences. Once the initial correspondences are established with

Figure 1. An example of a pair of oblique aerial images: The images are taken from (a) the North direction and (b) the West direction of the same scene. The red X marks the same building.
Figure 2. A sample of metadata file.
our proposed algorithm, the camera parameters can be refined.
3. Methodology
Figure 3 depicts the overall flowchart of the proposed system. Details of each section are provided next.
2EC Feature Extraction and Description
The main idea behind 2EC features is to utilize the geometrical traits of straight edges on the man-made structures and provide distinctive features that can be robustly matched between input images with large projective transformations. Here we introduce 2 Edges and one Corner (2EC) features, which consist of two connected line segments and their intersection. 2EC features could correspond to the boundaries of building rooftops. The procedures for detecting these features are explained in the order that they are implemented.
1) Straight line extraction: Here a set of straight-line segments are extracted from the image. The Burns line detector [20] is utilized, which uses both the gradient magnitude and the gradient orientation to form line support regions and eventually straight line segments. We briefly describe this procedure, however, we refer to [21] for more details. Burn’s method includes the following steps:
a) Partition image pixels into bins based on the gradient orientation values. A bin size of 45˚ was selected.
b) Run a connected-components algorithm to form line support regions from groups of 4-connected pixels that share the same shifted gradient orientation bin.
c) Eliminate line support regions that have an area smaller than 3 pixels.
d) Repeat steps a, b, and c by spatially shifting the gradient bins to produce a second set of line support regions. This accounts for the possibility that some true lines may have component pixels that lie on either side of an arbitrary gradient orientation boundary.
e) Use the voting scheme in [20] to select preferred lines from the two sets (the original set and the shifted set) of candidate lines.
f) For each line support region, compute the line represented by that region by performing a least square fit. The least-squares fit estimates planar model of each line using the gradient magnitude values.
2) Line linking: The objective of this step is to link collinear line segments that are separated by very small gaps. Following algorithm describes linking process:
a) Sort the lines in the order they would be encountered if a horizontal sweep was performed across the image.
b) Use a divide-and-conquer method to efficiently determine nearby pairs of lines.
c) Test each pair of nearby lines to determine whether they should be linked. Conditions (a) and (b) and one of the conditions of (c) and (d) in Figure 4 must be satisfied for a pair to be linked.
More details for this process can be found in [21] .
3) Obtaining edge map: Edge map serves as a clue to decide on the extension of a line and selection of its potential intersections. First, the original image is processed via Canny edge detector, followed by dilation with a 3 × 3 pixels square structuring element to widen edges and fill out narrow gaps. Next, isolated blobs with areas
Figure 3. Flowchart of the proposed system.


Figure 4. Four criteria for line linking process.
smaller than 1 m2 are removed. In aerial images, smaller blobs usually correspond to protuberant objects or texture on the surface of rooftops and they could be misleading when extending lines. Thus, they should be removed before the succeeding steps.
4) 2EC Feature extraction: Once the edge map is obtained, 2EC features are extracted by the following 6 steps:
a) Line extension: The objective of this step is to adjust the detected line segments according to the image’s edge map such that most of the corresponding edges of rooftops are covered, while as many as possible non- significant lines (lines on the grass regions or grounds) are removed. The extension of a line, on the other hand, should not be too long as it could incorrectly represent edges of multiple buildings along the same street/block and at a close proximity of each other. Only with meaningful and true line segments, the 2EC features can be constructed robustly. According to this principle, the line extension procedure has the following three steps:
· From the set of detected lines, the lines with less than 80% overlap with the edge map are identified and removed.
· To cover for those cases where partial occlusion or low contrast between the rooftop and the background have created breakage in the line segments, where they indeed correspond to complete building rooftop edges, each line segment is extended on both ends until it no longer overlaps with the edge map. The image boundaries are used in the cases where the extension of the line falls outside of the image area.
· Once all lines are extended, the endpoints of each extended line must be in close proximity of rooftop vertices, if it is from a real rooftop. However, in some cases, small discontinuities exist between the lines endpoints and the vertices that correspond to the rooftop corners. Those corners are supposed to be reached by further continuation of the lines. As a result, the extension of each line is continued by 10% of its length.
b) Line merge: In aerial images of urban scene, a rooftop edge often consists of several parallel lines, with each of them representing some parts of the edge. In order to avoid such ambiguity, nearby parallel lines are fused together to form one single continuous line that uniquely corresponds to the full length of a rooftop edge. If all the following three criteria are satisfied, the two line segments are assumed to be from one physical edge and therefore are merged together.
· They are parallel or almost parallel (a maximum cross angle of 5˚ is tolerated).
· The lateral distance between two lines is less than 1.5 pixels or 22.5 cm.
· When one line is projected onto the other, there exists at least at least 1 pixel overlap.
c) Line intersection: Using all the remaining line segments after the extension and merging procedures, the intersections of each line with all the other lines are found. An intersection is recorded only if it satisfies the following two conditions:
· The two intersected lines have an angle larger than 20˚ and less than 160˚.
· The intersection point lands on the edge map.
d) Endpoints redefinition: The definition of a 2EC feature includes two rooftop contour line segments and their intersection, which is obtained using previous steps. Each line segment starts from the intersection and ends at one of the endpoints of a line. However, the endpoints of each line might not be stable or might not precisely occur at its right place. Therefore, it is necessary to redefine the endpoints for each line. For this purpose, for each line, we detect all Harris corners [22] lie along the line and within 2 pixels lateral distances from it. Once all such corners are identified, they are projected onto the line to form potential locations where the line may end. All the projected points together with all the intersections on each line are sorted and the most left and most right points are chosen as the two endpoints of each line. Three parameters are used in Harris corner detector: standard deviation of smoothing Gaussian, quality level, and sensitivity factor. In our work, they are set to 1.5, 0.01, and 0.04 respectively.
e) Removal of unstable lines: Here, all the unstable lines are identified and removed. Based on our experiments and observations, we classify three conditions as unstable. Lines with at least one of these three conditions are labeled as unstable and removed iteratively until no more lines can be removed.
· Lines with only one intersection and missing at least one endpoint.
· Individual short lines (5 pixels of 0.75 cm or shorter).
· Short lines connected together forming a chain (if all connected lines are shorter than 5 pixels/0.75 cm).
f) 2EC feature extraction: At each intersection of a line, one or more features can be constructed. As shown in Figure 5, G is the intersection of l1 and l2. G13, G12, G11, and G21, G22 are all the other intersections and endpoints on l1 and l2. For G, there are 6 possible combinations of two line segments. In each combination, if both segments are longer than 15 pixels, a feature will be generated. In Figure 5, since GG13 is shorter than 15 pixels, it cannot be used to generate any feature. As a result, only four 2EC features are generated, which share the same intersection point G, but with different line segments combinations. These features are: G11GG21, G11GG22, G12GG21 and G12GG22.
Figure 5. 2EC feature generation for the intersection point G.
For each 2EC feature, we refer to the intersection as the center point, and the two endpoints of the lines as end points. As suggested by the name, the center point of 2EC feature could represent the corner of a rooftop where two rooftop boundary lines intersect. Considering the way 2EC features are extracted, more than one 2EC features may share a common center point, while they have line segments with different lengths. Since the center points are the most stable components of 2EC features (invariant to rotation and scale change), they are used as the point correspondences after 2EC feature correspondences are established. Figure 6 represents extracted features in one of our input images for a specific building structure.
4. Feature Correspondences Establishment
In this section, we present a matching process for matching 2EC features between images with wider view differences. Two assumptions are made here:
1) Each feature in one image can match only with one feature in the other image.
2) Not every feature has a correspondence.
For each feature in the first image, a search space is created by predicting the extracted location of that feature in the other image using the acquisition parameters in the metadata files. Both features’ shapes and image content are used to identify correspondences within the search space. Once the potential matches are obtained, a projective matrix optimization method is used to remove outliers. The matching process is repeated in an iterative way within smaller search spaces, which is computed based on the result of the first round of the projective matrix optimization. Following steps describe in details the proposed matching algorithm:
4.1. Feature Location Prediction
In this work, with each image a metadata file is associated that provides additional information including camera orientation (Yaw, Pitch and Roll angles) and location (latitude, longitude, and altitude), camera internal parameters, etc. Although these parameters are imprecise, they can still be used to roughly predict the shape and the position of each 2EC feature from one image to another.
1) Feature location estimation using metadata: Let us consider a pair of images taken by two cameras (C1 and C2) from different viewpoints. m is a point in I1, and m' is its actual corresponding location in I2. m can be transformed from I1 to I2 with a two-step transformation, which is computed using the imprecise camera parameters in the metadata files. The transformed location can then be used as a rough estimation of the location of m'.
Two assumptions are made in here. First, since the altitude of the camera (typically 1 km) is much higher than the heights of scene buildings, we assume that the building rooftops are located at the surface of the earth. Therefore, the depth of the image is assumed as the altitude of the camera, and the 3D location of any point in the image can be determined with a single image and its camera parameters. Second, since the ground region
Figure 6. Detected 2EC features. Red circle represent the center of each feature. Blue dots represent the end points and yellow lines are the edges of each feature.
covered by two cameras is small compared to the entire surface of the earth, we consider the ground as flat.
Based on these two assumptions, the model for two cameras and the ground region covered by their images are illustrated in Figure 7. Two steps are taken for this transformation: first, m in I1 is projected onto the 3D world (M), next M is projected back into 2D on I2. In order to implement such transformation, a world coordinate is used as the reference coordinate. Here, the center of the world coordinate system is located at the center of camera 1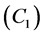 . The X axis is pointing to North, the Y axis is pointing to West, and the Z axis is pointing to the Earth Center. This means that the world coordinate system is the same as the first camera coordinate system, and its yaw, pitch, and roll angles are all zero. The transformation of a point
. The X axis is pointing to North, the Y axis is pointing to West, and the Z axis is pointing to the Earth Center. This means that the world coordinate system is the same as the first camera coordinate system, and its yaw, pitch, and roll angles are all zero. The transformation of a point 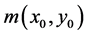 from I1 to the 3D world includes two procedures:
from I1 to the 3D world includes two procedures:
a) Transformation of the image coordinates of 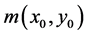 into the world coordinate system using the internal and external parameters of camera 1:
into the world coordinate system using the internal and external parameters of camera 1:
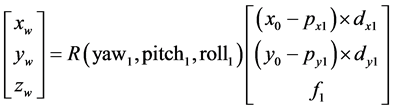 (1)
(1)
The values of yaw1, pitch1, and roll1 represent the orientation of camera 1. 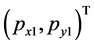 is the coordinate of the principal point in I1. dx1 and dy1 represent the conversion between the image pixel and metric world. f1 is the focal length of the first camera. 3D rotation
is the coordinate of the principal point in I1. dx1 and dy1 represent the conversion between the image pixel and metric world. f1 is the focal length of the first camera. 3D rotation 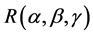 is defined by:
is defined by:
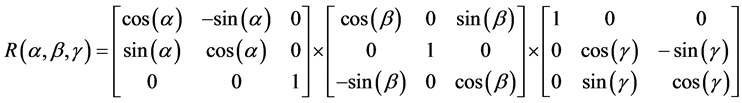 (2)
(2)
b) Projection of 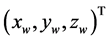 onto the ground by connecting it to the camera center and continuing it until it intersects with the ground. The relationship between the projected 3D point
onto the ground by connecting it to the camera center and continuing it until it intersects with the ground. The relationship between the projected 3D point 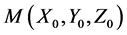 and
and 


Here alt1 is the altitude of camera 1 from metadata.
Next, according to [23] , 

In the above equations, K2 is the calibration matrix computed using the internal camera parameters:

Figure 7. The procedure of prediction of features from one image to another.
R2 is the orientation of the camera 2 with respect to the world coordinate system centered at C1. R2 can be computed by:

where lat1, lon1, lat2 and lon2 are the latitudes and longitudes of the two cameras. t2 is the coordinate of the second camera, C2, in the world coordinate system. It can be computed by:

Ccam1 and Ccam2 represent the 3D Cartesian coordinates of the two cameras with respect to ECEF (Earth-Centered, Earth-Fixed) coordinate system, and they are computed using the longitude and latitude of the two cameras according to [24] .
The above algorithm can be applied on each one of the 2EC features in I1 to predict its location and shape in I2. In fact, since we consider the ground as a plane, the corresponding points in the two image planes are related by a projective matrix Hm that can be found using the following steps:
· Four points are selected in



· Transform these four points to I2 using the method explained above. Let us assume the transformed points as



· With four corresponding points

During the matching process, the projective transformation Hm is applied to all 2EC features in I1 to predict their locations and shapes in I2.
Figure 8 shows an example of the prediction. The feature highlighted in the bottom image is transformed to the top image using the above transformation. The transformed feature is shown in the top image with red color and its corresponding true location is highlighted with green. One can notice that the predicted location is very close to its true location. Moreover, the lengths and orientations of the two are also similar.
2) Evaluation of prediction accuracy: To investigate the accuracy of prediction and provide a basis for selecting some of the thresholds required in the matching process, we applied the above transformation on 10 pairs of images. Among them, 5 pairs had 90˚ difference in yaw, and the other 5 pairs had 180˚ difference. For each pair of images, 120 matching points, which were uniformly spread over the entire images, were selected manually. Points in I1 were then transformed to I2 using the method explained in the above section and four measurements were calculated: 1) The distances between the transformed points and their ground truth locations. 2) For each point in I1, its epipolar line was computed according to [23] . The distances from the ground truth locations in I2 to their corresponding epipolar lines were calculated. 3) The lengths of the line segments, which were generated byany combination of two transformed points were computed and compared with that of the corresponding ground truth features. The length difference was measured as a percentage of the ground truth length. 4) The cross angles between the transformed line segments and their ground truth.
Figure 8. Transformation of a 2EC feature from I1 to I2.
The statistical values for the above measures are provided in Figures 9-12. One can see that the predicted positions have a maximum offset of 300 pixels from the ground truth locations. Also, the predicted epipolar lines are less than 150 pixels away from their true locations. Moreover, about 96.58% of the predicted line segments have less than 10% length differences compared to their corresponding ground truth line segments, and about 95.26% of the predicted line segments have less than 5˚ orientation differences. These errors are mainly induced by two sources: 1) the imprecise camera parameters provided in the metadata file, and 2) the assumption that all buildings in the images have zero heights. According to the epipolar geometry, each point in I1 can be mapped onto an epipolar line in I2. The location of the mapped point on the epipolar line, however, depends on the height of this point from the ground. Since the actual heights of the points vary in both images, their predicted locations
Figure 9. Histograms of distances between predicted locations and their ground truth (GT) locations for image pairs of 90˚ (left) and 180˚ (right) viewpoint variations.
Figure 10. Histograms of distances from GT locations to their estimated epipolar lines for image pairs of 90˚ (left) and 180˚ (right) viewpoint variations.
Figure 11. Histogram of differences in the length of the transformed line segments and their GT for image pairs of 90˚ (left) and 180˚ (right) viewpoint variations.

Figure 12. Histogram of orientation differences for transformed line segments and their GT for image pairs of 90˚ (left) and 180˚ (right) viewpoint variations.
in I2 would have different offsets from their ground truth locations.
4.2. Search Space Creation
Since the aerial images are large (2672 × 4008 pixels), it is very time consuming to search for correspondences over the entire image. Also, searching in a large domain means a higher chance of wrongly identifying matches. Therefore, creating a smaller search space that contains the correct correspondence is very critical to the process. Let’s Pabc represents a 2EC feature in I1. Its center point is denoted by cP and its two end points are denoted by aP and bP. The following two steps are designed to create its corresponding search space in I2:
1) Transform the center point cP to I2 using the method described in Section 4.1. Let’s denote the transformed point by


2) Compute the epipolar line of cP using the estimated fundamental matrix [23] . A window along the epipolar line is then created. The width of the window is chosen to be 

As shown in Figure 13, the intersection of the two areas generated above, denoted by

4.3. Filter Candidate Features Based on Feature Shape
Once the search space 

1) Transform Pabc to 


2) For the transformed feature

scriptor 







3) Given two 2EC features with their descriptors of 



Figure 13. Search space generation.
The thresholds 

4.4. Filter Candidate Features Based on Image Correlation
After the first round of filtering, for a typical feature in I1, there may be one or more qualified candidate features in I2. In order to identify the feature with the highest similarity, a correlation based method is incorporated. Since each 2EC feature, composed of three critical points (one center point and two end points), an image patch can be constructed by adding a fourth point to form a parallelogram with the other three points. The similarity between 2EC features can be evaluated by computing the correlation of their corresponding image patches. There are two reasons that make the use of correlation possible. 1) The images are taken by cameras from relatively high altitude, so rooftops can be seen in both images, even though they do go into projection and deformation. Since 2EC features represent the rooftop profiles of the buildings, they can be extracted in both images. 2) Since the rough camera parameters are provided via the metadata file, the image patches created by 2EC features can be transformed from I1 to I2.
Instead of using pixel intensity in the input images to compute correlation, we use the gradient images. The advantage of using gradient images is that they are less sensitive to the illumination variation. The Sobel operator is used to approximate the first derivative of the image in both horizontal and vertical directions. Magnitude of the gradients are then obtained by summing 

1) Consider that 



2) Compute vector



3) Translate each 



4) A similarity value for Pabc and Qabc is set by computing the correlation of the two sets of image gradient values: 



A similarity measure is assigned to each of the remaining candidate features in 
4.5. Removal of the Outliers
After the initial set of point correspondences is obtained, a statistical method is used to identify outliers among these point correspondences. Figure 14 shows the flowchart of this procedure.
Figure 14. Flowchart of the outlier removal process.
Consider the initial point matches as 








Next, point pairs with their distances larger than 




Once the above four iterations are exhausted, a new round of iteration is initiated. At each iteration, 5% of the matched pairs with the largest distance error are removed iteratively and the process stops if at least one of the following conditions is satisfied: 1) The maximum distance in 
At the end of this process, a new projective transformation 















5. Experimental Results
In this section, the stability and distinctiveness of 2EC features are investigated. The quality of 2EC features is evaluated by registration of slant aerial image that include wide variations in the viewing angles. The superiority of these features is shown by comparing the registration results for these features and those of the state of the art.
5.1. Feature Detection Results
Figure 16 shows the extracted 2EC features on a test image. In the figure, the red circles represent the locations of the center points of 2ECs. The yellow line segments are the lines attached to the center points. The blue stars at the end of the yellow lines are the end points of the 2EC features.
In this figure, 67 and 61 features were detected respectively. Among these features 13 common features exist between the two images. Figure 17 shows the results of SIFT features for the same building as in Figure 16. It can be noted that more SIFT features were detected in these images, however, most of the features were located on tree branches and cars. Compared with 2EC features, there were also more SIFT features detected on the
Figure 15. A pair of images with their corresponding matches. Corresponding features are labeled with the same number.
Figure 16. 2EC features for a building from different views.
Figure 17. SIFT features for a building from different views.
buildings. Not only did these features occur on the rooftop corners, but also they appeared on the white protuberant objects on the rooftops. Through a manual inspection we found only five common SIFT features were existing between the two views.
Here, we will evaluate the quality of 2EC features through establishing match correspondences in oblique aerial images. Considering the way these images are acquired, for one subject scene, there would be several images taken from North, East, South and West directions. If image pairs are captured from the similar directions, they will have similar yaw angles and therefore they mostly undergo a linear translation and a small projective transformation. For such images, it is very easy to process and establish match correspondences and usually most existing methods work well. However, two oblique aerial images taken from two different directions, for example, North and East, result in large projective transformation. Therefore, we only focus on image pairs with severe yaw angle variations from now on. Fifteen pairs of images were chosen from our database. Among them, five image pairs had a difference of 90˚ in yaw angle, five pairs had a difference of 180˚, and the other five pairs have 270˚ difference. All these images have pitch angles between 40˚ to 50˚. The combination of yaw and pitch angles variation leads to large projective transformations between these images.
For each image pair, 2EC features were first extracted and initial correspondences were established. Then the outliers were removed using optimized projective matrix. Finally, the matching procedure was repeated one more time based on the new search space that was created in each case using the optimized projection matrix. The original size of each image is 2672 × 4008 pixels. In our experiments, in order to reduce the running time and for the convenience of comparison with the state of the art, we have down-sampled the input images by a factor of 2. All the system parameters were kept the same for all the input images.
The results generated for the 15 image pairs are summarized in Table 1. In this table, the entry Yaw diff. represents the difference between the two capturing cameras in yaw angles. The No. of features column provides the number of 2EC features detected in each image (separated by a hyphen). The GT column represents the number of ground truth correspondences that are manually detected in both images. The next three entries of IC, CC, CR respectively present the number of Initial Correspondences, the number of correct correspondences, and the percentage of correct matches or the ratio of CC/IC. The statistics of the final results after the projective matrix optimization are presented in the next succeeding three entries (PMC, PCC, PCR). The last column of the table, Err, presents the accuracy of the established matches in pixels which are computed using the epipolar geometry. This column represents the average perpendicular distance in pixels from the ground truth points to their computed epipolar lines.
This measurement is estimated using the following steps:
1) Compute the fundamental matrix F over the input image pairs using the normalized 8-point algorithm [23] and the initial point correspondences obtained by matching the 2EC features.
2) For each ground truth pair




3) The distance of 


Table 1. Matching results in oblique aerial images using 2EC features.

where distance of 
As shown in columns PMC, PCC, and PCR of Table 1, even though the number of true correspondences is relatively small, the correct ratio in all image pairs is higher than 90%. An average correct rate of 96.41% is achieved, with an average residual error of 2.32 pixels. Since the purpose of establishing correspondences in aerial images is often to reconstruct 3D models, 8 pairs of match correspondences with high accuracy is sufficient for computing fundamental matrix. Therefore, as long as the number of correspondences is not too small, the results are considered meaningful. However, higher number of correct matches generally leads to more accurate fundamental matrix. Besides, match correspondences that are uniformly distributed all over the image result in a more accurate fundamental matrix. Since the ground truth correspondences used for the above measurements are spread all over the entire image, the residual error in the last column of the table can sometimes reflect the accuracy of the fundamental matrix computed using the found matches. Before applying the projective matrix optimization, the correct ratio is relatively low as shown in the entry CR. The projective matrix optimization step removes most of the outliers and successive iterations of the matching process adds in more true matches to the final results. Compared to the percentage shown in the column of CR, the results in PCR are improved significantly. It should be noted that some of the outliers could not be filtered out as they are too similar to the true matches.
Figure 18 shows an example of oblique aerial image pair with the correspondences established using 2EC features. The two images have yaw difference of about 180˚ and are taken with a pitch angle of about 50˚. The epipolar geometry is verified in Figure 18 (bottom). The three red dots are randomly selected. They represent the points that are used to generate the epipolar lines in both images. It can be seen that the corresponding epipolar lines have passed through the same image locations.
5.2. Comparison with the State of the Art
In order to compare the quality of 2EC features with that of the state of the art, three popular features including SIFT [25] , SURF [26] , and ASIFT [27] were utilized. We evaluated the quality of the features by finding match correspondences between images of wide view variations. For this purpose, the same 15 image pairs were utilized.
Tables 2-4 show the matching results for each of the above three algorithms. To assess the quality of the results, the accuracy of matching was inspected manually. The number of correspondences, the number of correct correspondences, and their ratio are given in the columns of Total Matches, Correct Matches, and Correct Rate. The average residual errors are provided in the last column of Error.
As shown in Table 2, SIFT achieved an average correct matching rate of 86.32%. Comparing to Table 1, one can see that 2EC features have higher correct matching rate than SIFT in all cases. For SIFT features, the average residual error over 15 pairs of input images is 10.81 pixels. Comparing the last column of Table 1 with that of Table 2, one can observe that the error for 2EC features is less than that of SIFT features in all the cases except row 3, which has very similar values for both 2EC and SIFT features. In conclusion, the proposed 2EC feature outperforms SIFT by an average correct rate of 10.09% in all the cases except one.
Figure 18. Results of matching 2EC features for an aerial image pair with 180˚ view difference: (Top) All 48 existing match correspondences are identified correctly by the proposed algorithm; (Bottom) The epipolar lines generated by the red dots.
Table 2. Matching results using SIFT features.
Table 3. Matching results using SURF features.
Table 4. Matching results using ASIFT features.
As shown in Table 3, the average correct rate for SURF is 75.31%. In all the cases of SURF, the correct rate and the residual error are worse than the proposed 2EC feature.
As for ASIFT feature, it has an average correct rate of 85.13%, with an average residual error of 68.07 pixels. It, however, outperforms 2EC feature in two cases (rows 3 and 13) with less residual error and similar correct rates. This is due to the fact that in those two cases the input scene included abundant texture on the ground and some rooftops and therefore correspondences were easily identified using ASIFT features. Also, the match correspondences for these two cases were spread all over images and as a result ASIFT resulted in a fundamental matrix with higher accuracy and less residual error.
6. Conclusion
In this work, 2EC features were proposed for the purpose of establishing match correspondences between oblique aerial images with large projective transformations. A complete solution for generating and matching 2EC features was proposed. The established correspondences could be used to accurately compute the fundamental matrix and obtain refined camera parameters that are used for image registration or 3D reconstruction purposes. The extraction of 2EC features required detecting straight lines in the input images and these lines were utilized as a medium to extract viewpoint invariant corners. Both lines and corners were encapsulated in the definition of 2EC features, such that each feature could potentially correspond to a vertex and two connected edges of a building rooftop. The geometrical characteristics of 2EC features ensured their surrounded image regions to be planar, and therefore viewpoint invariant under large viewpoint variations. In the matching process, both geometrical and visual properties of each feature were used. The experimental results showed the effectiveness of 2EC features to identify and locate true match correspondences between oblique aerial images under large projective transformation. The superiority of 2EC features was demonstrated by comparing it with the state of the art features.
References
- Xiao, J. and Shah, M. (2003) Two-Frame Wide Baseline Matching. Proceedings of the 9th IEEE International Conference on Computer Vision (ICCV 2003), Nice, 14-17 October 2003, 603-609.
- Lowe, D.G. (2004) Distinctive Image Features from Scale-Invariant Keypoints. International Journal of Computer Vision, 60, 91-110. http://dx.doi.org/10.1023/B:VISI.0000029664.99615.94
- Mikolajczyk, K. and Schmid, C. (2001) Indexing Based on Scale Invariant Interest Points. Proceedings of the 8th IEEE International Conference on Computer Vision (ICCV 2001), Vancouver, 7-14 July 2001, 525-531.
- Mikolajczyk, K. and Schmid, C. (2002) An Affine Invariant Interest Point Detector. Proceedings of the 7th European Conference on Computer Vision Part I, Copenhagen, 28-31 May 2002, 128-142.
- Mikolajczyk, K. and Schmid, C. (2004) Scale & Affine Invariant Interest Point Detectors. International Journal of Computer Vision, 60, 63-86. http://dx.doi.org/10.1023/B:VISI.0000027790.02288.f2
- Tuytelaars, T. and Gool, L.J.V. (2004) Matching Widely Separated Views Based on Affine Invariant Regions. International Journal of Computer Vision, 59, 61-85. http://dx.doi.org/10.1023/B:VISI.0000020671.28016.e8
- Matas, J., Chum, O., Urban, M. and Pajdla, T. (2002) Robust Wide Baseline Stereo from Maximally Stable Extremal regions. Image and Vision Computing, 22, 761-767.
- Mikolajczyk, K., Tuytelaars, T., Schmid, C., Zisserman, A., Matas, J., Schaffalitzky, F., Kadir, T. and Gool, L.J.V. (2005) A Comparison of Affine Region Detectors. International Journal of Computer Vision, 65, 43-72. http://dx.doi.org/10.1007/s11263-005-3848-x
- Ferrari, V., Tuytelaars, T. and Gool, L.J.V. (2003) Wide-Baseline Multiple-View Correspondences. Proceedings of the 2003 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, Madison, 18-20 June 2003, 718-728.
- Xie, J. and Tsui, H.-T. (2004) Wide Baseline Stereo Matching by Corner-Edge-Regions. Proceedings of the International Conference on Image Analysis and Recognition, Porto, 29 September 2004-1 October 2004, 713-720.
- Schmid, C. and Zisserman, A. (1997) Automatic Line Matching across Views. Proceedings of the 1997 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Juan, 17-19 June 1997, 666-671.
- Bay, H., Ferrari, V. and Gool, L.J.V. (2005) Wide-Baseline Stereo Matching with Line Segments. Proceedings of the 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Diego, 20-25 June 2005, 329-336.
- Wang, L., Neumann, U. and You, S. (2009) Wide-Baseline Image Matching Using Line Signatures. Proceedings of the 12th International Conference on Computer Vision, Kyoto, 29 September 2009-2 October 2009, 1311-1318.
- Tell, D. and Carlsson, S. (2002) Combining Appearance and Topology for Wide Baseline Matching. Proceedings of the 7th European Conference on Computer Vision, Copenhagen, 28-31 May 2002, 68-81.
- Ng, E.S. and Kingsbury, N.G. (2010) Matching of Interest Point Groups with Pairwise Spatial Constraints. Proceedings of the 17th IEEE International Conference on Image Processing (ICIP), Hong Kong, 26-29 September 2010, 2693- 2696.
- Mortensen, E.N., Deng, H. and Shapiro, L.G. (2005) A SIFT Descriptor with Global Context. Proceedings of the 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Diego, 20-25 June 2005, 184- 190.
- Lee, J.A., Yow, K.C. and Chia, A.Y.S. (2009) Robust Matching of Building Facades under Large Viewpoint Changes. Proceedings of the 12th International Conference on Computer Vision, Kyoto, 29 September 2009-2 October 2009, 1258-1264.
- Ding, M., Lyngbaek, K. and Zakhor, A. (2008) Automatic Registration of Aerial Imagery with Untextured 3DLiDAR Models. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Anchorage, 23-28 June 2008, 1-8.
- Wang, L. and Neumann, U. (2009) A Robust Approach for Automatic Registration of Aerial Images with Untextured Aerial LiDAR Data. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Miami, 20-25 June 2009, 2623-2630.
- Burns, J., Hanson, A. and Riseman, E. (1986) Extracting Straight Lines. IEEE Transactions on Pattern Analysis and Machine Intelligence, 8, 425-455. http://dx.doi.org/10.1109/TPAMI.1986.4767808
- Izadi, M. and Saeedi, P. (2012) Three-Dimensional Polygonal Building Model Estimation from Single Satellite Images. IEEE Transactions on Geoscience and Remote Sensing, 50, 2254-2272. http://dx.doi.org/10.1109/TGRS.2011.2172995
- Harris, C. and Stephens, M. (1988) A Combined Corner and Edge Detector. Proceedings of the 4th Alvey Vision Conference, Manchester, 31 August-2 September 1988, 147-151.
- Hartley, R. and Zisserman, A. (2003) Multiple View Geometry in Computer Vision. Cambridge University Press, Cambridge.
- Mularie, W. (2000) Department of Defense World Geodetic System 1984, Its Definition and Relationships with Local Geodetic Systems, National Geospatial-Intelligence Agency, Technical Report.
- Lowe, D.G. (1999) Object Recognition from Local Scale-Invariant Features. Proceedings of the 7th IEEE International Conference on Computer Vision, Kerkyra, 20-27 September 1999, 1150-1157.
- Bay, H., Tuytelaars, T. and Gool, L.J.V. (2006) SURF: Speeded up Robust Features. Proceedings of the 9th European Conference on Computer Vision, Graz, 7-13 May 2006, 404-417.
- Morel, J.M. and Yu, G. (2009) ASIFT: A New Framework for Fully Affine Invariant Image Comparison. SIAM Journal on Imaging Sciences, 2, 438-469. http://dx.doi.org/10.1137/080732730

















