International Journal of Geosciences
Vol.05 No.01(2014), Article ID:42202,13 pages
10.4236/ijg.2014.51008
Non-Rigid Rotation, Global Geodynamics and Free Nutation
Cheh Pan
Pan Filter Technology, Saratoga, USA
Email: cpan1@ix.netcom.com
Copyright © 2014 Cheh Pan. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited. In accordance of the Creative Commons Attribution License all Copyrights © 2014 are reserved for SCIRP and the owner of the intellectual property Cheh Pan. All Copyright © 2014 are guarded by law and by SCIRP as a guardian.
ABSTRACT
The rotation of the physical Earth not only obeys the law of conservation of angular momentum but follows also the three-finger rule of the right-handed system. The reference frame in the Earth is most essential. The generalized Eulerian equation of motion or the Liouville equation is to represent global geodynamics in general, which is examined directly through the observation of the Earth’s rotation and surface motions, with no additional assumptions after fundamental physics. Rotational acceleration, polar motion, plate tectonics, and seismicity observed on the Earth’s surface indicate that the Earth’s angular momentum is perturbed and adjusting independently of external torques. The internal torque or the rate of change of angular momentum in the absence of external torques represents the Earth’s conservation of perturbed angular momentum for a stable rotation of minimum energy configuration. The internal torques calculated from surface observations exhibit various magnitudes that reflect the overall global geodynamics. The secular components of internal torques are all on the order of 1023 ergs, which imply that the Earth’s angular momentum is conserved independently of external torques in a secular sense, and give an order-of-magnitude quantitative constraint to secular geodynamics in the interior. The equation of secular motion in the Earth is generalized for both internal and external perturbations. The equation approximates the global geodynamics that link polar motion with plate motion and mantle flow, while free nutation is induced to conserve the Earth’s angular momentum in the absence of external torques. The gyroscopic effect or gyricity dominates secular motion in the Earth. The kinematics of secular internal torques are consistent with the gross features of plate motion and mantle flow. Secular gyric torques are quadrupolar and continuous to the interior convectively according to the three-finger rule of the right-handed system, while secular rotational torque is toward the north. For a multilayered, deformable, energy-generating and dissipative Earth that allows motion and mass redistribution, stable rotation can be reached only when its major principal, rotation, and instantaneous figure axes are all completely aligned with each other to arrive at the minimum energy configuration of the system. Polar instability consists of incipient polar excitation that gains energy to commence polar instability, as well as polar motion and subsequent plate motion and mantle flow that dissipate energy for polar stability. Angular momentum perturbation via relative angular momentum supplies the excess energy at polar excitation, which can be episodic or continuous, internal and thermal or external and gravitational. Thermal buoyancy perturbs angular momentum, but as a secular motion it is also subject to gyricity, which consequently will guide thermal flow to conserve angular momentum. The Earth’s rotational energy of 2.16 × 1036 ergs is the largest energy reservoir that can be directly observed on the Earth’s surface; its slight fluctuation on the order of 1023 ergs is sufficient to supply power for any secular geodynamical processes in the Earth. After all, no geodynamics can be independent of the Earth’s perpetual rotation against fundamental physical laws.
Keywords
Global Geodynamics; Rotation Dynamics; Free Nutation; Angular Momentum Perturbation
1. Introduction
The Earth is a perpetually rotating heavenly body orbiting in space. The observation of polar motion, plate motion, seismicity, geological deformation, volcanism, as well as the multiple frequency-splits of the Chandler wobble [1,2] indicates that motion and mass redistribution are to occur in the solid Earth. The Earth is hence essentially a multilayered non-rigid heavenly body rotating according to the law of conservation of angular momentum, for which an additional physical rule, the three-finger rule of the right-handed system [3], also plays an equally important fundamental role. That is, in a rotating system allowing motion like the Earth, the rate of change of a vector in a reference frame rotating with the system relative to an inertial frame fixed in space differs from that in the inertial frame by a cross product of the angular velocity
 of the rotating frame with the vector. The differentiation operator
of the rotating frame with the vector. The differentiation operator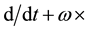 , therefore, applies to the whole rotating system. This is the gyroscopic effect, which has long been known but ignored in the study of solid Earth geodynamics.
, therefore, applies to the whole rotating system. This is the gyroscopic effect, which has long been known but ignored in the study of solid Earth geodynamics.
The importance of gyrodynamics comes in light of space dynamics [3]. From the observation of the orbiting of space vehicles, it was discovered that the rotation stability of a space vehicle can be significantly affected by the gyroscopic effect if there is energy dissipation in the vehicle [3-7]. D’Eleuterio and Hughes [7] hence include the gyroscopic effect, together with that of inertial (mass), dissipative (damping), and stiffness (elastic), as the four mechanical influences on the dynamics of flexible structures, and introduce the concept of gyricity to replace its conventional name under an instrument. Gyricity and gyric are adopted here as convenient shorthand for gyroscopic effect and gyroscopic. As the Earth is a multilayered, deformable, energy-generating, dissipative, and perpetually rotating heavenly body orbiting in space that allows motion and mass redistribution, its rotation dynamics are similar to, if not the same as, those of space vehicles, to obey the fundamental physical laws. The mechanical influences on geodynamics hence also include gyricity. As we shall see below, gyricity indeed dominates the rotation dynamics of a non-rigid Earth.
Any motion in the Earth, fast or slow, instantaneous or secular, is subject to gyricity according to the three-fin- ger rule of the right-handed system, just as that in any other rotating systems orbiting in space. The classic gyricity observed on the Earth is the Coriolis force, which was known to be negligibly small and hence led to the conventional belief that Coriolis effect played a very little role in geodynamics of the solid Earth. This is, analogous to the Earth’s rheology or deformability, indeed the case in an instantaneous sense as if the Earth were rigid, but not in a secular sense in a non-rigid Earth. A comparison may help to visualize. The Earth’s instantaneous rotation is at a rate of 1.46 × 1012 cm/year, while secular motion in the solid Earth is only a few cm/year. As we shall see below, gyricity in the Earth can be of great magnitude, and secular motion in a rotating Earth is not the same as that in an inertial or flat Earth.
Early observations [8-10] have already noticed that the torsional deformation of tectonic features on the ocean floors may be attributable to the Coriolis effect; likely are also the rotational inertia of the continents [11], as well as the “vertical axis rotation” of the crustal blocks [12,13]. Pan [14,15] has preliminarily studied the (secular) Coriolis and rotational torques in the Earth, and observes that the gross features of the present plate tectonics, such as plate distribution, plate motion, spread of oceanic ridges, and subduction of oceanic slabs, all reflect the quadrupolar nature of gyricity according to the three-finger rule of the right-handed system. This suggests that long-term gyricity may well be the primary driving mechanism for plate motion and mantle flow [15]. However, the study was yet preliminary and partial. The present paper concerns an overall examination of the fundamental physics that govern the rotation of the physical Earth, from there global geodynamics starts. It has two foundations: 1) The Liouville equation, as the generalized equation of motion for a rotating Earth orbiting in space that allows motion and mass redistribution, is to represent global geodynamics in general; and 2) direct observation of the Earth’s rotation and surface motions, without involving physical properties in the interior. It is practically a study of the Liouville equation directly through the Earth’s surface observations according to the three-finger rule of the right-handed system and the law of conservation of angular momentum, while the Earth’s non-rigidity is still treated as what the Liouville equation allows. The rotation of a non-rigid Earth is distinctly different from that of a biaxial or slightly triaxial rigid body, which is discussed elsewhere [1,2,14,16, 17].
2. Reference Frame, Liouville Equation and Global Geodynamics
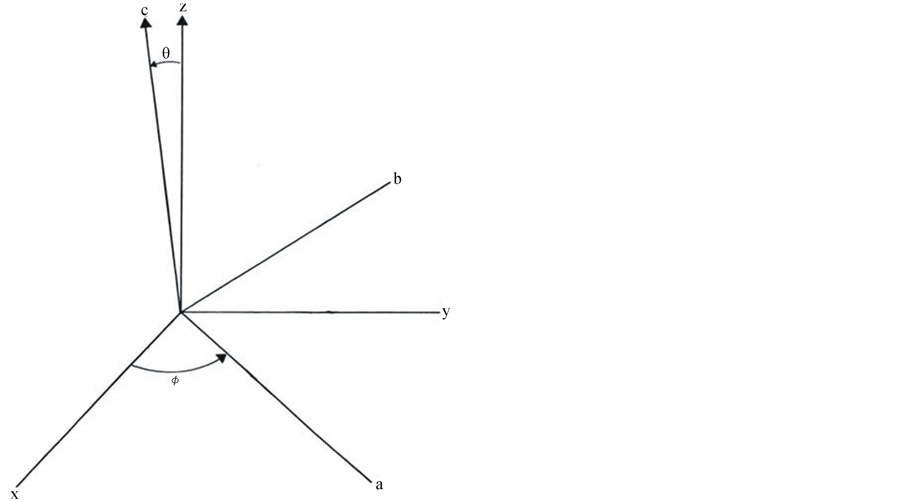
In the study of the rotation of a multilayered non-rigid Earth orbiting in space, the most essential and difficult problem is the choice of reference frame; otherwise it may end up not truly representing the physical Earth. So we repeat a brief review here to emphasize. Munk and MacDonald [18] have already pointed out that it is unlikely to find a truly body-fixed frame in the Earth. Chao [19] further points out that there is an inconsistency between the reference frame used for observation and those for theoretical calculation. Pan [17] observes that all conventional theoretical frames are idealized systems that are not truly located in the physical Earth. The Earth’s rotation must refer to an inertial frame fixed in space, but which can be assumed to be instantaneously coinciding with a frame located in the Earth without loss of generality [17,18,20]. Pan [14-17] demonstrates that a physically consistent theoretical frame has to be unique, physically located in the Earth, consistent with observation, and always associated with polar motion. A frame close to such conditions is adopted here. As depicted in Figure 1, the
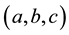 frame is the Earth’s principal axes prior to polar excitation, referring to which the inertia tensor was diagonal; whereas, the
frame is the Earth’s principal axes prior to polar excitation, referring to which the inertia tensor was diagonal; whereas, the
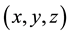 frame is the axes of the Earth’s inertia tensor that will appear simultaneously with polar excitation, referring to which the inertia tensor is not diagonal. The
frame is the axes of the Earth’s inertia tensor that will appear simultaneously with polar excitation, referring to which the inertia tensor is not diagonal. The
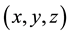 frame is the reference frame, which differs from the
frame is the reference frame, which differs from the
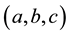 frame by the axial near-symmetry angle pair
frame by the axial near-symmetry angle pair , where
, where
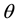 is the deviation angle between the c- and z-axes, and
is the deviation angle between the c- and z-axes, and
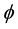 is the azimuth angle between corresponding equatorial axes of the two systems. The frame is geocentric. Its z-axis or instantaneous figure axis is aligned with the axis of reference [18] or the geographic axis [21] around which the rotation axis physically revolves, but which is, as Pan [2,14-17] points out, not a principal axis. Its y-axis is along the direction of secular polar drift, while x-axis is perpendicular to the y- and z-axes in the right-handed system. In this frame, the Earth is axially near-symmetrical and slightly triaxial even it was originally biaxial [2,14-16]. The Liouville equation is fully described in the frame.
is the azimuth angle between corresponding equatorial axes of the two systems. The frame is geocentric. Its z-axis or instantaneous figure axis is aligned with the axis of reference [18] or the geographic axis [21] around which the rotation axis physically revolves, but which is, as Pan [2,14-17] points out, not a principal axis. Its y-axis is along the direction of secular polar drift, while x-axis is perpendicular to the y- and z-axes in the right-handed system. In this frame, the Earth is axially near-symmetrical and slightly triaxial even it was originally biaxial [2,14-16]. The Liouville equation is fully described in the frame.
Received November 1, 2013; revised December 3, 2013; accepted January 2, 2014
The Liouville equation or the generalized Eulerian equation of motion [2,14-18,20,22] governs the rotation of a system that allows motion in the system. The Earth is such a rotating system; this is fundamental physics. The equation states that according to the law of conservation of angular momentum, the rate of change of total angular momentum or the internal torque [14] of a rotating system is equal to the external torque exerted on the system, while motion in the system follows the three- finger rule of the right-handed system. The Liouville equation can either be linearized to examine the polar excitation mechanism or rotation irregularities excited by motion and mass redistribution [1,2,14,16-18,20,22], or otherwise directly adopted as the Earth’s equation of motion for what after polar excitation or global geodynamics such as the driving mechanism of polar motion, plate motion and mantle flow [14,15], as well as free nutation in the absence of external torques. An incipient solution of the linearized Liouville equation [14,16,17] predicts the multiple splits of the Chandler frequency, as is confirmed by observation [1,2]. Pan [14,15] has also preliminarily demonstrated that two secular internal torques, the Coriolis and rotational torques, are likely the primary driving mechanisms for plate motion and mantle flow. The present paper is an introductory examination of the internal torques in the Liouville equation that
Figure 1.The coordinate systems of the Earth prior to and at polar excitation.
represent the overall global geodynamics, as well as an integration of global geodynamics with rotation dynamics.
Let
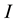 be the Earth’s inertia tensor,
be the Earth’s inertia tensor,
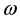 rotation velocity,
rotation velocity,
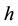 relative angular momentum arising from motion and mass redistribution [2,14,15,17], and
relative angular momentum arising from motion and mass redistribution [2,14,15,17], and
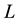 external torque. The Liouville equation in the
external torque. The Liouville equation in the
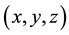 frame rotating relative to an instantaneously coinciding inertial frame fixed in space is, then,
frame rotating relative to an instantaneously coinciding inertial frame fixed in space is, then,
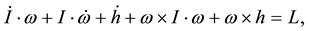 (1)
(1)
where the overdot designates
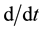 in the
in the
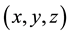 frame. Equation (1) represents global geodynamics in general. The left-side terms in the equation are the rate of change of angular momentum, a reaction to external torque that reflects the central-force dynamics in the Earth [23]. The terms can thus be called the internal torques of the system [14,15,24], though their dimension is not exactly in dyne-cm as that of a torque. Throughout this paper, we shall use erg as their unit for the convenience of direct conversion to energy, and for a more refined order- of-magnitude resolution. Observation of non-tidal rotational acceleration, polar motion, plate motion, and seismicity on the Earth’s surface indicates the Earth’s angular momentum is changing or adjusting independent of external torques. Internal torques therefore must exist in the Earth independent of external torques that can be calculated directly from surface observations, without involving physical properties in the interior [14,15]. The calculation is reliable at least on an order-of-magnitude sense, which allows us to quantitatively examine the internal torques from the Earth’s surface according to the three-finger rule of the right-handed system and the law of conservation of angular momentum. Order-of-magni- tude is not likely to change with new observations or the inclusion of the Earth’s rheology.
frame. Equation (1) represents global geodynamics in general. The left-side terms in the equation are the rate of change of angular momentum, a reaction to external torque that reflects the central-force dynamics in the Earth [23]. The terms can thus be called the internal torques of the system [14,15,24], though their dimension is not exactly in dyne-cm as that of a torque. Throughout this paper, we shall use erg as their unit for the convenience of direct conversion to energy, and for a more refined order- of-magnitude resolution. Observation of non-tidal rotational acceleration, polar motion, plate motion, and seismicity on the Earth’s surface indicates the Earth’s angular momentum is changing or adjusting independent of external torques. Internal torques therefore must exist in the Earth independent of external torques that can be calculated directly from surface observations, without involving physical properties in the interior [14,15]. The calculation is reliable at least on an order-of-magnitude sense, which allows us to quantitatively examine the internal torques from the Earth’s surface according to the three-finger rule of the right-handed system and the law of conservation of angular momentum. Order-of-magni- tude is not likely to change with new observations or the inclusion of the Earth’s rheology.
The first term
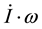 in Equation (1) arises from inertia changes due to motion and mass redistribution, notably secular polar drift, plate motion, and mantle flow, in a rotating Earth. According to the three-finger rule of the right-handed system, it belongs to gyricity but is not a typical gyric torque as that can be directly represented by the cross product of w with motion, and it will disappear if the Earth were rigid. Pan [14,15] names it the Coriolis torque and has quantitatively analyzed it in rather detail. Its magnitude is on the order of 1023 ergs, which, if converted to force, is about 12 to 80 times greater than the extensional force exerted at the bottom of the lithosphere by upper mantle thermal convection as calculated by Richter [25]. However, thermal flow, as a secular motion, can also induce such a gyric torque according to the three-finger rule of the right-handed system. The torque will then, for the sake of polar stability, guide the flow convectively to offset the perturbation to angular momentum from thermal buoyancy, which will be further explored below.
in Equation (1) arises from inertia changes due to motion and mass redistribution, notably secular polar drift, plate motion, and mantle flow, in a rotating Earth. According to the three-finger rule of the right-handed system, it belongs to gyricity but is not a typical gyric torque as that can be directly represented by the cross product of w with motion, and it will disappear if the Earth were rigid. Pan [14,15] names it the Coriolis torque and has quantitatively analyzed it in rather detail. Its magnitude is on the order of 1023 ergs, which, if converted to force, is about 12 to 80 times greater than the extensional force exerted at the bottom of the lithosphere by upper mantle thermal convection as calculated by Richter [25]. However, thermal flow, as a secular motion, can also induce such a gyric torque according to the three-finger rule of the right-handed system. The torque will then, for the sake of polar stability, guide the flow convectively to offset the perturbation to angular momentum from thermal buoyancy, which will be further explored below.
The second term
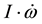 in Equation (1) arises from rotational acceleration and is non-gyric [15]. The term exists both in a rigid and a non-rigid Earth. Using the Earth’s moments and products of inertia calculated by Pan [16] and observed rotational acceleration [26-32], the different components of the torque are calculated and listed in Table 1, where α is the angular distance between the rotation and instantaneous figure axes, and β is the azimuth angle of the rotation axis. The calculation procedure is in Pan [15]. This torque has diverse components. Its periodic and irregular components are on the order of 1026 ergs, while its secular components, tidal and non-tidal, are on the order of 1023 ergs, the same as that of
in Equation (1) arises from rotational acceleration and is non-gyric [15]. The term exists both in a rigid and a non-rigid Earth. Using the Earth’s moments and products of inertia calculated by Pan [16] and observed rotational acceleration [26-32], the different components of the torque are calculated and listed in Table 1, where α is the angular distance between the rotation and instantaneous figure axes, and β is the azimuth angle of the rotation axis. The calculation procedure is in Pan [15]. This torque has diverse components. Its periodic and irregular components are on the order of 1026 ergs, while its secular components, tidal and non-tidal, are on the order of 1023 ergs, the same as that of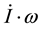
The third term
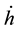
Table 1. Different components of
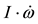
At α = 6.7 × 10−7 rad.
For instance, a
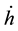
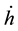
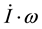

The fourth term
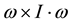
The fifth term


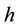

The above examination manifests that internal torques are of various magnitudes and are not all balanced by external torques, while the known reaction to external torques is order-of-magnitude greater than all the other internal torques. This indicates perturbation to the Earth’s angular momentum can be independent of external torques. Among the five internal torques in Equation (1),
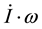


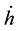
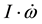
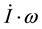

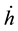
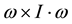

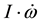
3. Generalization of the Earth’s Equation of Secular Motion
Pan [15] demonstrates that polar motion, plate motion, and mantle flow are interrelated and their interaction can be traced back to the evolution of polar instability. A special equation of secular motion in the Earth for internal perturbations [15] was derived according to the law of conservation of angular momentum and the three-finger rule of the right-handed system. The equation can be further generalized to account for both internal and external perturbations. Let

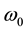

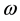
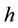
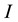

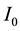
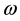
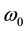
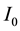
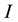
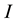


Equation (2) differs from Equation (3) in Pan [15] with the approximately equal sign
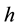
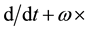
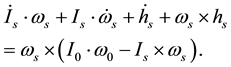
Equation (3) approximates the linkage between the Earth’s non-rigid rotation, secular global geodynamics as well as free nutation in the absence of external torques; it differs from the special equation of secular motion only for internal perturbations [15] by the approximately equal sign
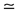
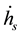
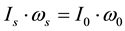
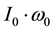
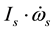
The left-side secular internal torques in Equation (3) exhibit the driving mechanism of secular motion in the Earth. Among which,
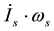

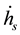
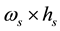
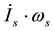

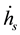
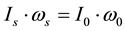
Pan [14,15] observes that since


4. Polar Stability
The polar or rotation stability implied in Equation (3) is different from that of a biaxial rigid body [2,3,17]. A biaxial rigid body can keep a stable rotation even its rotation axis is misaligned with its major principal axis, since it lacks either energy dissipation or motion and mass redistribution, while the equatorial bulge acts as a stabilizer. However, for a deformable, energy-generating and dissipative Earth that allows motion and mass redistribution, a stable rotation can be reached only when its major principal, rotation, and instantaneous figure axes are all completely aligned with each other [2,15,17]; i.e., only when
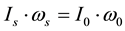
Polar instability consists of incipient polar excitation that gains energy, and subsequent polar motion that dissipates energy. Polar excitation, as we shall see below, can either be episodic or continuous, but polar motion is always continuous until a stable rotation is reached. The polar wandering mechanism discussed by Goldreich and Toomre [48] is a simplified account of polar instability, because it does not differentiate polar excitation from polar motion. The incipient solution of the Liouville equation [14,16] gives a static term for incipient polar excitation, as well as a secular polar drift term and a wobble term for subsequent polar motion. However, there is no clear distinction between the perturbation that excites polar instability and the subsequent adjustment that damps polar instability; both belong to mass redistribution in the Earth. One criterion for their physical division is that the mass redistribution that induces motion and products of inertia excites polar instability, and that reduces motion and products of inertia damps polar instability. Equation (3) expresses the latter. Nevertheless, if a motion, such as seasonal fluctuations of atmosphere or the atmospheric and oceanic excitation of the Earth’s wobbles [49,50], that induces little mass redistribution in the solid Earth, then there will be little change in the position of the principal axes in the solid Earth. However, according to the three-finger rule of the right-handed system, the relative angular momentum induced by the motion will force the rotation axis to revolve away from the major principal axis around an instantaneous figure axis that has been shifted to a new position at the excitation axis [2,17,18], about which the inertia tensor is no longer diagonal due to its axial near-symmetry[2,14,17]. Polar excitation by motion alone thus can also induce products of inertia in the solid Earth. In such a case, polar excitation is due to continuous motion as well as the
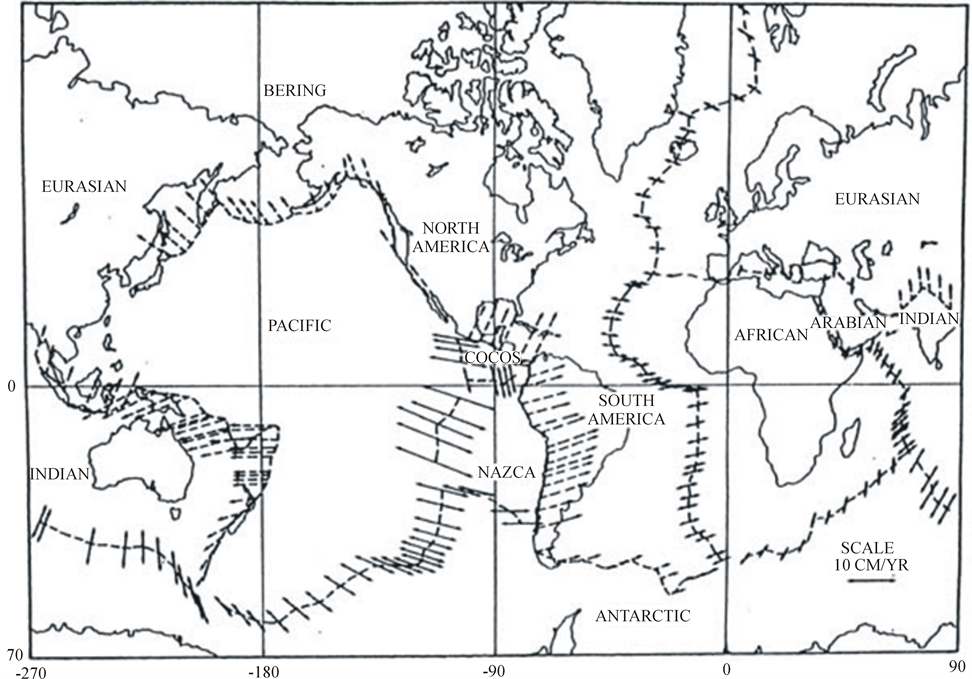
Figure 2. The present plate tectonics (after Minster et al., 1974).
products of inertia arising from the near-symmetry of the instantaneous figure axis at its new position, the excitation axis. The instantaneous figure axis thus will shift responding to either motion or mass redistribution, while the principal axes shift responding only to mass redistribution.
5. Perturbation and Energy Supply
We have so far demonstrated that secular internal torques are not the angular momentum perturbation that will excite polar instability, but represent the effort of an already perturbed Earth in search for a stable rotation through self-adjustment according to the three-finger rule of right-handed system for the sake of conservation of angular momentum. They thus dissipate energy and will appear in the Earth independent of external torques only after unstable rotation of higher energy configuration has already been excited. Pan [14,16] predicts the Chandler wobble possesses multiple frequency splits and is slow damping or quasi-permanent, as is confirmed by observation [1,2]. Polar motion hence does not need a simultaneous polar excitation to maintain. However, a quasi- permanent polar motion will still be damped out eventually for a stable rotation, if there is no repeated angular
momentum perturbation or episodic polar excitation to suspend it. Ahrens [40] and Wood [41] contend that the proto-Earth was formed through rapid and violent impact accretion of large planetsimals, which could repeatedly excite large polar motion or even a change of the Earth’s obliquity [51]. Pines and Shaham [42] suggest that some violent events in geological history, such as the escape of the Moon from the Earth or the impact of a giant meteorite, might have excited polar instability. Pan [17] demonstrates that the magnitude of polar excitation owing to meteorite or asteroid impact depends on the products of inertia that can be induced by the impact. For instance, if the impact asteroid was around 10 km in diameter [33], its polar excitation was about 1.15 × 10−5, slightly greater than the present Chandler wobble. In the above external perturbations, the energy supply is gravitational and mechanical. On the other hand, geological observation has long established that geological history was intersected by mountain buildings or diastrophisms between geological epochs. Pan [14,52-56] calculates that the diastrophisms are able to excite polar instability episodically on the order of 107 years, initiated by explosive release of excess thermal energy accumulated in the interior through gigantic failures along some susceptible zones in the lithosphere. The energy supply for such internal perturbations is thermal. The excess thermal energy that can be accumulated in the Earth in 107 years is on the order of 1035 ergs [52,53]. Pan [14] has quantitatively analyzed ten cases of such polar excitation, which can reach a magnitude as large as 10−2, four orders greater than the present Chandler wobble.
All above perturbations, internal or external, are episodic. Spada et al. [57] consider the excitation of polar wandering by subduction, while Steinberger and O’Connell [58] discuss changes of the Earth’s rotation axis owing to advection of mantle density heterogeneities. Gross [49] and Gross et al. [50] investigate the atmospheric and oceanic excitation of the Earth’s wobbles. For such cases, perturbation and consequent polar excitation are continuous, while energy supply is internal and thermal or gravitational. Polar excitation will occur simultaneously with polar motion until thermal convection or atmospheric and oceanic processes stop, but damping of polar motion will continue until a complete stable rotation is reached.
The Earth’s dissipation of excess energy for a stable rotation is independent of the loss of kinetic rotational energy through tidal friction. This is because, as we have noted above, secular rotational torque comes from non- tidal secular rotational acceleration. The energy dissipation through the Earth’s self-adjustment will stop as soon as the Earth has reached its complete stable rotation, but the loss of rotational energy through tidal friction will continue as long as external attractions are there. It is interesting that the magnitude of lunar tidal torque, according to Stacey [59], is 4.4 × 1023 ergs, on the same order of magnitude as that of secular internal torques. If the viscosity of the low-velocity layer is sufficiently low or the mantle is non-Newtonian [15], it cannot rule out that tidal torque might cause a secular lag of the lithosphere to induce apparent quadrupolar gyric motion of the tectonic plates over the low-velocity layer according to the three-finger rule of the right-handed system. If this were the case, then the driving mechanism of plate motion would involve also the exchange of angular momentum with the Moon, of which the energy supply is external and gravitational.
6. Convection
As has been pointed out above, secular gyric torques are continuous to the interior convectively according to the three-finger rule of the right-handed system. Pan [14,15] has preliminarily studied the (secular) Coriolis and rotational torques in the mantle and named the internal-tor- que-induced flow transvection, which is a form of convection induced by gyricity and is thus different from thermal convection, though both belong to secular motion in the mantle. Equation (3) and related discussions define transvection. It is a reaction of a deformable and dissipative Earth to angular momentum perturbation; i.e., it is the Earth’s effort to damp its products of inertia for a stable rotation to conserve angular momentum. Transvection is, therefore, a mass redistribution that occurs only after polar instability has been excited. On the other hand, thermal convection is an action of thermal buoyancy in the interior; i.e., it is a mass redistribution that induces products of inertia. In other words, thermal convection belongs to the angular momentum perturbation that supplies energy to excite polar instability, while transvection is the subsequent adjustment through gyricity that dissipates energy for polar stability. Transvection hence will guide thermal flow according to the quadrupolar rule of gyricity to offset the perturbation from thermal buoyancy for the sake of angular momentum conservation.
Mantle convection has long been believed to be the driving mechanism for plate motion. Convection models are generally divided into four categories: Thermal plumes [60,61], upper mantle convection [25,62-66], layered convection [67-72], and whole mantle convection [68,70,73-76]. A common problem for the various models is the physical properties in the interior; it is not yet certain whether the mantle is Newtonian or non-Newto- nian. Newtonian mantle prevails because we know more of Newtonian surface flows, and it is also easier to handle mathematically. However, observations and experiments also suggest that the rheological behavior of the upper mantle may be non-Newtonian [62,63,77-80]. Under the order-of-magnitude quantitative constraint from surface secular motion observations, a preliminary study [15] shows a non-Newtonian mantle is more compatible with secular internal torques. If the mantle is Newtonian, then the viscosity of the upper mantle used in that study was either too high or non-secular; otherwise, the viscous torque adopted for the upper mantle was inadequate [15]. Since the physical properties in the interior are deduced indirectly on the surface and are non-secular, how will they behave in the true physical conditions in the mantle in a geological time-frame is a good question. Calculation based on surface observations [15] shows that the driving effect of upper mantle thermal convection on plate motion is one order smaller than that of secular internal torques; only whole mantle convection is able to induce a torque that is on the order of 1023 ergs. This implies if thermal convection is to drive plate motion, it has to be whole mantle convection.
There is another concern for thermal convection, energy source or power supply. Heat from the core and radioactivity in the interior are believed to be the energy reservoirs. Nevertheless, the energy sources in the interior are indirectly estimated with assumptions [59], not like the rotational energy and secular internal torques that are directly observed on the Earth’s surface. The various thermal convection models are therefore more kinematical than dynamical. As a perturbation to angular momentum, thermal convection is a mass redistribution that will excite polar instability. However, as a secular motion, it has also to follow the three-finger rule of the right-handed system just like any other motions in a rotating Earth. This is to say, if thermal convection is to drive mantle flow, it will cause an inertia change to induce the secular Coriolis torque
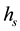
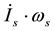
Secular internal torques are depth-dependent; i.e., they decrease with depth. In a non-Newtonian mantle, they are likely balanced by the viscoplastic torque about the bottom of the upper asthenosphere [15], which gives transvection an appearance analogous to the upper-man- tle or layered convection [72]; the 660-km discontinuity is thus not a barrier but a likely lower boundary for transvection. It is, therefore, not unreasonable to perceive that hot plumes may originate in the asthenosphere. The interaction between mantle thermal convection and the Earth’s rotation is worth an investigation. The fundamental physics that governs the flows in the Earth’s interior should not be much different from that for the more mobile layers, the atmosphere and oceans. Mantle dynamics cannot be independent of the Earth’s perpetual rotation.
7. More Discussions
Movements in the more rigid layer of the Earth, the lithosphere, are not in flows but in quadrupolar plates more or less 90˚-by-90˚ in dimension moving or subducting against each other according to the three-finger rule of the right-handed system, reflecting the quadrupolar nature of gyricity [15]. Secular internal torques therefore furnish dynamics to plate tectonics. The stress distribution in the lithosphere is expected to concentrate more along the confronting boundaries. This helps to explain the differences between intraplate and interplate seismicities; why the former is less frequent than the latter. The temporal variation of global seismicity can be correlated with secular internal torques, and such a correlation may help to learn about the global trend of seismic activity. On the other hand, neither plate motion nor flows in the different layers in the Earth will have much effect on the Earth’s principal gravity field, which is governed by Newton’s gravitational law [81]. Nevertheless, secular motion can affect the part of gravity that is due to rotation; i.e., it is responsible for the adjustment of the slight imbalances of the Earth’s gravity caused by its unstable rotation.
The energy required for secular motion in the Earth, as has been calculated above, is on the order of 1023 ergs, negligible in comparison to the Earth’s total rotational energy of 2.16 × 1036 ergs, which is the largest energy reservoir that can be directly observed on the Earth’s surface. This implies a slight fluctuation of the rotational energy, or an angular momentum perturbation that can provide to the Earth an unnoticeable amount of energy on the order of 1023 ergs, is sufficient to supply power for any secular dynamical processes in the Earth and maintain the presently observed polar motion, plate motion, and mantle flow. Similar to shaping a pottery on a wobbling turning table, the deformation and adjustment for the Earth to keep its near-spherical shape after gravitation reflect more of the effect of rotation rather than that of a dynamical process in the interior. We may have long overlooked this fact because we are too much used to our instantaneous life of twenty-four hours for a day and take it for granted. Dynamical processes in the interior can dominate mass redistribution only when the Earth is in a stable rotation of minimum energy configuration. Yet, whenever a dynamical process in the interior perturbs the Earth’s angular momentum, polar instability will be excited immediately. Secular internal torques will then appear accordingly, and rotation, subsequently gyricity, will again dominate secular motion in the Earth.
8. Conclusion
The physical Earth is a multilayered, deformable, energy- generating, dissipative, and perpetually rotating heavenly body orbiting in space according to the law of conservation of angular momentum, while motion in a rotating Earth follows the three-finger rule of the right-handed system. The Earth’s rotation dynamics is thus integrated with global geodynamics, and the generalized Eulerian equation of motion or the Liouville equation represents global geodynamics in general. An examination of the Liouville equation via observation of the Earth’s rotation and surface motions manifests that the Earth’s angular momentum is perturbed and adjusting independent of external torques. Secular internal torques represent the Earth’s effort to conserve its angular momentum for a stable rotation of minimum energy configuration, which appear in the Earth independent of external torques only after polar instability has been excited. Secular internal torques calculated from surface observations are all on the order of 1023 ergs, which gives a quantitative order- of-magnitude constraint to secular geodynamics in the interior. The Earth can be excited from a stable rotation of minimum energy configuration to an unstable rotation of higher energy budget by either internal or external perturbations. For the sake of conservation of angular momentum, internal torques in a perturbed Earth are balanced by free nutation in the absence of external torques. The Earth’s generalized equation of secular motion is an approximation of the global geodynamics that links polar motion, plate motion and mantle flow to free nutation. Gyricity dominates secular motion in the Earth, which, together with secular rotational torque, may well be the primary driving mechanism for plate motion and mantle flow. A deformable, energy-generating and dissipative Earth can reach a stable rotation of minimum energy configuration only when its major principal, rotation, and instantaneous figure axes are all completely aligned with each other; separation of the axes excites polar instability. Polar instability consists of incipient polar excitation that gains energy to commence polar instability, and subsequent polar motion, plate motion and mantle flow that dissipate energy for polar stability. The energy gained at polar excitation is supplied by angular momentum perturbation, which can be either episodic or continuous, internal and thermal or external and gravitational. According to the three-finger rule of the right-handed system, secular internal torques will induce transvection, a passive form of convection arising from gyricity that is different from active thermal convection. Thermal buoyancy supplies energy to excite polar instability, while transvection is the gyric effort of a rotating Earth to dissipate energy for polar stability. However, as a secular motion, thermal buoyancy is also subject to gyricity, which then guides the flow to follow the three-finger rule of the right-handed system for angular momentum conservation. The rotational energy of 2.16 × 1036 ergs is the largest energy reservoir that can be directly observed on the Earth’s surface; in comparison the energy supply for secular motion in the Earth is insignificant. An unnoticeable fluctuation of the Earth’s rotational energy on the order of 1023 ergs is sufficient to supply for any secular geodynamical processes in the Earth. No geodynamics in a deformable, energy-generating and dissipative Earth orbiting in space that allows motion and mass redistribution can be independent of its perpetual rotation, as long as the Liouville equation is its generalized equation of motion that follows the law of conservation of angular momentum and the three-finger rule of the right-handed system. This paper presents an introduction to the unification of global geodynamics with the Earth’s rotation dynamics through the Liouville equation under fundamental physical laws.
Acknowledgements
Discussions with Ben Chao helped me to clarify some fundamental concepts. I thank Liu Lanbo, Rob van der Voo, Bruce Buffett, David Gubbins, and Chen Yuntai for their review of the manuscript, Goetz Bokelmann for his review and discussions, and Giorgio Ranalli for his review, comments, and support. Sun Weidong suggested that tidal pull might cause a differential rotation between the lithosphere and the mantle. Special thanks are due to Professor Walter Munk for his kind review of an early version of the manuscript. High appreciation is due to the Editor-in-Chief and the anonymous reviewers for their comments and suggestions. The paper is in memory of Professors S. K. Runcorn, J. T. Wilson, and Ting-Ying H. Ma. Prof. Ma initiated my interest in the problem; Prof. Wilson supported my early studies; and Prof. Runcorn helped me in reaching conclusions. This particular paper took me nearly 25 years to evolve; I owe my dearest gratitude to my wife Wei for her understanding and support.
REFERENCES
[1] C. Pan, “Observed Multiple Frequencies of the Chandler Wobble,” Journal of Geodynamics, Vol. 44, No. 1-2, 2007, pp. 47-65. http://dx.doi.org/10.1016/j.jog.2006.12.004
[2] C. Pan, “Linearization of the Liouville Equation, Multiple Splits of the Chandler Frequency, Markowitz Wobbles, and Error Analysis,” International Journal of Geos- ciences, Vol. 3, No. 2, 2012, pp. 930-951. http://dx.doi.org/10.4236/ijg.2012.325095
[3] T. Thomson, “Introduction to Space Dynamics,” Wiley, New York, 1986, 317 p.
[4] R. E. Roberson, “The Equivalence of Two Classical Problems of Free Spinning Gyrostats,” Journal of Applied Mechanics, Vol. 38, No. 3, 1971, pp. 707-708.
[5] G. M. T. D’Eleuterio and P. C. Hughes, “Dynamics of a Flexible Vehicle with a General Angular Momentum distribution,” Progress Report at the III PVI and SU/AIAA Symposium on the Dynamics and Control of Large Flexible Spacecraft, Blacksburg, Virginia, 1981.
[6] H. B. Hablani, “Modal Analysis of Gyroscopic Flexible Spacecraft: A Continuum Approach,” Guidance, Control and Dynamics, Vol. 5, No. 5, 1982, pp. 448-457.
[7] G. M. T. D’Eleuterio and P. C. Hughes, “Dynamics of Gyro- Elastic Continua,” AIAA/ASME/ASCE/AHS 24th Struc- tures, Structural Dynamics & Materials Conference, 2-4 May 1983, 1983, 9 p.
[8] H. Rance, “Major Lineaments and Torsional Deformation of the Earth,” Journal of Geophysical Research, Vol. 72, No. 8, 1968, pp. 2213-2217. http://dx.doi.org/10.1029/JZ072i008p02213
[9] H. Rance, “Lineaments and Torsional Deformation of the Earth: Indian Ocean,” Journal of Geophysical Research, Vol. 74, No. 12, 1969, pp. 3271-3272. http://dx.doi.org/10.1029/JB074i012p03271
[10] B. F. Howell Jr., “Coriolis Force and the New Global Tectonics,” Journal of Geophysical Research, Vol. 75, No. 14, 1970, pp. 2769-2772. http://dx.doi.org/10.1029/JB075i014p02769
[11] M. F. Kane, “Rotational Inertia of Continents: A Pro- posed Link between Polar Wandering and Plate Tecton- ics,” Science, Vol. 175, No. 4028, 1972, pp. 1355-1357. http://dx.doi.org/10.1126/science.175.4028.1355
[12] K. W. Hudnut, “Geodetic Evidence for the Rotation of Crustal Blocks (Abstract), EOS,” Transactions― American Geophysical Union, Vol. 72, 1991, p. 124.
[13] D. E. Argus, and R. G. Gordon, “Rotation of the Sierra Nevada from VLBI data (Abstract), EOS,” Transac- tions―American Geophysical Union, Vol. 72, 1991, p. 124.
[14] C. Pan, “Polar Motion of a Triaxial Earth and Dynamical Plate Tectonics,” Tectonophysics, Vol. 25, No. 1-2, 1975, pp. 1-40. http://dx.doi.org/10.1016/0040-1951(75)90009-8
[15] C. Pan, “Polar Instability, Plate Motion, and Geodynam- ics of the Mantle,” Journal of Physics of the Earth, Vol. 33, No. 5, 1985, pp. 411-434. http://dx.doi.org/10.4294/jpe1952.33.411
[16] C. Pan, “The Multiple-Frequency Chandler Wobble,” Jour- nal of Physics of the Earth, Vol. 30, No. 5, 1982, pp. 389- 419. http://dx.doi.org/10.4294/jpe1952.30.389
[17] C. Pan, “Angular Momentum Perturbation, Polar Excita- tion, and Axial Near-Symmetry,” Geophysical Journal International, Vol. 137, No. 1, 1999, pp. 139-148. http://dx.doi.org/10.1046/j.1365-246x.1999.00782.x
[18] W. H. Munk and G. J. F. MacDonald, “The Rotation of the Earth,” Cambridge University Press, London, 1960, 323 p.
[19] B. F. Chao, “On the Excitation of the Earth’s Free Wob- ble and Reference Frames,” Geophysical Journal Interna- tional, Vol. 79, No. 2, 1984, pp. 555-563. http://dx.doi.org/10.1111/j.1365-246X.1984.tb02240.x
[20] H. Moritz and I. I. Mueller, “Earth Rotation: Theory and Observation,” The Ungar Publishing Company, New York, 1988, 617 p.
[21] M. L. Smith, “Wobble and Nutation of the Earth,” Geo- physical Journal International, Vol. 50, No. 1, 1977, pp. 103-140. http://dx.doi.org/10.1111/j.1365-246X.1977.tb01326.x
[22] K. Lambeck, “The Earth’s Variable Rotation: Geophysi- cal Causes and Consequences,” Cambridge University Press, London, 1980, 449 p. http://dx.doi.org/10.1017/CBO9780511569579
[23] R. A. Becker, “Introduction to Theoretical Mechanics,” McGraw-Hill, New York, 1954, 420 p.
[24] C. Pan, “The Earth’s Rotation Instability, Plate Motion, and Geodynamics of the Mantle (Abstract),” AGU Tran- sactions, Vol. 59, 1978, pp. 1202-1203.
[25] F. M. Richter, “Dynamical Model for Sea-Floor Spread- ing,” Reviews of Geophysics, Vol. 11, No. 2, 1973, pp. 223-287. http://dx.doi.org/10.1029/RG011i002p00223
[26] W. Markowitz, “Sudden Changes in Rotational Accelera- tion of the Earth and Secular Motion of the Pole,” In: L. Mansinha, D. E. Smylie and A. E. Beck, Eds., Earth- quake Displacement Fields and the Rotation of the Earth, Reidel, Dordrecht, 1970, pp. 69-81. http://dx.doi.org/10.1007/978-94-010-3308-4_7
[27] W. Markowitz, “Rotational Accelerations,” In: P. Mel- chior and S. Yumi, Eds., Rotation of the Earth, IAU Symposium No. 48, Reidel, Dordrecht, 1972, pp. 162-164.
[28] K. Lambeck, “Effects of Tidal Dissipation in the Oceans on the Moon’s Orbit and the Earth’s Rotation,” Journal of Geophysical Research, Vol. 80, No. 20, 1975, pp. 2917- 2925. http://dx.doi.org/10.1029/JB080i020p02917
[29] K. Lambeck, “Tidal Dissipation in the Oceans: Astro- nomical, Geophysical and Oceanographic Consequences, Philos,” Transactions of the Royal Society London A, Vol. 287, 1347, 1977, pp. 545-594. http://dx.doi.org/10.1098/rsta.1977.0159
[30] K. Lambeck and A. Cazenave, “The Earth’s Rotation and Atmosphere Circulation―I. Seasonal Variations,” Geo- physical Journal of the Royal Astronomical Society, Vol. 32, 1973, pp. 79-93.
[31] K. Lambeck and A. Cazenave, “The Earth’s Variable Rate of Rotation: A Discussion of Some Meteorological and Oceanic Causes and Consequences,” Philosophical Transactions of the Royal Society London A, Vol. 284, No. 1326, 1977, pp. 495-506. http://dx.doi.org/10.1098/rsta.1977.0025
[32] L. V. Morrison, “Tidal Deceleration of the Earth’s Rota- tion Deduced from Astronomical Observations in the Period A. D. 1600 to the Present,” In: P. Brosche and J. Sunder- man, Eds., Tidal Friction and the Earth’s Rotation, Springer-Verlag, Berlin, 1978, pp. 22-27.
[33] W. Alvarez and F. Asaro, “An Extraterrestrial Impact,” Scientific American, Vol. 263, No. 4, 1990, pp. 78-84. http://dx.doi.org/10.1038/scientificamerican1090-78
[34] T. Sasao, S. Okubo and M. Saito, “A Simple Theory on the Dynamical Effects of a Stratified Fluid Core upon Nutational Motion of the Earth,” In: E. P. Fedorov, M. L. Smith and P. L. Bender, Eds., Nutation and the Earth’s Rotation, IAU Symposium No. 78, Reidel, Dordrecht, 1980, pp. 165-184.
[35] T. Sasao and J. M. Wahr, “An Excitation Mechanism for the Free ‘Core Nutation’,” Geophysical Journal of the Royal Astronomical Society, Vol. 64, No. 3, 1981, pp. 729-746. http://dx.doi.org/10.1111/j.1365-246X.1981.tb02692.x
[36] S. Flodmark, “The Earth’s Polar Motion,” In: S. Flod- mark, Ed., New Approaches in Geomagnetism and the Earth’s Rotation, World Scientific, Singapore, 1991, pp. 3-52.
[37] S. Flodmark, “The Influence of Core Nutation on the Geogravitational Field and the Power Supply of Earth Dynamics,” Fysikum, Stockholm University, Stockholm, 1991.
[38] P. M. Mathews, T. A. Herring and B. A. Buffett, “Mo- deling of Nutation and Precession: New Nutation Series for Nonrigid Earth and Insights into the Earth’s Interior,” Journal of Geophysical Research, Vol. 107, No. B4, 2002, pp. ETG 3-1-ETG 3-26. B. F. Chao, “As the World Turns,” Eos, Transactions American Geophysical Union, Vol. 66, No. 46, 1985, pp. 766-770. http://dx.doi.org/10.1029/EO066i046p00766
[39] B. F. Chao, “As the World Turns,” Eos, Transactions American Geophysical Union, Vol. 66, No. 46, 1985, pp. 766-770. http://dx.doi.org/10.1029/EO066i046p00766
[40] T. J. Ahrens, “The Origin of the Earth,” Physics Today, Vol. 47, No. 8, 1994, pp. 38-45. http://dx.doi.org/10.1063/1.881436
[41] B. Wood, “The Formation and Differentiation of Earth,” Physics Today, Vol. 64, No. 12, 2011, pp. 40-45. http://dx.doi.org/10.1063/PT.3.1362
[42] D. Pines and J. Shaham, “Quadrupolar Analysis of Sto- rage and Release of Elastic Energy in the Mantle,” Nature (Physical Science), Vol. 243, No. 130, 1973, pp. 122-127.
[43] J. B. Minster, P. Molnar and E. Haines, “Numerical Mo- deling of Instantaneous Plate Tectonics,” Geophysical Journal International, Vol. 36, No. 3, 1974, pp. 541-576. http://dx.doi.org/10.1111/j.1365-246X.1974.tb00613.x
[44] R. G. Gordon, “Present Plate Motions and Plate Bounda- ries,” Global Earth Physics, A handbook of Physical Constants, AGU References Shelf I, 1995, pp. 66-87.
[45] S. R. Dickman, “Investigation of Controversial Polar Motion Features Using Homogeneous International Lati- tude Service Data,” Journal of Geophysical Research, Vol. 86, No. B6, 1981, pp. 4904-4912. http://dx.doi.org/10.1029/JB086iB06p04904
[46] R. S. Gross, “Earth Rotation: Long Period Variations,” In: T. A. Herring, Ed., Treatise of Geophysics, Vol. 3: Geo- desy, Elsevier, Oxford, 2007, pp. 239-294.
[47] T. Gold, “Instability of the Earth’s Axis of Rotation,” Nature, Vol. 175, 1955, pp. 526-529. http://dx.doi.org/10.1038/175526a0
[48] P. Goldreich and A. Toomre, “Some Remarks on Polar Wandering,” Journal of Geophysical Research, Vol. 74, No. 10, 1969, pp. 2555-2567. http://dx.doi.org/10.1029/JB074i010p02555
[49] R. S. Gross, “The Excitation of the Chandler Wobble,” Geophysical Research Letters, Vol. 27, No. 15, 2000, pp. 2329-2332. http://dx.doi.org/10.1029/2000GL011450
[50] R. S. Gross, I. Fukumori and D. Menemenlis, “Atmos- pheric and Oceanic Excitation of the Earth’s Wobbles during 1980-2000,” Journal of Geophysical Research, Vol. 108, No. B8, 2003, pp. 2370-2386. http://dx.doi.org/10.1029/2002JB002143
[51] L. Dones and S. Tremaine, “Why Does the Earth Spin Forward?” Science, Vol. 259, No. 5093, 1993, pp. 350- 354. http://dx.doi.org/10.1126/science.259.5093.350
[52] C. Pan, “A Preliminary Study on Relations between Polar Wandering and Seismicity,” Thesis, Department of Geo- logy and Geophysics, Massachusetts Institute of Tech- nology, Cambridge, 1963.
[53] C. Pan, “On the Dynamical Theory of Polar Wandering,” Tectonophysics, Vol. 5, No. 2, 1968, pp. 125-149. http://dx.doi.org/10.1016/0040-1951(68)90085-1
[54] C. Pan, “The Dynamical Evolution of a Layered Earth (Abstract),” Transactions, American Geophysical Union, Vol. 51, 1970, p. 430.
[55] C. Pan, “The Wandering of the Pole and the Earth’s Evo- lution Cycle (Abstract),” Transactions, American Geo- physical Union, Vol. 52, 1971, p. 355.
[56] C. Pan, “Polar Wandering and the Earth’s Dynamical Evolution Cycle,” In: P. Melchior and S. Yumi, Eds., Rotation of the Earth, IAU Symposium No. 48, Reidel, Dordrecht, 1972, pp. 206-211.
[57] G. Spada, Y. Ricard and R. Sabadini, “Excitation of True Polar Wander by Subduction,” Nature, Vol. 360, No. 6403, 1992, pp. 452-454. http://dx.doi.org/10.1038/360452a0
[58] B. Steinberger and R. J. O’Connell, “Changes of the Earth’s Rotation Axis Owning to Advection of Mantle Density Heterogeneities,” Nature, Vol. 387, No. 6629, 1997, pp. 169-173. http://dx.doi.org/10.1038/387169a0
[59] F. D. Stacey, “Physics of the Earth,” 3rd Edition, Brook- field Press, Brisbane, 1992, 513 pp.
[60] W. J. Morgan, “Convection Plumes in the Lower Mantle,” Nature, Vol. 230, No. 5288, 1971, pp. 42-43. http://dx.doi.org/10.1038/230042a0
[61] P. Olson and H. Singer, “Creeping Plumes,” Journal of Fluid Mechanics, Vol. 158, 1985, pp. 511-531. http://dx.doi.org/10.1017/S0022112085002749
[62] W. M. Elsasser, “Convection and Stress Propagation in the Upper Mantle,” In: S. K. Runcorn, Ed., The Applica- tion of Modern Physics to the Earth and Planetary Inte- riors, Wiley, New York, 1969, pp. 223-246.
[63] W. M. Elsasser, “Two-Layer Model of Upper Mantle Circulation,” Journal of Geophysical Research, Vol. 76, No. 20, 1971, pp. 4744-4753. http://dx.doi.org/10.1029/JB076i020p04744
[64] F. M. Richter, “Mantle Convection Models,” Annual Review of Earth and Planetary Sciences, Vol. 6, 1978, pp. 9-19. http://dx.doi.org/10.1146/annurev.ea.06.050178.000301
[65] M. Nakada, “Rheological Structure of the Earth’s Mantle Derived from Glacial Rebound in Laurentide,” Journal of Physics of the Earth, Vol. 31, No. 6, 1983, pp. 349-386. http://dx.doi.org/10.4294/jpe1952.31.349
[66] L. Fleitout and D. A. Yuen, “Steady State, Secondary Convection beneath Lithospheric Plates with Temperature- and Pressure-Dependent Viscosity,” Journal of Geophy- sical Research, Vol. 89, No. B11, 1984, pp. 9227- 9244. http://dx.doi.org/10.1029/JB089iB11p09227
[67] B. D. Marsh and J. G. Marsh, “On Global Gravity Ano- malies and Two-Layer Mantle Convection,” Journal of Geophysical Research, Vol. 81, No. 29, 1976, pp. 5267- 5280. http://dx.doi.org/10.1029/JB081i029p05267
[68] C. G. Sammis, “Effects of Polymorphic Phase Boundaries on Vertical and Horizontal Motions in the Earth’s Mantle,” Tectonophysics, Vol. 35, No. 1-3, 1976, pp. 169-182. http://dx.doi.org/10.1016/0040-1951(76)90036-6
[69] P. M. Kenyon and D. L. Turcotte, “Convection in a Two- Layer Mantle with a Strongly Temperature-Dependent Viscosity,” Journal of Geophysical Research, Vol. 88, No. B8, 1983, pp. 6403-6414. http://dx.doi.org/10.1029/JB088iB08p06403
[70] M. A. Richards and B. H. Hager, “Geoid Anomalies in a Dynamic Earth,” Journal of Geophysical Research, Vol. 89, No. B7, 1984, pp. 5987-6002. http://dx.doi.org/10.1029/JB089iB07p05987
[71] R. K. O’nions, “Relationships between Chemical and Convective Layering in the Earth,” Journal of the Geo- logical Society, Vol. 144, No. 2, 1987, pp. 259-274. http://dx.doi.org/10.1144/gsjgs.144.2.0259
[72] W. R. Peltier, “Layered Mantle Convection: New Pers- pectives on an Old Debate,” EOS, Vol. 80, 1999, p. S17.
[73] R. J. O’Connell, “On the Scale of Mantle Convection,” Tectonophysics, Vol. 38, No. 1-2, 1977, pp. 119-136. http://dx.doi.org/10.1016/0040-1951(77)90203-7
[74] W. M. Elsasser, P. Olson and B. D. Marsh, “Depth of Mantle Convection,” Journal of Geophysical Research, Vol. 84, No. B1, 1979, pp. 147-155. http://dx.doi.org/10.1029/JB084iB01p00147
[75] D. E. Loper, “A Simple Model of Whole-Mantle Convec- tion,” Journal of Geophysical Research, Vol. 90, No. B2, 1985, pp. 1809-1836. http://dx.doi.org/10.1029/JB090iB02p01809
[76] B. Travis and P. Olson, “Convection with Internal Heat Sources and Thermal Turbulence in the Earth’s Mantle,” Geophysical Journal International, Vol. 118, No. 1, 1994, pp. 1-19. http://dx.doi.org/10.1111/j.1365-246X.1994.tb04671.x
[77] J. Weertman, “The Creep Strength of the Earth’s Mantle,” Reviews of Geophysics, Vol. 8, No. 1, 1970, pp. 145-168. http://dx.doi.org/10.1029/RG008i001p00145
[78] S. H. Kirby and C. B. Raleigh, “Mechanisms of High- Temperature, Solid-State Flow in Minerals and Ceramics, and Their Bearing on the Creep Behavior of the Mantle,” Tectonophyiscs, Vol. 19, No. 2, 1973, pp. 165-194. http://dx.doi.org/10.1016/0040-1951(73)90038-3
[79] R. L. Post Jr. and D. T. Griggs, “The Earth’s Mantle: Evidence of Non-Newtonian Flow,” Science, Vol. 181, No. 4106, 1973, pp. 1242-1244. http://dx.doi.org/10.1126/science.181.4106.1242
[80] M. L. Bell, S. T. Crouch and A. Nur, “Non-Newtonian Anti-Phase Flow and Its Application to Plate Deforma- tion,” Tectonophysics, Vol. 39, No. 4, 1977, pp. 501-514. http://dx.doi.org/10.1016/0040-1951(77)90150-0
[81] W. A. Heiskanen and F. A. Vening Meinesz, “The Earth and Its Gravity Field,” McGraw-Hill, New York, 1958, 470 p.