Food and Nutrition Sciences
Vol.5 No.2(2014), Article ID:42105,5 pages DOI:10.4236/fns.2014.52020
Water Adsorption Isotherms of Amaranth (Amaranthus caudatus) Flour
Center for Food and Natural Products, Faculty of Science and Technology, San Simon University, Cochabamba, Bolivia.
Email: gabrielapena.b@fcyt.umss.edu.bo
Received August 7th, 2013; revised September 7th, 2013; accepted September 15th, 2013
ABSTRACT
Water sorption isotherms are unique for individual food materials and can be used directly to predict shelf life and determine proper storage conditions. In this context, the aim of this study was to determine the moisture adsorption isotherms of amaranth flour at 15˚C, 25˚C and 35˚C in a range of water activity from 0.1 to 0.9. Experimental data were modeled using five equations commonly applied in the foods field. The goodness of the fit for each isotherm model was evaluated through the coefficient of determination, the variance due to error and the confidence interval of the estimated parameters. All models can predict the adsorption isotherms of amaranth flour, but the GAB equation gives a better understanding of the observed sorption behavior. Estimated adsorption monolayer water contents ranged from 6.4 g to 7.2 g of water per 100 g of dry material. It was observed by a weak dependence of water activity with temperature. For ensuring microbiological stability, water content in amaranth flour should not be higher than 13 g of water per 100 g of dry material.
Keywords:Amaranth; Water Adsorption Isotherm; GAB Model
1. Introduction
Amaranth (Amaranthus caudatus) is a native plant in America, which has been domesticated, cultivated and used for over 6000 years [1]. This species is mainly cultivated in Bolivia, Peru and Ecuador. In Bolivia, the amaranth crop is geographically distributed from 17˚20' to 21˚28' south latitude and from 64˚13' to 69˚09' west longitude, having an altitudinal distribution between 1866 and 3050 meters above the sea level [2].
The grain of Amaranth is considered as a pseudocereal, because it has similar characteristics to cereal grains of true monocots [3]. Protein content found in amaranth grain is very similar to that of milk and is very close to the ideal protein balance proposed by FAO (Food and Agriculture Organization) for human consumption [4]. The high lysine and methionine concentrations support the great nutritional quality of the grain [5]; also amaranth has been recognized because of its high vitamin and mineral content [6].
For human consumption, amaranth flour is obtained from grinding and milling the plant grains. The flour has great nutritional properties and it is a major source for calories in the people’s diet of Andean regions; it is appreciated for preparing instant and fermented beverages and bakery/pastry products [7]. Due to its very low content in gluten, the flour has been successfully processed into baked products for celiac patients [8].
The quality of flour depends to a great extent upon its physical, chemical and microbiological stability. This stability is mainly a consequence of the relationship between the equilibrium water content of the food material and its corresponding water activity at a given temperature [9]. Water activity (aw) is a physicochemical parameter that indicates the availability of water in a food matrix for chemical and biochemical reactions (e.g. lipid oxidation, enzymatic and Maillard reactions) and for microbial growth [10]. For this reason, water activity is determinant for predicting the stability and shelf life of foods.
An adsorption isotherm relates the water content of a material with its water activity, which is in thermodynamic equilibrium. Under normal conditions, the water activity is equal to the relative humidity surrounding the material [11]. Besides from some fundamental models, several semi-empirical and empirical equations have been proposed for correlating the equilibrium water content and water activity of foods. For instance, the Guggenheim-Anderson-De Boer (GAB) equation has been recommended by the European Project Group COST 90 on Physical Properties of Food [12] as the fundamental equation for the characterization of water sorption in food materials [13-16]. This equation is based on the adsorption theory after Brunauer-Emmet-Teller (BET) for the monolayer, which gives a physicochemical explanation of the parameters involved [17].
Obtaining and modeling adsorption isotherms of foods are very important for determining suitable packaging materials and storage conditions, for evaluating the mixing with other powdered foods and for predicting its shelf life [18]. However, reliable experimental data of water sorption isotherms for amaranth flour are limited in the literature. Reference [19] determined desorption isotherms of amaranth flour by measuring the pressure exerted by flour samples. In other studies, the sorption isotherms for amaranth grains were obtained [4,20-22]. Analysis of the sorption characteristics of amaranth starch was conducted by [23]. Sorption isotherms and other physicochemical properties of nixtamalized amaranth flour were studied by [24].
The aim of this study was then to measure and model the water adsorption isotherms of amaranth flour at three temperatures, 15˚C, 25˚C and 35˚C. For the modeling, five mathematical equations were chosen from the literature for describing the experimental sorption behavior.
2. Materials and Methods
2.1. Sample Material
Amaranth flour was supplied by Andes Trópico, a food company in Cochabamba, Bolivia. The flour was further milled and homogenized in a laboratory knife mill (Retsch-GM200, Haan, Germany). Its water content was measured using an infrared moisture analyzer (Sartorius, MA30, Göttingen, Germany). The flour sample was then stored at room temperature in a polyethylene bag until the experiments were conducted.
2.2. Experimental Procedure
Adsorption isotherms of amaranth flour were measured using an alternative method to the classical approach [25], with the modifications described below.
To set up a moisture saturated environment, a glass desiccator filled with approximately 200 mL of distilled water was used. Temperature was controlled by a constant climate chamber (Memmert-HPP 108, Schwabach, Germany). The desiccator was introduced in the climate chamber at a preset temperature and allowed for 24 hours to equilibrate before each experiment.
Water activities were measured in a temperature controlled aw meter (Decagon-Aqualab 3TE, Washington, USA). Approximately 1.5 g of flour sample was placed in a disposable cup of the aw meter and then weighed exactly on an analytical balance (±0.001 g). The flour sample was further dehydrated in a drying oven (Binder-FD 53, Tuttlingen, Germany) at 45˚C for two hours. An initial water activity value was then measured in the aw meter previously preset at the temperature of the experiment. Immediately, the sample cup was weighed on the analytical balance to determine the corresponding initial water content by difference in weight.
The sample cup was introduced into the desiccator and allowed to adsorb water from the moisture saturated environment. After a short time, the sample was removed from the desiccator, transferred to the aw meter to measure its water activity and then weighed on the balance. Next, the sample was returned to the desiccator to continue adsorbing moisture, and the procedure was repeated until an aw value around 0.9 was obtained. At the beginning, the sample was allowed between 10 and 30 minutes to adsorb moisture, and the intervals increased from 60 to 120 minutes for the last measurements. The methodology was repeated for 15˚C, 25˚C and 35˚C.
2.3. Mathematical Modeling
Experimental adsorption equilibrium data of amaranth flour were modeled using the equations of GAB (Guggenheim, Anderson and De Boer), Henderson, Oswin, Chung-Pfost, and Peleg, which are listed in Table1
2.4. Statistical Analysis
The goodness of the fit for each proposed model was evaluated through three standards commonly used in the statistical analysis of nonlinear models: the coefficient of determination (R2), the variance due to error (S2) and the confidence interval of a parameter (CI).
The coefficient R2 is frequently used to judge whether the model correctly represents the data, implying that if the correlation coefficient is close to one the model is suitable. This parameter is defined as:
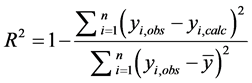 (1)
(1)
where yi,obs is the observed experimental datum at xi, yi,calc is the estimated datum at xi, and 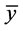 is the mean of the
is the mean of the
Xw is water content (dry basis); aw is water activity; Xm is monolayer water content; A, B, C, k, k1, k2, n1, n2 are constants.
observed values according to:
 (2)
(2)
The variance S2 is a recommended indicator to be used for comparing various models representing the same dependent variable. A model with smaller variance represents the data more accurately than a model with larger values of this indicator. This parameter is given by:
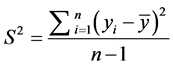 (3)
(3)
The CI measures the uncertainty in a parameter value. A narrow CI indicates that the parameter is significant in the model and thus the model is suitable for describing the experimental data.
3. Results and Discussion
Model parameters for each equation were estimated by nonlinear regression using the POLYMATH 6.1 software package. For the computations, we selected the Levenberg-Marquardt method [26,27]. Results were reported through R2, S2 and 95% CI.
Table 2 lists the parameter values and associated statistics for each model, which describe the adsorption experimental data of amaranth flour at 15˚C, 25˚C and 35˚C. All models are considered to be valid because they present high values of coefficients of determination (R2 > 0.97) and small values of variances (S2 < 1.2E−4). The results show that the Oswin, Henderson and Chung-Fost parameters do not vary significantly with temperature, whereas the Peleg and GAB equations show a temperature dependence of the amaranth flour isotherms.
Experimental data are plotted in Figure 1 and adsorption isotherms modeled by the GAB equation are show in Figure 2, which highlights the temperature dependence in the range of aw from 0.2 to 0.7. Below and above this aw range, the isotherms cross over each other; a similar behavior was observed in a study by [28].
Monolayer water content values, Xm, follow a usual trend with temperature as observed for most biopolymers; they decrease with temperature increasing [29]. In our study, we found Xm values from 0.072 to 0.064 between 15˚C and 35˚C.
Reference [23] modeled the equilibrium sorptional data but for amaranth starch at 25˚C, 35˚C and 50˚C. The GAB parameters they obtained at 25˚C are comparable to the parameters we found in this study, considering that amaranth flour is mainly composed of starch. Parameter values obtained by [4] but for amaranth grains reflect also a temperature dependence of the GAB equation.
Considering that microbiological stability could be ensured at aw < 0.6 [30], water content in amaranth flour should not be higher than 13 g of water per 100 g of dry material in the temperature range from 15˚C to 35˚C.
4. Conclusions
In this paper, moisture adsorption of amaranth flour has been measured at 15˚C, 25˚C and 35˚C, using an alternative experimental method. The experimental adsorption isotherms exhibited a sigmoidal trend and were satisfactorily fitted to well-known models. The GAB equation adjusted the data quite well and is recommended, due to its physical meaning, to describe the adsorption behavior of amaranth flour.
Results showed a weak dependence of aw with temperature in the range from 15˚C to 35˚C. This indicates that amaranth flour can be safely stored at different temperatures within this range. To be stable over time, the water content in amaranth flour should not be higher than 13 g of water per 100 g of dry material and needs to be kept under a surrounding environment with less than 60% relative humidity. Appropriate packing for the flour needs to be considered in environments with higher humidity than this limit.
The alternative experimental method for measuring adsorption isotherms we used has advantages over the traditional method. The time spent for obtaining experimental sorption equilibrium data is significantly reduced, it is not necessary to use expensive salts and more data points can be obtained. The method we introduced has proven to be competent with the traditional method proposed by the COST 90 project, providing reliable experimental data consistent with the theory developed in the field of water adsorption by natural biopolymers.
Acknowledgements
The authors gratefully acknowledge the financial support
Table 2 . Model parameters of nonlinear equations used to describe the water adsorption behavior of amaranth flour at 15˚C, 25˚C and 35˚C.
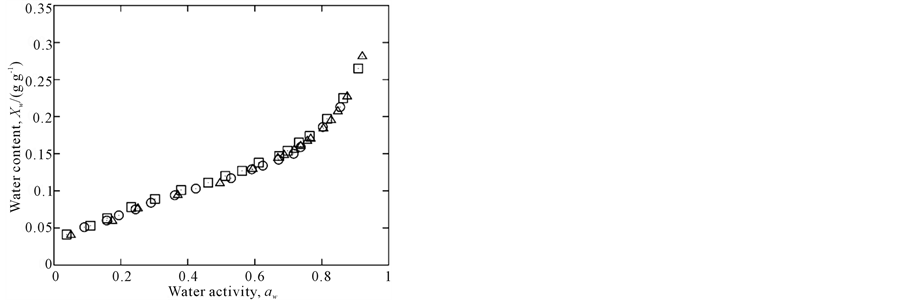
Figure 1. Experimental data of amaranth flour at 15˚C (™), 25˚C (r) and 35˚C (£).
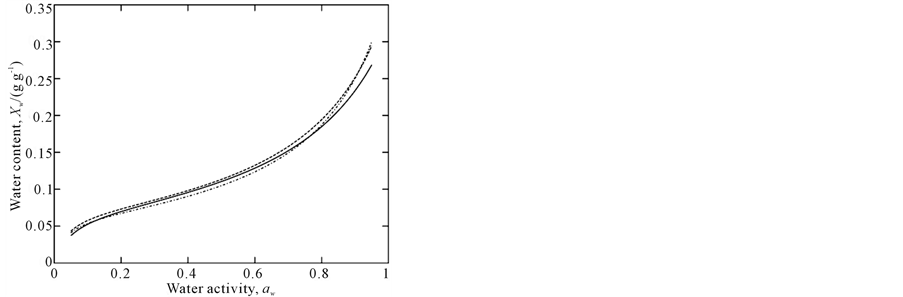
Figure 2. GAB isotherms for amaranth flour at 15˚C (–), 25˚C (– –) and 35˚C (•–).
of the Swedish International Development Agency (Sida).
REFERENCES
- J. D. Sauer. “Historical Geography of Crop Plants: A Select Roster,” CRC Press, México, 1993. pp. 121-128.
- M. Pinto, E. Mamani, L. Quispe and W. Rojas, “Caracterización y Análisis de la Variabilidad Fenotípica de la Colección de Germoplasma de Amaranto,” Informe Anual 2004/2005, Fundación Proimpa, Bolivia, 2005, pp. 78-88.
- R. Becerra, “El Amaranto: Nuevas Tecnologías para un Antiguo Cultivo,” Boletín Bimestral de la Comisión Nacional Para el Conocimiento y Uso de la Biodiversidad. Conabio, Vol. 30, No. 1, 2000, pp. 1-6.
- A. M. Pagano and R. H. Mascheroni, “Sorption Isotherms for Amaranth Grains,” Journal of Foodengineering, Vol. 67, No. 1, 2005, pp. 441-450. http://dx.doi.org/10.1016/j.jfoodeng.2004.05.012
- R. Teutonico and D. Knorr, “Amaranth: Composition, Properties, and Applications of a Rediscovered Food Crop,” Foodtechnology, Vol. 39, No. 4, 1985, pp. 49-60.
- R. S. Singhal and P. R. Kulkarni, “Review: Amaranths an Under-Utilized Resource,” International Journal Food Science and Technology, Vol. 23, 1988, pp. 125-139. http://dx.doi.org/10.1111/j.1365-2621.1988.tb00559.x
- P. Rocha, “Identificar Prácticas de Procesamiento y Obtención de Derivados de Amaranto (Millmi) a Nivel Familiar,” Informe Técnico Anual 2002-2003, Ipgri-Ifad, Fundación Proinpa, Bolivia, 2003, pp. 121-123.
- E. A. Tosi, M. C. Ciappini and R. Masciarelli, “Utilización de la Harina Integral de Amaranto (Amaranthuscruentus) en la Fabricación de Galletas para Celíacos,” Alimentaria, Vol. 33, 1996, pp. 49-55.
- P. Fellow, “Food Processing Technology. Principles and Practice,” 2nd Edition, Ellis Horwood, Chichester, 2003.
- J. Comaposada, P. Gou and J. Arnau, “The Effect of Sodium Chloride Content and Temperature on Pork Meat Isotherms,” Meat Science, Vol. 55, No. 3, 2000, pp. 291- 295. http://dx.doi.org/10.1016/S0309-1740(99)00154-0
- X. W. Zhang, X. Liu, D.-X. Gu, W. Zhou, R. L. Wang and P. Liu, “Desorption Isotherms of Some Vegetables,” Journal Science of Food Agriculture, Vol. 70, No. 3, 1996, pp. 303-306. http://dx.doi.org/10.1002/(SICI)1097-0010(199603)70:3<303::AID-JSFA494>3.0.CO;2-A
- W. Wolf, W. E. L. Spiesses and G. Jung, “Properties of Water in Foods in Relation to Quality and Stability,” D. Simatos and J. L. Multon, Eds., Martinusnijhoff Publishers, Dordrecht, 1985, pp. 661-679.
- H. Bizot, R. Jowitt, F. Escher, B. Hallstrom, H. Meffer, W. L. Spiess and G. Vos, “Using the Gab Model to Construct Sorption Isotherms,” Physical Properties of Foods, Applied Science Publishers, London, 1983, pp. 43-54.
- H. Weisser, “Influence of Temperature on Sorption Equilibrium,” In: D. Simatos and J. L. Multon, Eds., Properties of Water in Foods in Relation to Food Quality and Stability, Martinus Nijhoff Publishers, Dordrecht, 1985, pp. 95-118.
- Z. B. Maroulis, E. Tsami, D. Marinos-Kouris and G. D. Saravacos, “Application of the GAB Model to the Moisture Sorption Isotherms for Dried Fruits,” Journal of Food Engineering, Vol. 7, No. 1, 1988, pp. 63-70. http://dx.doi.org/10.1016/0260-8774(88)90069-6
- H. A. Iglesias and J. Chirife, “An Alternative to the GAB Model for the Mathematical Description of Moisture Sorption Isotherms of Foods,” Foods Research International, Vol. 28, No. 1, 1995, pp. 317-321. http://dx.doi.org/10.1016/0963-9969(94)00002-P
- C. T. Kiranoudis, Z. B. Maroullis, E. Tsami and D. Marinos-Kouris, “Equilibrium Moisture Content and Heat of Desorption of Some Vegetables,” Journal of Food Engineering, Vol. 20, No. 1, 1993, pp. 55-74. http://dx.doi.org/10.1016/0260-8774(93)90019-G
- J. Chirife and H. A. Iglesias, “Equations for Fitting Water Sorption Isotherm of Foods: Part I: A Review,” Journal of Food Technology, Vol. 13, No. 1, 1978, pp. 159-174.
- J. Alvarado, E. Toaza and G. Coloma, “Isotermas de Desorción en Harinas de Amaranto,” Archivos Latinoamericanos de Nutrición, Vol. 5, No. 1, 1990, pp. 387- 394 (Unpublished).
- A. Lema, D. Palumbo, J. Adaro and M. Lara, “Equilibrio de Sorción de Amaranto,” En Memorias del viii Congreso Latinoamericano de Transferencia de Calor y Materia LAT-CYM, Veracruz, 2001, pp. 184-189.
- M. L. Pollio, M. Tolaba and C. Suárez, “Measuring and Modeling Grain Sorption Equilibria of Amaranth Grains,” Cereal Chemistry, Vol. 75, No. 3, 1998, pp. 297-300. http://dx.doi.org/10.1094/CCHEM.1998.75.3.297
- E. A. Tosi, R. Masciarelli and M. Ciappini, “Humedades de Equilibrio del Amaranto (amarantuscruentus),” La alimentación Latinoamericana, Vol. 203, 1994, pp. 73- 76.
- A. Calzeta, R. J. Aguerre and C. Suárez, “Analysis of the Sorptional Characteristics of Amaranth Starch,” Journal of Food Engineering, Vol. 42, No. 1, 1999, pp. 51-57. http://dx.doi.org/10.1016/S0260-8774(99)00103-X
- J. A. Valdez-Niebla, O. Paredes-López, J. M. VargasLópez and D. Hernández-López, “Moisture Sorption Isotherms and Other Physicochemical Properties of Nixtamalized Amaranth Flour,” Food Chemistry, Vol. 46, No. 1, 1992, pp. 19-23. http://dx.doi.org/10.1016/0308-8146(93)90069-R
- T. C. Lima de Souza, A. H. Lima de Souza and R. A. da Silva-Pena, “A Rapid Method to Obtaining Moisture Sorption Isotherms of a Starchy Product,” Starch/Stärke, Vol. 65, No. 5-6, 2013, pp. 433-436.
- K. Levenberg, “A Method for the Solution of Certain Nonlinear Problems in Least Squares,” Quarterly of Applied Mathematics, Vol. 2, No. 1, 1994, pp. 164-168.
- D. W. Marquardt, “An Algorithm for Least-Squares Estimation of Nonlinear Parameters,” Journal of the Society for Industrial and Applied Mathematics, Vol. 11, No. 1, 1963, pp. 431-441. http://dx.doi.org/10.1137/0111030
- A. Gálvez, E. Aravena and R. Mondaca, “Isotermas de Adsorción en Harina de Maíz (Zeamays L.),” Ciência e Tecnologia de Alimentos, Campinhas, Vol. 26, No. 4, 2006, pp. 821-827. http://dx.doi.org/10.1590/S0101-20612006000400017
- H. A. Iglesias and J. Chirife, “Water Sorption Parameters of Food and Food Components,” In: Handbook of Food Isotherms, Academic Press, New York, 1982, pp. 23-87.
- L. B. Rockland and S. K. Nishi, “Influence of Water Activity on Food Product Quality and Stability,” Food Technology, Vol. 34, No. 1, 1980, pp. 42-59.


