International Journal of Medical Physics, Clinical Engineering and Radiation Oncology
Vol.06 No.02(2017), Article ID:76361,4 pages
10.4236/ijmpcero.2017.62017
A Radiotherapy Treatment Margin Formula When Systematic Positioning Errors are Relatively Small Compared to Random Positioning Errors: A First-Order Approximation
Kiyoshi Yoda
Research Physics, Elekta KK, Tokyo, Japan

Copyright © 2017 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: April 16, 2017; Accepted: May 20, 2017; Published: May 23, 2017
ABSTRACT
A radiotherapy treatment margin formula has been analytically derived when a standard deviation (SD) of systematic positioning errors S is relatively small compared to an SD of random positioning errors σ. The margin formula for 0 ≤ S ≤ σ was calculated by linearly interpolating two boundaries at S = 0 and S = σ, assuming that the van Herk margin approximation of k1S + k2σ is valid at S = σ. It was shown that a margin formula for 0 ≤ S ≤ σ may be approximated by k1σ + k2S, leading to a more general form of k1 max(S,σ) + k2 min(S,σ) which is a piecewise linear approximation for any values of S and σ.
Keywords:
Treatment Margin, Systematic Positioning Errors, Random Positioning Errors

1. Introduction
A radiotherapy treatment margin model proposed by van Herk was based on a two-Gaussian-process model comprising systematic positioning errors and random positioning errors. The coefficients of the model parameters were calculated in spherical coordinate system, leading to the following planning target volume (PTV) margin approximation, Mptv [1] [2] :
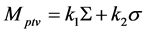 (1)
(1)
where S is a standard deviation (SD) of the systematic errors and σ is an SD of the random errors. The coefficient k1 depends on a given coverage probability of the patient population in a facility, whilst k2 varies with biological penumbra of the treatment fields. For example, k1 was set to 2.5, where 90% of the patients receive at least 95% of the prescribed dose in the clinical target volume (CTV) [1] [2] . The coefficient k2 was given as 0.7 for prostate treatment [1] [2] and 0.5 for typical lung treatment because the beam penumbra for lung treatment is broader than that for abdominal treatment [3] . The margin formula (1) was originally proposed for normal fractionation for body radiotherapy, when systematic errors were relatively large compared to random errors [1] [2] . After on-board cone-beam computer tomography (CBCT) was employed for tumor localization, the systematic errors were much reduced down to the level of the random errors [4] .
Meanwhile, a different formula was proposed for intracranial stereotactic radiotherapy, where a head fixation system comprising an integrated mask- mouthpiece was employed under CBCT image guidance [5] . In this case, the SD of the systematic errors was practically zero and thus S = 0. Looking back to the formula (1), the PTV margin giving the treatment coverage probability of 90% resulted from the systematic error distribution. When the systematic error is practically zero, the PTV margin needs to be calculated by the remaining random error distribution that follows a Gaussian distribution with an SD of σ. In other words, the following formula may hold [5] :
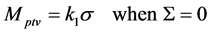 (2)
(2)
In this context, the coverage probability of 90% may have a different meaning. For the original van Herk formula, it means a patient population coverage, but for hypofractionated intracranial SRT, it can mean coverage probability of the number of fractions out of all the fractions delivered in the facility, where the random error distribution is assumed a single Gaussian distribution without inter-patient variability. The formula (2) was also graphically supported by Stroom et al. [6] , where a target dose volume histogram with S = 0 appeared favorable when a PTV margin was increased to 2σ. A natural interest is how to bridge the above two formulas (1) and (2) for an intermediate value of S. The purpose of this study was to derive this formula.
2. Derivation of the Formula
Assuming that formula (1) is valid when S goes down to σ [4] , Mptv for 0 ≤ S ≤ σ may be approximated by a first-order interpolation as described below. The formula (1) can be written as follows:
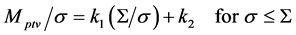 (3)
(3)
The formula (3) shows that Mptv/σ is a linear function of S/σ with a slope of k1 and an intercept of k2. Then, a linear interpolation function of Mptv/σ for 0 ≤ S ≤ σ may be assumed as
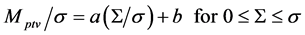 (4)
(4)
where a and b are unknown coefficients. The coefficients a and b can be solved
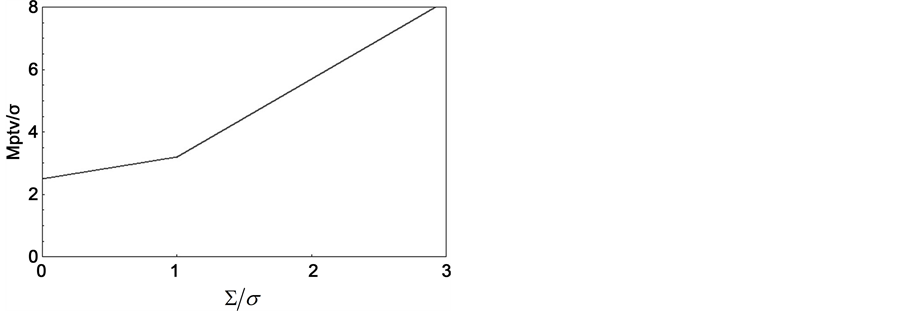
Figure 1. Calculated plot of piecewise-linearly-approximated normalized treatment margins MPTV as a function of normalized standard deviations of systematic positioning errors S, where each normalization was performed relative to the standard deviation of random positioning errors σ.
by using two boundary conditions of Mptv/σ = k1 with S = 0 from (2), and Mptv/σ = k1 + k2 with S = σ from (3), which results in a = k2 and b = k1. Consequently, we obtain the following formula:
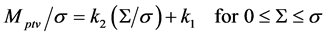 (5)
(5)
Equivalently,
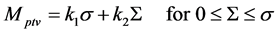 (6)
(6)
Figure 1 shows the resulting PTV margin plot as a function of S/σ with k1 = 2.5 and k2 = 0.7, where the PTV margin is also normalized relative to σ. The plot suggests that a use of (1) may be discouraged for 0 ≤ S ≤ σ because it may underestimate the PTV margins. The maximum amount of the underestimation may be (k1 − k2)σ when S = 0. To the author’s knowledge, this is the first report that provides a linearly approximated PTV margin formula for 0 ≤ S ≤ σ.
It is interesting to note that the two variables S and σ in the formulas (1) and (6) were swapped each other. This may be interpreted as follows: a coverage probability (either patient population or the number of fractions) of 90% is governed by a spatially-broader probability distribution between the systematic errors and the random errors, whilst a spatially-narrower probability distribution serves as an additive margin correction term.
3. Conclusion
A linearly approximated PTV margin formula of k1σ + k2S has been given when the systematic errors are relatively small compared to the random errors, which in turn leads to a more general form of k1 max(S, σ)+ k2 min(S, σ), a piecewise linear approximation for any values of S and σ.
Cite this paper
Yoda, K. (2017) A Radiotherapy Treatment Margin Formula When Systematic Positioning Errors are Relatively Small Compared to Random Po- sitioning Errors: A First-Order Approxima- tion. International Journal of Medical Phy- sics, Clinical Engineering and Radiation Oncology, 6, 193-196. https://doi.org/10.4236/ijmpcero.2017.62017
References
- 1. van Herk, M., Remeijer, P., Rasch, C. and Lebesque, J.V. (2000) The Probability of Correct Target Dosage: Dose-Population Histograms for Deriving Treatment Margins in Radiotherapy. International Journal of Radiation Oncology Biology Physics, 47, 1121-1135.
https://doi.org/10.1016/S0360-3016(00)00518-6 - 2. van Herk, M. (2004) Errors and Margins in Radiotherapy. Seminars in Radiation Oncology, 14, 52-64.
https://doi.org/10.1053/j.semradonc.2003.10.003 - 3. Jensen, H.R., Hansen, O., Hjelm-Hansen, M. and Brink, C. (2008) Inter- and Intra-fractional Movement of the Tumour in Extracranial Stereotactic Radiotherapy of NSCLC. Acta Oncologica, 47, 1432-1437.
https://doi.org/10.1080/02841860802251567 - 4. Smitsmans, M.H., de Bois, J., Sonke, J.J., Betgen, A., Zijp, L.J., Jaffray, D.A., Lebesque, J.V. and van Herk, M. (2005) Automatic Prostate Localization on Cone-Beam CT Scans for High Precision Image-Guided Radiotherapy. International Journal of Radiation Oncology Biology Physics, 63, 975-984.
https://doi.org/10.1016/j.ijrobp.2005.07.973 - 5. Mizukami, N. and Yoda, K. (2016) Intrafractional Positioning Accuracy during Stereotactic Brain Radiotherapy with a Modified Thermoplastic Mask System, On-Board Cone-Beam CT, and a Six-Degrees-of-Freedom Couch. Journal of Radiosurgery and SBRT, 4, 75-76.
- 6. Stroom, J.C. and Heijmen, B.J. (2002) Geometrical Uncertainties, Radiotherapy Planning Margins, and the ICRU-62 Report. Radiotherapy Oncology, 64, 75-83.
https://doi.org/10.1016/S0167-8140(02)00140-8