International Journal of Medical Physics, Clinical Engineering and Radiation Oncology
Vol.05 No.04(2016), Article ID:72098,19 pages
10.4236/ijmpcero.2016.54030
Radiation Beam Characterization and Dosimetry of Theratron Equinox-80 Telecobalt Machine Using BEAMnrc Monte Carlo Simulation Code
Narayan Prasad Patel1, Rahul Shukla2, Nagappan Balasubramanian1, Rajeev Atri1, Anil Kumar Dhull1, Hanuman Prasad Yadav2, Vivek Kaushal1
1Department of Radiotherapy, Pt. BDS Post Graduate Institute of Medical Sciences, Rohtak, India
2Department of Radiotherapy, GGS Medical College, Faridkot, India

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: September 3, 2016; Accepted: November 15, 2016; Published: November 18, 2016
ABSTRACT
The BEAMnrc code was used for the simulation of the Theratron Equinox-80 telecobalt machine. The phase space of radiation beam was generated at treatment distance of 80 cm for various field sizes. The phase spaces in air were analyzed by BEAMdp data processing program. The electron energy fluence with respect to photon energy was 0.09% and 0.34% for field size of 05 × 05 and 35 × 35 cm2 respectively and it was maximum at the central axis which gradually decreases beyond this. The profiles for photon fluence were in symmetry for all the fields. The full width at half maximum of profiles in photon energy fluence shows good agreement with the field size. The photon energy fluence was flat till the field size of 27 cm2, after which it decreases gradually till the edge in larger field sizes. The air-kerma output factor from the simulation was in good agreement with measured value. We analyzed the dose data scored in the voxels in a large water phantom by simulation using dosxyznrc code. The percentage depth dose for all field sizes was in good agreement with the BJR supplement 25 and the data supplied by the manufacturer of machine. Significant deviation of about 20% in isodose line near the edge of the profile was observed for 35 × 35 cm2 field size. The penumbra widths of all field sizes were comparable except for 35 × 35 cm2, which has a penumbra width of 4.1 cm at 10 cm depth. The significant under dose near the edge as compared to central axis for larger field sizes may be the indication for its careful use in treatment.
Keywords:
BEAMnrc Code, Simulation, Telecobalt Unit, Beam Profile, Depth Dose

1. Introduction
There is a long history of use of telecobalt unit in treatment of cancer. Due to its cost effectiveness, the unit is still being used for conventional treatment in radical and palliative radiotherapy treatment. The 3-D conformal radiation therapy is performed with the availability of the treatment planning system and radiation field analyzer. The new treatment modalities such as intensity modulated radiotherapy and image guided radiotherapy are also now facilitated in the telecobalt unit [1] [2] [3] . The dosimetry and treatment planning in the telecobalt unit is straightforward as compared to the linear accelerator. The dosimetric data published as supplement in British Journal of Radiology have been universally accepted for the dose calculation and as a reference for comparison [4] . The radiation field analyzer is used for the measurement of the depth-dose data and dose profiles for the purpose of input data in treatment planning system. Several authors have performed the simulation of various telecobalt units for the study of dosimetry parameters [5] - [12] .
Mora et al. studied the relative air kerma, influence of collimation system on the photon spectra, and the effect of electron contamination in output in Eldorado telecobalt unit using BEAMnrc code [6] . Sichani et al. used the MCNP code to simulate the Th-780E cobalt therapy unit to calculate the effects of each unit component on the photon spectrum at the phantom surface [7] . Miro et al. used MCNP code to study the photon spectra as a function of field size and the variation of the electron contamination of the 60Co beam in Theratron 780 (MDS Nordion) radiotherapy unit [8] . Shin et al. have performed the simulation of a 60Co radiotherapy unit with GEANT4 for different beam field sizes to generate the dose distributions inside the phantom [9] . Kumar et al. studied the Theratron Elite100 telecobalt machine using BEAMnrc Monte Carlo simulation code where photon energy spectrum is obtained at the bottom end of the primary collimator as well as at the top of the water phantom surface which is kept at 100 cm away from the radiation source [10] . Burns et al. compared the peak scatter factor from Monte Carlo calculated with the published BJR 17 data [11] . Tedgren et al. performed the simulation of 60Co unit at secondary standard dosimetry laboratory for comparison of results with the measurement data [12] .
The present study was planned to simulate the Theratron Equinox-80 telecobalt machine using BEAMnrc code for dosimetry purposes. In the process, first it was planned to generate the phase space of radiation beam for various field sizes at the treatment distance. The phase spaces were to be analyzed for the symmetry, flatness and geometric accuracy with the collimation system using BEAMdp program. The relative air kerma for various field sizes was to be calculated and to compare with the measured data. The phase space for various field sizes at treatment distance was planned to use as a source for the dose calculation in water phantom using dosxyznrc code. The BEAM- nrc as well as dosxyznrc code is coupled with EGSnrc user-code for the simulation of coupled electron-photon transport for particle energies ranging from 1 keV to 10 GeV for the accurate and precise dose calculation in medium [13] - [18] . The Monte Carlo calculation method takes prolonged time in dose calculation in the small voxels to achieve higher accuracy. The most of the authors have limited their simulation study over the calculation of few selected dosimetric data. The present study was planned for dose calculation in large scale for complete dosimetry in water phantom. The dose data calculated over the phantom were analyzed to derive the depth-dose curve and dose profiles at different depths for various field sizes.
2. Materials and Methods
2.1. Simulation of Telecobalt Unit
The present study uses the BEAMnrc Monte Carlo simulation code, designed for the modeling of radiation beams including high energy electron and photon beams from radiotherapy units such as telecobalt, linear accelerator etc. [13] . The Theratron Equinox-80 cobalt unit from Best Theratronics, Ottawa, Canada was simulated realistically for its various components such as source housing, source, fixed and movable collimators. The detail simulation configuration of the unit is shown in Figure 1(a) and Figure 1(b), respectively. The source consists of several pellets of Cobalt-60 radioactive material and it was simulated as per our assumption as cylindrical by CONESTAK module. The dimension of source was 2.0 cm in dia. and 2.0 cm in length encapsulated by iron of 0.5 cm thickness. The SLAB module was used to simulate the source housing made of lead material of 20 cm thickness all around. The tungsten was used for fixed collimator by PYRAMIDS module. The upper four pairs of X and Y movable jaws were simulated by lead. The last lower X and Y trimmer bar was simulated by tungsten. The surrounding medium was taken as air.
The five pairs of X and Y movable jaws and trimmer bar were configured for defining the field size as per the rule suggested by Mora et al. [6] . The center of the bottom face of the source is diagonally projected through lower edge of trimmer bar to define the field size as shown in Figure 1(a). The field sizes were defined from 05 × 05 to 35 × 35 cm2 in increments of 5 cm2 at 80 cm from the source. The z-dimension of end position of lower trimmer bar was 50.65 and 50.2 cm for field size of 10 × 10 and 25 × 25 cm2 respectively. The X-Z view of the actual dimension of the simulation for 10 × 10 cm2 field size is shown in Figure 1(b). The component module SLAB was used to simulate the air medium between the lower trimmer bar and treatment surface plane. The phase-space was generated at plane 1 below trimmer bar and at plane 2 at treatment distance of 80 cm from the source.
2.2. Simulation Process
The cylindrical cobalt-60 source was characterized for isotropic emission of bare Co-60 spectrum. The scoring plane for phase space was defined at below the last trimmer bar and the plane at treatment distance of 80 cm. The simulation of transport of particles from origin in the source to till the scoring in plane 1 and 2 was performed in a single stage. The most of the transport simulation parameters were set for default values. The cutoff energy for electron (ECUT) and photon (PCUT) were taken 0.7 MeV and 0.01 MeV respectively. The variance reduction techniques-range rejection of electron was


Figure 1.(a) The configuration of Theratorn Equinox-80 machine and water phantom for dose calculation and (b) Actual view of x-z plane of simulation geometry of Theratron Equinox-80 Telecobalt unit.
not opted. The statistical uncertainty of the output data from simulation directly depends up on the number of particle histories. Hence in order to improve the accuracy of the results and to minimize the error, total 1010 particle histories from the source were simulated for each field. The calculation time for each field was about 160 hours. The memory size of phase space files below the trimmer bar for field sizes from 05 × 05 to 35 × 35 cm2 varies from 3.0 MB to 4.5 MB per cm2. The photon flux scored at plane 2 for various field sizes were in the order of 118,835 to 163,147.
2.3. Analysis of Phase Space
BEAMdp (BEAM data processor) is a program, originally developed for the OMEGA (Ottawa Madison Electron Gamma Algorithm) project, to analyze the BEAM phase space data and to derive the spectral, planner fluence distributions for use by beam cha- racterization models [17] . The BEAMdp programme was utilized in the present study to analyze the following parameters:
1. Fluence vs. position: the total number of particle (Photon, electron, and both) scored in 200 spatial bins of equal area along the X-axis and Y-axis for various field sizes in a phase space files.
2. Energy fluence vs. position: the total particle (Photon, electron, and both) energy scored in 200 spatial bins of equal area along the X-axis and Y-axis for various field sizes in a phase space files. This is obtained by multiplying each particle weight by its kinetic energy before scoring in a bin.
3. Spectral distribution: the particle (Photon, electron, and both) scored in a user defined field vs. energy with 200 energy bins of equal bin width within a specified field size in X-axis and Y-axis for various field sizes. Fluence is normalized to the bin width and the number of incident particles.
4. Energy fluence distribution: the particle energy (Photon, electron, and both) fluence scored in user defined field vs. energy with 200 energy bins of equal bin width within a specified field size in X-axis and Y-axis for various field sizes. Fluence is normalized to the bin width and the number of incident particles.
5. Angular distribution: the total number of particles (Photon, electron, and both) scored in an angular bin of equal bin width within a specified field size in X-axis and Y-axis for various field sizes. Each data point in the data file represents the total number of particles scored within a given angular bin (the angle between the particle incident direction and the z-axis).
6. X-Y scatter plot from a phase-space data file (X-Y scatter plot): a plot of the X-Y positions of particles (Photon, electron, and both) having a user-specified charge and latch setting within a specified field size.
The BEAMdp programme generates the above data in text form. The data obtained from the phase space files is plotted using GRACE software. The GRACE is 2D graph plotting software for UNIX like operating system, which is a free WYSIWYG 2D graph plotting tool.
The air kerma at isocenter at 80 cm along the central axis from the source was calculated. The energy fluence data for photon and electron was derived from phase space. The energy fluence over 30 energy bins (i = 1 to 30) range from 0 to 1.4 MeV passes through cross section area of 1 cm2 along the central axis was derived. The air kerma was calculated using the following equation:
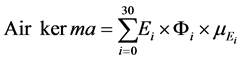
where 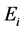 is the mean energy in energy bin I;
is the mean energy in energy bin I; 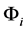 is the energy fluence in energy bin i and
is the energy fluence in energy bin i and 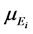 is the mass attenuation coefficient of air at energy
is the mass attenuation coefficient of air at energy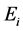 . The values of photon mass absorption coefficient in air were taken from publication by Hubbell [19] .
. The values of photon mass absorption coefficient in air were taken from publication by Hubbell [19] .
2.4. Dose Calculation in Water Phantom
The dose calculation in water phantom was performed using dosxyznrc code. The dosxyznrc is a general purpose Monte Carlo EGSnrc user-code for absorbed dose calculation in user defined medium in three dimensions [18] . The code simulates the transport of photons and electrons in a cartesian volume and scores the energy deposition in the defined voxels. The virtual water phantom consists of large number of user defined voxels in three dimensions. The phantom volume and the voxel size were taken variable depending upon the radiation field size, in order to maintain the accuracy due to scattering and to save the calculation time. The volume of the phantom for 05 × 05 cm2 field size was 30 × 30 × 40 cc, with voxels size of 0.1 × 0.1 × 0.1 cc uniformly distributed over the volume. The details of water phantom regarding volume, voxel size and the number of the dose scoring regions for various field sizes is shown in Table 1. All the voxels in the phantom were filled with water of density of 1 gm/cc. The phantom was saved as .egsphant file that contain the information of CT number with corresponding voxel number. The important voxels/regions were registered to get the dose information which generates the .egslst file. The dose data from .egslst file were analyzed to derive the depth-dose curve and dose profile. The dose calculation in water phantom was performed using phase space generated at plane 2 at 80 cm from the source. The phase space was virtually placed above the phantom with central axis directing at origin (x = 0, y = 0, z = 0) of the phantom. The cut off energy for electron (ECUT) and photon (PCUT) were 0.7 MeV 0.01 MeV respectively. The number of histories simulated from phase space depends upon the field size and phantom volume, which was 2.5 × 109 to 5 × 109 to achieve the reasonable accuracy. The accuracy achieved in dose calculation is higher at lower depths and decreases with increase in depth due to low photon fluence. After the calculation the dose detail in the phantom is saved in .3ddose file. The dosxyz_show program was then used to display the dose distribution in three dimensions x-z and y-z coordinates plane from .3ddose and .egsphant files. The .egslst file was used to extract the dose data along the central and off-axis at various depths for all the field sizes for analysis.
3. Results and Discussions
The phase space data were analyzed by generating profiles on various parameters along the X-off axis at mid plane of the field. The uncertainties in the result of photon energy fluence in different radial zones of the field were within ±0.02%. The profiles of photon
Table 1. The details of parameters used in design of water phantom for dosimetry study of various field sizes.
energy fluence vs. position and all particle (photon, electron and positron) energy fluence vs. position for 10 × 10 cm2 field size at 80 cm distance is shown in Figure 2(a) and Figure 2(b) respectively. The energy fluence for photon was 3.3e−06 MeV/incident particle. The full width at half maximum (FWHM) value for profile of photon energy fluence was 10 cm for 10 × 10 cm2 field size. The energy fluence vs. position for photon and electron for various field sizes is shown in Figure 3(a) and Figure 3(b) respectively. The electron energy fluence was 5.25e−09 MeV/incident particle for 10 × 10 cm2


Figure 2. Profiles along X axis at 80 cm distance for 10 × 10 cm2 field size (a) Photon energy fluence (MeV/cm2/N) vs. position and (b) Photon, electron & positron energy fluence (MeV/cm2/N) vs. position.


Figure 3. Profiles of (a) photon energy fluence (MeV/cm2/N) vs. position and (b) electron energy fluence (MeV/cm2/N) vs. position along X axis for various field sizes at 80 cm from the source.
field size. The contribution from electron to total energy fluence is about 0.16% at central axis of beam for 10 × 10 cm2 field size. The relative electron energy fluence increases with increase in field size. The electron energy contribution was fund to be 0.34% of photon energy for 35 × 35 cm2 field size. The energy fluence increases with increase in the field size, with the values from 1.77e−06 MeV/per incident particle for 05 × 05 cm2 to 11.16e−06 MeV for 35 × 35 cm2. The FWHM values were 10.0, 20.0 and 30.0 cm for the field sizes of 10.0, 20.0 and 30.0 cm2 respectively. The profiles were symmetric and flat for smaller field sizes over the field. The flatness in the profile is maintained till the field size of 25 × 25 cm2, however it is lost for higher field sizes as shown in profiles of 30 × 30 cm2 and 35 × 35 cm2 field size. The energy fluence in the profile gradually decreases at 13.5 cm off-axis either side of the central axis. This may be due to the optimum photon fluence through fixed collimator and the decrease in scatter component from the lower jaws and trimmer bar for field sizes higher than the 27 × 27 cm2. The electron energy fluence was maximum at central axis and decreases drastically towards the off-axis. The electron fluence out side of the field is also significant due to scatter of electron in air.
The air kerma calculated for various field sizes were normalized with the air kerma for reference field size of 10 × 10 cm2. The measurement of air kerma in Theratron Equinox-80 machine was performed using 0.6 cc ionization chamber placed at 80 cm along the central axis of beam. The field sizes taken in the measurement were similar to the field sizes in simulation study. The comparison of result of air kerma output factor from simulation and measurement is shown in Table 2. The results were in very good agreement. It is observed that the measured output factor increases with the increase in field size till 27 × 27 cm2 and thereafter saturates for higher field sizes. This justifies the findings in the profile of photon energy fluence vs. position, where the energy fluence decreases at 13.5 cm off-axis from the central beam.
The energy fluence (MeV/incident particle) distribution (i.e. vs. energy) for photon for 10 × 10 cm2 field size is shown in Figure 4(a). There are two photon energy fluence peaks at 1.17 and 1.33 MeV respectively. The contribution from the low energy scattered photon is very small, however, which increases with increase in photon energy. The detail analysis on scattered photon spectra have been presented by Mora et al. [6] , and Shin et al. [9] . The photon spectra in this study were in agreement with their results. The electron energy distribution for three different field sizes is shown in Figure 4(b). The energy fluence increases with increase in energy of electron and reaches maximum at particular energy and then decreases. The maximum energy of recoil electron was 1.2 MeV. It was observed that the electron energy of maximum fluence decreases with increase in the field size. The results of electron energy distribution for various field sizes in the present study were in agreement with the study of Mora et al. [6] . The mean energy (MeV) of photons in various field sizes is 1.02 MeV, which is much lower than the expected value of 1.25 MeV. The angular distribution of peak photon energy fluence (i.e. angle between photon direction and z-axis) were 2.0˚, 4.5˚, 7.0˚ and 11.0˚ for the field sizes of 05 × 05, 15 × 15, 25 × 25 and 35 × 35 cm2 respectively. The angle of maximum photon fluence increases with the increase in field size. The
Table 2. The comparison of air kerma output factor from measurement and simulation for various field sizes for Theratron Equinox-80 telecobalt unit.


Figure 4. Profiles for energy distribution (MeV/incident particle) of (a) photon for 10 × 10 cm2 and (b) electron for three field sizes at 80 cm from the source.
X-Y scatter plot for 20,000 photons for the field size of 10 × 10 cm2 at 80 cm distance is shown in Figure 5. The radiation beam of useful field size is clearly demarcated for X and Y axis for 10 cm width.
The details of simulation data of dose calculation in water phantom for various field sizes are shown in Table 3. It shows the no. of histories, calculation time, maximum dose par incident particle in any voxel and the accuracy. The calculation time increases with increase in the field size. The accuracy in the dose calculation varies with the field size and the depth of phantom. The accuracy in dose values was ˂±2% up to depth of
Figure 5. X-Y scatter plot of 20,000 photons at 80 cm for 10 × 10 cm2 field size.
Table 3. The detail of results of dose calculation in water phantom in the present study.
10 cm for all the field sizes. The accuracy varies from 1.5% - 2.5% for the depths between 10 cm and 20 cm. The accuracy was more than 2.5% at depths higher than 20 cm. The values were found about 5% at maximum depth of 40 cm. The number of histories simulated from the source in the present study was 1010, which is very high compare to 4 × 109 and 2 × 109 histories by Shin et al. [9] and Praveen et al. [10] respectively. The information of the radiation absorbed dose (Gy/per incident particle) calculated in the voxels over the phantom is saved in .3ddose file. The dosxyz_show code is used to display the dose distribution in different orientations from .3ddose and corresponding .egsphant file. The dose distribution in x-z and x-y plane for isodose line of 10, 20, 30, 40, 50, 60, 70 80, 90 and 100% is shown in Figure 6(a) and Figure 6(b) respectively.


Figure 6. The display of dose distribution for 10 × 10 cm2 field size by dosxyz_show program in (a) X-Z plane and (b) X-Y plane.
The central axis depth-dose in percentage for all field sizes up to 40 cm depth is shown in Figure 7(a). The surface layer of the phantom was made of thickness of 2.0 mm. The surface dose for 05 × 05 cm2 field size was 55.0%. The surface dose increases with increase in field size till 25 × 25 cm2 of 57.9% and then decreases with field size. The surface doses were 57.5% and 56.6% for field sizes of 30 × 30 cm2 and 35 × 35 cm2, respectively. The percentage depth dose for all the field sizes were compared with the data published by BJR supplement 25. The values of PDD were 98.4%, 78.9%, and 57.3% at depth of 1.0, 5.0 and 10.0 cm, respectively for field size of 10 × 10 cm2. The simulated data are in good agreement with the BJR supplement 25 and measured data supplied by the supplier of the equipment. The comparison of the central axis depth


Figure 7. Central axis depth dose curve in percentage (a) calculated for all the field sizes and (b) comparison in calculated and measured and BJR data for 10 × 10 cm2 field size.
dose from simulation, BJR 25 and supplied data from manufacturer is shown in Figure 7(b). The PDD values were in agreement within ±3% of the BJR data. This study calculates the PDD values up to 40 cm depth which is much higher compare to 30 cm as provided by the BJR and supplied data. Shin et al. have calculated the peak scatter factor and percentage depth dose for various field sizes and found that the results were in agreement with BJR supplement data [9] . Kumar et al. have derived the percentage depth dose curve for 05 × 05, 10 × 10 and 30 × 30 cm2 field sizes which were in well agreement with the BJR supplement data [10] .
The dose profile in water phantom for various field sizes at 0.5 cm depth is shown in Figure 8. The dose profiles were symmetrical for all the field sizes. The curve over the penumbra region is very smooth due to the small size voxel. The flatness was found within ±3% over the 80% of field for field sizes of 05 × 05, 10 × 10, 15 × 15 and 20 × 20 cm2. The flatness is lost near the edge of the field for higher field sizes. The dose profile at 0.5 cm depth for all the field sizes were compared with the data supplied by the manufacturer. The comparison of the dose profile for 05 × 05, 10 × 10, 30 × 30, 35 × 35 cm2 is shown in Figures 9(a)-(d), respectively. It is observed that the profiles from simulation were in good agreement with experimental for all the field sizes except 05 × 05 cm2 and 35 × 35 cm2. The small deviation in profile in penumbra region in 05 × 05 cm2 may be due to the fitting of the curve or variation in the simulation of collimator. However, there is large deviation in the dose profile for 35 × 35 cm2 field size between present study and experimental supplied data. The edge of the field shows 20% under dose in simulation study compare to the supplied data.
Similarly the dose profiles for all field sizes at 5.0 cm and 10.0 cm depth are shown in Figure 10(a) and Figure 10(b) respectively. The dose profiles at 5.0 and 10.0 cm depths were in similar character to the dose profile at 0.5 cm depth. The penumbra width for
Figure 8. Dose profile at 0.5 cm depth for various field sizes.


Figure 9. Comparison of depth dose profile at 0.5 cm depth between calculation and measured (a) for 05 × 05 cm2; (b) 10 × 10 cm2; (c) 30 × 30 cm2 and (d) 35 × 35 cm2 field sizes.
various field sizes at different depths is evaluated from the dose profile and shown in Table 4. The width is evaluated not only for isodose line between 80% and 20% but also between 90% and 20%. The penumbra width for profile of 10 × 10 cm2 field size at 0.5 cm depth was 1.15 (±0.05) cm which is comparable to the telecobalt unit Bhabhatran-I and Theratron Elite 80 [20] . It is observed that the penumbra width increases with increase in field size. The penumbra width for 35 × 35 cm2 field size is 3.5, 3.35 and 4.1 cm at depth of 0.5, 5.0 and 10 cm respectively, which significantly very high compare to the other field sizes. The penumbra width increases drastically for 30 × 30 and 35 × 35


Figure 10. Dose profile at (a) 5.0 cm and (b) 10.0 cm depth for all field sizes.
cm2 field sizes when the isodose line of 90% - 20% is taken. The comparison of dose profile between x and y axis at 5 cm depth for 10 × 10 cm2 field size is shown in Figure 11. The profiles show that the effect of the position of x and y trimmer bar in penumbra width is 2 mm.
The larger penumbra width in 30 × 30 cm2 and 35 × 35 cm2 field size shows that there is large deviation in the dose over the edge of the field. The unflatness is found 20% at the edge of the field. This is matter of concern in case of treatment using large
Table 4. The penumbra widths at two different isodose ranges for various field sizes at different depths.
Figure 11. Comparison of dose profile at 5.0 cm depth for 10 × 10 cm2 field size between X and Y axis.
field of more than 30 cm2, where the edge of the field receive doses about 20% less than the prescribed dose at central axis. In the previous study, the profile of photon energy fluence vs. position clearly shows the decrease in the photon energy fluence at 13.5 cm from the central axis. It means the photon fluence is found optimum for field size of 27 × 27 cm2 and it saturates or decreases for larger field sizes. The physical configuration of the fixed and movable collimator of the Equinox unit was rechecked for validation of the results. It was found the faces of the fixed collimator were exactly aligned with the moving collimators at field size of 27 × 27 cm2.
4. Conclusion
The present study performs the simulation of Theratron Equinox-80 telecobalt machine using BEAMnrc code for beam analysis and dose calculation in water phantom. The beam profiles in air show influence of the collimation system on the spectra of photon and electron. It was also found that the air kerma output factor saturates after certain field size which is comparable to the measurement data, also exhibits the accuracy of the realistic modeling of the Theratron Equinox-80 telecobalt machine. The relative electron energy fluence compared to photon increases with increase in the field size. The depth dose curves were in good agreement with the published data by BJR as well as measured data for Theratron Equinox-80 machine supplied by the supplier. The dose profiles at various depths were also in good agreement with the data provided by the supplier, except for the larger fields. A high dose gradient near the edge of the fields may be carefully planned for accurate and uniform dose delivery in larger field treatment.
Cite this paper
Patel, N.P., Shukla, R., Balasubramanian, N., Atri, R., Dhull, A. K., Yadav, H.P. and Kaushal, V. (2016) Radi- ation Beam Characterization and Dosimetry of Theratron Equinox-80 Telecobalt Machi- ne Using BEAMnrc Monte Carlo Simulation Code. International Journal of Medical Phy- sics, Clinical Engineering and Radiation On- cology, 5, 298-316. http://dx.doi.org/10.4236/ijmpcero.2016.54030
References
- 1. Ayyangar, K.M., Kumar, M.D., Narayan, P., Jesuraj, F. and Raju, M.R. (2010) Monte Carlo Simulation of a Multi-Lief Collimator Design for Telecobalt Machine Using BEAMnrc Code. Journal of Medical Physics, 31, 23-32.
- 2. Schreiner, L.J., Joshi, C.P., Darko, J., Kerr, A., Salomons, G. and Dhanesar, S. (2009) The Role of Cobalt-60 in Modern Radiation Therapy: Dose Delivery and Image Guidance. Journal of Medical Physics, 34, 133-136.
https://doi.org/10.4103/0971-6203.54846 - 3. Sahani, G., Sharma, S.D., Dash Sharma, P.K., Sharma, D.N. and Hussain, S.A. (2013) Monte Carlo Simulation Based Study of a Proposed Multilief Collimator for a Telecobalt Machine. Journal of Medical Physics, 40, Article ID: 0217051.
https://doi.org/10.1118/1.4773308 - 4. BJR Suppl. 25 (1996) Central Axis Depth Dose Data for Use in Radiotherapy. British Journal of Radiology, Suppl, 25, London.
- 5. Rogers, D.W.O., Ewart, G.M., Bielajew, A.F. and Van Dyk, G. (1988) Calculation of Electron Contamination in a Co60 Therapy Beam. Proceedings of the IAEA International Symposium on Dosimetry in Radiotherapy, 1, 303-312.
- 6. Mora, G.M., Maio, A. and Rogers, D.W.O. (1999) Monte Carlo Simulation of a Typical 60Co Therapy Source. Journal of Medical Physics, 26, 2494-2502.
https://doi.org/10.1118/1.598770 - 7. Teimouri Sichani, B. and Sohrabpour, M. (2004) Monte Carlo Dose Calculations for Radiotherapy Machines: Theratron 780-C Teletherapy Case Study. Physics in Medicine and Biology, 49, 807-818.
https://doi.org/10.1088/0031-9155/49/5/011 - 8. Miro, R., Soler, J., Gallardo, S., Campayo, J.M., Dyéz, S. and Verdu, G. (2005) MCNP Simulation of Theratron 780 Radiotherapy Unit. Radiation Protection Dosimetry, 116, 65-68.
https://doi.org/10.1093/rpd/nci125 - 9. Shin, J.W., Hong, S.W., LEE, C. and Suh, T.S. (2011) Application of a GEANT4 Simulation to a 60Co Therapy Unit. Journal of Korean Physical Society, 59, 12-19.
https://doi.org/10.3938/jkps.59.12 - 10. Praveen Kumar, R.D., Santosh, K.P. and Augustine, A. (2013) Monte Carlo Simulation of a Theratron Elite 100 Telecobalt Machine Using BEAMnrc Code. International Journal of Engineering Research and Applications, 3, 1574-1583.
- 11. Burns, J.E., Pritchard, D.H. and Knight, R.T. (1992) Peak Scatter Factors for 60Co Gammaradiation. Physics in Medicine and Biology, 37, 2309-2318.
https://doi.org/10.1088/0031-9155/37/12/013 - 12. Tedgren, A.C., de Luelmo, S. and Grindborg, J.E. (2010) Characterization of a 60Co Unit at Secondary Standard Dosimetry Laboratory-Monte Carlo Simulations Compared to Measurements and Results from the Literature. Medical Physics, 37, 2777-2287.
https://doi.org/10.1118/1.3392198 - 13. Rogers, D.W.O., Faddegon, B.A., Ding, G.X., Ma, C.M., Wei, J. and Mackie, T.R. (1995) BEAM: A Monte Carlo Code to Simulate Radiotherapy Treatment Units. Medical Physics, 22, 503-524.
https://doi.org/10.1118/1.597552 - 14. Kawrakow, I. and Rogers, D.W.O. (2003) EGSnrc Code System. NRCC Report PIRS-701, 194-239.
- 15. Rogers, D.W.O., Walters, B. and Kawrakow, I. (2006) BEAMnrc Users Manual. Ottawa, National Research Council of Canada. NRCC Report PIRS-0509(A), Revi, 78-79.
- 16. Nelson, W.R., Hirayama, H. and Rogers, D.W.O. (1985) The EGS4 Code System. Stanford Linear Accelerator Publication 265.
- 17. Ma, C.M. and Rogers, D.W.O. (2006) BEAMdp as a General Purpose Utility. NRCC Report PIRS-509(E) revA.
- 18. Walters, B., Kawrakow, I. and Rogers, D.W.O. (2009) DOSXYZnrc Users Manual. NRCC Report PIRS-794 revB.
- 19. Hubbell, J.H. (1982) Photon Mass Attenuation and Energy-Absorption Coefficients from 1KeV to 20 MeV. International Journal of Applied Radiation and Isotopes, 33, 1269-1290.
https://doi.org/10.1016/0020-708X(82)90248-4 - 20. Kumar, R., Sharma, S.D., Phurailatpam, R., Deshpande, D.D. and Kannan, S. (2005) Performance Characteristics of Indigenously Developed Bhabhatron-I Telecobalt Unit. Journal of Medical Physics, 30, 41-47.







