International Journal of Medical Physics, Clinical Engineering and Radiation Oncology
Vol.04 No.02(2015), Article ID:55898,12 pages
10.4236/ijmpcero.2015.42019
Biological Dose Estimation Model for Proton Beam Therapy
Vladimir Anferov1*, Indra J. Das2,3
1Pronova Solutions LLC, Knoxville, USA
2Indiana University School of Medicine, Indianapolis, USA
3IU Health Proton Therapy Center, Bloomington, USA
Email: *Vladimir.Anferov@pronovasolutions.com
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 14 January 2015; accepted 18 April 2015; published 23 April 2015
ABSTRACT
Purpose: The recommended value for the relative biological effectiveness (RBE) of proton beams is currently assumed to be 1.1. However, there is increasing evidence that RBE increases towards the end of proton beam range that may increase the biological effect of proton beam in the distal regions of the dose deposition. Methods: A computational approach is presented for estimating the biological effect of the proton beam. It includes a method for calculating the dose averaged linear energy transfer (LET) along the measured Bragg peak and published LET to RBE conversion routine. To validate the proposed method, we have performed Monte Carlo simulations of the pristine Bragg peak at various beam energies and compared the analysis with the simulated results. A good agreement within 5% is observed between the LET analysis of the modeled Bragg peaks and Monte Carlo simulations. Results: Applying the method to the set of Bragg peaks measured at a proton therapy facility we have estimated LET and RBE values along each Bragg peak. Combining the individual RBE-weighted Bragg peaks with known energy modulation weights we have calculated the RBE-weighted dose in the modulated proton beam. The proposed computational method provides a tool for calculating dose averaged LET along the measured Bragg peak. Conclusions: Combined with a model to convert LET into RBE, this method enables calculation of RBE-weighted dose both in pristine Bragg peak and in modulated beam in proton therapy.
Keywords:
Proton Beam Therapy, Relative Biological Effectiveness, Linear Energy Transfer

1. Introduction
Proton beams offer clinically favorable dose distribution due to their unique energy deposition characteristics in the form of the Bragg peak and finite penetration depth with near-zero dose beyond a certain depth known as range. These unique features provide possibilities for dose escalations to improve radiation outcomes with significant reduction in radiation related toxicities and complications [1] - [4] . The improved clinical outcome potentials of proton beams have driven interest in radiation oncology community, with clearly visible growth in the number of proton therapy facilities worldwide. While physical properties of proton beams are well established, the biological effects are still an active area of research with large uncertainties [5] [6] .
The majority of proton therapy facilities have adopted a constant value of 1.1 for the relative biological effectiveness (RBE) of proton beams based on international recommendations [6] [7] . However there are ample evidences that the RBE in particle beams is not constant rather depends on beam energy, location, dose fractionation and tissue type. Many experimental approaches in determining RBE of proton beam have been suggested depending upon the biological sample [8] - [15] as reflected in many publications that summarize the measured values [5] [6] . There is also a growing concern among clinicians who have observed adverse biological effect at the end of Bragg peak for brain and spinal cord irradiations [16] - [18] .
The experimentally measured RBE dependence on linear energy transfer (LET) suggests that the RBE value increases towards the end of beam range (as the energy decreases) that could increase the biological effect of proton radiation in the distal regions of the dose deposition [15] [19] [20] . To quantify this effect, the product of the deposited (physical) dose and the RBE, referred to as RBE-weighted dose, can be used. Radiobiological experiments [21] using monoenergetic proton beams have established general dependence of the RBE on the linear energy transfer (LET). Furthermore, phenomenological model [22] has been proposed linking the RBE effect with the proton dose per fraction, LET value, and tissue sensitivity to reference x-ray radiation expressed in α and β parameters of the linear-quadratic model [23] . The challenge remains to estimate the biological effect at the distal edge of the Bragg peak as the LET distributions can vary significantly depending on the hardware configuration and beam properties in the treatment nozzle [24] . In clinical practice, individual proton therapy nozzles are parameterized and calibrated by measuring depth dose distribution in water for a set of beam energies thus providing pristine Bragg peak measurements, which are specific to the proton beam-line design. These individual Bragg peaks can be combined with appropriate weighting factors to provide Spread Out Bragg Peak (SOBP) by selecting sequential beam energy reduction (or Bragg peak pull back), which would provide the required target coverage in depth. As variability of Bragg peak properties among treatment centers is well known [25] , one can also expect variation in RBE measurements at different facilities. A possible link of RBE variability with proton beam line design has been observed by Paganetti and Goitein [24] .
The main focus of this paper is to develop a computational method for RBE based on dose averaged LET (see Equation (2)) values from a measured depth dose data for clinical beam. While for the same treatment range Bragg peak shape may differ between different treatment centers, we do expect that the method presented here is universally applicable for converting measured Bragg peaks into RBE-weighted Bragg peaks. Once the RBE values are calculated along individual Bragg peaks, one can generate RBE-weighted SOBP dose distributions for clinical usage.
2. Materials and Methods
Ionization track structures and microdosimetric energy spectra of protons at various depths are typically analyzed to convert LET [26] - [30] of individual protons into an RBE value [13] [31] [32] , of a therapeutic beam. We propose a simple method that allows one to determine the dose averaged LET value at each point along the measured Bragg peak. Instead of integrating proton spectra with proton stopping power along each track, we take the ratio of the energy deposited per unit length to proton beam fluence (see Equation (2)) to define dose averaged LET. Assuming that the RBE-LET relationship is known, we can then calculate RBE values along the measured pristine Bragg peak to construct a “biological”, or RBE-weighted pristine Bragg peak. Applying the known pullbacks and respective energy modulation weights, one can determine the RBE-weighted dose in a modulated proton beam.
2.1. LET Calculation Model
The depth dose curve containing Bragg peak of the proton beam is divided into two regions: the proximal region from the surface to the dose maximum and the distal region from the maximum to near zero dose. For every depth, point x measured from the material surface in the proximal region, we can define the residual range RRES as:
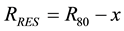 (1)
(1)
where R80 is the proton beam penetration range measured at the distal 80% dose level of the Bragg peak. Using the published energy-range tables [33] we can convert the residual penetration range at a given point into either the effective proton energy or into the effective stopping power. The linear energy transfer is defined by the energy deposited in the target media per unit length. Its primary contribution comes from the beam energy losses per unit length or the beam stopping power. However, LET also includes an additional small contribution that comes from short range secondary particles created in nuclear interactions of the primary proton beam with the target media [34] . We assumed a small but constant correction factor for nuclear interactions, which adds to beam stopping power and allows defining a dose averaged LET for each point in depth proximal to the Bragg peak. The correction factor value for nuclear interactions is determined in Section 2.2 using Monte-Carlo calculations.
It is important to note the small disagreement between various range-energy tables. For example, for the same energy of 250 MeV ICRU Report 49 [33] and Janni [35] predict proton ranges in water that differ by 3 mm. If we were to take water surface as our normalization point and assumed same energy proton beam at the entrance, then after passing the same slab of water the disagreement in the proton stopping power values from different range energy tables can exceed 10%near the Bragg peak. By introducing the residual range, we can set our nor- malization point at R80, which introduces very small discrepancy in initial beam energy at the water surface but brings the overall agreement of stopping power calculations from various range-energy tables to within 2% as illustrated in Figure 1.
Next we defined a method of calculating LET in the distal region of Bragg peak. Our most general assump- tion about distal region is that the dose averaged LET should be a smooth function of depth. The continuous slowing down approximation (CSDA) does not work beyond the Bragg peak since residual range becomes negative. Furthermore, the proton beam cannot be considered monoenergetic on the distal edge of the Bragg peak. Instead, the beam energy spectrum changes when it reaches energies below 3 MeV (residual range of 0.1 mm) as illustrated in Figure 2. Besides obvious asymmetry in the beam energy spectrum, the range of energies cor- responds to a wide range of LET values. Therefore, common RBE calculation methods include spectral analysis of the beam at every given point and integration of the dose deposition function with LET spectra [36] . This
Figure 1. Comparison of stopping power in different Range-Energy tables for water in log-log scale. The horizontal scale is reversed to emphasize the stopping power behavior along the Bragg peak.
Figure 2. Energy spectra on distal edge of 162 MeV Bragg peak obtained from Monte-Carlo calculations. Individual spectra at R05, R20, R50, R80 and R_peak were scaled down by factors of 1, 2, 3, 4, and 5 respectively.
LET spectral analysis works well in Monte Carlo but is not practical for analysis of clinically measured Bragg peaks. Looking for an alternative method, we have observed in our Monte Carlo simulations that the dose averaged LET exhibits a nearly linear increase with depth beyond the Bragg peak. Therefore, as a first approximation we assume that the dose averaged LET increases linearly with depth beyond the Bragg peak position and the slope of LET growth is defined by LET slope at the maximum dose point on the Bragg peak.
Furthermore, when the physical dose drops below 1% level the biological effect becomes important only at the theoretical level. When the physical dose is negligible, the RBE value becomes irrelevant from a clinical point of view. Therefore, beyond the distal 1% - 2% depth dose point we assume constant LET and RBE values. This prevents magnification of the experimental noise which could be present in the region beyond the Bragg peak.
2.2. Validation of the LET Calculation Model
To validate the proposed model for LET calculation we have carried out Monte Carlo simulation of the dose distribution along depth generated by 1 cm diameter source of mono-energetic proton shitting a water target. The Monte-Carlo calculations were carried out using MCNPx code [37] . Using a cylindrical detector mesh with 0.5 mm spacing in depth and 12 cm in diameter both the energy deposited and proton fluence in each cell was calculated. Instead of integrating the stopping power over the energy spectrum of the proton beam, we calculated the dose averaged LET through simple division of the energy deposited in each cell dE [MeV/cm3] by the proton beam fluence F [1/cm2]:
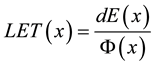 (2)
(2)
We have calculated the depth dose distribution and dose averaged LET for monoenergetic proton beams at three energies 116 MeV, 162 MeV and 201 MeV corresponding to the penetration range R80 in water of about 10 cm, 18 cm and 26 cm, respectively. We applied the LET calculation model outlined above to the Bragg peaks simulated with MCNPx to validate the proposed model. Thus, we could compare the LET model calculations to the MCNPx simulation results based on identical Bragg peaks. The comparison was first done for the proximal regions and then for the distal regions of the Bragg peaks.
2.3. LET to RBE Conversion
The most straight forward way to obtain RBE is to use experimental data from radiobiological experiment for a particular cell line. However, taking the data from published experiments [32] we would find that only a few data point lie in the clinically relevant for proton therapy LET range below 200 MeV/cm.
A more generic phenomenological model proposed by Wilkens and Oelfke [22] describing RBE as a function of proton dose Dp, the LET, and the tissue specific parameters α and β from a linear-quadratic cell survival parameterization:
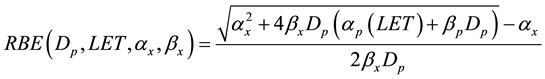 (3)
(3)
where subscripts p and x refer to proton and x-ray linear quadratic parameters, respectively. Analyzing published radiobiological experimental data Wilkens and Oelfke [22] concluded that in the LET region below 200 MeV/cm, which is most relevant for clinical applications, a linear dependence of αp on LET could be assumed, while βp is essentially independent of LET and equal to βx:
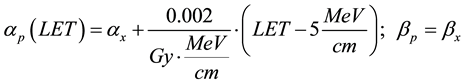 (4)
(4)
Note that such parameterization results in αp = αx at the entrance region of 170 MeV proton beam where the LET = 5 MeV/cm. In other words, monoenergetic proton beam has RBE = 1 at the entrance region into the water equivalent media. To estimate RBE variation in different tissues and for different dose fractionation regimes we have compiled a short table (Table 1) of alpha beta values for common treatment sites in proton therapy. We then studied how the selection of tissue or dose per fraction changes the RBE behavior in the range of LET values applicable for proton therapy.
2.4. RBE-Weighted Dose Calculation
Finally we computed the RBE-weighted dose along the Bragg peak as a product of measured physical dose at a given depth x, and RBE factor calculated using phenomenological model (Equation (3)) for LET value at the same point on Bragg peak assuming proton dose delivery with 2 Gy or 4 Gy per fraction. In these calculations we used head and neck tissue alpha beta parameters since it represents a typical treatment site in proton therapy. The case of 4 Gy per fraction was calculated to evaluate the effect of hypo-fractionation in proton therapy that has been observed in many publications [15] [38] .
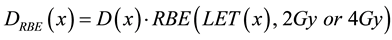 (5)
(5)
The physical depth dose measurements were taken with a Markus ion chamber in a water phantom while delivering pristine energy proton beams with field sizes exceeding 5 cm in diameter. The measured depth dose curves were smoothed with Gaussian algorithm imbedded into the water phantom data acquisition software to eliminate signal noise associated with beam intensity fluctuations. These measured Bragg peaks were part of the commissioning data set taken in uniform scanning nozzle as described Farr et al. [39] .
For proton beams modulated in depth, we calculated the RBE-weighted dose by combining RBE-weighted dose from individual Bragg peaks scaled according to monitor unit weights of individual energy layers.
Table 1. Radiosensitivity parameters for tissues representing common treatment sites in proton therapy.
3. Results
3.1. Validation of LET Calculation Model
To validate the proposed model for LET calculation we used Monte Carlo modeling to investigate the LET behavior around the proton Bragg peak. Figure 3 shows calculated LET values plotted against the residual range for three different energies of the incident proton beam 116 MeV, 162 MeV and 201 MeV.
The Monte Carlo simulation data indicate that LET behavior is nearly identical in the proximal region of the Bragg peak regardless of the incident beam energy. This pattern also agrees qualitatively with the LET predic- tions from the water range-energy tables. However, the stopping power values computed from the water range- energy table are consistently lower by about 7% due to missing contribution from the short range secondary particles created in the nuclear interactions. Similar nuclear buildup of about 6% has been observed experimentally at the entrance region of the Bragg peak.
Including the 7% correction into the model, we applied the LET calculation method to the set of Bragg peaks simulated with MCNPx [37] . Figure 4 shows comparison of the LET values along the 162 MeV Bragg peak calculated with the model and with Monte Carlo. Similar analysis was also carried out for proton beam energies of 116 MeV and 201 MeV. With the exception of distal tail region, where physical dose is less than 1% of the peak value, the model demonstrates good agreement with Monte Carlo simulations. The deviation between the model calculations and Monte Carlo does not exceed 4% in the proximal region of Bragg peak, while in the distal region of Bragg peak the LET values may differ by up to 8%. This can be attributed to simplified linear LET behavior, which the model assumes in the distal region.
3.2. RBE-Weighted Dose Calculation
With the method for calculating LET values along the measured Bragg peak, the next step is to calculate RBE based on LET values. We compared the RBE behavior in the range of LET values relevant in proton therapy for different tissues as shown in Figure 5(a). For the selected tissue types we found very small variation of RBE values within the LET range of interest. We also compared the RBE behavior for different dose per fraction. Negligible RBE variation with dose was observed for the LET values below 10 MeV/cm corresponding to proximal region of the Bragg peak. However, near the Bragg peak and in the distal region of the Bragg peak the
Figure 3. LET behavior on the proximal side of the Bragg peak calculated (Equation (2)) for three different proton beam energies and predictions from water range-energy tables. For each energy the position of Bragg peak is indicated with a triangle.
Figure 4. Comparison of the Monte Carlo simulated LET to the LET analysis applied to the simulated Bragg peak at 162 MeV. Similar data were obtained for Bragg peaks at 116 MeV and 201 MeV.


Figure 5. Proton beam RBE values calculated from Equation (3) are plotted as a function of LET: (a) For different tissues and same fractional dose of 2 Gy; and (b) For different fractional dose but same tissue type. Arrows on the top scale indicate expected residual range of protons in water for a given LET value.
RBE variation with dose become substantial and exceeds 10% for the LET values above 40 MeV/cm as shown in Figure 5(b).
Applying the proposed method to the set of experimentally measured Bragg peaks, we obtained the RBE-weighted absorbed dose as shown in Figure 6. Combining the RBE-weighted Bragg peaks we then estimated the biological dose in modulated beams that requires only the knowledge of weights of the individual Bragg peaks comprising the SOBP. Figure 7 shows physical and RBE-weighted SOBPs for large, medium and shallow proton beam penetration ranges and for two dose fractionation scenarios of 2 Gy and 4 Gy per fraction.
Figure 6. Physical and RBE-weighted dose distributions are plotted against depth in water for a 152 MeV pristine Bragg peak.
Figure 7. Comparison of the physical dose and RBE-weighted dose in modulated proton beams.
4. Discussions
Our LET calculation approach is based on the observation that for nearly monoenergetic proton beam, dose deposition per unit length on the proximal side of Bragg peak is defined by the proton stopping power and small contribution from secondary charged particles. While the shape of Bragg peak can vary depending on the hardware configuration and beam properties in the treatment nozzle, the LET behavior is the same on the proximal side of the Bragg peak and is defined by the residual range of the proton beam. On the distal side of the Bragg peak, LET slope does depend on beam properties (SAD, energy spread, etc.). However, we found that linear interpolation based on the LET slope calculated at the peak point of the Bragg peak gives reasonable approximation of the LET behavior on the distal side. Applying this approach to clinically measured Bragg peaks can give us dose averaged LET values at each point of the depth dose curve.
In our calculations of RBE-weighted dose, we rely on the phenomenological model proposed by Wilkens and Olfke [22] linking proton RBE with dose averaged LET values. Other RBE models exists that instead of simple linear relationship between proton and x-ray radio sensitivity parameters (α, β) assume stronger tissue dependence of RBE on α/β ratio, see Carabe et al. [40] . However, we feel that current experimental data do not warrant any proton RBE correlation with α/β ratio. This lack of correlation was also reported by Paganetti et al. [34] . In general, the phenomenological parameterization of Wilkens and Olfke [22] may need to be further generalized to wider sample of tissues but it gives the simplest way to link proton and x-ray therapies.
Applying our LET and RBE calculation model to the typical treatment sites in proton therapy, we found that tissue dependence of RBE is negligible. This result matches well with ICRU-78 recommendation of using tissue-independent mean RBE value of 1.1, which is based upon available in-vitro and in-vivo data. However, we suggest using caution since tissue-independence of proton RBE may not be applicable to all treatment sites and certainly may not be applicable to organs at risk adjacent to the treatment volume [15] . Instead, we suggest that a generic tissue-independent RBE-weighted set of Bragg peaks could be used to setup a machine configuration in treatment planning system for estimating RBE effects at typical treatment sites only.
Using the RBE-weighted set of Bragg peaks measured at our center, we have computed RBE-weighted dose distributions in modulated proton beam delivery. In the middle of computed SOBPs the RBE-weighted dose was found in reasonable agreement with a generic RBE value of 1.1 as recommended [6] . However, the RBE values can be as large as 1.3 at the distal edge and as low as 1.05 near the proximal edge of SOBP dose distribution. Our calculations also suggest that there could be up to 10% difference between RBE values on distal corner of SOBP at different beam energies. Furthermore, RBE value on the proximal corner is influenced by both the beam energy and the value of SOBP modulation. Our findings are consistent with predictions of other models of calculating RBE-weighted dose [26] .
Note that, the SOBP delivery implies superposition of Bragg peaks with different weighting factors. The Bragg peaks in the middle of SOBP deliver smaller dose than distal Bragg peaks to take into account dose already delivered by all those distal Bragg peaks. This may raise a concern about dose dependence of RBE. However, because of this “prior” dose from distal Bragg peaks and since the TOTAL physical dose within the SOBP is constant, we cannot apply dose effect to RBE weighted individual Bragg peaks comprising the SOBP.
Our method also predicts higher RBE at the distal edge of the dose distribution, which can lead to an apparent extension of the physical range by about 1 mm in depth. Table 2 summarizes the calculated RBE values and range extensions for the SOBP set. To compensate for elevated RBE at the distal end of SOBP, our calculations suggest reducing relative weight of the deepest Bragg peak and adding a negative slope of about 0.75%/cm to the physical dose within SOBP. The RBE-weighted dose calculations also suggest changes to common practice
Table 2. RBE values at different locations of SOBPs and range extension.
of maximizing the weight of the deepest Bragg peak to sharpen the distal fall off in favor of optimizing relative weights of the Bragg peaks to smooth out distal gradient and to compensate for the RBE rise on the distal edge of SOBP.
The analysis of hypo-fractionated proton dose delivery mode with 4 Gy per fraction indicates reduction of the biological effect in the SOBP region by about 7% compared with 2 Gy per fraction dose delivery mode as also noted by Carabe-Fernandez et al. [41] . Such calculations of the RBE-weighted dose could be used at the treatment planning stage for estimating the effect of fractionation scheme on the expected outcome in proton radiation therapy.
5. Conclusions
A computational model for estimating RBE-weighted dose based upon experimentally measured set of Bragg peaks is developed. The model allows one to calculate the dose averaged LET along the measured Bragg peak so that one can apply an LET to RBE conversion function. This routine can be applied to a set of Bragg peaks measured at any proton therapy facility. Combining the RBE-weighted pristine Bragg peaks according to the known weighting factors, one can obtain the RBE-weighted depth dose distribution in a modulated proton beam. The computed RBE-weighted absorbed dose exceeds physical dose by 5% - 30% over the SOBP region, depending on SOBP modulation width, maximum beam energy and depth along the SOBP.
The biological dose calculations strongly depend on the RBE versus LET relationship. However, we found that proton beam RBE tissue dependence is very small for four typical treatment sites. We also observed that the dose dependence of proton beam RBE has strongest effect mainly at the distal end of SOBP. The proposed method of computing the RBE-weighted dose in the proton beam may be useful in clinical practice for estimating the RBE-weighted dose delivered to the target and surrounding tissues, which could lead to treatment optimization and better definitions of safety margins during the treatment planning.
Acknowledgements
The authors are grateful to Dr. D. Nichiporov for useful discussions and critique that helped developing the computational method.
References
- Sheets, N.C., Goldin, G.H., Meyer, A.-M., Wu, Y., Chang, Y., Stuürmer, T., Holmes, J.A., Reeve, B.B., Godley, P.A., Carpenter, W.R. and Chen, R.C. (2012) Intensity-Modulated Radiation Therapy, Proton Therapy, or Conformal Radiation Therapy and Morbidity and Disease Control in Localized Prostate Cancer. JAMA, 307, 1611-1620. http://dx.doi.org/10.1001/jama.2012.460
- St. Clair, W.H., Adams, J.A., Bues, M., Fullerton, B.C., La Shell, S., Kooy, H.M., Loeffler, J.S. and Tarbell, N.J. (2004) Advantage of Protons Compared to Conventional x-Ray or Imrt in the Treatment of a Pediatric Patient with Medulloblastoma. International Journal of Radiation Oncology Biology Physics, 58, 727-734. http://dx.doi.org/10.1016/S0360-3016(03)01574-8
- Brown, A.P., Barney, C.L., Grosshans, D.R., McAleer, M.F., de Groot, J.F., Puduvalli, V.K., Tucker, S.L., Crawford, C.N., Khan, M., Khatua, S., Gilbert, M.R., Brown, P.D. and Mahajan, A. (2013) Proton Beam Craniospinal Irradiation Reduces Acute Toxicity for Adults with Medulloblastoma. International Journal of Radiation Oncology Biology Physics, 86, 277-284. http://dx.doi.org/10.1016/j.ijrobp.2013.01.014
- Moeller, B.J., Chintagumpala, M., Philip, J.J., Grosshans, D.R., McAleer, M.F., Woo, S.Y., Gidley, P.W., Vats, T.S. and Mahajan, A. (2011) Low Early Ototoxicity Rates for Pediatric Medulloblastoma Patients Treated with Proton Radiotherapy. Radiation Oncology, 6, 58. http://dx.doi.org/10.1186/1748-717X-6-58
- Blakely, E.A. and Chang, P.Y. (2009) Biology of Charged Particles. Cancer Journal, 15, 271-284. http://dx.doi.org/10.1097/PPO.0b013e3181b666c5
- ICRU Report 78 (2007) Prescribing, Recording, and Reporting Proton Beam Therapy. International Commission on Radiation Units and Measurements.
- IAEA TRS 461 (2008) Relative Biological Effectiveness in Ion Beam Therapy. International Atomic Energy Agency.
- Bashkirov, V. and Schulte, R.W. (2002) Dosimetry System for the Irradiation of Thin Biological Samples with Therapeutic Proton Beams. Physics in Medicine and Biology, 47, 409-420. http://dx.doi.org/10.1088/0031-9155/47/3/304
- Britten, R.A., Nazaryan, V., Davis, L.K., Klein, S.B., Nichiporov, D., Mendonca, M.S., Wolanski, M., Nie, X., George, J. and Keppel, C. (2013) Variations in the Rbe for Cell Killing along the Depth-Dose Profile of a Modulated Proton Therapy Beam. Radiation Research, 179, 21-28. http://dx.doi.org/10.1667/RR2737.1
- Gueulette, J., Blattmann, H., Pedroni, E., Coray, A., Decoster, B., Mahy, P., Wambersie, A. and Goitein, G. (2005) Relative Biologic Effectiveness Determination in Mouse Intestine for Scanning Proton Beam at Paul Scherrer Institute, Switzerland. Influence of Motion. International Journal of Radiation Oncology Biology Physics, 62, 838-845. http://dx.doi.org/10.1016/j.ijrobp.2005.03.048
- Gueulette, J., Bohm, L., De Coster, B.M., Vynckier, S., Octave-Prignot, M., Schreuder, A.N., Symons, J.E., Jones, D.T., Wambersie, A. and Scalliet, P. (1997) RBE Variation as a Function of Depth in the 200-MeV Proton Beam Produced at the National Accelerator Centre in Faure (South Africa). Radiotherapy and Oncology, 42, 303-309. http://dx.doi.org/10.1016/S0167-8140(97)01919-1
- Kagawa, K., Murakami, M., Hishikawa, Y., Abe, M., Akagi, T., Yanou, T., Kagiya, G., Furusawa, Y., Ando, K., Nojima, K., Aoki, M. and Kanai, T. (2002) Preclinical Biological Assessment of Proton and Carbon Ion Beams at Hyogo ion Beam Medical Center. International Journal of Radiation Oncology Biology Physics, 54, 928-938. http://dx.doi.org/10.1016/S0360-3016(02)02949-8
- Raju, M.R., Amols, H.I., Bain, E., Carpenter, S.G., Cox, R.A. and Robertson, J.B. (1978) A Heavy Particle Comparative Study. Part III: OER and RBE. British Journal of Radiology, 51, 712-719. http://dx.doi.org/10.1259/0007-1285-51-609-712
- Giantsoudi, D., Grassberger, C., Craft, D., Niemierko, A., Trofimov, A. and Paganetti, H. (2013) Linear Energy Transfer-Guided Optimization in Intensity Modulated Proton Therapy: Feasibility Study and Clinical Potential. International Journal of Radiation Oncology Biology Physics, 87, 216-222. http://dx.doi.org/10.1016/j.ijrobp.2013.05.013
- Carabe, A., España, S., Grassberger, C. and Paganetti, H. (2013) Clinical Consequences of Relative Biological Effectiveness Variations in Proton Radiotherapy of the Prostate, Brain and Liver. Physics in Medicine and Biology, 58, 2103-2117. http://dx.doi.org/10.1088/0031-9155/58/7/2103
- Pehlivan, B., Ares, C., Lomax, A.J., Stadelmann, O., Goitein, G., Timmermann, B., Schneider, R.A. and Hug, E.B. (2012) Temporal Lobe Toxicity Analysis after Proton Radiation Therapy for Skull Base Tumors. International Journal of Radiation Oncology Biology Physics, 83, 1432-1440. http://dx.doi.org/10.1016/j.ijrobp.2011.10.042
- Tilly, N., Johansson, J., Isacsson, U., Medin, J., Blomquist, E., Grusell, E. and Glimelius, B. (2005) The Influence of RBE Variations in a Clinical Proton Treatment Plan for a Hypopharynx Cancer. Physics in Medicine and Biology, 50, 2765-2777. http://dx.doi.org/10.1088/0031-9155/50/12/003
- Jones, B., Wilson, P., Nagano, A., Fenwick, J. and McKenna, G. (2012) Dilemmas Concerning Dose Distribution and the Influence of Relative Biological Effect in Proton Beam Therapy of Medulloblastoma. British Journal of Radiology, 85, e912-e918. http://dx.doi.org/10.1259/bjr/24498486
- Grassberger, C. and Paganetti, H. (2011) Elevated Let Components in Clinical Proton Beams. Physics in Medicine and Biology, 56, 6677-6691. http://dx.doi.org/10.1088/0031-9155/56/20/011
- Grassberger, C., Trofimov, A., Lomax, A. and Paganetti, H. (2011) Variations in Linear Energy Transfer within Clinical Proton Therapy Fields and the Potential for Biological Treatment Planning. International Journal of Radiation Oncology Biology Physics, 80, 1559-1566. http://dx.doi.org/10.1016/j.ijrobp.2010.10.027
- Belli, M., Campa, A. and Ermolli, I. (1997) A Semi-Empirical Approach to the Evaluation of the Relative Biological Effectiveness of Therapeutic Proton Beams: The Methodological Framework. Radiation Research, 148, 592-598. http://dx.doi.org/10.2307/3579735
- Wilkens, J.J. and Oelfke, U. (2004) A Phenomenological Model for the Relative Biological Effectiveness in Therapeutic Proton Beams. Physics in Medicine and Biology, 49, 2811-2825. http://dx.doi.org/10.1088/0031-9155/49/13/004
- Neary, G.J. (1965) The Relation between the Exponent of Dose Response for Chromosome Aberrations and the Relative Contribution of “Two-Track” and “One-Track” Processes. Mutation Research, 2, 242-246. http://dx.doi.org/10.1016/0027-5107(65)90035-7
- Paganetti, H. and Goitein, M. (2000) Radiobiological Significance of Beamline Dependent Proton Energy Distributions in a Spread-Out Bragg Peak. Medical Physics, 27, 1119-1126. http://dx.doi.org/10.1118/1.598977
- His, W.C., Moyers, M.F., Nichiporov, D., Anferov, V., Wolanski, M., Allgower, C.E., Farr, J.B., Mascia, A.E. and Schreuder, A.N. (2009) Energy Spectrum Control for Modulated Proton Beams. Medical Physics, 36, 2297-2308. http://dx.doi.org/10.1118/1.3132422
- Frese, M.C., Yu, V.K., Stewart, R.D. and Carlson, D.J. (2012) A Mechanism-Based Approach to Predict the Relative Biological Effectiveness of Protons and Carbon Ions in Radiation Therapy. International Journal of Radiation Oncology Biology Physics, 83, 442-450. http://dx.doi.org/10.1016/j.ijrobp.2011.06.1983
- Kantemiris, I., Karaiskos, P., Papagiannis, P. and Angelopoulos, A. (2011) Dose and Dose Averaged LET Comparison of 1H, 4He, 6Li, 8Be, 10B, 12C, 14N, and 16O Ion Beams Forming a Spread-Out Bragg Peak. Medical Physics, 38, 6585- 6591. http://dx.doi.org/10.1118/1.3662911
- Nikjoo, H., Uehara, S., Wilson, W.E., Hoshi, M. and Goodhead, D.T. (1998) Track Structure in Radiation Biology: Theory and Applications. International Journal of Radiation Biology, 73, 355-364. http://dx.doi.org/10.1080/095530098142176
- Ottolenghi, A., Merzagora, M. and Paretzke, H.G. (1997) DNA Complex Lesions Induced by Protons and α-Particles: Track Structure Characteristics Determining Linear Energy Transfer and Particle Type Dependence. Radiation and Environmental Biophysics, 36, 97-103. http://dx.doi.org/10.1007/s004110050060
- Zaider, M., Brenner, D.J. and Wilson, W.E. (1983) The Applications of Tack Calculations to Radiobiology I. Monte Carlo Simulation of Proton Tracks. Radiation Research, 95, 231-247. http://dx.doi.org/10.2307/3576252
- Barendsen, G.W. (1994) RBE-LET Relationships for Different Types of Lethal Radiation Damage in Mammalian Cells: Comparison with DNA Dsb and an Interpretation of Differences in Radiosensitivity. International Journal of Radiation Biology, 66, 433-436. http://dx.doi.org/10.1080/09553009414551411
- Belli, M., Cera, F., Cherubini, R., Dalla Vecchia, M., Haque, A.M., Ianzini, F., Moschini, G., Sapora, O., Simone, G., Tabocchini, M.A. and Tiveron, P. (1998) RBE-LET Relationships for Cell Inactivation and Mutation Induced by Low Energy Protons in v79 Cells: Further Results at the LNL Facility. International Journal of Radiation Biology, 74, 501- 509. http://dx.doi.org/10.1080/095530098141375
- ICRU (1993) ICRU Report 49, Stopping Powers and Ranges for Protons and Alpha Particles. International Commission on Radiation Units and Measurements.
- Paganetti, H., Niemierko, A., Ancukiewicz, M., Gerweck, L.E., Goitein, M., Loeffler, J.S. and Suit, H.D. (2002) Relative Biological Effectiveness (RBE) Values for Proton Beam Therapy. International Journal of Radiation Oncology Biology Physics, 53, 407-421. http://dx.doi.org/10.1016/S0360-3016(02)02754-2
- Janni, J.F. (1966) Calculations of Energy Loss, Range, Pathlength, Straggling, Multiple Scattering, and the Probability of Inelastic Nuclear Collisions for 0.1- to 1000-MeV Protons. Air Force Weapons Laboratory, Technical Report No. AFWL-TR-65-150.
- Gomà, C., Andreo, P. and Sempau, J. (2013) Spencer-Attix Water/Medium Stopping-Power Ratios for the Dosimetry of Proton Pencil Beams. Physics in Medicine and Biology, 58, 2509-2522. http://dx.doi.org/10.1088/0031-9155/58/8/2509
- Pelowitz, D.B., Hendricks, J.S., Durkee, J.W., Fensin, M.L., James, M.R., McKinney, G.W., Mashnik, S.G. and Waters, L.S. (2008) MCNPX User’s Manual. Version 2.6.0, National Laboratory, Los Alamos.
- Matsuura, T., Egashira, Y., Nishio, T., Matsumoto, Y., Wada, M., Koike, S., Furusawa, Y., Kohno, R., Nishioka, S., Kameoka, S., Tsuchihara, K., Kawashima, M. and Ogino, T. (2010) Apparent Absence of a Proton Beam Dose Rate Effect and Possible Differences in RBE between Bragg Peak and Plateau. Medical Physics, 37, 5376-5381. http://dx.doi.org/10.1118/1.3490086
- Farr, J.B., Mascia, A.E., His, W.C., Allgower, C.E., Jesseph, F., Schreuder, A.N., Wolanski, M., Nichiporov, D.F. and Anferov, V. (2008) Clinical Characterization of a Proton Beam Continuous Uniform Scanning System with Dose Layer Stacking. Medical Physics, 35, 4945-4954. http://dx.doi.org/10.1118/1.2982248
- Carabe, A., Moteabbed, M., Depauw, N., Schuemann, J. and Paganetti, H. (2012) Range Uncertainty in Proton Therapy Due to Variable Biological Effectiveness. Physics in Medicine and Biology, 57, 1159-1172. http://dx.doi.org/10.1088/0031-9155/57/5/1159
- Carabe-Fernandez, A., Dale, R.G., Hopewell, J.W., Jones, B. and Paganetti, H. (2010) Fractionation Effects in Particle Radiotherapy: Implications for Hypo-Fractionation Regimes. Physics in Medicine and Biology, 55, 5685-5700. http://dx.doi.org/10.1088/0031-9155/55/19/005
- Kramer, M. and Scholz, M. (2000) Treatment Planning for Heavy-Ion Radiotherapy: Calculation and Optimization of Biologically Effective Dose. Physics in Medicine and Biology, 45, 3319-3330. http://dx.doi.org/10.1088/0031-9155/45/11/314
- Carlson, D.J., Stewart, R.D., Li, X.A., Jennings, K., Wang, J.Z. and Guerrero, M. (2004) Comparison of in Vitro and in Vivo Alpha/Beta Ratios for Prostate Cancer. Physics in Medicine and Biology, 49, 4477-4491. http://dx.doi.org/10.1088/0031-9155/49/19/003
- Travis, E.L., Thames Jr., H.D., Tucker, S.L., Watkins, T.L. and Kiss, I. (1986) Protection of Mouse Jejunal Crypt Cells by WR-2721 after Small Doses of Radiation. International Journal of Radiation Oncology Biology Physics, 12, 807- 814. http://dx.doi.org/10.1016/0360-3016(86)90040-4
- Girinsky, T., Lubin, R., Pignon, J.P., Chavaudra, N., Gazeau, J., Dubray, B., Cosset, J.M., Socie, G. and Fertil, B. (1993) Predictive Value of in Vitro Radiosensitivity Parameters in Head and Neck Cancers and Cervical Carcinomas: Preliminary Correlations with Local Control and Overall Survival. International Journal of Radiation Oncology Biology Physics, 25, 3-7. http://dx.doi.org/10.1016/0360-3016(93)90137-K
- Stuschke, M. and Thames, H.D. (1999) Fractionation Sensitivities and Dose-Control Relations of Head and Neck Carcinomas: Analysis of the Randomized Hyperfractionation Trials. Radiotherapy and Oncology, 51, 113-121. http://dx.doi.org/10.1016/S0167-8140(99)00042-0
NOTES

*Corresponding author.








