ABSTRACT

The simulation of oat grain productivity does not contemplate the use of efficient models that involve important management with meteorological elements. The objective of the study is to propose a mathematical model capable of simulating the oat grain productivity through the management of nitrogen and growth regulator with variables related to the plant and to meteorological elements. In this study, two experiments were conducted in the years of 2013, 2014 and 2015: one to quantify biomass productivity and another to determine grain productivity and lodging at the management doses of nitrogen and growth regulator. The experimental design was a randomized block with four replications in a 4 × 3 factorial scheme for 0, 200, 400 and 600 mL∙ha⁻¹ growth regulator doses and 30, 90 and 150 kg∙ha⁻¹ nitrogen doses, respectively. During the crop cycles, the meteorological variables thermal sum, radiation and rainfall were quantified. The mathematical model proposed, which combines polynomial regression of the harvest index with multiple linear regression of the biological productivity, is efficient in the simulation of oat grains productivity with the use of growth regulator, nitrogen and meteorological elements. Thus, it adds to the conventional models of simulation and becomes an aid tool for making decisions regarding the management of oats culture.

Keywords:

Avena sativa, Biomass, Lodging, Trinexapac-Ethyl, Regression

1. Introduction

Oat is a cereal of multiple purposes, mainly due to the great demand for its derivatives in food production [1] [2] . Oat grains productivity is dependent on the genetic potential of the cultivars, management technologies, climate and favorable soil [3] [4] . Among the management technologies, nitrogen plays a decisive role on the productivity of biomass and grains [5] [6] . The new biotypes of oats are highly responsive to the use of nitrogen in the productivity expression [2] [3] [4] . On the other hand, the increase of nitrogen doses, along with favorable meteorological conditions, increases the vegetative development, potentializing lo- dging [5] [6] [7] .

Lodging is the phenomenon in which the plant loses its vertical position, bends and falls to the ground [8] , directly affecting grain productivity and quality, as well as hindering the harvest [1] . An alternative used in cereals such as rice [9] , wheat [10] and oats [6] , is the use of growth regulators, which are chemical compounds that make stem more resistant to breaking and lodging without decreasing grain productivity [11] .

Although there are mathematical models for the estimation of grain productivity in cereals [13] [14] , few are used to simulate the productivity of oats. Also, they do not simultaneously involve plant-related variables, the meteorological condition, and important management practices that affect grain productivity [4] - [15] . Therefore, the elaboration of an efficient simulation model of oat grain productivity through the nitrogen use, growth regulator and variables related to plant and climate can be an important tool in the definition of more efficient forms of management, as well as allowing the development of applications for productivity simulation in mobile devices and for harvest estimation in inspections from warranty programs of agricultural activity. In this context, the objective of the study is to propose a mathematical model capable of simulating oat grain productivity through nitrogen management and growth regulator with variables related to plant and meteorological elements.

2. Material and Methods

The field work was developed in the agricultural years of 2013, 2014 and 2015 in Augusto Pestana (28˚26'30'' South latitude and 54˚00'58'' West longitude), RS, Brazil. The soil of the experimental area is classified as typical dystroferric red latosol, and the climate, according to Köppen classification [12] , type Cfa, with hot summer without dry season. Ten days before sowing, soil analysis was performed and the following chemical characteristics were identified [16] : pH = 6.2, P = 33.9 mg∙dm⁻³, K = 200 mg∙dm⁻³, Organic Matter = 3.0%, Al = 0.0 cmolc∙dm⁻³, Ca = 6.5 cmolc∙dm⁻³and Mg = 2.5 cmolc∙dm⁻³. Sowing was performed with seeder/fertilizer machine in soybean/oat system with the plot composed of 5 lines of 5 m in length and spacing of 0.20 m between lines, forming the experimental unit of 5 m². At sowing, 30 and 20 kg∙ha⁻¹ of P₂O₅ and K₂O were applied, respectively, based on soil P and K contents for expected grain productivity of 3 T∙ha⁻¹ and N at the base with 10 kg∙ha⁻¹, with the remainder aiming at contemplating the doses proposed in the study, applied in the stage of fourth leaf expanded with nitrogen available in the form of urea. The seeds were submitted to germination and vigor tests in laboratory in order to correct the density of 400 viable seeds m⁻² of the Barbarasul cultivar. During the execution of the study, two applications of the fungicide tebuconazole (commercial name FOLICUR^®CE) at the dosage of 750 mL∙ha⁻¹ were made. In addition, weed control was carried out with metsulfuron-methyl herbicide (commercial name ALLY^®) at the dosage of 4 g∙ha⁻¹ and additional weeds whenever necessary.

Two experiments were conducted in each cultivation year. One to quantify the rate of biomass production by the cuts made every 30 days until the harvest point and another to the harvest aiming at the estimation of grain productivity and lodging. In the two experiments, the experimental design was a randomized block with four replications in a 4 × 3 factorial scheme, in the sources of variation of growth regulator doses (0, 200, 400 and 600 mL∙ha⁻¹) and N-fertilizer doses (30, 90 and 150 kg∙ha⁻¹), respectively, totaling 96 experimental units. The growth regulator (Trinexapac-Ethyl) was sprayed at constant pressure of 30 lb∙pol⁻² by compressed CO₂ with flat fan tips at the stage of 1st and 2nd visible node of the stem.

The harvest of the experiments to estimate the grain productivity occurred manually by cutting the three central lines of each plot. The time of grain harvest was also defined as the last cut of the experiment directed to the analysis of biomass productivity (120 days), near the harvest point, with grain moisture around 15% [17] . The plots were harvested with a stationary harvester and the harvested material was taken to the laboratory for the correction of grain moisture to 13% and obtention of grain productivity. Lodging was visually estimated before the harvest and expressed as a percentage, considering the angle formed in the vertical position of the stem of the plants in relation to the soil and to the area of lodged plants. For this estimation was used the methodology suggested by [18] , modified, with lodging (LODG) defined from the following equation:

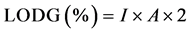
where: I is the degree of inclination of the plants, ranging from 0 to 5, 0 (zero) indicating the absence of inclination and 5 indicating that all the plants are completely lodged; “A” is the area with lodged plants in the plot, which varies from 0 to 10, 0 (zero) corresponding to the absence of lodged plants and 10 to the plants lodged in the whole plot, regardless of their inclination. Thus, this equation weighs the incidence and severity of the plants lodging. In the experiments aiming at quantifying biomass productivity by cuts along the development of the plants, the harvest of plant material was performed close to the soil, from the collection of a linear meter of the three central lines of each plot, in the period of 30, 60, 90 and 120 days after the emergence, totaling four cuts. The samples with the green mass were weighed on a precision scale and directed to a forced air heater at 65˚C until reaching constant weight, for estimation of the total dry mass converted into kg∙ha⁻¹. The values of the general averages along with the information on temperature and rainfall were used to classify the years as unfavorable, intermediate and favorable to cultivation. The meteorological data of thermal sum, radiation and pluviometric precipitation were obtained through a meteorological station located at approximately 500 m of the experiments. It should be noted that the thermal sum (Ts) was obtained from the emergence of plants by the following model:

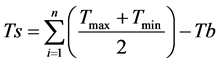(1)

where T_max = maximum temperature (˚C); T_min = minimum temperature (˚C); n = number of days of the period of emergence-harvest; Bt = base temperature. The oat base temperature was that presented by [19] , considering the value of 4˚C.

Catering to the assumptions of homogeneity and normality through Bartlett tests, variance analysis was performed to detect the main and interaction effects. An adjustment of linear regression equation was performed for the estimation of the ideal growth regulator dose for lodging of oat plants by the increase of growth regulator doses. As it is an equation that describes the linear behavior of lodging, it was considered the possibility of plant lodging at a maximum of 5%, value added to the parameter “y” of the equation, obtained by:

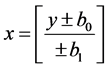(2)

According [20] , the value of up to 10% of lodging of oat plants does not cause significant losses on grain productivity. After that, was performed the adjustment of second degree regression equation to estimate oat harvest index (HI) as a function of growth regulator doses in conditions reduced (30 kg∙ha⁻¹), high (90 kg∙ha⁻¹) and very high (150 kg∙ha⁻¹) of fertilization with nitrogen.

(3)

where a, b and c are coefficients obtained by polynomial regression 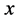and and 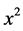are the growth regulator doses.

For the composition of the multiple linear regression model in the estimation of oat biomass productivity, involving meteorological variables (radiation, thermal sum and rainfall), growth regulator doses and nitrogen, the choice of the potential variables was made via Stepwise technique. This procedure iteratively constructs a sequence of regression models by adding and removing variables, selecting those that have the largest relation with the main variable (y), using the partial F statistic, according to the model:

(4)

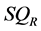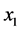where is the quadratic sum of the regression and is the quadratic average of the error for the model containing the variables and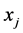. The variables selected through Step Wise were used to determine the multiple linear regression equation for the simulation of oat biomass productivity (BP), provided by an equation of the type:

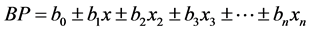(5)

where 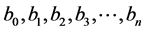are coefficients obtained by multiple linear regression and 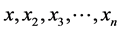are variables classified as significant by the Step Wise model. The equation in matrix form is described as:

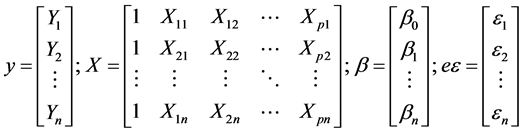(6)

From these matrices, the value of the regression coefficients is obtained, with

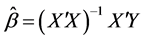(7)

and the variance of these coefficients is obtained by the covariance matrix of the regression coefficients vector:

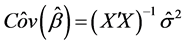(8)

(9)

where is the number of equations and is the number of parameters. The hypothesis test has verified vs, expressed by:

(10)

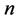
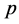
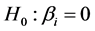
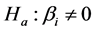
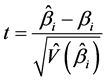
However, since oat grain productivity is the product between biomass productivity and harvest index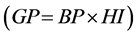, Equation (11) represents the proposed model for simulation of grain productivity of oats, given by the multiplication between Equation (5) and Equation (3), expressed by:

(11)

All data processing method have been performed using the statistical software Genes.

3. Results and Discussion

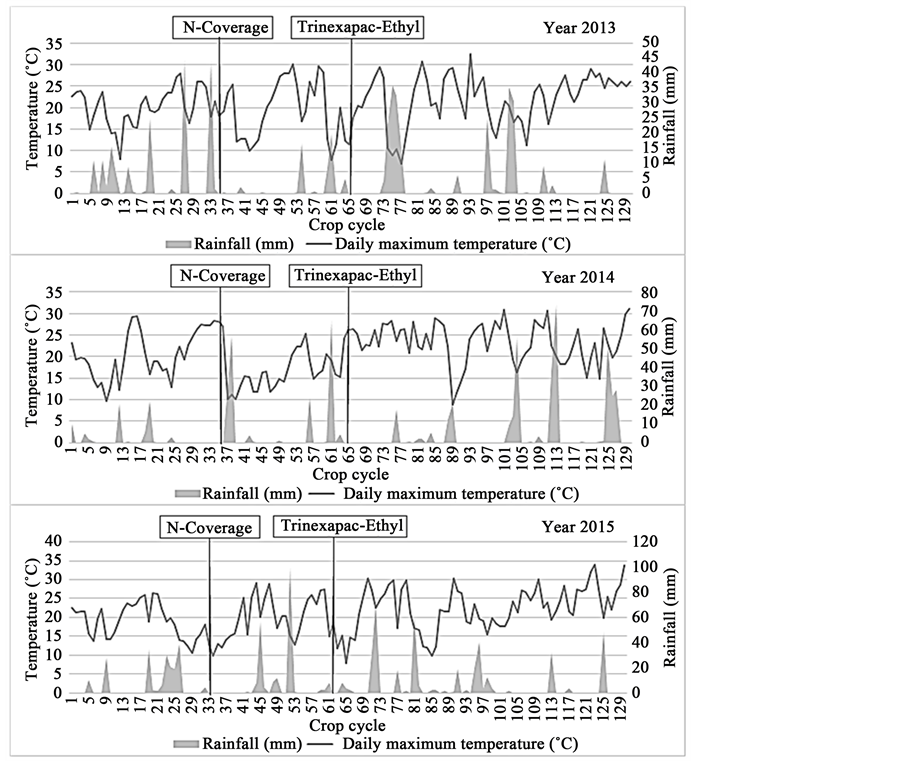
In Figure 1, it is observed that at the time of nitrogen application in 2014, the maximum temperature averages were higher (±27˚C) in relation to 2015 and

2013. In addition, fertilizer application was followed by rainfall volume greater than 50 mm, volume also observed near grain harvest.

These facts justify the lower productivity obtained in this year (Table 1), either due to loss of nutrients by leaching and losses due to excessive rainfall during maturation, characterizing an unfavorable year (UY) of cultivation. In 2015, the maximum temperature near to nitrogen application was the lowest (±12˚C) in relation to other years.

At the moment of nitrogen application, the soil presented adequate humidity conditions due to accumulation of rainfall on the previous days (Figure 1). The high volume of rain during the cycle provided periods of less insolation, what reduces the efficiency of photosynthesis by the plant. Therefore, the average grain productivity of Table 1 justifies a reasonable productivity, characterizing an intermediate year (IY) of cultivation. In 2013, the maximum temperature ob- tained at the time of nitrogen application was around 20˚C and in favorable conditions of soil moisture (Figure 1). In this condition, according to Table 1, although the total rainfall volume was the lowest, the adequate distribution of

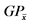
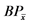
* = Historical rainfall average obtained in the months of May to October of 1990 to 2015; Averages followed by same letter in the column do not differ from each other in the probability of 5% error by the Scott-Knott test; FY = favorable year; UY = unfavorable year; IY = intermediate year; Temperature (˚C); Precipitation (mm); = grain productivity (kg∙ha⁻¹); = biomass productivity (kg∙ha⁻¹).

rainfall over the cycle (Figure 1) was decisive to the higher grain productivity, higher than 4 T∙ha⁻¹, characterizing the year as favorable to cultivation (FY).

Of all the segments of the economy, agriculture is the one that shows greater dependence on meteorological variables, generating production oscillations over the years [21] . Rainfall has been the main meteorological variable that affects agricultural productivity, although temperature, light and solar radiation are also important [22] . The temperature acts as a catalyst for biological processes, which is why plants require a minimum and maximum temperature for normal physiological activities [23] . According [24] , the maximum temperature for the development of the oat crop is 35˚C, and the minimum temperature is 0˚C. In oats, the favorable climate is described as one with milder temperatures and radiation quality in favor of tillering and grain filling, without occurrence of rains in great quantity and intensity, however, favoring the adequate supply of moisture stored in the soil [4] - [19] . Reference [25] points out that the condition of favorable and unfavorable year in the wheat crop is defined mainly by the distribution of rainfall during the crop cycle. Therefore, stress caused by lack or excess of water in the soil adversely affects the development of wheat and oats [5] - [26] .

The productivity simulation, when dependent on the condition of the agricultural year, does not contemplate efficient forecasting models, considering the strong variation in each year of cultivation (Table 1 and Figure 1). Therefore, in the elaboration of the presented models were considered the cumulative effects of variability among the years. In the estimation of the ideal growth regulator dose by lodging expression (Table 2), the regression equations tested showed a

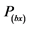
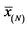
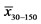
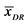
* = Significant at 5% probability of error, respectively, by the probability of F; = parameter that measures the slope of the line; LODG= lodging; R² = coefficient of determination; ( ) = consideration of the possibility of plant lodging at 5%; = average obtained in the three years of study; = general average of; y_E = estimated value; Ideal dose = dose of regulator that allows plant lodging in less than 5%.

linear trend, regardless of the year and nitrogen dose. For this estimation, was taken into account the possibility of plant lodging at a maximum of 5%, value added to the parameter “y” of each equation. Regardless of the condition of the year of cultivation, the optimal doses of use of oat growth regulator are 460, 500 and 520 mL∙ha⁻¹ for the reduced, high and very high condition of nitrogen fertilization, respectively. Overall, regardless of nitrogen condition, the ideal growth regulator dose was adjusted to 495 mL∙ha⁻¹.

In wheat [27] [28] and rice [9] - [29] was observed a reduction of plant lodging with the 400 mL∙ha⁻¹ dose of regulator. In crotalaria [30] and soybean [31] , efficient reduction of lodging was obtained with the application of 500 mL∙ha⁻¹. Reference [11] and [32] , studying the effects of growth regulator on grain productivity and oat seed quality, state that the dose of 500 mL∙ha⁻¹ reduces plant stature in up to 60% and efficiently reduces lodging.

In the analysis of the harvest index (Table 3), regardless of the year of cultivation and the nitrogen dose, the second degree equations showed to be appropriate as a function of the doses of growth regulator. In these equations, the inclusion of the optimal dose of the regulator presented in Table 2 indicated a lower harvest index in the year of 2013 (FA).

An expected event, since grain productivity evidenced quadratic behavior, and biomass productivity, steady growth. Therefore, the linear favoring of the straw

P(b_x) = parameter that measures the slope of the line by the probability of T at 5% error; R² = coefficient of determination; * = Significant at 5% probability of error, respectively, by the F test; 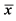= general average; y_E = estimated value.

biomass expression with the stability in the grain elaboration promoted reduction in the harvest index. In oats, the lowest harvest index is not always reflected in lower grain productivities, since it is natural for the favorable cultivation condition to promote greater straw production than grains. Reference [33] studying the genetic variability of the physiological parameters of production in oats, observed harvest index between 0.33 and 0.45. The results found by these authors are in agreement with those obtained in this study, which, in general, regardless of the condition of the agricultural year, showed a harvest index of 0.43, 0.37 and 0.42 for the reduced, high and very high condition of nitrogen fertilization, respectively. In addition, in the estimation of the oat harvest index, considering the cumulative effect of variability between the years, the use of the adjusted dose of growth regulator at 495 mL∙ha⁻¹ reported a harvest index of 0.40.

The harvest index is an important indicator of productivity, dimensioning how much of the total biomass produced was directed to the elaboration of biomass straw and biomass grains [20] . Seed density [20] , nitrogen fertilization [5] and growth regulator [6] are the main management factors that affect the expression of the harvest index of oats. Reference [2] point out that the reduction in the oat harvest index in favorable year to cultivation is due to the greater favoring of the expression of the vegetative growth, although the grain productivity also increased, therefore, justifying that the increase in grain productivity does not express a behavior similar to that of the biological productivity, reducing the harvest index due to the higher volume of biomass straw. In wheat [28] and oats [6] , the growth regulator increased the expression of the harvest index by the reduction of the straw biomass and the shortening of the stem.

In Table 4, the sum of the meteorological values obtained at each biomass cut-off point is shown along with the productivity averages. At 30 and 60 days after emergence, there were no differences in biomass productivity with the increase of the growth regulator doses in each nitrogen use condition (Table 4).

This fact was expected, since the application of the regulator happened around 65 days after emergence, with the appearance of the first and second visible node of the main stem, according to recommendation. The response to the use of regulator on biomass expression was shown to be effective at 90 days after emergence. At this moment, there was a significant reduction of the biomass productivity at 400 and 600 mL∙ha⁻¹, not differing from each other, regardless of the nitrogen fertilization condition. In the conditions of 30 and 90 kg∙ha⁻¹ of nitrogen, the biomass cut with 120 days after emergence, indicated the greatest reduction of biomass productivity with the use of a 600 mL∙ha⁻¹ dose of the regulator product. At the highest N-fertilizer condition, biomass productivities were strongly reduced with the doses of 400 and 600 mL∙ha⁻¹. In Table 5 presents the variables to be tested by the Step Wise technique for the composition of the multiple linear regression model.

Therefore, the variables radiation, thermal sum and rainfall presented significance in all conditions of use growth regulator and nitrogen. The possibility of simulation of biomass productivity with the use of a growth regulator dose in the

DAE = days after emergence; R Dose = doses of applied growth regulator; N Dose = doses of nitrogen applied in coverage; Averages followed by the same letter in the column do not differ statistically from each other in a 5% probability of error according to the Scott-Knott test.

* = Significant at 5% probability of error, respectively, by the probability of F; Thermal sum (day degrees); Rainfall (mm∙m⁻²); Radiation (V∙m⁻¹); Regulator Dose = ideal dose of regulator for lodging estimate of less than 5% (mL∙ha⁻¹); N = Nitrogen (kg∙ha⁻¹).

range from 0 to 600 mL∙ha⁻¹ was also significant, regardless of the nitrogen dose. However, in the elaboration of a more complete model, involving the use of growth regulator, meteorological variables and the use of the nitrogen dose, the significance of all these elements were confirmed to compose the multiple linear regression model in the biomass productivity simulation.

The Step Wise method for choosing variables to compose the multiple linear regression model is considered as one of the corrective actions for multicollinearity problems [34] . It allows the selection of potential variables for multiple linear regression simulation [2] - [35] . Therefore, a decisive technique in the elaboration of reliable models for the simulation [36] . Reference [37] using the Step Wise technique, identified that in wheat, the variables temperature, radiation and rainfall were the most important elements for simulation of productivity by multiple linear regression. The potential variables for simulation obtained by these authors is in agreement with the results found in this study.

Table 6 shows the multiple linear regression equations for simulation of oat biomass productivity. In this simulation, were used the values observed at 120 days of the plant cycle, along with the meteorological values (Table 4) and adjusted dose of the growth regulator for lodging (Table 2), under the different N-fertilizer conditions. At the dose of 30 kg∙ha⁻¹ of nitrogen, the increase of the growth regulator dose resulted in a decrease of biomass productivity. It is noteworthy that this same behavior was observed with the simulation, a tendency that occurred in the other doses of N-fertilizer use. The equations tested proved to be efficient in the simulation of biological productivity with values similar to those observed.

In the simulation of biological productivity with the inclusion of the growth regulator dose in the multiple model (Table 6), in the interval from 0 to 600 mL∙ha⁻¹ (PB_0-600), the use of the optimum dose of the regulator in each condition

BP = biological productivity (kg∙ha⁻¹); T = thermal sum (day degrees); r = rainfall (mm∙m²); R = radiation (V∙m⁻¹); O = observed; E = estimated; LL = lower limit; UL = upper limit; N = nitrogen (70 kg∙ha⁻¹); RD = ideal dose of regulator (mL∙ha⁻¹); CI = confidence interval.

of N-fertilization (Table 2) indicated that the simulated values were very close to those observed and in the confidence interval of the average. In the analysis of the general model, the simulation of the biomass productivity in the inclusion of the optimum dose of the regulator (495 mL∙ha⁻¹) and the proposed nitrogen dose of 70 kg∙ha⁻¹ showed simulated productivity of 9345 kg∙ha⁻¹, near to that of 9640 kg∙ha⁻¹ observed and in the established confidence interval. Therefore, the use of the general model of biological productivity is efficient in the simulation of the biomass productivity involving the main managements in oats through the use of growth regulator and nitrogen with meteorological variables.

The simulation by multiple linear regression is a tool that allows efficient estimation of productivity [38] . Reference [2] using multiple linear regression, were successful in the simulation of oat productivity via panicle components. Reference [39] accurately simulated the productivity of wheat in dry conditions using the multiple linear regression model. Also using multiple linear regression, reference [40] estimated the productivity of rice grains according to the soil attributes efficiently.

Considering that grain productivity is the product between biological productivity (determined by multiple linear regression) and the harvest index (determined by polynomial regression of second degree), Table 7 presents the results that validate the proposed model to simulate grain productivity.

GP = grain productivity (kg∙ha⁻¹); T = thermal sum (day degrees); r = rainfall (mm∙m²); R = radiation (V∙m⁻¹); N = nitrogen (70 kg∙ha⁻¹); RD = ideal dose of regulator (mL∙ha⁻¹); GPO = grain productivity observed in the field; GPE = grain productivity estimated by the model.

For these simulations, were used the values of the meteorological elements presented in Table 4 and the adjusted growth regulator dose for lodging, according to Table 2. Therefore, in the reduced (30 kg∙ha⁻¹), high (90 kg∙ha⁻¹) and very high (150 kg∙ha⁻¹) doses of nitrogen, the equations present estimated values of grain productivity very close to those observed in the field, condition also observed in the simulation with the equations that use the adjusted doses of growth regulator in each condition of nitrogen use. All the results presented so far provide reliability support for the creation of the general model that guides the main objective of this study, according to Equation (11). However, in the grain productivity simulation involving simultaneously the management of growth regulator and nitrogen with meteorological elements, the results of the simulation were highly predictable, with an estimated productivity of 3760 kg∙ha⁻¹ and observed at 3685 kg∙ha⁻¹, confirming the quality of the model proposed for estimating oat grain productivity.

The use of mathematical models to estimate agricultural productivity is an important tool for crop forecasting systems [14] . Besides, combined simulation models allow us to analyze different scenarios, considering several factors that influence the productivity of each crop [41] . Thus, the integration of two or more models aims to obtain a more efficient model for the prediction of agricultural crops [42] . Reference [43] combined the expolinear-logistic model and the Gompertz model to estimate the variation of shoot dry matter accumulation in sugarcane cultivars. Reference [42] combined models of Fuzzy Logic and Neural Networks to estimate wheat productivity as a function of nitrogen fertilization. Reference [41] using the combination of mathematical models were able to predict satisfactorily the grain productivity of the soybean crop, evidencing the best irrigation strategies that result in high grain productivity. Reference [44] combined simple linear regression with the InfoCrop model to simulate grain productivity of the irrigated rice crop, obtaining satisfactory performance in the simulations.

Acknowledgements

To CAPES, CNPq, FAPERGS and UNIJUÍ for the resources to the development of the research and for the scientific, technological initiation and productivity scholarships.

Cite this paper

Marolli, A., da Silva, J.A.G., Scremin, O.B., Mantai, R.D., Trautmann, A.P.B., de Mamann, Â.T.W., Car- bonera, R., Kraisig, A.R., Krüger, C.A.M.B. and Arenhardt, E.G. (2017) A Proposal of Oat Productivity Simulation by Meteorological Elements, Growth Regulator and Ni- trogen. American Journal of Plant Scien- ces, 8, 2101-2118. https://doi.org/10.4236/ajps.2017.89141

References