American Journal of Climate Change
Vol.06 No.02(2017), Article ID:77021,14 pages
10.4236/ajcc.2017.62018
Integration of Spatial Prediction in the Assessment of Vegetation Productivity in the Northern Part of Nigeria
Sadiq Abdullahi Yelwa1*, Umar Usman2
1Department of Geography, Usmanu Danfodiyo University, Sokoto, Nigeria
2Department of Mathematics, Usmanu Danfodiyo University, Sokoto, Nigeria

Copyright © 2017 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: January 12, 2017; Accepted: June 17, 2017; Published: June 20, 2017
ABSTRACT
Climate change is one of the greatest threats facing the global community and has been mainly induced by increasing atmospheric concentrations of greenhouse gases resulting from fossil fuel energy use and change in vegetation cover. This study used modelling techniques to determine how changes in climate could affect vegetation productivity in the northern part of Nigeria. Climatic parameters (Rainfall, Minimum and Maximum Temperatures) as well as coarse Normalised Difference Vegetation Index (NDVI) data for the growing seasons of 1981-2009 were utilised. Because of the relationship between climatic parameters and vegetation, Spatial method of data interpolation was tested. Results from the prediction elevation values ranged from −3e−9 to 2e−9. It was observed from prediction variance map that the values were higher in the upper portion of the study area which comprised Gusau (GS), Jos (JS), Katsina (KT), Minna (MN) and Zaria (ZR) and lower in the middle and lower parts of the study area which comprised mainly Funtua, Kano, Maiduguri and Sokoto. Further studies are encouraged with high resolution imageries and more meteorological data to cover the montane and forest zone of the country to determine the level of climatic impacts particularly on vegetation productivity in general.
Keywords:
Climate Change, Regression-Kriging (RK) and Normalized Difference Vegetation Index (NDVI), Linear Model, Digital Elevation Model (DEM)

1. Introduction
Climate change is one of the greatest threats facing the global community in the current century, and has been mainly induced by increasing atmospheric concentrations of greenhouse gases resulting from fossil fuel energy use and continuous increase in the decline of vegetation cover. Although the changes being witnessed in the general land cover globally may be attributed to the changing climate with both their negative and positive effects, these are often not given attention to. For example, the increasing global temperatures are translating into either increased or decreased vegetation productivity depending on environment conditions. Furthermore, because of the sensitivity of global and regional climatic models, there is more increasing attention in research in these areas. Geostatistics for example, is based on the theory of regionalized variables [1] [2] and [3] , which allows one to capitalize on the spatial correlation between neigh- bouring observations to predict attribute values at unsampled locations. For example, [4] has shown that the geostatistical prediction technique (kriging) provides better estimates of rainfall than conventional methods. [5] found that the results depend on the sampling density and that, for high-resolution networks (e.g. 13 rain gauges over a 35 km2), the kriging method does not show significantly greater predictive skill than simpler techniques, such as the inverse square distance method. Similar results were found by [6] when they compared kriging and multiquadratic surface fitting for various gauge densities. In fact, besides providing a measure of prediction error (kriging variance), a major advantage of kriging over simpler methods is that the sparsely sampled observations of the primary attribute could be complemented by secondary attributes that were more densely sampled. For rainfall, secondary information was taken in the form of weather-radar observations. A multivariate extension of kriging, known as cokriging, has been used for merging rain gauge and radar-rainfall data e.g. [7] and [8] .
Geostatistical interpolators can also be used to make spatial predictions of continuous variables using field samples. Predicted values for unsampled locations are determined by a combination of the surrounding samples weighted by their distance to the unknown location [9] . Kriging, originally developed by [10] for mineral exploration, is one of the most widely used geostatistical interpolators because of its fidelity to the sample data. Thus, kriging uses a model of the spatial dependence between samples (i.e., how autocorrelation changes as a function of distance between samples) as well as the distance to neighbouring sample points to create estimates at unknown locations [11] . The number and distribution of sample points affect the scale of predictions that can be made via statistical interpolators. This is especially true for kriging, as sample points of varying distances apart are needed to estimate spatial autocorrelation. Given the cost and time required to collect field samples, it is often difficult to obtain enough samples to make spatial predictions at a scale that is useful to rangeland managers using statistical interpolators alone [11] .
2. Conceptual Framework
In recent years, there has been an increasing interest in hybrid interpolation techniques which combine two conceptually different approaches to modelling and mapping spatial variability [12] : 1) interpolation relying solely on point observations of the target variable; and 2) interpolation based on regression of the target variable on spatially exhaustive auxiliary information. Several studies have shown that hybrid techniques can give better predictions than either single approach [11] [13] [14] [15] [16] [17] . These interpolators are currently used in a variety of applications, ranging from modelling spatial variability in tropical rainforest soils [17] [18] mapping of leaf area index (LAI) using Landsat ETM+ data [19] , modelling spatial distribution of human diseases [20] , mapping water table [21] [22] , mapping abundance of fish in the ocean [23] , mapping rainfall over Great Britain [16] , and mapping rainfall erosivity in the Algarve region of Portugal [3] . One of these hybrid interpolation techniques is known as regression-kriging (RK) [24] [25] . It first uses regression on auxiliary information and then uses simple kriging (SK) with known mean (0) to interpolate the residuals from the regression model. This allows the use of arbitrarily-complex regression methods, including generalized linear models. In spite of this and other attractive properties of RK, it is not as widely used in geosciences as might be expected.
Universal kriging (UK) model that was said to have been introduced by [26] and by many statisticians considered to be the (only) best linear unbiased prediction model of spatial data [27] , Section 6. Originally, UK was intended as a generalized case of kriging where the trend is modelled as a function of coordinates, within the kriging system. Thus, some authors e.g. [28] [29] [30] reserve the term Universal Kriging for this case. If the drift is defined externally as a linear function of some auxiliary variables, rather than the coordinates, the term Kriging with External Drift (KED) is preferred [29] [31] . In the case of UK or KED, the predictions are made as with kriging, with the difference that the covariance matrix of residuals is extended with the auxiliary predictors [32] . However, the drift and residuals can also be estimated separately and then summed. This procedure was suggested [33] as well as [24] but later named regression- kriging, while [2] used the term Kriging with a trend model to refer to a family of interpolators and refers to RK as simple kriging with varying local means. KED and RK differ in the computational steps used; however, the resulting predictions and prediction variances are the same, given the same point set, auxiliary variables, regression functional form, and regression fitting method.
Although the KED seems, at first glance, to be computationally more straight- forward than RK, the variogram parameters for KED must also be estimated from regression residuals, thus requiring a separate regression modelling step. This regression should be GLS because of the likely spatial correlation between residuals, although many analysts used it instead of the OLS residuals, which may not be too different from the GLS residuals [17] . However, they are not optimal if there is any spatial correlation, and indeed may be quite different in the case of highly correlated clustered sample points. Also a limitation of KED is the instability of the extended matrix in the case that the covariate does not vary smoothly in space [2] . RK has the advantage that it explicitly separates trend estimation from residual interpolation, allowing the use of arbitrarily complex forms of regression, rather than the simple linear techniques that can be used with KED. In addition, it allows the separate interpretation of the two interpolated components. For these reasons we advocate the use of the term regression-kriging over universal kriging. Hence, RK is a more descriptive synonym of the same generic interpolation method [12] .
The variable used in the Regression and Kriging analysis should be normally distributed for better kriging estimates. In many studies, however, the variables show skewed non-normal distribution, which then reflect on residuals [32] . Skewed data can be made more appropriate for geospatial prediction modelling by the means of data transformation which generally improves the Kriging estimates [34] .
[35] used another geostatistical technique with an external drift, to combine both types of information. In that study, another valuable and cheaper source of secondary information was considered i.e., a digital elevation model (DEM). Precipitation tends to increase with increasing elevation, mainly because of the orographic effect of mountainous terrain, which causes the air to be lifted vertically, and the condensation occurred due to adiabatic cooling. For example, [36] reported a significant 0.75 correlation between average annual precipitation and elevation recorded at 62 stations in Nevada and south-eastern California. In that experiment a multivariate version of kriging, called cokriging to incorporate elevation into the mapping of rainfall was utilised. However, according to [37] a more straightforward approach exists which consist of estimating rainfall at a DEM grid cell through a regression of rainfall versus elevation. In another study using simple modelling approach, [38] analysed the mean and inter-seasonal variation during growing season across the Kano region using only rainfall and NDVI datasets. However, they neither utilised DEM data nor a complex regression technique in their assessment.
As for [39] who examined different models namely, thiessen polygons, inverse distance, second order polynomial, ordinary kriging and universal kriging for distribution of monthly rainfall in southern Florida, ordinary kriging method was found to have the lowest error (1.32), though in comparison, [40] showed that the method of thin plate smoothing splines was the most accurate method for interpolation particularly if soil salinity is incorporated. However, when [41] compared the performance of three interpolation methods (nearest neighbour, ordinary kriging, and cokriging) for soil moisture retention, ordinary kriging and cokriging were found to be very promising techniques.
3. The Study Area
The study area is centered on the northern part of Nigeria where data obtained from 12 climatological stations were utilised. This area falls within Latitude 8˚N to 14˚N and Longitude 2.5˚E to 14˚E (Figure 1). The area can be described as a mixture of wet and dry type. Rainfall varies from the extreme northern part, central and southern part of the study area. Depending on the location within
Figure 1. Map of the study area showing the climatological stations.
the study area, annual rainfall is as low as to 800 mm to a maximum of 5000 mm during the wet year while vegetation is mixed savannah and montane types.
The objectives of this research are to examine Regression-Kriging (RK) using some climatic variables that are likely to affect the changing climate in the study area during growing season.
4. Data and Methods
Data from the nearest 12 meteorological stations administrated by the Nigerian Meteorological Agency (Nimet) was sourced and utilised for this study. The dataset covering the growing seasons (June to September 1981-2009) for the study area in the form of monthly rainfall, minimum and maximum temperatures were used variables for the analysis in addition Normalised Difference Vegetation Index (NDVI) dataset of the same time series and digital elevation data (DEM). The meteorological stations are regularly distributed over the study area and represent all land cover types found there as described by [38] .
4.1. Regression-Kriging
In the geostatistical approach, predictions are commonly made by calculating some weighted average of the observations based on [32] :
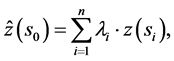 (1)
(1)
where 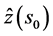 is the predicted value of the target variable at an unvisited location s0 given its map coordinates, the sample data
is the predicted value of the target variable at an unvisited location s0 given its map coordinates, the sample data 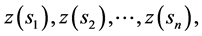 and their coordinates. The weights
and their coordinates. The weights  are chosen such that the prediction error variance is minimized, yielding weights that depend on the spatial autocorrelation structure of the variable. This interpolation procedure is popularly known as ordinary kriging (OK). An alternative to kriging is the regression approach, which makes predictions by modelling the relationship between the target and auxiliary environmental variables at sample locations, and applying it to unvisited locations using the known value of the auxiliary variables at those locations. Common auxiliary environmental predictors are land surface parameters, remote sensing images, and geological, soil, and land-use maps [42] . A common regression approach is linear multiple regressions [43] [44] , where the prediction is again a weighted average, this time of the predictors:
are chosen such that the prediction error variance is minimized, yielding weights that depend on the spatial autocorrelation structure of the variable. This interpolation procedure is popularly known as ordinary kriging (OK). An alternative to kriging is the regression approach, which makes predictions by modelling the relationship between the target and auxiliary environmental variables at sample locations, and applying it to unvisited locations using the known value of the auxiliary variables at those locations. Common auxiliary environmental predictors are land surface parameters, remote sensing images, and geological, soil, and land-use maps [42] . A common regression approach is linear multiple regressions [43] [44] , where the prediction is again a weighted average, this time of the predictors:
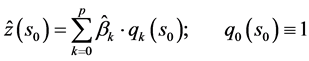 (2)
(2)
where 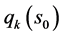 the values of the auxiliary variables at the target location are,
the values of the auxiliary variables at the target location are, 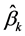 are the estimated regression coefficients and p is the number of predictors or auxiliary variables. (To avoid confusion with geographical coordinates, we use the symbol q, instead of the more common x, to denote a predictor.) RK combines these two approaches: regression is used to fit the explanatory variation and SK with expected value 0 is used to fit the residuals, i.e. unexplained variation [25] :
are the estimated regression coefficients and p is the number of predictors or auxiliary variables. (To avoid confusion with geographical coordinates, we use the symbol q, instead of the more common x, to denote a predictor.) RK combines these two approaches: regression is used to fit the explanatory variation and SK with expected value 0 is used to fit the residuals, i.e. unexplained variation [25] :
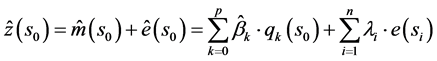 (3)
(3)
where  is the fitted drift,
is the fitted drift, 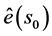 is the interpolated residual,
is the interpolated residual, 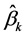 are estimated drift model coefficients (
are estimated drift model coefficients (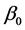 is the estimated intercept),
is the estimated intercept), 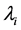 are kriging weights determined by the spatial dependence structure of the residual and where e(si) is the residual at location si. The regression coefficients
are kriging weights determined by the spatial dependence structure of the residual and where e(si) is the residual at location si. The regression coefficients 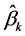 are estimated from the sample by some fitting method, e.g. ordinary least squares (OLS) or, optimally, using generalized least squares (GLS), to take the spatial correlation between individual observations into account [45] :
are estimated from the sample by some fitting method, e.g. ordinary least squares (OLS) or, optimally, using generalized least squares (GLS), to take the spatial correlation between individual observations into account [45] :
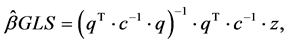 (4)
(4)
where 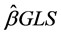 is the vector of estimated regression coefficients, C is the covariance matrix of the residuals, q is a matrix of predictors at the sampling locations, and z is the vector of measured values of the target variable. Once the trend has been estimated the residual can be interpolated with kriging and added to the estimated trend. In matrix notation, this is written as [27] :
is the vector of estimated regression coefficients, C is the covariance matrix of the residuals, q is a matrix of predictors at the sampling locations, and z is the vector of measured values of the target variable. Once the trend has been estimated the residual can be interpolated with kriging and added to the estimated trend. In matrix notation, this is written as [27] :
 , (5)
, (5)
where 




where 

Initially an iterative process was used to estimate the residuals using OLS, followed by utilising the covariance function of the residuals to obtain the GLS coefficients. These were used later to re-compute the residuals, from which an updated covariance function was computed, and so on. Although this has been recommended by many geostatisticians as the proper procedure, [46] showed that use of the covariance function derived from the OLS residuals (i.e. a single iteration) is often satisfactory.
4.2. Variogram Modelling of Residuals
In this study, residuals were estimated from the difference between predicted and observed values, which are generally assumed to be normally distributed. Fitting of the variogram was achieved with the aid of R software package. The residuals were analyzed for spatial autocorrelation structure using variogram modeling. First the semi variance was determined to be the difference between the two points in a point pair, while the variogram cloud was formed and later grouped in to lags based on some separation range and finally a residual variogram was derived.
5. Results and Discussion
Figure 2 indicated that residuals estimated from the difference between predicted and observed values, and is assumed to be normally distributed. The regression residuals are obtained from the multiple regression analysis of predictor and target variables. These regression residuals are modelled as residual variogram and the trend line added to get the final overall prediction results. The result shows that with increase distance the semi variance value increases and reached maximum and flattens.
5.1. Spatial Prediction
After fitting the parameters of regression model or deterministic part of variation (significant predictor variables and their coefficients) and the residual variogram or stochastic, spatially-auto correlated part of variation (sill, nugget and range) using the “R” programming codes the model was run. The resulting output values were back transformed to obtain spatially predicted values.
From Figure 3, the Ordinary Kriging predicted elevation values ranges from
Figure 2. Regression residuals from modelled variogram.
Figure 3. Spatial prediction from sampled locations.
265.3 to 635 and Regression-Kriging predicted elevation values ranges from 8.345e+69 to 2.97e+274. The regression-kriging map shows a much more local detail. Hence, to determine which method is more accurate the leave-one-out cross validation method was utilised as implemented in the krige.cv method of gstat package [47] . Amount of variation explained by this model is therefore 84% which shows that it has good fit.
5.2. Long Term Changes in Vegetation Productivity
In assessing the long term changes in vegetation productivity for the period 1981-2009 the annual NDVI integrals were computed for the entire growing season and a trend of the predicted changes were determined as described by [48] . Although trend analysis was conducted by [49] on vegetation across Sokoto state during the growing season within the current study area under examination, their study was only limited to one meteorological data station. In the current study the output was a slope and intercept images (presented as long term changes in predicted vegetation productivity using AVHRR and MODIS time series dataset as slope of changes presented as R-images) (Figure 4) instead of ordinary trend image presented in their study. The slope image captures long-term trend covering the study area. From a statistical point of view the trend itself represent an actual situation because the entire data population is known. This cannot be compared with linear regression techniques used to show correlation between samples of observations. For the same reason, the regression correlation coefficient for the trend line here gives information about the variation in the data set, whether or not the trend is likely to represent a real world situation.
From the results of the model (predicted vegetation changes), the relationships between the time-series AVHRR and MODIS datasets were examined. As can be seen from these R-images, green indicates positive trend while the yellow-brown and red are indicative of negative trend. The analysis of variance (ANOVA) of the LM results shows that the identified trends are significant in large parts of southern part of the study area covering the northern part of Nigeria. It is very clear that trends are weak mostly in the southern part of the study area. Furthermore, spatial patterns of the coefficient of variations of R2 appear to correspond exactly with patterns of vegetation cover although the R2 decreases from shrubs and desert vegetation in the northern part of the study area, to guinea vegetation in the south (for the AVHRR dataset and a mixture of this for the MODIS dataset). These results indicate a major degree of temporal variation in the relationship between NDVI and rainfall in the study area which suggests likely impacts of both anthropogenic and the changing climate.
The strength of relationship between NDVI and rainfall, along with the use of regression statistics, provides useful information for assessment of land cover performance. In the dry regions particularly in the northern part of Nigeria with
Figure 4. Predicted long term vegetation changes from AVHRR and MODIS datasets. (a) AVHRR-NDVI dataset (1981 to 2000). (b) MODIS-NDVI data (2000-2009).
exceptionally low NDVI-rainfall, the correlation identify sites where vegetation cover decreased with a likelihood of land degradation going on [50] . A look at the time-series of regression statistics, such as R2, the ability of the land surface to respond to rainfall over the time period can be implied. Thus, a decrease of R² over the study period would indicate a decreasing dependence of the vegetation cover on rainfall patterns and an increasing dependence on others factors such as temperature patterns or human influence. This negative trend indicated an area with vegetation cover undergoing certain negative change relationships between series. On relationships between other series the contrary is that an increase of R2 over time suggests a surface with an increasingly response of the vegetation cover to rainfall and a decreasing role of other predictive factors. There is no doubt however, that any change in land cover or in land use would be reflected in a change of R2 value. Hence, abandonment or expansion of cultivated areas as well as converting virgin lands into agricultural use should be noticeable in the time-series of the R2.
6. Conclusion
This study has identified and evaluated methods appropriate to environmental assessment in the northern part of Nigeria. The assessment therefore determined that long term changes in vegetation productivity or otherwise can be assessed by integrating spatial prediction. The spatially averaged time-series of growing season NDVI exhibited a statistically significant upward trend with an increase of 0.5% for all vegetated pixels over the period 1981-2009. The coefficient of determination of the trend is relatively high (R2 = 0.17). The growing season NDVI images exhibited significant upward trends for each land-cover type with an exception of semi-arid section falling in the extreme northern part of the study area. Thus, bearing in mind that a relationship between NDVI and climatic parameters exists, spatial prediction was integrated and tested so as to assess the impact of the changing climate on NDVI vegetation productivity in the northern part of Nigeria. From prediction variance map (Figure 3) values are higher in the middle (upper portion of the study area which comprises Gusau, Katsina, Jos and Minna) and low values are found in the lower parts of the map (lower portion of the study area which comprising of Funtua, Kano, Maiduguri and Sokoto. However, further assessments are encouraged in this regard so as to incorporate high spatial resolution NDVI data, and more meteorological stations from the northeast and southeast of the study area (considering the wide spacing of the stations) so as to determine the level of climatic impacts or otherwise particularly in the montane and forest zones of the country in terms of vegetation productivity in general.
Acknowledgements
The authors acknowledge the Clarks Lab for providing the NOAA/NASA- MODIS/NDVI/EVI/CMD and AVHRR monthly dataset as well as the USGS for the use of the 90 meter DEM derived from the Shuttle Radar Topography Mission instrument which were all utilised in this study. They are also grateful to Nigerian Meteorological Agency (NIMET) for providing the rainfall and temperature data utilised in this assessment.
Cite this paper
Yelwa, S.A. and Usman, U. (2017) Integration of Spatial Prediction in the Assessment of Vegetation Productivity in the Northern Part of Nigeria. American Journal of Climate Change, 6, 360-373. https://doi.org/10.4236/ajcc.2017.62018
References
- 1. Journel, A.G. and Huijbregts, J.C. (1978) Mining Geostatistics. Academic Press, Inc., London.
- 2. Goovaerts, P. (1997) Geostatistics for Natural Resources Evaluation. Oxford University Press, New York, 483 p.
- 3. Goovaerts, P. (1999) Geostatistics in Soil Science: State-of-the-Art and Perspectives. Geoderma, 89, 1-46.
- 4. Tabios, G.Q. and Salas, J.D. (1985) A Comparative Analysis of Techniques for Spatial Interpolation of Precipitation. Journal of the American Water Resources Association, 21, 365-380.
https://doi.org/10.1111/j.1752-1688.1985.tb00147.x - 5. Dirks, K.N., Hay, J.E., Stow, C.D. and Harris, D. (1998) High-Resolution Studies of Rainfall on Norfolk Island Part II: Interpolation of Rainfall Data. Journal of Hydrology, 208, 187-193.
- 6. Borga, M. and Vizzaccaro, A. (1997) On the Interpolation of Hydrologic Variables: Formal Equivalence of Multiquadratic Surface Fitting and Kriging. Journal of Hydrology, 195, 160-171.
- 7. Creutin, J.D., Delrieu, G. and Lebel, T. (1988) Rain Measurement by Raingauge-Radar Combination: A Geostatistical Approach. Journal of Atmospheric and Oceanic Technology, 5, 102-115.
https://doi.org/10.1175/1520-0426(1988)005<0102:RMBRRC>2.0.CO;2 - 8. Azimi-Zonooz, A., Krajewski, W.F., Bowles, D.S. and Seo, D.J. (1989) Spatial Rainfall Estimation by Linear and Non-Linear Cokriging of Radar-Rainfall and Rain Gauge Data. Stochastic Hydrology and Hydraulics, 3, 51-67.
https://doi.org/10.1007/BF01543427 - 9. Fortin, M.J. and Dale, M.R.T. (2005) Spatial Analysis. Cambridge University Press, Cambridge.
- 10. Krige, D.G. (1966) Two-Dimensional Weighted Moving Average Trend Surfaces for Ore Valuations. Proceedings of Symposium on Mathematical Statstics and Computer Applications, Ore Valuation, 13-38.
- 11. Bailey, T.C. and Gatrell, A.C. (1995) Interactive Spatial Data Analysis. Longman Scientific & Technical; J. Wiley, Harlow Essex, England.
- 12. Hengl, T., Gerard, B.M. and Rossiter, D.G. (2007) About Regression-Kriging: From Equations to Case Studies. Computers & Geosciences, 33, 1301-1315.
https://doi.org/10.1016/j.cageo.2007.05.001 - 13. Knotters, M., Brus, D. and Voshaar, J. (1995) A Comparison of Kriging, Co-Kriging and Kriging Combined with Regression for Spatial Interpolation of Horizon Depth with Censored Observations. Geoderma, 67, 227-246.
https://doi.org/10.1016/0016-7061(95)00011-C - 14. Bishop, T. and Mc Bratney, A. (2001) A Comparison of Prediction Methods for the Creation of Field-Extent Soil Property Maps. Geoderma, 103, 149-160.
https://doi.org/10.1016/S0016-7061(01)00074-X - 15. Bourennane, H. and King, D. (2003) Using Multiple External Drifts to Estimate a Soil Variable. Geoderma, 114, 1-18.
https://doi.org/10.1016/S0016-7061(02)00338-5 - 16. Lloyd, C.D. (2005) Assessing the Effect of Integrating Elevation Data into the Estimation of Monthly Precipitation in Great Britain. Journal of Hydrology, 308, 128-150.
https://doi.org/10.1016/j.jhydrol.2004.10.026 - 17. Yemefack, M., Rossiter, D.G. and Njomgang, R. (2005) Multi-Scale Characterization of Soil Variability within an Agricultural Landscape Mosaic System in Southern Cameroon. Geodermal, 25, 117-143.
https://doi.org/10.1016/j.geoderma.2004.07.007 - 18. Leopold, U., Heuvelink, G.B., Tiktak, A., Finke, P.A. and Schoumans, O. (2005) Accounting for Change of Support in Spatial Accuracy Assessment of Modelled Soil Mineral Phosphorous Concentration. Geoderma, 130, 368-386.
https://doi.org/10.1016/j.geoderma.2005.02.008 - 19. Berterretche, M., Hudak, A.T., Cohen, W.B., Maiersperger, T.K., Gower, S.T. and Dungan, J. (2005) Comparison of Regression and Geostatistical Methods for Mapping Leaf Area Index (LAI) with Landsat ETM Data over a Boreal Forest. Remote Sensing of Environment, 96, 49-61.
https://doi.org/10.1016/j.rse.2005.01.014 - 20. Pleydell, D.R.J., Raoul, F., Tourneux, F., Danson, F.M., Graham, A.J., Craig, P.S. and Giraudoux, P. (2004) Modelling the Spatial Distribution of Echinococcusmultilo cularis Infection in Foxes. Acta Tropica, 91, 253-265.
https://doi.org/10.1016/j.actatropica.2004.05.004 - 21. Desbarats, A.J., Logan, C.E., Hinton, M.J. and Sharpe, D.R. (2002) On the Kriging of Water Table Elevations Using Collateral Information from a Digital Elevation Model. Journal of Hydrology, 255, 25-38.
https://doi.org/10.1016/S0022-1694(01)00504-2 - 22. Finke, P.A., Brus, D.J., Bierkens, M.F.P., Hoagland, T., Knotters, M. and Vries, F. (2004) Mapping Groundwater Dynamics Using Multiple Sources of Exhaustive High Resolution Data. Geoderma, 123, 23-39.
https://doi.org/10.1016/j.geoderma.2004.01.025 - 23. Rivoirard, J. (2002) On the Structural Link between Variables in Kriging with External Drift. Mathematical Geology, 34, 797-808.
- 24. Odeh, I., McBratney, A. and Chittleborough, D. (1995) Further Results on Prediction of Soil Properties from Terrain Attributes: Heterotopic Cokriging and Regression-Kriging. Geoderma, 67, 215-226.
https://doi.org/10.1023/A:1020972510120 - 25. Hengl, T., Heuvelink, G. and Stein, A. (2004) A Generic Framework for Spatial Prediction of Soil Variables Based on Regression-Kriging. Geoderma, 122, 75-93.
https://doi.org/10.1016/0016-7061(95)00007-B - 26. Matheron, G. (1969) Le krigeage universel (Universal kriging) Vol. 1. Cahiers du Centre de Morphologie Mathematique, Ecole des Mines de Paris, Fontainebleau, 83 p.
https://doi.org/10.1016/j.geoderma.2003.08.018 - 27. Christensen, R. (2001) Linear Models for Multivariate Time Series and Spatial Data. 2nd Edition. Springer, New York, 398 p.
- 28. Deutsch, C. and Journel, A. (1998) GSLIB: Geostatistical Software and User’s Guide. 2nd Edition, Oxford University Press, New York, 369 p.
- 29. Wackernagel, H. (1998) Multivariate Geostatistics: An Introduction with Applications. 2nd Edition, Springer, Berlin, 291 p.
https://doi.org/10.1007/978-3-662-03550-4 - 30. Papritz, A. and Stein, A. (1999) Spatial Prediction by Linear Kriging. In: Stein, A., van der Meer, F. and Gorte, B., Eds., Spatial Statistics for Remote Sensing, Kluwer Academic Publishers, Dodrecht, 83-113.
https://doi.org/10.1007/0-306-47647-9_6 - 31. Chiles, J. and Delfiner, P. (1999) Geostatistics: Modeling Spatial Uncertainty. Wiley, New York, 695 p.
https://doi.org/10.1002/9780470316993 - 32. Webster, R. and Oliver, M. (2001) Geostatistics for Environmental Scientists Statistics in Practice. Wiley, Chichester, 271 p.
- 33. Ahmed, S. and de Marsily, G. (1987) Comparison of Geostatistical Methods for Estimating Transmissivity Using Data on Transmissivity and Specific Capacity. Water Resources Research, 23, 1717-1737.
https://doi.org/10.1029/WR023i009p01717 - 34. Wu, J., Norvell, W.A. and Welch, R.M. (2006) Kriging on Highly Skewed Data for DTPA-Extractable Soil Zn with Auxiliary Information for pH and Organic Carbon. Geoderma, 134, 187-199.
https://doi.org/10.1016/j.geoderma.2005.11.002 - 35. Raspa, G., Tucci, M. and Bruno, R. (1997) Reconstruction of Rainfall Fields by Combining Ground Rain Gauges Data with Radar Maps Using External Drift Method. In: Baafi, E.Y. and Schofield, N.A., Eds., Geostatistics Wollongong’96, Kluwer Academic, Dordrecht, 941-950.
https://doi.org/10.1007/978-94-011-5726-1_57 - 36. Hevesi, J.A., Flint, A.L. and Istok, J.D. (1992) Precipitation Estimation in Mountainous Terrain Using Multivariate Geostatistics. Part I: Structural Analysis. Journal of Applied Meteorology, 31, 661-676.
https://doi.org/10.1175/1520-0450(1992)031<0661:PEIMTU>2.0.CO;2 - 37. Daly, C., Neilson, R.P. and Phillips, D.L. (1994) A Statistical Topographic Model for Mapping Climatological Precipitation over Mountainous Terrain. Journal of Applied Meteorology, 33, 140-158.
https://doi.org/10.1175/1520-0450(1994)033<0140:ASTMFM>2.0.CO;2 - 38. Dakata, F.A.G. and Yelwa, S.A. (2012) An Assessment of Mean and Inter-Seasonal Variation during Growing Season across Kano Region, Nigeria Using Normalized Difference Vegetation Index Derived from SPOT Satellite Data. Global Advanced Research Journal of Social Sciences, 3, 059-064.
- 39. Abtew, W., Obeysekera, J. and Shih, G. (1993) Spatial Analysis for Monthly Rainfall in South Florida. Water Resources Bulletin, 29, 179-188.
https://doi.org/10.1111/j.1752-1688.1993.tb03199.x - 40. Hosseini, E., Gallichand, J. and Marcotte, D. (1994) Theoretical and Experimental Performance of Spatial Interpolation Methods for Soil Salinity Analysis. Transaction of the ASAE, 36, 1799-1807.
https://doi.org/10.13031/2013.28269 - 41. Voltz, M. and Goulard, M. (1994) Spatial Interpolation of Soil Moisture Retention Curves. Geoderma, 62, 109-123.
https://doi.org/10.1016/0016-7061(94)90031-0 - 42. McKenzie, N. and Ryan, P. (1999) Spatial Prediction of Soil Properties Using Environmental Correlation. Geoderma, 89, 67-94.
https://doi.org/10.1016/S0016-7061(98)00137-2 - 43. Draper, N. and Smith, H. (1981) Applied Regression Analysis. 2nd Edition, Wiley, New York, 709 p.
- 44. Christensen, R. (1996) Plane Answers to Complex Questions: The Theory of Linear Models. 2nd Edition, Springer, New York, 452 p.
https://doi.org/10.1007/978-1-4757-2477-6 - 45. Cressie, N. (1993) Statistics for Spatial Data. Revised Edition, Wiley, New York, 900 p.
- 46. Kitanidis, P. (1994) Generalized Covariance Functions in Estimation. Mathematical Geo-logy, 25, 525-540.
https://doi.org/10.1007/BF00890244 - 47. Pebesma, E.J. (2004) Multivariable Geostatistics in S: The GSTAT Package. Computers and Geosciences, 30, 683-691.
https://doi.org/10.1016/j.cageo.2004.03.012 - 48. Fuller, D.O. (1998) Trends in NDVI Time Series and Their Relationship to Rangeland and Crop Production in Senegal, 1987-1993. International Journal of Remote Sensing, 19, 2013-2018.
https://doi.org/10.1080/014311698215135 - 49. Yelwa, S.A. and Isah, A.D. (2010) Analysis of Trends in Vegetation AVHRR-NDVI Data across Sokoto State 1982-1986 Using Remote Sensing and GIS. Nigerian Journal of Basic and Applied Science, 18, 90-96.
https://doi.org/10.4314/njbas.v18i1.56849 - 50. Li, B., Tao, S. and Dawson, R.W. (2002) Relation between AVHRR NDVI and Eco-Climatic Parameters in China. International Journal of Remote Sensing, 23, 989-999.
https://doi.org/10.1080/014311602753474192
List of Abbreviations
ANOVA Analysis of Variance
AVHRR Advanced Very High Resolution Radiometer
CMD Climate Modelling Grid
CK Cokriging
DEM Digital Elevation Model
GIS Geographical Information Systems
GLS Generalized Least Squares
KED Kriging with External Drift
LAI Leaf Area Index
MODIS Moderate Resolution Imaging Spectrometer
NASA National Aeronautics Space Administration
NDVI Normalised Difference Vegetation Index
NIMET Nigerian Meteorological Agency
NOAA National Oceanic Atmospheric Administration
OLS Ordinary Least Square
RK Regression-Kriging
SK Simple kriging
SRTM Shuttle Radar Topography Mission
Tmax Maximum Temperature
Tmin Minimum Temperature
UK Universal kriging
USGS United States Geological Survey





