American Journal of Climate Change
Vol.3 No.1(2014), Article ID:43994,12 pages DOI:10.4236/ajcc.2014.31008
Analysis of Change Point in Surface Temperature Time Series Using Cumulative Sum Chart and Bootstrapping for Asansol Weather Observation Station, West Bengal, India
Ansar Khan1, Soumendu Chatterjee2, Dipak Bisai1, Nilay Kanti Barman1
1Department of Geography and Environment Management, Vidyasagar University, Midnapore, India
2Department of Geography, Presidency University, Kolkata, India
Email: khanansargeo@gmail.com, scgeovu@yahoo.co.in, dbisai@gmail.com, nilay@csws.in
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/


Received 22 October 2013; revised 23 November 2013; accepted 27 December 2013
ABSTRACT
This paper aims to detect the short-term as well as long-term change point in the surface air temperature time series for Asansol weather observation station, West Bengal, India. Temperature data for the period from 1941 to 2010 of the said weather observatory have been collected from Indian Meteorological Department, Kolkata. Variations and trends of annual mean temperature, annual mean maximum temperature and annual minimum temperature time series were examined. The cumulative sum charts (CUSUM) and bootstrapping were used for the detection of abrupt changes in the time series data set. Statistically significant abrupt changes and trends have been detected. The major change point in the annual mean temperatures occurred around 1986 (0.57˚C) at the period of 25 years in the long-term regional scale. On the other side, the annual mean maximum and annual mean minimum temperatures have distinct change points at level 1. There are abrupt changes in the year 1961 (Confidence interval 1961, 1963) for the annual mean maximum and 1994 (Confidence interval 1993, 1996) for the annual mean minimum temperatures at a confidence level of 100% and 98%, respectively. Before the change, the annual mean maximum and annual mean minimum temperatures were 30.90˚C and 23.99˚C, respectively, while after the change, the temperatures became 33.93˚C and 24.84˚C, respectively. Over the entire period of consideration (1941-2010), 11 forward and backward changes were found in total. Out of 11, there are 3 changes (1961, 1986 and 2001) in annual mean temperatures, 4 changes (1957, 1961, 1980 and 1994) in annual mean maximum temperatures, and rest 4 changes (1968, 1981, 1994 and 2001) are associated with annual mean minimum temperature data set.
Keywords:Bootstrapping; Change Point; CUSUM; Temperature Time Series

1. Introduction
Climate change and global warming are recognized worldwide as the most crucial environmental dilemma that the world is experiencing today [1] -[3] . Concern in climate change and global warming by the international community, non-government organizations and governments has brought great interest to climate scientists leading to several studies on climate trend detection at global, hemispherical and regional scales [3] -[5] . Nowadays, study of long-term temperature variability has been a topic of particular attention for climate researchers as temperature affects straightaway human activities in all domains. Increase in anthropogenic greenhouse gases’ concentrations in the atmosphere is mainly due to human activities such as deforestation, burning of fossil fuel and the conversion of the Earth’s land to urban uses driven largely by the rapid growth of the human population that are major causes of warming of the climate system and of the process of climate change [4] -[6] . Several studies of long-term time series of temperatures have been done [7] -[9] . Results have shown that the Earth’s surface air temperature has increased by 0.6˚C - 0.8˚C during the 20th century, along with changes in the hydrologic cycle. Temperatures in the lower troposphere have augmented between 0.13˚C and 0.22˚C per decade since 1979, according to satellite temperature measurements [10] . In an analysis of a time series combining global land and marine surface temperature records from 1850 to 2010 developed by the Climate Research Unit (CRU), the year 2005 was seen as the second warmest year, behind 1998 with 2003 and 2010 tied for third warmest year [8] [11] -[14] . The two most recent decades were compared with the period 1979-1990. Warming has been observed to be concentrated in the most recent decade, from 2001 to 2010. The results were attributed to natural variability of the climate and/or to human activity but not to the El Niño-Southern Oscillation as previously suggested by other authors [13] -[15] . Generally, there is consent among scientists that most of the observed increase in globally averaged temperatures since the mid-20th century is unequivocal and very likely due to the observed increase in anthropogenic greenhouse gas concentrations. The 10 warmest years of the 20th century all occurred in the last 15 years of the century, 1998 being the warmest. The Intergovernmental Panel on Climate Change (IPCC, 2007) projected that the average global surface temperature will continue to increase to between 1.4˚C and 5.8˚C above 1990 levels,by 2100 [2] . To some extent, other factors, such as variations in solar radiation [8] and land use at regional scale, are also considered to be among the causes of the observed global warming [16] -[22] . Though some studies have been done on climate change in different regions of India and whole of the adjacent sub-continent, the lack of reliable surface observational climate data still constitute a foremost gap affecting the detection capacity of impacts resulting from long-term climate changes. An effort is, therefore, required in maintaining existing observatories and increasing networks, and cooperation between countries. Regardless of the limited surface observational climate data, results from those studies indicate, in general, an increasing trend in temperature and a decreasing trend in rainfall during the last century. But key sources of errors in the detection of abrupt changes in climate data habitually consist of change of location of observatory; changes of instruments, change in observation times, missing data, and methods used to calculate daily means and increased urbanized and/or industrialized areas. Inhomogeneities in climate data time series can bring inaccuracies and make possible misinterpretation in the investigation of climate change over a region when analyzing a given climate parameter. Hence, there is a need for detecting change points in temperature time series and adjustment of data thereby.
2. Study Area
Asansol (23˚40'48"N and 86˚59'24"E) is situated in the Burdwan District of West Bengal It is Located between the Damodar and Ajay rivers over the extended part of Chhota Nagpur plateau, while the plateau proper occupies most of the state of Jharkhand. Another river, Barakar, joins the Damodar near Dishergarh. A small rivulet, Nunia, flows past Asansol. Dhanbad district lies on the western side of Asansol while, Durgapur sub division of Bardhman district lies on the eastern side and to the south, across the Damodar river are the Purulia and Bankura districts. To the north of Asansol are Dumka (Jharkhand) and Birbhum (West Bengal) districts. Dhanbad district across the Barakar river in Jharkhand is also a major mining area and has close links with Asansol. Both Dhanbad and Asansol lies in the Damodar valley. Mean an annual day time maximum temperature generally reaches as high as 31˚C. At night, the average annual minimum temperature drops down to around 22˚C. The average annual relative humidity is around 65%. The Heat Index is extreme and one can guess how hot it feels when relative humidity is added to actual air temperature. The average monthly amount of precipitation in rainy season has been recorded at around 78 mm. The average monthly wind speed around 2 km/h or 1 knot, approximately. In recent years, the maximum sustained wind speed has reached 56 km/h, or 30 knot.
3. Data Base and Method
3.1. Data Base
The data used in this study were collected from the Eastern Regional Centre of Indian Meteorological Department, Kolkata. They consisted of time series of year wise monthly average of maximum and minimum surface air temperature for the period ranging from 1941 to 2010 for the Asansol weather observatory. Those data were statistically processed and then condensed to annual mean values for further analysis. Studies of long-term climate change require that data be homogenous. Observed climate abrupt changes in a homogenous climate time series are caused only by variations in weather and climate [23] . Several studies have been conducted on quality control and homogenization of climatological data for the detection of climate trends [24] -[27] . Detailed explanations on the methods to be followed for data analysis are as under.
3.2. Cumulative Sum Charts (CUSUM) and Bootstrapping
The cumulative sum charts (CUSUM) and bootstrapping were performed as suggested by Taylor [28] . Let,  represent
represent 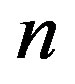 data points of a time series, and
data points of a time series, and 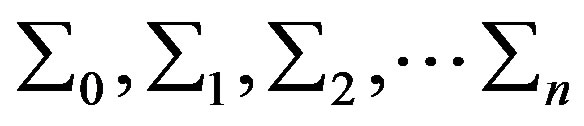 are iteratively computed as follows a) The average
are iteratively computed as follows a) The average 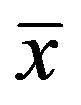 of
of 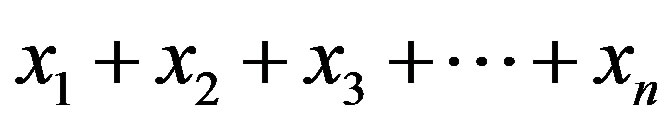 is given by
is given by
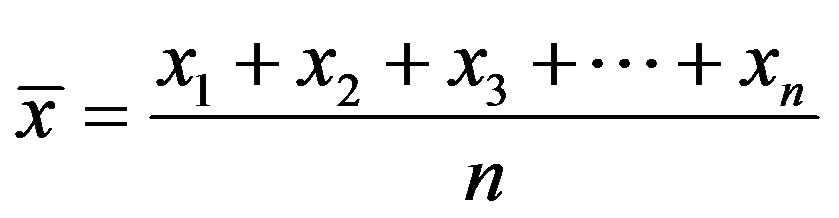 (1)
(1)
b) Let, 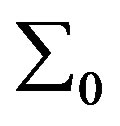 be equal to zero.
be equal to zero.
c) 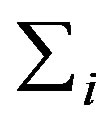 are computed recursively as follows
are computed recursively as follows
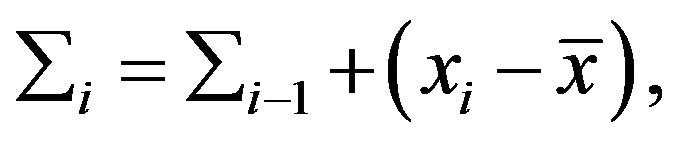 (2)
(2)
where,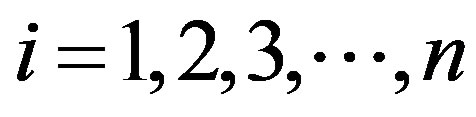 .
.
Actually, the cumulative sums are not the cumulative sums of the values. Instead they are the cumulative sums of differences between the values and the average. These differences sum to zero so the cumulative sum always ends at zero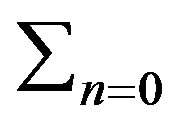 .
.
The confidence level can be determined for the apparent change by performing a bootstrap analysis [29] [30] . Before performing the bootstrap analysis, an estimator of the magnitude of the change is required. One choice, which works well regardless of the distribution and despite multiple changes is,  which is defined as
which is defined as
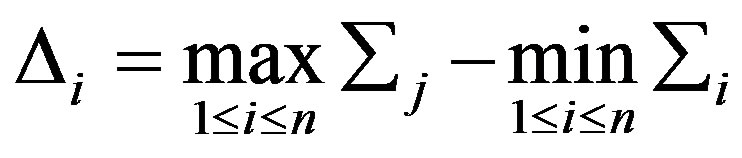 (3)
(3)
Once the estimator of the magnitude of the change has been selected, the bootstrap analysis can be performed. A single bootstrap is performed by a) Generating a bootstrap sample of n data points of time series, denoted as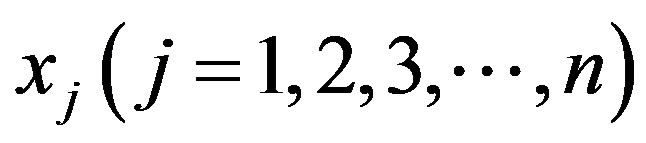 , by randomly reordering the original
, by randomly reordering the original 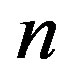 values. This is called sampling without replacement (SWOR).
values. This is called sampling without replacement (SWOR).
b) Based on the bootstrap sample, the bootstrap CUSUM is calculated following same method and denoted as,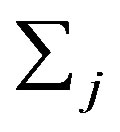 .
.
c) The maximum, minimum, and difference of the bootstrap CUSUM are calculated and the difference between the maximum and minimum bootstrap CUSUM is defined as,
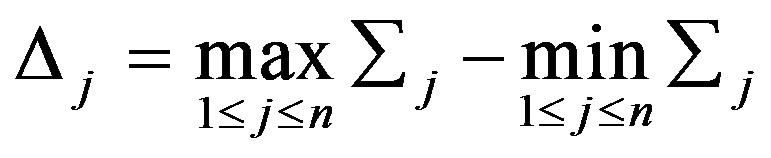 (4)
(4)
d) Determine whether, .
.
The bootstrap analysis consists of performing a large number of bootstraps and counting the number of bootstraps for which difference bootstrap 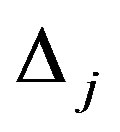 less than the original difference
less than the original difference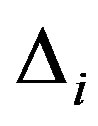 . Let
. Let 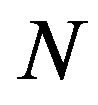 is the number of bootstrap samples performed and let K be the number of bootstraps for which
is the number of bootstrap samples performed and let K be the number of bootstraps for which . Then the confidence level that a change occurred as a percentage is calculated as follows Confidence Level
. Then the confidence level that a change occurred as a percentage is calculated as follows Confidence Level
 (5)
(5)
Bootstrapping is a distribution free approach with only a single assumption, that of an independent error structure.
Once a change has been detected, an estimate of when the change occurred can be made. One such estimator is the CUSUM estimator. Let, 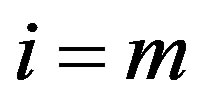 , such that
, such that
 (6)
(6)
Then m is the point furthest from zero in the CUSUM chart. The point m estimates last point before the change occurred. The point 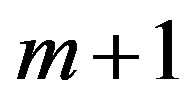 estimates the first point after the change. The second estimator of when the change occurred is the mean square error (MSE) estimator. Let MSE (
estimates the first point after the change. The second estimator of when the change occurred is the mean square error (MSE) estimator. Let MSE (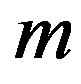 ) be defined as MSE
) be defined as MSE
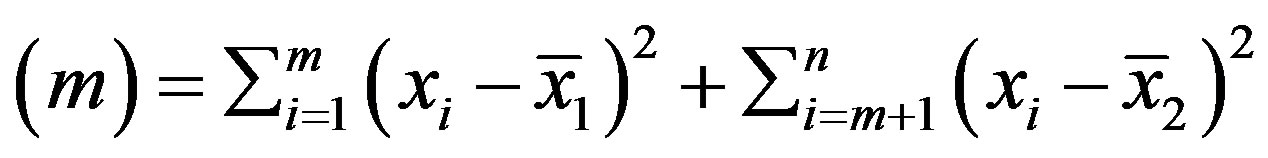 (7)
(7)
where
 and
and 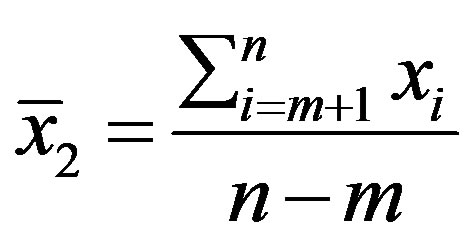
In MSE error estimation, the data series is split into two segments, 1 to m, and 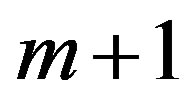 to n, then it is estimated that how well the data in each segment fits their corresponding averages. The value of m, for which MSE (m) is minimized, gives the best estimate of the last point before change, while the point
to n, then it is estimated that how well the data in each segment fits their corresponding averages. The value of m, for which MSE (m) is minimized, gives the best estimate of the last point before change, while the point 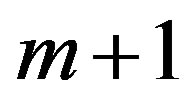 denotes the first point after change. In the same way, data of each segment can be passed through the above method to find level 2 change points that divides corresponding segments into sub-segments. Repetition of the procedure mentioned above helps finding significant change points at subsequent levels for each of which associated confidence limits and levels can be determined by bootstrapping. In this manner multiple change points can be detected by incorporating additional change points each at successive passes that will continue to split the segments into two. Once the change points, along with associated confidence levels, have been detected a backward elimination procedure is then used to eliminate those points that no longer qualify test of significance. To reduce the rate of false detection, when a point is eliminated, the surrounding change points are re-estimated along with their significance level. Thus the significant change points have been detected for the temperature time series considered for this study.
denotes the first point after change. In the same way, data of each segment can be passed through the above method to find level 2 change points that divides corresponding segments into sub-segments. Repetition of the procedure mentioned above helps finding significant change points at subsequent levels for each of which associated confidence limits and levels can be determined by bootstrapping. In this manner multiple change points can be detected by incorporating additional change points each at successive passes that will continue to split the segments into two. Once the change points, along with associated confidence levels, have been detected a backward elimination procedure is then used to eliminate those points that no longer qualify test of significance. To reduce the rate of false detection, when a point is eliminated, the surrounding change points are re-estimated along with their significance level. Thus the significant change points have been detected for the temperature time series considered for this study.
Variations and trends of annual mean temperature, annual mean minimum temperature and annual minimum temperature values time series were examined following the method mentioned above. The cumulative sum charts (CUSUM) and bootstrapping were used for the detection of abrupt changes. Section of the CUSUM chart with an ascending trend indicates a period when the values remaining above the overall average. Likewise, a section with a descending trend indicates a period of time where the values lie below the overall average. The confidence level can be determined by performing bootstrap analysis.
4. Results and Discussion
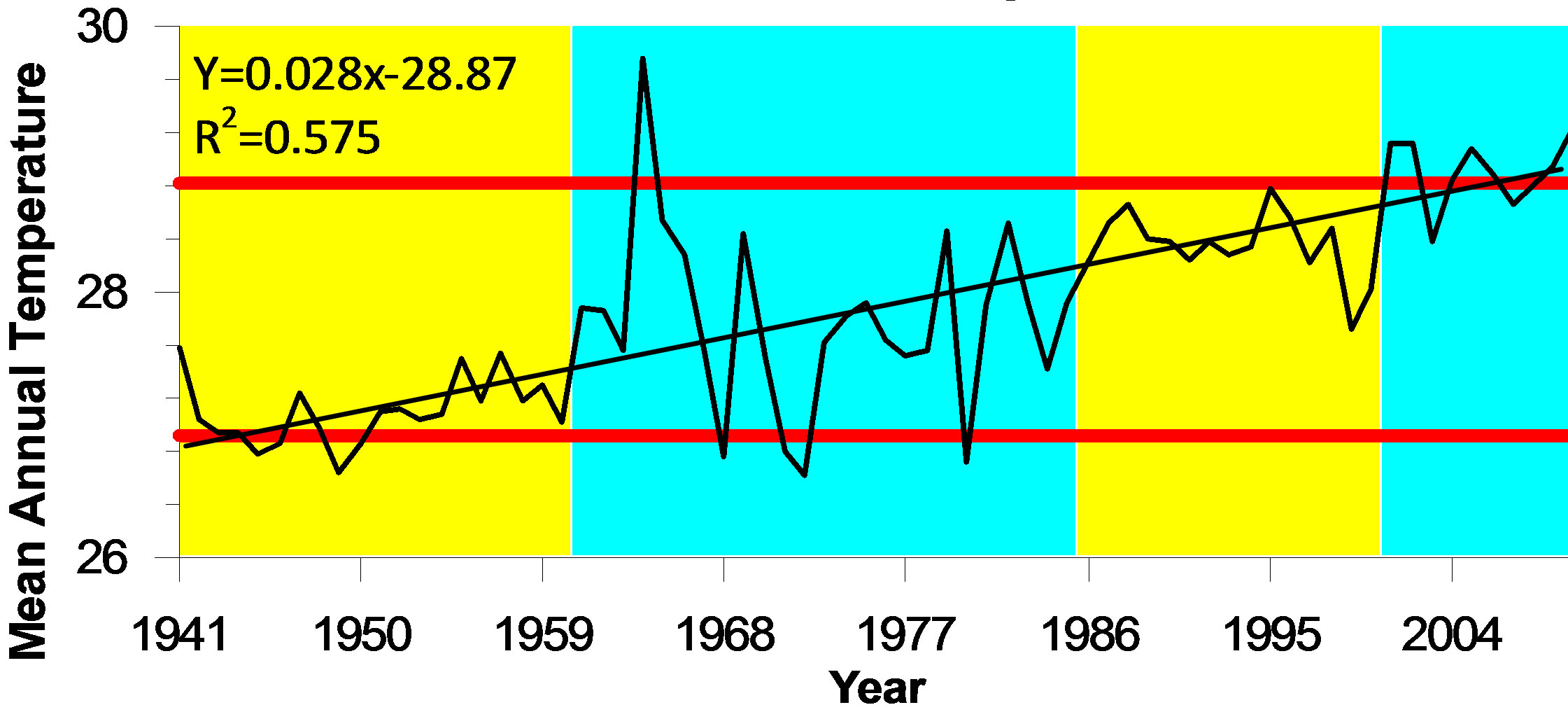
Before the change point analysis, a simple regression model has been applied to show the long term trends of annual mean temperature series, annual mean maximum temperature series and annual mean minimum temperature series and results shows that the annual mean minimum temperature has been remarkably increasing trend than the annual mean maximum temperature in Figures 1(b) and (c). In both the cases, Adjusted R² values are 0.21 and 0.06, respectively. But annual mean temperature tend to be seriatim manner and it meets with Adjusted R² 0.58 in Figure 1(a).
 (a)
(a)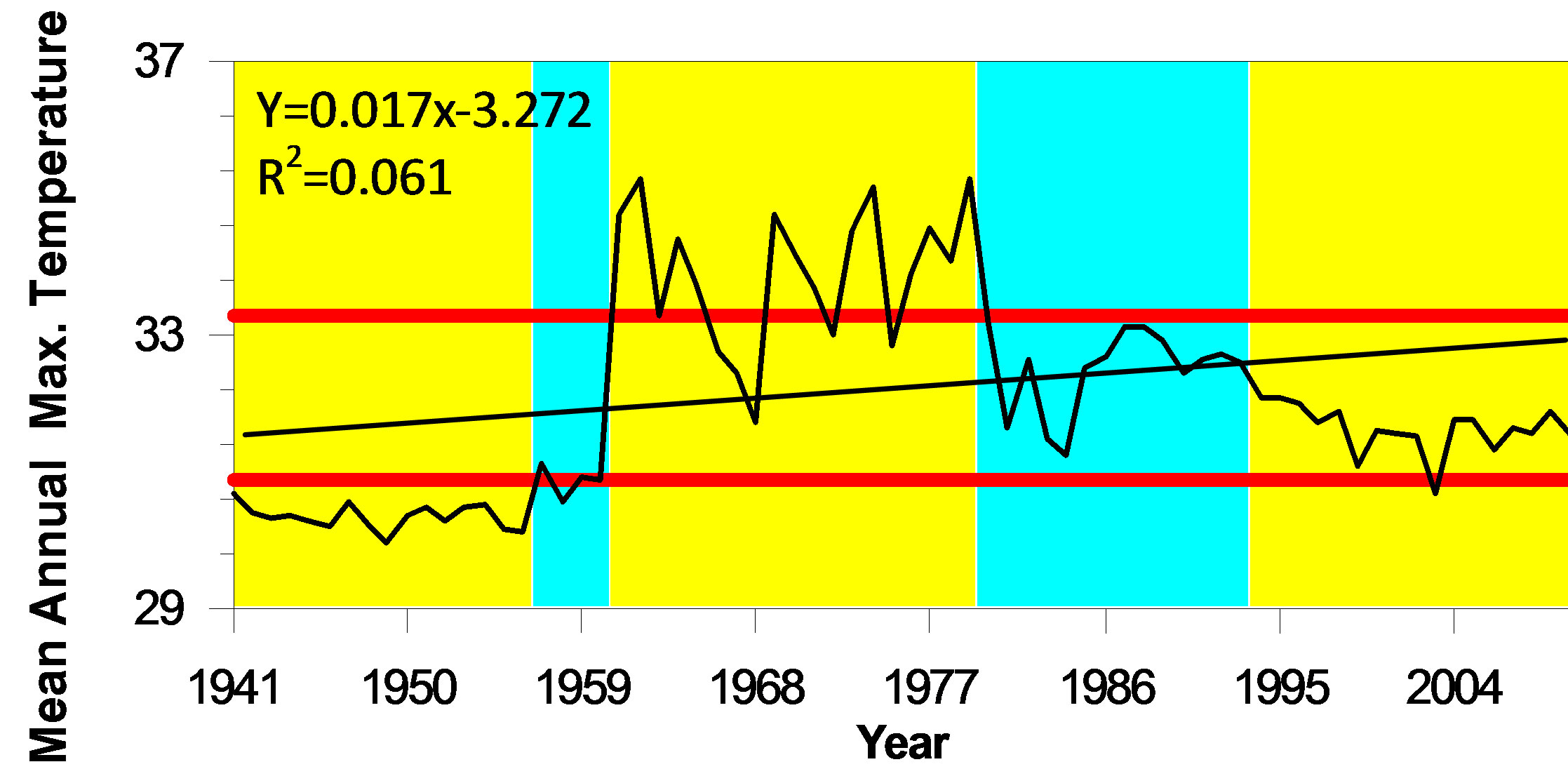 (b)
(b)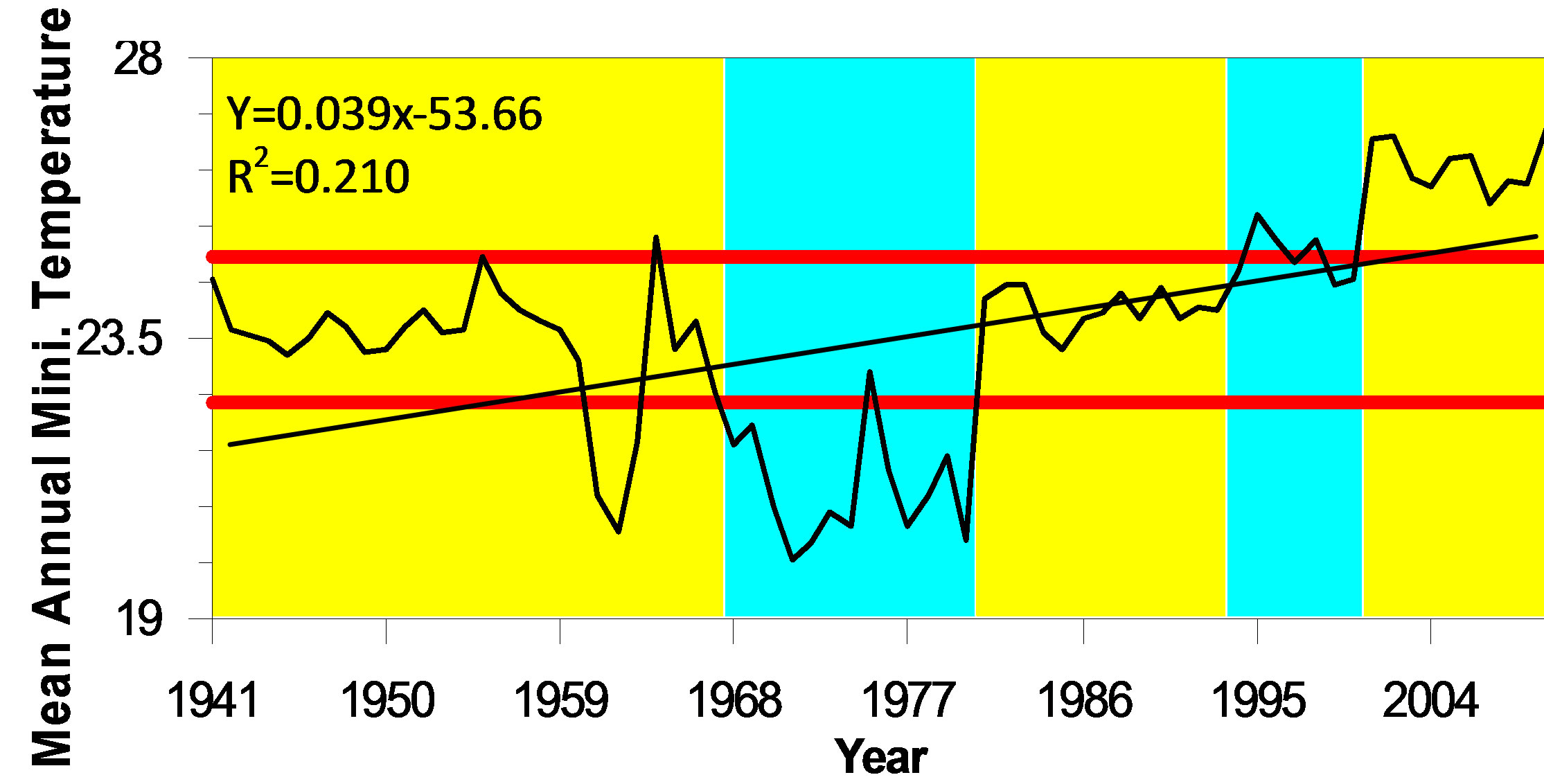 (c)
(c)
Figure 1. Regression of adjusted long term time series of (a) mean annual temperature, (b) mean annual maximum temperature, and (c) mean annual minimum temperature (1941-2010) for Asansol Weather Observatory.
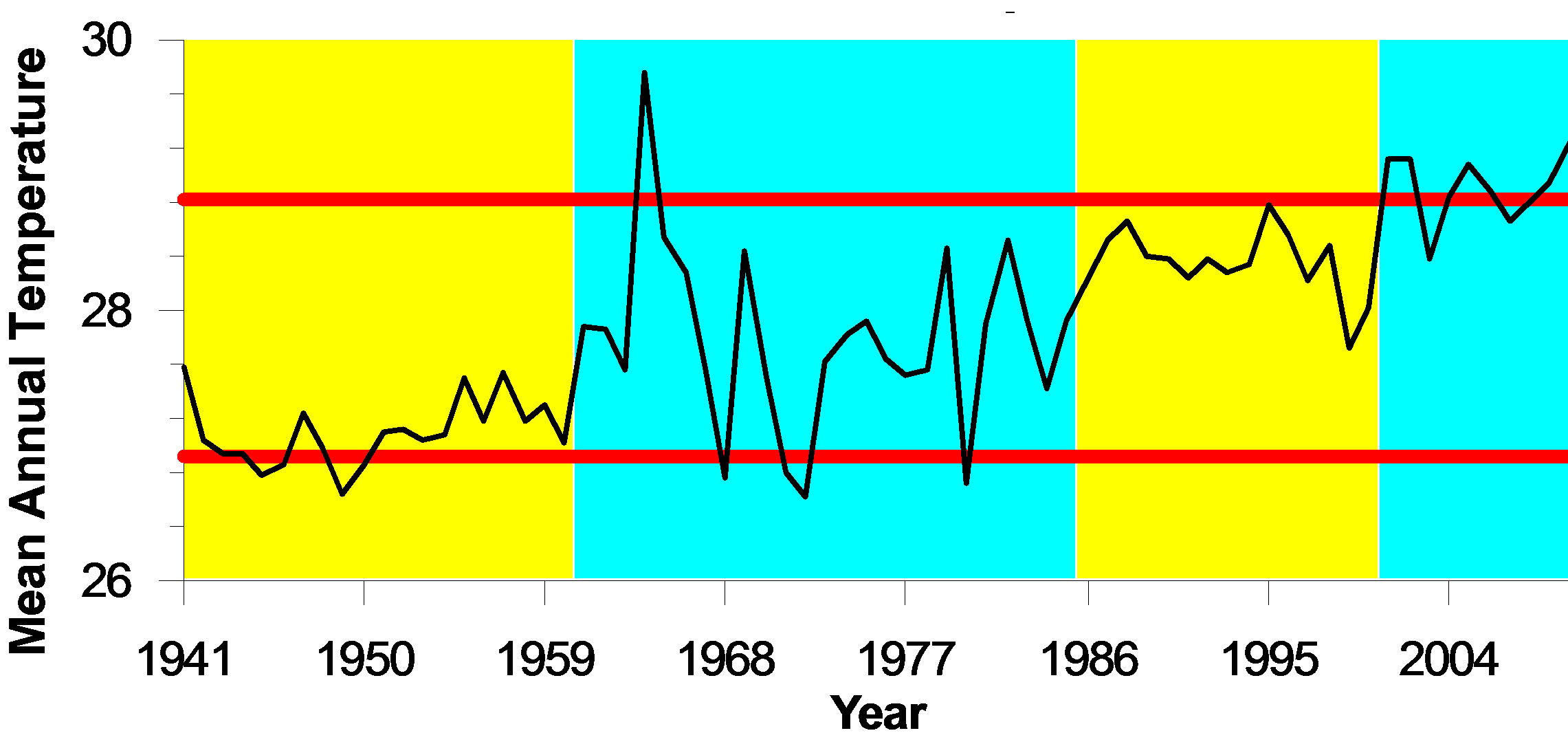
The results of change-point analysis for the annual mean temperature, annual mean minimum temperature and annual mean maximum temperature for Asansol weather observatory are presented in Figure 2 where period of change has been indicated with shaded background. In Table 1, confidence levels of those changes are mentioned. The table also gives a level associated with each change which is a measure of importance of the change. The level 1 change signifies the first change detected which is most visibly apparent in the CUSUM charts. Level 2 changes are detected on second pass of the data. There are as many numbers of levels as the numbers changes found. By means of the change point analysis from the independent error structure no outlier’s assumptions were made in annual mean maximum and annual mean minimum temperature trend in one hand. On the other hand, the annual mean temperature appears to violate the assumption of independence error. The confidence levels and confidence interval may be affected. The errors are positively correlated, meaning that if single value is above average temperature trend, the next several values will also tend to be above average. As a result,
 (a)
(a) (b)
(b)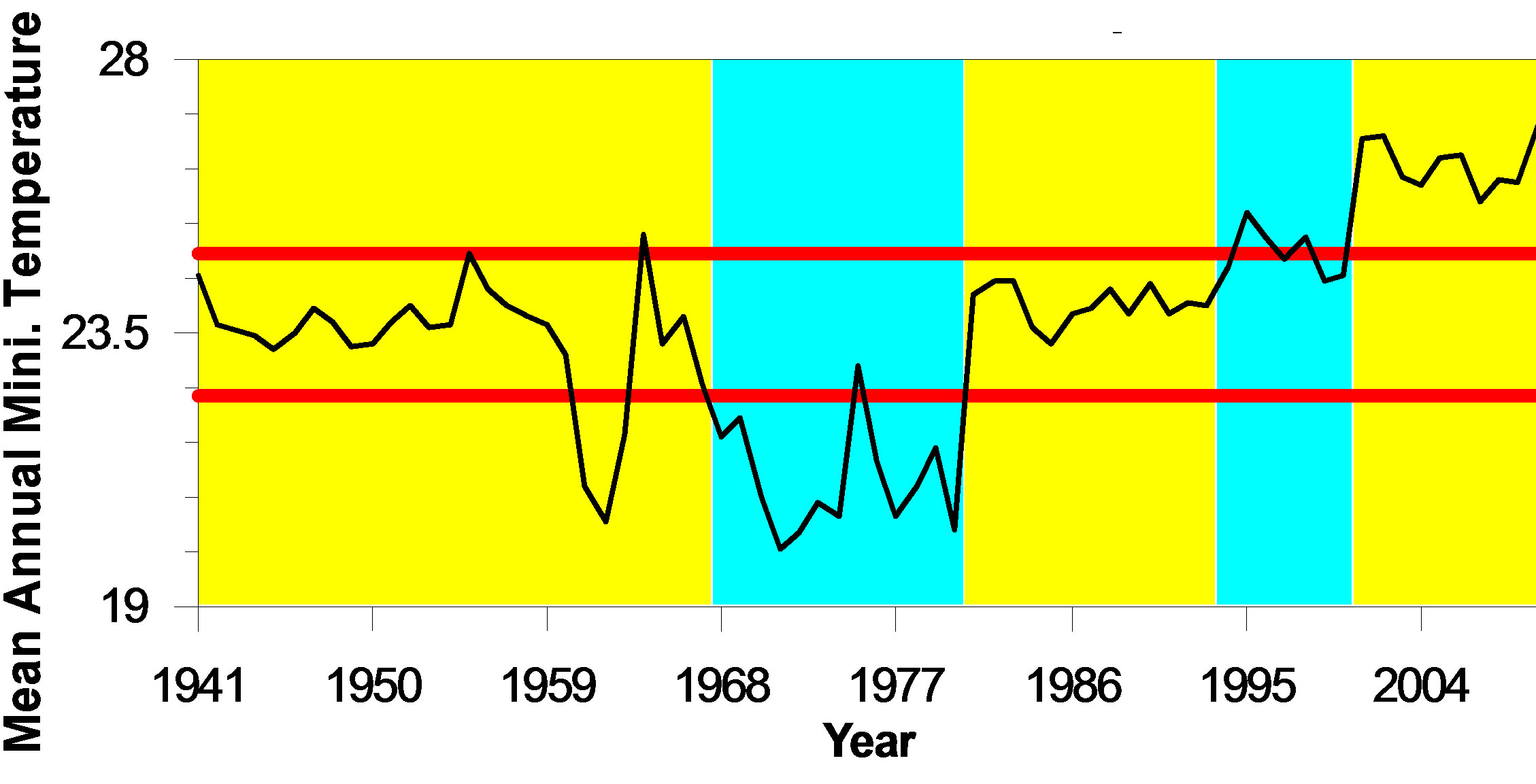 (c)
(c)
Figure 2. Temperature trends for (a) mean annual temperature, (b) mean annual maximum temperature, and (c) mean annual minimum temperature with maximum range of temperature fluctuation indicated by red lines under the situation of no change in trend.
the analysis may incorrectly indicate that a change has taken place. But the associated level of confidence obtained from bootstrapping may confirm the change to have occurred. This analysis shows that the annual mean temperature reveal a quasi-change in the year of 2001 (Confidence interval 1999, 2003) at a confidence level of 100%, at level 2. Prior to the change in 2001, annual mean temperature was 28.36˚C; while subsequent to the change the average became 28.92˚C. It has been also noted that an abrupt change in mean annual temperature in the years of 1961 (Confidence interval 1960, 1978), and 1986 (Confidence interval 1962, 1987); at a confidence level of 98% and 99% respectively, at level 3 and 1. Prior to changes 1961 and 1968, the annual mean temperatures for the two changing years were 27.11˚C and 27.79˚C respectively, while after the change the temperature became 27.79˚C and 28.36˚C respectively.
Table 1. Significant changes in (a) mean annual temperature (b) mean annual maximum temperature and (c) mean annual minimum temperature.
But largest change of temperatures is associated with 1986 (0.57˚C) at the period of 25 years in the long term regional scale are presented in Table 1(a) and Figure 2(a). On the other side the annual mean maximum and annual mean minimum temperature series also have distinct change points and presents in Table 1(b), Figure 2(b) and Table 1(c), Figure 2(c) respectively. The annual mean maximum temperatures time series exhibits a level 1 change in the year 1961 (Confidence interval 1961, 1963) at a confidence level of 100%, while for the annual mean minimum temperature series a level 1 changes is found to occur in 1994 (Confidence interval 1993, 1996) at a confidence level of 98%. Before these changes in 1961 and 1994, the annual mean maximum and annual mean minimum temperatures were 30.90˚C and 23.99˚C respectively, while after the change the mean temperatures became 33.93˚C and 24.84˚C, respectively. Over the entire period of consideration (1994-2010), 11 forward and backward changes were found. Out of 11, there are 3 changes (1961, 1986 and 2001) in annual mean temperature, 4 changes (1957, 1961, 1980 and 1994) in annual mean maximum temperature and rest 4 changes (1968, 1981, 1994 and 2001) in annual mean minimum temperature.
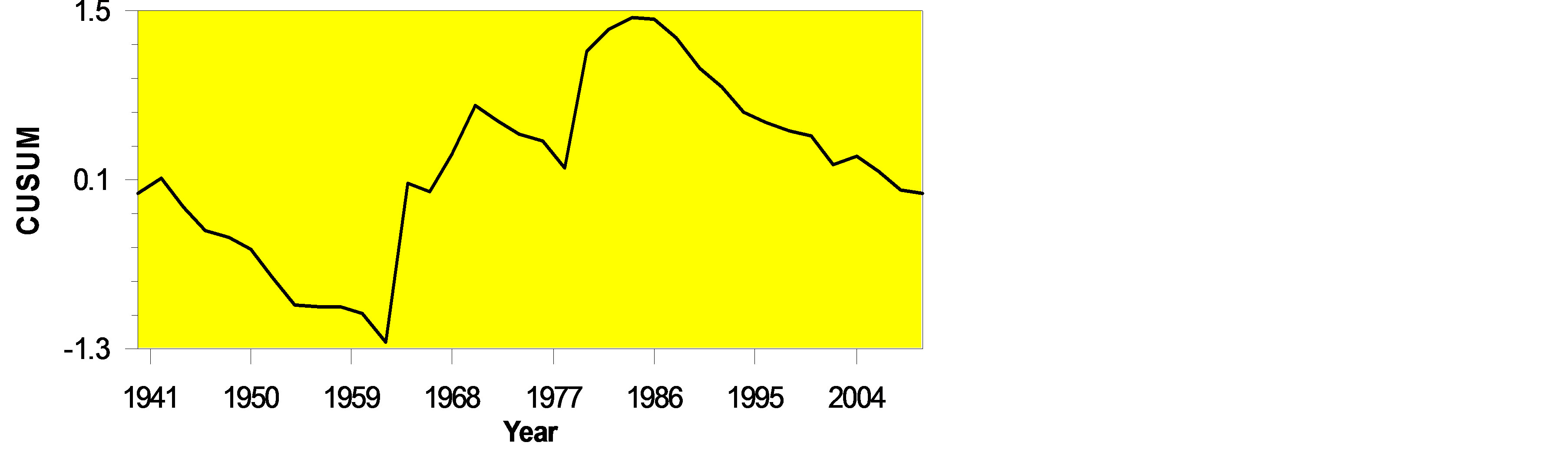
The CUSUM charts are presented in Figure 3. It is important to analyze the single or multiple change points within the entire period of a time series. The annual mean temperature CUSUM chart in Figure 3(a) exhibits an abrupt change in the year 1986; afterward the remaining section of the forwarded chart line shows an increasing trend where the values tend to be above the overall average (27.86˚C). But, in case of annual mean maximum temperatures the CUSUM chart in Figure 3(b) reveals an abrupt change in 1961. After 1961, the chart line goes upward till 1994; then again forwarded chart line gradually goes downward indicating the values tend to be below the overall average of annual maximum temperatures (32.10˚C). The annual mean minimum temperature CUSUM chart in Figure 3(c) presents quasi-intersecting or sinusoidal changing character between annual mean and annual maximum temperature outliers. As such, annual mean minimum temperatures also exhibits an abrupt
 (a)
(a)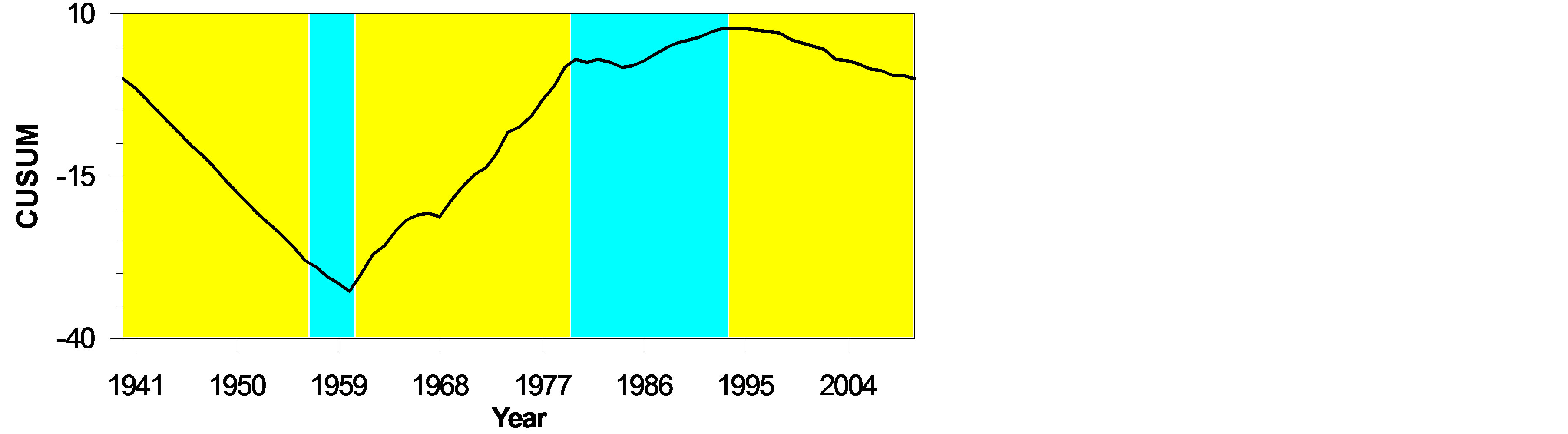 (b)
(b)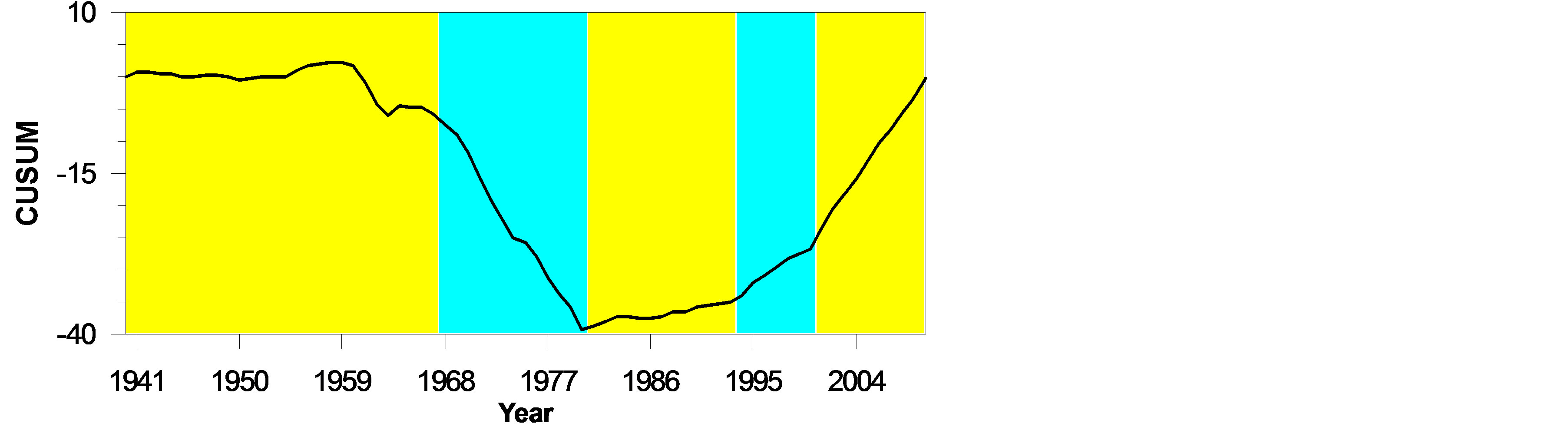 (c)
(c)
Figure 3. CUSUM charts for (a) mean annual temperature, (b) mean annual maximum temperature, and (c) mean annual minimum temperature.
change in the year 1994 and chart line again gradually raises upward indicating values to be above the overall average of annual mean temperature (23.66˚C).
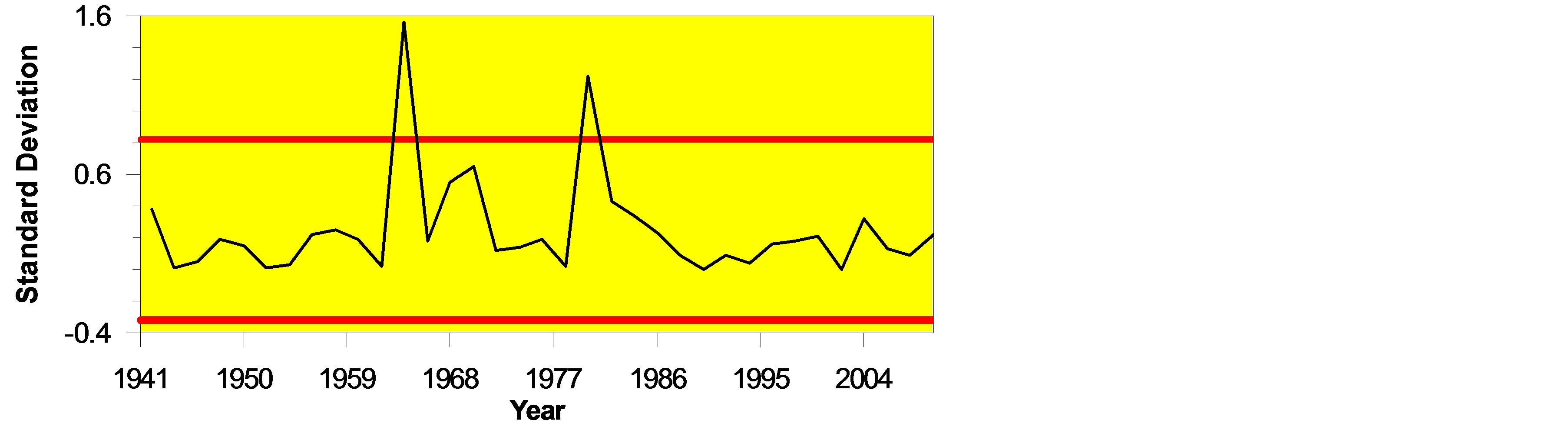
The Figure 4 with 4(a) and 4(c) presents that there is no significant change in annual mean and annual mean minimum temperature standard deviations and estimated standard deviations are 0.32˚C and 0.48˚C, respectively. But, a significant change in Table 2 and Figure 4 with 4(b) in annual means maximum temperature standard deviation was found. The CUSUM chart exhibits an abrupt change of level 1 category in the year 1963 (Confidence interval 1961, 1979) at a confidence level of 96% (Table 2). Prior to the change in 1963, annual mean maximum temperature standard deviation was 0.21˚C, while after the change the standard deviation of annual mean maximum temperature became 0.89˚C and another change in the year 1983 can be identified. Linear trends of standard deviations for each of the three data sets for the period (1941-2010) in question have been shown in Figure 5 with 5(a)-5(c) by simple plots of standard deviations against the years.
5. Conclusion
70-year time series of annual mean, annual mean maximum and annual mean temperature have been compiled
 (a)
(a)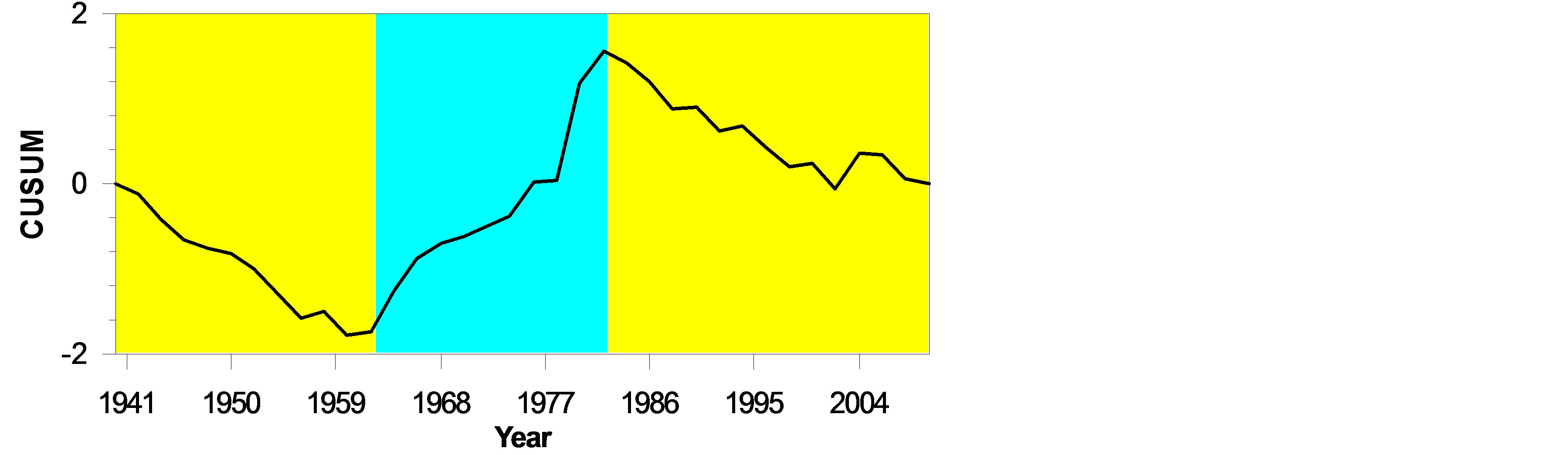 (b)
(b) (c)
(c)
Figure 4. CUSUM charts for (a) mean annual temperature standard deviation, (b) mean annual maximum temperature standard deviation, and (c) mean annual minimum temperature standard deviation.
Table 2. Significant changes in mean annual maximum temperature standard deviation.
and statistically analyzed. CUSUM charts have been prepared to identify the change points in the series, and bootstrapping technique has been employed to determine significance level associated with each of the detected change points. The analyses confirm a major change in mean annual temperature of Asansol to have occurred around 1986. For the mean maximum and mean minimum temperatures, such major changes have occurred somewhere around 1961 and 1994, respectively. Inspection of CUSUM Charts clearly demonstrates resemblance
 (a)
(a)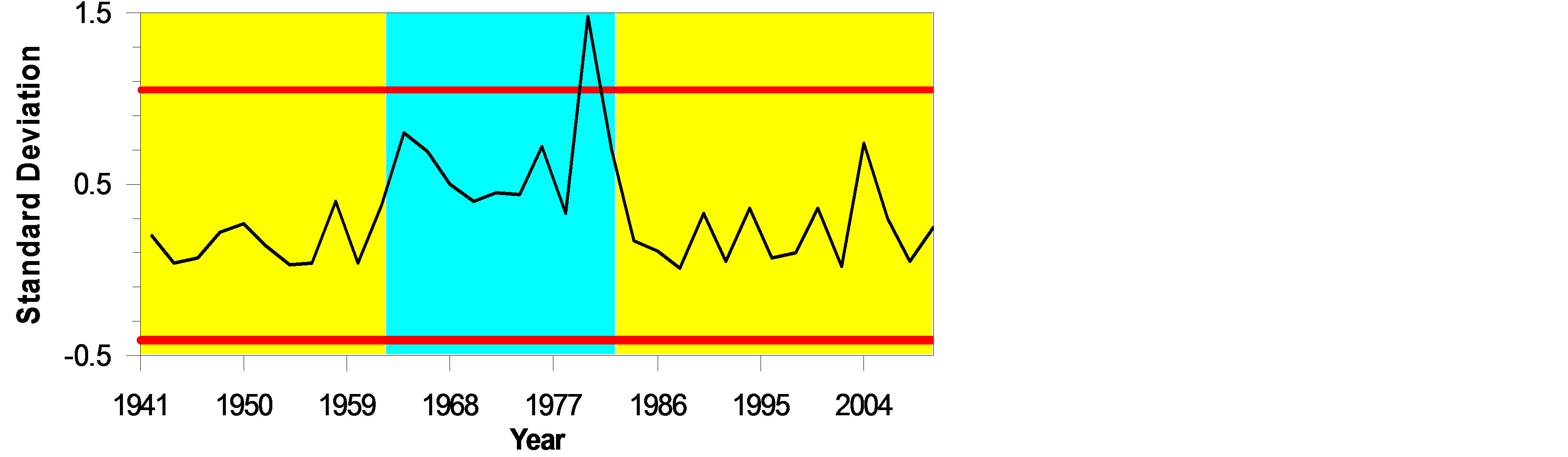 (b)
(b)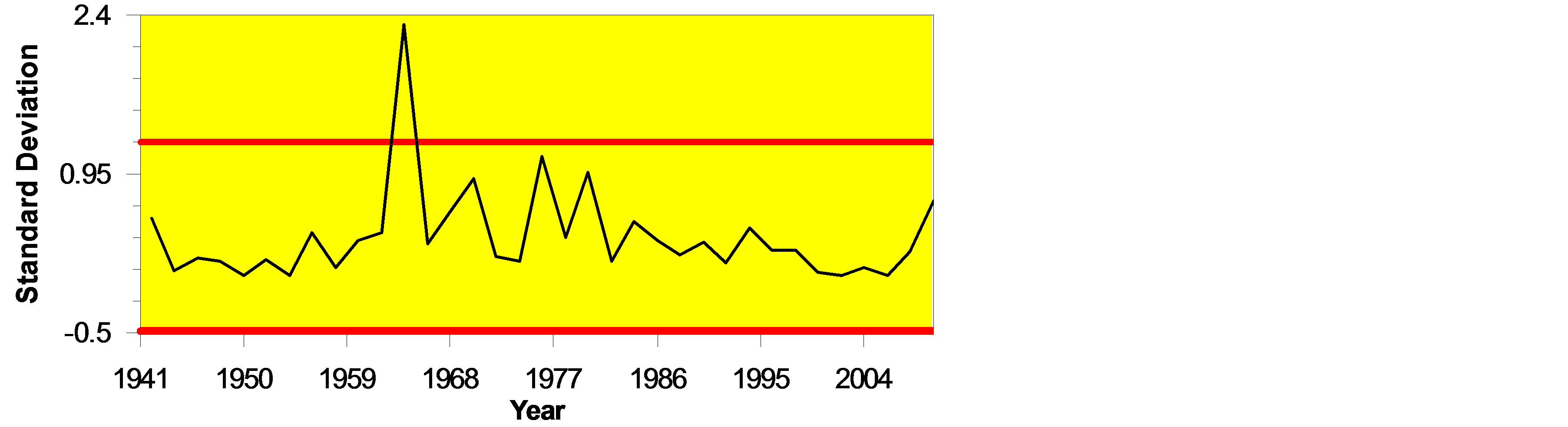 (c)
(c)
Figure 5. Temperature trends for (a) mean annual temperature standard deviation, (b) mean annual maximum temperature standard deviation, and (c) mean annual minimum temperature standard deviation with maximum range of temperature fluctuation indicated by red lines under the situation of no change in trend.
between mean annual and mean minimum temperature trends. The inhomogeneity in an unadjusted temperature time series is often attributed to change in instrumental arrangements and/or measuring conditions. But if such was the case in the present context, all the data sets would have supposedly indicated changes within approximately common range of years which could not be found in case of Asansol. Hence, the change in temperature trend may be due to rapid industrialization and expansion of mining activities and subsequent urbanization since 1980s. Above all, those activities took a huge toll of large-scale forest destructions which may be responsible for local level increase in mean annual and mean maximum temperature. But drawing such inferences does require inclusion of more data from larger number of stations in the analyses and adjustment or homogenization of data sets before employing them in change point analysis.
References
- IPCC (2007) Climate Change 2007: Synthesis Report. In: R. K. Pachauri and A. Reisinger, Eds., Contribution of Working Groups I, II and III to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change (IPCC), Cambridge University Press, Cambridge.
- IPCC (2007) Climate Change 2007: The Physical Science Basis. In: S. Solomon, D. Qin, M. Manning, Z. Chen, M. Marquis, K. B. Averyt, M. Tignor and H. L. Miller, Eds., Contribution of Working Group I to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change (IPCC), Cambridge University Press, Cambridge.
- IPCC (2007) Climate Change 2007: Impacts, Adaptation and Vulnerability. In: M. L. Parry, O. F. Canziani, J. P. Palutikof, P. J. van der Linden and C. E. Hanson, Eds., Contribution of Working Group II to the Fourth Assessment Report of the Intergovernmental Panel on Climate Change (IPCC), Cambridge University Press, Cambridge.
- Joeri, R., William, H., Jason, H.L., van Vuuren, D.P., Keywan, R., Mathews, B.M., Tatsuya, H., Kejun, J. and Malte, M. (2011) Emission Pathways Consistent with a 2˚C Global Temperature Limit. Nature Climate Change, 1, 413-418. http://dx.doi.org/10.1038/nclimate1258
- Spencer, R.W. (2008) The Discovery of Global Warming. American Institute of Physics, Harvard University Press, Cambridge. http://www.aip.org/history/climate/co2.htm
- (2005) Joint Science Academies’ Statement: Global Response to Climate Change. http://nationalacademies.org/onp/06072005.pdf
- Parker, D.E. and Alexander, L.V. (2002) Global and Regional Climate in 2001. Weather, 57, 328-340. http://dx.doi.org/10.1256/00431650260283505
- Brohan, P., Kennedy, J.J., Harris, I., Tett, S.F.B. and Jones, P.D. (2006) Uncertainty Estimates in Regional and Global Observed Temperature Changes: A New Dataset from 1850. Journal of Geophysical Research, 111, Article ID: D12106. http://dx.doi.org/10.1029/2005JD006548
- Jones, P.D. and Moberg, A. (2003) Hemispheric and Large-Scale Surface Air Temperature Variations: An Extensive Revision and Update to 2001. Journal of Climate, 16, 206-223.
- Soon, W., Baliunas, S., Posmentier, E.S. and Okeke, P. (2000) Variations of Solar Coronal Hole Area and Terrestrial Lower Tropospheric Air Temperature from 1979 to Mid-1998: Astronomical Forcing of Change in Earth’s Climate. New Astron, 4, 563-579. http://dx.doi.org/10.1016/S1384-1076(00)00002-6
- Landscheidt, T. (2000) Solar Wind near Earth: Indicator of Variations in Global Temperature. Proceedings of the 1st Solar and Space Weather Euro conference on the Solar Cycle a Tenerife, Tenerife, 25-29 September 2000, 497-500.
- Vinnikov, K.Y. andGrody, N.C. (2003) Global Warming Trend of Mean Troposphere Temperature Observed by Satellites. Science, 302, 269-272. http://dx.doi.org/10.1126/science.1087910
- Jones, P.D., Parker, D.E., Osborn, T.J. and Briffa, K.R. (2011) Global and Hemispheric Temperature Anomalies-Land and Marine Instrumental Records. Trends: A Compendium of Data on Global Change. http://cdiac.ornl.gov/trends/temp/jonescru/jones.html
- Nicholson, S.E. (2001) Climatic and Environmental Change in Africa during the Last Two Centuries. Climate Research, 17, 123-144. http://dx.doi.org/10.3354/cr017123
- Nicholson, S.E. and Kim, J. (1997) The Relationship of the E Niño Southern Oscillation to African Rainfall. International Journal of Climatology, 17, 117-135.
- Pielke, R.A. (2005) Land Use and Climate Change. Science, 310, 1625-1626. http://dx.doi.org/10.1126/science.1120529
- Robert Jr., R.C. and Sandra, W.B. (1987) The Impact of Rapid Urbanization on Pan Evaporation in Phoenix, Arizona. Journal of Climatology, 7, 593-597. http://dx.doi.org/10.1002/joc.3370070607
- Aguilar, E., Auer, I., Brunet, M., Peterson, T. and Wieringa, J. (2003) Guidelines on Climate Metadata and Homogenization. WMO TD. No. 1186 (WCDMP2), World Meteorological Organization, Geneva.
- He, W.P., Feng, G.L. and Wu Chou, Q. (2011) A New Method for Abrupt Dynamic Change Detection of Correlated Time Series. International Journal of climatology, 32, 1604-1614. http://dx.doi.org/10.1002/joc.2367
- Menne, M.J. and Williams Jr., C.N. (2009) Homogenization of Temperature Series via Pairwise Comparisons. Journal of Climate, 22, 1700-1717. http://dx.doi.org/10.1175/2008JCLI2263.1
- Brunet, M., et al. (2007) Temporal and Spatial Temperature Variability and Change over Spain during 1850-2005. Journal of Geophysical Research, 112, Article ID: D12117. http://dx.doi.org/10.1029/2006JD008249
- Della-Marta, P.M. and Wanner, H. (2006) A Method of Homogenizing the Extremes and Mean of Daily Temperature Measurements. Journal of Climate, 19, 4179-4197. http://dx.doi.org/10.1175/JCLI3855.1
- Serra, C., Burgueno, A. and Lana, X. (2001) Analysis of Maximum and Minimum Daily Temperatures Recorded at Fabra Observatory (Barcelona, Ne S 1917-1998. International Journal of Climatology, 21, 617-636. http://dx.doi.org/10.1002/joc.633
- Peterson, T.C., Easterling, D.R., Karl, T.R., et al. (1998) Homogeneity Adjustments of in Situ Atmospheric Climate Data: A Review. International Journal of Climatology, 18, 1493-1517. http://dx.doi.org/10.1002/(SICI)1097-0088(19981115)18:13<1493::AID-JOC329>3.0.CO;2-T
- Karl, T.R. and Williams Jr., C.N. (1987) An Approach to Adjusting Climatological Time Series for Discontinuous In-TACT>2.0.C homogeneities. Journal of Climate & Applied Meteorology, 26, 1744-1763.
- H. Alexanderson, () A Homogeneity Test Applied to Precipitation Data. Journal of Climatology, Vol. 6, 1986, pp. 661-675. http://dx.doi.org/10.1002/joc.3370060607
- Buishan, T.A. (1982) Some Methods for Testing the Homogeneity of Rainfall Records. Journal of Hydrology, 58, 11- 27. http://dx.doi.org/10.1016/0022-1694(82)90066-X
- Taylor, W. (2000) Change-Point Analysis: A Powerful Tool for Detecting Changes. Taylor Enterprises, Libertyville. http://www.variation.com/cpa/tech/changepoint
- Taylor, W. (2000) Change-Point Analyzer 2.3 Software Package. Taylor Enterprises Inc., Libertyville. http://www.variation.com/cpa/tech/changepoint
- Davison, A.C. and Hinkley, D.V. (1997) Bootstrap Methods and Their Application. Cambridge University Press, Cambridge. http://dx.doi.org/10.1017/CBO9780511802843


