ABSTRACT

This work seeks to describe intra-solution particle movement system. It makes use of data obtained from simulations of patients on efavirenz. A system of ordinary differential equations is used to model movement state at some particular concentration. The movement states’ description is found for the primary and secondary level. The primary system is found to be predominantly an unstable system while the secondary system is stable. This is derived from the state of dynamic eigenvalues associated with the system. The saturated solution-particle is projected to be stable both for the primary potential and secondary state. A volume conserving linear system has been suggested to describe the dynamical state of movement of a solution particle.

Keywords:

Ordinary Differential Equations, Stability, Nonautonomous Linear System, Concentration-Varying Eigenvalues, Solution Particle

1. Introduction

The intra-solution-particle movement system is described in this work. A system which consists of the primary and secondary movement states that is proposed in Nemaura (2015) is investigated. Differential Equations are used to describe dynamical systems. Most systems are described relative to time [1] [2] [3] . In this work, they are used to describe a dynamical system of the state of a solution particle relative to concentration.

Multiple compartmental modelling finds its use in fields such as Physiologically Based Pharmacokinetics, Engineering and Mathematical Biology [1] [3] [4] . Other researchers work with constant parameters that are obtained for autonomous linear systems. In this work, a simple system (nonautonomous linear system) whose parameters vary according to concentration is considered [5] [6] . The mixing problems have been widely studied by the use of ordinary differential equations [4] [7] [8] . Additionally, some researchers consider probable systems that arise from these mixing problems [7] [8] . This work proposes a system of linear ordinary differential equations that potentially govern the state of solution particle and shares a relation to the mixing problems. In addition, there is consideration of a volume conserving state of a solution particle. The dynamic eigenvalues from the corresponding matrix and stability of the concentration varying linear systems are proposed. The dynamic eigenvalues have found applications for linear time-varying systems [2] .

This work highlights possible intra-particle movement potential/states inferred to be present in the solution particle, at primary and secondary level and attempts to give mathematical form as in Nemaura (2015) [9] . It proposes multiple-compartmental models, one for the primary level and the other for the secondary level. The resultant form gives a general representation of movement within a solution particle.

2. Methods

The primary and secondary movement system of projected simulated data from patients who had been on efavirenz is used [9] . The software used, were R and Mathematica.

2.1. The Primary System

The primary system is a sub-system of the secondary and describes potential. It is projected to consist of four main movement entities that is convection, saturation, passive and advection. The form entity being the advective component [9] .

2.2. The Primary System of Solution Particle

A solution particle with concentration (x) is made up of four movement components (variables) at primary level C-convective, A-advective, P-Passive, and S-Saturation at primary level satisfying

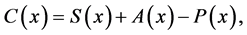(1)

(2)

where

We analyse the following system of differential equations in order to infer on the overall process occuring in describing state of movement in a solution particle (See Figure 1).

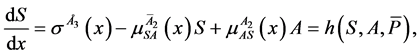(3)

(4)

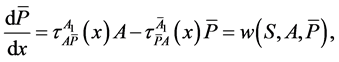(5)

Subject to,

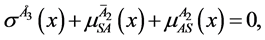
And

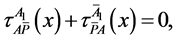
With 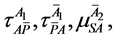and are the variable parameters. These two conditions allows no net change in the volumetric consituencies of the four movement components, where

―single phase third generation solution sub-particle at primary level, form inducing movement interaction with four main movement entities,

―single phase second generation solution sub-particle at primary level with four main movement entities, and

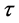―altering phase(s) first generation solution sub-particle at primary level with three main movement entities.

Solving the primary system above (1 - 5) in terms of advective components,

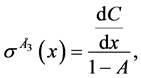
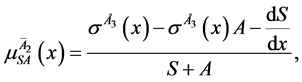
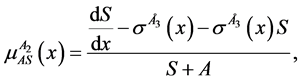
2.3. Stability Analysis of the Primary System

The equlibrium, steady state points are constant solutions, , and

which satisfy the nonlinear system of equations and These

points govern the behaviour of physical models. Thus we obtain (form potential), (space accesory potential), and (negative binding-orientation potential). It is important to note that the convective potential at equilibrium (primary level) is negative (nullifying/compensating accesory potential). Furthermore, it has the value of −1.

Local Analysis near Steady-State Points

Local analysis is studied near each steady state point. We begin by the following,

(6)

(7)

(8)

where, and are small.

(9)

(10)

(11)

The partial derivatives are evaluated at the equilibrium point. The stability of the steady state point is investigated by studying the eigenvalues of the Jacobian matrix (A matrix of the partial derivatives). The Jacobian matrix for the primary system is given by,

(12)

Ÿ (I)Undisturbed potential, where

. The characteristic equation of J is given by,

Eigenvalues of this system are given by,. The equilibrium point has neutral stability. Thus the primary unique space interacting potential has a neutral equilibrium before “disturbances”.

Ÿ (II) Disturbed (dissolving) potential,

The dynamic eigenvalues follows from the characteristic equation of J given by,

which is similar,

Thus the eigenvalues for this system are,

And

where, and

Ÿ (III) Saturated potential (:, , ). The characteristic equation is given by,

2.4. The Secondary System of Solution Particle

The product of advective primary interaction potential with its unique space (the relative uptake) results in a secondary advective movement system [9] . A solution particle with concentration (x) is made up of three movement components (variables) at secondary level―convective,―advective, and―Saturation at secondary level satisfying

(13)

This is represented by the following constituent system (See Figure 2),

(14)

(15)

Subject to,

With (variable parameters). The condition allows no net change in the volumetric consituents of the movement components. Where,

―single phase third generation solution sub-particle at secondary level, form

inducing movement interaction with four main movement entities,

―single phase second generation solution sub-particle at secondary level with four main movement entities.

Solving the secondary system above (13) - (15),

2.5. Stability Analysis of the Secondary System

The equlibrium, steady state points are constant solutions, and, which

satisfy the nonlinear system of equations and. It is shown that this

system is orbitally stable, which signifies that the solutions remain near the equilibrium point.

Local Analysis near Steady-State Points

Considering,

Thus we obtain, (form state), and

(space accessory state). It is important to note that the convective movement at secondary level is a stable state which is 0 (nullifying/stabilising accessory state). We study local analysis near each steady state point for Equations (14) & (15). We begin by the following,

(16)

(17)

where and are small. Next we substitute Equations (16) & (17) into (18) & (19).

(18)

(19)

The Jacobian matrix for the secondary system is given by,

(20)

The eigenvalues and for this system are given by and

respectively. The secondary system gives a form of neutral stability.

3. Results

3.1. Numerical Projections of Sub-Particle and Particle of Solution for the Primary System

The graphical representation of the advective components (sub-systems) are shown (see Figure 3). The solution is developed from the primary system equation in Nemaura (2015) and the system (1 - 5).

The primary system and sub-system equations and estimated parameters are given (See Equations (21) - (27) and Table 1).

Primary system equation,

(21)

Primary―sub-particle equation given by,

(22)

Primary―sub-particle equation given by,

(23)

Primary―sub-particle equation given by,

(24)

Primary―sub-particle equation given by,

(25)

where

Primary―sub-particle equation given by,

(26)

Primary―sub-particle equation given by,

(27)

where is the point when the system is projected to show considerable loss of homogeneity-potential.

Furthermore,

3.2. Numerical Projections of Sub-Particle and Particle of Solution Movement for the Secondary System

The graphical representation of the advective components (sub-systems) are shown (see Figure 4). The solution is developed from the secondary system equation in Nemaura (2015) and the system (13 - 15).

The secondary system and sub-system equations and estimated parameters are given (See Equations (28) - (31) and Table 2). Secondary system equation is given by,

(28)

Secondary―sub-particle equation given by,

(29)

Secondary―sub-particle equation given by,

(30)

Secondary―sub-particle equation given by,

(31)

3.3. Stability Numerical Analysis for Secondary System

Let and the plot of against x is given (See Figure 5). The results show that for almost all values of concentration (x). The following is proposed where is the error term in estimating

. The system is inferred to be stable.

4. Discussion

A nonautonomous linear system is developed that enables characterisation of the projected movement in a solution-particle [5] [6] . There are four main movement potential components at primary level with respect to advection. They are held together by the sub-system also a potential which is inferred to have five distinct systems (that is the two, s and two). While, the secondary system consists of two and s. The variable parameters in the system of ordinary differential equations are inferred to describe (advective) form components of movement. The movement description gives the state of solution particle and there is suggestion of the constituent entities.

The primary system is generally projected to be an unstable system relative to concentration. The saturated system is inferred to have stable potential. The reaction allowing state (non-saturated concentration) has unstable equilibrium potential at primary level. However, the secondary system is stable.

This work has managed to describe the possible state of kinetics of a solution-particle of efavirenz. It has shown that a saturated state can be equated to a stable state both at primary and secondary level. The constructed matrix in this case is traceless that is it has zero trace. The volume conserving systems have been considered in modelling of the physical systems and the theoretical framework is also developed in Lie Theory [10] [11] .

Acknowledgements

The author would like to thank the following; C. Nhachi, C. Masimirembwa, and G. Kadzirange, AIBST and The College of Health Sciences, University of Zimbabwe.

Cite this paper

Nemaura, T. (2016) Modelling the Dynamical State of the Projected Primary and Secondary Intra-Solu- tion-Particle Movement System of Efavirenz In-Vivo. International Journal of Modern Nonlinear Theory and Application, 5, 235- 247. http://dx.doi.org/10.4236/ijmnta.2016.54021

References