International Journal of Modern Nonlinear Theory and Application
Vol.3 No.3(2014), Article
ID:48633,8
pages
DOI:10.4236/ijmnta.2014.33015
On Slide Mode Control of Chaotic Rikitake Two-Disk Dynamo
—Chaotic Simulations of the Reversals of the Earth’s Magnetic Field
Ahmad Harb, Nabil Ayoub
School of Natural Resources Engineering, German Jordanian University, Amman, Jordan
Email: aharb48@gmail.com
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 5 June 2014; revised 3 July 2014; accepted 11 July 2014
ABSTRACT
The modern nonlinear theory, bifurcation and chaos theory are used in this paper to analyze the dynamics of the Rikitake two-disk dynamo system. The mathematical model of the Rikitake system consists of three nonlinear differential equations, which found to be the same as the mathematical model of the well-known Lorenz system. The study showed that under certain value of control parameter, the system experiences a chaotic behaviour. The experienced chaotic oscillation may simulate the reversal of the Earth’s magnetic field. The main objective of this paper is to control the chaotic behaviour in Rikitake system. So, a nonlinear controller based on the slide mode control theory is designed. The study showed that the designed controller was so effective in controlling the unstable chaotic oscillations.
Keywords:Chaos Theory, Nonlinear Control, Magnetic Theory, Sliding-Mode Control Theory

1. Introduction
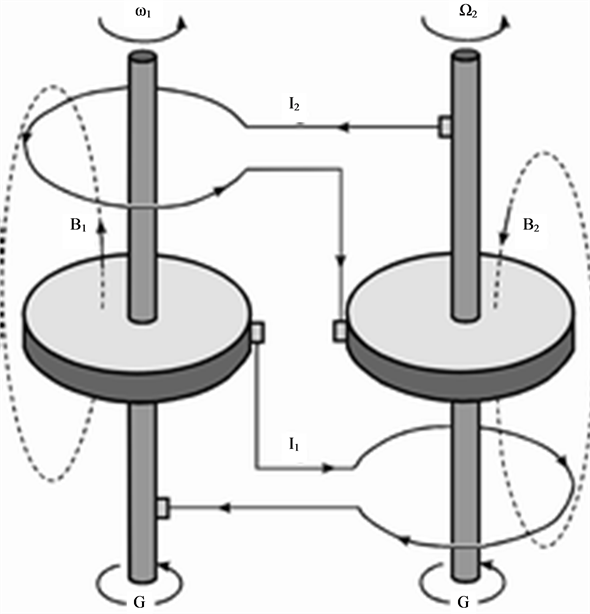
Figure 1 [1] [2] shows the Rikitake two-disk dynamo. As shown in Figure 1, two conducting disks, 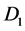 (Left) and
(Left) and ![]() (Right) are subjected to a common torque of magnitude G. Disks
(Right) are subjected to a common torque of magnitude G. Disks 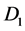 and
and ![]() rotate in the same sense. Disk
rotate in the same sense. Disk 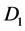 has an angular velocity,
has an angular velocity, 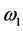 , around the axis of rotation
, around the axis of rotation 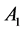 and
and ![]() has an angular velocity,
has an angular velocity, 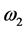 , around the axis of rotation
, around the axis of rotation . Current loop
. Current loop  is coaxial with disk
is coaxial with disk ![]() with axis
with axis 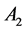 and
and 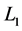 is below
is below![]() , while current loop
, while current loop 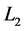 is coaxial with disk
is coaxial with disk  with axis
with axis 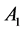 and
and 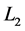 is above
is above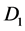 . Currents
. Currents ![]() and
and  both run upwards in the axial wires
both run upwards in the axial wires 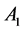 and
and  respectively. From the configuration of Figure 1 we see that current
respectively. From the configuration of Figure 1 we see that current ![]() runs radially outward in Disk
runs radially outward in Disk 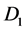 while current
while current 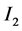 runs radially inward in Disk
runs radially inward in Disk![]() . Loop
. Loop 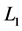 is connected to Disk
is connected to Disk 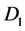 and its axis of rotation
and its axis of rotation 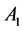 by conducting brushes, similarly loop
by conducting brushes, similarly loop 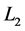 is connected to
is connected to
Disk ![]() and its axis of rotation
and its axis of rotation 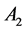 by conducting brushes. Current loop
by conducting brushes. Current loop  causes a magnetic field
causes a magnetic field 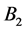 to pierce through the rotating disk
to pierce through the rotating disk![]() , and current loop
, and current loop  causes a magnetic field
causes a magnetic field  to pierce through the rotating disk
to pierce through the rotating disk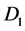 . According to Faraday’s law and Lenz’s law magnetic field
. According to Faraday’s law and Lenz’s law magnetic field 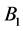 crossing disk
crossing disk 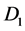 induces an emf between the center of
induces an emf between the center of 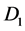 and its rim causing an induced inward current
and its rim causing an induced inward current 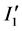 to occur in the opposite direction to
to occur in the opposite direction to ![]() which reduces the original current
which reduces the original current![]() . A similar situation happens in disk
. A similar situation happens in disk ![]() and magnetic field
and magnetic field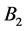 , but of opposite polarity to that of
, but of opposite polarity to that of 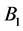 and
and , where the induced emf is also between the center of
, where the induced emf is also between the center of ![]() and its rim causing an induced outward current
and its rim causing an induced outward current 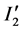 to occur in the opposite direction to
to occur in the opposite direction to 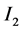 which reduces the original current
which reduces the original current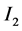 . This process will result in electric current reversals in both loops which causes a reversal in the corresponding magnetic fields. Chaos shall result under particular initial conditions.
. This process will result in electric current reversals in both loops which causes a reversal in the corresponding magnetic fields. Chaos shall result under particular initial conditions.
The dynamics of Rikitake system has been discussed by many researchers. E. C. Bullard [3] -[7] has extensively discussed the behavior of earth’s magnetic field and its simulation with dynamos. He first discussed the magnetic field within the earth [5] , then the similar behavior between a set of homogeneous dynamos and terrestrial magnetism [6] and in 1955 [7] discussed the stability of a homopolar dynamo. Liu Xiao-Jun, et al. [8] analyzed the dynamics of Rikitake two-disk dynamo to explain the reversals of the Earth’s magnetic field. They concluded that the chaotic behavior of the system can be used to simulate the reversals of the geomagnetic field. The Rikitake chaotic attractor was studied by several authors. T. McMillen [9] has studied the shape and dynamics of the Rikitake attractor. J. Llibre et al. [10] used the Poincare compactification to study the dynamics of the Rikitake system at infinity. Chien-Chih Chen et al. [11] have studied the stochastic resonance in the periodically forced Rikitake dynamo.
Many researchers start working on controlling the chaotic behaviors. Harb and Ayoub [12] have designed a nonlinear controller based on backstepping nonlinear theory to control the chaotic behaviour in Rikitake system. Harb and Harb [13] have designed a nonlinear controller to control the chaotic behavior in the phase-locked loop by means of nonlinear control. Harb and Abdel-Jabber [14] used both linear and nonlinear control to mitigate the chaotic oscillations in electrical power system. Nayfeh et al. [15] , Chiang et al. [16] and Abed et al. [17] have controlled the chaotic oscillations in power systems using nonlinear control. Chang and Chen [18] investigated bifurcation characteristics of nonlinear systems under a PID controller. The main objective of control is to stabilize and delay a chaotic oscillation and reduce the amplitude of bifurcation solution. In [19] , they used a control law to transform an unstable subcritical bifurcation point into a stable supercritical bifurcation point.
Lately, the control aspect of the Rikitake chaotic attractor was studied through self coupling of single state variable and nonlinear feedback controller with partial systems states [20] .
In this paper, we used the nonlinear control based on slide mode control to control the chaotic oscillations of the Rikitake two-disk dynamo.
2. Mathematical Model
As shown in Figure 1, the Rikitake two-disk system consists of two conducting rotating disks. These disks are connected into two coils. The current in each coil feeds the magnetic field of the other. The self inductance 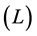 and resistance
and resistance 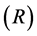 are the same in each circuit. An external constant mechanical torque
are the same in each circuit. An external constant mechanical torque 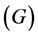 for each circuit is applied on the axis to rotate with an angular velocity. The
for each circuit is applied on the axis to rotate with an angular velocity. The ![]() circuit equations as shown in Figure 1 are given as:
circuit equations as shown in Figure 1 are given as:
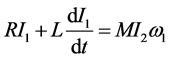 (1)
(1)
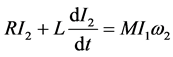 (2)
(2)
where 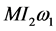 and
and 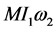 are the rotation voltages
are the rotation voltages 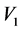 and
and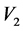 .
. ![]() is the mutual inductance.
is the mutual inductance.
If the moment of inertia of each disk, 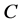 is considered, the system mathematical model can be written after [3] as follows:
is considered, the system mathematical model can be written after [3] as follows:
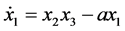 (3)
(3)
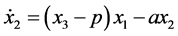 (4)
(4)
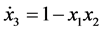 (5)
(5)
where  and
and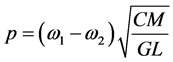 .
.
3. Uncontrolled System
Simulation Results and Discussion
The equilibrium solution or constant solution of the system can be found if we let the set of Equations (3)-(5) to be zero. One will end up with a set of nonlinear algebraic equations. One of the solutions of this set of equations willbe function of one of the control parameters. The stability of this constant solution, can be studied by using eigenvalue analysis which is based on the Jacobian matrix derived based on linearization. The eigenvalues of the Jacobian matrix of the set of Equations (3)-(5) evaluated at the equilibrium point. In this paper, we used our own program for calculating and analyzing the stability of the fixed points and their bifurcations rather than using software packages in the market.
On the other hand, the stability of the periodic solution is studied by means of the Floquet theory. At the value of the control parameter![]() , we found that the system is experiencing chaotic oscillations as shown in Figure 2 and Figure 3. In this paper, the main objective is to find a way to eliminate the chaotic oscillations. So, a nonlinear controller based on backstepping nonlinear theory control is designed. In the next section, the nonlinear controller design will be discussed.
, we found that the system is experiencing chaotic oscillations as shown in Figure 2 and Figure 3. In this paper, the main objective is to find a way to eliminate the chaotic oscillations. So, a nonlinear controller based on backstepping nonlinear theory control is designed. In the next section, the nonlinear controller design will be discussed.
4. Controlled System
4.1. Slide Mode Nonlinear Controller
Sliding mode control (SMC) is a variable structure control utilizing a high-speed switching control law to drive a system state trajectory onto a specified and user chosen surface, so called sliding surface, and to maintain the
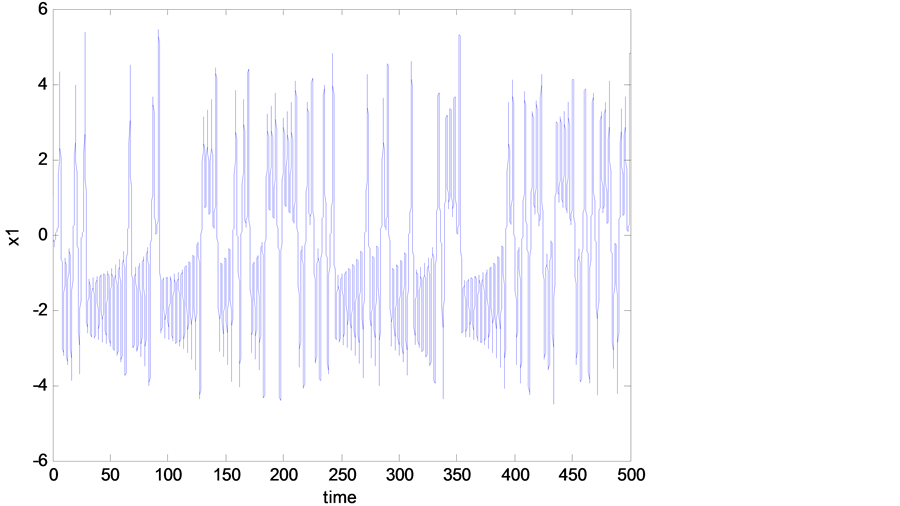
Figure 2. Time history (chaotic behavior, without controller).
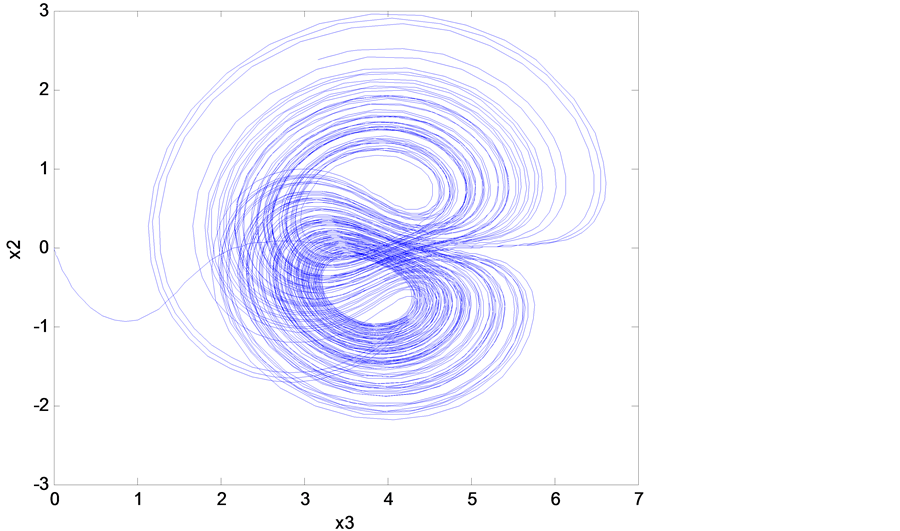
Figure 3. State space trajectory projection (chaotic behavior, without controller).
system state trajectory on the sliding surface at subsequent times. Many researchers have been used such a controller, for example; Korondi et al. [21] , Hung et al. [22] , Slotine and Sastry [23] , and Slotine and Li [24] .
To this end, let us rewrite the Equations (3)-(5) as follows:
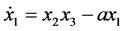 (6)
(6)
 (7)
(7)
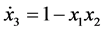 (8)
(8)
where![]() , is the control signal need to be designed.
, is the control signal need to be designed.
The two separate phases of the sliding mode design method are:
Phase 1:
Sliding-surface design: an appropriate sliding surface must be selected to yield desirable performance.
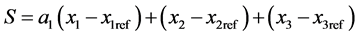 (9)
(9)
where  is Tuning parameter.
is Tuning parameter.
Phase 2:
Sliding-reachability condition design
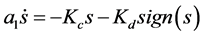 (10)
(10)
where ![]() and
and 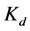 are positive constant design parameters.
are positive constant design parameters.
4.2. Construction of the Control Law
By differentiating the sliding surface and equating with the reachability condition and solving out for![]() , the control signal will be:
, the control signal will be:
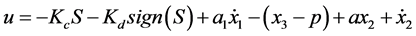 (11)
(11)
4.3. Simulation Results and Discussion
As mentioned previously, the Rikitake system is experiencing a chaotic behavior as shown in Figure 2, Figure 3, and this was when no control signal added to the system. But once we add the designed control signal 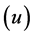 in Equation (11) to the mathematical model of the Rikitake system Equations (6)-(8), one can see that all the chaotic oscillations, shown in Figure 2 and Figure 3, have been eliminated as shown in Figures 4-7. Figure 6 and Figure 7 show the time history of the system when the designed controller
in Equation (11) to the mathematical model of the Rikitake system Equations (6)-(8), one can see that all the chaotic oscillations, shown in Figure 2 and Figure 3, have been eliminated as shown in Figures 4-7. Figure 6 and Figure 7 show the time history of the system when the designed controller![]() , is applied after 50 sec. One can see how effective the controller in eliminating the chaotic oscillations.
, is applied after 50 sec. One can see how effective the controller in eliminating the chaotic oscillations.
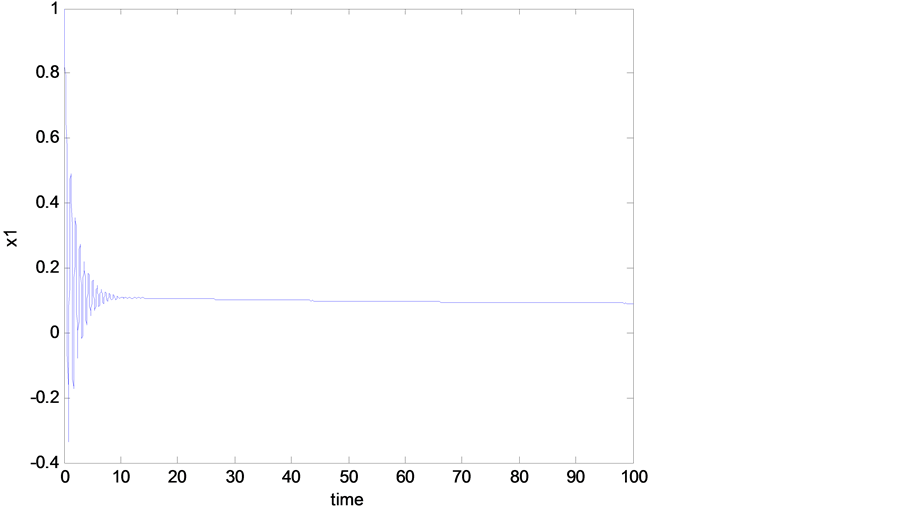
Figure 4. Time history (with controller).
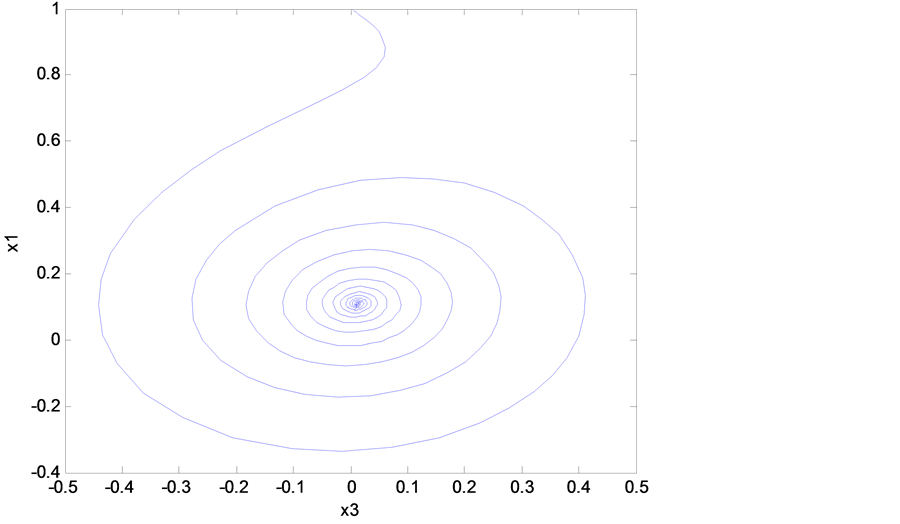
Figure 5. State space trajectory projection (with controller).
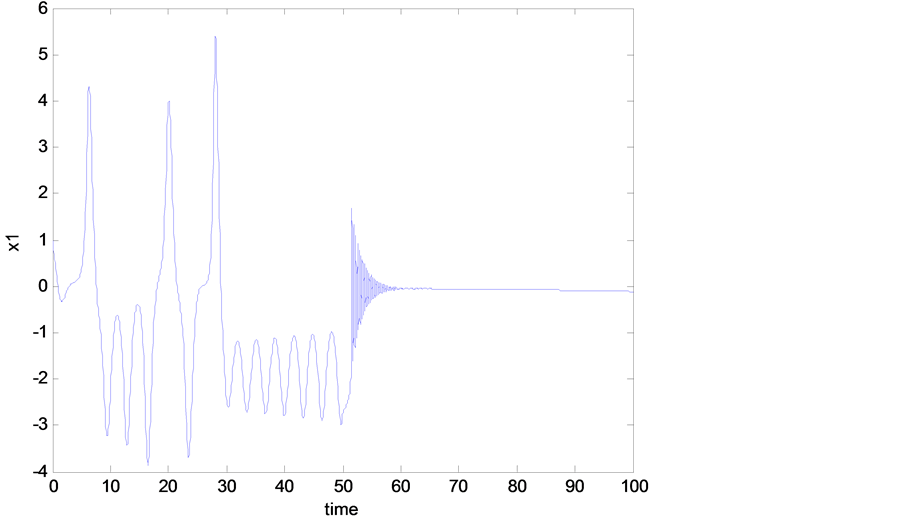
Figure 6. State space trajectory projection (with controller).
5. Conclusion
Bifurcation and chaos theory was used to investigate dynamics of the Rikitake two-disk dynamo. Rikitake system mathematical model consists of three nonlinear differential equations, which found to be the same as the mathematical model of the well known Lorenz system. This system is experiencing a chaotic behavior at certain value of the control parameter. The experienced chaotic oscillation can simulate the reversal of the Earth magnetic field. To control chaotic behavior, a nonlinear controller based on the slide mode control theory was
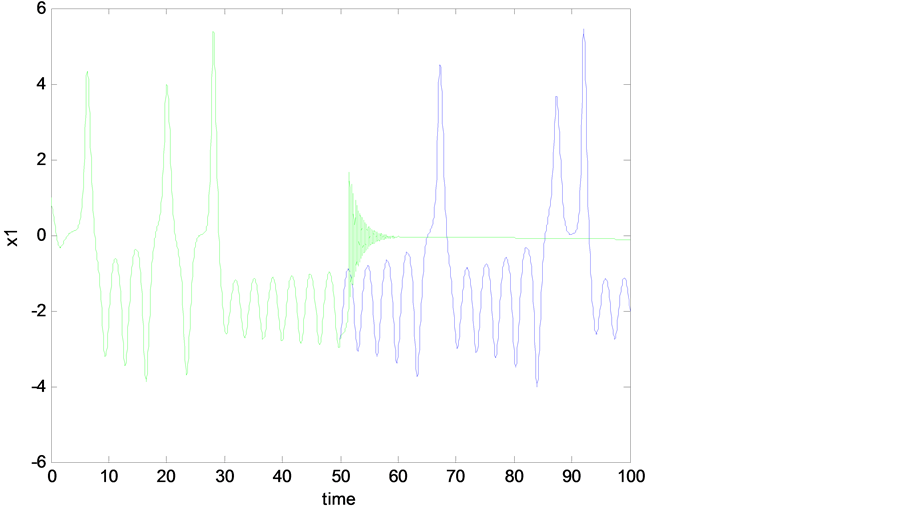
Figure 7. Comparison of state space trajectory projection between two cases (with and without controller, and the controller applied after 50 sec).
designed. The study showed that the designed controller was so effective to eliminate the unstable chaotic oscillations of the Rikitake two-disk dynamo.
References
- Rikitake, T. (1958) Oscillations of a System of Disk Dynamos. Proceedings of the Cambridge Philosophical Society, 54, 89-105. http://dx.doi.org/10.1017/S0305004100033223
- http://oen.dydaktyka.agh.edu.pl/dydaktyka/matematyka/c_fraktale_i_chaos/chaos.php?rozdzial=8
- Danca, M.-F. and Codreanu, S. (2011) Finding the Rikitake’s Attractors by Parameter Switching. arXiv:1102.2164v1
- Danca, M.-F. and Codreanu, S. (2012) Modeling Numerically the Rikitake’s Attractors. Journal of the Franklin Institute, 349, 861-878.
- Bullard, E.C. (1949) The Magnetic Field within the Earth. Proceedings of the Royal Society, 197, 433-453.http://dx.doi.org/10.1098/rspa.1949.0074
- Bullard, E.C. and Gellman, H. (1954) Homogeneous Dynamos and Terrestrial Magnetism. Philosophical Transactions of the Royal Society of London A, 247, 213-278.
- Bullard, E.C. (1955) The Stability of a Homopolar Dynamo. Proceedings of the Cambridge Philosophical Society, 51, 744-760. http://dx.doi.org/10.1017/S0305004100030814
- Liu, X.-J., Li, X.-F., Chang, Y.-X. and Zhang, J.-G. (2008) Chaos and Chaos Synchronism of the Rikitake Two-Disk Dynamo. 4th International Conference on Natural Computation, IEEE Computer Society, Jinan, 18-20 October 2008, 613-617.
- McMillen, T. (1999) The Shape and Dynamics of the Rikitake Attractor. The Nonlinear Journal, 1, 1-10.
- Llibre, J. and Messias, M. (2009) Global Dynamics of the Rikitake System. Physica D, 238, 241-252.http://dx.doi.org/10.1016/j.physd.2008.10.011
- Chen, C.-C. and Tseng, C.-Y. (2007) A Study of Stochastic Resonance in the Periodically Forced Rikitake Dynamo. Terrestrial, Atmospheric and Oceanic Sciences, 18, 671-680. http://dx.doi.org/10.3319/TAO.2007.18.4.671(T)
- Harb, A. and Ayoub, N. (2010) Nonlinear Control of Chaotic Rikitake Two-Disk Dynamo. International Journal of Nonlinear Science, 9, 1-8.
- Harb, A. and Harb, B. (2004) Chaos Control of Third-Order Phase-Locked Loops Using Backstepping Nonlinear Controller. Chaos, Solitons & Fractals, 20, 719-723.
- Harb, A. and Abedl-Jabbar, N. (2003) Controlling Hopf Bifurcation and Chaos in a Small Power System. Chaos, Solitons & Fractals, 18, 1055-1063.
- Nayfeh, A.H., Harb, A.M. and Chin, C. (1996) Bifurcation in a Power System Model. International Journal of Bifurcation and Chaos, 6.
- Abed, E.H., Alexander, J.C., Wang, H., Hamdan, A.H. and Lee, H.C. (1992) Dynamic Bifurcation in a Power System Model Exhibiting Voltage Collapse. Proceedings of the 1992 IEEE International Symposium on Circuits and Systems, San Diego, 10-13 May 1992, 2509-2512. http://dx.doi.org/10.1109/ISCAS.1992.230476
- Chiang, H.-D., Dobson, I., Thomas, R.J., Thorp, J.S. and Fekih-Ahmed, L. (1990) On Voltage Collapse in Electric Power Systems. IEEE Transactions on Power Systems, 5, 601-611. http://dx.doi.org/10.1109/59.54571
- Chang, H.-C. and Chen, L.-H. (1984) Bifurcation Characteristics of Nonlinear Systems under Conventional PID Control. Chemical Engineering Science, 39, 1127-1142. http://dx.doi.org/10.1016/0009-2509(84)85075-7
- Abed, E.H. and Fu, J.-H. (1986) Local Feedback Stabilization and Bifurcation Control, I. Hopf Bifurcation. Systems Control Letters, 7, 11-17. http://dx.doi.org/10.1016/0167-6911(86)90095-2
- Jian, J., Shen, Y. and Yu, H. (2008) Synchronization of Rikitake Chaotic Attractor via Partial System States. Proceedings of the 9th International Conference for Young Computer Scientists, Hunan, 18-21 November 2008, 2919-2924.
- Korondi, P., Hashimoto, H. and Utkin, V. (1994) Proceedings of the Asian Control Conference, 381 Lee, S. 1995.
- Hung, J.Y., Gao, W. and Hung, J.C. (1993) Variable Structure Control: A Survey. IEEE Transactions on Industrial Electronics, 40, 2-22. http://dx.doi.org/10.1109/41.184817
- Slotine, J.-J.E. and Sastry, S.S. (1983) Tracking Control of Non-Linear Systems Using Sliding Surfaces, with Application to Robot Manipulators. International Journal of Control, 38, 465-492.http://dx.doi.org/10.1080/00207178308933088
- Slotine, J.-J.E. and Li, W. (1991) Applied Nonlinear Control. Prentice Hall, New Jersey.