International Journal of Modern Nonlinear Theory and Application
Vol.2 No.4(2013), Article ID:41228,11 pages DOI:10.4236/ijmnta.2013.24034
The Effects of Void-Reactivity Feedback and Neutron Interaction on the Nonlinear Dynamics of a Nuclear-Coupled Boiling System
Nuclear Science and Technology Development Center, National Tsing Hua University, Hsinchu, Taiwan
Email: ctlee2@mx.nthu.edu.tw
Copyright © 2013 Jin Der Lee. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received October 31, 2013; revised November 30, 2013; accepted December 6, 2013
Keywords: Multiple Channel; Multi-Point Reactor; Void-Reactivity; Neutron Interaction; Nonlinear Oscillation
ABSTRACT
The present study explores the effects of void-reactivity feedback and neutron interaction on the nonlinear phenomena of a seven-nuclear-coupled boiling channel system with a constant total flow rate. The results show that the void-reactivity feedback and the neutron interaction both have significant effects on the nonlinear characteristics of this system. The complex nonlinear phenomena may depend on the magnitudes of the void-reactivity coefficient and neutron interaction parameter. The results demonstrate that complex nonlinear phenomena, i.e. various complex periodic oscillations and complex chaotic oscillations, can appear in the present system as the variations over certain values of void-reactivity coefficient and neutron interaction parameter under some specific operating states. These imply multiple complex periodic and chaotic attractors, with very interesting and peculiar shapes on the phase space, exist in this system.
1. Introduction
Complex nonlinear phenomena, significantly chaotic oscillations, may exist in different two-phase flow systems. Rizwan-Uddin and Dorning [1] reported theoretically a chaotic attractor in a two-phase flow system with periodically oscillating external pressure drop. Clausse and Lahey [2] identified a chaotic attractor occurring in a boiling channel with very low inlet flows. Lin et al. [3] illustrated a series of period-doubled bifurcation at high inlet subcoolings in an autonomous nuclear-coupled boiling system. Eventually, chaotic oscillations appeared in their forced circulation system. Lee and Pan [4] recognized a route from the periodic oscillation to the chaotic oscillation through period-doubled bifurcation for a nuclear-coupled boiling natural circulation loop with a strong void-reactivity feedback. Prasad and Pandey [5] also reported such a route to chaos through period-doubled bifurcation in a nuclear-coupled natural circulation system. Moreover, Wu et al. [6] presented experimental observations on the evolution of periodic oscillations toward chaos at high inlet subcoolings in a low pressure, two-phase natural circulation loop.
Most two-phase flow systems, i.e. boiling water reactors (BWRs), have multiple parallel boiling channels. If the multiple channels are subject to substantially different thermal and hydraulic conditions, strong interactions can occur in these channels. The channels may oscillate with different phases and magnitudes among each other. Such interaction induced instability between parallel channels is unique for multi-channel systems [7]. A distinctive type of chaotic attractor, the so-called complex strange attractor, can be induced by the interactions among multiple loops or multiple boiling channels under some specific operating conditions. A complex strange attractor evolved from the Lorenz attractor as a result of loop interactions was reported by [8] in their singlephase natural circulation double loop system. Lee and Pan [9] reported another type of complex strange attractor evolved from the Rossler attractor due to the coupled channel-to-channel thermal-hydraulic and subcore-tosubcore neutron interactions. Recently, Lee and Pan [10] also investigated the nonlinear dynamics and possible oscillation types of a single or multiple nuclear-coupled boiling channel system subject to strong void-reactivity feedbacks. The results demonstrated a route from periodic oscillations to chaotic oscillations through the perioddoubled bifurcation for a single nuclear-coupled boiling channel by strengthening the nuclear-coupled effects. Complex nonlinear phenomena, such as various periodic oscillations and complex Rossler type chaotic oscillations, might appear in the system of three boiling channels coupled with a three-point reactor under the condition of strong void-reactivity feedbacks and weak subcore-to-subcore neutron interactions.
The above brief review reveals complex and interesting nonlinear phenomena in different two-phase flow systems investigated in the literature. In a multiple nuclear-coupled boiling channel system, there are two coupling and competing nuclear effects on the system stability, i.e. the unstable effect of the void-reactivity feedback versus the stable effect of the neutron interactions [9]. Our previous studies [9,10] suggested that these two effects might have prominent influences on the dynamic characteristics of a nuclear-coupled boiling system. And, their effects on the nonlinear dynamics of a seven nuclear-coupled boiling channel system will be further investigated in the present study.
2. The Model
On the basis of the design of an advanced boiling water reactor (ABWR) [11], the multiple boiling channel model coupled with multi-point reactors [9] are adopted to analyze the nonlinear dynamics of the system numerically. The present study considers the multiple coupling dynamics among multiple channels, fuel rods and multi-point reactors as shown in Figure 1. The dynamics of multi-channel thermal-hydraulics may affect the dynamics of neutron field through void-reactivity feedbacks. This can further affect the dynamics of fuel rod heat transfer resulted by the dynamic heat generation rates. The dynamics of fuel rod can produce effects on the multi-channel thermal-hydraulics with the dynamic heat fluxes and on the neutron field dynamics through Doppler-reactivity feedbacks, and etc.
2.1. Multi-Channel Thermal Hydraulics
By adopting the homogeneous two-phase flow model and considering the j-th channel in the system of M parallel channels shown in Figure 1(a), the following dimensionless set of ordinary differential equations for the dynamics of multiple boiling channels, with a constant total mass flow rate and the same dynamic channel pressure drop, can be derived [12]:
 (1)
(1)

Figure 1. The multiple coupling feedbacks and interactions among multiple channels, fuel rods and multi-point reactors.
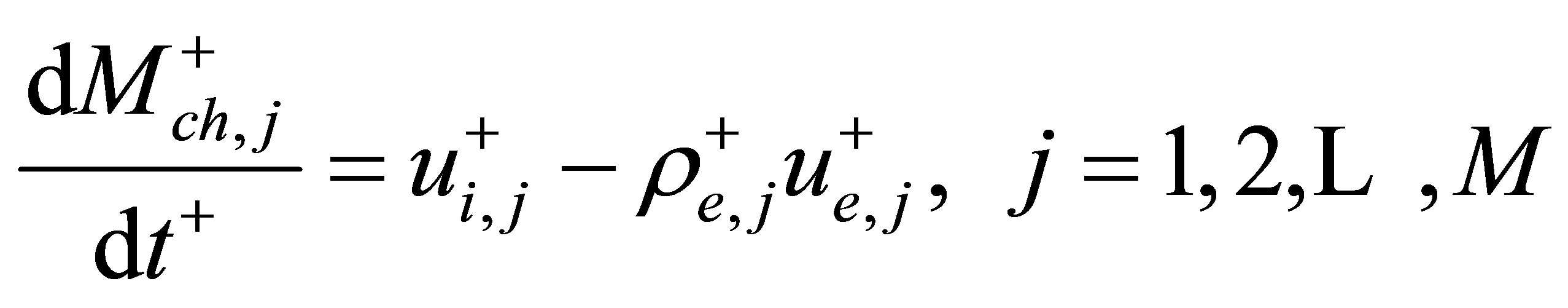 . (2)
. (2)
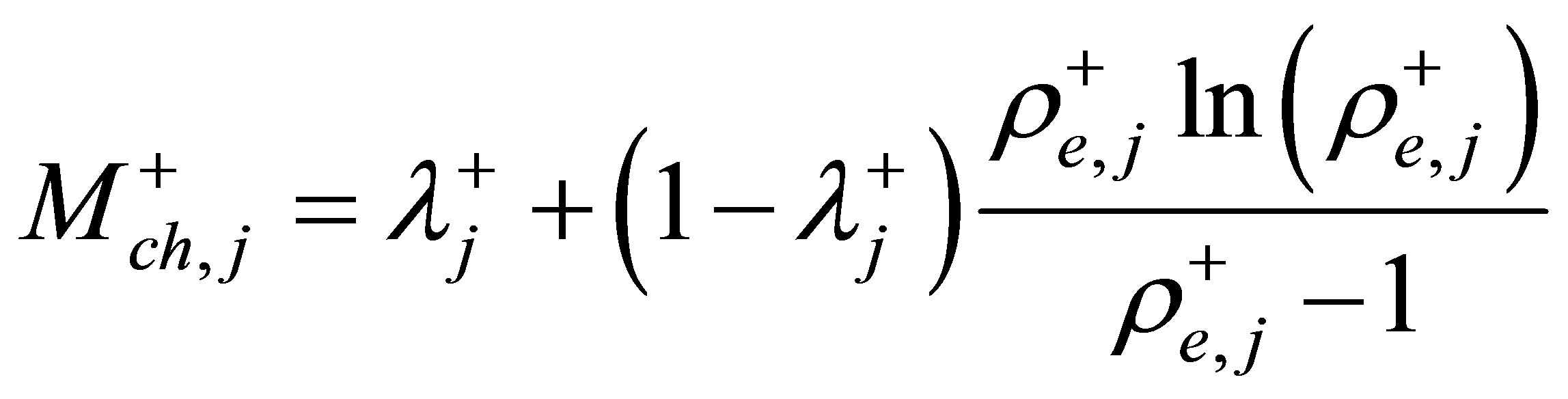 (3)
(3)
 (4)
(4)
 (5)
(5)
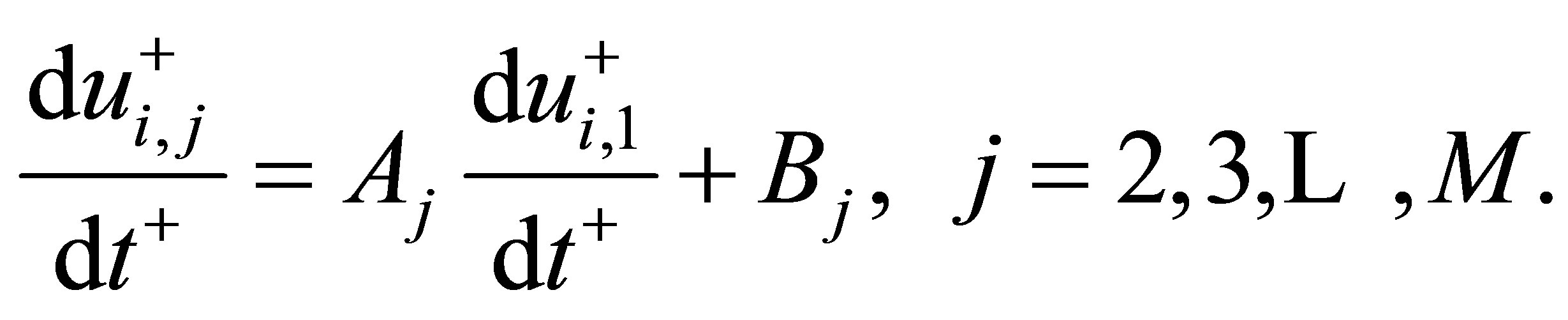 (6)
(6)
 (7)
(7)
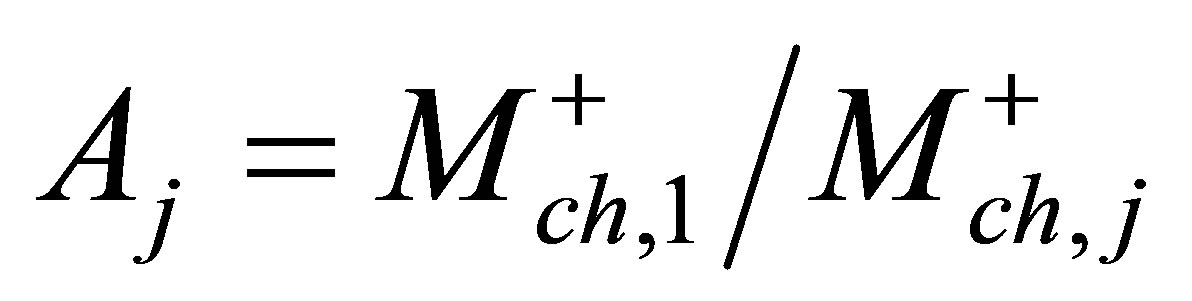 (8)
(8)
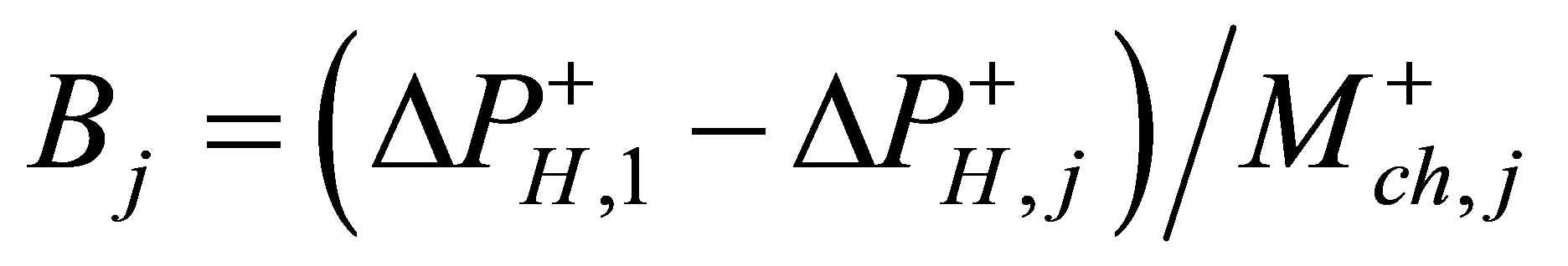 (9)
(9)
2.2. Dynamics of Fuel Rod Heat Transfer
Treating the fuel rod by a two-node lumped system revealed in Figure 1(b), the dynamics of fuel rod heat transfer can be described by the following two dimensionless dynamic equations for the average temperature of the fuel pellet 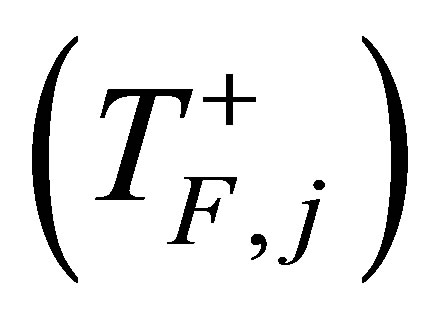 and cladding
and cladding 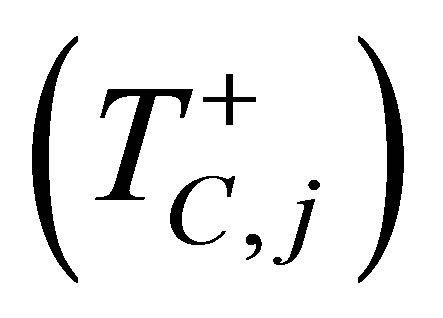 respectively in the j-th subcore [3]:
respectively in the j-th subcore [3]:
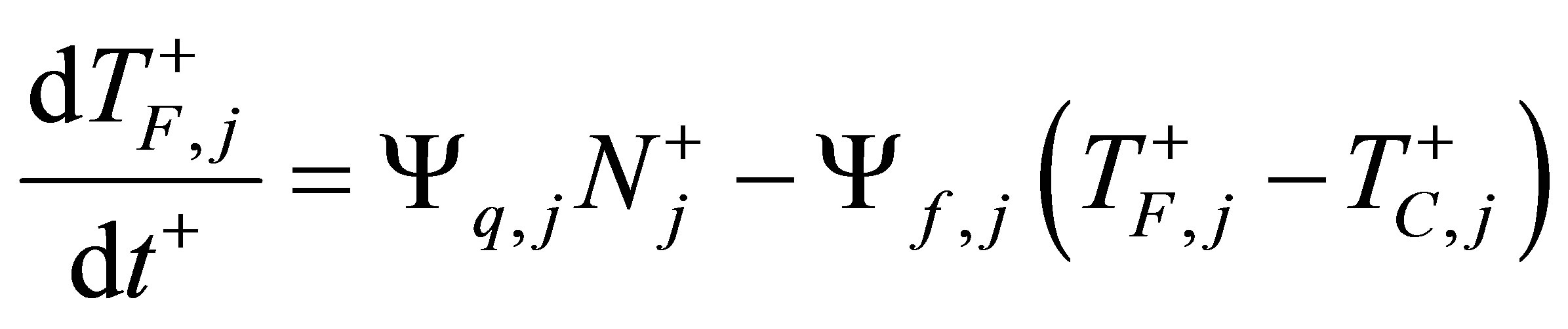 (10)
(10)
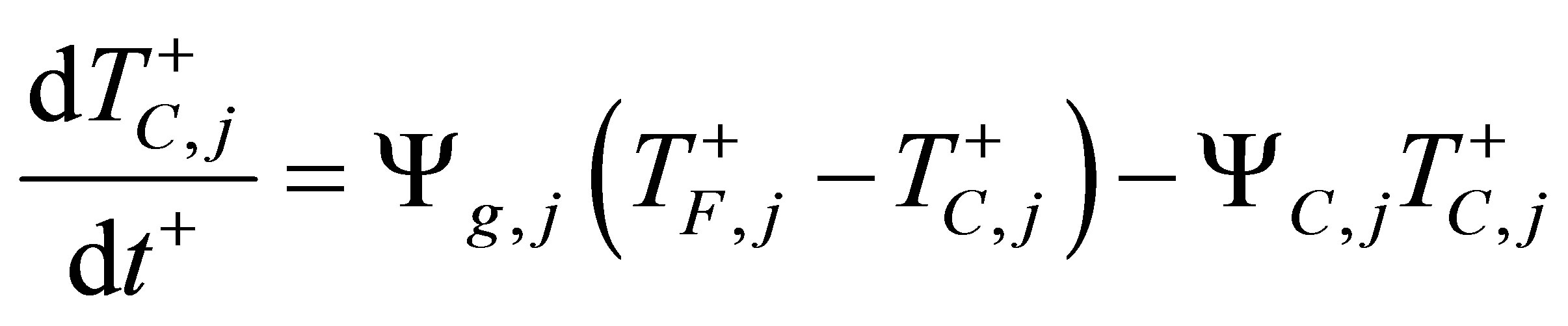 (11)
(11)
where
 (12)
(12)
 (13)
(13)
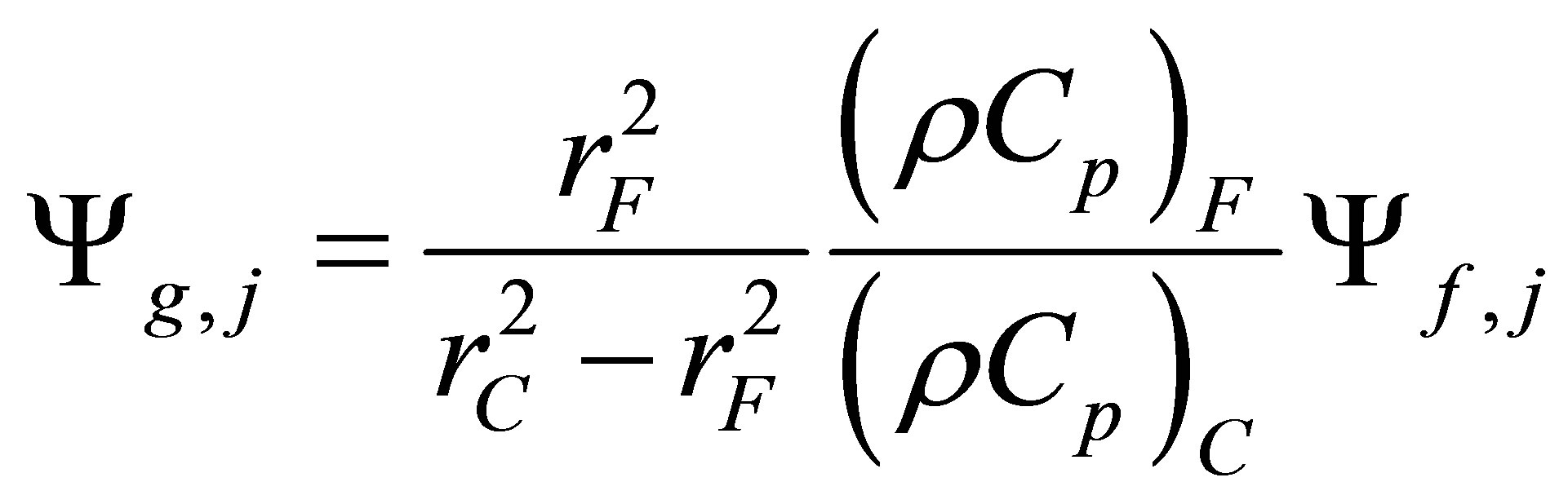 (14)
(14)
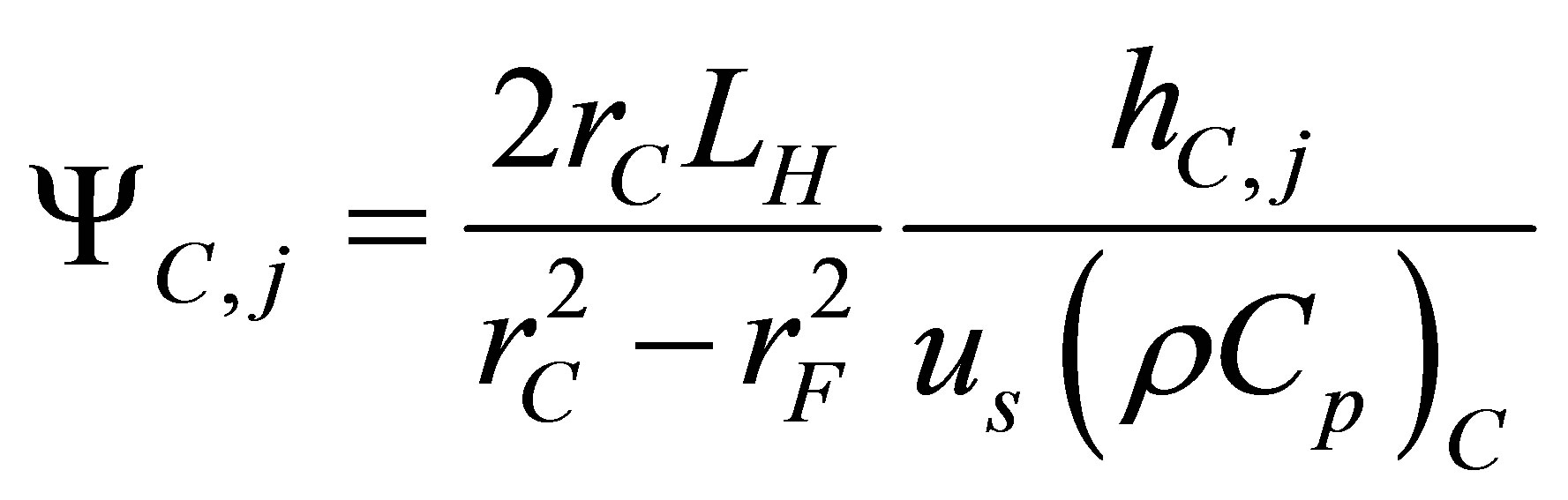 (15)
(15)
As a result, the dynamic heat flux on the j-th fuel rod surface can be expressed as in [3]:
 (16)
(16)
2.3. Multi-Point Neutron Dynamics
Considering the neutron interactions among subcores illustrated in Figure 1(c), the dimensionless dynamic equation for the neutron density in the j-th subcore can be expressed as in [9]:
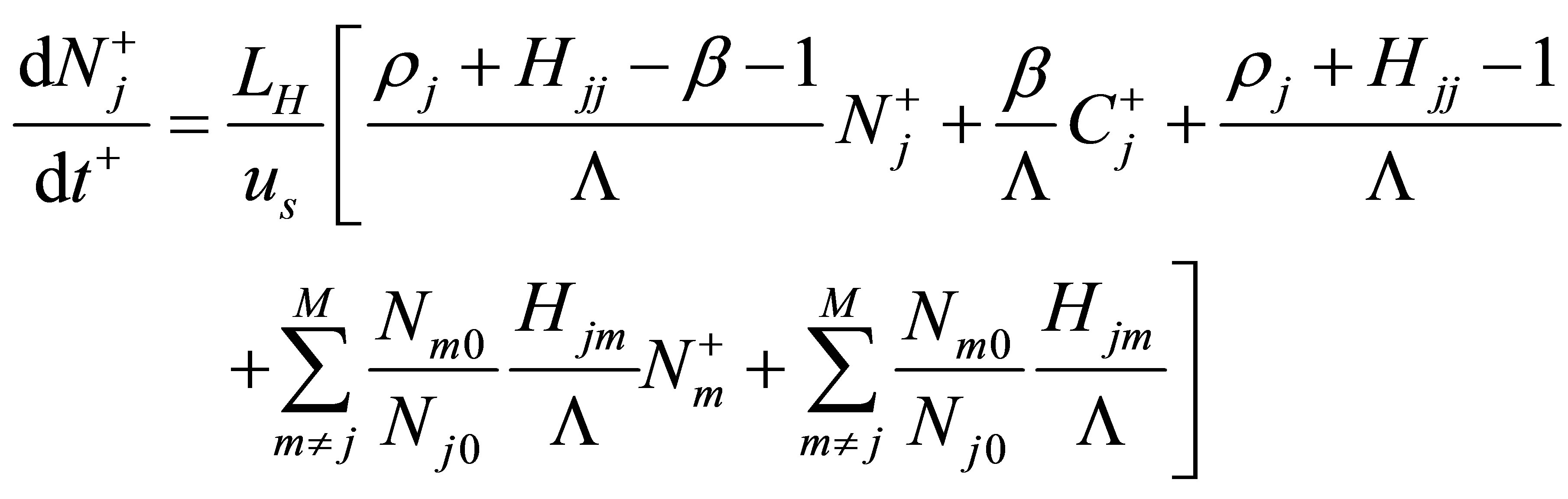 (17)
(17)
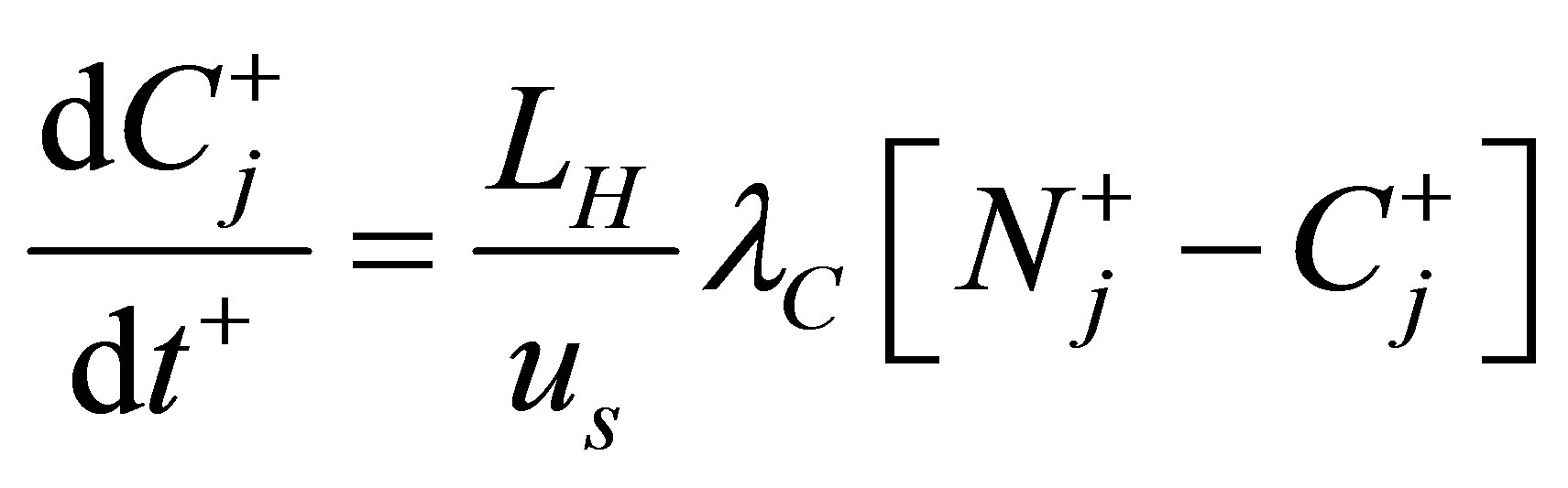 (18)
(18)
where the delayed neutrons are treated by the one-group approximation. The interaction coefficient, 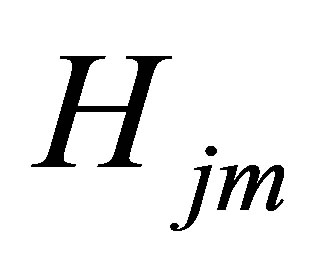 , accounts for the fraction of neutrons generated in the m-th subcore that migrate to the j-th subcore. The modified definition of
, accounts for the fraction of neutrons generated in the m-th subcore that migrate to the j-th subcore. The modified definition of  given by [9] can be applied to the case no matter what each subcore has an equal or a different steady-state heat generation rate. Thus,
given by [9] can be applied to the case no matter what each subcore has an equal or a different steady-state heat generation rate. Thus,
 (19)
(19)
where  is the neutron interaction parameter. If the definition of
is the neutron interaction parameter. If the definition of 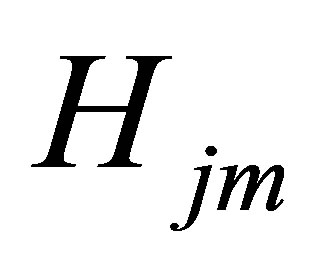 in Equation (19) for
in Equation (19) for  is adopted to describe the neutron interactions among the different subcores,
is adopted to describe the neutron interactions among the different subcores,  should be defined differently to satisfy the zero initial conditions [9].
should be defined differently to satisfy the zero initial conditions [9].
 (20)
(20)
Neglecting Doppler-reactivity feedback, the reactivity change is calculated on the basis of the following equation:
 (21)
(21)
The void-reactivity coefficient  is, in general, a function of the void fraction in the j-th channel; however, it is assumed to be constant in the present study.
is, in general, a function of the void fraction in the j-th channel; however, it is assumed to be constant in the present study.
3. Solution Method
The numerical model totally consists of  nonlinear, ordinary differential equations. By setting the parameter values of
nonlinear, ordinary differential equations. By setting the parameter values of 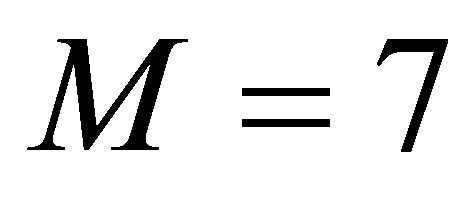 and
and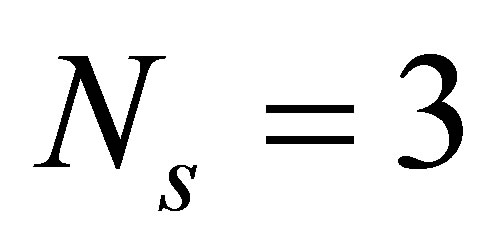 , these dynamic equations are treated by the same solution method as in [9]. The numerical simulations will be performed on the platform of Visual Fortran Composer. The steady-state inlet velocity of each channel and the other variables are determined by solving the set of equations with time derivative terms set to zero, thereby resulting in a set of nonlinear algebraic equations. This set of equations is solved numerically using the subroutine SNSQE of [13], employing the Powell Hybrid Scheme. The nonlinear dynamics of the system at a given initial steady state are obtained by solving the set of nonlinear, ordinary differential equations by perturbing the inlet velocity in one of the channels using the subroutine SDRIV2 of [13]. The SDRIV2 employs the Gear multi-value method.
, these dynamic equations are treated by the same solution method as in [9]. The numerical simulations will be performed on the platform of Visual Fortran Composer. The steady-state inlet velocity of each channel and the other variables are determined by solving the set of equations with time derivative terms set to zero, thereby resulting in a set of nonlinear algebraic equations. This set of equations is solved numerically using the subroutine SNSQE of [13], employing the Powell Hybrid Scheme. The nonlinear dynamics of the system at a given initial steady state are obtained by solving the set of nonlinear, ordinary differential equations by perturbing the inlet velocity in one of the channels using the subroutine SDRIV2 of [13]. The SDRIV2 employs the Gear multi-value method.
4. Results and Discussion
Table 1 lists the geometries and properties used in the present study. This set of data is extracted from the Pre liminary Safety Analysis Report of an ABWR [11]. For a seven nuclear-coupled boiling channel system considering in this study, a radial heat flux distribution of 1.3:1.2:1.1:1.0:0.9:0.8:0.7 is set on the basis of a given average heat flux. The inlet loss coefficient in each channel, as listed in Table 2, is selected such that all the heated channels have approximately the same exit quality at a typical normal operating condition given in Table 1.

Table 1. The geometries and properties used in the present study [11].
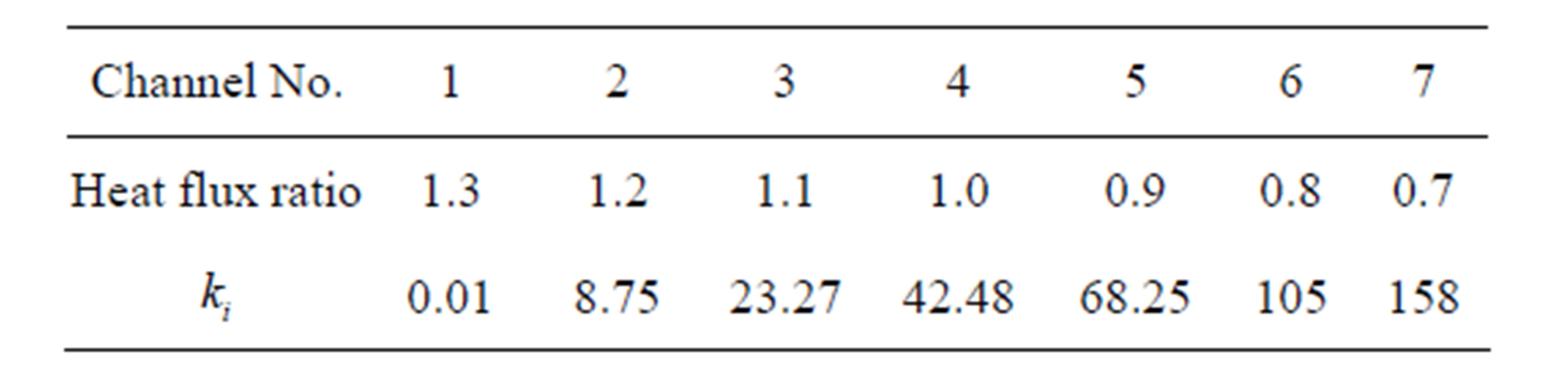
Table 2. The condition for a seven nuclear-coupled boiling channel system under the normal operating condition given in Table 1, 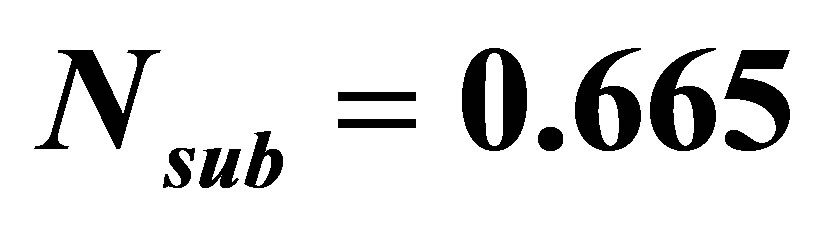 and
and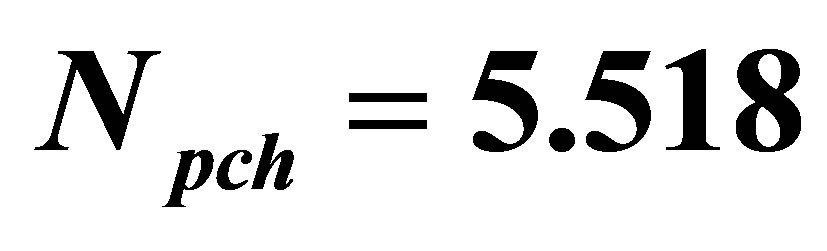 .
.
4.1. The Effects of Void-Reactivity Feedback on the Nonlinear Phenomena
By considering the channel-to-channel interactions among the multiple channels and the neutron interactions among the subcores, the transient responses for each channel and the corresponding subcore can be examined by the time evolutions of dependent variables following a perturbation in the inlet velocity of one channel, i.e. channel 1, at given steady state conditions. For a given value of neutron interaction parameter, 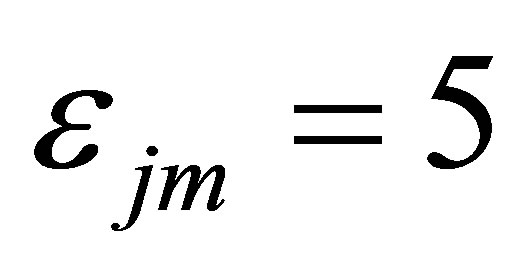 , which corresponds to a weak subcore-to-subcore neutron interaction condition, the effects of void-reactivity feedback on the system dynamics are evaluated at a fixed subcooling number,
, which corresponds to a weak subcore-to-subcore neutron interaction condition, the effects of void-reactivity feedback on the system dynamics are evaluated at a fixed subcooling number,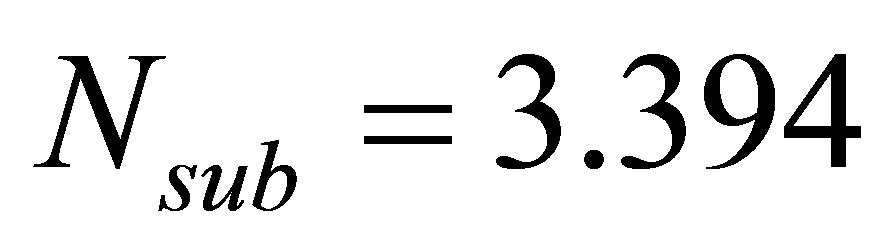 . Four select operating states, with an average phase change number of
. Four select operating states, with an average phase change number of , 5.715, 5.741 and 5.774 respectively, are considered in the present analysis. For such four analytical cases, Figure 2 illustrates the nonlinear oscillations of inlet velocity
, 5.715, 5.741 and 5.774 respectively, are considered in the present analysis. For such four analytical cases, Figure 2 illustrates the nonlinear oscillations of inlet velocity 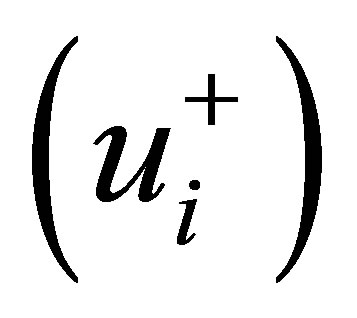 in the representative channel (channel 1) of this seven nuclear-coupled boiling channel system with a heat flux ratio of 1.3:1.2:1.1:1.0:0.9:0.8:0.7 under different voidreactivity coefficients. By setting the void-reactivity coefficient at
in the representative channel (channel 1) of this seven nuclear-coupled boiling channel system with a heat flux ratio of 1.3:1.2:1.1:1.0:0.9:0.8:0.7 under different voidreactivity coefficients. By setting the void-reactivity coefficient at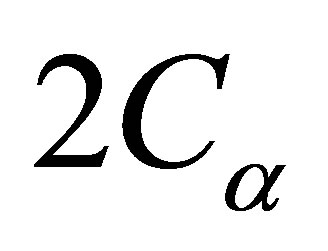 , two times of the reference void-reactivity coefficient given in Table 1, the results in Figure 2(a) reveal that the magnitudes of the oscillations in all the four cases are dampened out and the system quickly returns to the corresponding initial steady state. Thus, these four cases belong to stable operating states. By tripling the magnitude of the reference void-reactivity coefficient
, two times of the reference void-reactivity coefficient given in Table 1, the results in Figure 2(a) reveal that the magnitudes of the oscillations in all the four cases are dampened out and the system quickly returns to the corresponding initial steady state. Thus, these four cases belong to stable operating states. By tripling the magnitude of the reference void-reactivity coefficient , the results in Figure 2(b) show that strengthening void-reactivity feedback leads to an unstable effect on the system dynamics. The magnitudes of nonlinear oscillations in one typical channel (channel 1) for all the four cases grow to certain values and then remain unchanged during the transients. It demonstrates that the system present a type of limit cycle oscillations. If the magnitude of the void-reactivity coefficient is raised by four times, i.e.
, the results in Figure 2(b) show that strengthening void-reactivity feedback leads to an unstable effect on the system dynamics. The magnitudes of nonlinear oscillations in one typical channel (channel 1) for all the four cases grow to certain values and then remain unchanged during the transients. It demonstrates that the system present a type of limit cycle oscillations. If the magnitude of the void-reactivity coefficient is raised by four times, i.e. , the results in Figure 2(c) indicate that increasing the void-reactivity coefficient can further enhance the unstable effect of void-reactivity feedback and thus induce distinct effect on the individual operating state. For the case of
, the results in Figure 2(c) indicate that increasing the void-reactivity coefficient can further enhance the unstable effect of void-reactivity feedback and thus induce distinct effect on the individual operating state. For the case of , the system responses finally evolve to periodic oscillations with a periodic cycle of six, so-called “complex P-6 oscillations” as a result of the channel-to-channel interactions and subcore-to-subcore
, the system responses finally evolve to periodic oscillations with a periodic cycle of six, so-called “complex P-6 oscillations” as a result of the channel-to-channel interactions and subcore-to-subcore
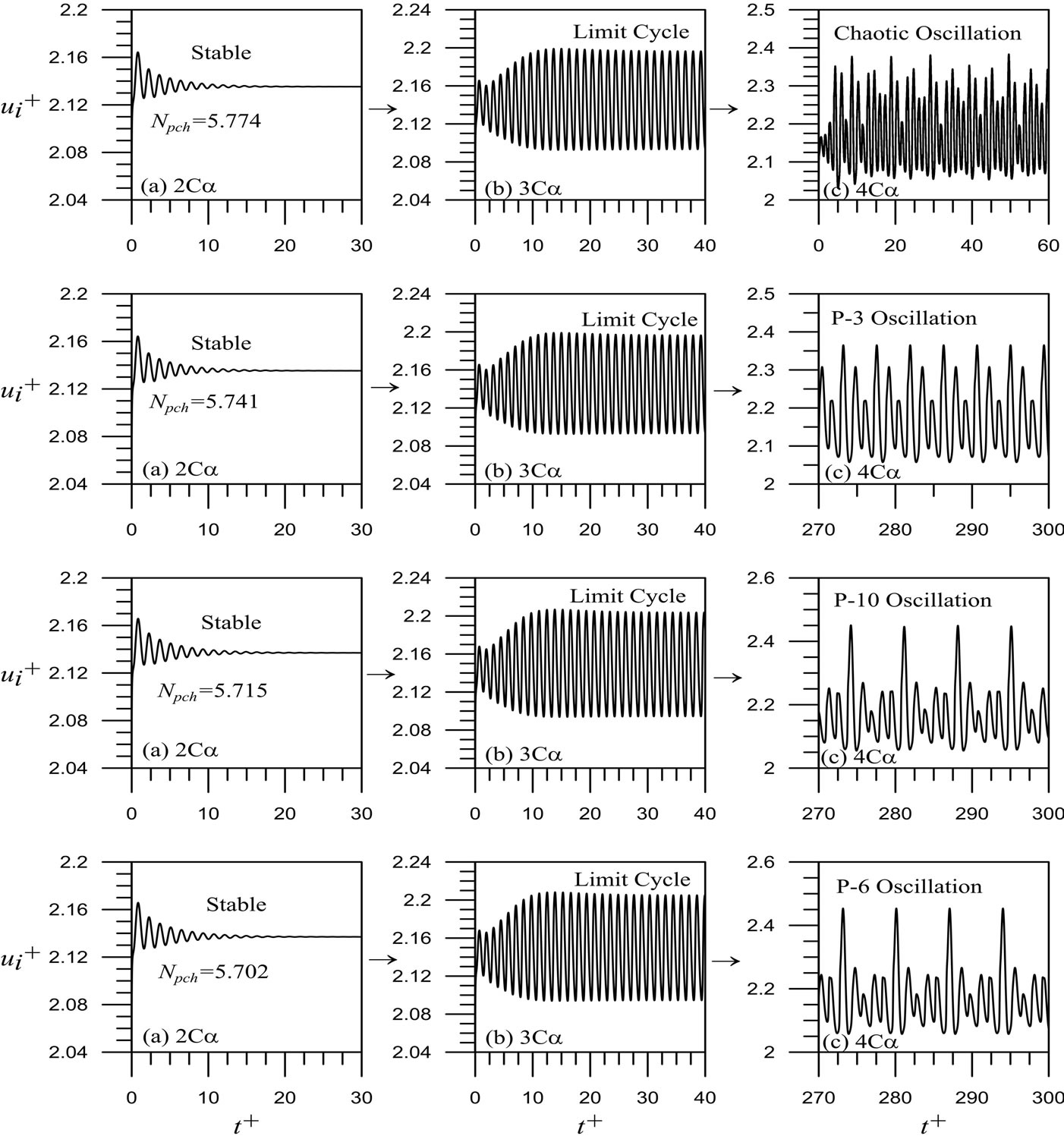
Figure 2. The effects of different void-reactivity coefficients on the nonlinear phenomena of the seven nuclear-coupled boiling channel system with a heat flux ratio of 1.3:1.2:1.1:1.0:0.9:0.8:0.7 and fixed values of 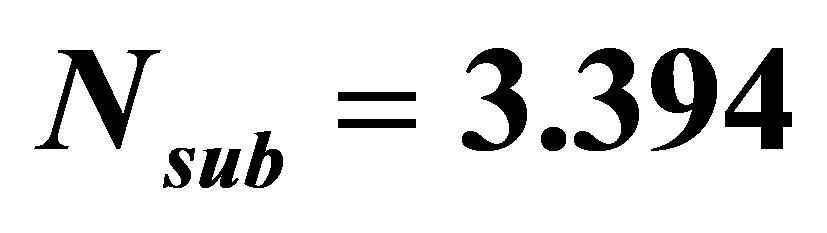 and
and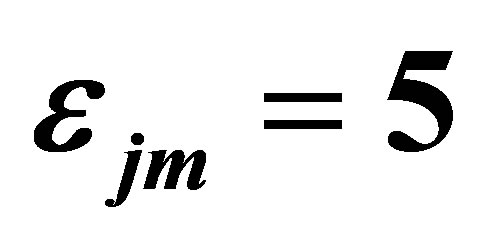 .
.
neutron interactions. Another special type of complex P-10 (period-10 orbit) oscillations is found in the state of  and the other unique type of complex P-3 (period-3 orbit) oscillations is identified in the state of
and the other unique type of complex P-3 (period-3 orbit) oscillations is identified in the state of 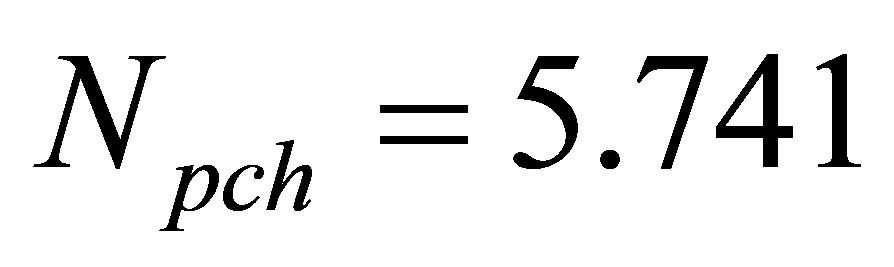 as illustrated in Figure 2(c). Moreover, for the state of
as illustrated in Figure 2(c). Moreover, for the state of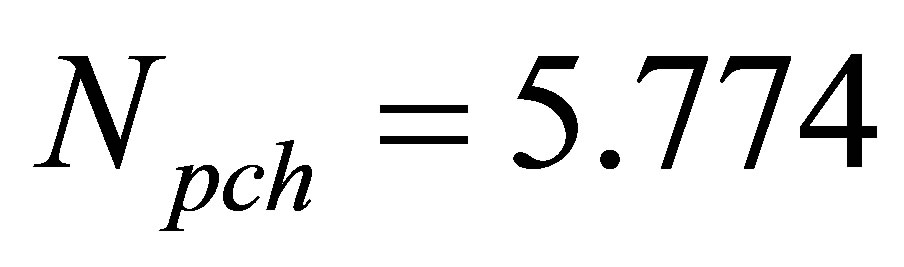 , the results in Figure 2(c) show that the nonlinear oscillations of the system present chaotic behavior. This can be classified into a type of complex Rossler type chaotic oscillations as reported in [9-10].
, the results in Figure 2(c) show that the nonlinear oscillations of the system present chaotic behavior. This can be classified into a type of complex Rossler type chaotic oscillations as reported in [9-10].
Under a weak subcore-to-subcore neutron interaction condition of , the above discussions suggest that enlarging void-reactivity feedback can lead to a significant effect on the nonlinear dynamics of the present system with seven nuclear-coupled boiling channels.
, the above discussions suggest that enlarging void-reactivity feedback can lead to a significant effect on the nonlinear dynamics of the present system with seven nuclear-coupled boiling channels.
4.2. The Effects of Neutron Interaction on the Nonlinear Phenomena
In order to evaluate the effects of the neutron interaction on the nonlinear dynamics of this nuclear-coupled boiling system, the magnitude of the void-reactivity coefficient is kept constant and at a given value of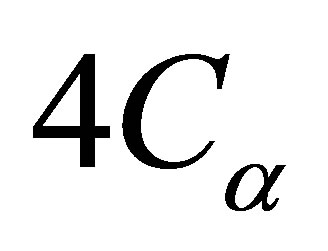 . With a fixed subcooling number of
. With a fixed subcooling number of , four select operating states, with an average phase change number of
, four select operating states, with an average phase change number of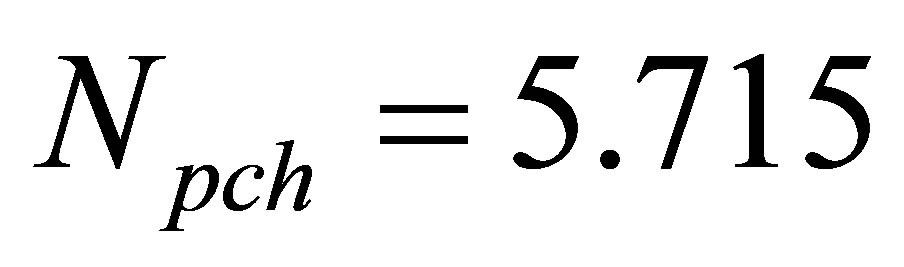 , 5.728, 5.741 and 5.774 respectively, are considered in the present analysis. For such four analytical cases, Figure 3 displays the influences of neutron interaction on the nonlinear dynamics of inlet velocity
, 5.728, 5.741 and 5.774 respectively, are considered in the present analysis. For such four analytical cases, Figure 3 displays the influences of neutron interaction on the nonlinear dynamics of inlet velocity 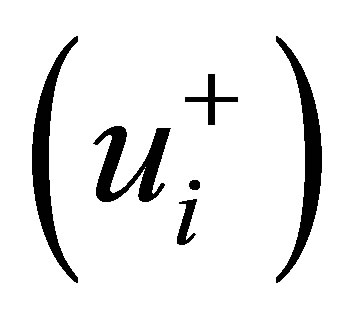 in one typical channel (channel 1) of this seven nuclear-coupled boiling channel system under different values of neutron interaction parameters
in one typical channel (channel 1) of this seven nuclear-coupled boiling channel system under different values of neutron interaction parameters . If the value of
. If the value of  is more large, the corresponding neutron interaction is more weak and thus the system is more unstable [9].
is more large, the corresponding neutron interaction is more weak and thus the system is more unstable [9].
Considering the condition of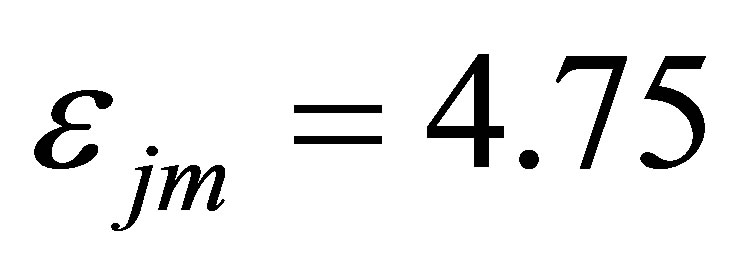 , the results in Figure 3(a) indicate that the transient responses of all the four operating states present a type of limit cycle oscillations, so-called complex P-1 (period-1 orbit) oscillations later. By step change the value of neutron interaction parameter
, the results in Figure 3(a) indicate that the transient responses of all the four operating states present a type of limit cycle oscillations, so-called complex P-1 (period-1 orbit) oscillations later. By step change the value of neutron interaction parameter  from 4.75, 5.0 to 5.1, this will induce an
from 4.75, 5.0 to 5.1, this will induce an
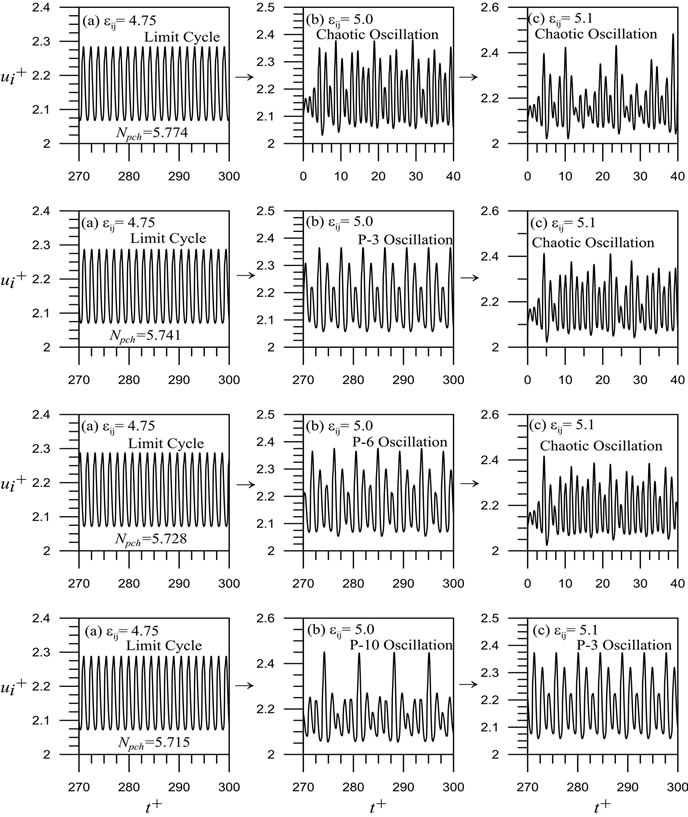
Figure 3. The effects of different neutron interaction parameter values on the nonlinear phenomena of the seven nuclearcoupled boiling channel system with a heat flux ratio of 1.3:1.2:1.1:1.0:0.9:0.8:0.7 and fixed values of  and
and .
.
increasing unstable effect on the stability and distinct influence on the nonlinear dynamics of the system. As the increase in the value of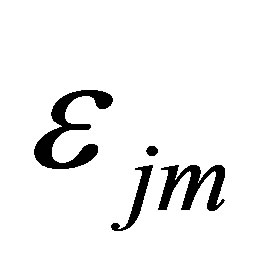 , the results in Figure 3 reveal that the system with the operating state of
, the results in Figure 3 reveal that the system with the operating state of 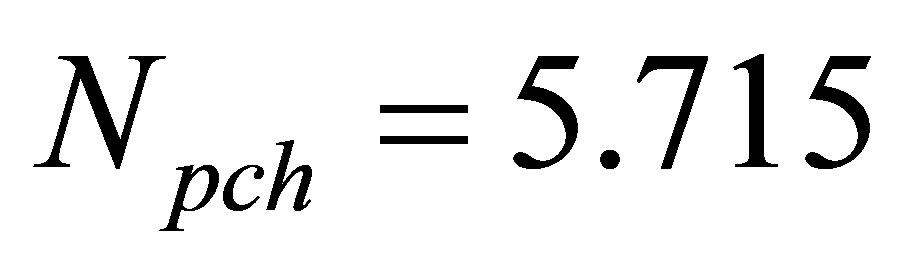 experiences different nonlinear oscillation types of complex P-1, complex P-10 and complex P-3, respectively. For another operating state of
experiences different nonlinear oscillation types of complex P-1, complex P-10 and complex P-3, respectively. For another operating state of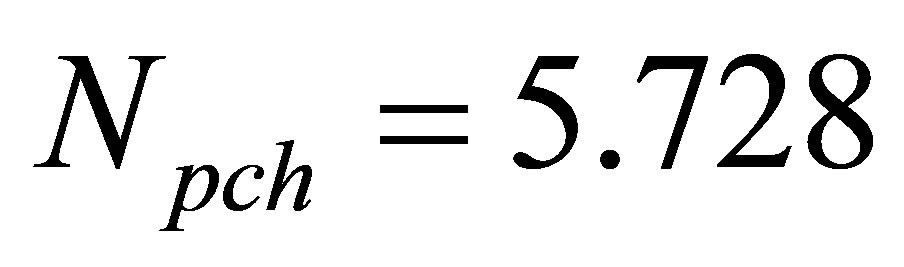 , the system exhibits the corresponding nonlinear oscillation types of (complex P-1, complex P-6, complex chaos) in response to the change in
, the system exhibits the corresponding nonlinear oscillation types of (complex P-1, complex P-6, complex chaos) in response to the change in  as shown in Figure 3. In addition, the nonlinear oscillation types, with respect to the increasing
as shown in Figure 3. In addition, the nonlinear oscillation types, with respect to the increasing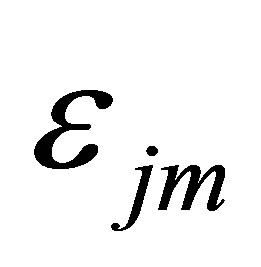 , are of (complex P-1, complex P-3, complex chaos) at the operating state of
, are of (complex P-1, complex P-3, complex chaos) at the operating state of 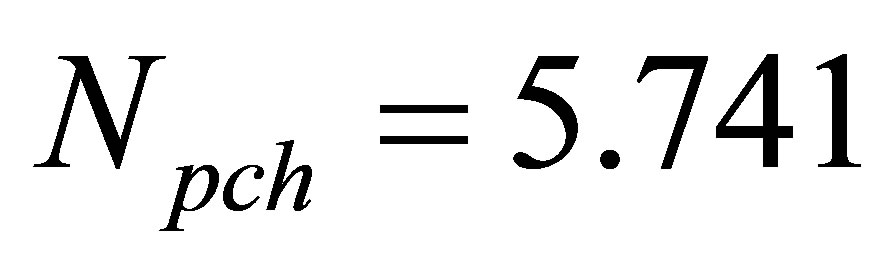 and (complex P-1, complex chaos, complex chaos) at the operating state of
and (complex P-1, complex chaos, complex chaos) at the operating state of , respectively.
, respectively.
Under the condition of strong void-reactivity feedbacks, i.e. , the preceding discussions demonstrate that the effect of the neutron interaction on the nonlinear dynamics of the present system is more significant as the more large value of
, the preceding discussions demonstrate that the effect of the neutron interaction on the nonlinear dynamics of the present system is more significant as the more large value of , i.e. more weaker neutron interaction. The multiple types of periodic and chaotic oscillations are unique and interesting through the complex and coupling interactions among the channels and the subcores. The distinct characteristics of those nonlinear phenomena, i.e. periodic and chaotic attractors, will be further plotted on the phase space and analyzed by chaotic measures as an example of
, i.e. more weaker neutron interaction. The multiple types of periodic and chaotic oscillations are unique and interesting through the complex and coupling interactions among the channels and the subcores. The distinct characteristics of those nonlinear phenomena, i.e. periodic and chaotic attractors, will be further plotted on the phase space and analyzed by chaotic measures as an example of 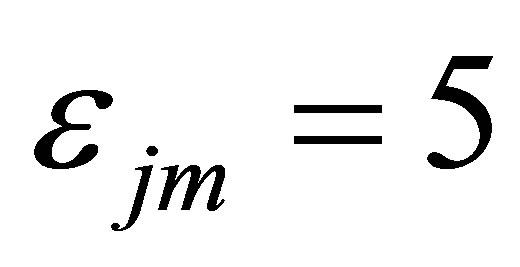 in Section 4.3.
in Section 4.3.
4.3. Complex Periodic and Chaotic Attractors
Considering the system with the void-reactivity coefficient quadrupled 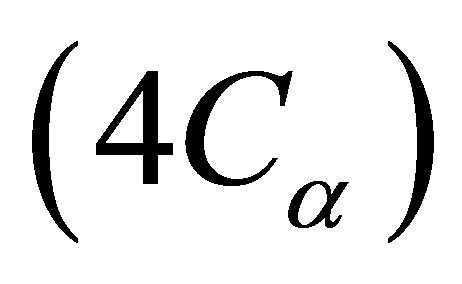 and neutron interaction parameter of
and neutron interaction parameter of , some interesting nonlinear dynamics can be identified in the present system of seven nuclearcoupled boiling channels. At the state of
, some interesting nonlinear dynamics can be identified in the present system of seven nuclearcoupled boiling channels. At the state of 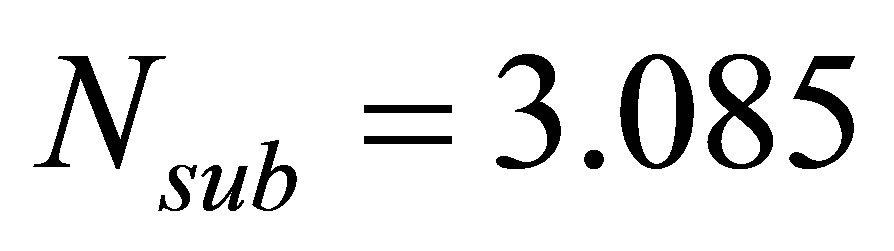 and
and , a special oscillation type of complex P-2 (period-2 orbit) occurs in the system as illustrated in Figure 4 as a result of the channel-to-channel interactions and subcore-to-subcore neutron interactions. The results indicate that the corresponding phase diagram onto the
, a special oscillation type of complex P-2 (period-2 orbit) occurs in the system as illustrated in Figure 4 as a result of the channel-to-channel interactions and subcore-to-subcore neutron interactions. The results indicate that the corresponding phase diagram onto the 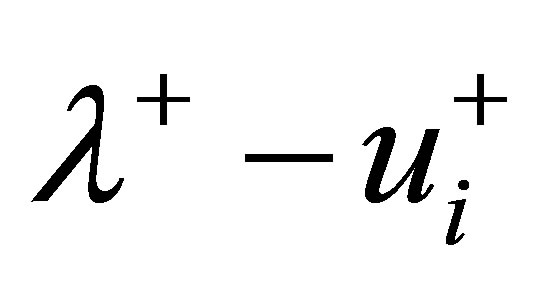 plane for each channel and the transient response of fuel cladding temperature
plane for each channel and the transient response of fuel cladding temperature  for one select subcore (subcore 1). The figures on the phase plane in each channel reveal very interesting and peculiar shapes of complex P-2 attractor.
for one select subcore (subcore 1). The figures on the phase plane in each channel reveal very interesting and peculiar shapes of complex P-2 attractor.
If the inlet subcooling is further increased to , much more nonlinear oscillation types can take place depending on the operating conditions. Figure 5 illustrates that the phase diagrams onto the
, much more nonlinear oscillation types can take place depending on the operating conditions. Figure 5 illustrates that the phase diagrams onto the  plane for the transients of the representative channel (channel 2) at different operating conditions.
plane for the transients of the representative channel (channel 2) at different operating conditions.
The results in Figures 5(a)-(d) display some distinctive periodic and chaotic attractors, i.e. complex P-3 attractor at , complex P-6 attractor at
, complex P-6 attractor at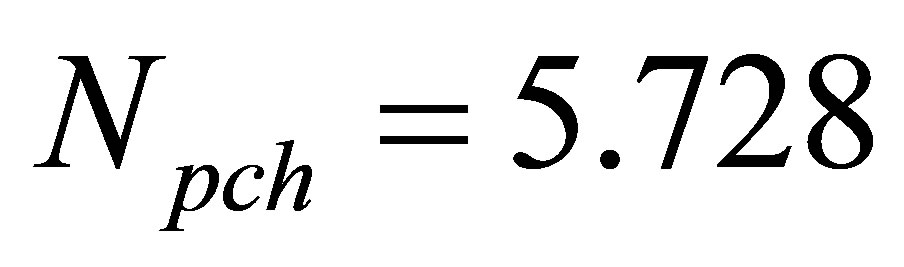 , complex P-10 attractor at
, complex P-10 attractor at 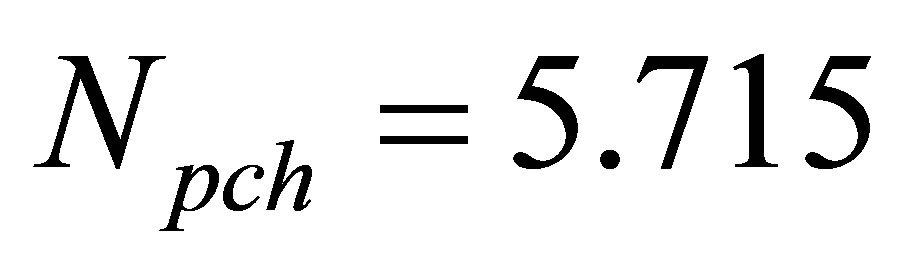 and complex chaotic attractor at
and complex chaotic attractor at , respec-
, respec-

Figure 4. The phase trajectories of complex P-2 oscillations and transient response of fuel cladding temperature 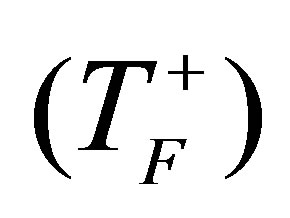 in subcore 1 occur in the state of
in subcore 1 occur in the state of 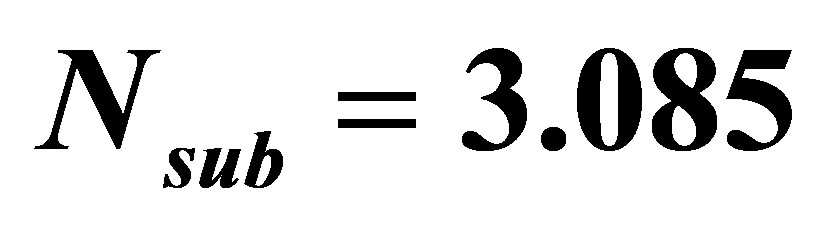 and
and  with
with  and
and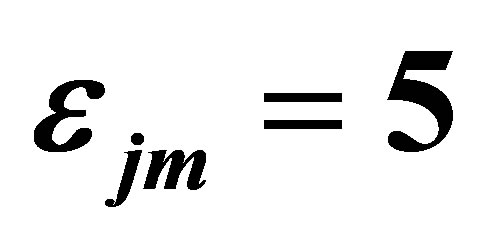 .
.
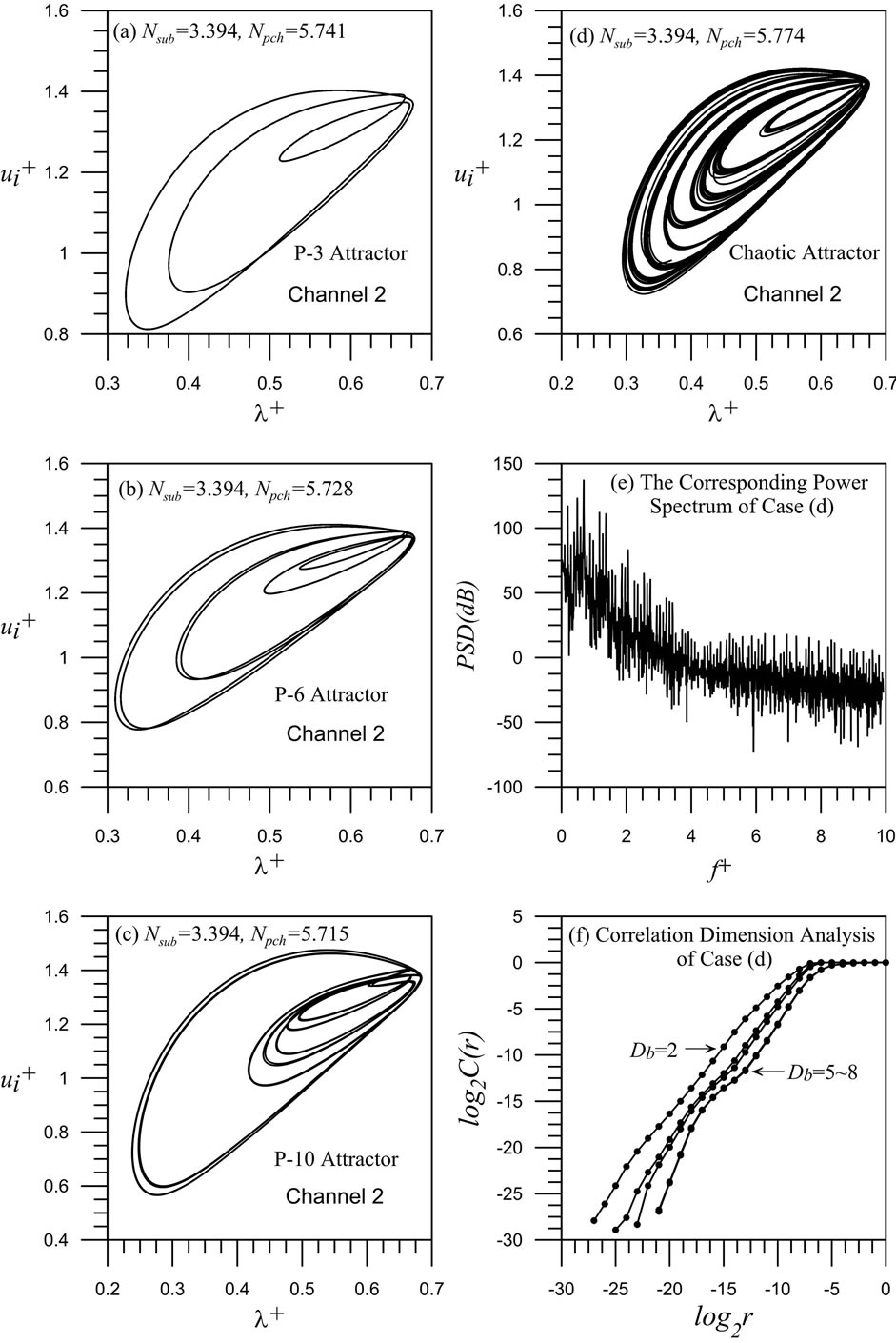
Figure 5. The phase trajectories onto the  plane of the representative channel for various complex periodic and chaotic oscillations exist in the system with
plane of the representative channel for various complex periodic and chaotic oscillations exist in the system with  and
and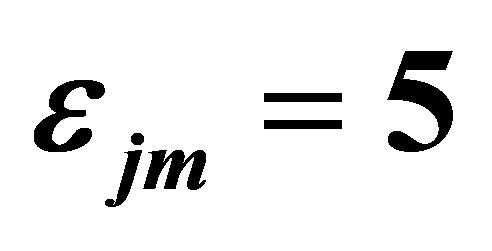 , and the corresponding power spectrum and correlation dimension analysis of case (d).
, and the corresponding power spectrum and correlation dimension analysis of case (d).
tively. Figure 5(e) illustrates the corresponding power spectrum of complex chaotic oscillation in Figure 5(d) through FFT analysis. The analytical result shows that the power spectrum has no well-defined peaks and falls off rapidly as the frequency increases. Furthermore, the correlation dimension of this complex strange attractor is estimated following the procedure in [14]. Using the dimension 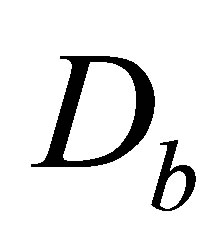 as a parameter, the
as a parameter, the 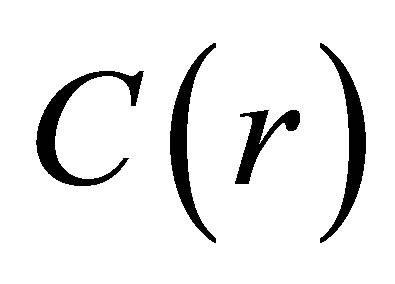 in a log–log plot is shown in Figure 5(f). The results exhibit the slope of the curve is almost unchanged after
in a log–log plot is shown in Figure 5(f). The results exhibit the slope of the curve is almost unchanged after . It implies an imbedding dimension of 5 [15]. The slope of the least-square fitting straight line for
. It implies an imbedding dimension of 5 [15]. The slope of the least-square fitting straight line for 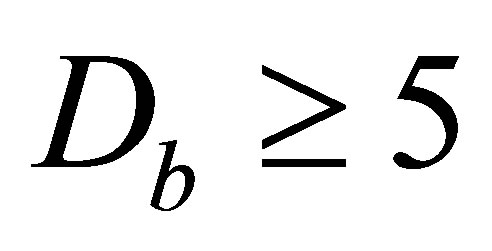 in Figure 5(f) suggests a fractal dimension of
in Figure 5(f) suggests a fractal dimension of . This further confirms that a complex chaotic attractor exist in this system. Such complex chaotic oscillations for the operating state of Figure 5(d) are further projected onto a three dimensional phase plane of
. This further confirms that a complex chaotic attractor exist in this system. Such complex chaotic oscillations for the operating state of Figure 5(d) are further projected onto a three dimensional phase plane of 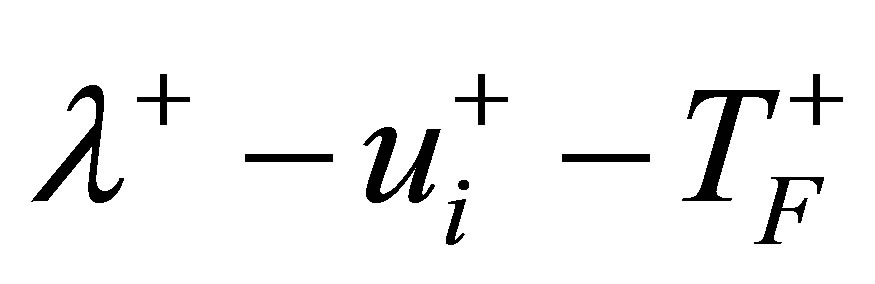 as shown in Figure 6. These 3D phase trajectories for all channels demonstrate that such complex chaotic attrac-
as shown in Figure 6. These 3D phase trajectories for all channels demonstrate that such complex chaotic attrac-
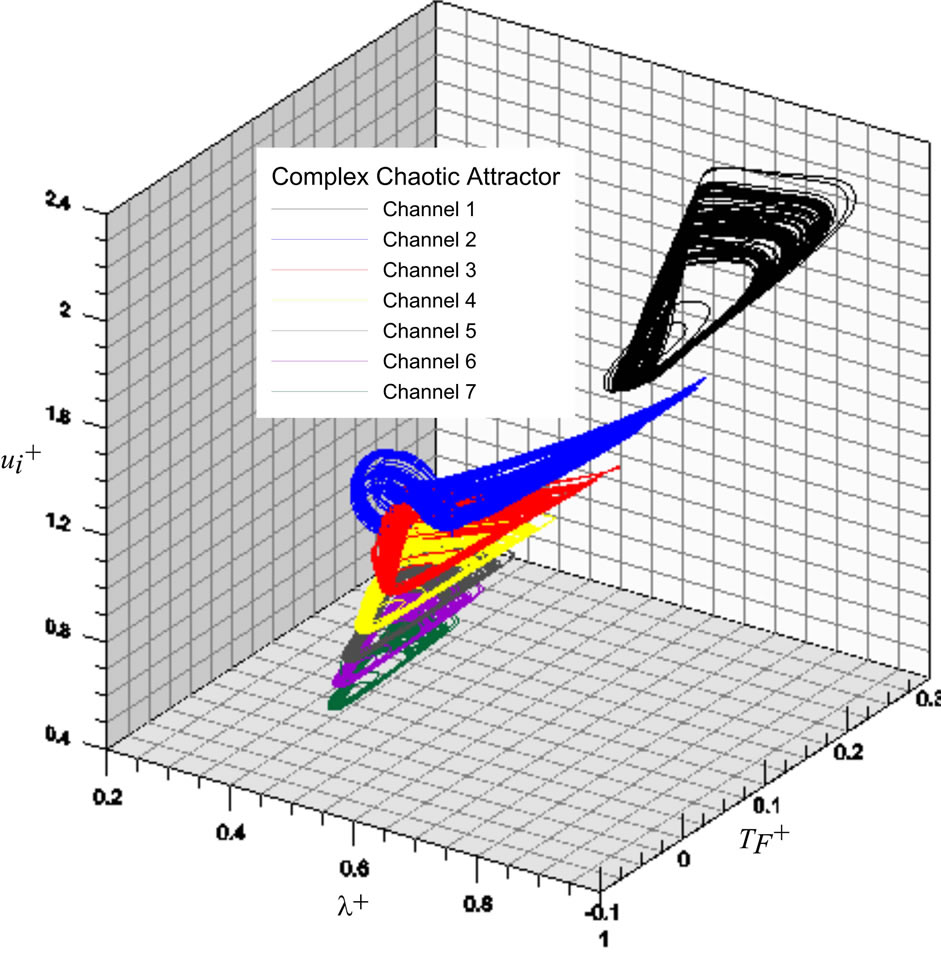
Figure 6. The 3D phase trajectories onto the 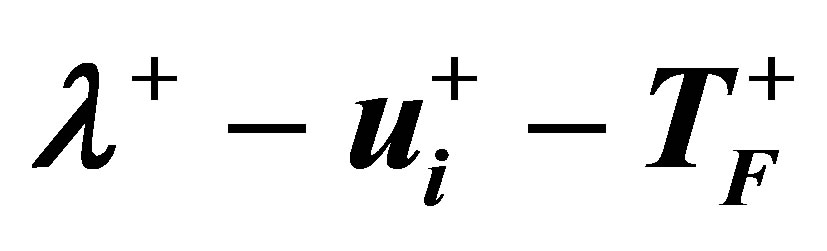 plane for complex chaotic oscillations appear in the operating state of Figure 5(d).
plane for complex chaotic oscillations appear in the operating state of Figure 5(d).
tors have distinctive phase shapes constrained by the boundary conditions of a constant total mass flow rate and the same dynamic pressure drop among channels.
5. Conclusions
By considering multi-channel thermal hydraulics, fuel rod dynamics and multi-point neutron dynamics, this study investigates the effects of the void-reactivity feedback and the neutron interaction on the nonlinear phenomena of a seven-nuclear-coupled boiling channel system with a constant total flow rate. The characteristic feature of the multiple coupling feedback and nonlinear interaction among sub-models can induce complex and interesting nonlinear phenomena in this nuclear-coupled boiling system. The following conclusions may be drawn from the results:
1) The void-reactivity feedback has a significant effect on the nonlinear phenomena of the present system. The increase in the value of the void-reactivity coefficient can lead to an unstable effect on the system dynamics. For the system with a weak subcore-to-subcore neutron interaction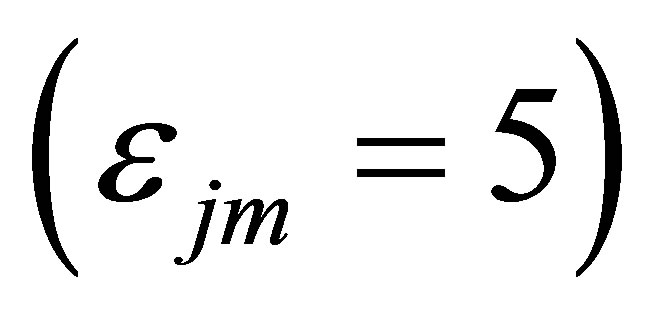 , it will result in a series of changes in nonlinear oscillation types from the steady oscillations, complex periodic oscillations, to complex chaotic oscillations depending on the system states with different void-reactivity coefficients of
, it will result in a series of changes in nonlinear oscillation types from the steady oscillations, complex periodic oscillations, to complex chaotic oscillations depending on the system states with different void-reactivity coefficients of ,
, 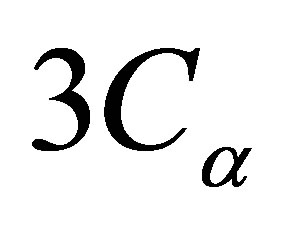 and
and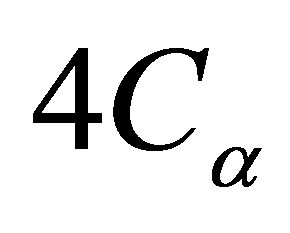 , respectively.
, respectively.
2) Increasing the value of neutron interaction parameter  will debilitate the neutron interaction among subcores and make the system more unstable. The results indicate that the effect of neutron interaction has a great influence on the nonlinear phenomena of the present system. For the system subject to a strong void-reactivity feedback
will debilitate the neutron interaction among subcores and make the system more unstable. The results indicate that the effect of neutron interaction has a great influence on the nonlinear phenomena of the present system. For the system subject to a strong void-reactivity feedback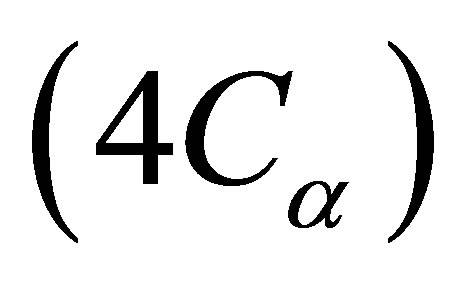 , various complex periodic oscillations and complex chaotic oscillations depending on the system states can evolve through the step increase in the parameter value of
, various complex periodic oscillations and complex chaotic oscillations depending on the system states can evolve through the step increase in the parameter value of  from 4.75, 5.0 to 5.1.
from 4.75, 5.0 to 5.1.
3) Multiple types of periodic and chaotic oscillations are unique as a result of the complex and coupling interactions among the channels and the subcores. Multiple complex periodic attractors and complex chaotic attractors can simultaneously appear in this seven-nuclear-coupled boiling channel system under some specific operating conditions.
REFERENCES
- Rizwan-uddin and J. J. Dorning, “A Chaoic Attractor in a Periodically Forced Two Phase Flow System,” Nuclear Science and Engineering, Vol. 100, No. 4, 1988, pp. 393-404.
- A. Clausse and R. T. Lahey Jr., “An Investigation of Periodic and Strange Attractors in Boiling Flows Using Chaos Theory,” Proceedings of the Ninth International Heat Transfer Conference, Vol. 2, Jerusalem, 19-24 August 1990, pp. 3-8.
- Y. N. Lin, J. D. Lee and C. Pan, “Nonlinear Dynamics of a Nuclear-Coupled Boiling Channel with Forced Flows,” Nuclear Engineering and Design, Vol. 179, No. 1, 1998, pp. 31-49. http://dx.doi.org/10.1016/S0029-5493(97)00242-2
- J. D. Lee and C. Pan, “Nonlinear Analysis for a Nuclear-Coupled Two-Phase Natural Circulation Loop,” Nuclear Engineering and Design, Vol. 235, No. 5, 2005, pp. 613-626. http://dx.doi.org/10.1016/j.nucengdes.2004.09.008
- G. V. Durga Prasad and M. Pandey, “Stability Analysis and Nonlinear Dynamics of Natural Circulation Boiling Water Reactors,” Nuclear Engineering and Design, Vol. 238, No. 1, 2008, pp. 229-240. http://dx.doi.org/10.1016/j.nucengdes.2007.05.004
- C. Y. Wu, S. B. Wang and C. Pan, “Chaotic Oscillations in Low Pressure Two-Phase Natural Circulation Loop under Low Power and High Inlet Subcooling Conditions,” Nuclear Engineering and Design, Vol. 162, No. 2-3, 1996, pp. 223-232. http://dx.doi.org/10.1016/0029-5493(95)01127-7
- M. Aritomi, S. Aoki and A. Inoue, “Instabilities in Parallel Channel of Forced-Convection Boiling Upflow System (II) Experimental Results,” Journal of Nuclear Science and Technology, Vol. 14, No. 2, 1977, pp. 88-96. http://dx.doi.org/10.1080/18811248.1977.9730730
- A. Satoh, K. Okamoto and H. Madarame, “Instability of Single-Phase Natural Circulation under Double Loop System,” Chaos, Solitons & Fractals, Vol. 9, No. 9, 1998, pp. 1575-1585. http://dx.doi.org/10.1016/S0960-0779(97)00117-3
- J. D. Lee and C. Pan, “Dynamic Analysis of Multiple Nuclear-Coupled Boiling Channels Based on a MultiPoint Reactor Model,” Nuclear Engineering and Design, Vol. 235, No. 22, 2005, pp. 2358-2374. http://dx.doi.org/10.1016/j.nucengdes.2005.05.031
- J. D. Lee and C. Pan, “Periodic and Chaotic Oscillations in the Nuclear-Coupled Boiling Channel System Subject to Strong Void-Reactivity Feedbacks,” Annals of Nuclear Energy, Vol. 36, No. 5, 2009, pp. 793-801. http://dx.doi.org/10.1016/j.anucene.2009.01.016
- Taiwan Power Company, “Preliminary Safety Analysis Report,” Lungmen Nuclear Power Station Units 1 & 2, Taipei, Taiwan, 1997.
- J. D. Lee and C. Pan, “Dynamics of Multiple Parallel Boiling Channel Systems with Forced Flows,” Nuclear Engineering and Design, Vol. 192, No. 1, 1999, pp. 31- 44. http://dx.doi.org/10.1016/S0029-5493(99)00085-0
- D. Kahaner, C. Moler and S. Nash, “Numerical Methods and Software,” Prentice Hall, Upper Saddle River, 1989.
- T. S. Parker and L. O. Chua, “Practical Numerical Algorithms for Chaotic Systems,” Chapter 7, Springer, New York, 1989. http://dx.doi.org/10.1007/978-1-4612-3486-9
- F. C. Moon, “Chaotic and Fractal Dynamics, an Introduction for Applied Scientists and Engineers,” Wiley, New York, 1992, pp. 358-359.
Nomenclature
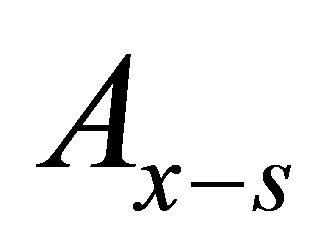 cross sectional area of the channel
cross sectional area of the channel 
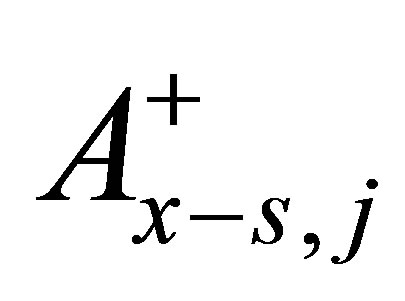 non-dimensional cross sectional area of the j-th heated channel,
non-dimensional cross sectional area of the j-th heated channel, 
 non-dimensional precursor concentration in j-th subcore
non-dimensional precursor concentration in j-th subcore
 constant pressure specific heat
constant pressure specific heat 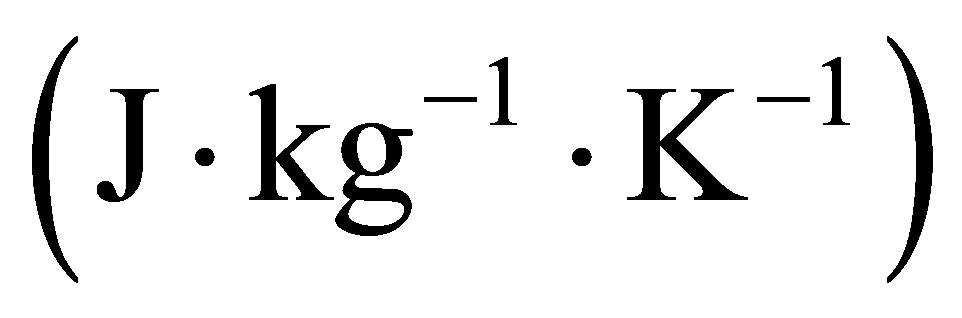
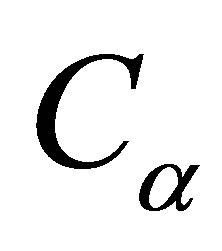 void-reactivity coefficient
void-reactivity coefficient 
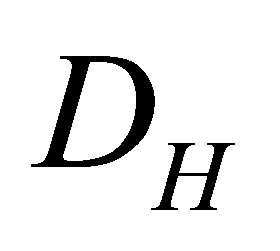 diameter of the channel
diameter of the channel 
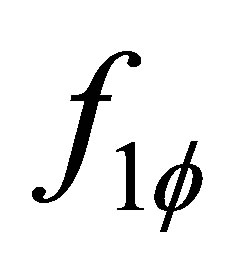 single-phase friction factor
single-phase friction factor
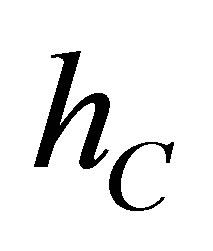 clad-to-coolant heat transfer coefficient
clad-to-coolant heat transfer coefficient 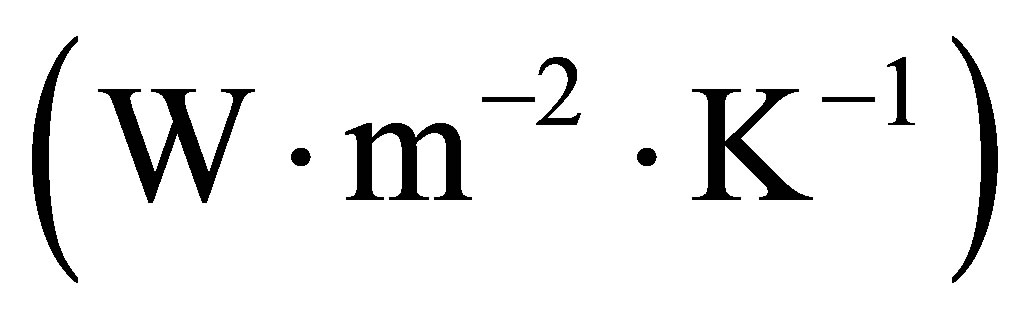
 Pellet-to-clad gap conductance
Pellet-to-clad gap conductance 
 saturated liquid enthalpy
saturated liquid enthalpy 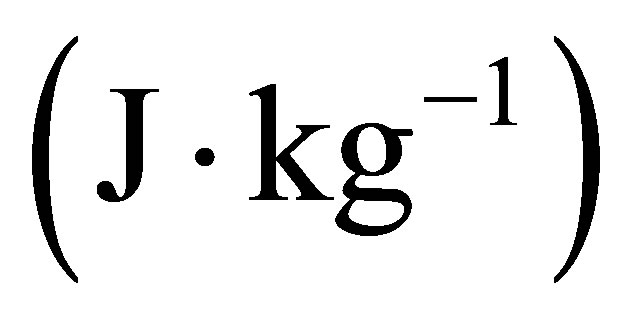
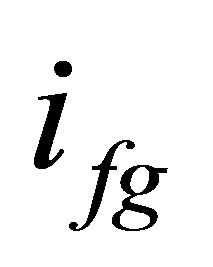 latent heat of evaporation
latent heat of evaporation 
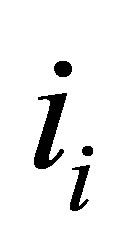 inlet liquid enthalpy
inlet liquid enthalpy 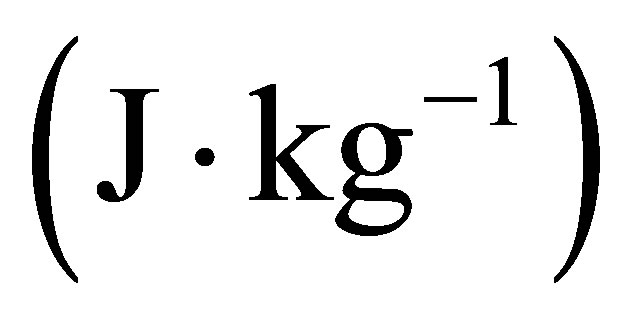
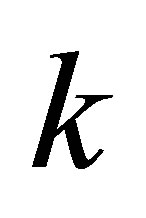 thermal conductivity
thermal conductivity  or loss coefficient
or loss coefficient
 channel length
channel length 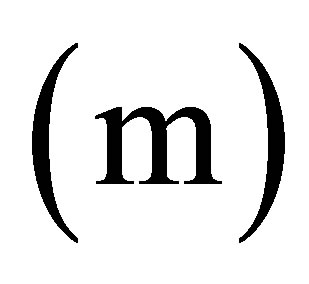
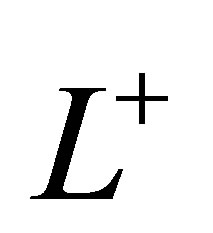 non-dimensional length
non-dimensional length
 non-dimensional mass
non-dimensional mass
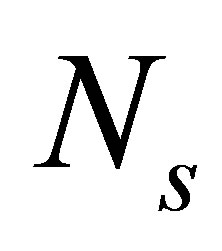 number of nodes in the single-phase region
number of nodes in the single-phase region
 phase change number for j-th channel,
phase change number for j-th channel,
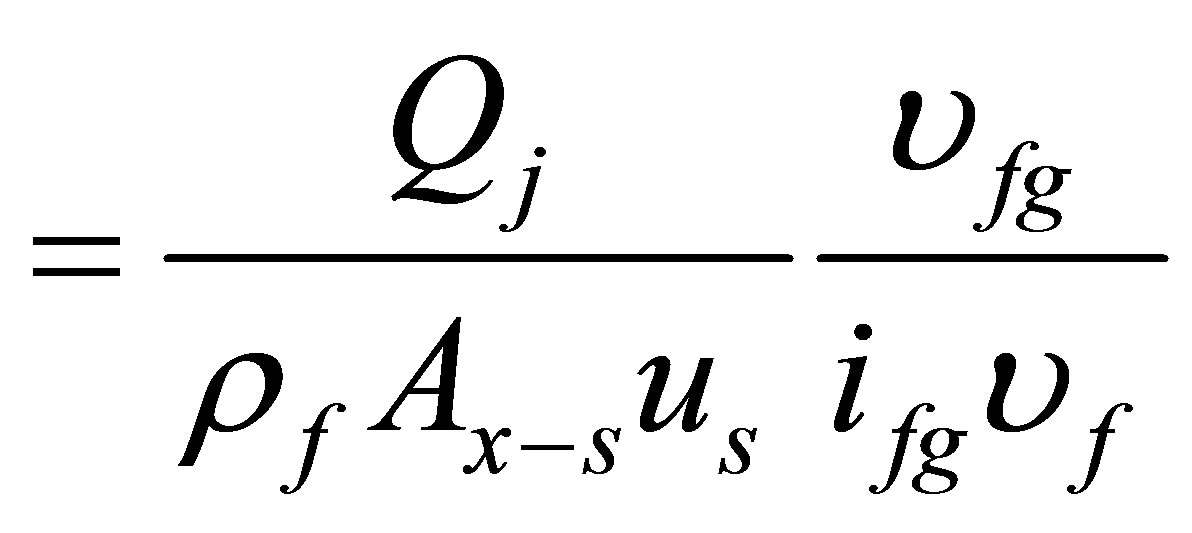
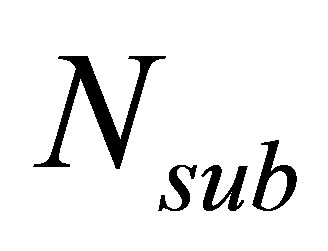 subcooling number,
subcooling number, 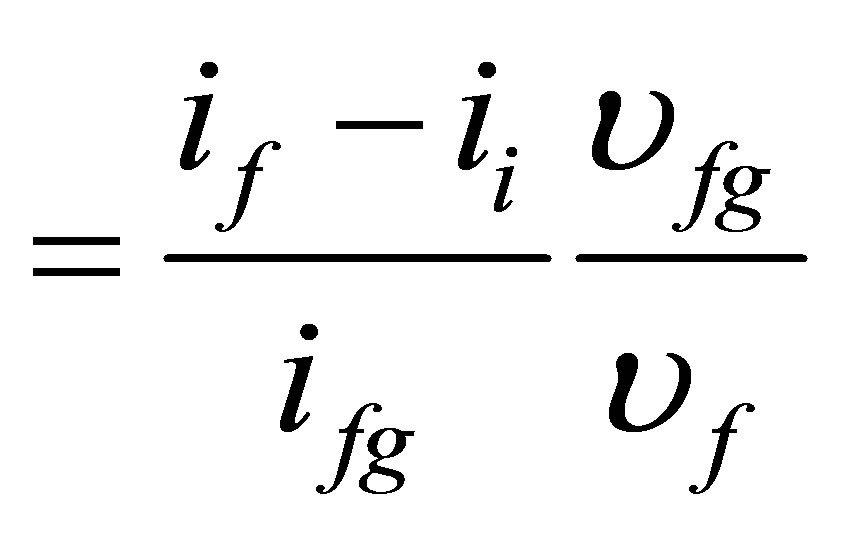
 non-dimensional neutron density in j-th subcore
non-dimensional neutron density in j-th subcore
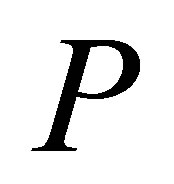 system pressure
system pressure 
 heating power in j-th channel
heating power in j-th channel 
 steady-state heating power
steady-state heating power 
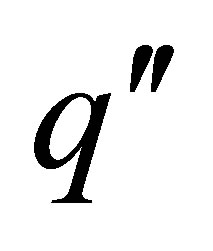 heat flux
heat flux 
 steady state heat flux
steady state heat flux 
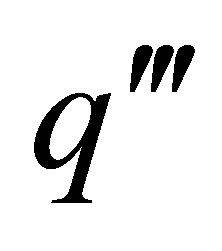 volumetric heat generation rate
volumetric heat generation rate 
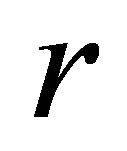 radius
radius 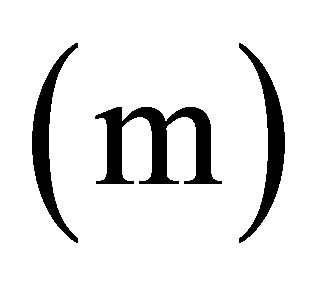
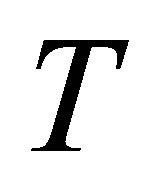 temperature
temperature 
 saturation temperature
saturation temperature 
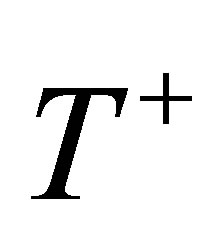 non-dimensional temperature
non-dimensional temperature
 non-dimensional time
non-dimensional time
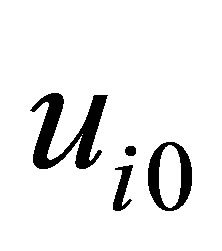 steady state inlet velocity
steady state inlet velocity 
 velocity scale,
velocity scale, 
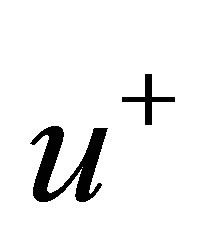 non-dimensional velocity
non-dimensional velocity
 specific volume of saturated liquid
specific volume of saturated liquid 
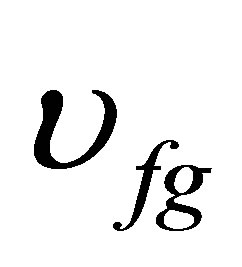 difference in specific volume of saturated liquid and vapor
difference in specific volume of saturated liquid and vapor 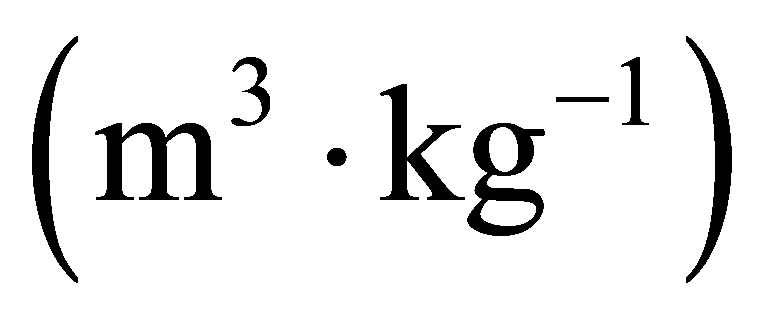
Greek symbols
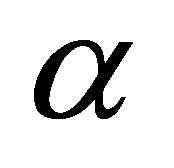 void fraction or thermal diffusivity
void fraction or thermal diffusivity
 delayed neutron fraction
delayed neutron fraction
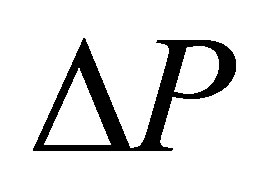 pressure drop
pressure drop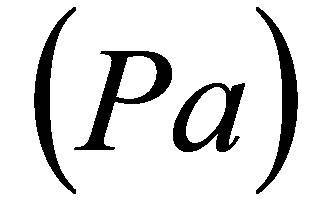
 non-dimensional pressure drop
non-dimensional pressure drop
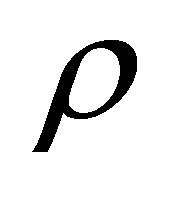 density
density 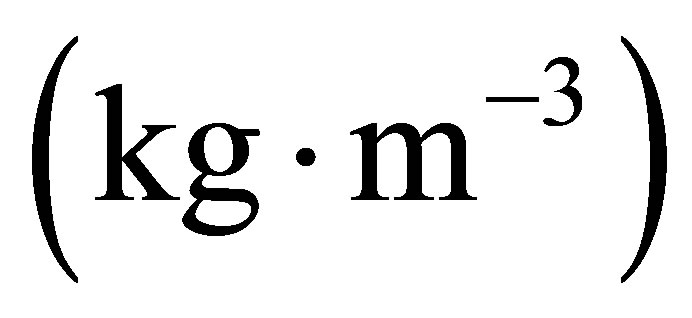 or reactivity (
or reactivity (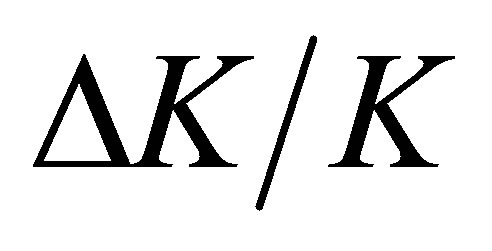 , where
, where  is multiplication factor )
is multiplication factor )
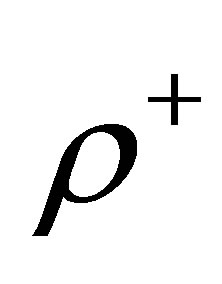 non-dimensional density
non-dimensional density
 density of saturated liquid
density of saturated liquid 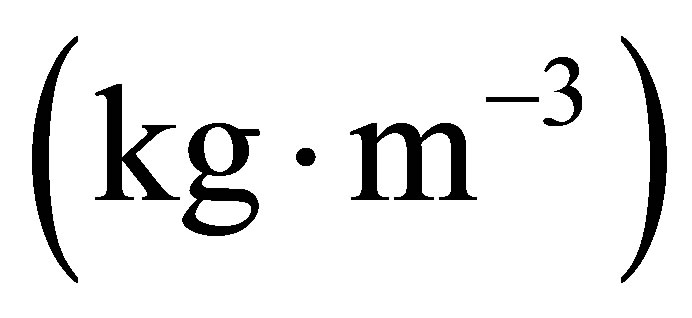
 neutron generation time
neutron generation time 
 boiling boundary
boiling boundary 
 non-dimensional boiling boundary
non-dimensional boiling boundary
 decay constant of delayed neutron precursor
decay constant of delayed neutron precursor 
Subscripts
 channel
channel
 exit of the channel
exit of the channel
 inlet of the channel
inlet of the channel
 j-th channel or subcore
j-th channel or subcore
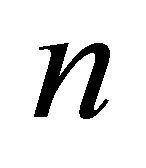 n-th node in the single-phase region 0 steady state
n-th node in the single-phase region 0 steady state
 fuel pellet
fuel pellet
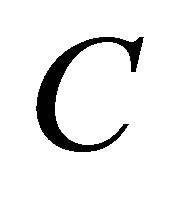 cladding
cladding

