Open Journal of Fluid Dynamics
Vol.06 No.03(2016), Article ID:70792,20 pages
10.4236/ojfd.2016.63019
Streaming Caused by Oscillatory Flow in Peripheral Airways of Human Lung
Bing Han, Hiroyuki Hirahara, Sho Yoshizaki
Graduate School of Science and Engineering, Saitama University, Saitama City, Japan
Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: August 14, 2016; Accepted: September 18, 2016; Published: September 22, 2016
ABSTRACT
Oscillatory flow facilitates gas exchange in human respiration system. In the present study, both numerical calculation and PIV (Particle Image Velocimetry) measurement indicate that, under the application of HFOV (High Frequency Oscillatory Ventilation), apparent steady streaming is caused and augmented in distal airways by the continuous oscillation, i.e., the core air moves downwards and the peripheral air evacuates upwards within bronchioles. The net flow of steady streaming serves to overcome the lack of tidal volume in HFOV and delivers fresh air into deeper lung region. Also, numerical calculations reveal that the intensity of steady streaming is mainly influenced by the geometry of airways with provided oscillatory frequency and tidal volume, and it rises with Re and Wo up to a Re of about 124 and Wo of about 5. Steady streaming is considered as an important factor for the ventilation efficiency of HFOV.
Keywords:
Oscillatory Flow, Steady Streaming, HFOV, Bronchioles, Womersley Number

1. Introduction
Oscillatory flow is a widespread phenomenon and plays an important role in many fields, e.g. pneumatic propulsion, piston-drived flow, and acoustic oscillation are commonly used in mechanical engineering; pulsatile blood circulation, respiratory flow in lung, and capillary waves are of much interest in bio-mechanics; seasonal reversing wind, ocean circulations as well as tide flow are of high concern in meteorology, etc. More than mere oscillation or repetition, mass, momentum, and energy may be transferred via these reciprocating movements. The present study focuses on the effect of reciprocal motion in peripheral human lung airways that is much more complex than in a cylindrical channel. If Poiseuille flow is oscillated in a uniform duct, no net flux will occur when the flow restores, although the Stokes layer may vary unsteadily and the flow is in sinusoidal motion during the oscillation.
However, for the oscillatory flow in non-uniform channels, fluid elements would not in general return to original locations at the end of oscillation. This displacement is the integrated result from steady component of oscillation, and often referred to as steady streaming that can be defined as
 (1)
(1)
where 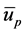 is the Lagrangian velocity of fluid particle initially at
is the Lagrangian velocity of fluid particle initially at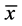 , during the flow cycle of period T.
, during the flow cycle of period T.  is expected to be non-zero for almost all fluid particles moving through the non-uniform cross section.
is expected to be non-zero for almost all fluid particles moving through the non-uniform cross section.
Recently, this time-averaged effect (steady streaming) has gradually been found important and functional in many fields. Steady streaming generated by no slip boundary conditions was surveyed with respect to flows in blood vessels by Padmanabhan and Pedley [1] . In the hearing process, Lighthill found that acoustic streaming associated with ossicle-produced waves might help to transform acoustic signals to neural activity [2] . Leibovich studied the streaming flow raised in the boundary layer attached to a vibrating free boundary and showed that the streaming flow acted on the instability of a particular ocean circulation [3] . Lyne investigated the oscillatory flow in a curved tube with circular cross section, found that there was a steady streaming at the boundary from the inside to the outside bend when the characteristic Reynolds number was much greater than 1 [4] . Hall studied the flow along a pipe of slowly varying cross section driven by an oscillatory pressure difference at ends, and a net flow was produced toward the wide end of the pipe [5] . Haselton and Scherer showed a steady streaming displacement of fluid elements in oscillatory flow through a Y-shaped tube bifurcation model with Reynolds and Womersley numbers could exist in human bronchial airways [6] . Eckmann and Grotberg analyzed and solved the motion equations of oscillatory flow in a curved tube by means of a regular pertubation method over a range of Womersley number, and a substantial time-average axial transport was demonstrated with respect to pulmonary gas exchange [7] . Fresconi et al. illustrated the transport profiles in the conducting airways of the human lung by laser-induced fluorescence experiment and numerical calculation, they concluded that the simple streaming was relatively more important to convective dispersion than augmented dispersion, and presented an explanation for steady streaming based on geometric asymmetries associated with a bifurcation network [8] . Gaver and Grotberg surveyed the oscillatory flow in a tapered channel under conditions of fixed stroke volume and reported a bidirectional streaming in the channel by means of both calculation and experiment [9] . The similar bidirectional steady streaming was also predicted by Goldberg et al. in their analysis of oscillatory flow at the entrance region of a semi-infinite tube of circular cross section [10] .
The flow phenomena induced by oscillatory respiration are quite complex in human lung, due to the complicated pulmonary structure, different respiration scenarios, mechanical properties of lung tissue, and the interaction with organs or body parts, etc. The Reynolds number varies from thousands at the trachea drastically to lower than 0.1 in the alveoli sacs during our rest breathing, and the flows may differ more when the gas is oscillated by faster frequency even with lower tidal volume because the Reynolds number could be increased by higher-frequency vibration in airways, which indicates the flow is more turbulent in the upper lung channels, and if the oscillation is fast enough, out-of-phase flow would be induced mainly in the intermediate airways. Currently, the studies of airflow under HFOV (High-Frequency Oscillatory Ventilation) basically center on the upper or intermediate lung region due to the flow particularity there.
Anatomically, an adult human lung bifurcates from trachea to alveoli 23 times and thus forms a multi-branching structure with 24 generations (G0 - G23) according to Weibel’s lung model [11] , as illustrated in Figure 1. The airways above G18 act as conducting zone where no gas exchange between oxygen and carbon dioxide occurs, the gas exchange commences from G18 to the terminals. In our normal breathing, the inhaled air can easily arrive under G18 because the tidal volume (about 500 mL) is sufficient enough to deliver air to the respiratory region directly. However, in application of HFOV, the gas is oscillated with fast frequency (3 - 25 Hz) and shallow tidal volume (30 - 150 mL) that is normally smaller than the dead space (inner volume of conducting zone), which implies each oscillation barely can directly deliver fresh air to respiratory zone via the conducting airways, while HFOV is widely reported for being efficient in ventilation for injured lungs. The green color in Figure 1 denotes the achievable region of tidal volume in HFOV.
Figure 1. Schematic of lung bifurcations and the directly achievable region (green) for tidal volume of HFOV.
Therefore, we assume that there might be progressive or cumulative net flow, aside from molecular diffusion, to overcome the shortage of tidal volume in HFOV and bring fresh air to the alveoli indirectly. Whether or not steady streaming acts in the transitional bronchioles where the low tidal volume cannot reach needs to be confirmed, which is the first purpose of the present study. If the steady streaming is found working within this zone, its importance and reason need to be analyzed and illustrated, which is the second purpose of this study. The relevant investigations implemented by Haselton and Scherer [6] , Fresconi, Wexler, and Prasad [8] , Gaver and Grotberg [9] imply the close relation between airway geometry and steady streaming in oscillatory flow. To clarify reason of steady streaming, different airway geometries (cylinder, cone, bifurcation, and multi-bifurcations), a series of Womersley numbers and the corresponding Reynolds numbers will be investigated to testify their influences on steady streaming.
2. Exact Solutions of Oscillatory Flow in Uniform Channels
For the oscillatory flow in channels of uniform cross section, it is relatively convenient to figure out the exact solution of velocity distribution. One of the classic oscillatory problems is the Stokes’ second problem which deals with the velocity distribution of viscous flow over an oscillatory plate, as shown in Figure 2(a). Because of the no-slip condition at y = 0, the fluid on the surface follows plate movement and its velocity is , where U,
, where U, 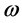 , t are velocity amplitude, angular frequency, and time, respectively. While at the very far
, t are velocity amplitude, angular frequency, and time, respectively. While at the very far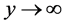 , the flow velocity attenuates to zero. By substituting these boundary conditions to Navier-Stokes equation, the flow velocity can be solved as
, the flow velocity attenuates to zero. By substituting these boundary conditions to Navier-Stokes equation, the flow velocity can be solved as , where
, where 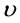 denotes kinematic viscosity, and
denotes kinematic viscosity, and  is illustrated at various phases in Figure 2(b), and the velocity profiles are enveloped by dash curves
is illustrated at various phases in Figure 2(b), and the velocity profiles are enveloped by dash curves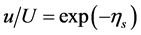 .
.
Another noted oscillatory flow is the unsteady oscillatory flow in cylindrical channel, in a cylindrical coordinate, the governing equation can be expressed by
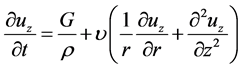 ,
,
where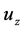 ,
, 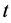 ,
, 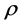 ,
,  ,
,  , and
, and 


poiseuille, 

While for Wo


K represents the acceleration per unit mass,



Figure 2. Distribution of flow velocity close to an oscillating wall in Stokes’ second problem.
Figure 3. Velocity distribution of oscillating flow in pipe with uniform cross section at different phases in one cycle.
gas as shown in Figure 3.
In the case of oscillatory flow in pipe of uniform rectangular cross section, similarly, we assume the central axis in X direction, the flow velocity 
solved by substituting into the governing equation
boundary conditions for the flow are

proximation of poiseuille velocity distribution is
where



strated in Figure 4.
These cases share one characteristic in common that the flows are oscillated in uniform channel. Velocity distribution varies at different instant of a cycle, however, the net flow is zero after integral cycles of oscillation due to the symmetry of velocity distribution at incoming and outgoing phases, which also means the resultant steady streaming is zero. While in a non-uniform channel, the steady streaming is generally nonzero after the oscillations, a coefficient [6] of this convective exchange process is defined for the normal plane at tube position X as

where 


In non-uniform channels, it is not convenient to find the exact solution of velocity distribution and the coefficient 
Figure 4. Velocity distribution of Poiseuille flow in pipe with uniform rectangular cross section at
with respect to the coefficient


3. CFD Calculation and PIV Experiment of Oscillatory Flow in Bifurcating Airways
As foresaid, a progressive mechanism is expected to act under the application of HFOV, and further to deliver fresh gas into the transitional zone. Therefore, a cluster model of transitional bronchioles airways needs to be built numerically or realistically, for clarifying the flow feature during oscillations. Figure 5 shows the dimensions of airway branch (Figure 5(a)) and its mesh (Figure 5(b)) used in numerical calculation, and Figure 6 depicts the airway model used in PIV measurement. Both the numerical and realistic model are based on geometry of Weibel’s model from G18 to G20 (G stands for the generation in anatomical lung structure). The inflow channel and four outflow channels have been extended for fully developing the internal flow. In this study, we basically adopt two scenarios i.e., rest breathing (sinusoidal, 0.2 Hz with 500 mL tidal volume) and HFOV (sinusoidal, 10 Hz with 50 mL tidal volume).
In numerical model, the top inlet is fed with oscillatory gas, the four outlets are connected to the pressure boundary conditions. The calculations are implemented by Star-ccm+® which is based on the FVM (finite volume method) algorithm. The governing equations for the gas flow in airway model are:


where 

Figure 5. Numerical model of lung branch from G18 to G20.
Figure 6. Experimental airways from G18 to G20.
convective terms are discretized by MARS method in second order. Initial temperature and pressure are set at 293.10 K and 101.3 kPa, respectively. Because the flow velocity is lower than 0.1 m/s, and local Reynolds number is less than 10 in this distal region, incompressible Newtonian fluid and laminar flow are selected as the flow properties.
For the numerical inlet boundary, gas velocity is used based on the feature of oscillatory Poiseuille flow, Equation (5) is employed to guarantee 50 mL tidal volume for sinusoidal oscillation with different frequencies in HFOV, where uz and 2.5 × 10−4 (m) indicate velocity in z direction and the radius of G18 airway.

For the four outlets at the bottom, gas pressure is assigned as the boundary condition, which comprises lung compliance C, laminar resistance in airway Rj and volumetric flow rate in bronchi for a given generation q as demonstrated in Equation (6). And lung compliance C is defined as the ratio of volume difference 


where the suffix i indicates the generation number of interest, and j counts from i+1 to the terminal.
Both Lagrangian method and VOF (Volume of Fluid) scheme are employed in calculation to demonstrate the internal flow. VOF method is normally used to distinguish the interface between different species of fluid. The gas property in the airways is homogeneous without species difference, however, VOF can be employed here for judging the net flow which is based on the deformation of fictive interface. In VOF setting, the effect of molecular diffusion is neglected to clearly show the interface between different fluids, and all the fluids share identical physical properties.
Similarly, in the experimental setup, as illustrated in Figure 7 and Figure 8, the upper inlet is connected to a buffer tank which acts as lung dead space, the other side of the buffer tank is connected to HFOV supplier directly. The four ends are coupled with
Figure 7. Schematic of PIV experiment.
Figure 8. Experimental setup of airways model.
four truncated elastic tubes, to simulate the compliances of following airways. Additionally, in G18 - G20, the Reynolds number is less than 10, and Womersley number is lower than 1, the Peclet number is about 1 in the HFOV application, which indicates that viscous laminar flow and parabolic quasi-steady flow are dominant in this region, also the advective transport rate and diffusive transport rate are generally in the same order of magnitude.
Our rest breathing normally takes 5 seconds for one cycle of respiration, while the HFOV achieves 50 oscillations within the same duration. As shown in Figure 9, Figure 10 and Figure 11, the numerical results illustrate that after long stretching, almost all
Figure 9. Initial Lagrangian particles.
Figure 10. End of 5-second rest breathing.
the gas particles returned to their original locations after one cycle of rest breathing. While in the case of HFOV, a regular redistribution of gas particles is presented after 50 fast and shallow oscillations-the core particles move downwards while the peripheral particles evacuate upwards, and the ones extremely close to the wall do not relocate apparently due to the no-slip condition, which obviously is a time-averaged mechanism.
Similar phenomenon is revealed by means of VOF as demonstrated in Figure 12, Figure 13, and Figure 14. Four fluids with identical properties are initially arrayed in the airway model in parallel. After a cycle of rest breathing, majority of gas parcels return to initial locations, and the rearrangement of these gas parcels is irregular. While the HFOV redistribute the gas parcels in a much more regular way after 5-sceond oscillations, and apparent streaming net flow has been induced as shown in Figure 14. Accordingly, HFOV produces more apparent net flow than in rest breathing.
Figure 11. End of 5-second HFOV.
Figure 12. Initial VOF setting.
Figure 13. End of 5-second rest breathing.
Figure 14. End of 5-second HFOV.
To confirm this phenomenon of net flow induced by HFOV, PIV measurement is thereafter carried out by using the realistic airway model, the gas-feeding pattern is set identical to the numerical calculation-sinusoidal oscillation with 10 Hz frequency and 50 mL tidal volume. After obtaining velocity distribution at different phases in a cycle, the particle dislocations can be produced by integrating the velocity distribution at different instants of the cycle as shown in Figure 15. Figure 16 depicts the particle dislocations in one cycle with same settings, except that the frequency is raised up to 20 Hz. As expected, obvious net flow of streaming has been found in 10 Hz and 20 Hz HFOV. For other combinations of frequency and tidal volume in HFOV, semblable patterns of particle movement have been obtained as well. The phenomena revealed by PIV measurement are highly similar to the numerical calculation, although the experimental results are not as neat as the computational results. The existence of steady streaming in
Figure 15. Particle dislocations in PIV measurement (10 Hz).
Figure 16. Particle dislocations in PIV measurement (20 Hz).
HFOV has been confirmed by PIV experiment. According to the particle tracks obtained in experiment, it can be found that the down-coming and up-going routes do not superpose each other for every particle, which implies the oscillatory flow is remarkably irreversible in distal airways. And the irreversible pattern gives rise to the net flow or steady streaming.
4. The Influence of Channel Geometry on Oscillatory Flow
The steady streaming phenomenon which is caused by irreversible flow has been confirmed by both CFD calculation and PIV measurement. In bifurcation geometry, the steady streaming is assumed to be mainly affected by the asymmetric geometry in airway, according to the assumption of F. E. Fresconi et al. [8] . We will examine the assumption by means of comparing the effect of various geometries. In this step, the VOF calculation is adopted with identical inlet boundary condition (oscillatory velocity) and outlet boundary condition (total pressure) for these geometries. The strength of steady streaming CEX will be investigated under sinusoidal oscillation with 10 Hz frequency and 50 mL tidal volume in one-second HFOV application. Also, the molecular diffusion is neglected for clearly observing the interface between the nominal fresh air and used air.
As illustrated in Figure 17, four different airway geometries including cylinder, cone, bifurcation, and multi-bifurcations, are built and connected to the upper straight channel numerically. The interfaces between fresh and used gas are initially arranged on the geometry connections. The numerical results show that steady streamings enhanced gradually in each non-uniform geometry by oscillation, and an obvious transition of steady streaming in these shapes can be seen that more divergent channel brings greater steady streaming. The variation extent of cross section is considered as a crucial factor to the development of net flow. It basically confirms the assumption―the non- uniform geometry mainly generates the steady streaming.
Cylinder
Cone
Bifurcation (2 generations)
Branch (3 generations)
Shapes in volume mesh






Figure 17. Steady streaming in different channel shapes caused by oscillatory flow (sinusoidal, 10 Hz, 50 mL) in 1second.
Moreover, the volume of net flow (Vnf) which denotes the volume of fresh gas left in the following region after oscillation has been calculated along with the coefficient CEX, as listed in Table 1. In the cylinder channel, the steady streaming is supposed to be zero after integral cycles of oscillation because of the uniform channel, a slight deviation occurs in the numerical calculation due to the approximate treatment in iterations. More divergent geometry gives greater Vnf and higher CEX. The CEX of branch model is as high as 0.164, which means 16.4% of the tidal volume has been thrusted into the lower region after 10 oscillations, this lung-like airways apparently is more suitable to be a steady-streaming generator. In addition, the tidal volume at G18 is 50 mL/218 = 1.91 × 10−4 mL, because the tidal volume is normally applied to trachea in clinical application of HFOV. For the distal airways, the volume of oscillatory flow is quite limited due to the huge number of branches.
Both bifurcation model and branch model consist of bifurcating channels, however, the volume of net flow and CEX are much higher in the branch model. Therefore, it is considered that more following bifurcations bring greater net flow and stronger steady streaming, this cumulative effect implies that steady streaming may be much more considerable in HFOV application due to the multi-bifurcating structure in the real human lung which bifurcates 23 times from trachea all the way to alveoli.
5. The Influence of Womersley Number and Reynolds Number on Steady Streaming
In clinical field, the airway geometry has been defined already, a series of Wo and corresponding Re are then selected and applied to check their influences on CEX, which may be instructive to HFOV application. The oscillatory frequency is changed to regulate the magnitude of Wo, and the changed velocity then determines Re, while the tidal volume is kept at 50 mL at trachea. Figure 18 depicts shapes of different gas segment after three cycles of oscillation under various Womersley numbers. The internal gas is initially divided into four parts by nominal interfaces in VOF scheme, and the molecular diffusion is neglected as well. It can be seen from the results that the high Wo brings apparent deformation and deep penetration in longitudinal direction.
The variation of penetration volume for three-cycle oscillation (sinusoidal, 50 mL tidal volume) under different Womersley numbers (from 0.1 to 10) are illustrated in Figure 19. All the curves reach up to almost the same peak values due to the identical
Table 1. Volume of net flow and CEX by oscillatory flow (sinusoidal, 10 Hz, 50 mL) in one second.













Figure 18. Movements of different sections of internal gas after 3 cycles of oscillation under various Womersley numbers.
Figure 19. Penetration volumes under different Wo in oscillatory flow (sinusoidal with 50 mL tidal volume) within 3 cycles.
tidal volume, while at the end of each oscillation, the values of penetration volume diverge from each other because of the different magnitudes of streaming net flow in airways, which means different amounts of fresh air are left in the following region after the oscillation. The curves indicate that the net flows are relatively low when Wo < 1, while for Wo > 1, the magnitudes of net flow rise drastically as Womersley number grows up to about 5, then fall down gradually when Wo further increases. This trend can be noticed clearly in Figure 20 that directly shows the relation between Vnf and Wo in three cycles. For all the three cycles, net flow maximizes at about Wo = 5 as well.
The detailed values of oscillatory frequency, Wo, Re, Vnf, and CEX after three cycles are listed in the following Table 2. Both Wo and Re are calculated on the basis of oscillatory frequency. The CEX reaches a maximum 0.345 when Wo = 5, Re = 123.6, the corresponding frequency is as high as 955.0 Hz. The net flows are compared for different frequencies in same cycles here, if it is compared in an identical duration, the difference will be much greater because the higher frequency accomplishes more cycles in a certain duration. This result indicates that the steady streaming in lung can be enhanced drastically by increasing the oscillatory frequency up to nearly one thousand, which may further give an improvement direction for current HFOV.
Haselton and Scherer investigated streaming magnitude in a single bifurcation channel whose sizes are much greater than our airway models, they found the maximum streaming displacement increases with Re and Wo up to a Re of about 100 and Wo of about 5, after which a gradual decline occurs [6] . Although they regulated the value of Re and Wo also by changing the flow viscosity, we achieved it by merely changing the oscillatory frequency, the critical values of Re and Wo they found are very close to our calculation results. Their measurement was accomplished within a big single bifurcation while our model is much smaller and multi-bifurcated, which may indicate that steady streaming acts throughout the lung airways of different sizes. Gaver
Figure 20. Volume of net flow under different Wo in oscillatory flow (sinusoidal with 50 mL tidal volume) within 3 cycles.
Table 2. Influence of Re and Wo on steady streaming after three cycles of oscillation (sinusoidal with tidal volume).
and Grotberg [9] experimentally investigated oscillatory flow in a tapered channel and demonstrated that the deformation of a dye streak is different in the cases of Wo < 5 and Wo > 10. Therefore, it is considered that a peak steady streaming appears when Wo reaches about 5 and Re is close to 100 or slightly over 100 in bifurcation airways.
Obviously, the Womersley number can be changed by changing either frequency or viscosity within a provided geometry. But only oscillatory frequency has been altered to change Wo in this study, one reason is in clinical field, the viscosity of ventilating gas is almost constant, another reason is that we anticipate faster oscillation could incur better ventilation efficiency by causing more turbulence in upper lung region as well as more steady streaming. From Table 2, it can be seen that the intensity of steady streaming increases with oscillatory frequency up to nearly 1000 Hz, it may imply the possibility of super-fast HFOV in the future.
6. Discussion and Conclusions
A common scenario of HFOV (sinusoidal with 10 Hz frequency and 50 mL tidal volume) has been investigated by both CFD calculation and PIV measurement in the present study. An apparent time-averaged net flow phenomenon has been found in peripheral lung airways which help to deliver the fresh air into deeper region centrally and discharge the used air peripherally. It demonstrates that even though the tidal volume is smaller than dead space of lung in HFOV, steady streaming works to thrust the fresh gas deeply and thereby overcome the lack of tidal volume. The distal lung region is therefore more convective than previously expected. In view of steady streaming found in upper lung airways by other researchers, it is considered that steady streaming may exist in the whole lung tract and is an important factor of HFOV effect.
A series of airway geometry have been numerically surveyed to clarify the influence of geometry on steady streaming. It is found that more divergent channels bring stronger steady streaming, and the multi-bifurcated channel causes greater steady streaming than the single bifurcation does, which indicates the magnitude of steady streaming in real lung may be much greater than that in the truncated branch model under HFOV application.
By changing the oscillatory frequency, different Womersley numbers and corresponding Reynolds numbers have been obtained to testify their influences on steady streaming. It has been found that the streaming magnitude rises with Re and Wo up to a Re of about 124 and Wo of about 5, which is in a good agreement with the experimental results brought out by other researchers. Moreover, the volume of net flow maximizes when the frequency reaches nearly 1000, which may imply the feasibility of super-fast HFOV in the future.
Acknowledgements
The authors are grateful to Kohei Morita and Tomonori Yamamoto for assistance in numerical calculation and PIV measurement.
Cite this paper
Han, B., Hirahara, H. and Yoshizaki, S. (2016) Streaming Cau- sed by Oscillatory Flow in Peripheral Airways of Human Lung. Open Journal of Fluid Dynamics, 6, 242-261. http://dx.doi.org/10.4236/ojfd.2016.63019
References
- 1. Padmanabham, N. and Pedley, T.J. (1987) Three-Dimensional Steady Streaming in a Uniform Tube with an Oscillating Elliptical Cross-Section. Journal of Fluid Mechanics, 178, 325-343.
http://dx.doi.org/10.1017/S0022112087001241 - 2. Lighthill, M.J. (1991) Biomechanics of Hearing Sensitivity. Journal of Vibration and Acoustics, 113, 1-13.
http://dx.doi.org/10.1115/1.2930149 - 3. Leibovich, S. (1983) The Form and Dynamics of Langmuir Circulations. Annual Review of Fluid Mechanics, 15, 391-427.
http://dx.doi.org/10.1146/annurev.fl.15.010183.002135 - 4. Lyne, W.H. (1971) Unsteady Viscous Flow in a Curved Pipe. Journal of Fluid Mechanics, 45, 13-31.
http://dx.doi.org/10.1017/S0022112071002970 - 5. Hall, P. (1974) Unsteady Viscous Flow in a Pipe of Slowly Varying Cross-Section. Journal of Fluid Mechanics, 64, 209-226.
http://dx.doi.org/10.1017/S0022112074002369 - 6. Haselton, F.R. and Scherer, P.W. (1982) Flow Visualization of Steady Streaming in Oscillatory Flow through a Bifurcating Tube. Journal of Fluid Mechanics, 123, 315-333.
http://dx.doi.org/10.1017/S0022112082003085 - 7. Eckmann, D.M. and Grotberg, J.B. (1988) Oscillatory Flow and Mass Transport in a Curved Tube. Journal of Fluid Mechanics, 188, 509-527.
http://dx.doi.org/10.1017/S0022112088000825 - 8. Fresconi, F.E., Wexler, A.S. and Prasad, A.K. (2008) Transport Profiles in the Conducting Airways of the Human Lung. International Journal of Heat and Mass Transfer, 51, 5552-5561.
http://dx.doi.org/10.1016/j.ijheatmasstransfer.2008.04.014 - 9. Gaver, D.P. and Grotberg, J.B. (1986) An Experimental Investigation of Oscillating Flow in a Tapered Channel. Journal of Fluid Mechanics, 172, 47-61.
http://dx.doi.org/10.1017/S0022112086001647 - 10. Goldberg, I.S., Zhang, Z. and Tran, M. (1999) Steady Streaming of Fluid in the Entrance Region of a Tube during Oscillatory Flow. Physics of Fluids, 11, 2957-2962.
http://dx.doi.org/10.1063/1.870154 - 11. Weibel, E.R. (1963) Morphometry of the Human Lung. Springer Verlag and Academic Press, New York.
http://dx.doi.org/10.1007/978-3-642-87553-3
Nomenclature

C: Compliance [m3/Pa]
f: Frequency [Hz]
G: external force [N]
p: Pressure [Pa]
Q: Flow rate [m3/s]
Pe: Peclet number
r: radial position [m]
Re: Reynolds number


t: time [s]
T: flow cycle period [s]
u: oscillatory velocity [m/s]
U: velocity amplitude [m/s]

uz: velocity in z direction [m/s]
VT: tidal volume [m3]
Wo: Womersley number

υ: kinematic viscosity [m2/s]
ω: angular frequency [rad/s]
ρ: fluid density [kg/m3]


Subscript
i: ith generation of lung
j: jth generation of lung
z: z-direction





































