Open Journal of Fluid Dynamics
Vol.05 No.01(2015), Article ID:54410,9 pages
10.4236/ojfd.2015.51008
Rheological Properties of Casting Solutions for Starch Edible Films Production
Po Huo1*, Tatsiana Savitskaya2, Lizaveta Gotina2, Ivan Reznikov2, Dzmitry Grinshpan3
1College of Biology and Environmental Engineering, Zhejiang Shuren University, Hangzhou, China
2Faculty of Chemistry, Belarusian State University, Minsk, Belarus
3Research Institute for Physical and Chemical Problems, Minsk, Belarus
Email: *xka-8@163.com, savitskayaTA@bsu.by
Copyright © 2015 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 10 February 2015; accepted 1 March 2015; published 5 March 2015
ABSTRACT
Rheological properties of corn starch and sodium alginate blend solutions have been measured at different polymer ratios in the temperature range from 303 to 343 K bya R/S Brook field rheometer with аcoaxial cylinder measuring unit. Dynamic viscosity of blends has been shown to decrease with shear rate increase and to increase with sodium alginate content increase. The influence of shear rate on activation energy of viscous flow depends on sodium alginate content and is different for below and over 5% (mass) content. Applicability of Ostwald-de-Waele, Herschel-Bulkley, Bingham and Casson models for the description of CS:SA blend solutions flow has been analyzed. Rheological properties of CS:SA blend solutions allow one to look at them as an alternative to starch solutions for edible films casting and production by dry method.
Keywords:
Corn Starch, Sodium Alginate, Polymer Blend Solutions, Rheological Properties, Activation Energy of Viscous Flow, Edible Films Casting Solutions

1. Introduction
The food industry has recently taken a growing interest in the application of edible food films for food packaging which should solve problems like preserving food quality and ensuring biological human safety. In the meantime the era of biodegradable films, which can be destroyed in the result of biological processes in the human body without any harmful effects has not yet begun. Nevertheless such an idea attracts attention both from researchers and industrial manufacturers. Starch being a biodegradable polymer with excellent biocompatibility and non-toxicity can be considered as a basic raw material for such purposes [1] [2] . There are two macromolecular components in starch: amylose and amylopectin. Amylose is a linear polymer of α-1,4 anhydroglycose units whereas amylopectin is a highly branched polymer of short α-1,4 chains linked by α-1,6 glucosidic branching points occurring every 25 - 30 glucose units. The ratio of these two polysaccharides varies according to the botanical origin of the starch. Good film forming ability of starch determines its wide use in the food packaging area. But when comparing mechanical properties of freshly prepared films and stored starch films the need of modification is evident for the removal of the recrystallization phenomenon that makes starch films more rigid and less stretchable during storage and subsequent use [3] .
Corn starch (CS) modification by means of blending with other food polymers has to be taken into account for solving the problems mentioned above. Presently there are many polymers that can be regarded to as feedstock for the production of such bicomponent films on an industrial scale [4] - [6] . Sodium alginate (SA) widely used for food purposes is of special interest for such a strategy line. Sodium alginate is a water soluble salt of alginic acid, a naturally occurring non-toxic polysaccharide found in all species of brown algae [7] . It contains two uronic acids, (1-4)-linked β-D-mannuronic acid (M) and (1-4)-linked α-L-guluronic acid (G). It is composed of homopolymeric blocks M-M or G-G, and blocks with an alternative sequence of M-G blocks.
Films based on CS and SA blends show promising results for application as edible packaging in food industry. Rheological properties of casting solutions must be known to control the manufacturing process of bicomponent films. The influence of such variable parameters as overall concentration of polymers, polymer blending ratio, shear stress, temperature and others on solution viscosity must be taken into account [8] - [10] . In the current research the effect of SA addition on the rheological properties of CS solutions was focused on with the following bodies of interest: the influence of temperature, polymer blending ratio and total concentration of two polymers, as well as their simultaneous effects. Several rheological models were used to estimate the fitting of the experimental data and the activation energy of viscous flow was calculated.
2. Materials and Methods
2.1. Solutions Preparation
The CS solutions were prepared by dispersing starch powder in distilled water under mechanical stirring during 15 min at room temperature, followed by heating of the dispersion at 90˚C for 30 minutes under stirring. IKA Werke equipment was used for stirring. The concentration of CS in the solutions was 5%, 6%, 8% and 10% (mass). Pure CS produced in China that contains 25% of amylose with water content ≤ 14% was used. The SA solutions were prepared by dissolving sodium alginate powder in distilled water under stirring during 45 min at room temperature. The concentrations of SA solutions under study were 2%, 3% and 4% (mass). We used pure sodium alginate (SA) extracted from sea plant Kelp (sea tangle), produced in China with water content ≤ 14%. The following ratio of polymers in CS:SA blends were investigated: CS:SA = 100:0; 99:1; 98:2; 95:5; 90:10; 80:20; 70:30; 60:40; 50:50; 0:100. The total concentration of polymers in the solution was taken 8 % (mass) as the most suitable concentration for film casting and production by drying. Polymer blend solutions were prepared by simultaneous dispersion of starch and sodium alginate in distilled water at stirring during 15 min, followed by heating of dispersion at 90˚C for 30 minutes under stirring. The overall polymer concentration was 8% (mass) at different blending ratio of CS:SA.
2.2. Rheological Measurements
Rheological measurements were carried out using a CC25 coaxial cylinder measuring unit of the R/S Brookfield rotational rheometer with a constant shear rate regime. The shear stress was measured as a function of shear rate that varied from 0.5 to 1000 s−1. Seventeen milliliters of solution were loaded into the cylindrical cup and cooled in a water bath to specific temperature. All analyses were performed at least three times between 20% - 80% full torque scales. Data were analyzed using MS-Excel and Mathematica software. Measurements were made starting at 343 K followed by consistent cooling to 333 K, 323 K, 313 K and 303 K at which the measurements were ended.
2.3. Activation Energy of Viscous Flow Calculation
The value of measured viscosity is a measure of a fluid’s resistance to flow. In order for the solution to flow, certain amount of energy is required to overcome the resistance and allow molecular motion to occur. This energy is known as the “activation energy of viscous flow” Ea and can be calculated using Eyring’s Equation (1) [11] . The equation explains the physical meaning of the activation energy of viscous flow, as the required energy for the molecule to pass through the energy barrier that surrounds motionless molecules. The number of molecules having this energy is in correlation with the Boltzmann factor, hence the viscosity of the liquid can be expressed by Equation (1).
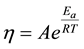 (1)
(1)
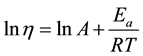 (2)
(2)
To calculate the activation energy of viscous flow at constant shear rate we used the dependence of viscosity versus reverse value of temperature. In the case of linear plot simple mathematical operations were performed, suggesting that A is constant within a narrow range of temperatures (Equation (2)):
2.4. Theoretical Viscosity Calculation
Theoretical viscosity was calculated according to the following formula:
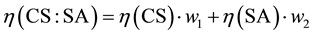
where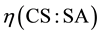 −blend viscosity,
−blend viscosity,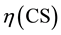 −CS viscosity,
−CS viscosity, −SA viscosity,
−SA viscosity,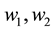 ―mass content of CS and SA respectively. The dualistic possibility of viscosity growth was taken into account, thus both linear and exponential theoretical viscosity value was calculated.
―mass content of CS and SA respectively. The dualistic possibility of viscosity growth was taken into account, thus both linear and exponential theoretical viscosity value was calculated.
3. Results and Discussion
The rheological behavior of individual CS, SA and polymer blend solutions can be described as the behavior of non-Newtonian fluids that are shear thinning (viscosity decreases with shear rate increase) in the concentration range under study. Figure 1 shows the viscosity rheograms, i.e. plots of viscosity versus shear rate for the solutions of CS and SA with different polymer concentrations. From this figure it can be noticed that 8% CS and 2% SA solutions have very close values of viscosity at shear rate over 300 s−1, while 10 % CS and 3% SA solutions have very closed values of viscosity at very low values of shear rate. This data predicts very high viscosity of 8% SA solution. Preparation of such a solution in practice turned out to be impossible hence less concentrated solutions of SA had to be used for films casting and rheological measurements.
As follows from Figure 2 both polymers solutions exhibit a non-linear growth of viscosity with polymer concentration increase.
As it can be seen from Figure 2, the intensive viscosity growth according to exponential law starts for SA solutions from the lower concentration than for CS solutions. The parameters of the exponential equation η = aexp(bC) are shown in Table 1.
These results can be useful in making a prediction of polymer solutions viscosity.
As seen from Figure 2 for SA solutions the dependence of viscosity from polymer concentration becomes more and more linear with the increase of temperature. When describing exponential fitting for SA solutions, it was taken into account that SA concentrations in the solutions under study were taken in a narrow band. According to Taylor’s theorem (Equation (3)):
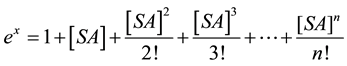 (3)
(3)
So at low SA concentrations a certain flat region can be explained by Taylor’s theorem (Equation (3)). The parameters of the exponential equations are shown in Table 2 from which it is evident that at low temperature exponential behavior fits experimental data with a higher correlation coefficient.
Figure 3 illustrates the impact of SA content on the viscosity of CS:SA blend solutions measured at 303 and 343 K. The viscosity increases with SA content increase and its growth becomes rather dramatic over 25% SA content in the blend. Because of high viscosity that exceeded the value possible to measure for the given measuring unit the viscosity of solutions with high SA content was measured at 343 K only.
Figure 1. Viscosity of pure SA (1, 2) and CS (3, 4) solutions versus shear rate at 343 K. Concentration of the solutions: 1% - 2%, 2% - 3%, 3% - 8%, 4% - 10%.

Figure 2. Plot of viscosity versus overall polymer concentration for CS (a), SA (b) solutions at different temperatures at shear rate 1000 s−1: 1−343 K, 2−323 K, 3−303 K.
Figure 3. Dependence of viscosity on SA content in 8% CS/SA solutions at different temperaturesat shear rate 1000 s−1: 1−343 K, 2−303 K.
The shear rate dependence of viscosity in double logarithmic scale for CS and SA solutions of different concentrations is presented at Figure 4. As follows from the figure, the viscosity of CS solutions decreases more sharply as the shear rate increases. The difference in the curve’s shape can be explained by different configuration of the initial macromolecules [12] : linear for SA and branched for CS. There are two types of starch macromo-
Table 1. Exponential equation parameters for viscosity ( )−concentration (C) dependence.
Table 2. Correlation coefficients for SA solutions at different temperatures.

Figure 4. Viscosity vs. shear rate in double logarithmic scale for CS (a), SA (b) solutions of different con- centrations at 343 K. The concentrations are as follows: (a) 1−5%, 2−6%, 3−8%, 4−10%; (b) 1−4%, b− 3%, 3−2%.
lecules: amylase and amylopectin. Amylose is an essentially linear, isotactic polymer of a-D-glucopyranosyl units linked


Variation of solution viscosity with shear stress for 8% solutions of polymer blends with different blending ratio CS:SA at a temperatures range from 303 to 343 K is represented at Figure 5 in 3D scale. Represented data makes it clear that the more the content of SA for equiconcentrated solutions the higher the viscosity and the value of shear stress of the start of fluid flow.
The comparison of experimental and theoretical evaluated solutions viscosity is shown in Table 3. As Table 3 follows, the theoretically calculated viscosity values are lower than experimental values and increase with SA content increase. The probable reason for this is interaction between polymer macromolecules in a blend by hydrogen bonding.
Activation energy of viscous flow (flow activation energy) for CS:SA blend solutions was evaluated from the slope of the straight line in the Arrhenius plot, i.e. the plot of logarithmic viscosity at constant shear rate against reversed temperature. Flow activation energy is defined as minimum energy required to overcome the energy barrier before the elementary flow can occur. The viscous flow occurs as a sequence of events which are shifts of particles in the direction of the shear force action from one equilibrium position to another. As it could be seen from Figure 6, flow activation energy of polymers blend solutions has minimum value at blending ratio CS:SA = 98:2. Data represented at Figure 6 correspond to average value of activation energy for the interval of

Figure 5. Variation of 8% (mass) solution viscosity with shear stress for different polymer ratio for CS:SA blends and temperatures: (a)−303 K, (b)−323 K, (c)−343 K.
Figure 6. Activation energy of viscous flow at constant shear rate versus SA content in 8% (mass) solutions of CS:SA blends.
Table 3. Experimental and calculated polymers blend solutions viscosity.
where ηl―linear theoretical viscosity, ηe―exponential theoretical viscosity, ηexp―experimental value.
shear rate 4 - 140 s−1. The average value of flow activation energy for this interval of shear rate is represented at the figure. Flow activation energy versus polymer blend composition curves determined at 310, 660 and 1000 s−1 follow the similar trend. The decreasing of activation energy at small amount of SA are thought to be due by the destruction of intermolecular hydrogen bonds between starch hydroxyl groups as a result of the action of SA macromolecules as a high molecular weight plasticizer. Increasing of flow activation energy at more than 10% SA content in the solution follows by the increasing of the concentration of a component with higher flow activation energy. One can compare the numerical values of flow activation energy for 8% starch solution and 2% SA solution: 10.6 and 15.8 kJ/mol correspondingly.
The unusual behavior of this blend was discovered by the dependence of flow activation energy versus shear rate at different blending ratio of CS:SA as well. In order to demonstrate the picture a 3D diagram of flow activation energy dependence on both shear rate and SA content in the solutions (Figure 7) was built. As can be seen from the diagram the flow activation energy is constant with shear rate increasing for this blend only. The activation energy of viscous flow was found to increase for CS solution and to decrease for CS:SA blend solutions when SA content is over 5%. The growth of activation energy of viscous flow with growth of shear rate for CS solutions can be connected with the degradation of undestroyed residues of CS granules.
Rheological flow curve for the solution at blending ratio CS:SA = 98:2 is not typical in the comparison with other compositions as follows from Figure 8. At a limited area of small shear rates they show Newtonian flow with a constant zero-shear viscosity (curve 4).
Figure 7. Dependence of activation energy of viscous flow on both the shear rate (x) and SA content in 8% (mass) solutions (y).

Figure 8. Flow curves in double logarithmic scales at 323 K (a) and 343 K (b) for CS (1) and CS/SA solutions: 2−99.5/0.5, 3−99/1, 4−98/2, 5−95/5, 6−90/10, 7−80/20, 8−70/30, 9−60/40, 10− 50/50.
Table 4 illustrates fitting of the shear stress versus shear rate experimental data to different rheological models:
Table 4. Suitability of rheological models for CS/SA blend solutions.
Ability of the models to follow the data has been analyzed. It was shown, that power equations fit the curves with a higher correlation coefficient, than Bingham (Equation (6)) or Casson equation (Equation (7)). Within the power equations, the more parameters there are, the higher the coefficient of determination, so Herschel-Bul- kley equation (Equation (5)) describes experimental data better, than Ostwald-de Waele (Equation (4)). With increasing SA concentration Ostwald-de Waele and Herschel-Bulkley equations remains high correlation, whereas the effect of high alginate concentration appears significant. As parameter n is less than1, all solutions are pseudoplastic fluids. For most of the cases certain fitting increasing is noticed with temperature increasing. As power law can be used to describe the

Considering n as a flow behavior index, that describes deviation from Newtonian fluids about flow behavior, it was found, that the value with increasing SA contents changes its behavior from a curve with strongly marked maximums, through a curve with feebly marked minimum to monotonic decreasing curves. Similar to K parameter, spoken above, for isothermal conditions the dependences with a maximum n value are widely presented.
It was found, that the Herschel-Bulkley equation has the best correlation with experimental data. Nevertheless, the values of τ0 ≤ 0 doesn’t make much sense and may only represent, that the equation fits most of the data at

The K parameter in the Herschel-Bulkley equation tends to decrease with increasing temperature at low SA concentrations, followed by almost similar values to increasing dependences, analogue to K parameter in power law equation, furthermore, the higher the SA concentration, the sharper the K variation within the temperature series. Parameter n in the Herschel-Bulkley equation varies similar to parameter K of the same equation.
4. Conclusions
Experimental results show that the rheological properties of individual CS, SA and CS:SA blend solutions are controlled by temperature, overall polymer concentration and alginate content in the solutions within the temperature range of 303 - 343 K, alginate content up to 40% and overall concentration of individual CS 5% - 10%, SA 2% - 4% and overall 8% (mass) concentration of polymers for polymer blends. The rheological behavior of individual CS, SA and polymer blend solutions can be described as the behavior of non-Newtonian liquids that are pseudoplastic, where their viscosity decreases with increasing shear rate.
Dependence of viscosity on individual CS, SA solution concentration fits an exponential law. Viscosity depends more sharply on concentration for SA solution than CS solutions. SA content in blends makes the solution much more viscous. Such a tendency is due to the fact that the SA component contributes significantly to the viscosity of the solution. When the SA content exceeds 25 (wt%) viscosity value starts a drastic growth in comparison to low SA content, where the viscosity changes relatively little.
Because CS and CS:SA blends have similar character of rheological curve it is possible to use CS:SA blend solutions for modified starch edible films casting. But the overall polymers concentration has to be reduced from the point of view of viscosity limitation for casting process. The required concentration can be calculated.
The activation energy of viscous flow calculated for all investigated CS/SA blend solutions shows a minimum value at a SA 2% content with the following increase. Polymer blend of this composition demonstrates the independence of activation energy of viscous flow on shear rate and small Newtonian area on rheological curve. This suggests that at this polymer ratio SA macromolecules probably work as a high molecular weight plasticizer.
The flow curves (shear stress against shear rate) for CS/SA blend solutions were fitted to theoretical models proposed for pseudoplastic fluids: Ostwald-de Waele and Herschel-Bulkley. Bingham and Casson models are less suitable. The applicability of models depends on blend composition and temperature as well.
Acknowledgements
The authors would like to thank Science and Technology Department of Zhejiang Province, State Administration of Foreign Experts Affairs, Zhejiang Administration of Foreign Experts Affairs and Zhejiang Shuren University for financial support.
Cite this paper
PoHuo,TatsianaSavitskaya,LizavetaGotina,IvanReznikov,DzmitryGrinshpan, (2015) Rheological Properties of Casting Solutions for Starch Edible Films Production. Open Journal of Fluid Dynamics,05,58-67. doi: 10.4236/ojfd.2015.51008
References
- 1. Thakore, I.M., et al. (2001) Studies on Biodegradability, Morphology and Thermo-Mechanical Properties of LDPE/ Modified Starch Blends. European Polymer Journal, 37, 151-160.
http://dx.doi.org/10.1016/S0014-3057(00)00086-0 - 2. Lu, D.R., Xiao, C.M. and Xu, S.J. (2009) Starch-Based Completely Biodegradable Polymer Materials. Express Polymer Letters, 3, 366-375.
http://dx.doi.org/10.3144/expresspolymlett.2009.46 - 3. Jimknez, A., Fabra, M., Taw, P. and Chiralt, A. (2012) Edible and Biodegradable Starch Films. Food and Bioprocess Technology, 5, 2058-2076.
http://dx.doi.org/10.1007/s11947-012-0835-4 - 4. Scatto, M., et al. (2013) Plasticized and Nanofilled poly(lactic acid)-Based Cast Films: Effect of Plasticizer and Organoclay on Processability and Final Properties. Journal of Applied Polymer Science, 127, 4947-4956.
http://dx.doi.org/10.1002/app.38042 - 5. Lund, A. (2010) Melt Spinning of poly(vinylidene fluoride) Mono-and Bicomponent Fibres and Yarns—The Formation of Piezoelectric Beta-Phase Crystallinity. Lic. Thesis, Chalmers University of Technology, Chalmers.
- 6. Wu, P.C., et al. (2007) Novel Microporous Films and Their Composites. Journal of Engineered Fibers and Fabrics, 2, 49-59.
http://www.jeffjournal.org/papers/Volume2/Wu.pdf - 7. Harnsilawat T., Pongsawatmanit, R. and McClements, D.J. (2006) Characterization of β-lactoglobulin-sodium Alginate Interactions in Aqueous Solutions: A Calorimetry, Light Scattering, Electrophoretic Mobility and Solubility Study. Food Hydrocolloids, 20, 577-585.
http://dx.doi.org/10.1016/j.foodhyd.2005.05.005 - 8. Che, L.M., Li,D., Wang, L.J., Ozkan, N., Chen, X.D. and Mao, Z.H. (2008) Rheological Properties of Dilute Aqueous Solutions of Cassava Starch. Carbohydrate Polymers, 74, 385-389.
http://dx.doi.org/10.1016/j.carbpol.2008.03.007 - 9. Lagarrigue, S. and Alvarez, G. (2001) The Rheology of Starch Dispersions at High Temperatures and High Shear Rates: A Review. Journal of Food Engineering, 50, 189-202.
http://dx.doi.org/10.1016/S0260-8774(00)00239-9 - 10. Marcotte, M., Taherian, A.R. Trigui, M. and Ramaswamy, H.S. (2001) Evaluation of Rheological Properties of Selected Salt Enriched Food Hydrocolloids. Journal of Food Engineering, 48, 157-167.
http://dx.doi.org/10.1016/S0260-8774(00)00153-9 - 11. Gedde, U.L.F. (1999) Polymer Physics. Springer, Berlin.
http://dx.doi.org/10.1007/978-94-011-0543-9 - 12. Kasehagen, L.J. and Macosko, C.W. (1998) Nonlinear Shear and Extensional Rheology of Long-Chain Randomly Branched Polybutadiene. Journal of Rheology, 42, 1303-1327.
http://dx.doi.org/10.1122/1.550892
NOTES
*Corresponding author.













