Open Journal of Fluid Dynamics
Vol.4 No.2(2014), Article
ID:46732,19
pages
DOI:10.4236/ojfd.2014.42016
The Stability of a Rotating Cartesian Plume in the Presence of Vertical Boundaries
Khaled S. Al-Mashrafi1, Ibrahim A. Eltayeb2
1Section of Applied Sciences, Department of Human Resources Development, General Directorate of Education in Eastern Region, Ministry of Education, Sur, Oman
2Department of Mathematics and Statistics, College of Science, Sultan Qaboos University, Muscat, Oman
Email: P001175@student.squ.edu.om
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 15 April 2014; revised 15 May 2014; accepted 22 May 2014
ABSTRACT
The effect of two fixed vertical boundaries, a finite distance apart, on the dynamics of a column of buoyant fluid rising in a less buoyant fluid is investigated in the presence of vertical rotation. It is shown that the presence of the boundaries introduces two main effects on a rotating plume. They tend to stabilise the plume but succeed only reducing the value of the growth rate and the plume remains unstable for all finite values of the distance between the boundaries and the plume. In the absence of the sidewalls, two modes of the instability were found known as the sinuous mode and the varicose mode. The influence of the boundaries is such that it reduces the growth rate of the varicose mode more than that of the sinuous mode and consequently the modified sinuous mode is always preferred in the presence of the boundaries.
Keywords:Compositional Plumes, Stability, Growth Rate, Bounded Domain, Rotation

1. Introduction
The study of the dynamics of compositional plumes is important for many real life applications in industry ([1] - [6] ), geophysics ([7] -[25] ) and environment ([26] -[34] ). While the presence of the compositional plumes can be harmful (e.g., in iron bars), it is useful in geophysics (e.g., the hot compositional plumes, that rise from the inner core boundary of the Earth into the outer core interact with the rotation and magnetic field of the Earth and may contribute to the Geodynamo). Such a wide range of applications has motivated many studies on various aspects of the dynamics of compositional plumes. These studies are experimental and theoretical. The experimental works on the dynamics of compositional plumes observed that the plume flow seems to be stable (Sample and Hellawell [35] ; Chen and Chen [36] ; Hellawell et al. [37] ). The laboratory studies by Hellawell et al. [37] find that the plumes are thin and long, and its top part tends to break up and disappears. Classen et al. [38] experimentally studied the dynamics of compositional plumes under the influence of vertical rotation to find that the plumes are unstable and break into blobs. On the other hand, the theoretical works on the stability of the plumes showed that the Cartesian plume is always unstable in the absence of rotation (Eltayeb and Loper [16] ) and in the presence of rotation (Eltayeb and Hamza [18] ). These studies assumed that the plume rises vertically in a fluid of unbounded domains. While the experimental studies were conducted in bounded regions to show that the plume was stable, the theoretical models were conducted in unbounded domains to find that the plume was unstable. Thus it is of interest to examine the influence of the vertical boundaries on the dynamics of the plumes. The mathematical model by Al Mashrafi and Eltayeb [6] investigated the influence of the two fixed vertical boundaries on the dynamics of the plumes. They tested the stability of non-rotating Cartesian plumes in a bounded domain to find that the presence of two vertical boundaries affects the stability, but the plumes remain unstable. Moreover, they found that the plume was stable when it was close to the boundary but had a large thickness and the material diffusion is potent in the thin layer between the plume and the nearest boundary.
Motivated by real life applications and laboratory results, we study here the influence of vertical rotation on the dynamics of bounded Cartesian plume. In general, the purpose of this study is to extend the theoretical model by Al Mashrafi and Eltayeb [6] on the dynamics of a Cartesian compositional plume in bounded regions to include the action of vertical rotation. The model by Al Mashrafi and Eltayeb [6] consisted of a column of buoyant fluid of finite thickness,  , rising vertically in another less buoyant fluid bounded by two fixed vertical walls located at
, rising vertically in another less buoyant fluid bounded by two fixed vertical walls located at  and
and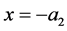 . The system was infinite in the
. The system was infinite in the ![]() and
and 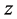 directions. In the current study, we consider that the whole system rotates about the vertical with a uniform angular speed,
directions. In the current study, we consider that the whole system rotates about the vertical with a uniform angular speed, 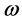 (see Figure 1).
(see Figure 1).
In Section 2, we formulate the model mathematically and state the boundary conditions of the system. The presence of rotation introduces an additional parameter, 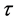 , which is a measure of the Coriolis force relative to the viscous force, and this parameter referred to hereinafter as the rotation parameter, defined by
, which is a measure of the Coriolis force relative to the viscous force, and this parameter referred to hereinafter as the rotation parameter, defined by
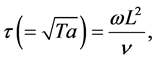 (1)
(1)
where ![]() is the Taylor number,
is the Taylor number, 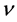 is the kinematic viscosity and
is the kinematic viscosity and 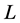 is the unit of length (see Equation (6) below). In Section 3, we investigate the influence of the vertical boundaries on the linear stability of a rotating
is the unit of length (see Equation (6) below). In Section 3, we investigate the influence of the vertical boundaries on the linear stability of a rotating
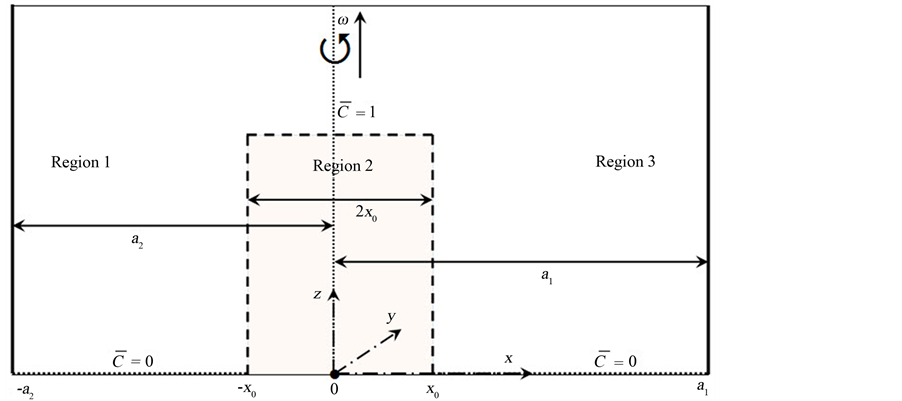
Figure 1. The geometry of the problem showing the profile of the basic state concentration of light material,  , representing a plume of width,
, representing a plume of width, 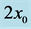 , and concentration, 1 , rising vertically in a finite fluid of width,
, and concentration, 1 , rising vertically in a finite fluid of width, 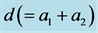 , and concentration, 0. The system rotates uniformly about the vertical with angular speed,
, and concentration, 0. The system rotates uniformly about the vertical with angular speed, . The plume divided the system into three regions: region 2 represents the plume whereas regions 1 and 3 represent the surrounding fluid.
. The plume divided the system into three regions: region 2 represents the plume whereas regions 1 and 3 represent the surrounding fluid.
bounded Cartesian plume. The problem of the rotating plume was studied by Eltayeb and Hamza [18] in the absence of boundaries. In Section 4, we discuss the effect of the boundaries on the stability of a rotating plume. The growth rate is maximised over the wave numbers plane 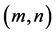 in the parameter space. In Section 5, we make some concluding remarks.
in the parameter space. In Section 5, we make some concluding remarks.
2. Formulation of the Problem
We consider a two-component fluid, in which the concentration of the solvent component (light material) is ![]() and the temperature is
and the temperature is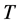 , rotating uniformly about the vertical with angular velocity
, rotating uniformly about the vertical with angular velocity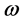 . The fluid has kinematic viscosity,
. The fluid has kinematic viscosity, 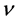 , and thermal diffusivity,
, and thermal diffusivity, 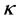 , and material diffusion is negligible. The dimensionless equations of the system have been derived by Eltayeb and Hamza [18] . They are
, and material diffusion is negligible. The dimensionless equations of the system have been derived by Eltayeb and Hamza [18] . They are
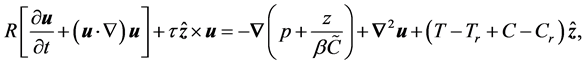 (2)
(2)
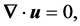 (3)
(3)
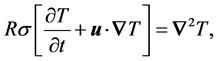 (4)
(4)
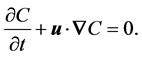 (5)
(5)
Here R,  and
and 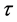 are the Grashoff number, the Prandtl number and the rotation parameter, respectively, defined by
are the Grashoff number, the Prandtl number and the rotation parameter, respectively, defined by
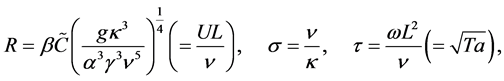 (6)
(6)
where ![]() is the Taylor number and
is the Taylor number and![]() ,
, 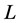 and
and 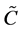 are characteristic units of velocity, length and concentration, respectively (Al Mashrafi and Eltayeb [6] ), and
are characteristic units of velocity, length and concentration, respectively (Al Mashrafi and Eltayeb [6] ), and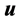 ,
, ![]() ,
, ![]() ,
, 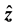 ,
, 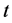 ,
, 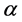 ,
, 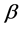 ,
, ![]() ,
, ![]() are the velocity vector, the pressure, the constant gravitational acceleration, the upward unit vector, the time, the thermal expansion coefficient, the compositional expansion coefficient, the density, the uniform temperature gradient and the subscript “
are the velocity vector, the pressure, the constant gravitational acceleration, the upward unit vector, the time, the thermal expansion coefficient, the compositional expansion coefficient, the density, the uniform temperature gradient and the subscript “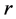 ” in the Equation (2) refers to reference values.
” in the Equation (2) refers to reference values.
We consider a basic concentration profile
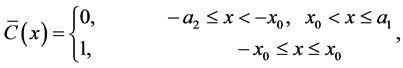 (7)
(7)
which defines a plume of thickness, 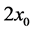 , rising with velocity
, rising with velocity 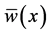 in the presence of mean temperature
in the presence of mean temperature 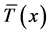 and mean pressure
and mean pressure 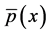 such that
such that
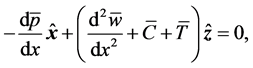 (8)
(8)
 (9)
(9)
which are the same equations obtained in the absence of rotation. The presence of rotation does not affect the basic state, and the solution of (8) and (9) is the same as in the absence of rotation. We include it here for easy reference:
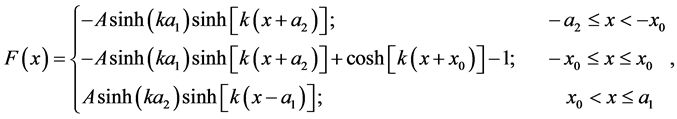 (10)
(10)
where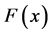 ,
, 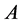 and
and 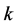 are defined by
are defined by
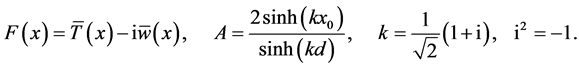 (11)
(11)
3. The Stability Analysis
In this section, we use the perturbation Equations (14)-(17) to investigate the linear stability of the basic state solution given by (10). We assume that the interface at the plane 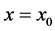 is given a small harmonic disturbance of the form
is given a small harmonic disturbance of the form
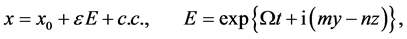 (12)
(12)
where 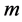 and
and 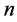 are the wavenumber components in the
are the wavenumber components in the 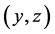 plane,
plane, ![]() is the growth rate and
is the growth rate and 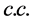 refers to the complex conjugate.
refers to the complex conjugate.
The disturbance (12) will propagate into the fluid, and affect the second interface and the variables of the system to produce the perturbations. Consequently, the interface at 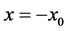 can be written in the form
can be written in the form
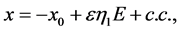 (13)
(13)
where 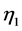 is a measure of the amplitude of the interface and it is evaluated as a part of the solution. The perturbations introduced into the system are governed by the dimensionless equations (see Al Mashrafi and Eltayeb [6] )
is a measure of the amplitude of the interface and it is evaluated as a part of the solution. The perturbations introduced into the system are governed by the dimensionless equations (see Al Mashrafi and Eltayeb [6] )
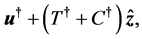
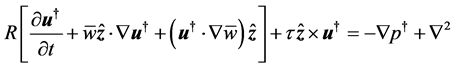 (14)
(14)
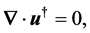 (15)
(15)
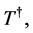
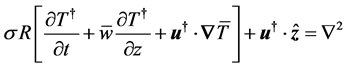 (16)
(16)
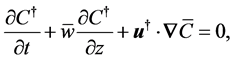 (17)
(17)
where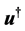 ,
, 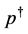 ,
, 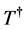 and
and 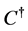 are the perturbations in velocity, pressure, temperature and concentration, respectively.
are the perturbations in velocity, pressure, temperature and concentration, respectively.
The perturbation variables take the form
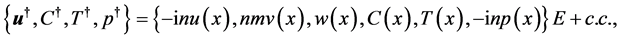 (18)
(18)
in which the factors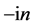 ,
, 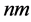 , and
, and 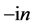 are introduced in the variables
are introduced in the variables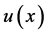 ,
, 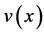 and
and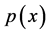 , respectively, for convenience.
, respectively, for convenience.
Substituting the variables (18) into the Equations (14)-(17) and after some arrangements we get the following equations
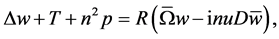 (19)
(19)
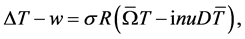 (20)
(20)
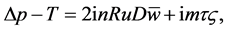 (21)
(21)
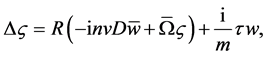 (22)
(22)
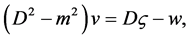 (23)
(23)
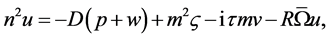 (24)
(24)
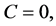 (25)
(25)
subject to the boundary conditions
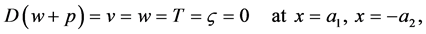 (26)
(26)
 (27)
(27)
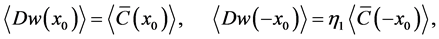 (28)
(28)
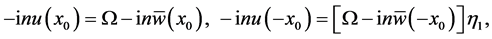 (29)
(29)
where the variable ![]() is related to the vertical component of vorticity and is defined as
is related to the vertical component of vorticity and is defined as
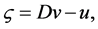 (30)
(30)
and we have introduced the notation
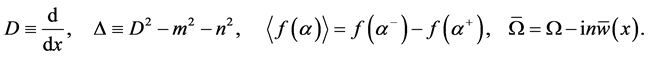 (31)
(31)
(cf. Al Mashrafi and Eltayeb [6] ).
We use the same method adopted in Al Mashrafi and Eltayeb [6] and expand the perturbation variables and the growth rate in the small parameter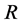 , thus
, thus
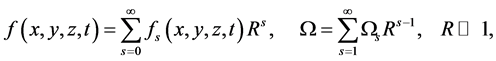 (32)
(32)
where 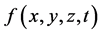 indicates any of the perturbation variables
indicates any of the perturbation variables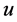 ,
,  ,
, 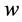 ,
, ![]() ,
, ![]() and
and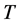 .
.
It turned out that the leading order terms in the equations determines the stability of the system. The relevant equations and the boundary conditions are then obtained from (19)-(24) and (26)-(29) by neglecting the terms with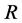 . In order to facilitate comparison with the results of the non-rotating case, we shall maintain the subscript 0. The equations are given by
. In order to facilitate comparison with the results of the non-rotating case, we shall maintain the subscript 0. The equations are given by
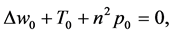 (33)
(33)
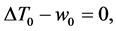 (34)
(34)
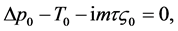 (35)
(35)
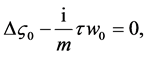 (36)
(36)
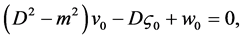 (37)
(37)
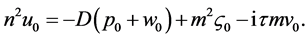 (38)
(38)
The associated boundary conditions are obtained from (26)-(29) by introducing the subscript 0 to all the variables and the subscript 1 to![]() .
.
The system (33)-(38) together with the boundary conditions poses an eigenvalue problem for the growth rate, ![]() , which determines the stability of the system. The real part
, which determines the stability of the system. The real part 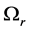 governs the variations of the amplitude of the disturbance with time, and hence it determines the stability of the disturbance. If it is negative for all possible values of the wavenumbers
governs the variations of the amplitude of the disturbance with time, and hence it determines the stability of the disturbance. If it is negative for all possible values of the wavenumbers 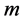 and
and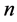 , then the plume is stable, while if at least one pair of
, then the plume is stable, while if at least one pair of 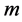 and
and 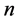 gives a positive value, then the plume is unstable. If
gives a positive value, then the plume is unstable. If 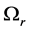 vanishes for all values of the wavenumbers, the plume is neutrally stable. If the preferred mode occurs for
vanishes for all values of the wavenumbers, the plume is neutrally stable. If the preferred mode occurs for ,
, 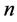 both non-zero, it is referred to as a 3-dimensional mode (oblique), and if
both non-zero, it is referred to as a 3-dimensional mode (oblique), and if![]() , it is called 2-dimensional (vertical). The case
, it is called 2-dimensional (vertical). The case ![]() and
and ![]() is found not to occur. The imaginary part
is found not to occur. The imaginary part 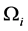 determines the phase speed of the disturbance. The vertical phase speed
determines the phase speed of the disturbance. The vertical phase speed ![]() and the horizontal phase speed
and the horizontal phase speed ![]() are defined as
are defined as
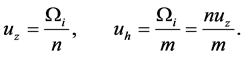 (39)
(39)
We note that ![]() is defined only if
is defined only if![]() .
.
We operate on Equation (33) with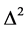 , and use Equations (34)-(36) to get
, and use Equations (34)-(36) to get
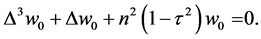 (40)
(40)
The general solution of the differential Equation (40) can be written in the form
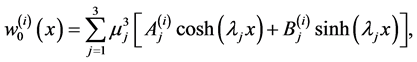 (41)
(41)
where the superscript  refers to the three regions of the system (see Figure 1),
refers to the three regions of the system (see Figure 1), 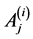 ,
, 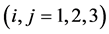
 are constants, and
are constants, and 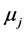 are the roots of the cubic equation
are the roots of the cubic equation
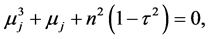 (42)
(42)
with ![]() is given by
is given by
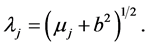 (43)
(43)
We use the Equations (34)-(36) and the solution (41) to obtain
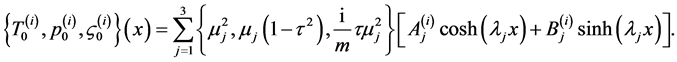 (44)
(44)
The Equation (37) can be solved in the form a complementary function and particular solution to find
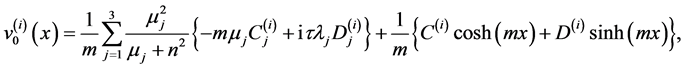 (45)
(45)
where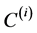 ,
, 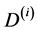 are constants, and
are constants, and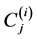 ,
, 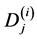 are given by
are given by
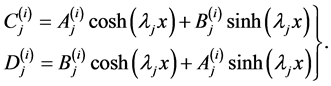 (46)
(46)
Now we apply the boundary conditions at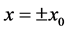 ,
,  ,
, 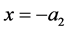 and solve the resulting algebraic equations for the constants
and solve the resulting algebraic equations for the constants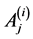 ,
, 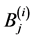 ,
, 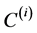 ,
, 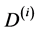 for
for 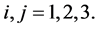 The details of the solution are given in the Appendix A.
The details of the solution are given in the Appendix A.
The growth rate is given by the quadratic equation
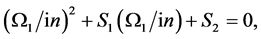 (47)
(47)
where 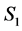 and
and ![]() are given in the Appendix A.
are given in the Appendix A.
Solving Equation (47) yields
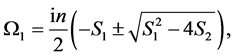 (48)
(48)
and the displacement  is given by
is given by
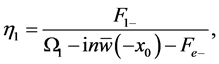 (49)
(49)
in which  and
and 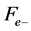 are defined in the Appendix A.
are defined in the Appendix A.
We note that, as in the absence of rotation, the system has two modes. The upper sign in the expression (48) corresponds to the modified varicose mode (MV) and the lower sign refers to the modified sinuous mode (MS).
4. Discussions of the Results
The growth rate (48) is evaluated numerically in the 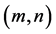 plane as a function of the parameters
plane as a function of the parameters![]() ,
, ![]() ,
, 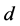 and
and ![]() for both modes. The contours of
for both modes. The contours of 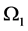 in the
in the 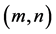 plane are plotted for sample values of the parameters
plane are plotted for sample values of the parameters![]() ,
, ![]() ,
, ![]() and
and 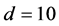 in the Figures 2-4.
in the Figures 2-4.
In Figure 2, we present a comparison between the contours of the two modes MV and MS for different values of the Taylor number, ![]() , when
, when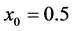 ,
, 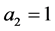 and
and . We note that the MV mode always possesses a minimum with negative growth rate and one or two maxima with positive growth rates while the MS mode has
. We note that the MV mode always possesses a minimum with negative growth rate and one or two maxima with positive growth rates while the MS mode has
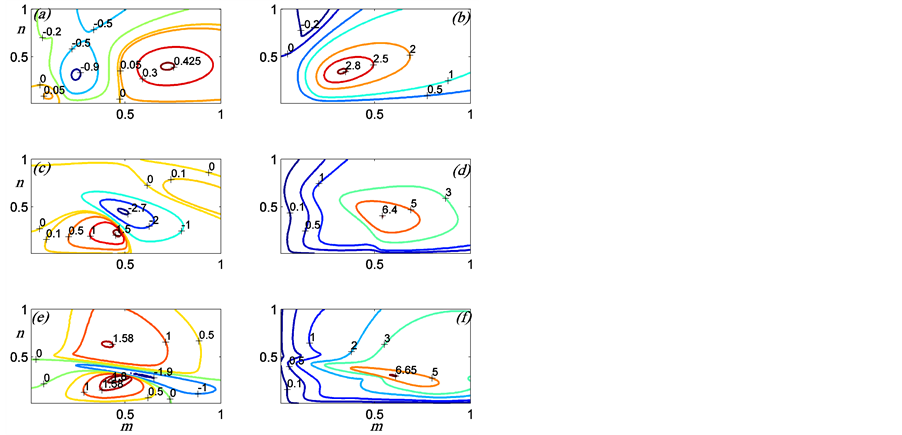
Figure 2. Contours of the growth rate ,  , of the modes MV, as in (a), (c), (e) and MS, as in (b), (d), (f) for the rotating bounded Cartesian plume where
, of the modes MV, as in (a), (c), (e) and MS, as in (b), (d), (f) for the rotating bounded Cartesian plume where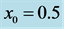 ,
, 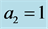 ,
,![]() . Here
. Here ![]() for (a), (b);
for (a), (b); ![]() for (c), (d); and
for (c), (d); and ![]() for (e), (f). Note that the preferred mode is MS.
for (e), (f). Note that the preferred mode is MS.
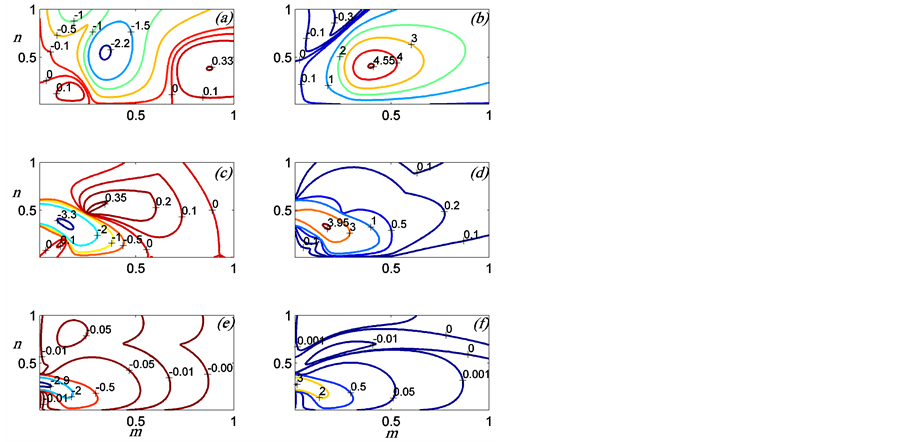
Figure 3. Contours of the growth rate,  , of the modes MV, as in (a), (c), (e) and MS, as in (b), (d), (f) for
, of the modes MV, as in (a), (c), (e) and MS, as in (b), (d), (f) for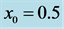 ,
, ![]() ,
,![]() . Here
. Here 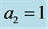 for (a), (b);
for (a), (b);  for (c), (d); and
for (c), (d); and 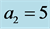 for (e), (f). Note that the preferred mode of the instability is 2-dimensional when
for (e), (f). Note that the preferred mode of the instability is 2-dimensional when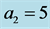 .
.
a minimum with negative growth rate only when ![]() is small and one maximum with positive growth rate which is larger than that of the corresponding MV mode. This indicates that the MS mode is preferred for this set of parameters. The local maxima correspond to 3-dimensional modes and the largest maximum always increases with the increase in the rotation parameter
is small and one maximum with positive growth rate which is larger than that of the corresponding MV mode. This indicates that the MS mode is preferred for this set of parameters. The local maxima correspond to 3-dimensional modes and the largest maximum always increases with the increase in the rotation parameter![]() .
.
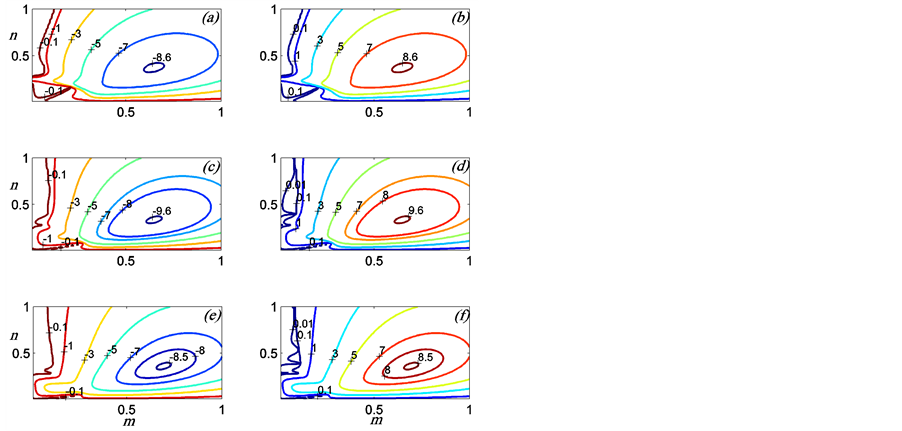
Figure 4. Isolines of the growth rate , 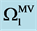 , as in (a), (c), (e) and
, as in (a), (c), (e) and 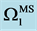 as in (b), (d), (f) for
as in (b), (d), (f) for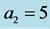 ,
, ![]() ,
,![]() . Here
. Here 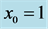 for (a), (b);
for (a), (b); 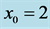 for (c), (d); and
for (c), (d); and 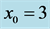 for (e), (f). Note that at fixed point
for (e), (f). Note that at fixed point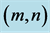 , the values of
, the values of 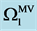 and
and 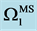 are nearly same but there different in the sign.
are nearly same but there different in the sign.
Figure 3 presents the influence of the distance ![]() between the plume and the nearest sidewall on the stability of the plume when the thickness of the plume and the rotation parameter are held fixed at
between the plume and the nearest sidewall on the stability of the plume when the thickness of the plume and the rotation parameter are held fixed at 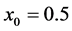 and
and![]() . The figure is plotted for three different values of
. The figure is plotted for three different values of![]() :
: 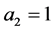 for subfigures (a), (b);
for subfigures (a), (b); 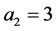 for subfigures (c), (d); and
for subfigures (c), (d); and 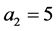 for subfigures (e), (f). When the plume is situated half-way between the sidewalls
for subfigures (e), (f). When the plume is situated half-way between the sidewalls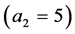 , the MV mode has a negative growth rate everywhere and hence stable while the MS mode has a growth rate that is positive everywhere and hence is preferred. The local maximum possesses a vanishing horizontal wave number and hence propagates vertically. As the plume moves towards a wall, the growth rates of both modes increase and the MV mode develops local maxima with positive growth rates but they are not preferred because the MS mode local maximum increases as well and becomes 3-dimenaional.
, the MV mode has a negative growth rate everywhere and hence stable while the MS mode has a growth rate that is positive everywhere and hence is preferred. The local maximum possesses a vanishing horizontal wave number and hence propagates vertically. As the plume moves towards a wall, the growth rates of both modes increase and the MV mode develops local maxima with positive growth rates but they are not preferred because the MS mode local maximum increases as well and becomes 3-dimenaional.
Figure 4 illustrates the influence of the plume thickness on the contours of the growth rate for fixed values of the rotation parameter and the distance between the two sidewalls when the plume is situated half-way between the two sidewalls. As ![]() increases from
increases from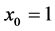 , the growth rate for MS mode, which is positive everywhere, increases and that of the MV mode, which is negative everywhere, decreases until
, the growth rate for MS mode, which is positive everywhere, increases and that of the MV mode, which is negative everywhere, decreases until ![]() reaches a critical value,
reaches a critical value, 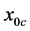 , when the growth rate of the MS mode decreases and that of the MV mode increases.
, when the growth rate of the MS mode decreases and that of the MV mode increases.
The contours of Figures 2-4 indicate that the preferred mode of instability is the modified sinuous (MS) mode. This indication is quantified by calculating the maximum growth rate and the associated wave numbers and phase speeds for different values of the parameters. For fixed values of![]() ,
, ![]() ,
, 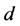 and
and![]() , we maximize over the wave numbers
, we maximize over the wave numbers 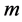 and
and 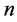 by demanding that
by demanding that
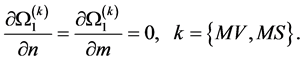 (50)
(50)
The solution of (50) gives the values  and
and ![]() at maximum growth rate,
at maximum growth rate, 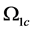 , calculated from (48) for these values of
, calculated from (48) for these values of 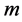 and
and  to give, together with the corresponding value
to give, together with the corresponding value 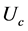 of the phase speed, the parameters
of the phase speed, the parameters 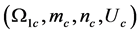 of the preferred mode. For fixed parameters
of the preferred mode. For fixed parameters![]() ,
, ![]() ,
,  and
and![]() , and particular mode, all possible local maxima of
, and particular mode, all possible local maxima of  are identified and the largest value taken together with the corresponding wavenumbers and phase speeds as defining the preferred mode for that set of parameters for that mode. This is carried out for both modified varicose (MV) and modified sinuous (MS) modes, and the largest is chosen as the preferred mode. A sample of the results is given in Figures 5-9.
are identified and the largest value taken together with the corresponding wavenumbers and phase speeds as defining the preferred mode for that set of parameters for that mode. This is carried out for both modified varicose (MV) and modified sinuous (MS) modes, and the largest is chosen as the preferred mode. A sample of the results is given in Figures 5-9.
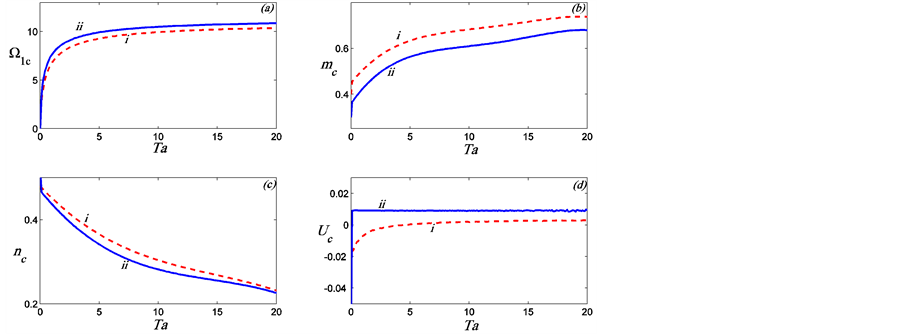
Figure 5. The preferred mode parameters 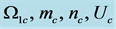 are plotted in (a), (b), (c), (d) as a function of
are plotted in (a), (b), (c), (d) as a function of ![]() , for
, for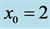 , and two different values of
, and two different values of ![]() and the plume half-way between the sidewalls. The roman numbers
and the plume half-way between the sidewalls. The roman numbers ![]() and
and 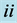 refer to
refer to 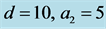 and
and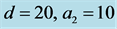 , respectively.
, respectively.
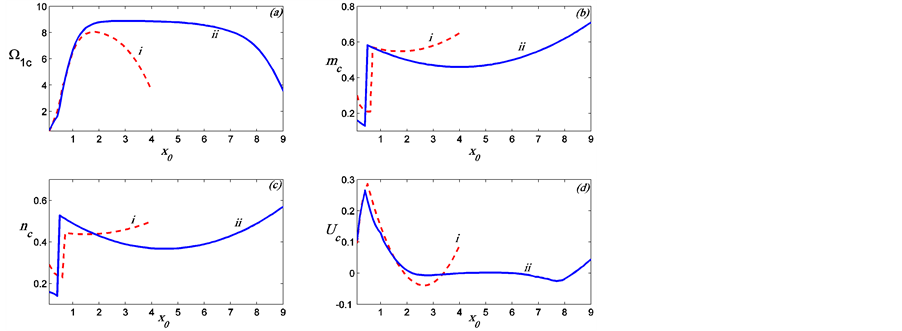
Figure 6. The preferred mode parameters 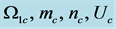 are plotted in (a), (b), (c), (d) as a function of
are plotted in (a), (b), (c), (d) as a function of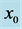 , for
, for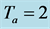 , and two different values of
, and two different values of ![]() and the plume half-way between the sidewalls. The roman numbers
and the plume half-way between the sidewalls. The roman numbers ![]() and
and 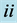 refer to
refer to 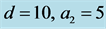 and
and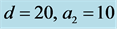 , respectively.
, respectively.
Figure 5 and Figure 6 illustrate the influence of the distance between the boundaries on the preferred mode of instability of the rotating plume. In Figure 5, the preferred mode parameters are plotted as a function of ![]() for fixed
for fixed ![]() and two values of the distance between the sidewalls,
and two values of the distance between the sidewalls, 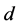 , for a plume situated half-way between the sidewalls. It is found that the preferred mode is the MS mode and the influence of the boundaries tends to stabilise the plume but only reduces the growth rate slightly. The horizontal and vertical wavenumbers are increased while the phase speeds are reduced as the distance,
, for a plume situated half-way between the sidewalls. It is found that the preferred mode is the MS mode and the influence of the boundaries tends to stabilise the plume but only reduces the growth rate slightly. The horizontal and vertical wavenumbers are increased while the phase speeds are reduced as the distance, 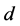 , between the two walls is reduced.
, between the two walls is reduced.
Figure 6 presents the preferred mode of instability as a function of ![]() and fixed
and fixed ![]() where the plume is equidistant from the two walls and
where the plume is equidistant from the two walls and 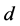 takes the values 10 and 20. The growth rate increases rapidly as
takes the values 10 and 20. The growth rate increases rapidly as ![]() increases from zero until it reaches a maximum when the plume occupies the middle half of the region between the sidewalls. As the thickness of the plume increases further, the growth rate decreases if
increases from zero until it reaches a maximum when the plume occupies the middle half of the region between the sidewalls. As the thickness of the plume increases further, the growth rate decreases if 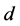 is small but stays at the maximum value for increasing
is small but stays at the maximum value for increasing ![]() if the distance
if the distance 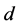 is large. In both case, the growth rate drops to zero as the wall is approached and the plume nearly fill the whole region between the sidewalls. The wavenumbers decrease as
is large. In both case, the growth rate drops to zero as the wall is approached and the plume nearly fill the whole region between the sidewalls. The wavenumbers decrease as ![]() increases from zero but they soon jump to larger values and increase with
increases from zero but they soon jump to larger values and increase with![]() . In both cases the MS mode is preferred.
. In both cases the MS mode is preferred.
Figure 7. The preferred mode parameters  are plotted in (a), (b), (c), (d), respectively, as a function of
are plotted in (a), (b), (c), (d), respectively, as a function of![]() , for
, for ,
, ![]() and two different values of
and two different values of . The solid curves refer to
. The solid curves refer to 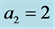 and the broken curves refer to
and the broken curves refer to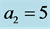 . Note that preferred mode is MS in all cases.
. Note that preferred mode is MS in all cases.

Figure 8. The preferred mode parameters 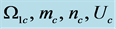 are plotted in (a), (b), (c), (d), respectively, as a function of
are plotted in (a), (b), (c), (d), respectively, as a function of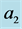 , for
, for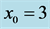 ,
, ![]() and for two different values of
and for two different values of![]() . The roman numbers
. The roman numbers ![]() and
and 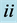 refer to
refer to ![]() and
and![]() , respectively. Note that the maximum growth decreases as the plume moves away from the wall to the centre.
, respectively. Note that the maximum growth decreases as the plume moves away from the wall to the centre.
Figure 7 illustrates the dependence of the preferred mode on ![]() for
for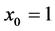 ,
, 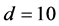 and
and ![]() takes two values:
takes two values: 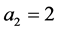 and
and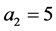 . As the Taylor number increases from
. As the Taylor number increases from![]() , the maximum growth rate
, the maximum growth rate 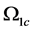 increases rapidly until
increases rapidly until ![]() reaches a certain value that increases as the distance between plume and the nearest sidewall increases, after which the growth rate varies much more slowly. The wavenumbers of the preferred mode show sudden changes at a small value of
reaches a certain value that increases as the distance between plume and the nearest sidewall increases, after which the growth rate varies much more slowly. The wavenumbers of the preferred mode show sudden changes at a small value of ![]() indicating a change of local maximum as
indicating a change of local maximum as![]() , increases through a value,
, increases through a value,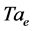 . The horizontal wavenumber,
. The horizontal wavenumber, 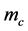 , is zero for small
, is zero for small ![]() corresponding to 2-dimensional motions, but as
corresponding to 2-dimensional motions, but as ![]() reaches
reaches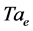 ,
, 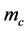 jumps to a nonzero value and increases thereafter. The vertical wavenumber increases rapidly as
jumps to a nonzero value and increases thereafter. The vertical wavenumber increases rapidly as ![]() increase to
increase to 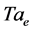 and then decreases as
and then decreases as ![]() increases further. The vertical phase speed of the preferred mode also suffers a change at
increases further. The vertical phase speed of the preferred mode also suffers a change at 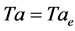 and the jump depends on how far the plume is from the nearest sidewall.
and the jump depends on how far the plume is from the nearest sidewall.
In Figure 8, we present the dependence of the preferred mode on the distance ![]() between the plume and the nearest sidewall. We note that the growth rate decreases when the plume moves towards the location half-way
between the plume and the nearest sidewall. We note that the growth rate decreases when the plume moves towards the location half-way

Figure 9. The preferred mode parameters 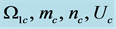 are depicted in (a), (b), (c), (d) as a function of
are depicted in (a), (b), (c), (d) as a function of 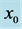 , for
, for 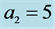 and
and![]() . The solid (broken) curves refer to
. The solid (broken) curves refer to . Note that the preferred mode of instability is modified sinuous mode in all cases. When the plume is wide, the growth rate decreases whenever the plume moves to the wall.
. Note that the preferred mode of instability is modified sinuous mode in all cases. When the plume is wide, the growth rate decreases whenever the plume moves to the wall.
between the two sidewalls. Both wavenumber components increase steadily as the distance between plume and the nearest sidewall increases. The vertical phase speed however behaves differently as ![]() increases; it decreases steadily with increasing
increases; it decreases steadily with increasing ![]() if
if ![]() is small but when
is small but when ![]() is large, it decreases slowly reaching a minimum before it increases at a moderate rate. In all cases, it is the MS mode that provides the preferred mode.
is large, it decreases slowly reaching a minimum before it increases at a moderate rate. In all cases, it is the MS mode that provides the preferred mode.
Figure 9 shows the dependence of the critical modes 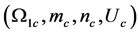 on
on![]() . The growth rate increases gradually until
. The growth rate increases gradually until ![]() reaches a critical thickness,
reaches a critical thickness, 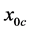 , and then it decreases. This indicates that there is a critical thickness representing the most unstable plume. The behaviour of the wavenumber components and phase speed with
, and then it decreases. This indicates that there is a critical thickness representing the most unstable plume. The behaviour of the wavenumber components and phase speed with ![]() is quite complicated. The horizontal wavenumber vanishes for small
is quite complicated. The horizontal wavenumber vanishes for small ![]() when
when ![]() is small. For large,
is small. For large, 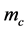 , behaves in a similar way when
, behaves in a similar way when ![]() is close to
is close to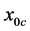 . The vertical wavenumber, on the other hand decreases as
. The vertical wavenumber, on the other hand decreases as ![]() increases from zero and jumps to a larger value when the local maximum changes, and then varies very slowly until
increases from zero and jumps to a larger value when the local maximum changes, and then varies very slowly until ![]() is almost 4, when
is almost 4, when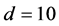 .
.
5. Conclusions
The dynamics of a fully developed plume of buoyant fluid, in the form of a channel of finite width, 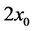 , rising in a less buoyant fluid contained between two parallel vertical walls, a distance
, rising in a less buoyant fluid contained between two parallel vertical walls, a distance  apart, and two fluids rotate uniformly about the vertical have been investigated.
apart, and two fluids rotate uniformly about the vertical have been investigated.
In the absence of boundaries ([18] ), it was found that the stability problem depended on the parameters: the Grashoff number,  , the Taylor number,
, the Taylor number, ![]() , and the thickness of the plume,
, and the thickness of the plume,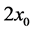 . The magnitude of the growth rate was of the order
. The magnitude of the growth rate was of the order 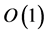 for
for 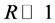 and the instability took one of the two types: sinuous mode or varicose mode.
and the instability took one of the two types: sinuous mode or varicose mode.
The presence of the vertical boundaries here introduces two dimensionless parameters: the distance between the plume and the nearest wall, ![]() , and the distance between the two vertical sidewalls,
, and the distance between the two vertical sidewalls,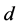 . The introduction of the boundaries modifies the two modes to be the modified sinuous mode (MS) and the modified varicose mode (MV). It is shown here that the boundaries introduce two main effects to the rotating Cartesian plume studied by Eltayeb and Hamza [18] . First, the sidewalls tends to stabilise the plume but succeed only reducing the growth rate and the plume remains unstable for all values of the Taylor number and the distance from the nearest sidewall. Second, the presence of the sidewalls suppresses the modified varicose mode and allows the modified sinuous only to be unstable. The preferred mode can be 3-dimensional or 2-dimensional depending on the values of the parameters of the system. When the preferred mode is 2-dimensional, propagation can be upwards or downwards.
. The introduction of the boundaries modifies the two modes to be the modified sinuous mode (MS) and the modified varicose mode (MV). It is shown here that the boundaries introduce two main effects to the rotating Cartesian plume studied by Eltayeb and Hamza [18] . First, the sidewalls tends to stabilise the plume but succeed only reducing the growth rate and the plume remains unstable for all values of the Taylor number and the distance from the nearest sidewall. Second, the presence of the sidewalls suppresses the modified varicose mode and allows the modified sinuous only to be unstable. The preferred mode can be 3-dimensional or 2-dimensional depending on the values of the parameters of the system. When the preferred mode is 2-dimensional, propagation can be upwards or downwards.
References
- McDonald, R.J. and Hunt, J.D. (1970) Convection Fluid Motion within the Interdendritic Liquid of a Casting. Metallurgical Transactions, 1, 1787-1788. http://dx.doi.org/10.1007/BF02642039
- Copley, S.M., Giamel, A.F., Johnson, S.M. and Hornbecker, M.F. (1970) The Origin of Freckles Inunidirectionally Solidified Castings. Metallurgical Transactions, 1, 2193-2204. http://dx.doi.org/10.1007/BF02643435
- Emms, P.W. and Fowler, A.C. (1994) Compositional Convection in the Solidification of Binary Alloys. Journal of Fluid Mechanics, 262, 111-139. http://dx.doi.org/10.1017/S0022112094000443
- Worster, M.G. (1997) Convection in Mushy Layers. Annual Review of Fluid Mechanics, 29, 91-122. http://dx.doi.org/10.1146/annurev.fluid.29.1.91
- Aussillous, P., Sederman, A.J., Gladden, L.F., Huppert, H.E. and Worster, M.G. (2006) Magnetic Resonance Imaging of Structure and Convection in Solidifying Mushy Layers. Journal of Fluid Mechanics, 522, 99-125. http://dx.doi.org/10.1017/S0022112005008451
- Al Mashrafi, K.S. and Eltayeb, I.A. (2014) The Influence of Boundaries on the Stability of Compositional Plumes. Open Journal of Fluid Dynamics, 4, 83-102. http://dx.doi.org/10.4236/ojfd.2014.41007
- Verhoogen, J. (1961) Heat Balance of the Earth’s Core. Geophysical Journal of the Royal Astronomical Society, 4, 276- 281. http://dx.doi.org/10.1111/j.1365-246X.1961.tb06819.x
- Morgan, W.J. (1971) Convection Plumes in the Lower Mantle. Nature, 230, 42-43. http://dx.doi.org/10.1038/230042a0
- Gubbins, D. (1977) Energetics of the Earth’s Core. J. Geophys., 43, 453-464.
- Loper, D.E. (1978) The Gravitationally Powered Dynamo. Geophysical Journal of the Royal Astronomical Society, 54, 389-404. http://dx.doi.org/10.1111/j.1365-246X.1978.tb04265.x
- Loper, D.E. and Roberts, P.H. (1978) On the Motion of an Iron-Alloy Core Containing a Slurry. I. General Theory. Geophysical & Astrophysical Fluid Dynamics, 9, 289-321. http://dx.doi.org/10.1080/03091927708242333
- Loper, D.E. and Roberts, P.H. (1981) A Study of Conditions at the Inner Core Boundary of the Earth. Physics of the Earth and Planetary Interiors, 24, 302-307. http://dx.doi.org/10.1016/0031-9201(81)90117-5
- Loper, D.E. and Stacey, F.D. (1983) The Dynamical and Thermal Structure of Deep Mantle Plumes. Physics of the Earth and Planetary Interiors, 34, 304-317. http://dx.doi.org/10.1016/0031-9201(83)90047-X
- Moffatt, H.K. (1989) Liquid Metal MHD and the Geodynamo. In: Lielpeteris, J. and Moreau, R., Eds., Liquid Metal Magneto-Hydrodynamics, Kluwer Academic Publishers, Dordrecht, 403-412.
- Eltayeb, I.A. and Loper, D.E. (1991) On the Stability of Vertical Double-Diffusive Interfaces. Part 1. A Single Plane Interface. Journal of Fluid Mechanics, 228, 149-181.
- Eltayeb, I.A. and Loper, D.E. (1994) On the Stability of Vertical Double-Diffusive Interfaces. Part 2. Two Parallel Interfaces. Journal of Fluid Mechanics, 267, 251-273. http://dx.doi.org/10.1017/S0022112094001175
- Eltayeb, I.A. and Loper, D.E. (1997) On the Stability of Vertical Double-Diffusive Interfaces. Part 3. Cylindrical Interfaces. Journal of Fluid Mechanics, 353, 45-66. http://dx.doi.org/10.1017/S0022112097007374
- Eltayeb, I.A. and Hamza, E.A. (1998) Compositional Convection in the Presence of Rotation. Journal of Fluid Mechanics, 354, 277-299. http://dx.doi.org/10.1017/S0022112097007696
- Eltayeb, I.A. (1999) The Stability of Compositional Plumes in a Rotating Magnetic Fluid. Physics of the Earth and Planetary Interiors, 110, 1-19.
- Eltayeb, I.A. (2006) The Stability of a Compositional Plume Rotating in the Presence of a Magnetic Field. Geophysical & Astrophysical Fluid Dynamics, 100, 429-455. http://dx.doi.org/10.1080/03091920600799541
- Kumagai, I. (2002) On the Anatomy of Mantle Plumes: Effect of the Viscosity Ratio on Entrainment and Stirring. Earth and Planetary Science Letters, 198, 211-224. http://dx.doi.org/10.1016/S0012-821X(02)00513-7
- Shimizu, H., Poirier, J.P. and Le Mouel, J.L. (2005) On Crystallization at the Inner Core Boundary. Physics of the Earth and Planetary Interiors, 151, 37-51. http://dx.doi.org/10.1016/j.pepi.2005.01.001
- Kerr, R.C., Mériaux, C. and Lister, J.R. (2008) Effect of Thermal Diffusion on the Stability of Strongly Tilted Mantle Plume Tails. Journal of Geophysical Research, 113, Article ID: B09401. http://dx.doi.org/10.1029/2007JB005510
- Al-Lawatia, M.A., Elbashir, T.B.A., Eltayeb, I.A., Rahman, M.M. and Balakrishnan, E. (2011) The Dynamics of Two Interacting Compositional Plumes in the Presence of a Magnetic Field. Geophysical & Astrophysical Fluid Dynamics, 105, 586-615. http://dx.doi.org/10.1080/03091929.2010.518316
- Eltayeb, I.A. and Elbashir, T.B.A. (2013) The Stability of Two Interacting Compositional Plumes under the Influence of Inclined Rotation.
- Stern, M.E. (1960) The “Salt Fountain” and Thermohaline Convection. Tellus, 12, 172-175. http://dx.doi.org/10.1111/j.2153-3490.1960.tb01295.x
- Bennington, K.O. (1963) Some Crystal Growth Features of Sea Ice. Journal of Glaciology, 4, 669-689.
- Lake, R. and Lewis, E. (1970) Salt Rejection by Sea Ice during Growth. Journal of Geophysical Research, 75, 583-597. http://dx.doi.org/10.1029/JC075i003p00583
- Holyer, J.Y. (1984) The Stability of Long, Steady, Two-Dimensional Salt Fingers. Journal of Fluid Mechanics, 147, 169-185. http://dx.doi.org/10.1017/S0022112084002044
- Howard, L.N. and Veronis, G. (1992) Stability of Salt Fingers with Negligible Salt Diffusivity. Journal of Fluid Mechanics, 239, 511-522. http://dx.doi.org/10.1017/S0022112092004518
- Wettlaufer, J.S., Worster, M.G. and Huppert, H.E. (1997) Natural Convection during Solidification of an Alloy from above with Application to the Evolution of Sea Ice. Journal of Fluid Mechanics, 344, 291-316. http://dx.doi.org/10.1017/S0022112097006022
- Schmitt, R.W. (2003) Observational and Laboratory Insights into Salt-Finger Convection. Progress in Oceanography, 56, 419-433. http://dx.doi.org/10.1016/S0079-6611(03)00033-8
- Feltham, D.L., Untersteiner, N., Wettlaufer, J.S. and Worster, M.G. (2006) Sea Ice Is a Mushy Layer. Geophysical Research Letters, 33, Article ID: L14501. http://dx.doi.org/10.1029/2006GL026290
- Notz, D. and Worster, M.G. (2008) In Situ Measurements of the Evolution of Young Sea Ice. Journal of Geophysical Research, 113, Article ID: C03001. http://dx.doi.org/10.1029/2007JC004333
- Sample, A.K. and Hellawell, A. (1984) The Mechanisms of Formation and Prevention of Channel Segregation during Alloy Solidification. Metallurgical Transactions A, 15, 2163-2173. http://dx.doi.org/10.1007/BF02647099
- Chen, C.F. and Chen, F. (1991) Experimental Study of Directional Solidification of Aqueous Ammonium Chloride Solution. Journal of Fluid Mechanics, 227, 567-586. http://dx.doi.org/10.1017/S0022112091000253
- Hellawell, A., Sarazin, J.R. and Steube, R.S. (1993) Channel Convection in Partly Solidified Systems. Philosophical Transactions of the Royal Society A. London, 345, 507-544. http://dx.doi.org/10.1098/rsta.1993.0143
- Classen, S., Heimpel, M. and Christensen, U. (1999) Blob Instability in Rotating Compositional Convection. Geophysical Research Letters, 26, 135-138. http://dx.doi.org/10.1029/1998GL900227
Appendix A: The Derivation of the Dispersion Relation
In this appendix, we apply the boundary conditions (26)-(28) when the subscript is 0 for the variables (41), (44) and (45) to evaluate the constants of the solution. Application of the boundary conditions at the interface 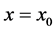 gives
gives
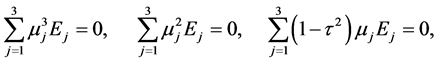 (A:1)
(A:1)
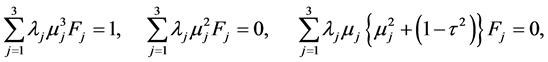 (A:2)
(A:2)
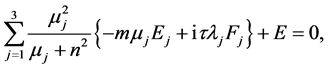 (A:3)
(A:3)
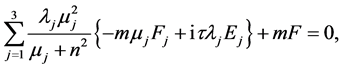 (A:4)
(A:4)
where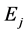 ,
, 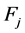 ,
, 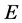 and
and 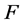 are defined by
are defined by
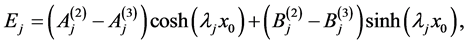 (A:5)
(A:5)
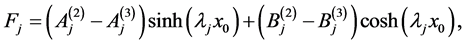 (A:6)
(A:6)
 (A:7)
(A:7)
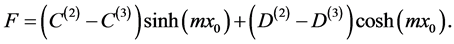 (A:8)
(A:8)
We use the Equations (A:5)-(A:8) to obtain
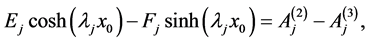 (A:9)
(A:9)
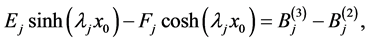 (A:10)
(A:10)
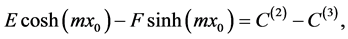 (A:11)
(A:11)
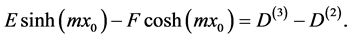 (A:12)
(A:12)
Similarly, at the interface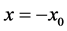 , we find
, we find
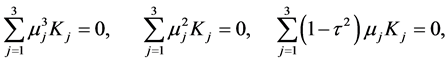 (A:13)
(A:13)
 (A:14)
(A:14)
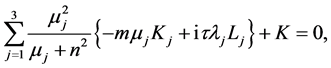 (A:15)
(A:15)
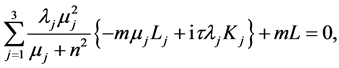 (A:16)
(A:16)
in which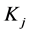 ,
, 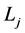 ,
, ![]() and
and  are given by
are given by
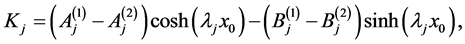 (A:17)
(A:17)
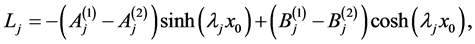 (A:18)
(A:18)
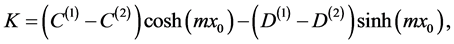 (A:19)
(A:19)
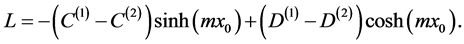 (A:20)
(A:20)
Equations (A:17)-(A:20) give
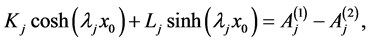 (A:21)
(A:21)
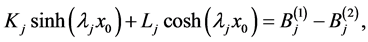 (A:22)
(A:22)
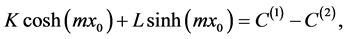 (A:23)
(A:23)
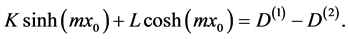 (A:24)
(A:24)
The boundary conditions at the boundaries 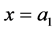 and
and 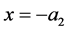 give
give
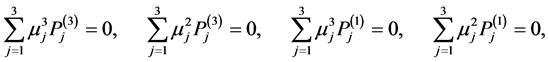 (A:25)
(A:25)
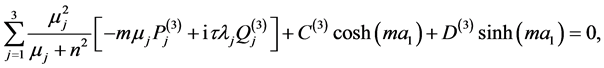 (A:26)
(A:26)
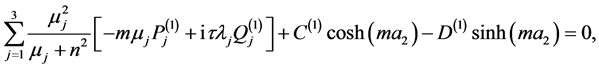 (A:27)
(A:27)
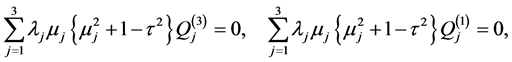 (A:28)
(A:28)
such that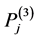 ,
, 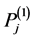 ,
, 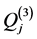 and
and 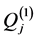 are defined by
are defined by
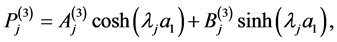 (A:29)
(A:29)
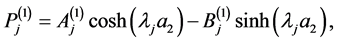 (A:30)
(A:30)
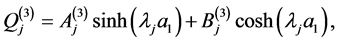 (A:31)
(A:31)
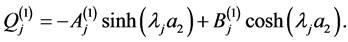 (A:32)
(A:32)
The equations and can be solved to find
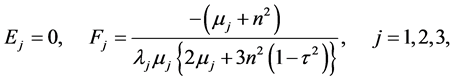 (A:33)
(A:33)
since the roots 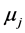 are distinct. Hence Equations (A:3)-(A:5) give
are distinct. Hence Equations (A:3)-(A:5) give
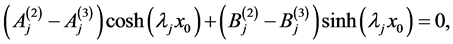 (A:34)
(A:34)
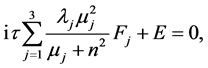 (A:35)
(A:35)
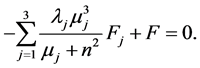 (A:36)
(A:36)
Using the expression for 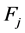 in , and the properties of the 3 roots of the cubic Equation (42) to simplify the expressions (A:35), (A:36). The simplifications lead to
in , and the properties of the 3 roots of the cubic Equation (42) to simplify the expressions (A:35), (A:36). The simplifications lead to
![]() (A:37)
(A:37)
Hence the expressions (A:9)-(A:12) reduce to
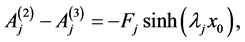 (A:38)
(A:38)
 (A:39)
(A:39)
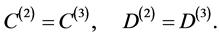 (A:40)
(A:40)
The same method can be applied to the conditions at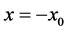 . The Equations (A:13)-(A:16) leads to
. The Equations (A:13)-(A:16) leads to
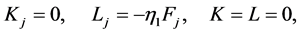 (A:41)
(A:41)
thus the expressions (A:21)-(A:24) give
 (A:42)
(A:42)
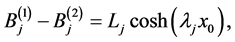 (A:43)
(A:43)
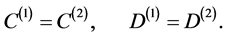 (A:44)
(A:44)
The expressions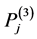 ,
, 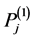 ,
, 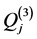 and
and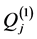 , given in (A:29)-(A:32), can be simplified by using the relations (A:38), (A:39) and (A:42), (A:43) to find
, given in (A:29)-(A:32), can be simplified by using the relations (A:38), (A:39) and (A:42), (A:43) to find
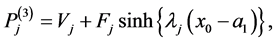 (A:45)
(A:45)
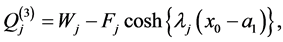 (A:46)
(A:46)
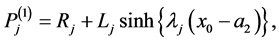 (A:47)
(A:47)
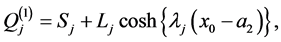 (A:48)
(A:48)
where we have defined the notation
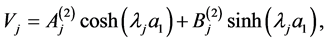 (A:49)
(A:49)
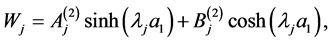 (A:50)
(A:50)
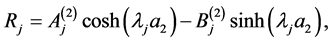 (A:51)
(A:51)
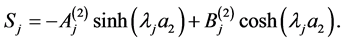 (A:52)
(A:52)
The Equations (A:49)-(A:52) give
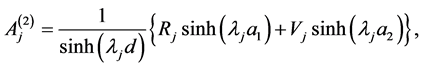 (A:53)
(A:53)
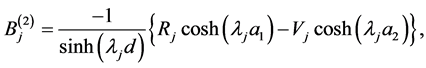 (A:54)
(A:54)
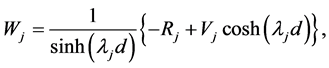 (A:55)
(A:55)
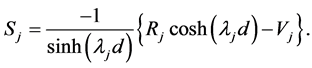 (A:56)
(A:56)
The boundary conditions at 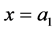 and
and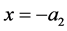 , given in (A:25) and (A:28), can be written by using (A:45)-(A:48) and (A:55) and (A:56) to obtain
, given in (A:25) and (A:28), can be written by using (A:45)-(A:48) and (A:55) and (A:56) to obtain
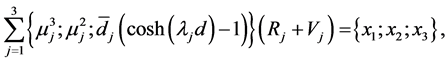 (A:57)
(A:57)
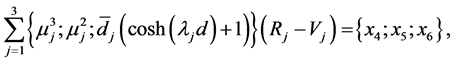 (A:58)
(A:58)
in which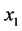 ,
, ![]() ,
, 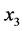 ,
, ![]() ,
, ![]() and
and ![]() are defined by
are defined by
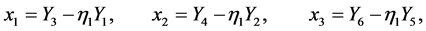 (A:59)
(A:59)
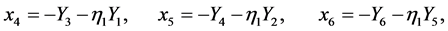 (A:60)
(A:60)
and we have defined 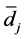 and
and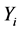 ,
, ![]() as
as
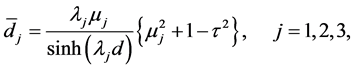 (A:61)
(A:61)
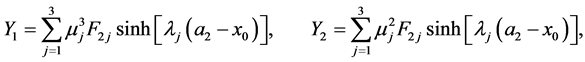 (A:62)
(A:62)
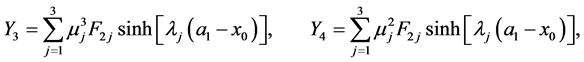 (A:63)
(A:63)
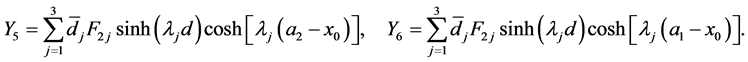 (A:64)
(A:64)
The algebraic system (A:57) and (A:58) can be solved by elimination to find
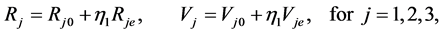 (A:65)
(A:65)
in which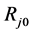 ,
,  ,
,  and
and 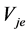 are given by
are given by
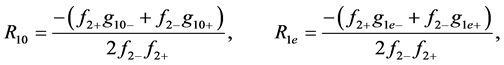 (A:66)
(A:66)
 (A:67)
(A:67)
 (A:68)
(A:68)
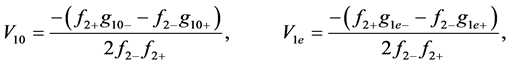 (A:69)
(A:69)
 (A:70)
(A:70)
 (A:71)
(A:71)
and we have defined the following notation
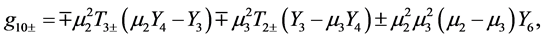 (A:72)
(A:72)
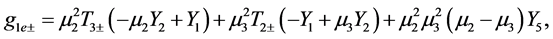 (A:73)
(A:73)
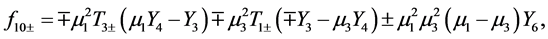 (A:74)
(A:74)
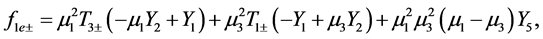 (A:75)
(A:75)
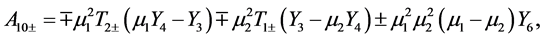 (A:76)
(A:76)
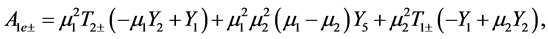 (A:77)
(A:77)
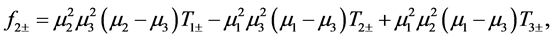 (A:78)
(A:78)
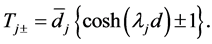 (A:79)
(A:79)
The constants 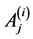 and
and 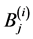 for
for  can easily evaluated using (A:38), (A:39), (A:42), (A:43), (A:53), (A:54). The next step is to find the expressions of the constants
can easily evaluated using (A:38), (A:39), (A:42), (A:43), (A:53), (A:54). The next step is to find the expressions of the constants 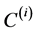 and
and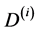 . The Equations (A:26), (A:27), (A:40) and (A:44) give
. The Equations (A:26), (A:27), (A:40) and (A:44) give
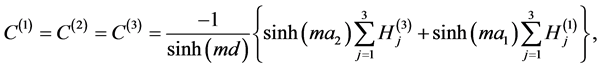 (A:80)
(A:80)
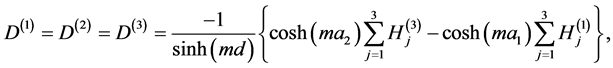 (A:81)
(A:81)
where 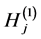 and
and 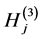 are defined by
are defined by
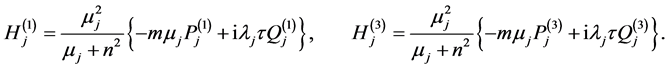 (A:82)
(A:82)
The application of the boundary condition (29) gives
 (A:83)
(A:83)
such that 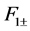 and
and 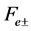 are given by
are given by
 (A:84)
(A:84)
where  for
for 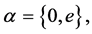
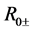 and
and 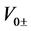 are defined by
are defined by
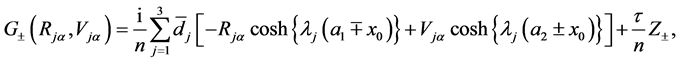 (A:85)
(A:85)
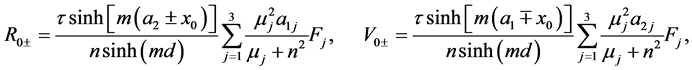 (A:86)
(A:86)
and we have used the notation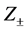 ,
, 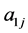 ,
, 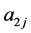 ,
, 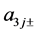 ,
, 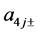 ,
, 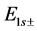 and
and 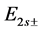
 (A:87)
(A:87)
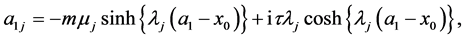 (A:88)
(A:88)
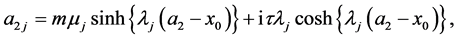 (A:89)
(A:89)
 (A:90)
(A:90)
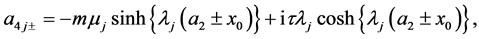 (A:91)
(A:91)
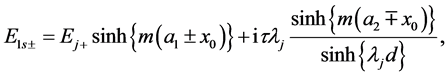 (A:92)
(A:92)
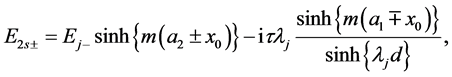 (A:93)
(A:93)
and 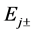 has the form
has the form
 (A:94)
(A:94)
Now the growth rate 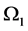 and the displacement
and the displacement 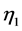 can be evaluated by solving the Equation (A:83) to find
can be evaluated by solving the Equation (A:83) to find
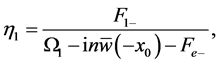 (A:95)
(A:95)
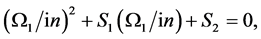 (A:96)
(A:96)
where 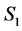 and
and ![]() are defined by
are defined by
 (A:97)
(A:97)
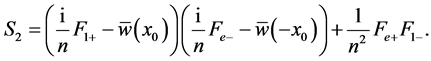 (A:98)
(A:98)

