Open Journal of Fluid Dynamics
Vol.3 No.2(2013), Article ID:33643,4 pages DOI:10.4236/ojfd.2013.32011
Similarity Solution of the Influence of the Thermal Radiation and Heat Transfer on Steady Compressible Boundary Layer Flow
1Mathematical Science Department, Federal University of Technology, Akure, Nigeria
2King Fahd University of Petroleum and Mineral, Dhahran, Saudi Arabia
Email: sanmialao@yahoo.com, samson.bfolarin@yahoo.com
Copyright © 2013 Felix Ilesanmi Alao, Samson Babatunde Folarin. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received January 25, 2013; revised February 28, 2013; accepted March 8, 2013
Keywords: Radiation; Heat Transfer; Stewartson Transformation; Roseland Approximation
ABSTRACT
This paper determines the influence of the radiation and heat transfer on the compressible boundary layer flow using similarity solutions approach. The Roseland approximation is used to describe the radiative heat flux in the energy equation and the compressible boundary layer equations are transformed using Stewartson transformation. Similarity (invariant) solutions for the governing partial differential equations system are constructed. The shooting method is employed to transform the resulting non-linear boundary value problem into initial value problem, which is solved numerically. The effects of various parameters on the velocity and temperature profiles as well as the Falkner skan exponent and Prandtl number are shown graphically.
1. Introduction
The analysis of heat transfer through a laminar boundary layer in the flow of a viscous fluid over arbitrary specified surface temperature contributes a very important problem in the field of heat transfer. The prediction of heat transfer under such condition encompasses a wide range of technological applications, such as calculation of heat transfer at the front portion of the projectile, aircraft or other body moving through the atmosphere. Radiative effects have important applications in physics and engineering, and its effects on different flows are very important in space technology and high temperature processes. But very little is known about the effects of radiation on the boundary layer flow. Thermal radiation effects may play an important role in controlling heat transfer in polymer processing industry where the quality of the final product depends on the heat controlling factors to some extent. High temperature plasmas, cooling of nuclear reactors, liquid metal fluids, power generation systems are some important applications of radiative heat transfer from a wall to conductive gray fluids. Although this problem has been successfully studied in the past, to our best knowledge, only little research work has been conducted to investigate the effect of radiation with heat transfer on compressible boundary layer flow. T. C. Chaim [1], discusses the heat transfer in a fluid with variable thermal conductivity over stretching sheet. J. C. Crepeau and R. Clarksean [2], examine the similarity solution of natural convection with internal generation of heat. The effect of radiation on heat transfer problems has been studied by Hossain and Takhar [3]. S. Mukhopadhyay [4], studies the effect of radiation and variable fluid viscosity on flow and heat transfer along a symmetric wedge. The present work deals with the influence of the thermal radiation and heat transfer on steady compressible boundary layer flow.
2. Governing Equations
We consider a steady, two-dimensional, laminar boundarylayer flow of viscous compressible fluid, given as,
 (2.1)
(2.1)
 (2.2)
(2.2)
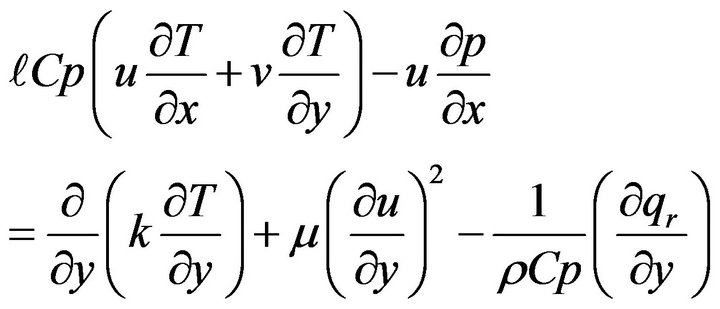 (2.3)
(2.3)
Boundary conditions are:
 at
at  (2.4)
(2.4)
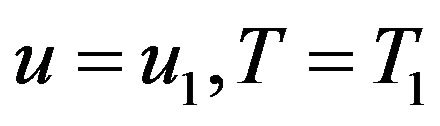 at
at 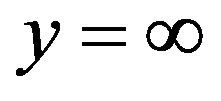 (2.5)
(2.5)
where, 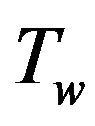 is the constant wall temperature,
is the constant wall temperature, 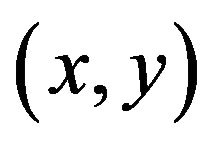 are the Cartesian coordinates with x and y axes along and normal to the surface of the cylinder respectively,
are the Cartesian coordinates with x and y axes along and normal to the surface of the cylinder respectively, 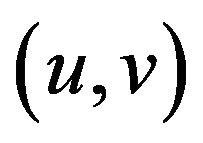 are the velocity components along x and y axes, p is the pressure,
are the velocity components along x and y axes, p is the pressure,  is the density, k is the thermal conductivity,
is the density, k is the thermal conductivity,  is the specific heat at constant pressure, R is the gas constant and the suffix o, refers to some standard state, say
is the specific heat at constant pressure, R is the gas constant and the suffix o, refers to some standard state, say .
.
3. Method of Solution
Stewartson transformation variables of the reduced Equations (2.1)-(2.3) is given as,
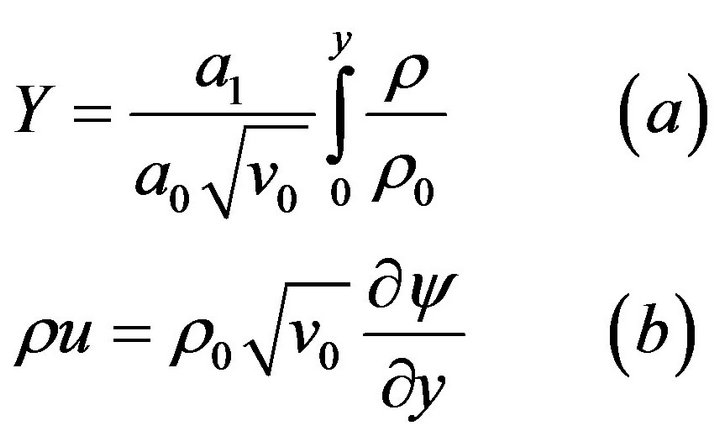 (3.1)
(3.1)
Then,
 (3.2)
(3.2)
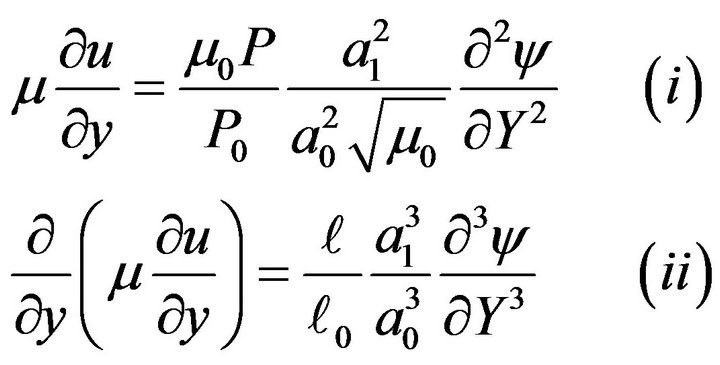 (3.3)
(3.3)
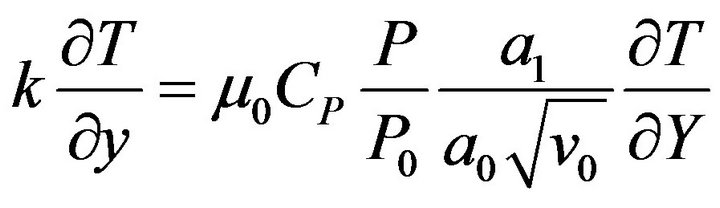 (3.4)
(3.4)
see Stewartson [5], with
 (3.5)
(3.5)
By applying the stewartson transformation variables on Equations (2.1)-(2.6), we obtained
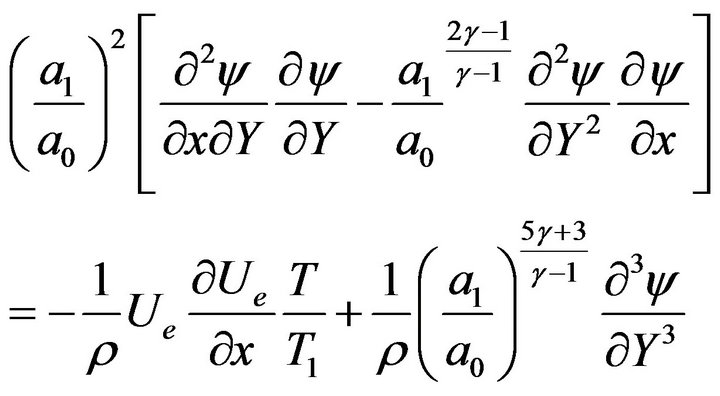 (3.6)
(3.6)
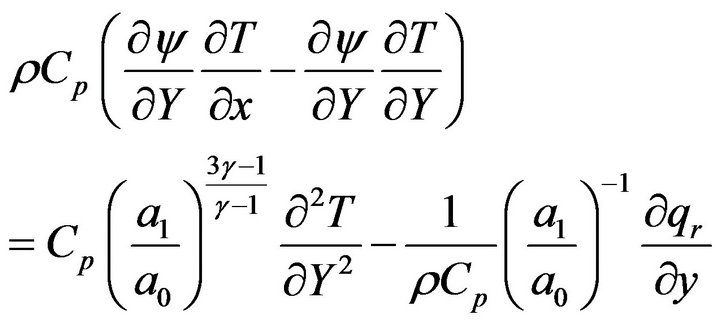 (3.7)
(3.7)
where  is the stream function, a1 and a0 are velocities of sounding main stream.
is the stream function, a1 and a0 are velocities of sounding main stream.
The roseland approximation for radiation is given by
 (see Mukhopadhyay [4])
(see Mukhopadhyay [4]) 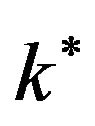 is the absorption coefficient and
is the absorption coefficient and  is the Stefan-Boltzman constant. Assuming the temperature within the flow is such that,
is the Stefan-Boltzman constant. Assuming the temperature within the flow is such that, 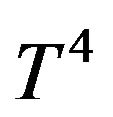 may be expanded in Taylor series about
may be expanded in Taylor series about  (free stream temperature) and neglecting the higher orders terms, we have,
(free stream temperature) and neglecting the higher orders terms, we have,
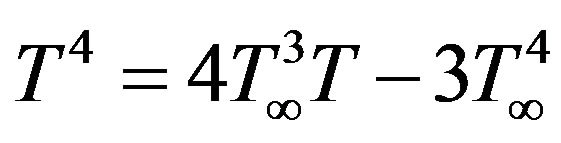 (3.8)
(3.8)
replacing  by unity and using roseland approximation on Equations (3.6) and (3.7), gives
by unity and using roseland approximation on Equations (3.6) and (3.7), gives
 (3.9)
(3.9)
 (3.10)
(3.10)
The non dimensionalized form of Equation (3.10) with the transformed boundary conditions using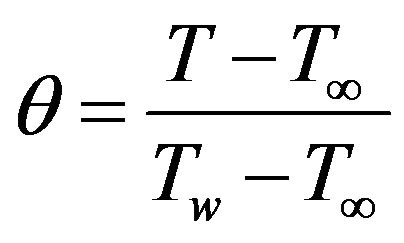 becomes
becomes
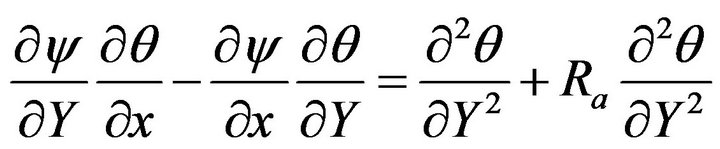 (3.11)
(3.11)
With the boundary conditions
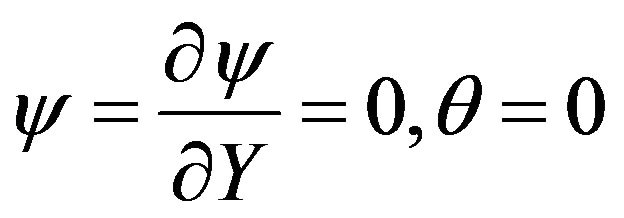 at
at 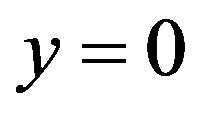 (3.12)
(3.12)
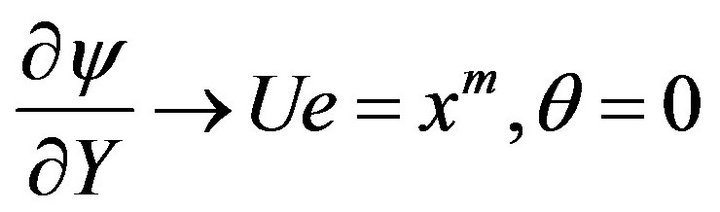 at
at  (3.13)
(3.13)
where 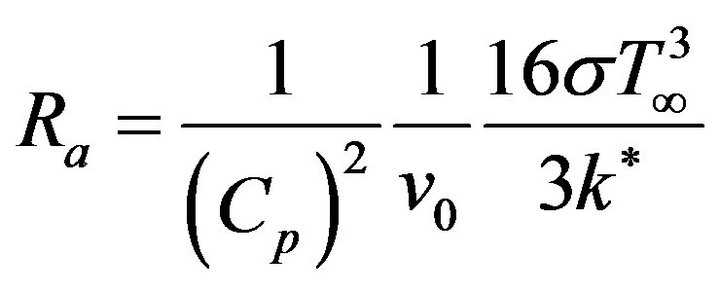 (radiative term).
(radiative term).
The similarity variables defined below, are used to transformed Equations (3.9)-(3.13)
 (3.14)
(3.14)
The transformations gives the below coupled non linear ordinary differential equations
 (3.15)
(3.15)
 (3.16)
(3.16)
because of the presence of temperature T, we define the function S relating to the absolute temperature, with Mach number as
 (3.17)
(3.17)
where, 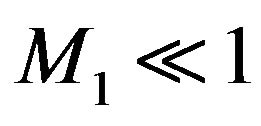 (subsonic flow),
(subsonic flow), 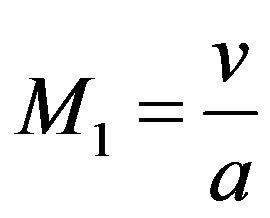 simplifying Equation (3.17) and substituting it into Equations (3.15) and (3.16), we obtained
simplifying Equation (3.17) and substituting it into Equations (3.15) and (3.16), we obtained
 (3.18)
(3.18)
 (3.19)
(3.19)
With the boundary conditions,
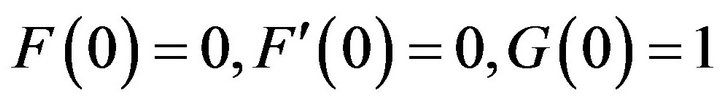 at
at 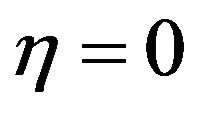 (3.20)
(3.20)
 at
at  (3.21)
(3.21)
where 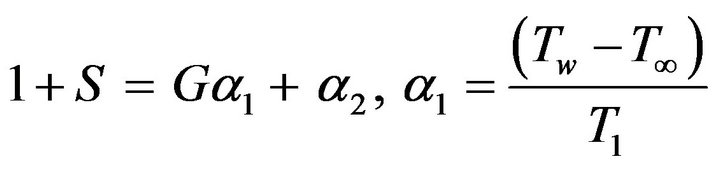 and
and 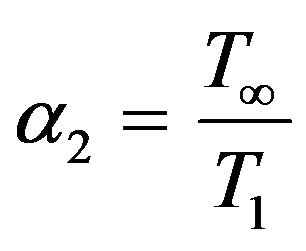
finally we have Equations (3.18)-(3.21) as
 (3.22)
(3.22)
 (3.23)
(3.23)
With boundary conditions,
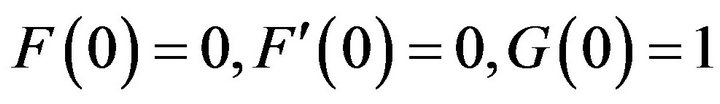 at
at 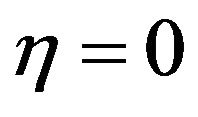 (3.24)
(3.24)
 at
at 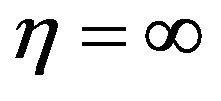 (3.25)
(3.25)
4. Numerical Solution
Shooting method was employed to transform Equations (3.25)-(3.28) into coupled initial value problems. The approximate solution is constructed using Runge-Kutta fourth order technique. Furthermore, the resulting higher order non-linear coupled differentials are decomposed into systems of first order differential equations given below
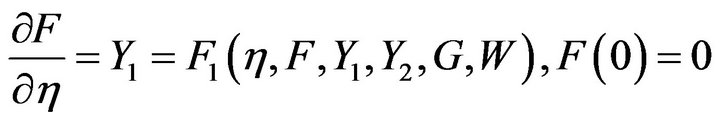 (4.1)
(4.1)
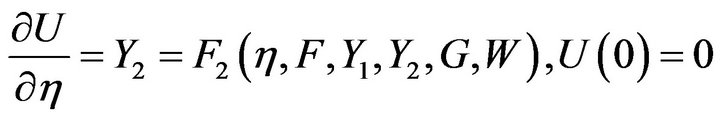 (4.2)
(4.2)
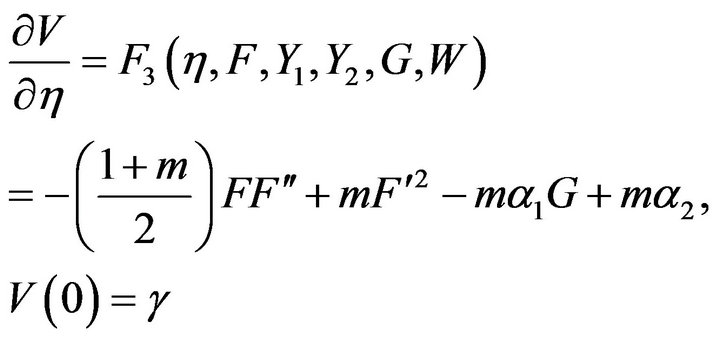 (4.3)
(4.3)
Also
 (4.4)
(4.4)
 (4.5)
(4.5)
5. Results
Discussion of Results
In order to illustrate the results, numerical values were plotted in Figures 1-3). In all cases, we considered the parameters, 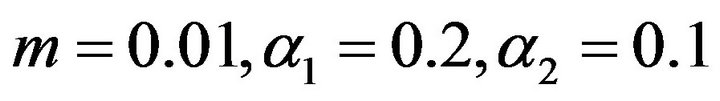 and
and . Others are
. Others are 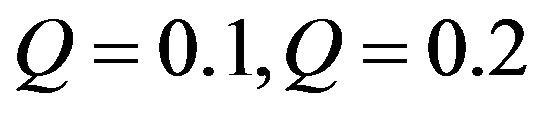 and
and .
.
Figure 1 demonstrates the effect of radiative parameter on velocity field, with fixed Falkner skan exponent m, and Prandtl number Pr on both region of the boundary layer flow. It is discovered that, increase in radiation has insignificant effect on the velocity field of the boundary layer. Also, Figure 2 shows the effect of radiation on the velocity field, Radiation has insignificant effect on the fluid flow on the boundary layer.
Furthermore, Figure 3 shows the effects of the radia-
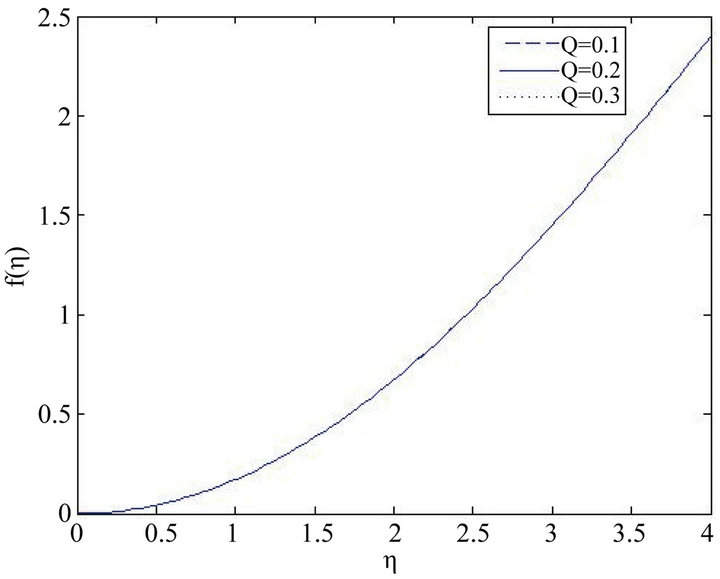
Figure 1. Variation of the velocity profile f(η) with η for several values of Q’s with fixed other parameters.
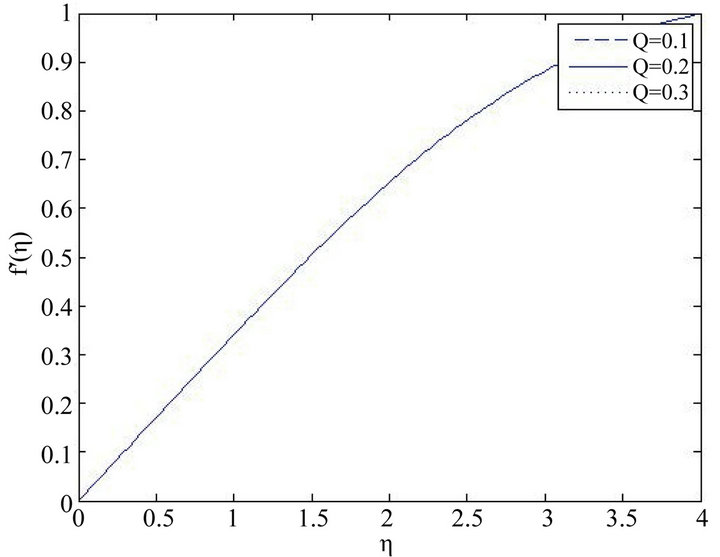
Figure 2. Variation of the velocity profile f’(η) with η for several values of Q’s with fixed other parameter.

Figure 3. Variation of the temperature profile G(η) with η for several values of Q’s with the other parameter fixed.
tive parameters Q on the temperature field in the presence of some fixed parameter. The temperature 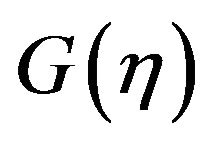 decreases as the thermal radiation Q increases. This is in agreement with the physical fact that the thermal boundary layer decreases with increasing Q.
decreases as the thermal radiation Q increases. This is in agreement with the physical fact that the thermal boundary layer decreases with increasing Q.
6. Conclusion
The present study gives the similarity solution with the approximate solution using the shooting method to determine radiative the heat transfer on the boundary layer flow. Our results show that due to radiation, the rate of heat transfer increases. It is found that the effect of thermal radiation is insignificant in the fluid velocity. The flow separation can be controlled in the presence of lower radiation. The temperature of the boundary layer decreases with increasing thermal radiation.
REFERENCES
- T. C. Chaim, “Heat Transfer in a Fluid with Variable Thermal Conductivity over Stretching Sheet,” Acta Mechanica, Vol. 129, No. 1-2, 1998, pp. 63-72. doi:10.1007/BF01379650
- J. C. Crepeau and R. Clarksean, “Similarity Solution of Natural Convection with Internal Generation of Heat,” Journal of Heat Transfer, Vol. 119, No. 1, 1997, pp. 183- 185. doi:10.1115/1.2824086
- M. A. Hossain and H. S. Takhar, “Radiation Effect on Mixed Convection along a Vertical Plate with Uniform Surface Temperature,” International Journal of Heat and Mass Transfer, Vol. 31, No. 4, 1996, pp. 243-248. doi:10.1007/BF02328616
- S. Mukhopadhyay, “Effect of Radiation and Variable Fluid Viscosity on Flow and Heat Transfer along a Symmetric Wedge,” Journal of Applied Fluid Mechanics, Vol. 2, No. 2, 2009, pp. 29-34.
- K. Stewartson, “Correlated Incompressible and Compressible Boundary Layers,” Proceedings of the Royal Society of London A, Vol. 200, No. 1060, 1949, pp. 84-100.

