Received 28 September 2015; accepted 26 October 2015; published 29 October 2015

ABSTRACT

Minimization of transportation time is a great concern of the transportation problems like the cost minimizing transportation problems. In this writing, a transportation algorithm is developed and applied to obtain an Initial Basic Feasible Solution (IBFS) of transportation problems in minimizing transportation time. The developed method has also been illustrated numerically to test the efficiency of the method where it is observed that the proposed method yields a better result.

Keywords:

Transportation Problem, Initial Basic Feasible Solution, Minimizing, Transportation Time

1. Introduction

A special class of Linear Programming Problem is transportation problem, where the main objective is to minimize the cost of distributing a product from a number of sources to a number of destinations. This type of problem is known as cost minimizing transportation problem. The problem of minimizing transportation cost has been studied since long and is well known by [1] -[15] .

Again, in the process of transporting of urgent material, such as weapons used in military operations, rescue equipments, equipments used for dealing with emergency, medical treatment things and the fresh foods with short storage period, where the speed of delivery is more important than the transportation cost. This type of transportation problem is known as time minimizing transportation problem where the objective is to minimize the transporting time rather than the cost of transportation.

An initial basic feasible solution for minimizing the time of transportation can be obtained by using any well known methods such as, North West Corner Method (NWCM), Least Cost Method (LCM), Vogel’s Approximation Method (VAM) and Extremum Difference Method (EDM). The time minimizing transportation problem had also been studied by a good number of researchers [16] - [20] and they introduced various algorithms for solving time minimizing transportation problems. Garfinkel and Rao in 1971 solved time minimizing transportation problems [21] . Hammer [16] and Szwarc [22] used labeling techniques to solve such kind of problems respectively in 1969 and 1971. In [23] , Nikolic proposed an algorithm to obtain the minimum of the total transportation time. Very recently M. Sharif Uddin [18] has developed an efficient technique of minimizing the time of a transportation problem.

2. Proposed Procedure of Finding an Initial Basic Feasible Solution

It is considered that the readers are well acquainted with transportation problem. Basing on this consideration, a new procedure of finding an initial basic feasible solution of the time minimizing transportation problems is been illustrated below:

Ÿ Step-1: Identify the Largest Element (LE) of every row and every column in the transportation table and write down them in outer column of the supply and lower row of the demand.

Ÿ Step-2: Determine the magnitude of the difference of row largest element and column largest element corresponding to each element.

Ÿ Step-3: Place the value obtained in step-2 on the right bottom of the corresponding elements.

Ÿ Step-4: Place the Row Distribution Indicators (RDI) and the Column Distribution Indicators (CDI) just after and below the supply limits and demand requirements respectively within first bracket, which are the difference of the largest and nearest-to-largest (Second largest) of right bottom entries. If there are two or more largest entries, the RDI or CDI is to be considered as zero.

Ÿ Step-5: Identify the largest number among the RDI and CDI in each level. Choose the smallest time unit along the highest RDI or CDI. If there are two or more number of highest RDI or CDI; choose that highest indicator along which the smallest time element is present. If there are two or more number of smallest time element, choose any one of those arbitrarily.

Ÿ Step-6: Allocate minimum of supply/demand values on the left top of the corresponding smallest time unit selected in Step-5.

Ÿ Step-7: Check whether exactly one of the row/column corresponding to the selected cell has zero supply/ zero demand, respectively. If so, delete the row/column which has the zero supply/zero demand. Again if it is found that both the supply and demand has become zero corresponding to the selected cell, delete either the row or column but not both.

Ÿ Step-8: Match the supply/demand of the left out row/column with the remaining demands/supplies of the undeleted columns/row.

Ÿ Step-9: Repeat Step: 4 to 6 until all the rim requirements are satisfied.

Ÿ Step-10: Determine the largest time T_k corresponding to basic cells.

3. Algorithm for Optimality Test

Algorithm for finding the optimal time for time minimization transportation problems are described below:

Ÿ Step-1: Determine an initial basic feasible solution using above method.

Ÿ Step-2: Determine the largest time T_k corresponding to the basic cells and cross off all non-basic cells.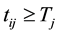

Ÿ Step-3: Construct a loop for the basic cells corresponding to largest time T_k including a non-basic cell in such a way that the allotment in the cell with T_k can be shifted to the non-basic cell in the loop by readjustment of row and column sum, the value at T_k cell is zero and no variables becomes zero or negative. If no such loop can be formed, the solution under test is optimum. Otherwise move to the next step.

Ÿ Step-4: Repeat the procedure until an optimum basic feasible solution is obtained.

4. Illustrative Example

4.1. Example-1

Table 1 shows the time required to shift a load from origins to destinations. It is required to find the optimum plan for shipment to minimize the time of shipment.

4.1.1. Initial Basic Feasible Solution

From the above table it is seen that total supply and total demand are equal. Hence the given transportation problem is a balanced one. Obtaining IBFS for Example-1 using the Proposed Algorithm is shown in Table 2.

We see that the number of basic variables is 5 = (3 + 3 − 1) and the set of basic cells do not contain a loop. Thus the solution obtained is a basic feasible solution and the initial basic feasible solution is x₁₂ = 2, x₁₃ = 11, x₂₁ = 12, x₂₂ = 8, x₃₂ = 5 and the shipping time of basic cells are t₁₂ = 21, t₁₃ = 14, t₂₁ = 8, t₂₂ = 12, t₃₂ = 17.

Therefore, in order to complete the shifting it takes the time T₁ = max{t₁₂, t₁₃, t₂₁, t₂₂, t₃₂} = max{21, 14, 8, 12, 17}= 21 units of time.

4.1.2. Optimality Test

Ÿ Iteration-1: From the IBFS, it is found that the largest time is T₁ = 21, therefore we cross off the non-basic cell (2, 3) which contains equal time unit to T₁. Let us construct a loop for the basic cells corresponding to the largest time T₁ = 21 including the non-basic cell (1, 1) which is called entering cell. The constructed loop in this iteration is shown in Table 3.

The allocation is readjusted in the corner of the loop and a new solution is obtained which is shown in Table 4.

Ÿ Iteration-2: Now largest time is T₂ = 17, therefore we cross off the cells (1, 2) and (3, 3) which contain larger time units than T₂. Let us construct a loop for the basic cells corresponding to the largest time T₂ = 17 including the non-basic cell (3, 1). The constructed loop in this iteration is shown in Table 5.

Readjust the allocation in the corner of the loop, we obtain a new solution which is shown in Table 6.

Ÿ Iteration-3: Now largest time is T₃ = 15, therefore the cell (3, 2) which contains larger time unit than T₃ is crossed off. Now all the crossed off cells including the crossed off cell in this stage is shown in Table 7.

Now no loop can be formed originating from the cell (3, 1). Thus the obtained solution x₁₁ = 2, x₁₃ = 11, x₂₁ = 5, x₂₂ = 15, x₃₁ = 5 is optimum and the optimum shipment time is max {13, 14, 8, 12, 15} = 15 time units.

4.2. Example-2

Some equipment is to be transported from three origins to three destinations. The supply at the origins, the demand at the destinations and the time of shipment are shown in Table 8.

It is required to find the optimum plan for shipment to minimize the total time of shipment.

4.2.1. Initial Basic Feasible Solution

From Table 8, it is seen that total supply and total demand are equal. Hence the given transportation problem is a balanced one. Obtaining IBFS for Example-2 using the Proposed Algorithm is shown in Table 9.

It is seen that the number of basic variables is 5 (=3 + 3 − 1) and the set of basic cells do not contain a loop. Thus the solution obtained is a basic feasible solution and the initial basic feasible solution is x₁₁ = 2, x₁₂ = 10, x₂₁ = 3, x₂₃ = 14, x₃₁ = 7 and the shipping time of basic cells are t₁₁= 15, t₁₂ = 7, t₂₁= 8, t₂₃ = 14, t₃₁ = 17.

Therefore, in order to complete the shipment, it takes the time T₁ = max{t₁₁, t₁₂, t₂₁, t₂₃, t₃₁} = max{15, 7, 8, 14, 17} = 17 units of time.

4.2.2. Optimality Test

Ÿ Iteration-1: Now largest time is T₁ = 17, therefore the non basic cells, (1, 3), (3, 2) and (3, 3) containing larger time units than T₁ are crossed off. These crossed off cells are shown in Table 10.

Now no loop can be formed originating from the cell (3, 1). Thus the obtained solution x₁₁ = 2, x₁₂ = 10, x₂₁ = 3, x₂₃ = 14, x₃₁ = 7 is optimum and the optimum shipment time is max {15, 7, 8, 14, 17} = 17 units of time.

5. Comparative Study of the Results

After obtaining an IBFS by the proposed method, the obtained result is compared with the solution obtained by other existing methods that how many number of iterations are to be required to obtain an optimum solution. This is shown in Table 11.

6. Conclusion

In this writing, an algorithm has been discussed to solve time minimizing transportation problems. Efficiency of the developed algorithm is also been justified by solving numerical problems. During this process, a comparative study among the proposed method and the other existing methods is also carried out; where it is observed that the proposed method requires minimum number of iterations to obtain the optimal transportation time. Therefore, the proposed algorithm claims its wide application in the field of optimization in solving the time minimizing transportation problem.

Cite this paper

Mollah MesbahuddinAhmed,Md. AmirulIslam,MomotazKatun,SabihaYesmin,Md. SharifUddin, (2015) New Procedure of Finding an Initial Basic Feasible Solution of the Time Minimizing Transportation Problems. Open Journal of Applied Sciences,05,634-640. doi: 10.4236/ojapps.2015.510062

References