Received 10 August 2015; accepted 25 August 2015; published 28 August 2015

ABSTRACT

In order to accurately measure the pressure and the pressure difference between two points in the vacuum chamber, a large number of experimental data were used to research the performance of the three capacitance diaphragm gauge and analysis the main influences of the uncertainly degree of pressure in the process. In this paper, three kind of uncertainty, such as the single uncertainty, the synthesis uncertainty and the expanded uncertainty of the three capacitance diaphragm gauges are introduced in detail in pressure measurement. The results show that the performance difference of capacitance diaphragm gauge can be very influential to the accuracy of the pressure difference measurement and the uncertainty of different pressure can be very influential to pressure measurement. That for accurately measuring pressure and pressure difference has certain reference significance.

Keywords:

Capacitance Diaphragm Gauges, Pressure Measurement, Measurement Uncertainty

1. Introduction

The progress of science and technology depends on the development of microelectronics and semiconductor technology that the upgrading and renewing of equipment and technology of microelectronics and semiconductor consequently grow rapidly. This attracted some researchers to study on it. Regardless of from equipment research and development or technological parameters on the need to measure pressure in integrated circuit (IC) processing chamber.

Evaluation of uncertainty is widely used in the test, measurement and other fields of engineering research [1] [2] . Capacitance film gauges (CDGs) measuring the pressure have some advantages such as high accuracy, good linearity and measurement result has nothing to do with the gas composition and types so that it can be applied to measure pressure in IC processing chamber. Due to the difference in manufacture, using time and over-pressure environment that will cause the performance difference [3] . To study the pressure difference in vacuum chamber during dynamic gas flow when the inlet flow rate is low, differential pressure sometimes is only a fraction of Pa. Therefore, the uncertainty factors of capacitance film gauge are very important for the pressure measurement.

This paper based on ASME PTC 19.2-2010 “Pressure Measurement Instruments and Apparatus Supplement” of China as the standard for studying the uncertainty of pressure measurement. This experiment adopts three capacitance film gauges which come from INFICON Instruments Inc., USA and its range is 1333 Pa. Through the experiment, pressure difference between film gauges in measuring pressure is got. Various factors [4] which influence the uncertainty are analyzed and the results provide a base for measuring pressure or pressure differences.

2. Experimental Apparatus

The experimental system mainly includes the gas intake system, pressure measurement system, extraction system. The height of the chamber is 320 mm while its inner diameter is 580 mm (capacity = 84.5 L) as shown in Figure 1. And the vacuum chamber made of 304 stainless steel that is pumped by a high vacuum pumping system is composed of a turbo molecular pump with pumping speed 300 L∙s⁻¹ for N₂ backed by a 82 m³∙s⁻¹ roots pump. The chamber is extracted through a flapper valve of diameter 100 mm. At first, the vacuum chamber wall would suffer two hours’ baking (about 100 degrees Celsius) by a heating jacket, then, the chamber would be extracted for about four hours. It could be achieved that the pressure of the chamber was less than 2 ´ 10⁻⁴ Pa. Based on the static pressure boosting method, the overall leak rate of the chamber was 8.84 ´ 10⁻⁶ Pa∙m²∙s⁻¹ [5] .

For this purpose, three capacitance diaphragm gauges (CGG1, CGG2, CGG3, zero pressure less than 4 ´ 10⁻⁴ Pa) are flanged joint on the cavity wall as shown in Figure 2.

3. Experimental

3.1. Experimental Process

Experimental research on pressure in the range of 10 - 100 Pa, it is necessary to investigate pressure difference in static environment of the three film gauge. Setting the static pressure values such as 20 Pa, 30 Pa, 40 Pa, 50 Pa, 60 Pa, 70 Pa, 80 Pa, 90 Pa, 100 Pa and recording readings of the CDGs, to find out the difference between them. Specific process is as follows: firstly, increasing chamber pressure to over 100 Pa through the vent valve. Secondly, only starting the roots pump to make the pressure at setting value, stopping evacuating. Finally, Please wait until this date is stable and record data.

In the above experiment system, controlling strictly the influence of other experimental factors, such as, keeping the indoor temperature at 20˚C ± 0.2˚C and the humidity at 50% ± 2% RH, ensuring the Experiments occur in the condition that in absence of noise and vibration situation. In order to exclude specific situation, repeat the experiment 10 times.

3.2. Experimental Results

The experimental data are dealt with error processing, and the conclusions from these are compared. For example, in terms of 20 Pa, the average measured data, the residual error of the CDG can be obtained, respectively. The average of residual error in 10 times test to obtain average residual error of every CDG at 20 Pa shown in Table 1. The data processing steps of other pressure are as same as the condition of static pressure 20 Pa, the results as shown in Table 1.

Table 1 shows the average residual error difference of CDGs, for examples, 1 - 2 means difference between CDG1 and CDG2, others like them. The hydrostatic pressure difference of CDGs is shown in Table 2.

The static pressure of chamber should be equal. Table 2 shows that there are performance differences among CDGs, so the measurement results are corrected based on the pressure difference.

4. Uncertainty Calculation

4.1. Mathematical Model Established

The pressure measurement mathematical model of CDG is denoted from the simple relation.

(1)

where P_u (P_a) is the Instrument measurements; δP_s is the instrument error; δP_t is the environment error.

4.2. Uncertainty Evaluation

The experiment experience shows that the significant factors affecting the CDG accurate measurement such as measurement repeatability, apparatus, and temperature. Analysis of the uncertainty characteristics, the components (μ₁) is type A evaluation of standard uncertainty and components (μ₂, μ₃) are type B.

4.2.1. The Components (μ₁) of the Uncertainty Caused by the Repeatability

Using a Bessel method to calculate a single measure standard deviation and the results are shown in Table 3.

The standard deviation of CDG2 is the smallest of the three at same pressure that explaining its stability is best. On the contrary, the stability of the CDG1 is the worst.

The average standard deviation, that is to say, The components of the uncertainty caused by the repeatability,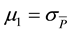. The results are as follows (Table 4).

The degrees of freedom υ₁ = n − 1 = 9

4.2.2. The Components (μ₂) of the Uncertainty Caused by the Apparatus

According to the instrument specifications, CDGs’ indication error (δ) is 0.2% readings. The indication error of setting pressure is shown in Table 5. According to uniformly distributed, the components of the uncertainty caused by the apparatus can be calculated as following.

Due to the stability of the instrument is reliable, the degrees of freedom υ₂ = ∞.

4.2.3. The Components (μ₃) of the Uncertainty Caused by the Temperature

According to the instrument specifications, CDGs’ error is 0.0050% F.S/˚C. Due to the indoor temperature at 20˚C ± 0.2˚C, the error δ = 0.0050% × 1333 Pa/˚C × 0.4˚C = 0.027 Pa. According to uniformly distributed, the components of the uncertainty caused by the temperature can be calculated from the simple relation.

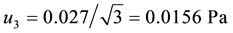
Due to the stability of the instrument is reliable, Degrees of freedom υ₂ = ∞.

4.2.4. Combined Uncertainty

The uncertainty components such as u₁, u₂, u₃ are independent of each other, that is to say, ρ_ij = 0. The combined uncertainty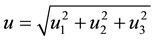, the results are as follows (Table 6).

The free degree of synthetic standard uncertainty was calculated from the following formula.

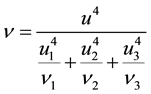(2)

The data in Table 7 are large number can explain the evaluation of uncertainty is better.

4.2.5. Expanded Uncertainty

Taking confidence probability P = 0.95, through the degrees of freedom in Table 7 to check the t distribution table [6] , t_0.95(υ) = 1.96, that is to say, coverage factor k = 1.96. The expanded uncertainty of pressure measurement is shown in Table 8.

4.2.6. Discussion and Analysis

The results show the combined uncertainty and expanded uncertainty of CDGs are considered equal at same pressure. Relative to components μ₂ and μ₃, components μ₁ is much smaller. That is to say, the experiment error caused by the repeatability is minimum. The CDG adopted in the experiment is the most accurate to measure vacuum pressure in the market. Lacking of a more precise instrument for reference, it is difficult to determine which regulate has the highest accuracy through experiment result but its stability can be judged by the standard deviation. Learn from the hydrostatic pressure difference of the CDG in this experiment, Follow-up experiments can accurately measure the pressure difference between two points of interior chamber.

5. Conclusion

In a follow-up experiment, the measurement uncertainty was evaluated based on the results in Tables 6-8 when the CDG was used to measure the chamber pressure. The measurement results are corrected based on the hydrostatic pressure difference and measurement uncertainty when measuring pressure differences. The uncertainty evaluation process of measuring pressure can provide reference for vacuum measurement in the future and measurement pressure difference between two points of vacuum chamber can provide data support for designing process parameters.

Acknowledgements

The research work was supported by grant No.2011ZX02403-004 of the National Key Technology Research and Development Program of the Ministry of Science and Technology of China. A simulate system and experimental platform of IC Equipment including Process Chamber, supported by Multidisciplinary Collaborative Designing.

Cite this paper

YulinZhou,XinQuan,TieniuYang, (2015) The Evaluation of Measurement Uncertainty and Its Application in the Vacuum Pressure Measurement. Open Journal of Applied Sciences,05,495-500. doi: 10.4236/ojapps.2015.58048

References

NOTES

^*Corresponding author.