Open Journal of Applied Sciences
Vol. 3 No. 2 (2013) , Article ID: 33376 , 10 pages DOI:10.4236/ojapps.2013.32028
TABLE I.
Phytoremediation Dynamic Model as an Assessment Tool in the Environmental Management*
1School of Science and Technology, Universidad del Turabo, Gurabo, Puerto Rico
2Department of Natural Science and Mathematics, Inter American University, Bayamon, Puerto Rico
Email: rrcanales@bayamon.inter.edu
Copyright © 2013 Rafael R. Canales-Pastrana, Marlio Paredes. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received January 16, 2013; revised February 18, 2013; accepted February 27, 2013
Keywords: Phytoremediation; Plant Physiology Model; System Dynamics; Environmental Management
ABSTRACT
Phytoremediation is considered a viable and cost effective emerging technology to clean-up trace elements. This approach has not been fully commercialized due the existence of various concerns about it. Those can be summarized as the uncertainty of the system behaviors at different scenarios, such as: contaminant, contaminant concentration and the behaviors of the physiology in the plant. Previous approaches have implemented diverse mathematical algorithms to characterize phytoremediation systems, such as: differential equation solution sets, statistical correlation and system dynamics approach. Phytoremediation Dynamic Model (PDM) employed the classical plant structure to simulate plantsoil-pollutant interaction. This model has proved its capability to mimic phytovolatilization processes of mercury chloride, obtaining more than 95% of correlation between the experimental data, and also provides the capability to know the contaminant flow rate and its concentration in plant tissue. The differential equations system which describes the model includes a comprehensive parameter which encapsulates plant bioavailability dependence in the contaminantmedia interaction as a novel approach because this has not been found on the literature previously. PDM has proved the ability to mimic plant response as a function of contaminant concentration and the applicability as an assessment tool for phytoremediation system performance.
1. Introduction
Since the Industrial Revolution the pollution has been exacerbated, increasing their intrusion probability in the food web [1]. Heavy metal should be a priority to environmental scientist, they are not easily degraded; rather they are bioaccumulated [2-4]. Frequently found in contaminated sites: Cd, Cr, Cu, Pb, Hg, Ni and Zn [5-7], they can be transformed by microorganism interactions into a more bioavailable forms like methyl and dimethyl compounds [8,9].
Mercury was taken as key example of heavy metal contamination, and exposure to different mercury species can inflict a variety of threats to human health, including an irreversible damage to nervous system [6,10]. The global mercury budget has increased 3.3 times in postindustrial times which can be ascribed to the exploitation of precious metals (gold and silver) and coal burning [11-13].
The environmental scientific community has the responsibility to analyze contamination issues to develop standardized protocols. Those analyses mainly consist in site contaminant characterization and construction of mathematical or graphical models, in which multivariate sequential probabilities can be exhibited and map the contaminant dispersion based on background information [12]. These components are crucial to understand their possible contaminant interactions, the establishment of the final stage goal, and the evaluation procedure on the remediation process [7,14]. These kinds of approaches have been implemented to determine the environmental hazard index or a heavy metal risk parameter linked to a specific site location map [15]. This paper discusses previous knowledge on heavy metal cleanup techniques and mathematical model for their evaluation, then presents a novel model approach to characterize phytoremediation dynamic.
2. Previous Knowledge on Heavy Metal Cleanup Technique and Mathematical Model
Cleanup of contaminated soil is an important issue to: the environment, economy and public health. Particularly, chemical degradation affects around 12% of the total degraded soil worldwide [16]. Around the world, countries have been applying environmental strategies to prevent further soil degradation and restoring deteriorated soils, in which the cost implications are considered [17]. Besides the risk of water body contamination by soil washout runoff, there is also the risk of plants growing on contaminated soils, which then extract and translocate pollutants [18,19]. For example, vegetables have the capability to accumulate heavy metals, promoting the intrusion in the food web [19,20]. Environmental scientists have been developing traditional and non-traditional techniques.
2.1. Traditional Cleanup Technique
The traditional cleanup techniques include: flushing, chemical reduction/oxidation, excavation and capping, and stabilization and solidification [21-23]. Excavation and capping is the most commonly used and has an estimate price of $2.5 million/hectare treated [16]. Soil remediation methods for heavy metals contamination, are environmentally invasive, expensive and inefficient, especially when applied to large areas [21,24].
2.2. Non-Traditional Cleanup Technique
Bioremediation is the non-traditional cleanup technique, in which living organisms are implemented (e.g. bacteria, algae, fungi and plant) to extract or confine contaminants from the contaminated media [23,25]. The viable emerging technology to cleanup heavy metal is phytoremediation [6,26,27]. Phytoremediation employs plants for this task and has been promoted as an aesthetically pleasing and solar driven passive technique [28].
2.3. Phytoremediation
This technique can be sub-divided into: phytodegradation or phytotransformation, phytovolatilization, phytoextraction, rhizofiltration and phytostabilization [29,30]. Phytodegradation breaks down contaminants as a consequence of having a catalytic enzyme production by the root. Phytovolatilization is the uptake of a contaminant, later release through transpiration. In phytoextraction (or phytoaccumulation) plants mine and translocate the contaminant from the root to above ground tissues and fix it. Rhizofiltration refers to the absorption or adsorption of the contaminant by the plant root, while phytostabilization involves immobilization of contaminants in the root zone [31,32]. These techniques have been tested to clean up metals, pesticides and hydrocarbons on engineered wetlands [28].
Some plants, like hydrophytes, have intrinsic cleanup capabilities, but their efficiency varies significantly between species [30,33-35]. To achieve a higher efficiency, plants can be genetically modified [23,30,36]. Examples of this approach include the modification of Arabidopsis thaliana, Nicotiana tabacum and Liriodendron tulipifera with the insertion of merA and merB, two bacterial genes employed to increase the mercury remediation potential [36-40].
The implementation of this methods can cost less than one tenth of the price of traditional techniques [16,27,39] and are environmentally friendly. Therefore, their performance has been considered a highly site-specific technology [6,41], seeing the wide variation of contaminants and soil properties which affect the plant interaction [30, 34,42,43]. The most important concerns about phytoremediation are: 1) metal bioavailability within the rhizosphere; 2) uptake rate of metal by roots; 3) proportion of metal “fixed” within the roots; 4) rate of xylem loading/ translocation to shoots; and 5) cellular tolerance to toxic metals [29,30,44]. For those concerns phytoremediation has not been fully commercially implemented.
2.4. Mathematical Models
The implementation of the mathematical model on environmental science helps to evaluate different scenarios to make an objective decision without affecting the environment. Also, can bypass the human rationality, which in some cases promotes an error and/or biases [45]; particularly in complex systems such as: plant-soil interaction.
Several mathematical approaches have been used to understand the soil-plant interaction during the last forty years [46], those can be applied for modeling the phytoremediation cleanup route. Diverse mathematical algorithms have been implemented to reinforce phytoremediation process understanding. A variety of diffusion laws implementation and statistical correlations, aiming to understand the phenomena in a comprehensive way, have been found [47-52]. These models are mathematically intensive and very specialized. System Dynamic Approach (SDA) has been applied, providing a differential equations solution set, defined by models for compartmentalization of the plant physiology [53-55].
All implementations have been constructed using STELLA (system thinking software of isee systems), considering the internal interactions of the contaminant according to the plants’ metabolism. However, these add an excessive complexity to the model, given the number of parameters considered, ranging from 30 to 43 variables per model [53-55]. Those variables are categorized: calibrated, estimated and assumed. These amounts of variables and their differences in the categorization enhance the model’s complexity.
3. Phytoremediation Dynamic Model
The construction of Phytoremediation Dynamic Model was made considering the previous model approaches; it is an implementation of SDA and a plant physiological structure. However, simpler plant structure interaction has been used. Figure 1 shows the plant schematic representation of the phytoremediation process; which is composed of four structural blocks and three processes. Each block has the intent to mimic the contaminant concentration as a function of plant physiological section (root, shoot, leaf) and soil interaction. The arrows steps are to indicate the net contaminant flow between blocks. Extraction section represents the root capability to remove the contaminant from soil. Translocation is the term typically used for the contaminant movement from the root to plant upper tissue [56]. In order to have a clear distinction, this process has been divided in two steps. Translocation 1 represents the contaminant flow from root to shoot (stem), and translocation 2 characterizes the contaminant flow from shoot to leaf.
3.1. Methodology
The development of the Phytoremediation Dynamic Model (PDM) was performed using STELLATM a dynamic software that implements the pictographic modeling representation, based upon four basic components: stocks (level variables), flows (rates), connectors (relationship) and converters (auxiliary variables) [53,55].
The plant was represented by three functional parts (root, shoot, leaf) as stocks (level variables) interconnected, mimicking its anatomy and physiology; two
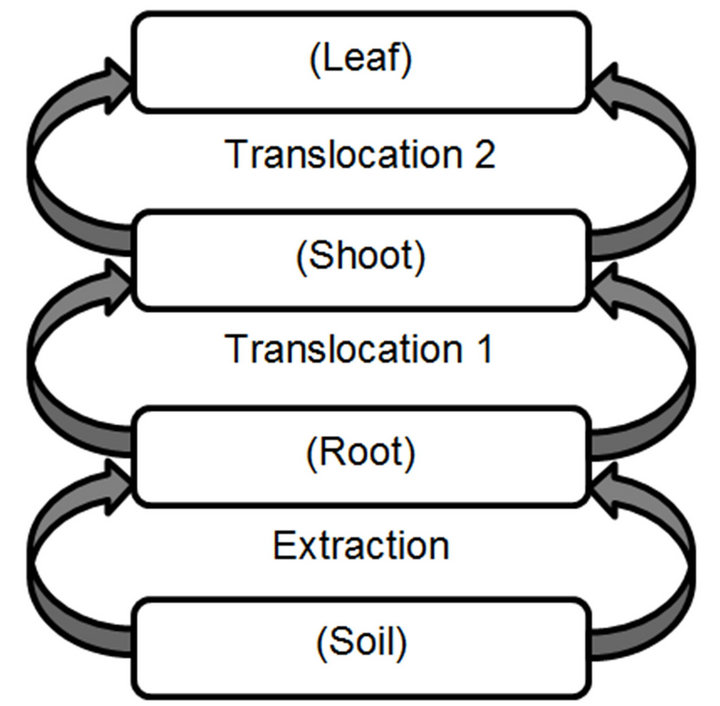
Figure 1. Basic schematic representation of plant physiology, which represents the phytoremediation process.
stocks represent abiotic factors (soil, atmosphere) of the environment (Figure 2). A similar structural representation can be found in a different phytoremediation modeling approach [11,50,55].
PDM combines, the dynamic structural diagram between biotic and abiotic environmental component with the schematic representation of the plant physiology. The model behavior will be governed by the fundamental assumption stated as follows:
1) Fluxes (rates) depend on the contaminant concentration of the previous stocks (level variables), which relate with section rates and threshold concentration. Sections rates is a calibration variable. Threshold concentration is an estimated variable, which value establishes the minimum concentration that previous stock has to achieve to allow the contaminant flow to the next stocks. Once thresholds concentrations are achieved, the value should be maintained during the time frame modeled (Root threshold concentration, Shoot threshold concentration, Leaf threshold concentration). This works as osmotic concentration levels, which is a phenomenon observed as a function of plant species and contamina
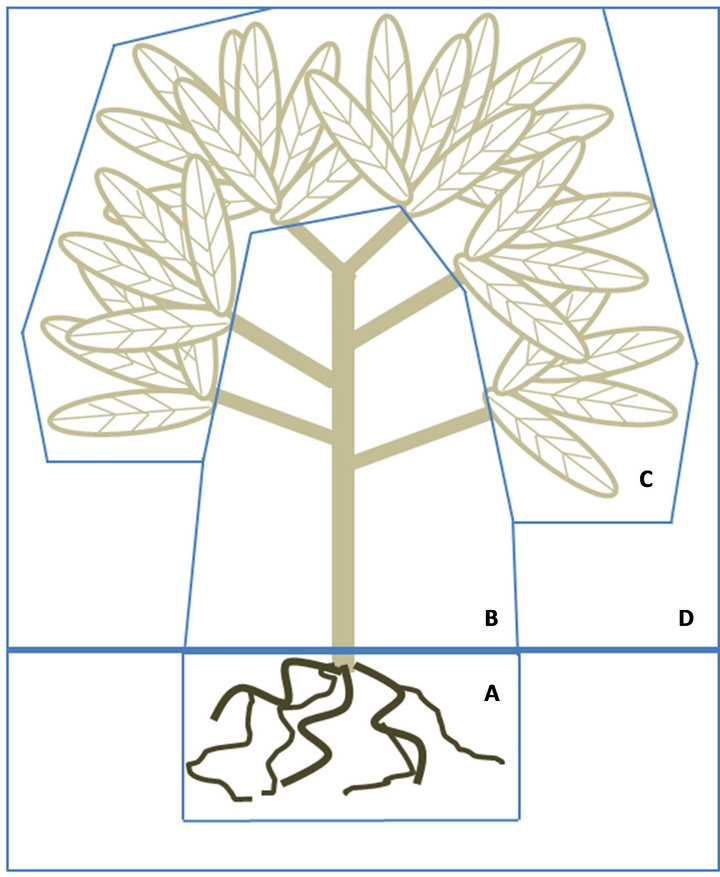
Figure 2. Dynamic structure diagram for the Phytoremediation Dynamic Model (PDM), in which the system has been divided in the compartments to be considered. The compartments can be classified as above or below the ground. The (A) Compartment represents the soil-plant interaction at the root zone, which is the below the ground section involving two stocks: soil and root. The above ground segment; are composed by three stocks: (B) Shoots; (C) Leaf; and (D) Atmosphere.
tion, as reported for plant tissues [27,30,59].
2) Once the threshold concentration is achieved the section flow rates is constant during the time frame modeled (Extraction rate, Translocation rate, Incorporation rate, Volatilization rate), around plant transport capacity. In plant physiology it is well known that ions in solution are moved through transporters. These are characterized mainly by their transport capacity (Vmax) and affinity for the ion (Km) [56].
3) Initial level concentrations in different stocks are zero, except for the stock which represents contaminated soil.
4) Contaminant bioavailability depends on the exponential ratio between the current and initial contaminant concentration in soil. This dependence was represented in the flow equation in PMD soil section and is called Fraction. This soil-plant includes factors such as plant transporters and soil physical-chemical properties. The Km measures the transporter affinity for a specific ion, where high values represent low affinity. The contaminant bioavailability has complex interactions with soil pH, organic matter, carbonates, electrical conductivity and grain distribution [46]. The pH is one of the most important chemical properties of the soil because affects the bioavailability of the contaminant, through the modification of the cation exchange capacity [56]. The heavy metal concentration as a function of pH, has a strong correlation coefficient on a logarithmic lineal regression [28, 57,58].
Once the assumptions have been established the schematic representation of PDM was developed, using STELLATM. It was composed by five stocks, four flows and eight auxiliary variables as depicted in Figure 3. The stocks (levels variables) represent structural reservoirs of the plant physiology and environment, while flows (rates) characterize the upward net contaminant exchange between its compartments. The literature, do not make a distinction between the flows that supplies substance to shoot or leaf, both of them were called translocation as shown in Figure 1 [56]. To be explicit on PMD, translocation-2 was renamed as incorporation, which is the flow that supplies the substance to the leaf. Also, Figure 3
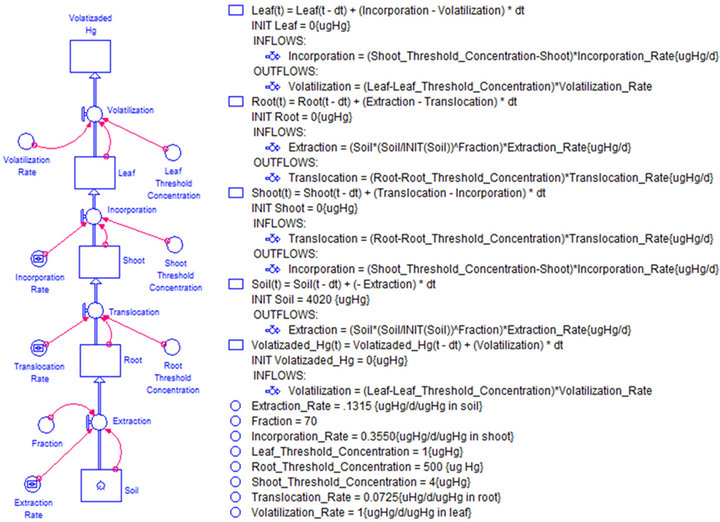
Figure 3. (a) The forrester diagram schematic representation of the phytoremediation dynamic model; (b) The differential equation system of the phytoremediation process.
shows the system of differential equations, which governs the model behavior. The differential equations were rewritten according to the standard of mathematical notations, depicted in Table 1.
S_, and ThC_ functions represent stocks and threshold concentration, respectively. These functions have their respective sub-index (Soil, Root, Shoot, Leaf or Atm for atmosphere) to identify the model section which they represent. R_ represents the rates at which the contaminant moves, ones the threshold was attained. The function of the threshold, flux rates and the gradient in concentration between their neighbors’ stocks was represented by F_. Each one of these functions has a sub-index which identifies the interaction in the model (Ext = Extraction, Tran = Translocation, Inc = Incorporation, Vol = Volatilization). The expression Init_SSoil, corresponds to the initial contaminant concentration in the soil, which is implemented as a constant to calculate the bioavailability as time evolves.
The schematic representation of PMD using STELLATM is simpler that previous UTCSP phytoremediation model [55] and generate similar systems of differential equations [11,50]. The differential equation for the soil model section can be solve by the separation of variables technique but the other equation constitutes a linear differential equation system, which can be tackle with a numerical integration solving method, such as Euler.
3.2. Qualitatively Validation
The PDM validation has been developed to mimic phy-
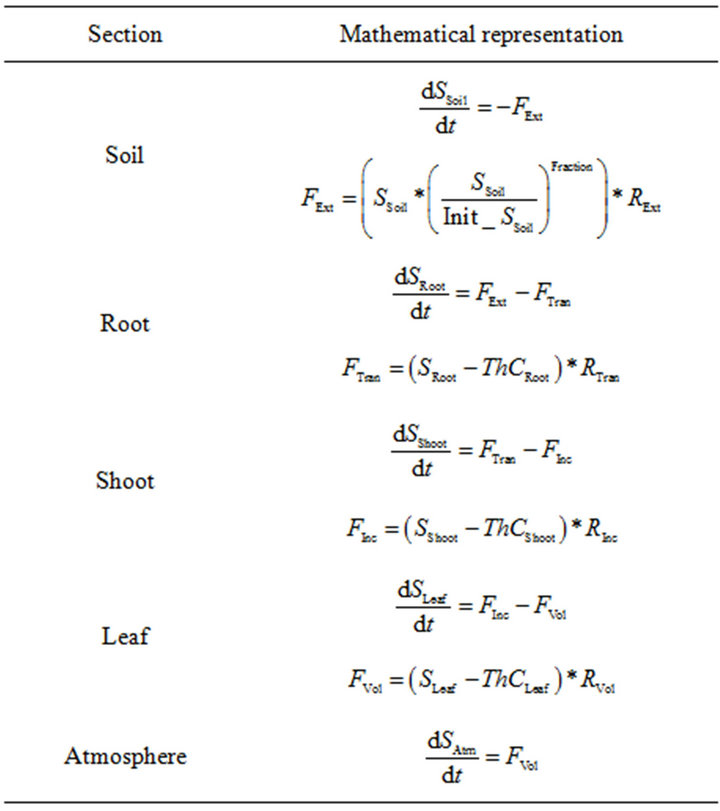
Table 1. Differential equation system describing PDM.
tovolatilization because, is the most comprehensive process which includes all physiologic section of the plant. Heavy metal accumulation and hyperaccumulation plants have been studied extensively [30], only a few research have been performed on heavy metal phytovolatilization [38,40,60,61]. The accumulated amount of heavy metal concentration in each physiological section of the plant [38,60,61], was used to establish a feasible threshold values.
Hussein et al. (2007) showed a comprehensive phytovolatilization experiment for mercury chloride (HgCl2) and phenyl mercury acetate. They tested the remediation capability for two genetically modify tobacco plant in comparison of wild types. In the article, the contaminant can be found in the plants tissue and the volatilization as time evolves. The volatilization data for the two genetically modified lines are shown in Figure 4, for mercury chloride. The pLDR-merAB data set was employed for validation purposes, because they represent the simpler gene expression and present more behavioral changes in comparison with pLDR-merAB3’UTR (Figure 4).
According to the environmental point of view, the amount of mercury extracted from soil is important, but as well the amount released to the atmosphere. In order to analyze amount of total mercury releases to the atmosphere (cumulative volatilized mercury) a sub model was constructed, implementing SDA (Figure 5). The qualitatively validation of PDM, was performed. In the Figure 6 depicted the likeness between the model and the experimental data values. This high similarity between the model and the experimental data validate: 1) the fundamental assumptions of the model; and 2) the value of the auxiliary variable in the base scenario which are reasonable and feasible (Table 2). The model has
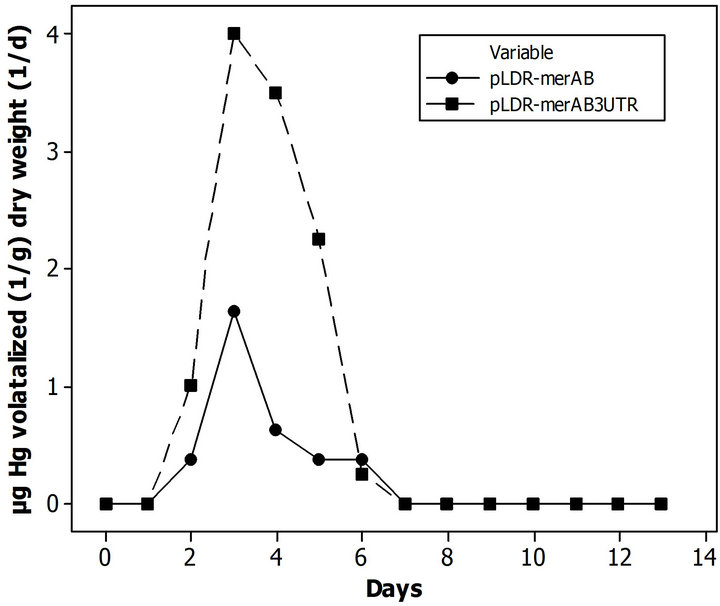
Figure 4. Volatilization data by genetically modified tobacco plant on contaminated soil with 100 µM of HgCl2 (Adapted from [40]).
eight auxiliary variables that have been categorized; four as estimated and four as calibrated. The categorization was performed according to the way in which their value was obtained, estimated for the value extracted from the literature and calibrated for the variables values modified to adjust model behaviors to the experimental data. Those variables are also divided in three groups: threshold, rates and bioavailability constant (Fraction).
3.3. Quantitative Validation and Statistical Analysis
The cumulative volatilized mercury concentration data was selected to perform the quantitative analysis because of the environmental relevance of those emissions that can enhance mercury concentration in the atmosphere and summarize the results of the volatilized data. Table 3 depicts the descriptive statistical analysis for the experimental and model data. The percent of difference between experimental data and model for each analysis did not exceed 0.9%.
Figure 7 shows a regression fit analysis, demonstrating a strong correlation (99.4%). The slope of the regression line differed in 0.9% in comparison with the theoretical one. The analysis shows the prediction and confidence intervals as well. The prediction interval represents a range of new observation is likely to be and confidence interval represents a range that the mean will response, in both intervals that behaviors is according to the established percentage of precision. All data points achieved the 99% prediction interval; however one data point (7%) was overlapped with the line that constringes the interval, although 86% of data points are inside the confidence interval, one (7%) is touching the lines that limit the interval and another (7%) is completely outside the interval.
With the results of the descriptive and regression analysis, we can be hypothesized that the difference between PDM and the experimental analysis is less than one data units. A sign test was employed as a non-parametric statistic to examine the mean difference. The Sign Test demonstrated that the null hypothesis can be rejected with a significant confidence level of 95%, having a median of 0.0200 and a p-value of 0.0001.

Table 2. Auxiliary variable categorization and base scenario values.

Figure 5. Schematic representation of stock (level variables) and flow model to obtain the cumulative volatilized mercury, using experimental data.
 (a)
(a) (b)
(b)
Figure 6. Comparison between experimental data and PDM. (a) Volatilized µg Hg; (b) Cumulative volatilized µg Hg.
The statistical analysis demonstrates that Phytoremediation Dynamic Model (PDM) has the ability to reproduce the experimental results of phytoremediation experiment with excellent degree of accuracy and statistical significance. The differential equations system summarizes the interaction between biotic and abiotic, including bioavailability, flows rates and metal concentration. These factors are some of the most influential concerns about phytoremediation that tackles the fully commercially implementation [29,30,44]. The bioavailability factors are represented in the soil section of the model; which is governed by the Fraction calibration variable. The value of this adimensional variable represents the percentage of the contaminant, which is not available for the plant to be removed on each time steps. The calibrated value for this scenario is 70, which mean that only the 30% of the mercury chloride is accessible for the removal on each time steps. The concentration of the metal that is retained on each plants physiological section is represented in the value of the threshold variables. The contaminant flow through the phytoremediation system is characterized by the rate variables. All of those variable values were depicted in Table 2.
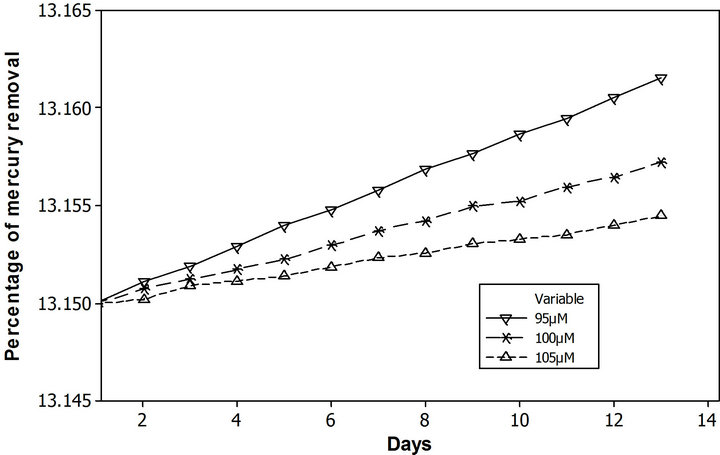
PDM can be also implemented as a performance tools for the technique, calculating the percentage of contaminant removed. To assess this approach, a family of runs fluctuating the mercury chloride initial concentration in the range of 10 µM to 100 µM, with an increment of 10 µM, was performed. Likewise, it have been done with two more runs ±5% of the base scenario initial contaminant concentration in soil. The Figure 8 illustrates the performance behavior for both scenarios, according to the percentage of mercury removed. The effectiveness of this phytoremediation system shows invers dependence as function of contaminant soil concentration. In the range of 10 µM to 100 µM, the amount of mercury removed varied from 31% to 13%, but close to 100 µM (± 5%) these amounts of total mercury removal varied in the hundredth. These types of analysis increased the system understanding at the time to make a decision of which kind of technique is better for a specific situation. It also provides comprehensive information for the regulators about system’s functionality.
5. Acknowledgements
The first author would like to thank the Computational
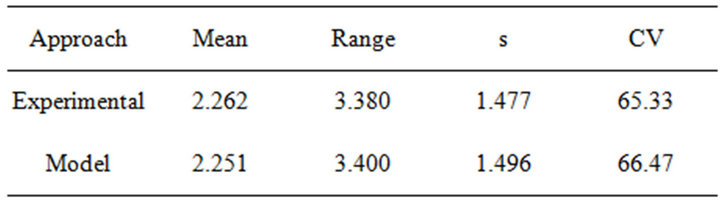
Table 3. Descriptive statistical analysis for cumulative mercury concentration (µHg) by approach (standard deviation (s); coefficient of variation (CV)).
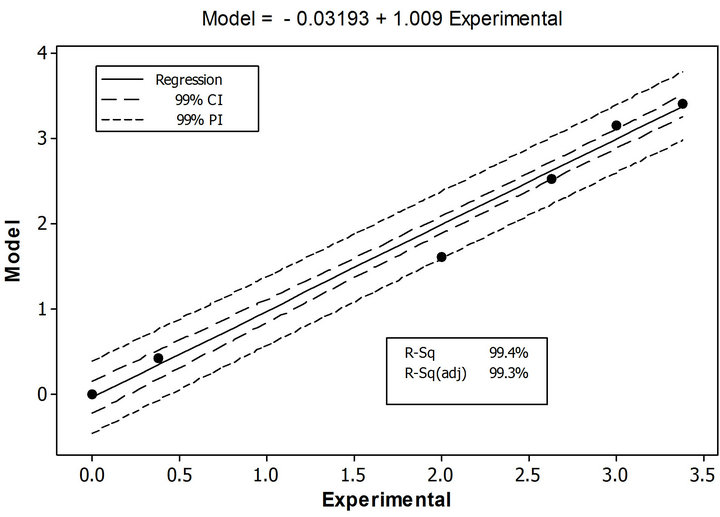
Figure 7. Regression fit analysis between experimental data and PDM, showing the prediction (PI) and confidence (CI) intervals for cumulative mercury concentration.
 (a)
(a) (b)
(b)
Figure 8. Percentage of mercury removal as a function of initial soil contaminant concentration. (a) From 10 µM to 100 µM, with an increment of 10 µM; (b) 100 µM ± 5%.
Scientific Laboratory at Inter American University, Bayamon Campus for providing us the computational resources and to Yamaris Pacheco-Moctezuma for reviewing this manuscript at early stages.
REFERENCES
- Environment Canada, “Global Mercury Circulation,” 2010. http://www.ec.gc.ca/mercure-mercury/default.asp?lang=En&n=A177A336-1Environment
- N. Piorrone and K. R. Mahaffey, “Where We Stand on Mercury Pollution and Its Health Effects on Regional and Global Scales,” In: N. Piorrone and K. R. Mahaffey, Eds., Dynamics of Mercury Pollution on Regional and Global Scales: Atmospheric Processes and Human Exposures around the World, Springer Science + Business Media, Inc., New York, 2006, pp. 1-21.
- J. Sardans, F. Montes and J. Peñuelas, “Determination of As, Cd, Cu, Hg, and Pb in Biological Samples by Modern Electrothermal Atomic Absorption Spectrometry,” Spectrochimica Acta Part B, Vol. 65, No. 2, 2010, pp. 97-112. doi:10.1016/j.sab.2009.11.009
- B. Pezzarossa, F. Gorini and G. Petruzzelli, “Heavy Metal and Selenium Distribution and Bioavailability in Contaminated Sites: A Tools for Phytoremediation,” In: H. Magdi, Ed., Dynamics and Bioavailability of Heavy Metals in the Roots Zone, CRC Press Taylor & Francis Group, Florida, 2011, pp. 93-127. doi:10.1201/b10796-5
- “World Commission on Environment and DevelopmentUnited Nation Our Common Future,” United Nation, 1987. http://www.un-documents.net/wced-ocf.htm
- J. R. Henry, “An Overview of the Phytoremediation of Lead and Mercury,” US Environmental Protection Agency Office of Solid Waste and Emergency Response Technology Innovation, Washington DC, 2000, p. 55.
- I. Renberg, C. Bigler, R. Bindler, M. Norberg, J. Rydberg and U. Segreström, “Environmental History: A Piece in the Puzzle for Establishing Plans for Environmental Management,” Journal of Environmental Management, Vol. 90, No. 8, 2009, pp. 2794-2800. doi:10.1016/j.jenvman.2009.03.008
- J. M. Wood, “Biological Cycles for Toxic Elements in the Environment,” Science, Vol. 183, No. 4129, 1974, pp. 1049-1052. doi:10.1126/science.183.4129.1049
- W. P. Redley, L. J. Dizikes and J. M. Wood, “Biological Cycles for Toxic Elements in the Environment,” Science, Vol. 197, No. 4301, 1977, pp. 329-332. doi:10.1126/science.877556
- A. Shafaghat, F. Salimi, M. Valiei, J. Salehzadeh and M. Shafaghat, “Removal of Heavy Metals (Pb2+, Cu2+ and Cr3+) from Aqueous Solutions Using Five Plants Materials,” African Journal of Biotechnology, Vol. 11, No. 4, 2012, pp. 852-855.
- S. E. Sundberg, J. J. Ellington, J. J. Evans, D. A. Keys and J. W. Fisher, “Accumulation of Perchlorate in Tobacco Plants: Developments of a Plant Kinetic Model,” Journal of Environmental Monitoring, Vol. 5, No. 3, 2003, pp. 505-512. doi:10.1039/b300570d
- N. V. Smith-Downey, E. M. Sunderland and D. J. Jacob, “Anthropogenic Impacts on Global Storage and Emissions of Mercury from Terrestrial Soils: Insights from a New Global Model,” Journal of Geophysical Research, Vol. 115, No. G3, 2010, pp. 1-11.
- E. S. Corbitt, D. J. Jacob, C. D. Holmes, D. G. Streets and E. M. Sunderland, “Global Source-Receptor Relationship for Mercury Deposition under Present-Day and 2050 Emissions Scenarios,” Environmental Science & Technology, Vol. 45, No. 24, 2011, pp. 10477-10484. doi:10.1021/es202496y
- S. Polasky, S. R. Carpenter, C. Folke and B. Keeler, “Decision-Making under Great Uncertainty: Environmental Management in an Era of Global Change,” Trends in Ecology and Evolution, Vol. 26, No. 8, 2011, pp. 398-404. doi:10.1016/j.tree.2011.04.007
- C. Franco, A. Soares and J. Delgado, “Geostatistical Modeling of Heavy Metal Contamination in the Topsoil of Guadiamar River Margins (S Spain) Using a Stochastic Simulation Technique,” Geoderma, Vol. 136, No. 3-4, 2006, pp. 852-864. doi:10.1016/j.geoderma.2006.06.012
- C. Bini, “Frorm Soil Contamination to Land Restoration,” Nova Science Publisher, New York, 2010.
- European Commission, “Soil Protection: The Story Behind the Strategy,” EU: European Communities, Luxembourg, 2006.
- M. J. McLaughlina, D. R. Parkerb and J. M. Clarkec, “Metals and Micronutrients—Food Safety Issues,” Field Crops Research, Vol. 60, No. 1-2, 1999, pp. 143-163. doi:10.1016/S0378-4290(98)00137-3
- F. Mapanda, E. N. Mangwayana, J. Nyamangara and K. E. Gillera, “The Effects of Long-Term Irrigation Using Wastewater on Heavy Metal Contents of Soils under Vegetables Harare, Zimbabwe,” Agriculture, Ecosystems & Environment, Vol. 107, No. 2-3, 2005, pp. 151-165. doi:10.1016/j.agee.2004.11.005
- Y. Cui, Y. Zhu, R. Zhai, D. Chen, Y. Huang, Y. Qui and J. Liang, “Transfer of Metals from Soil to Vegetables in an Area near a Smelter in Nanning, China,” Environmental International, Vol. 30, No. 6, 2004, pp. 785-791. doi:10.1016/j.envint.2004.01.003
- S. Kärenlampi, H. Schat, J. Vangronsveld, J. A. C. Verkleij, D. Lelie, M. Mergeay and A. I. Tervahauta, “Genetic Engineering in the Improvement of Plants for Phytoremediation of Metal Polluted Soil,” Environmental Pollution, Vol. 107, No. 2, 2000, pp. 225-231. doi:10.1016/S0269-7491(99)00141-4
- J. Hinton and M. Veiga, “Mercury Contaminated Sites: A Review of Remedial Solutions,” Proceeding of National Institute for Minamata Disease, Minamata, 19-20 March 2001. http://www.nimd.go.jp/english/kenkyu/nimd_forum/nimd_forum_2001.pdf
- G. Wu, H. Kang, X. Zhang, H. Shao, L. Chu and C. Ruan, “A Critical Review on the Bio-Removal of Hazardous Heavy Metals from Contaminated Soils: Issues, Progress, Eco-Environmental Concerns and Opportunities,” Journal of Hazardous Materials, Vol. 174, No. 1-3, 2010, pp. 1-8. doi:10.1016/j.jhazmat.2009.09.113
- E. Meers, F. M. G. Tack, S. Van Slycken, A. Ruttens, G. Du Laing, J. Vangronsveld and M. G. Verloo, “Chemically Assisted Phytoextraction: A Review of Potential Soil Amendments for Increasing Plant Uptake of Heavy Metals,” International Journal of Phytoremediation, Vol. 10, No. 5, 2008, pp. 390-414. doi:10.1080/15226510802100515
- M. H. Fulekar and J. Sharma, “Bioinformatics Applied in Bioremediation,” Innovative Romanian Food Biotechnology, Vol. 2, No. 2, 2008, pp. 28-36.
- O. V. Singh, S. Labana, G. Pandey, R. Budhiraja and R. K. Jain, “Phytoremediation: An Overview of Metallic Ion Decontamination from Soil,” Applied Microbiology and Biotechnology, Vol. 61, No. 5-6, 2003, pp. 405-412.
- C. D. Jadia and M. H. Fulekar, “Phytoremediation of Heavy Metals: Recent Techniques,” African Journal of Biotechnology, Vol. 8, No. 6, 2009, pp. 921-928.
- M. Zhang, Z. Liu and H. Wang, “Use of Single Extraction Method to Predict Bioavailability of Heavy Metals in Polluted Soils to Rice,” Communications in Soil Science and Plant Analysis, Vol. 41, No. 7, 2010, pp. 820-831. doi:10.1080/00103621003592341
- Environmental Protection Agency, “Introduction to Phytoremediation,” Environmental Protection Agency, Ohio, 2000, pp. 1-72.
- H. Sarma, “Metal Hyperaccumulation in Plants: A Review Focusing on Phytoremediation Technology,” Journal of Environmental Science and Technology, Vol. 4, No. 2, 2011, pp. 118-138. doi:10.3923/jest.2011.118.138
- A. D. Pueke and H. Rennenberg, “Phytoremediation: Molecular Biology, Requirements for Application, Environmental Protection, Public Attention and Feasibility,” European Molecular Biology Organization, Vol. 6, No. 6, 2005, pp. 497-501.
- Technology Innovation Program-Environmental Protection Agency, Environmental Protection Agency, 2008. http://clu-in.org/techfocus/default.focus/sec/Phytotechnologies/cat/Overview/
- X.-B. Zhang, P. Liu, Y.-S. Yang and W.-R. Chen, “Phytoremediation of Urban Wastewater by Model Wetlands with Ornamental Hydrophytes,” Journal of Environmental Science, Vol. 19, No. 8, 2007, pp. 902-909. doi:10.1016/S1001-0742(07)60150-8
- C. Lafabrie, K. M. Major, C. S. Major and J. Cebrián, “Arsenic and Mercury Bioaccumulation in the Aquatic Plant, Vallisneria neotropicallis,” Chemosphere, Vol. 82, No. 10, 2011, pp. 1393-1400. doi:10.1016/j.chemosphere.2010.11.070
- P. Zornoza, R. Millán, M. J. Sierra and E. Esteban, “Efficiency of White Lupin in the Removal of Mercury from Contaminated Soils: Soil and Hydroponic Experiments,” Journals of Environmental Science, Vol. 22, No. 3, 2010, pp. 421-427. doi:10.1016/S1001-0742(09)60124-8
- A. Harfouche, R. Meilan and A. Altman, “Tree Genetic Engineering and Applications to Sustainable Forestry and Biomass Production,” Trends in Biotechnology, Vol. 29, No. 1, 2011, pp. 9-17. doi:10.1016/j.tibtech.2010.09.003
- A. C. P. Heaton, C. L. Rugh, N. J. Wang, R. B. Meagher, “Phytoremediation of Mercury and Methylmercury-Polluted Soils Using Genetically Engineered Plants,” Journal of Soil Contamination, Vol. 7, No. 4, 1988, pp. 497-509.
- C. L. Rugh, H. D. Wilde, N. M. Stack, D. M. Thomson, A. O. Summers and R. B. Meagher, “Mercuric Ion Reduction and Resistance in Transgenic Arabidopsis thaliana Plants Expressing a Modified Bacterial merA Gene,” Proceeding of National Science, Vol. 93, No. 8, 1996, pp. 3182-3187. doi:10.1073/pnas.93.8.3182
- U. Krämer, “Phytoremediation: Novel Approaches to Cleaning up Polluted Soils,” Current Opinion in Biotechnology, Vol. 16, No. 2, 2005, pp. 133-141. doi:10.1016/j.copbio.2005.02.006
- H. S. Hussein, O. N. Ruiz, N. Terry and H. Daniell, “Phytoremediation of Mercury and Organomercurial in Choloplast Transgenic Plants: Enhanced Roots Uptake, Translocation to Shoots, and Volatilization,” Environmental Science Technology, Vol. 41, No. 24, 2007, pp. 8439- 8446. doi:10.1021/es070908q
- N. A. Sorkhoh, N. Ali, H. Al-Awadhi, N. Dashti, D. M. Al-Mailem, M. Eliyas and S. S. Radwan, “Phytoremediation of Mercury in Pristine and Crude Oil Contaminated soil: Contributions of Rhizobacteria and Their Host Plants to Mercury Removal,” Ecotoxicology and Environmental Safety, Vol. 73, No. 8, 2010, pp. 1998-2003. doi:10.1016/j.ecoenv.2010.08.033
- M. Israr, A. Jewell, D. Kumar and S. V. Sahi, “Interactive Effects of Lead, Copper, Nickel and Zinc on Growth, Metal Uptake and Antioxidative Metabolism of Sesbania drummondii,” Journal of Hazardous Materials, Vol. 186, No. 1-2, 2011, pp. 1520-1526. doi:10.1016/j.jhazmat.2010.12.021
- X. Wang. L. Q. Ma, B. Rathinasabapathi, Y. Liu and G. Zeng, “Uptake and Translocation of Arsenite and Arsenate by Pteris vittata L.: Effects of Silicon, Boron and Mercury,” Environmental and Experimental Botany, Vol. 68, No. 2, 2010, pp. 222-229. doi:10.1016/j.envexpbot.2009.11.006
- J. V. Deuren, T. Lloyd, S. Chhetry, R. Liou and J. Peck, “Remediation Technologies Screening Matrix and Reference Guide: Version 4.0. Federal Remediation Technology Roundtable,” 2006.
- J. D. Sterman, “Misperceptions of Feedback in Dynamic Decision Making,” Organizational Behavior and Human Decision Process, Vol. 43, No. 3, 1989, pp. 301-335. doi:10.1016/0749-5978(89)90041-1
- D. K. Benbi and R. Nieder, “Handbook of Processes and Modeling in Soil-Plant System,” Food Products Press and The Haworth Reference Press, Binghamton, 2003, p. 762.
- S. C. McCutcheon and J. L. Schnoor, “Phytoremediation: Transformation and Control of Contaminants,” Wiley-Interscience Inc., Hoboken, 2003, p. 987.
- B. Robinson, J. E. Ferández, P. Madejón, T. Marañón, J. M. Murillo, S. Green and B Clothier, “Phytoextraction: An Assessment of Biogeochemical and Economic Viability,” Plant and Soil, Vol. 249, No. 1, 2003, pp. 117-125. doi:10.1023/A:1022586524971
- S. Trapp, “Plant Uptake and Transport Models for Neutral and Ionic Chemical,” Environmental Science and Pollution Research, Vol. 11, No. 1, 2004, pp. 33-39. doi:10.1065/espr2003.08.169
- D. M. Thomas, L. Vandemuelebroeke and K. Yamaguchi, “A Mathematical Evolution Model for Phytoremediation of Metals,” Discrete and Continuous Dynamical System Series B, Vol. 5, No. 2, 2005, pp. 411-422.
- J. Japenga, G. F. Koopmans, J. Song and P. F. A. M. Römkens, “A Feasibility Test to Estimate the Duration of Phytoextraction of Heavy Metals from Polluted Soils,” International Journals of Phytoremediation, Vol. 9, No. 2, 2007, pp. 115-132. doi:10.1080/15226510701232773
- H. Qu, Q. Zhu, M. Guo and Z. Lu, “Simulation of Carbon-Based Model for Virtual Plants as Complex Adaptive System,” Simulation Modeling Practice and Theory, Vol. 18, No. 6, 2010, pp. 677-695. doi:10.1016/j.simpat.2010.01.004
- Y. Ouyang, “Phytoremediation: Modeling Plant Uptake and Contaminant Transport in the Soil-Plant-Atmosphere Continuum,” Journal of Hydrology, Vol. 266, No. 1-2, 2002, pp. 66-82. doi:10.1016/S0022-1694(02)00116-6
- Y. Ouyang, C. H. Huang, D. Y. Huang, D. Lin and L. Cui, “Simulating Uptake and Transport of TNT by Plants Using STELLA,” Chemosphere, Vol. 69, No. 8, 2007, pp. 1245-1252. doi:10.1016/j.chemosphere.2007.05.081
- Y. Ouyang, “Modeling the Mechanisms for Uptake and Translocation of Dioxane in a Soil-Plant Ecosystem with STELLA,” Journal of Contaminant Hydrology, Vol. 95, No. 1-2, 2008, pp. 17-29. doi:10.1016/j.jconhyd.2007.07.010
- M. M. Lasat, “Phytoextraction of Metal from Contaminated Soil: A Review of Plant/Soil/Metal Interaction and Assessment of Pertinent Agronomic Issues,” Journal of Hazardous Substance Research, Vol. 2, No. 5, 2000, pp. 1-25.
- M. L. Almendras, M. Carballa, L. Diels, K. Vanbroekhoven and R. Chamy, “Prediction of Heavy Metal Mobility and Bioavailability in Contaminated Soil Using Sequential Extraction and Biosensors,” Journal of Environmental Engineering, Vol. 135, No. 9, 2009, pp. 839-844. doi:10.1061/(ASCE)0733-9372(2009)135:9(839)
- J. A. Rodríguez, A. Vázquez, J. M. Grau, C. Martínez and M. López, “Factors Controlling the Spatial Variability of Mercury Distribution in Spain Topsoil,” Soil & Sediment Contamination, Vol. 18, No. 1, 2009, pp. 30-42.
- H. Yu, J. Ge, X. Zhong, M. Czakó and L. Márton, “Differential Mercury Volatilization by Tobacco Organs Expressing a Modified Bacterial merA Gene,” Cell Research, Vol. 11, No. 3, 2001, pp. 231-236. doi:10.1038/sj.cr.7290091
- [61] S. Bizily, C. C. Rugh, A. O. Summers and R. B. Meagher, “Phytoremediation of Methylmercury Pollution: merB Expression in Arabidopsis thaliana Plants Confer Resistance to Organomercurial,” Proceeding of National Academy of Science of the United States of America, Vol. 96, No. 12, 1999, pp. 6808-6813. doi:10.1073/pnas.96.12.6808
- [62] O. N. Ruiz, H. S. Hussein, N. Terry and H. Daniell, “Phytoremediation of Organomercurial Compounds via Chloroplast Genetic Engineering,” Plant Physiology, Vol. 132, No. 3, 2003, pp. 1344-1352. doi:10.1104/pp.103.020958
NOTES
*This paper is based on an unpublished doctoral dissertation: Phytoremediation Dynamic Model for Environmental Management.

