Advances in Linear Algebra & Matrix Theory
Vol.3 No.4(2013), Article ID:40927,4 pages DOI:10.4236/alamt.2013.34013
Commuting Outer Inverses
1Department of Mathematics, Faculty of Science, Kanagawa University, Kanagawa, Japan
2Department of Research and Graduate Studies, Linda Vista University, Pueblo Nuevo Solistahuacán, Mexico
Email: chiyom01@kanagawa-u.ac.jp, gkantun@ulv.edu.mx
Copyright © 2013 Muneo Chō, Gabriel Kantún-Montiel. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received November 12, 2013; revised December 9, 2013; accepted December 16, 2013
Keywords: Generalized Inverse; Koliha-Drazin Inverse; Outer Inverse
ABSTRACT
The group, Drazin and Koliha-Drazin inverses are particular classes of commuting outer inverses. In this note, we use the inverse along an element to study some spectral conditions related to these inverses in the case of bounded linear operators on a Banach space.
1. Introduction
Several of the useful properties of the group, Drazin and Koliha-Drazin inverses can be related to their spectral characterizations. Some of these can be traced to the property of being commuting outer inverses.
Let 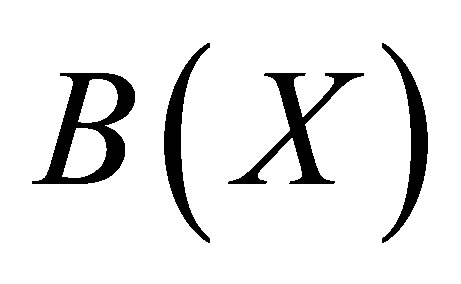 be the set of bounded linear operators on a Banach space
be the set of bounded linear operators on a Banach space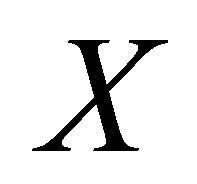 , and let
, and let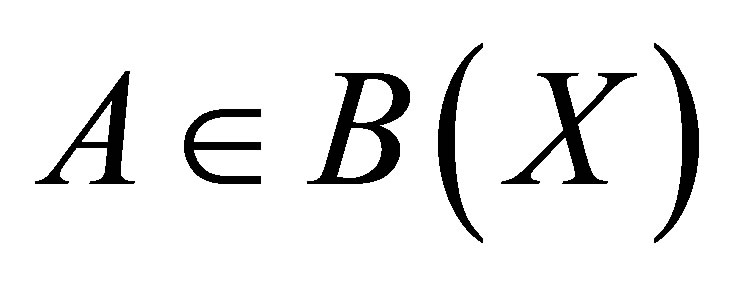 . We denote the range by
. We denote the range by  and the null space of
and the null space of  by
by .
.
Let 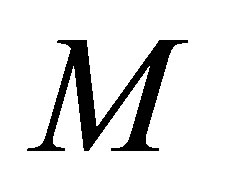 and
and 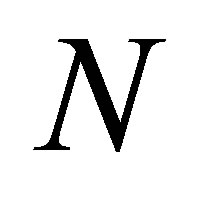 be closed subspaces of
be closed subspaces of . The outer inverse with prescribed range
. The outer inverse with prescribed range 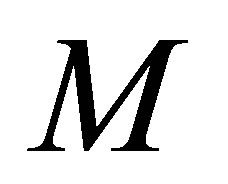 and null space
and null space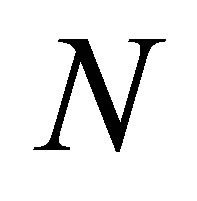 , denoted
, denoted 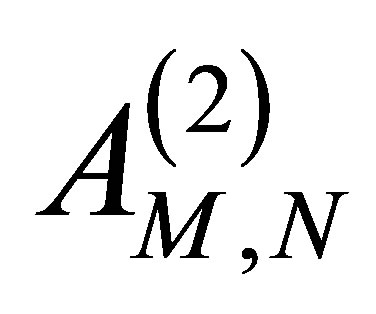 is the unique operator
is the unique operator  which satisfies:
which satisfies:
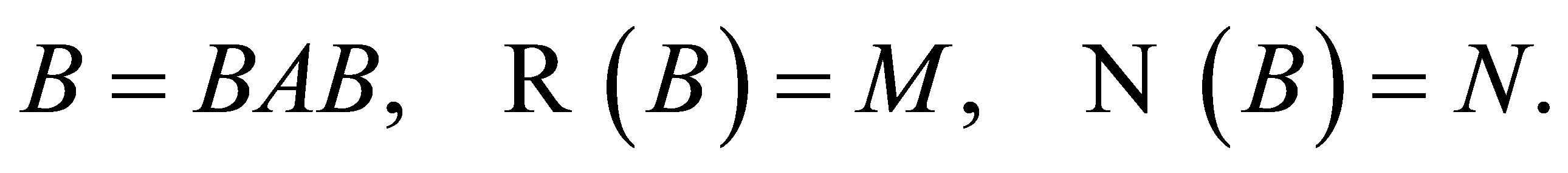
There is some advantage in prescribing the null space and range of an outer inverse by means of a third operator. In doing so, we will use the notion of invertibility along an element introduced by X. Mary ([1]). We say  is invertible along
is invertible along 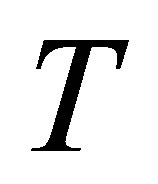 if there exists
if there exists 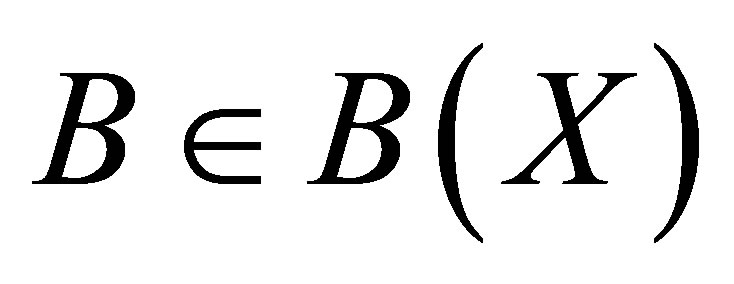 such that
such that

In this case, the inverse along 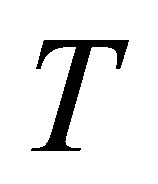 is unique and we write
is unique and we write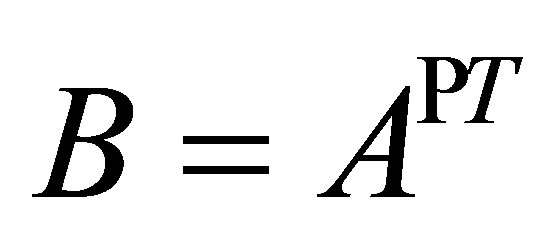 .
.
From 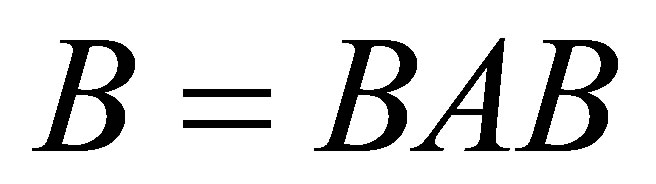 we have that BA and AB are projections such that
we have that BA and AB are projections such that 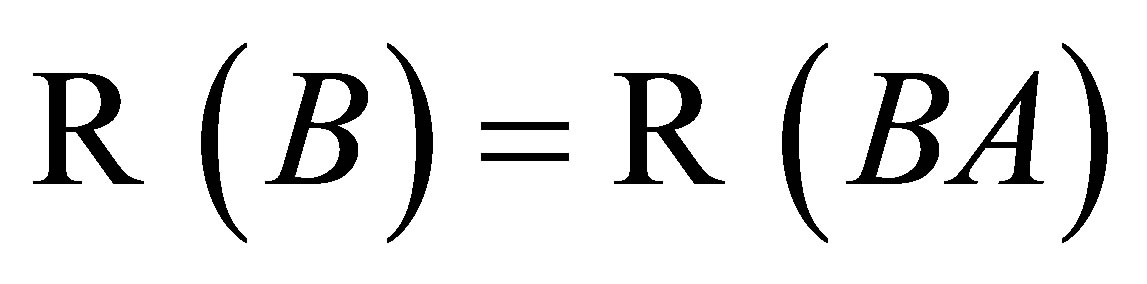 and
and 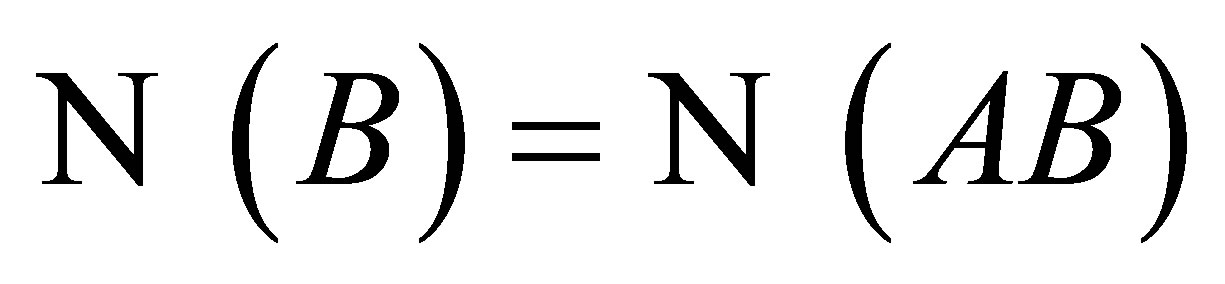 . Thus, we are effectively prescribing the range of the projection
. Thus, we are effectively prescribing the range of the projection 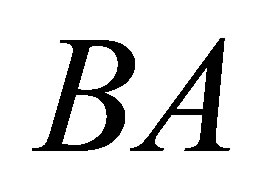 and the null space of the projection
and the null space of the projection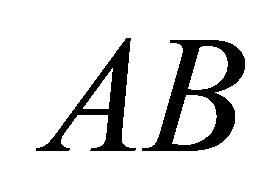 .
.
One of the useful properties of a generalized inverse is that, although the operator is not invertible, there is a subspace for which the reduction of the operator to that subspace is indeed invertible:
Theorem 1. ([2, Theorem 2]) Let 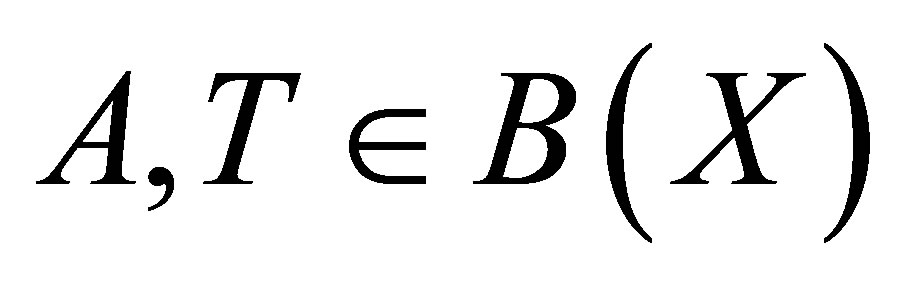 be nonzero operators. The following statements are equivalent.
be nonzero operators. The following statements are equivalent.
1.  is invertible along
is invertible along .
.
2. 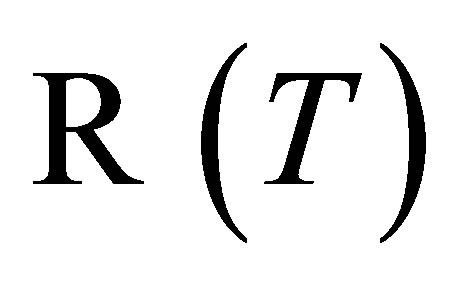 is a closed and complemented subspace of
is a closed and complemented subspace of ,
, 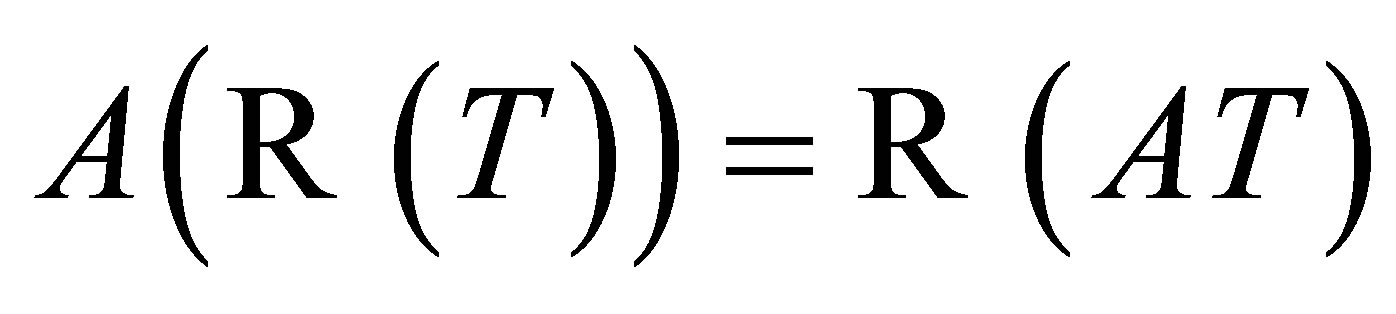 is closed such that
is closed such that  and the reduction
and the reduction 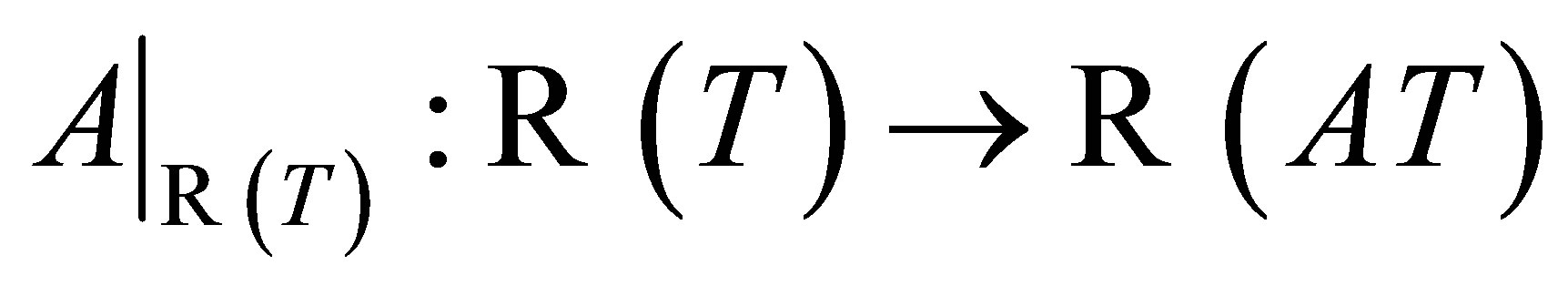 is invertible.
is invertible.
Recall an operator 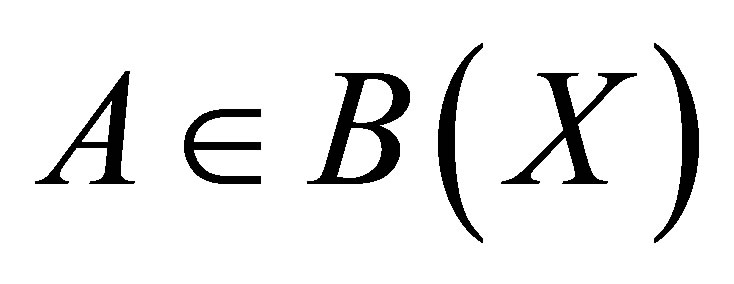 is said to be group invertible if there exists
is said to be group invertible if there exists 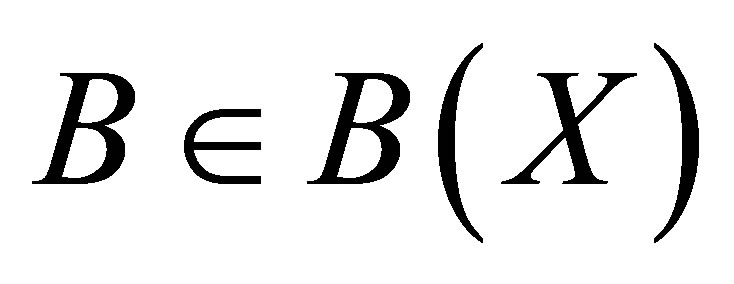 such that
such that
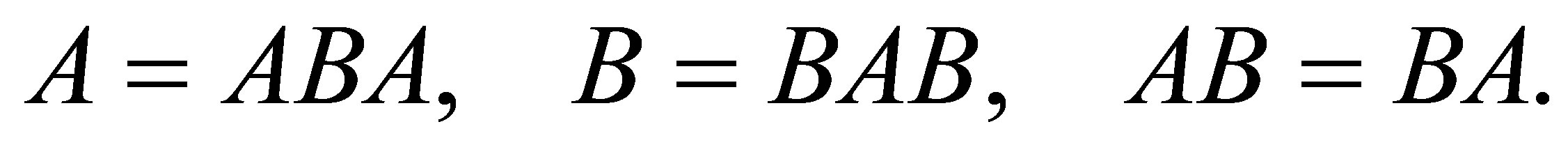
In this case, such 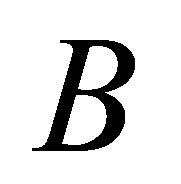 is unique and we write
is unique and we write 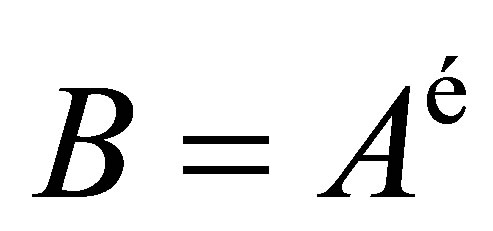 for the group inverse of
for the group inverse of .
.
Proposition 2. ([2, Theorem 3]) If  is invertible along
is invertible along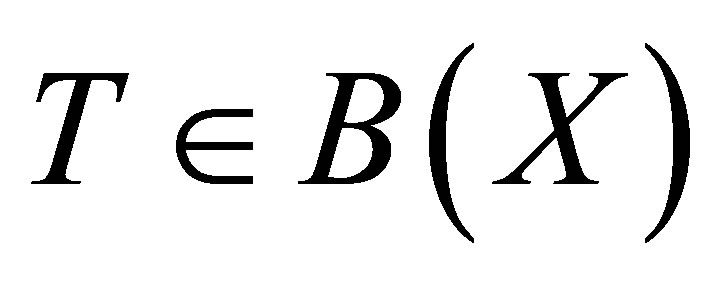 , then AT and TA are group invertible and
, then AT and TA are group invertible and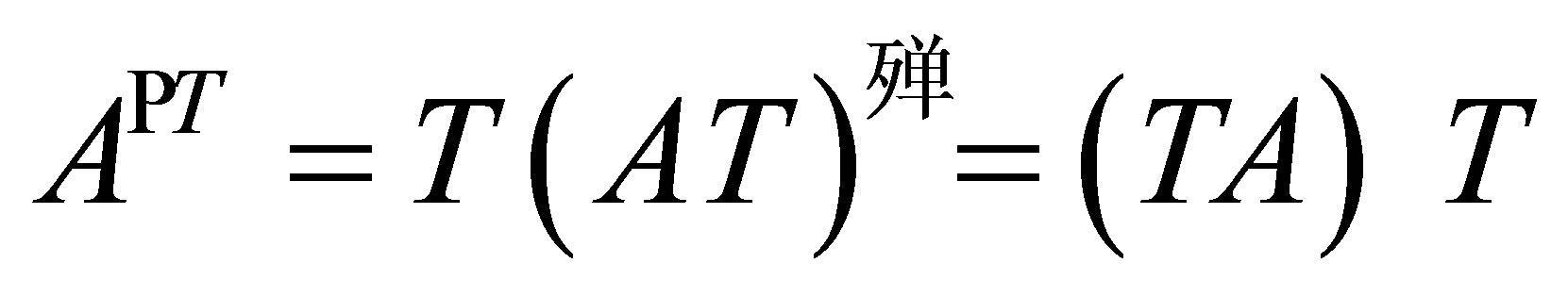 .
.
Example 3. Let  the space of square-summable sequences. Let
the space of square-summable sequences. Let 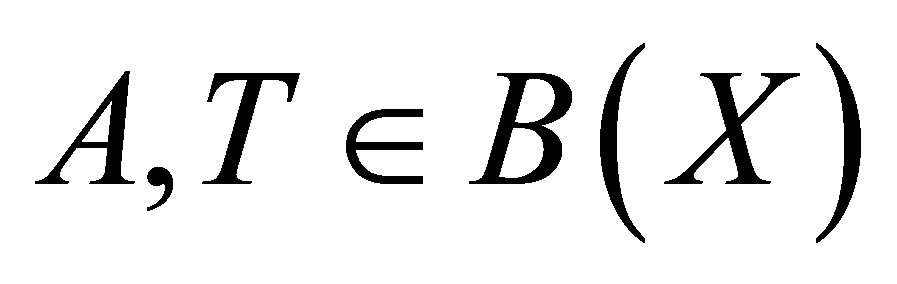 be defined by
be defined by  and
and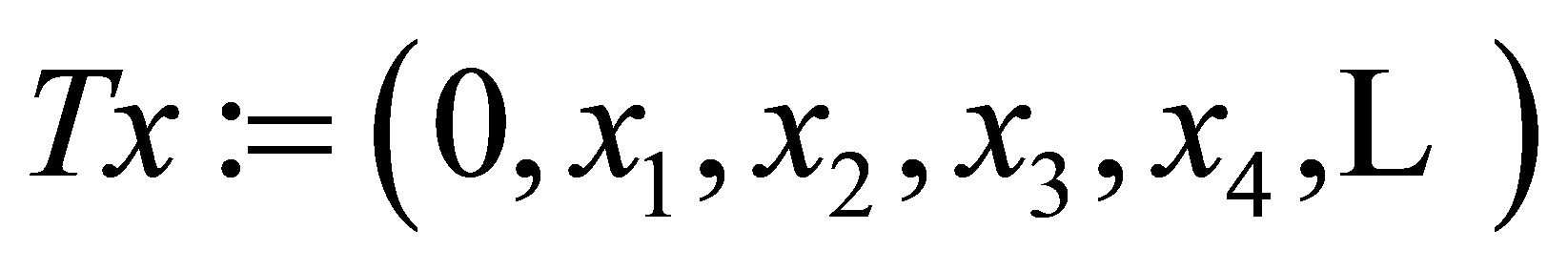 .
.
Then  is invertible along
is invertible along 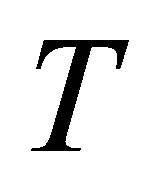 with
with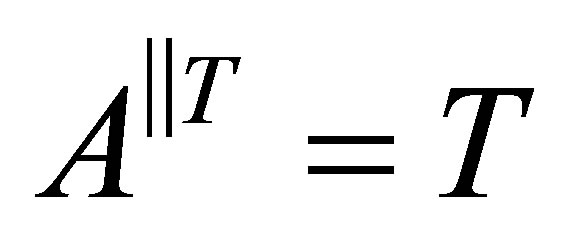 .
.
In the following section, we study an operator  such that
such that  is invertible along
is invertible along 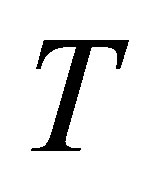 with
with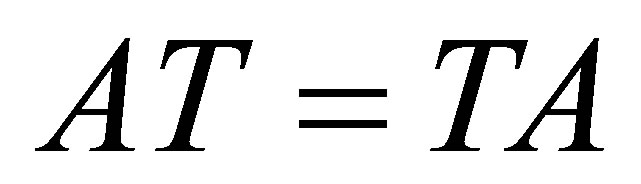 . Then, in Section 3 we study some projections related to the outer inverse with prescribed range and null space. Finally, in Section 4 we specialize to spectral projections, covering results from Dajić and Koliha ([3]).
. Then, in Section 3 we study some projections related to the outer inverse with prescribed range and null space. Finally, in Section 4 we specialize to spectral projections, covering results from Dajić and Koliha ([3]).
2. Invertibility along a Commuting Operator
Proposition 4. Let  be invertible along
be invertible along . If
. If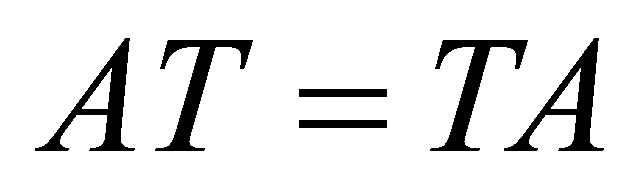 , then
, then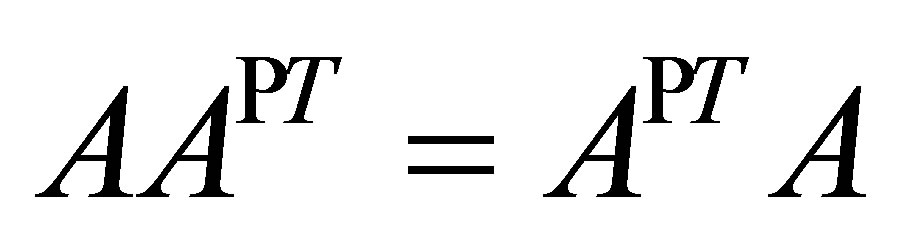 .
.
Proof. From Proposition 2 we have:

If  is invertible along
is invertible along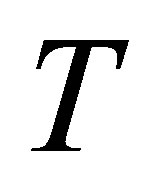 , then we have the following matrix form ([2]):
, then we have the following matrix form ([2]):

where 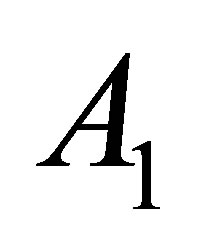 is invertible and
is invertible and 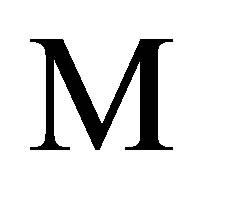 is a complement of
is a complement of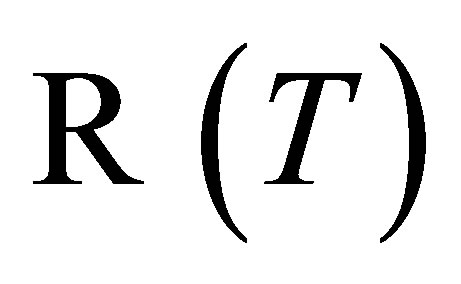 , that is,
, that is,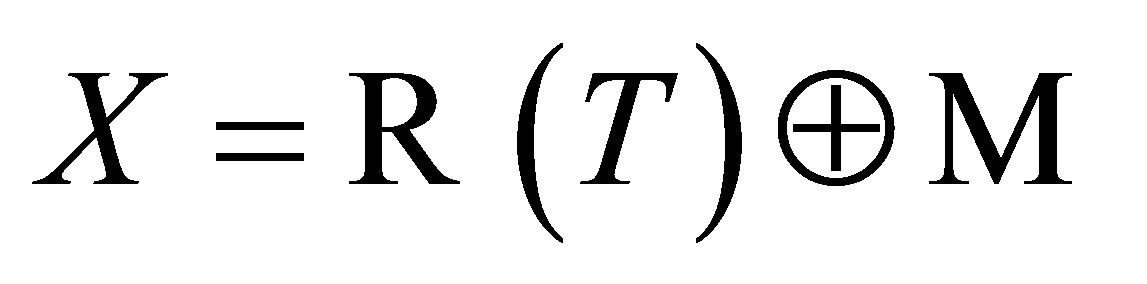 .
.
When  and
and 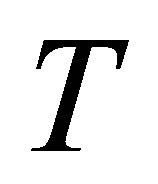 commute, we can say a little more:
commute, we can say a little more:
Theorem 5. Let  be invertible along
be invertible along  and
and . Then there exist an invertible operator
. Then there exist an invertible operator 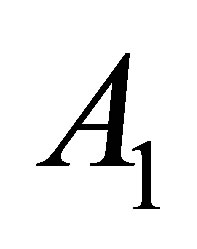 on
on  and an operator
and an operator 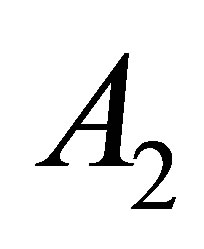 on
on 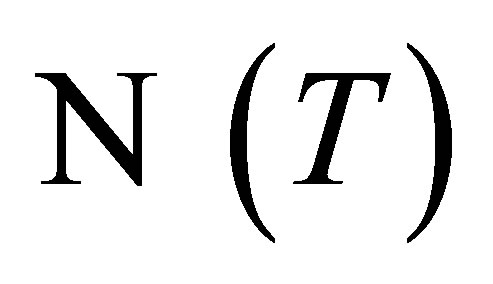 such that
such that
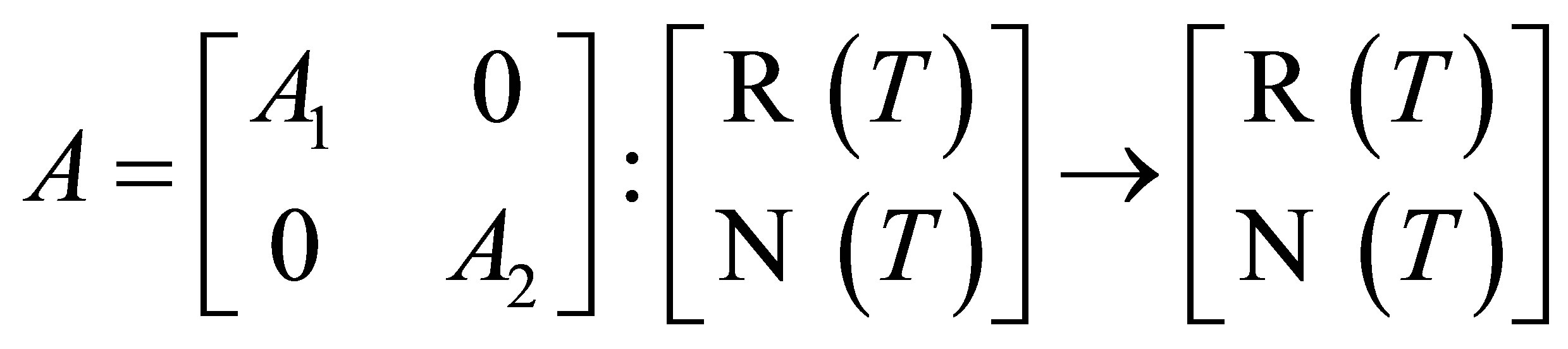
and 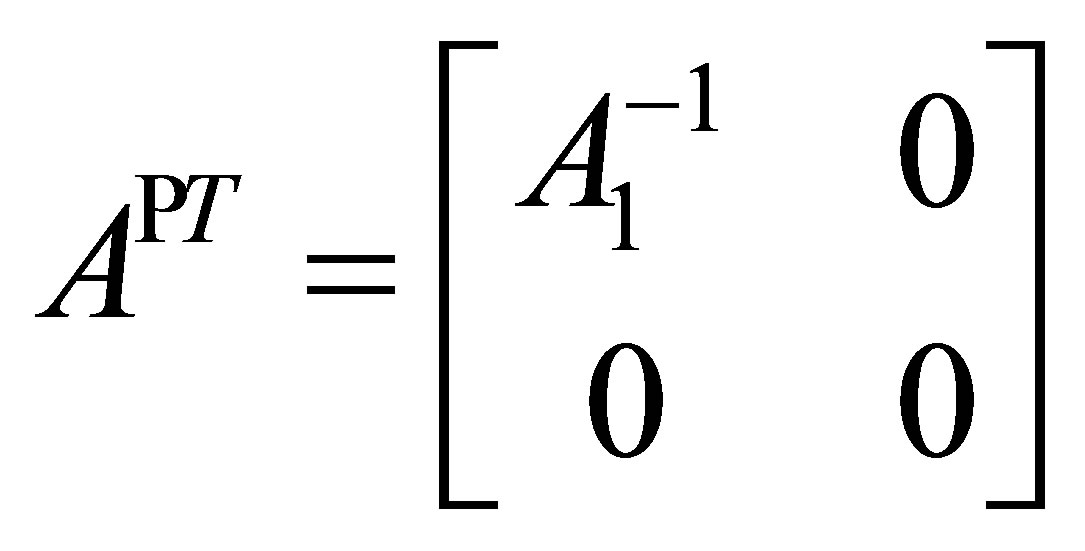
Proof. Suppose  is invertible along
is invertible along 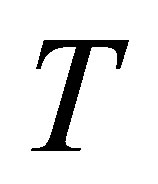 and
and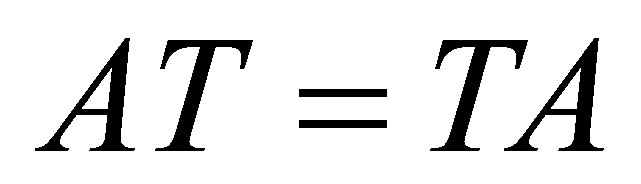 . Then by Proposition 4
. Then by Proposition 4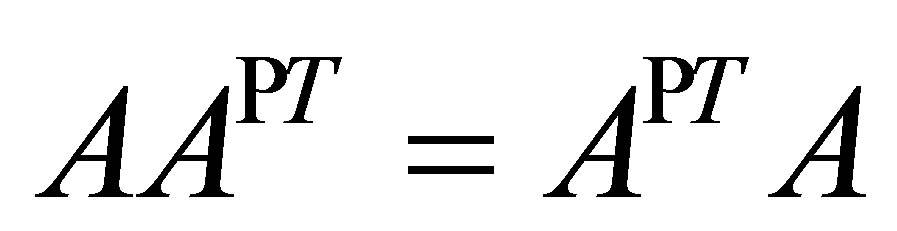 . Thus, since
. Thus, since 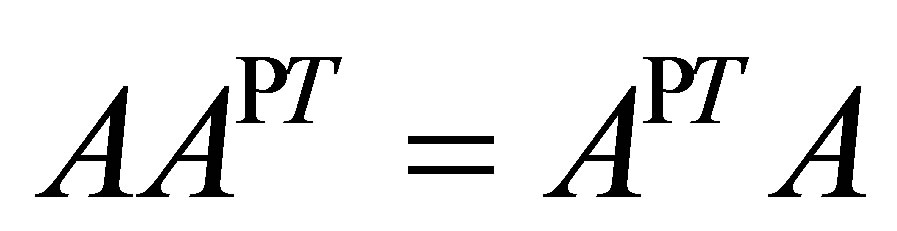 is a projection, we have that
is a projection, we have that
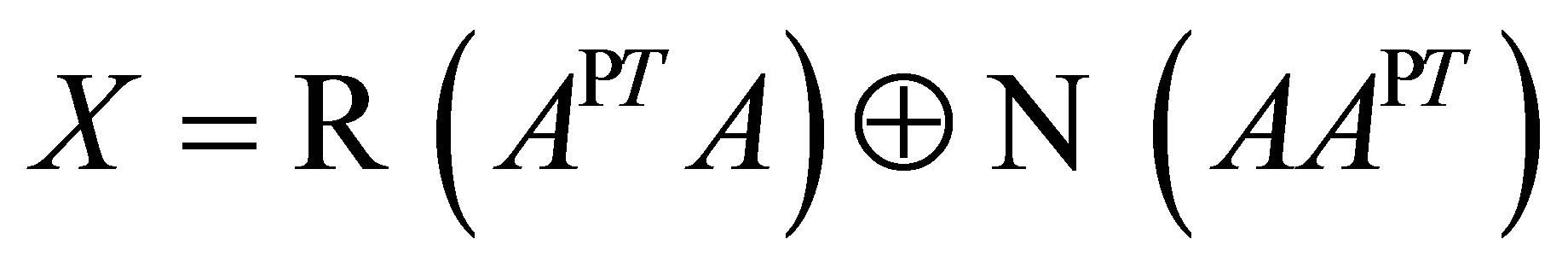 .
.
Since

and
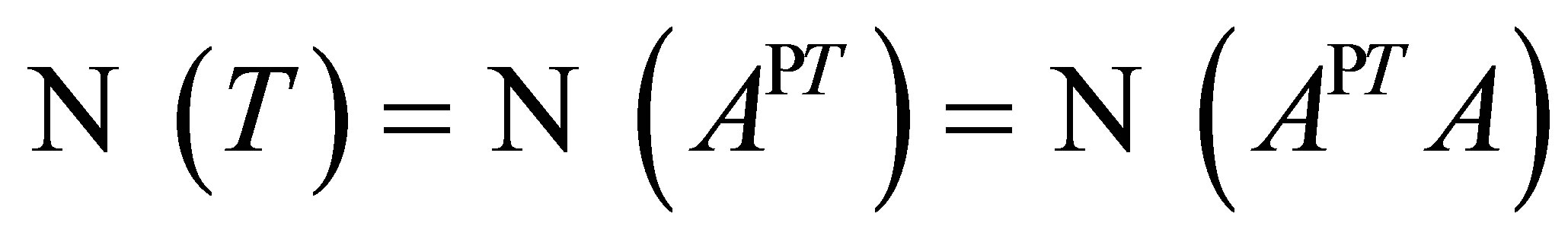
we also have
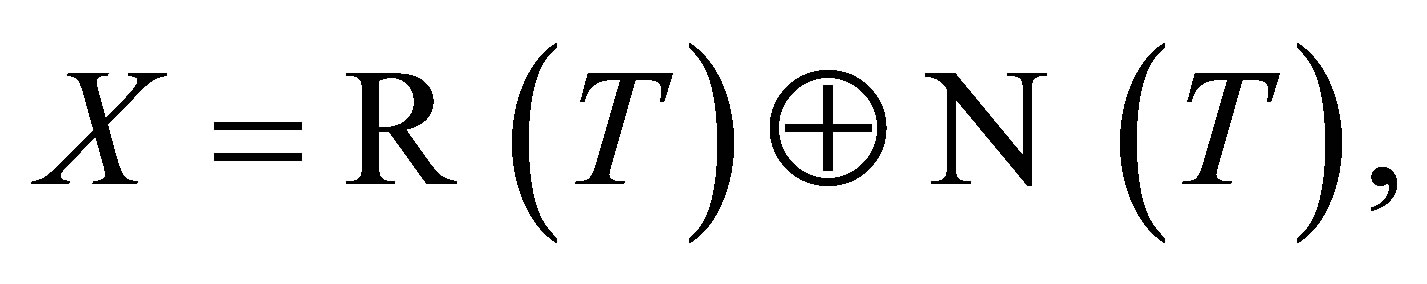
and hence we can consider the following matrix decomposition of :
:
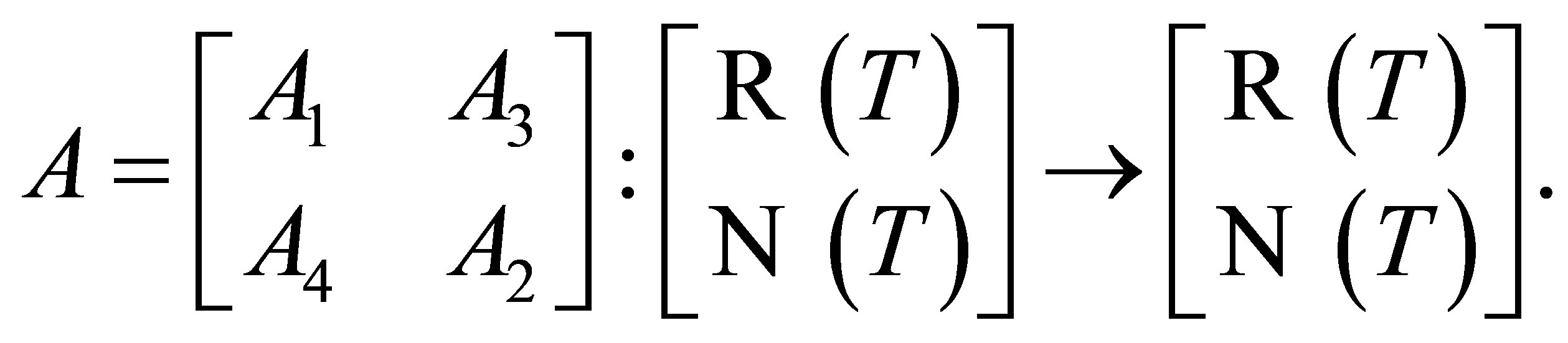
In this case,  ,
, 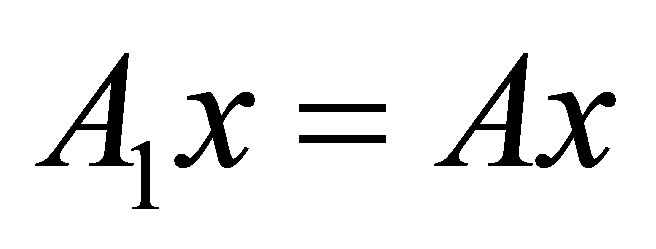 , is invertible. Indeed, to see that it is onto note that since
, is invertible. Indeed, to see that it is onto note that since  and
and
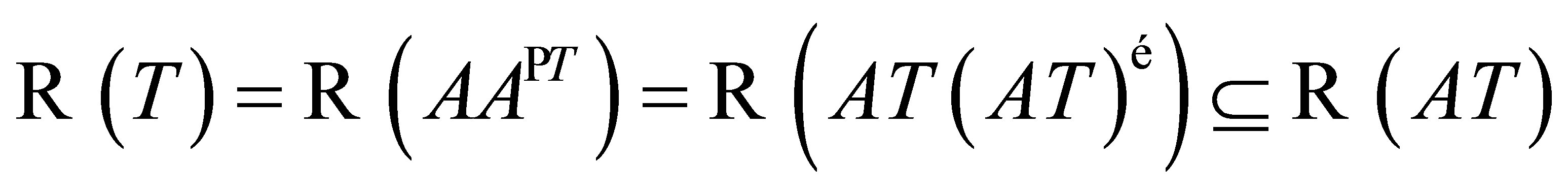 , we have
, we have 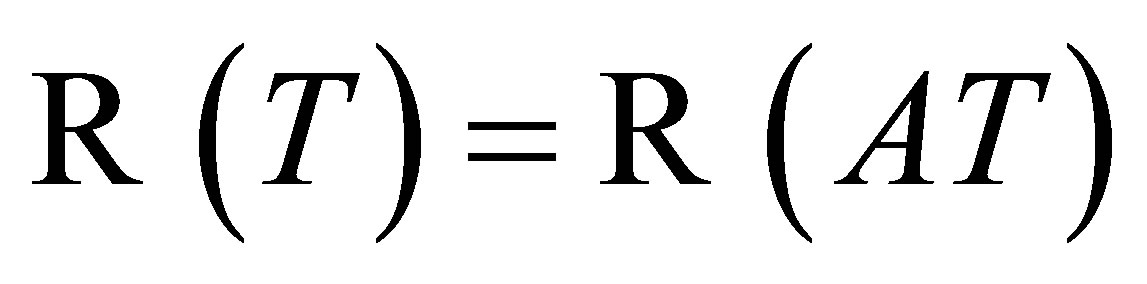 and hence
and hence 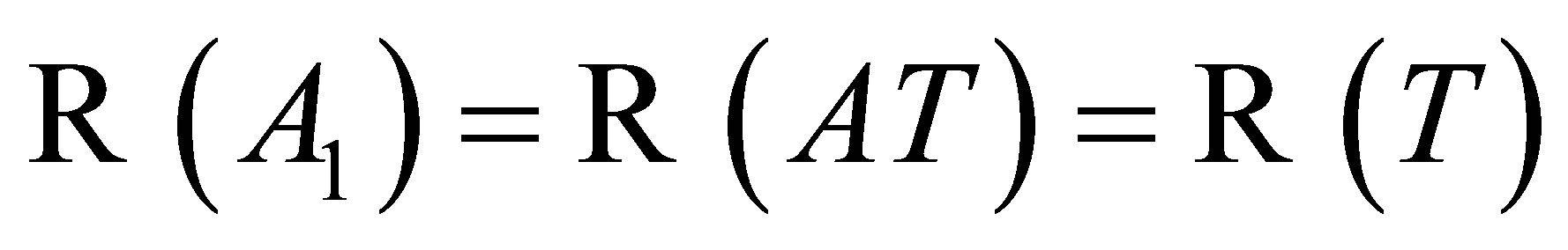 . To see that it is also 1-1, let
. To see that it is also 1-1, let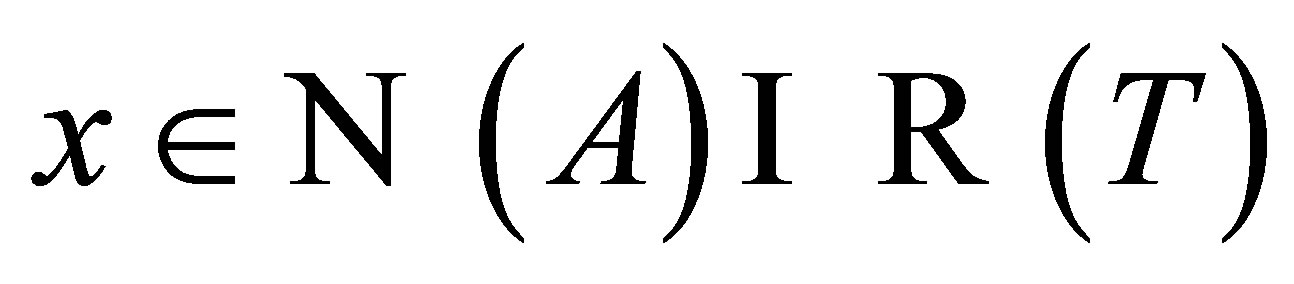 . Since
. Since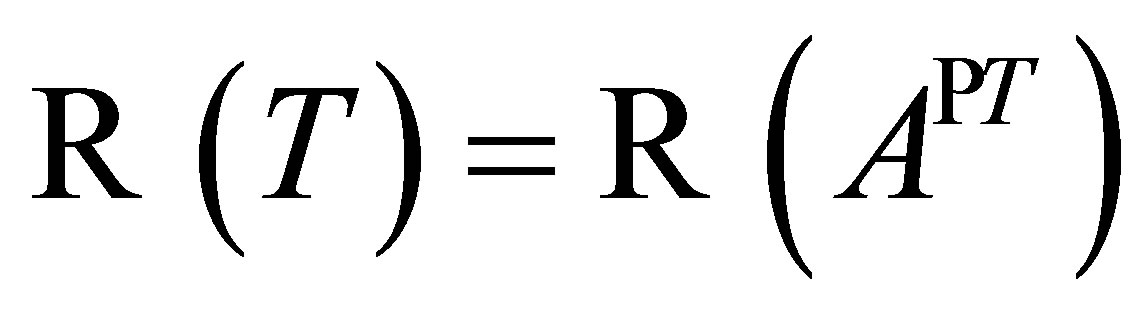 , there exists
, there exists 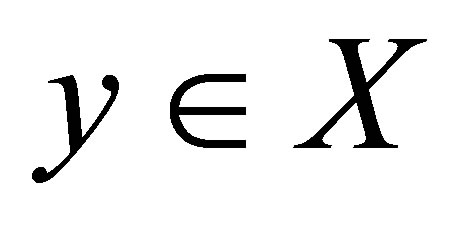 such that
such that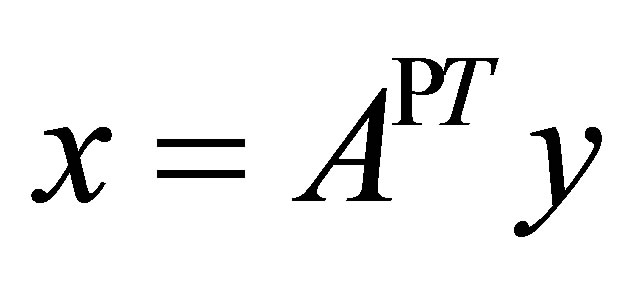 . Then,
. Then, 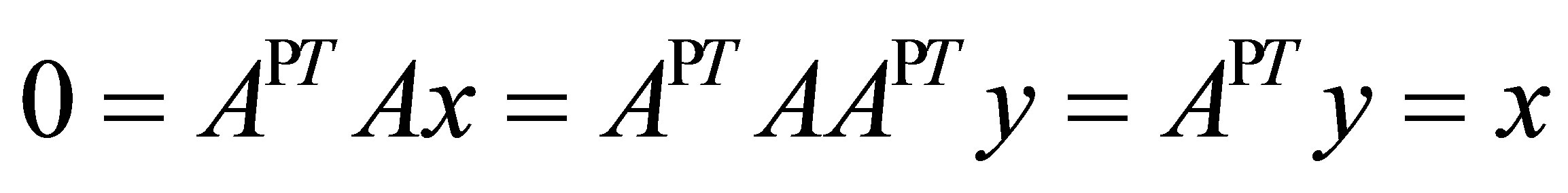 .
.
Moreover, since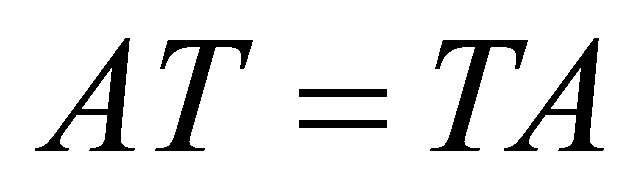 , subspaces
, subspaces 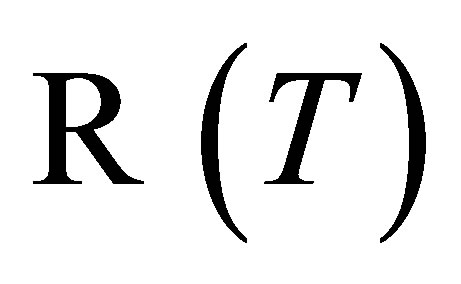 and
and 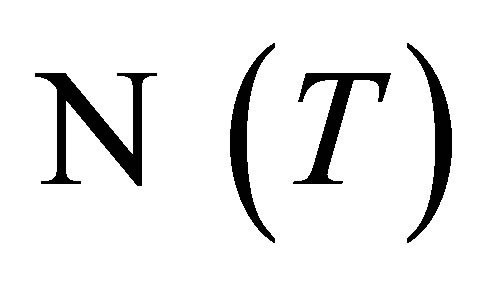 are
are  -invariant and
-invariant and  maps
maps  onto
onto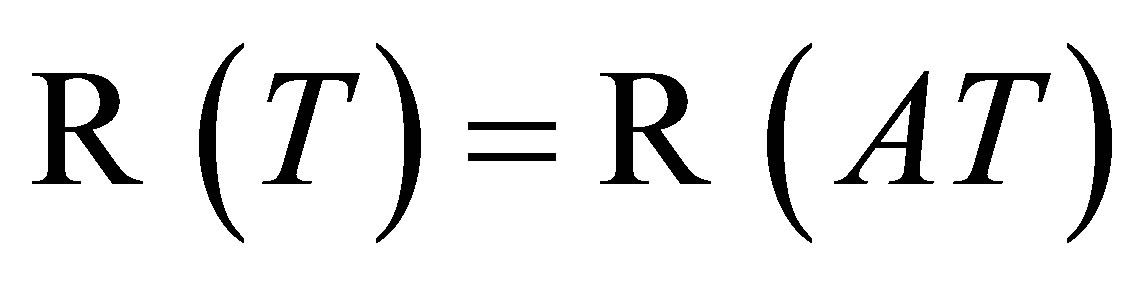 , we get
, we get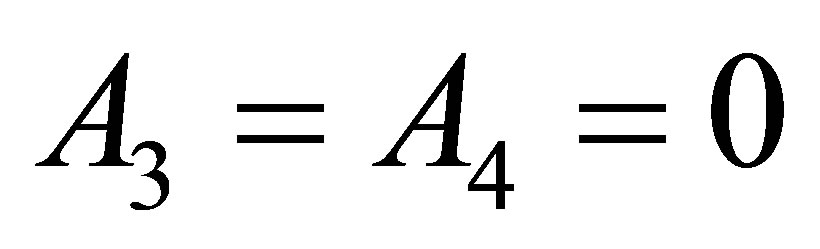 . Thus,
. Thus,
 and clearly
and clearly 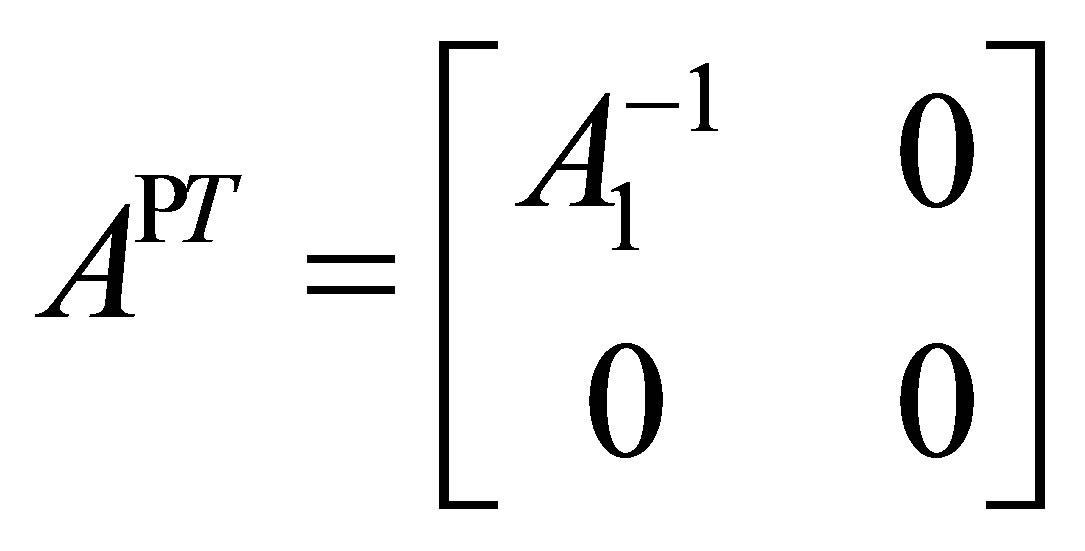 .
.
Example 6. Let 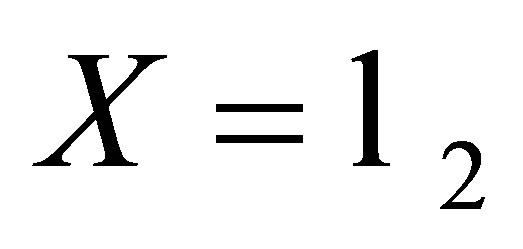 the space of square-summable sequences. Let
the space of square-summable sequences. Let 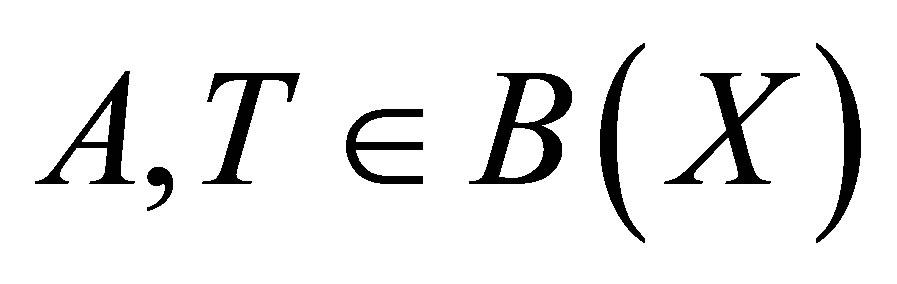 be defined by
be defined by
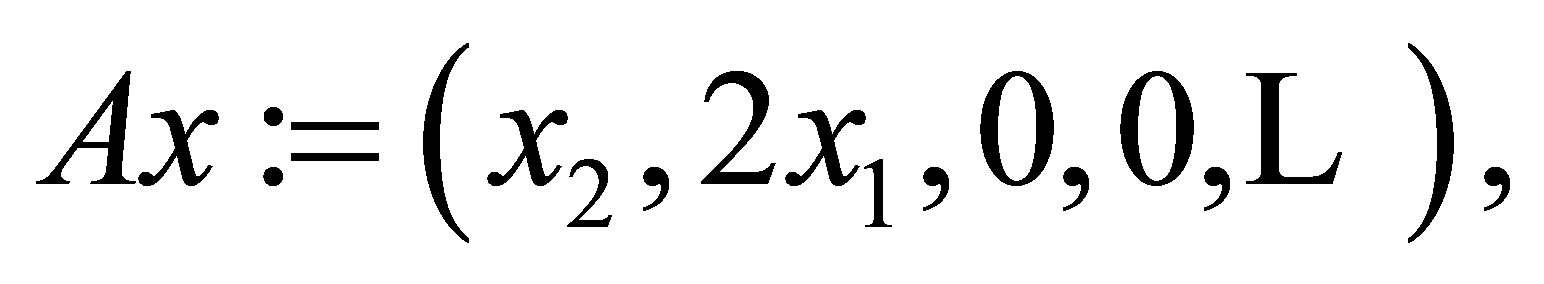

Then it is easy to verify that  is the operator such that
is the operator such that
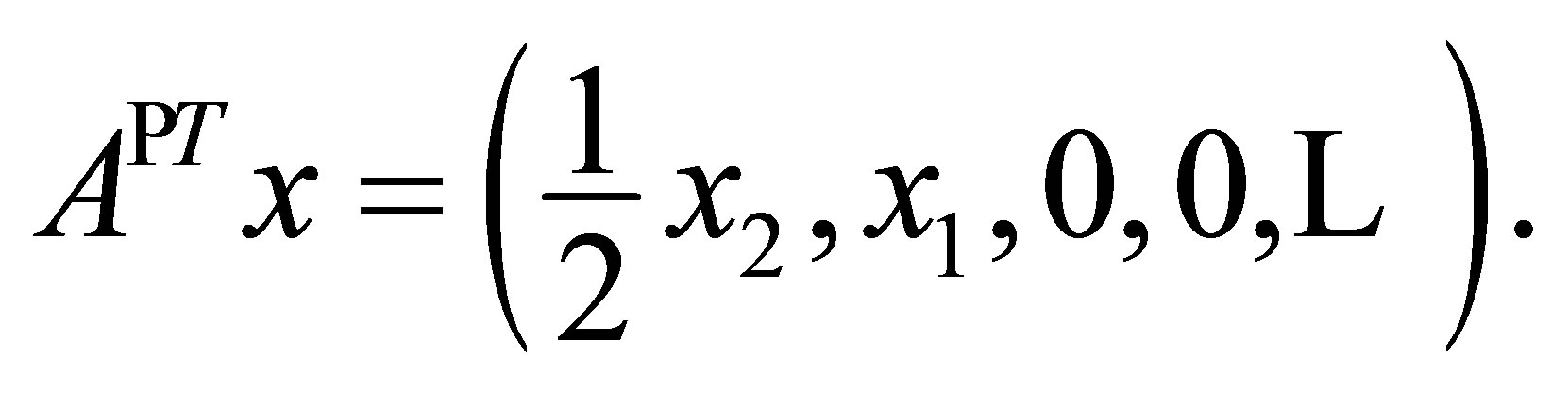
It is clear that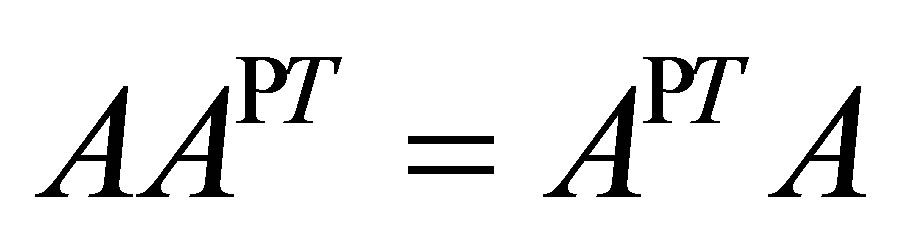 , but we have
, but we have
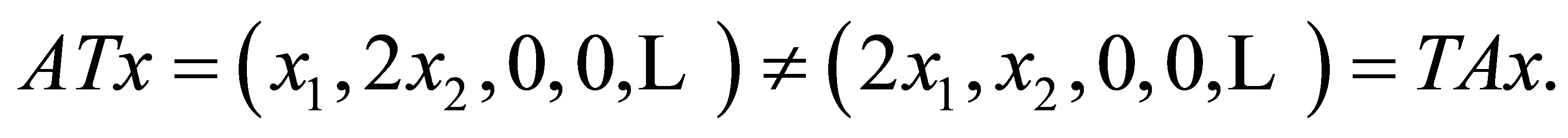
3. Projections
Commuting outer inverses are naturally linked to projections.
Proposition 7. Let . If
. If  is invertible along
is invertible along 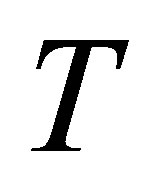 and
and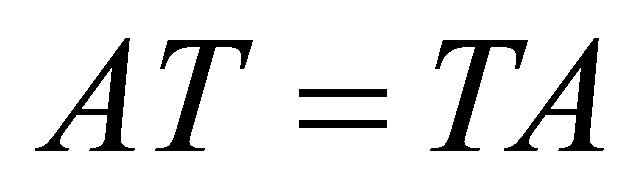 , then there exists a bounded projection
, then there exists a bounded projection 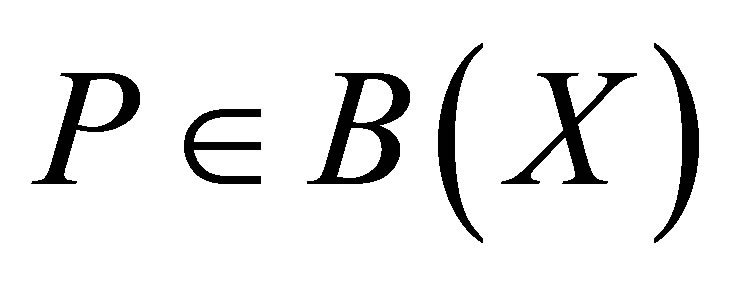 such that
such that  is invertible along
is invertible along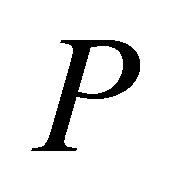 .
.
Proof. From Theorem 5 we have that if  is invertible along
is invertible along 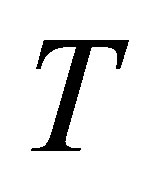 and
and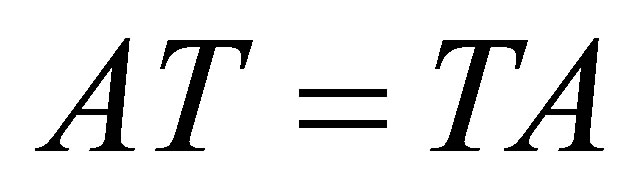 , then
, then
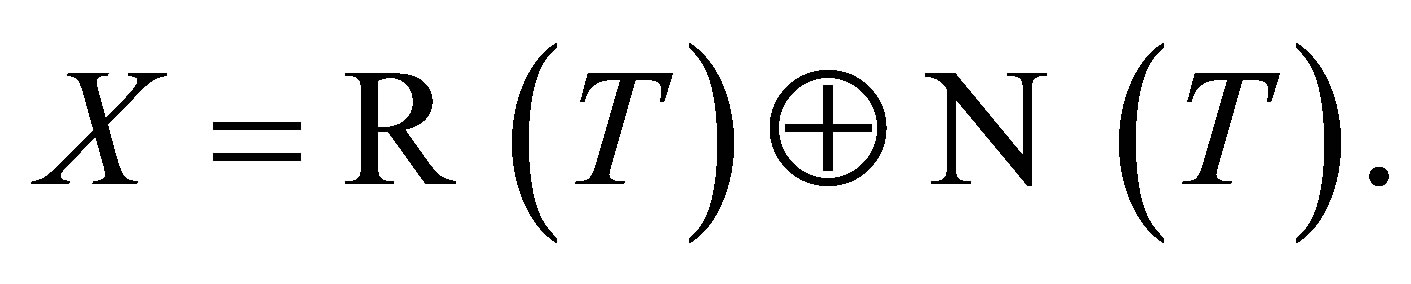
Thus, there exists a bounded projection  such that
such that  and
and . Hence,
. Hence,  is invertible along
is invertible along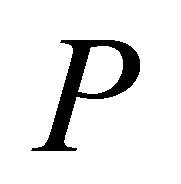 .
.
For a sort of converse, we give a necessary condition in Theorem 9.
Example 8. An operator  and a projection
and a projection 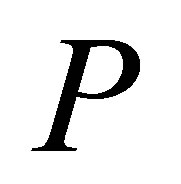 such that
such that  is invertible along
is invertible along  and
and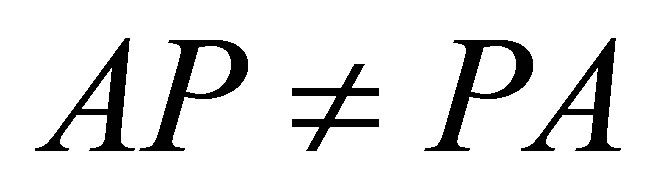 .
.
Let 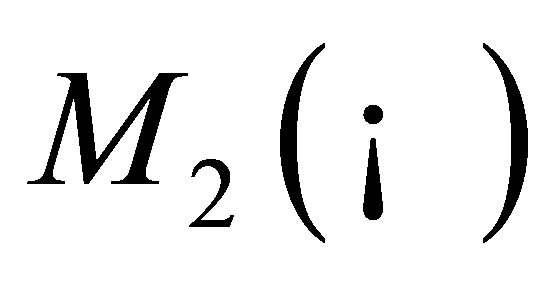 be the set of two by two matrices with real entries. Let
be the set of two by two matrices with real entries. Let 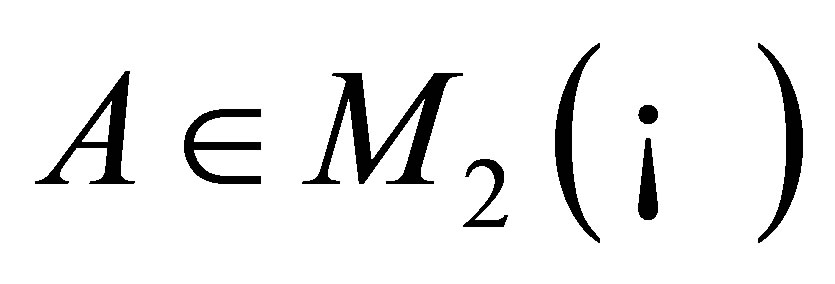 be the (rotation) matrix defined by
be the (rotation) matrix defined by
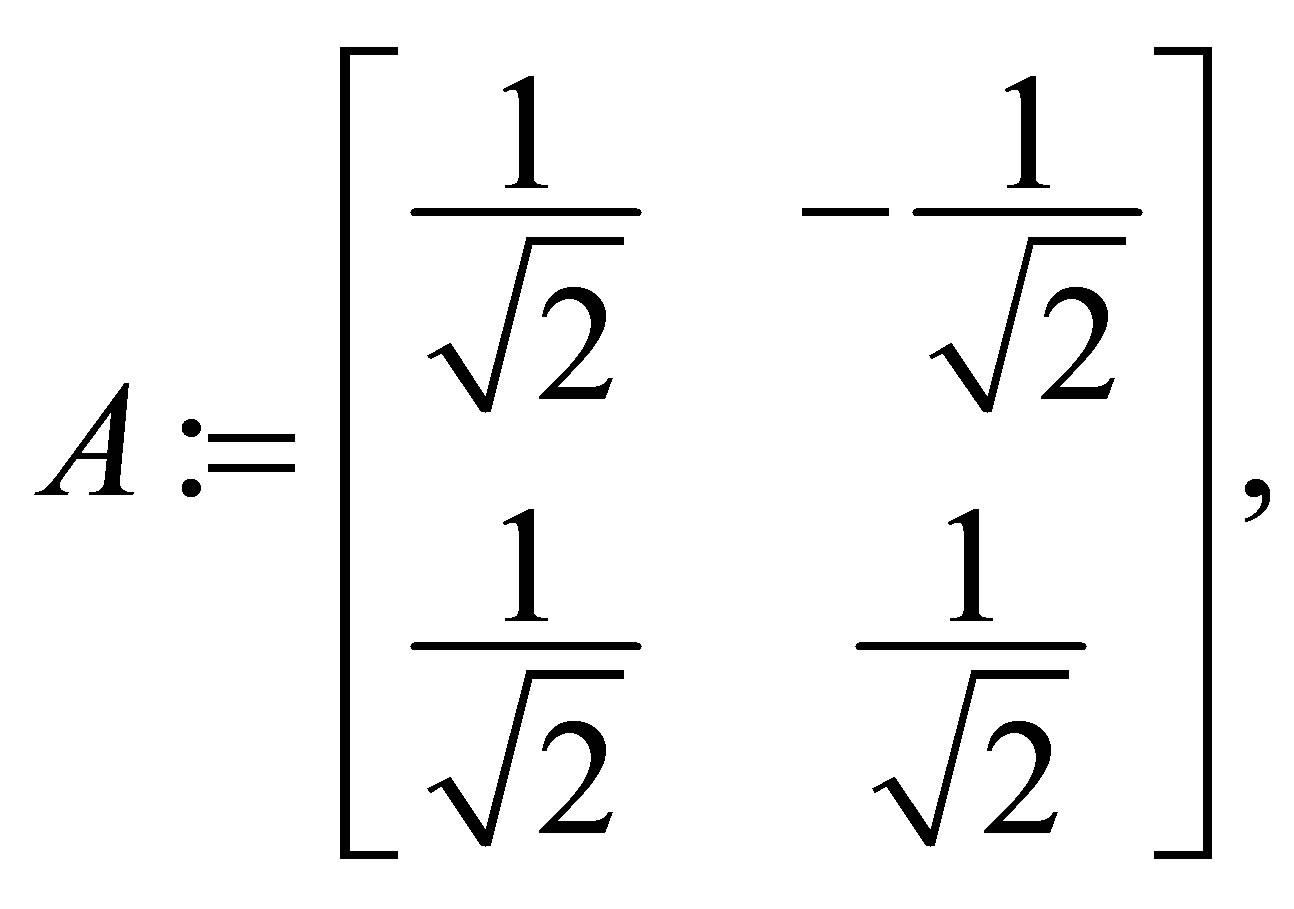
and let 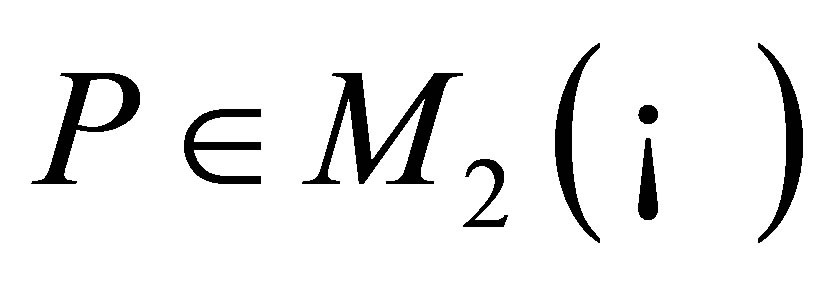 be the projection defined by
be the projection defined by
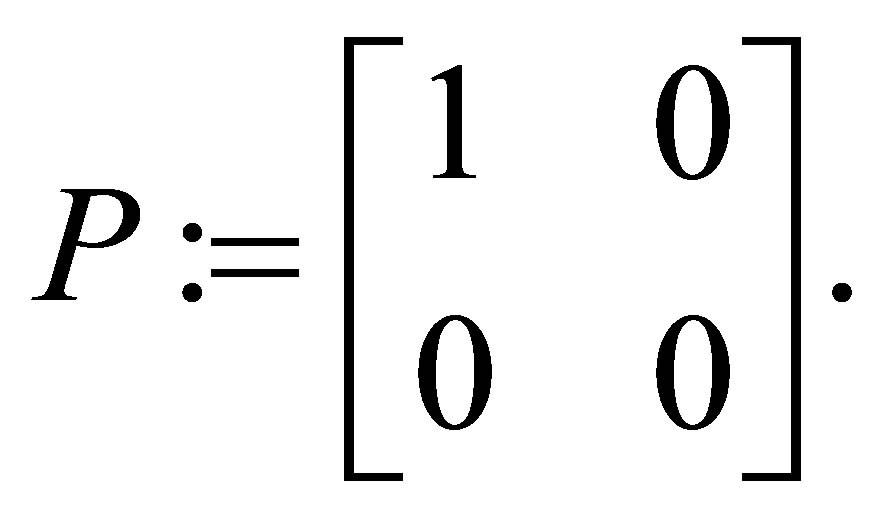
Then, it is easy to check that 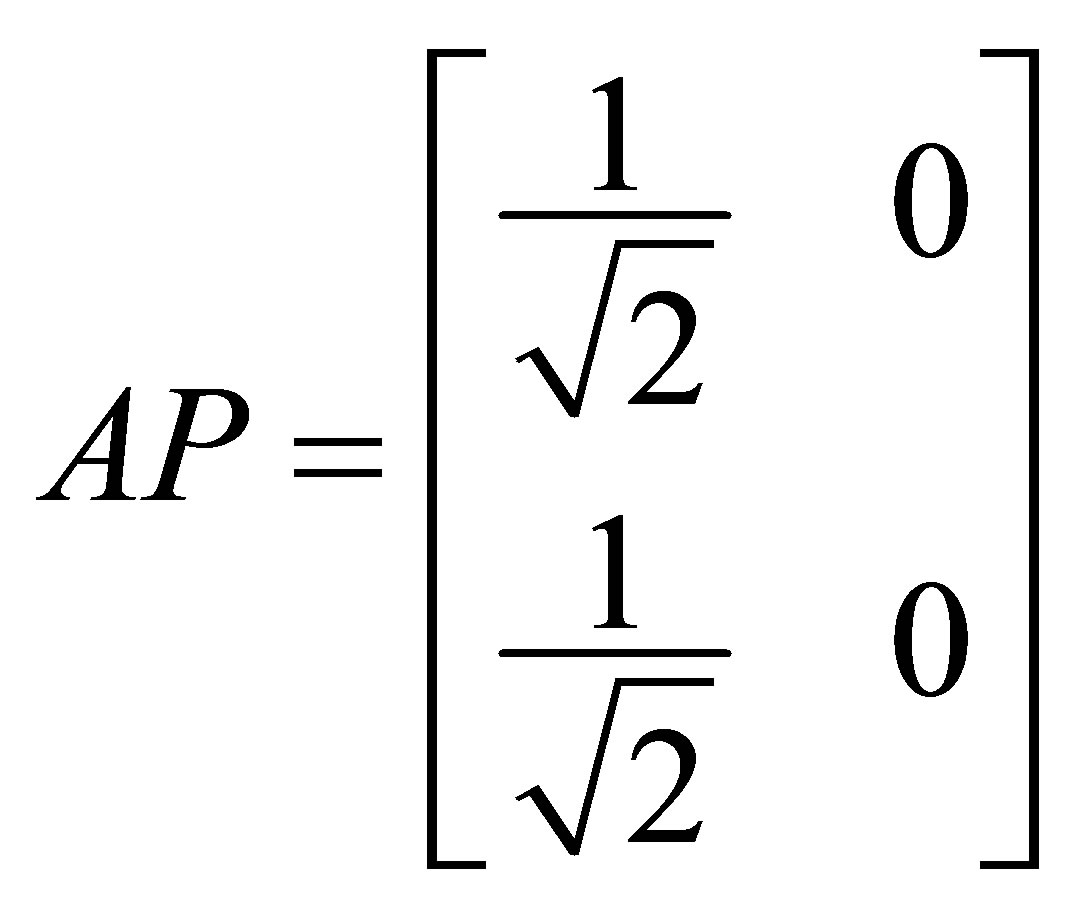 is group invertible, with group inverse
is group invertible, with group inverse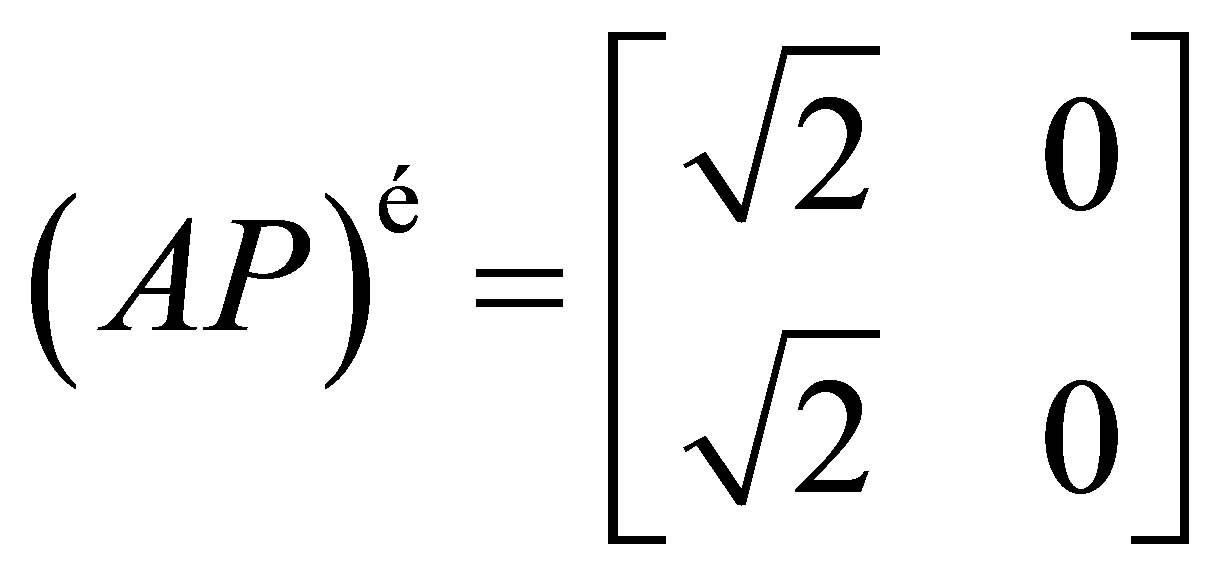 .
.
We have
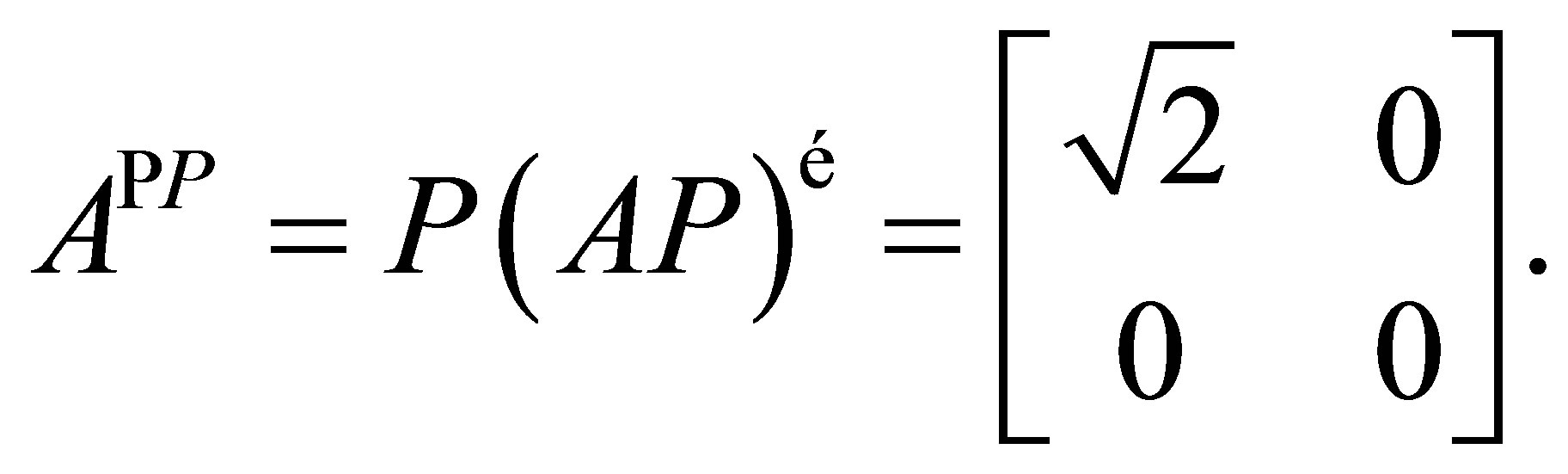
Thus,  is invertible along
is invertible along 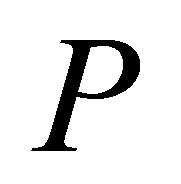 but since
but since
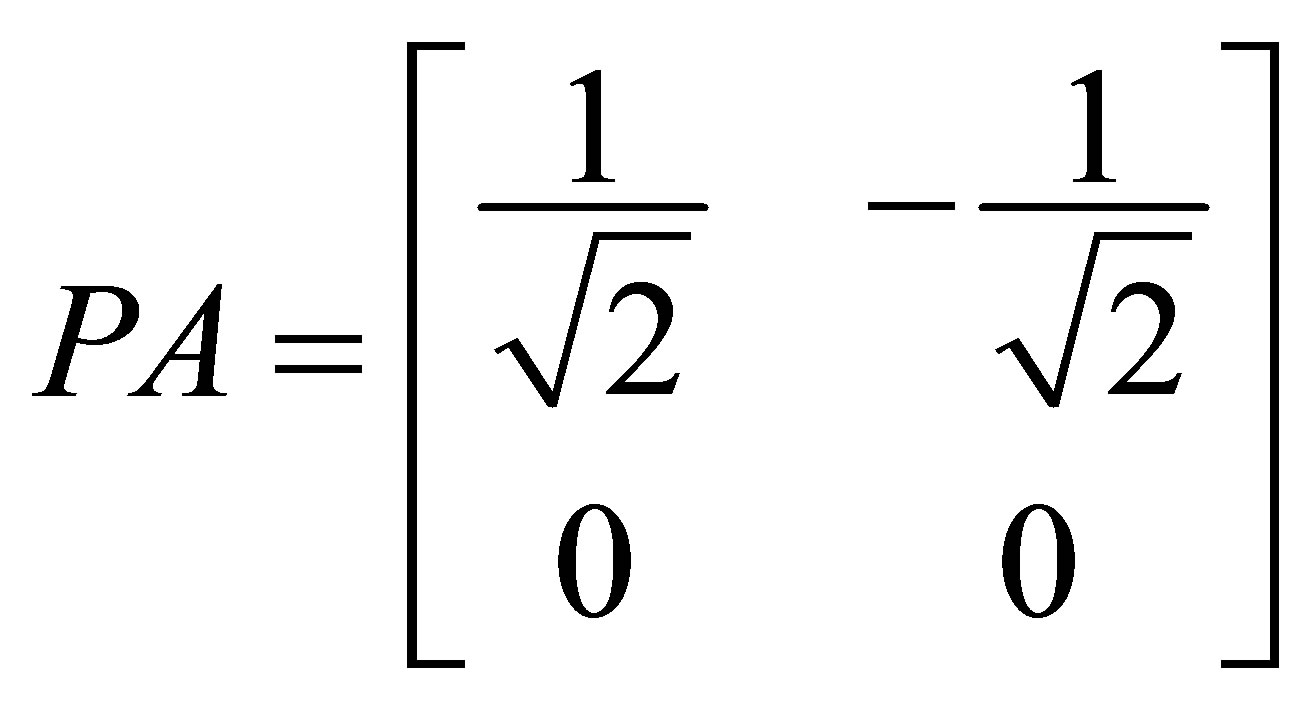 , we see
, we see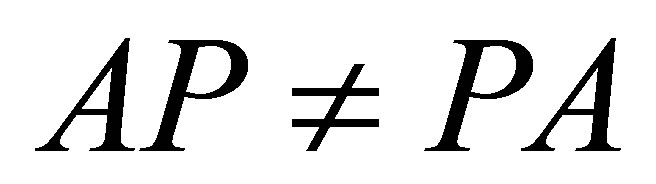 . Notice that
. Notice that
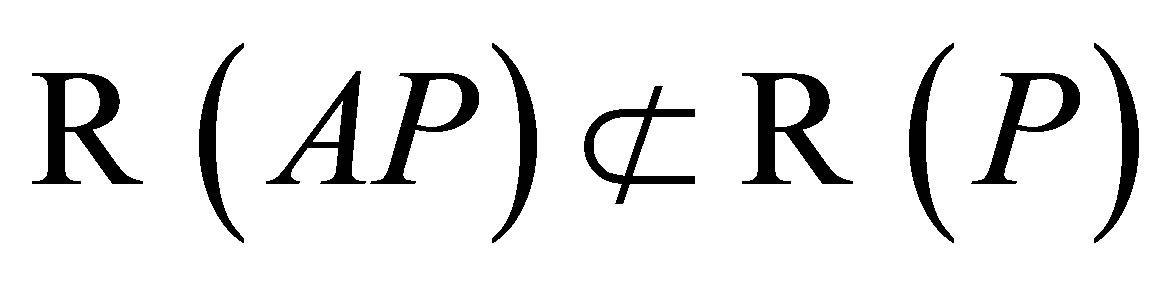 .
.
Theorem 9. Let  be a projection and suppose
be a projection and suppose 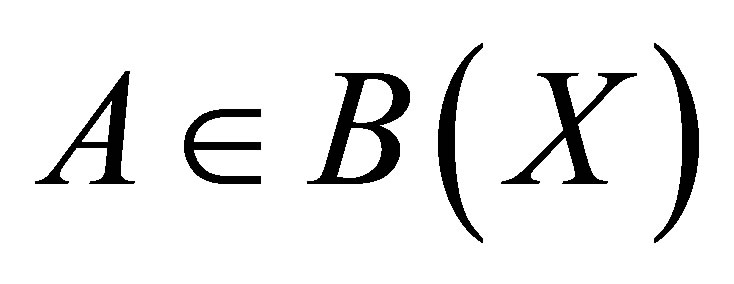 is invertible along
is invertible along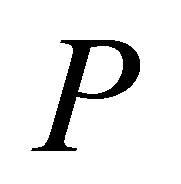 . If
. If 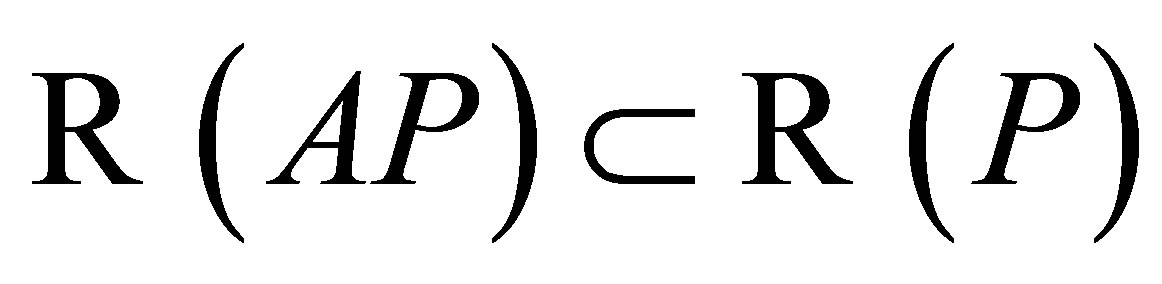 , then
, then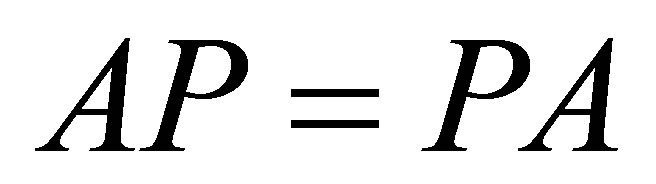 .
.
Proof. Since 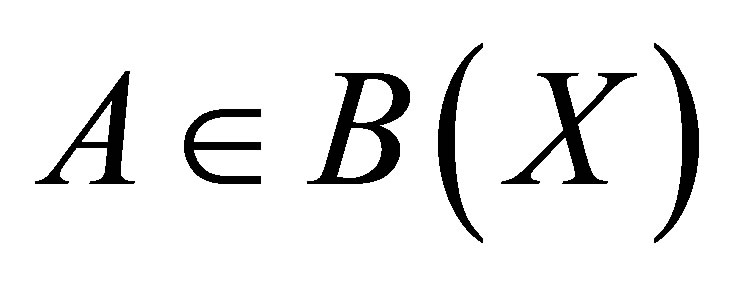 is invertible along
is invertible along ,
,  has the following matrix form [2, Corollary 1]:
has the following matrix form [2, Corollary 1]:
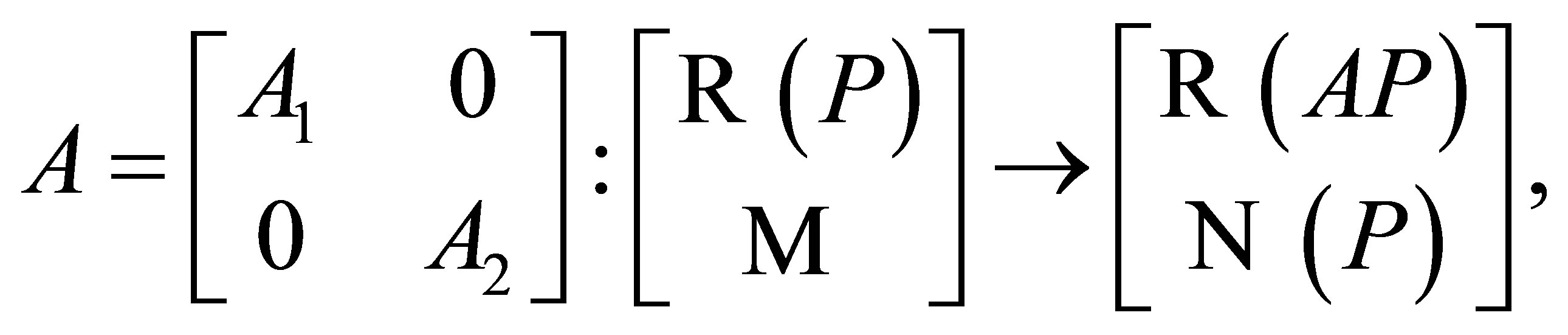
where 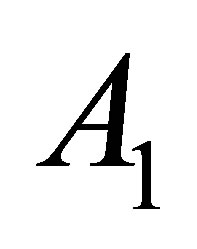 is invertible and
is invertible and 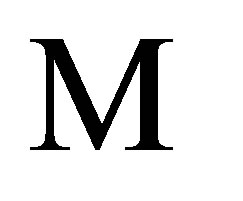 is the complement of
is the complement of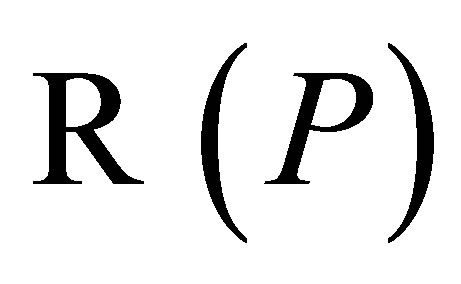 , that is,
, that is,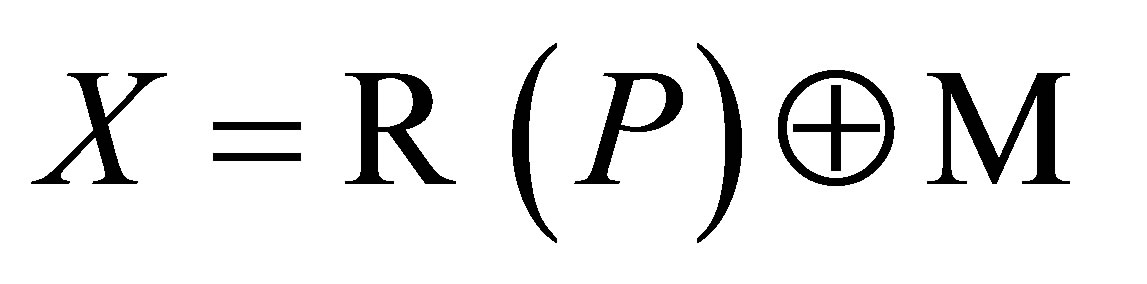 .
.
Since 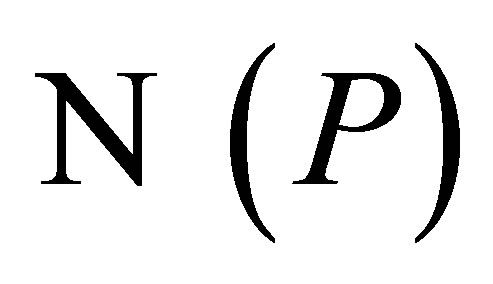 is a complement for
is a complement for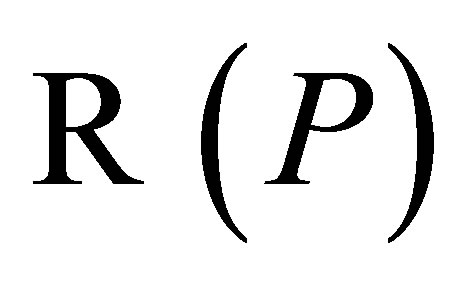 , we can take
, we can take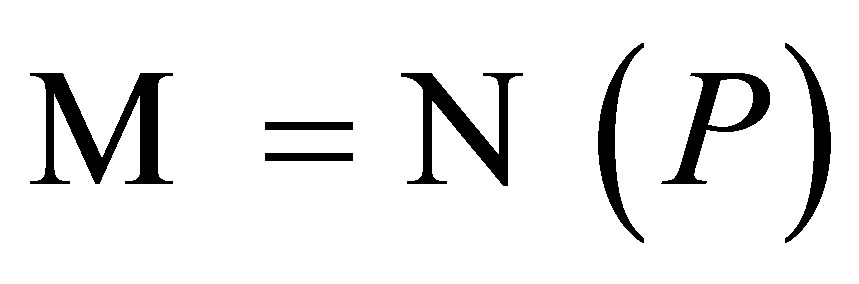 . Then, we have
. Then, we have
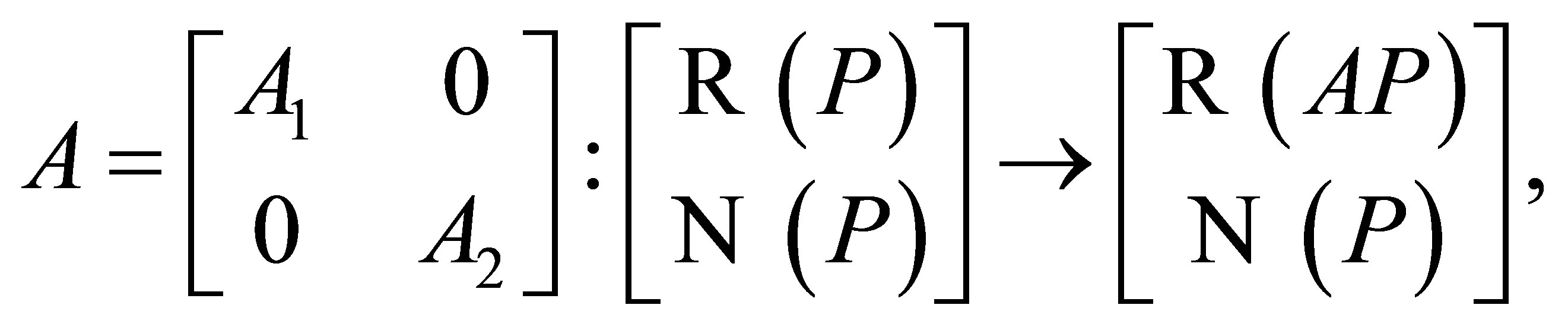
Now, suppose . From Theorem 1 we know that
. From Theorem 1 we know that 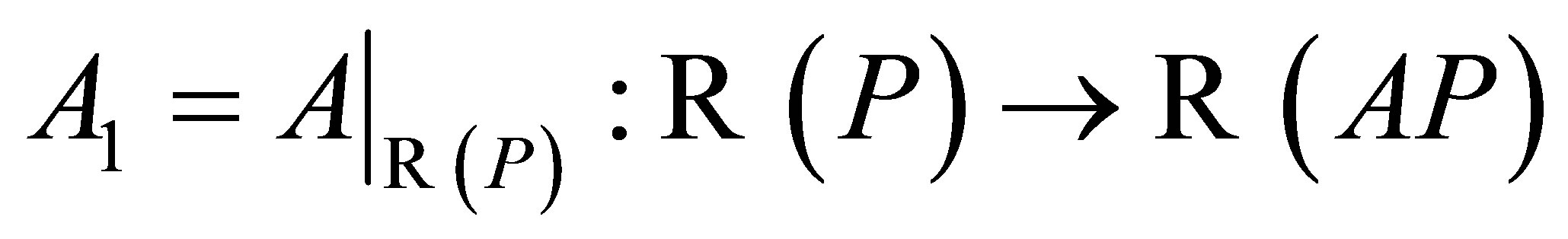 is invertiblewhich implies
is invertiblewhich implies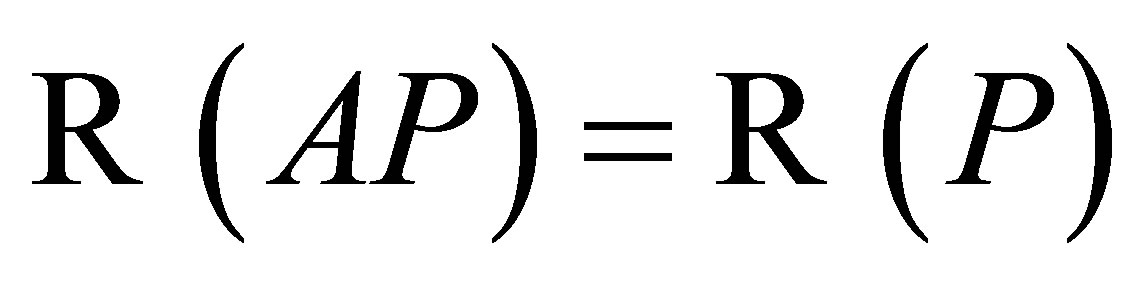 . Thus,
. Thus,
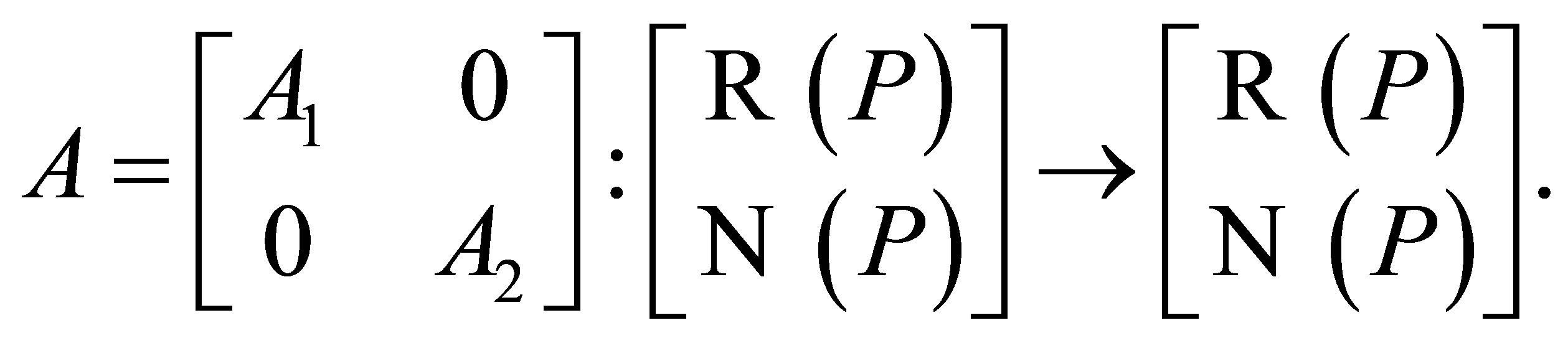
It follows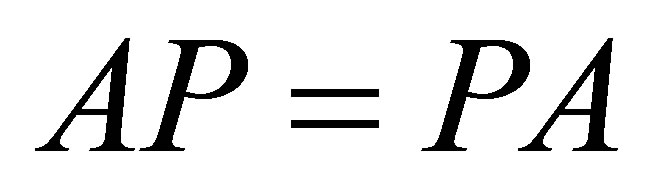 .
.
Note that the theorem above together with Proposition 4 implies that if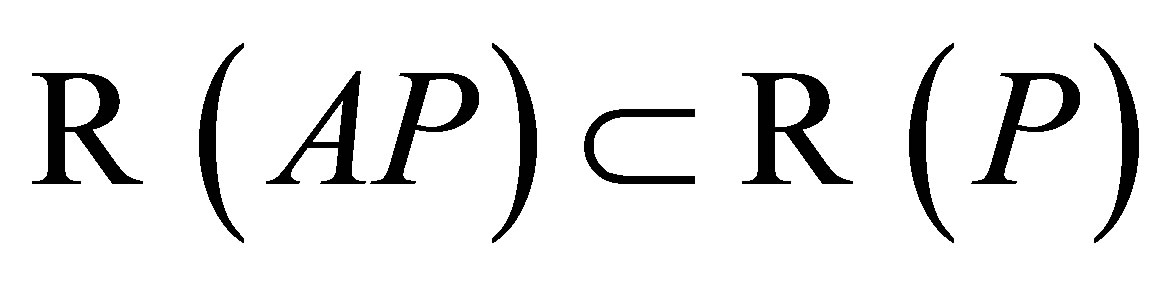 , then
, then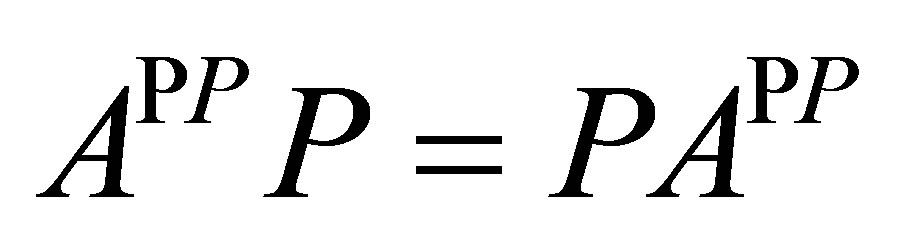 . However, we can prove:
. However, we can prove:
Proposition 10. Let 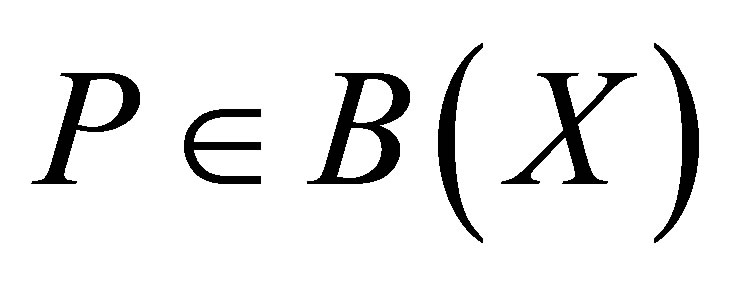 be a projection, and suppose
be a projection, and suppose  is invertible along
is invertible along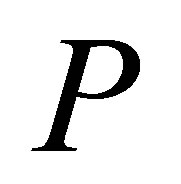 . Then
. Then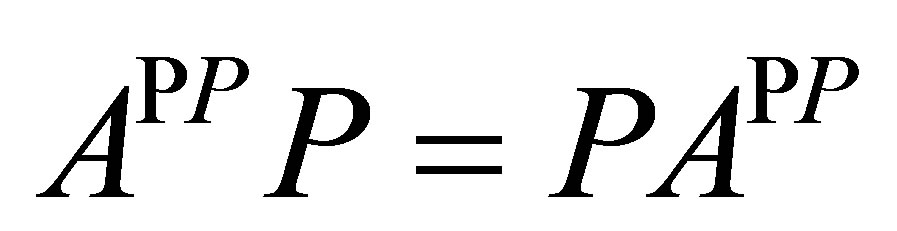 .
.
Proof. Using Proposition 4,
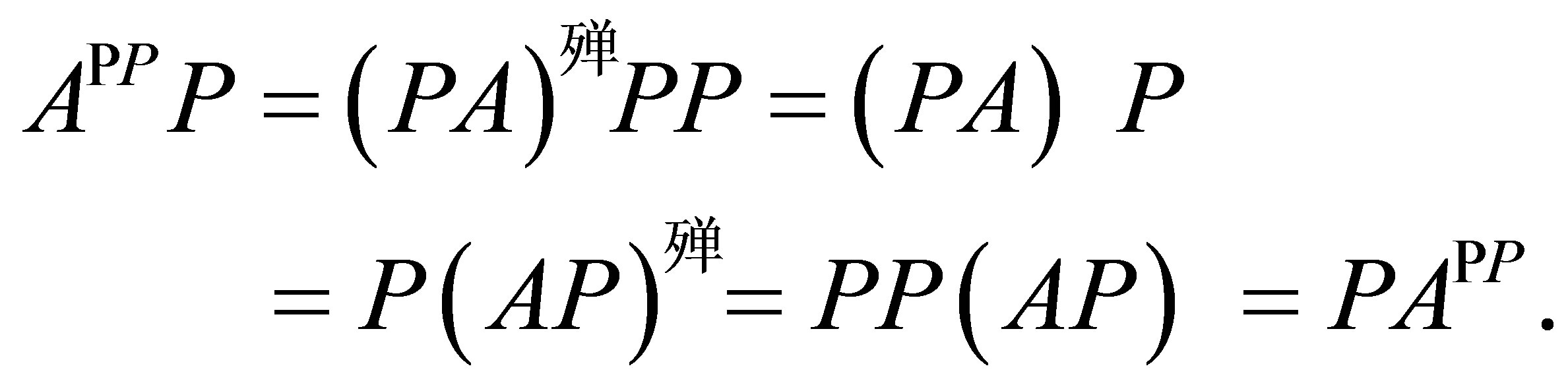
Example 11. An operator 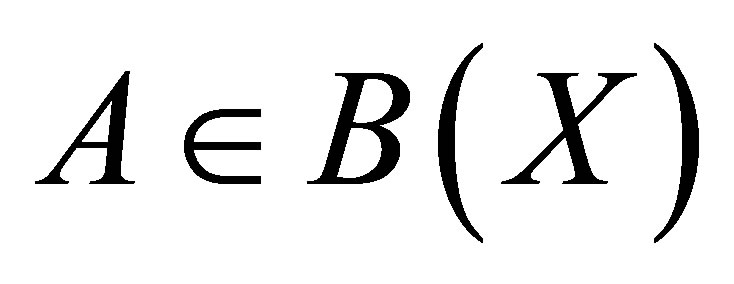 and a projection
and a projection 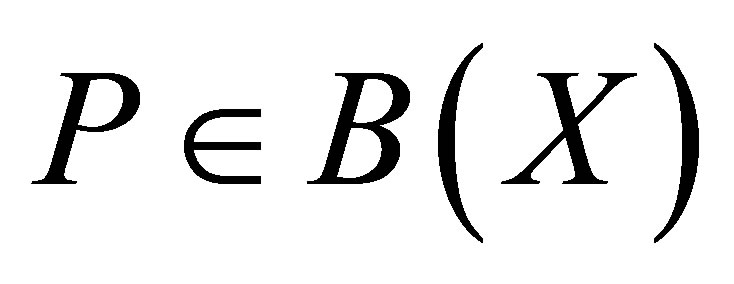 such that
such that  but
but  is not invertible along
is not invertible along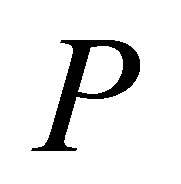 .
.
Let 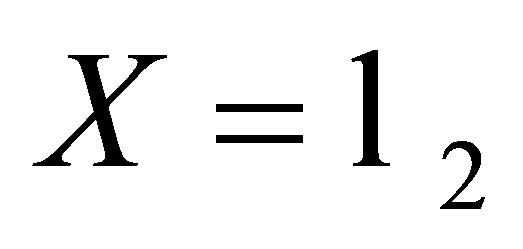 and let
and let 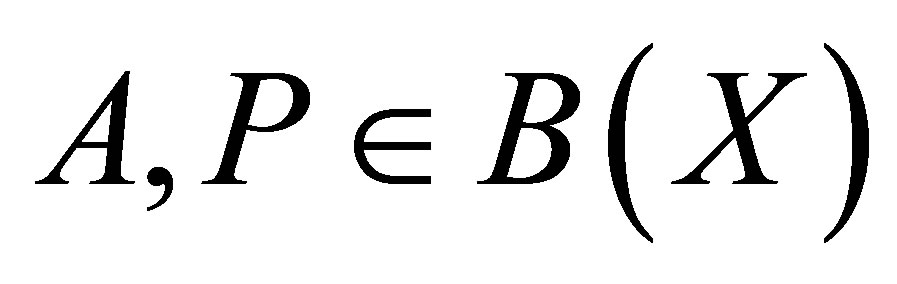 be defined by
be defined by
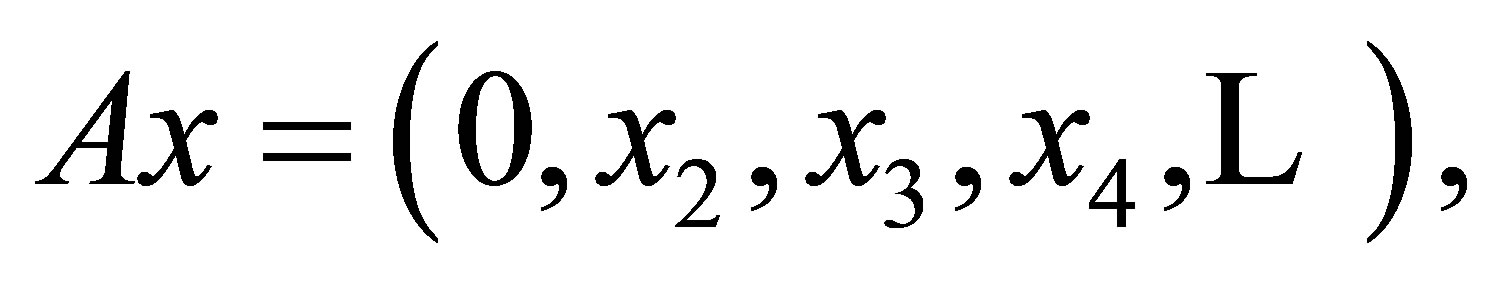
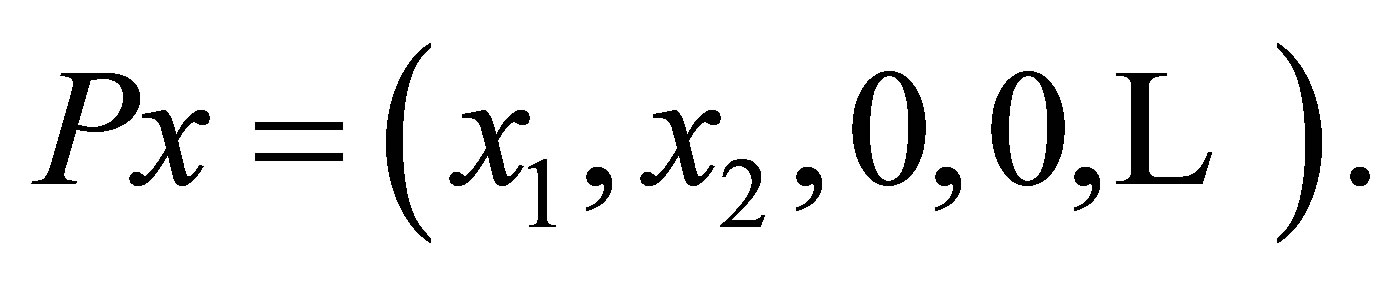
Then
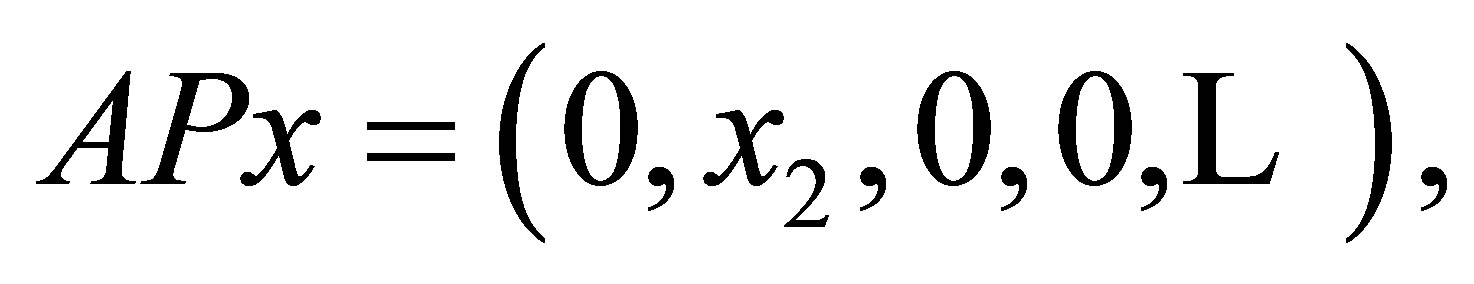
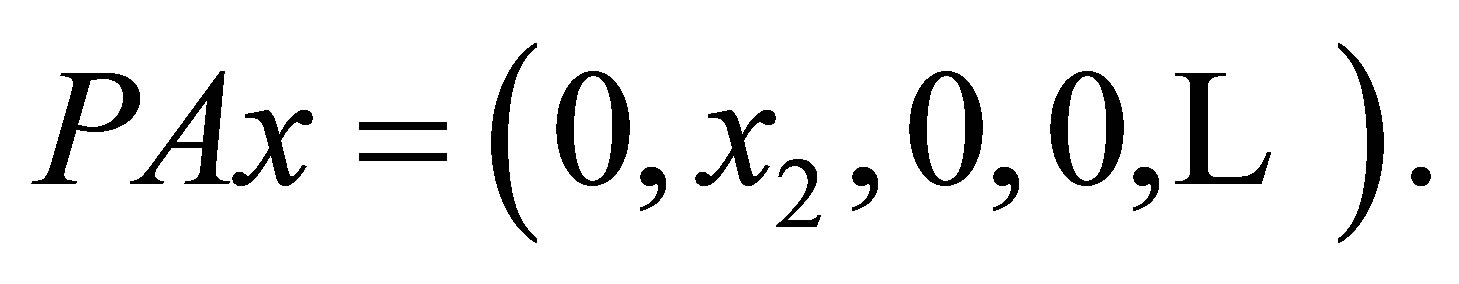
However, the reduction 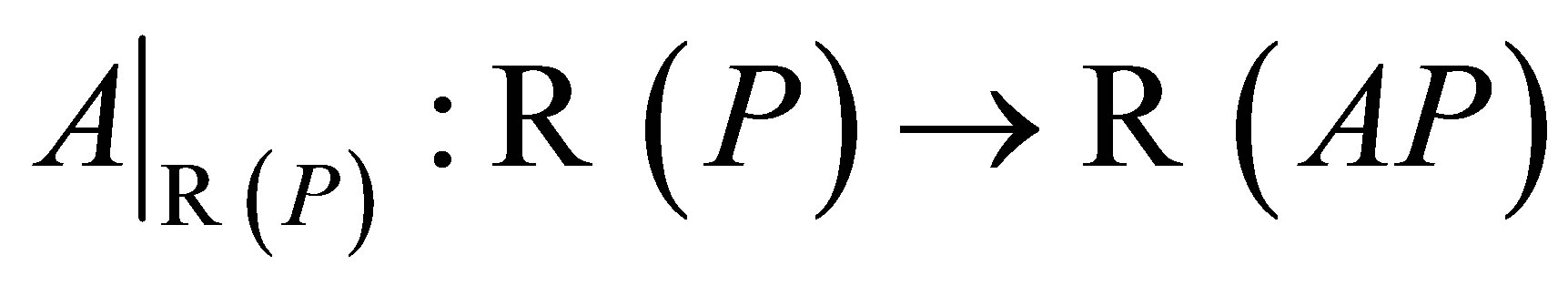 can not be invertible, and by Theorem 1
can not be invertible, and by Theorem 1  is not invertible along
is not invertible along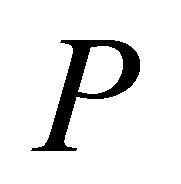 .
.
Theorem 12. Let 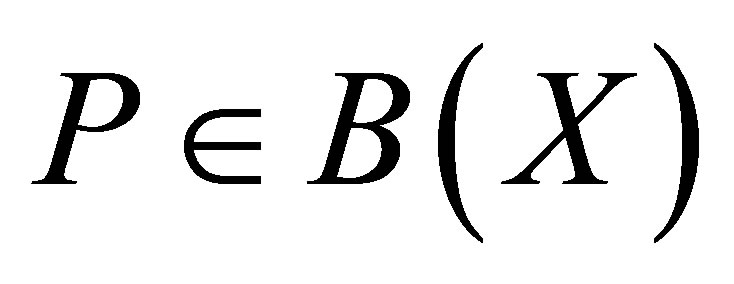 be a projection and
be a projection and 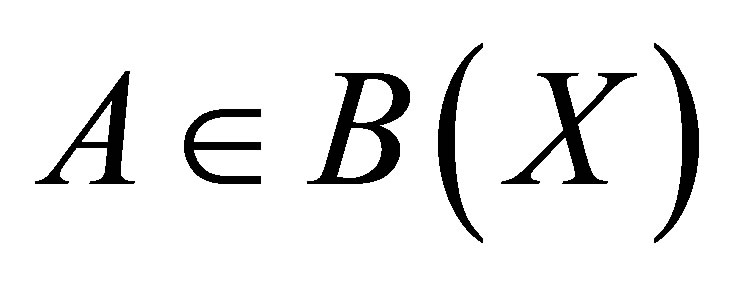 be such that
be such that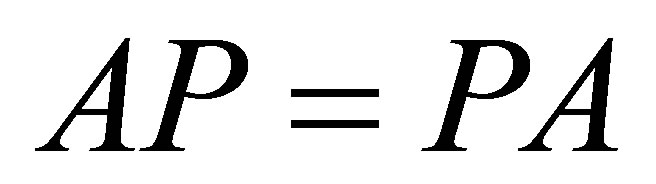 . Then,
. Then,  is invertible along
is invertible along  if and only if
if and only if 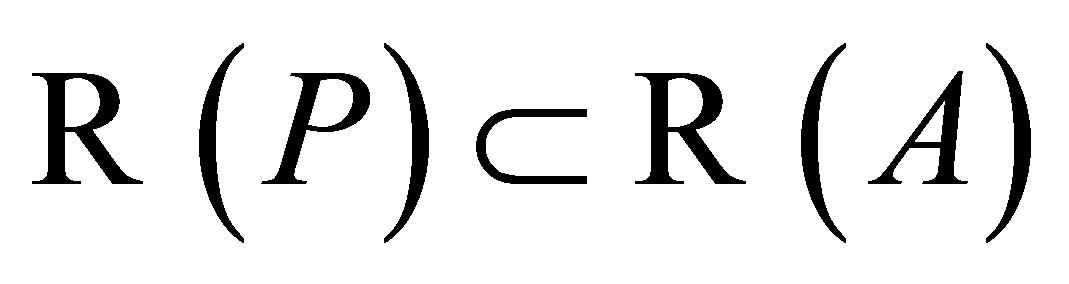 and
and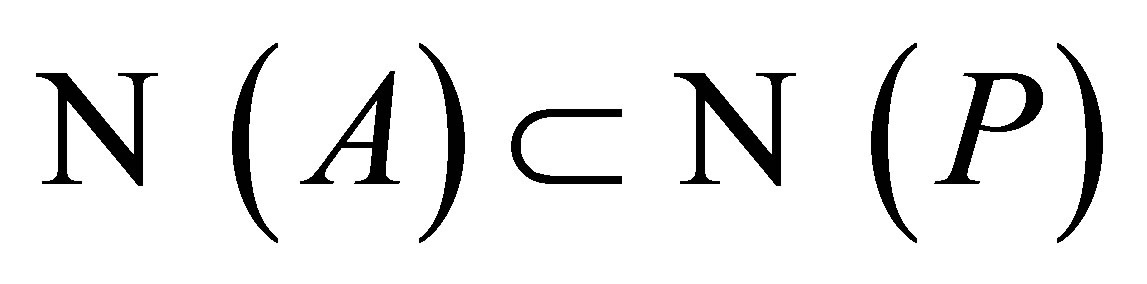 .
.
Proof. Suppose  is invertible along
is invertible along . Since
. Since 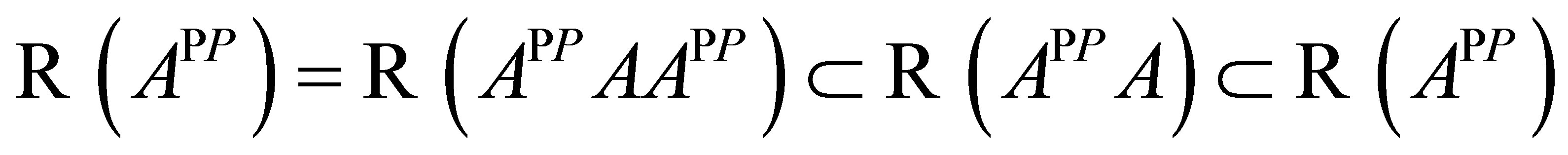 and from Proposition 4 and the definition of
and from Proposition 4 and the definition of  we have
we have
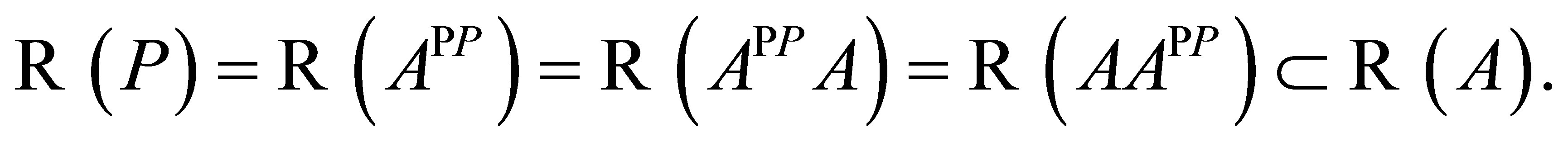
Similarly, from
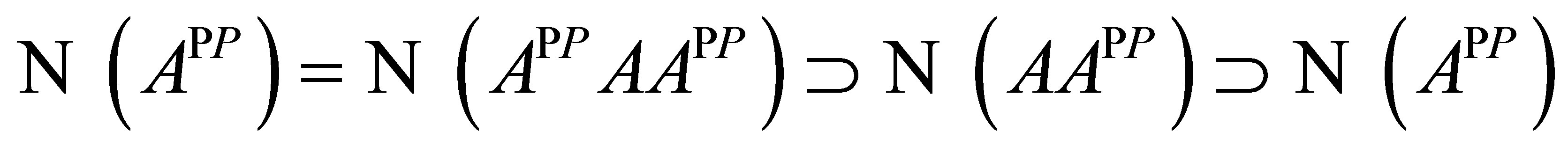 Proposition 4 and the definition of
Proposition 4 and the definition of  we get
we get

Conversely, suppose 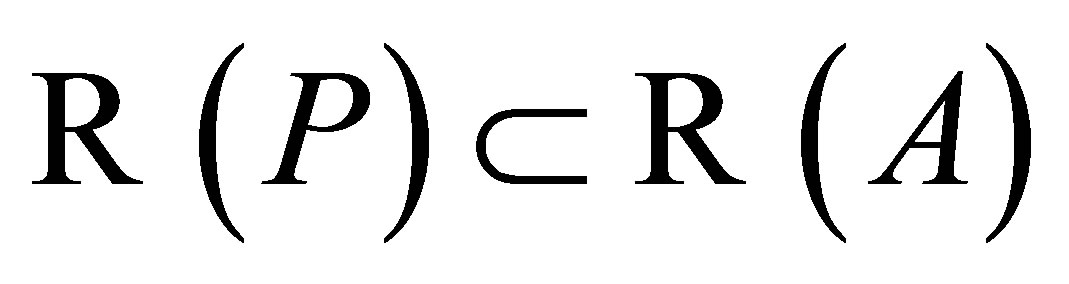 and
and  . We use Theorem 1. The reduction
. We use Theorem 1. The reduction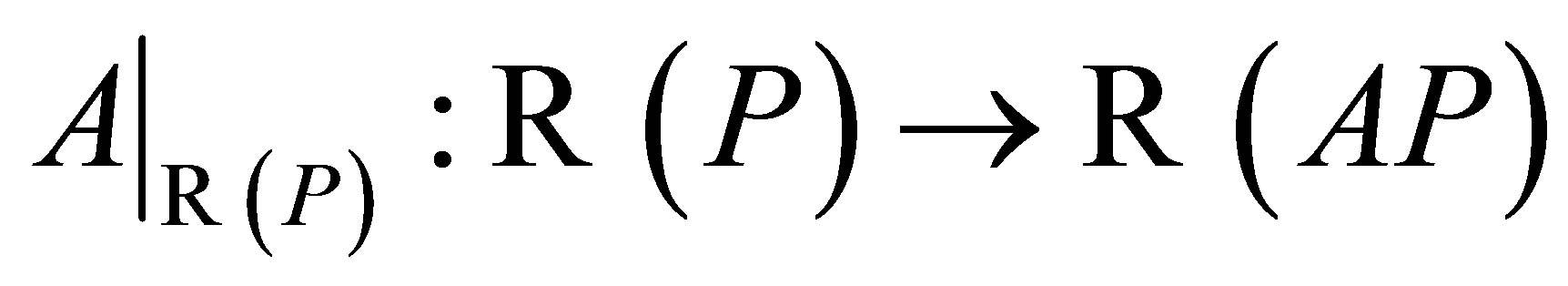 is clearly onto. From
is clearly onto. From  and
and  we get that it is also 1-1.To see that
we get that it is also 1-1.To see that  is closed and
is closed and  we will show
we will show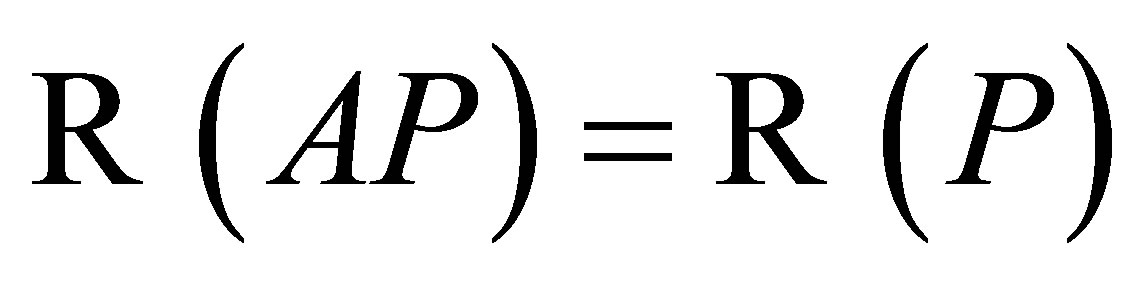 . It is clear that
. It is clear that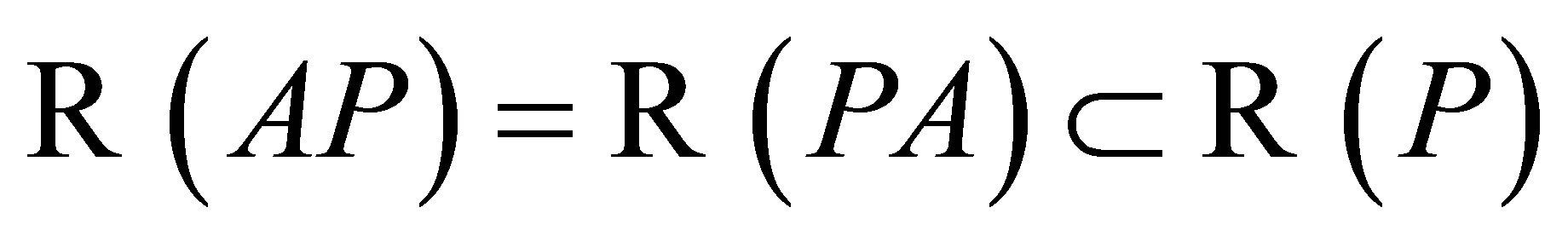 . For the other inclusion, let
. For the other inclusion, let . Since
. Since , there exists
, there exists 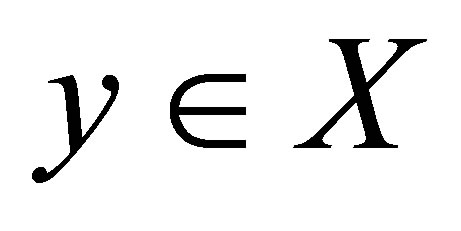 such that
such that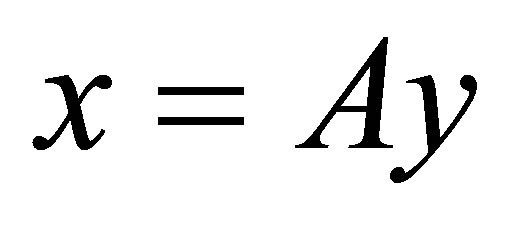 . Then, from
. Then, from 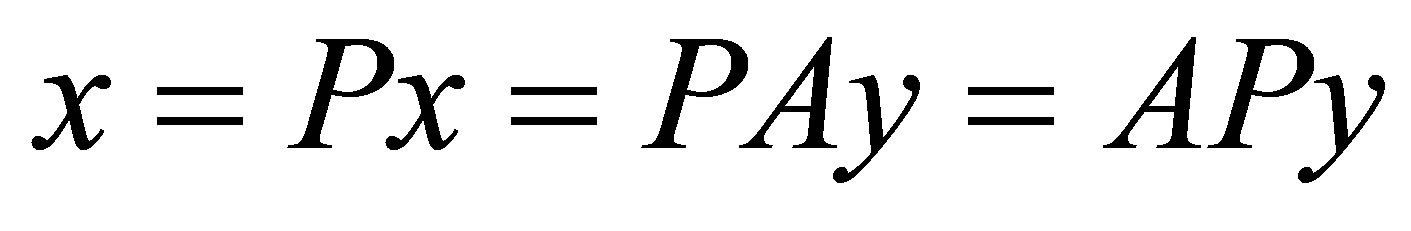 it follows that
it follows that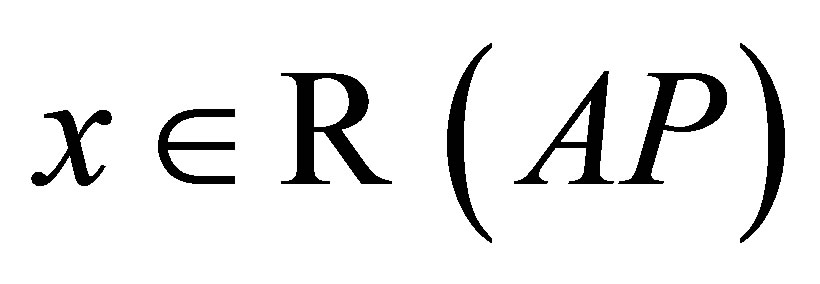 . Thus,
. Thus, . Finally, it is clear that
. Finally, it is clear that  is closed and complemented. Hence
is closed and complemented. Hence  is invertible along
is invertible along .
.
4. Spectral Projections
Recall the spectrum 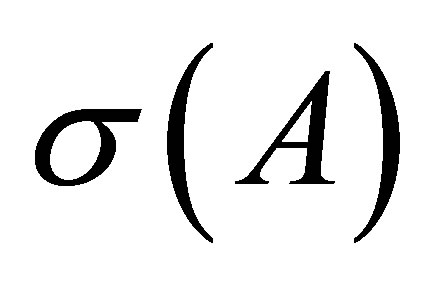 of an operator
of an operator 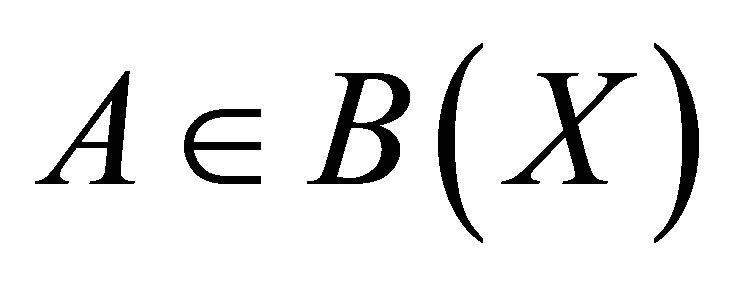 is the set
is the set 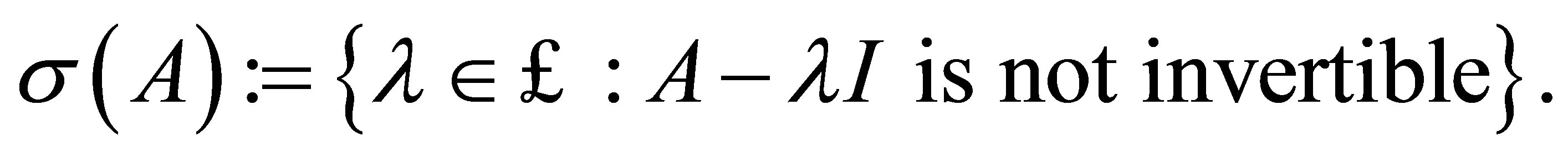
Suppose  is invertible along
is invertible along 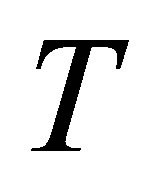 and
and . Then we have the matrix form
. Then we have the matrix form
 .
.
From 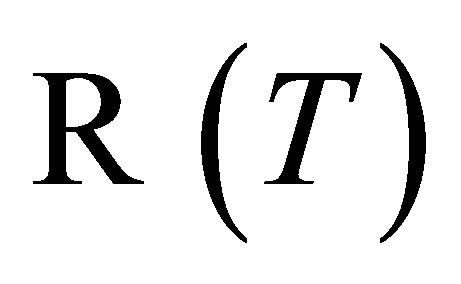 and
and 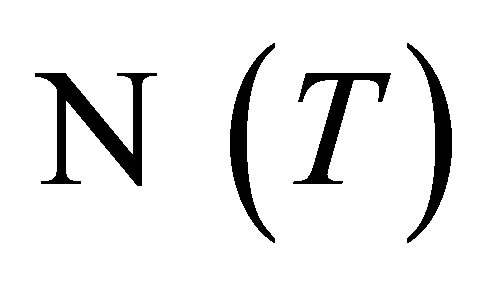 are invariant under
are invariant under , we have:
, we have:
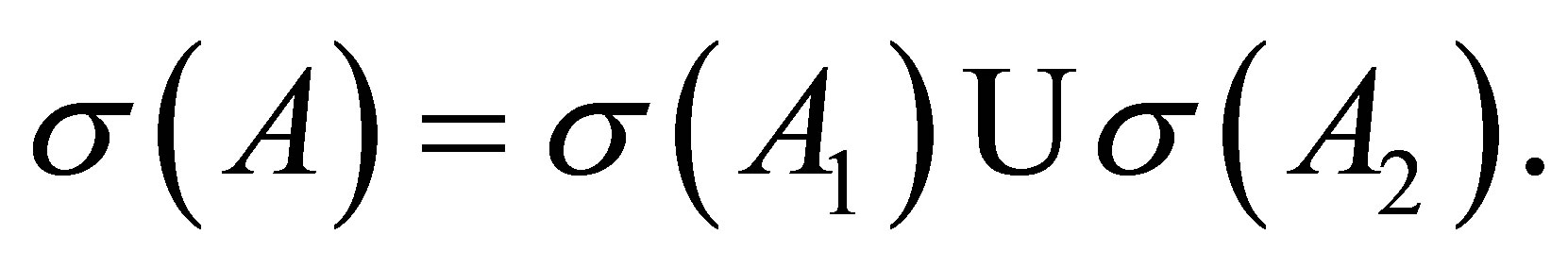
Since 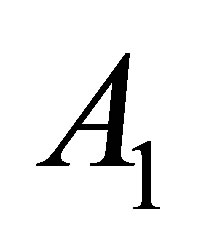 is invertible but
is invertible but  is not, we know that
is not, we know that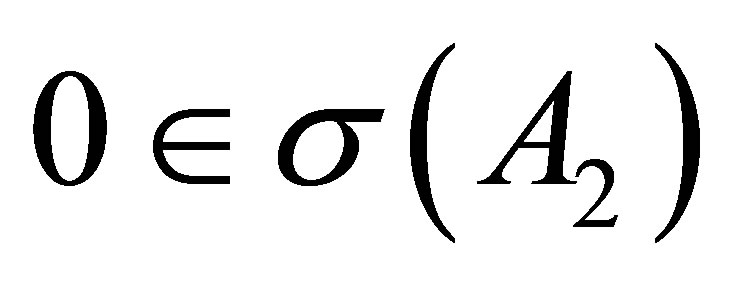 .
.
Note that from 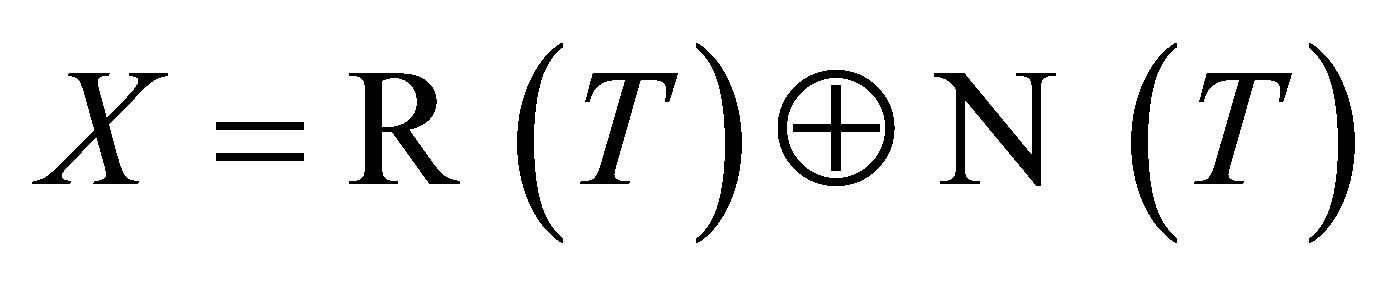 and the matrix form of
and the matrix form of , there exists a projection
, there exists a projection 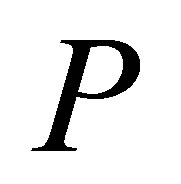 such that
such that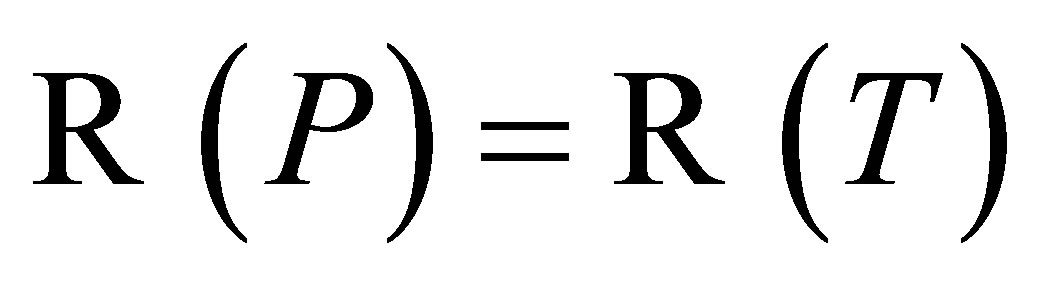 ,
, 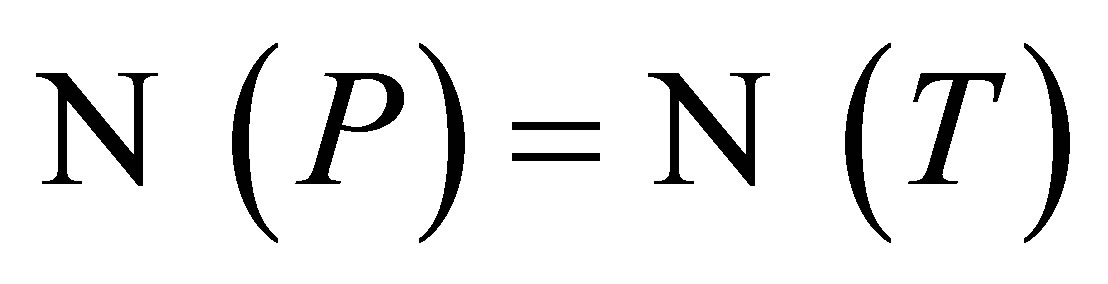 and
and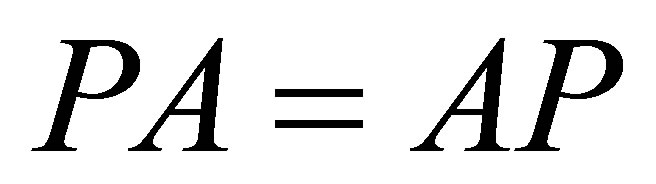 . Thus, without loss of generality, we can suppose
. Thus, without loss of generality, we can suppose  is invertible along a projection
is invertible along a projection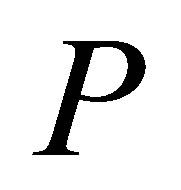 . A very important class of projections which commutes with
. A very important class of projections which commutes with  is a class of spectral projections, which we now discuss.
is a class of spectral projections, which we now discuss.
The resolvent set 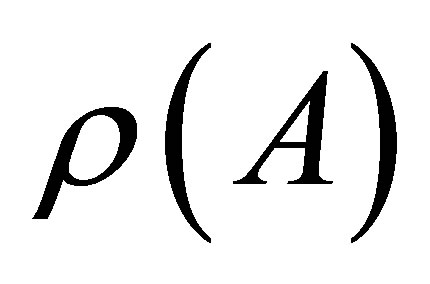 of
of  is
is 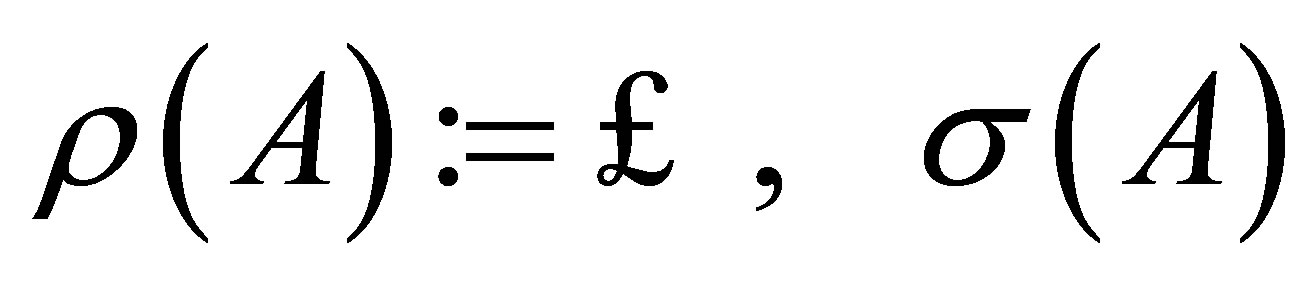 and for
and for  the resolvent function
the resolvent function  is
is
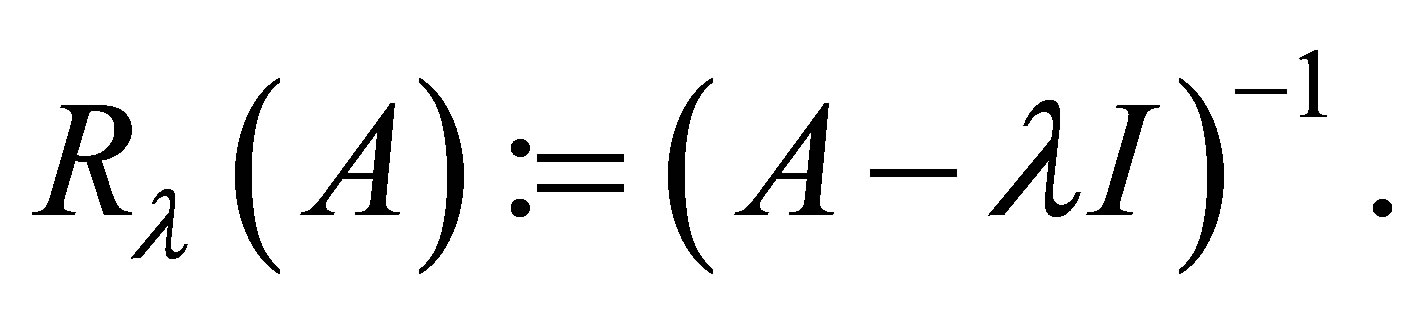
A subset 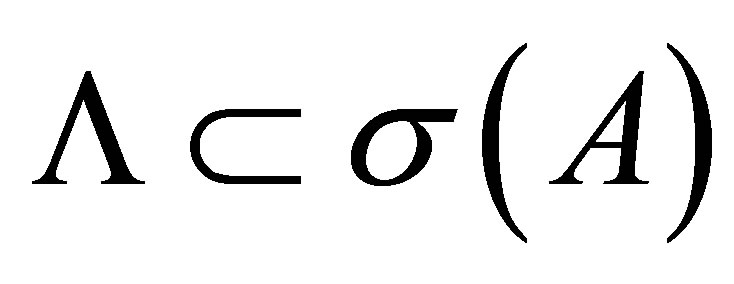 is said to be a spectral set of
is said to be a spectral set of  if
if  and
and 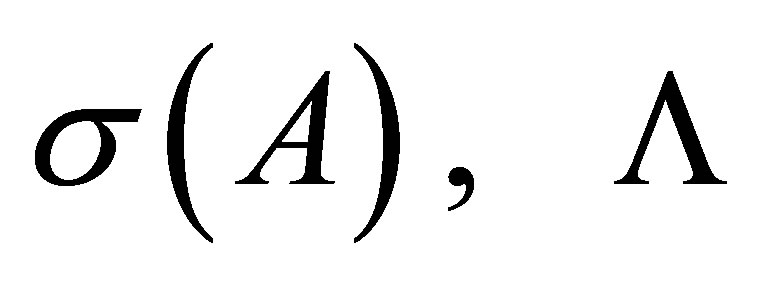 are both closed in
are both closed in . For a spectral set
. For a spectral set  of
of ,
, 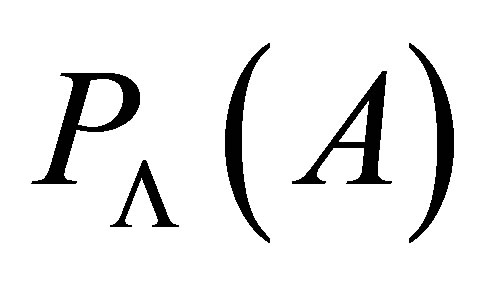 the spectral projection associated with
the spectral projection associated with  is defined by
is defined by
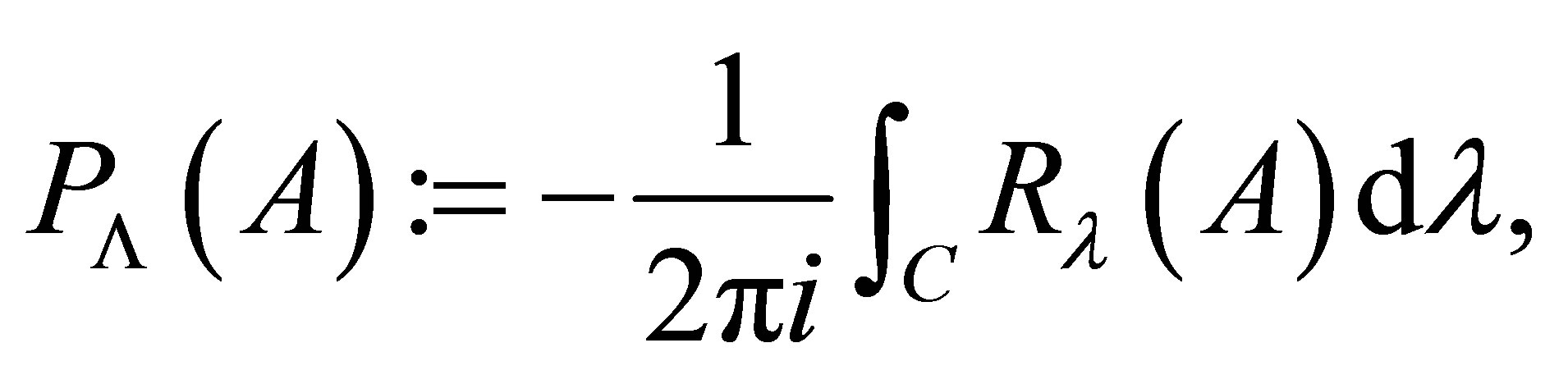
where  is a Cauchy contour that separates
is a Cauchy contour that separates  from
from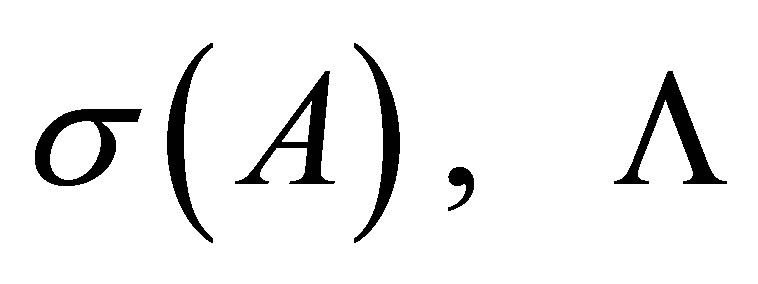 .
.
If 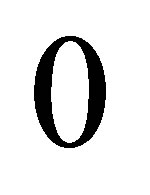 is a point of the resolvent set or an isolated point of the spectrum
is a point of the resolvent set or an isolated point of the spectrum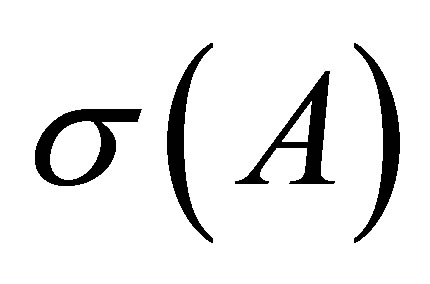 , then the operator
, then the operator  is called quasipolar. Let
is called quasipolar. Let  be quasipolar and let
be quasipolar and let  be the spectral projection associated with the spectral set
be the spectral projection associated with the spectral set , then ([4]):
, then ([4]):
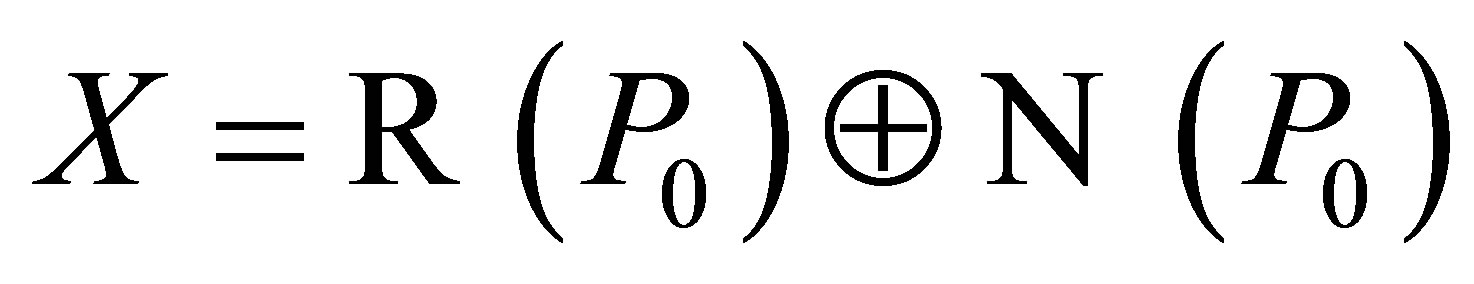
Let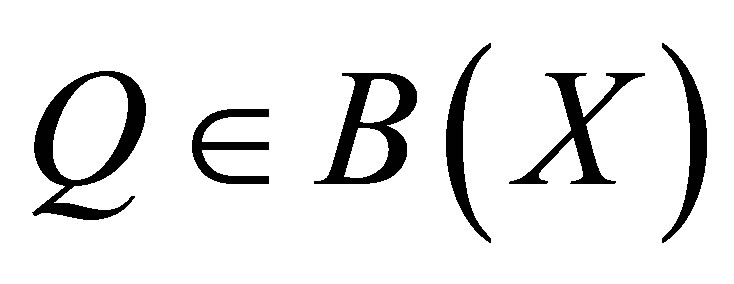 . If
. If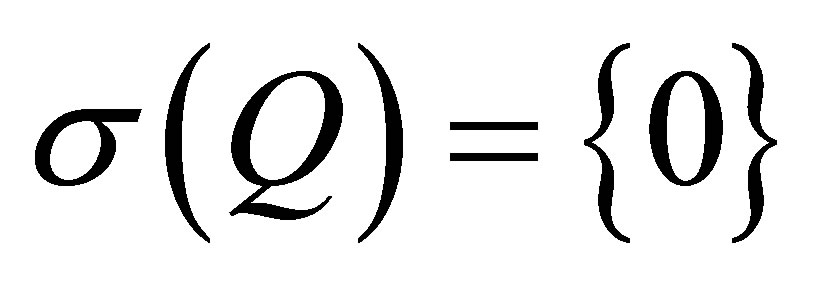 , then we say that
, then we say that  is a quasinilpotent operator. Recall that
is a quasinilpotent operator. Recall that  is nilpotent if
is nilpotent if 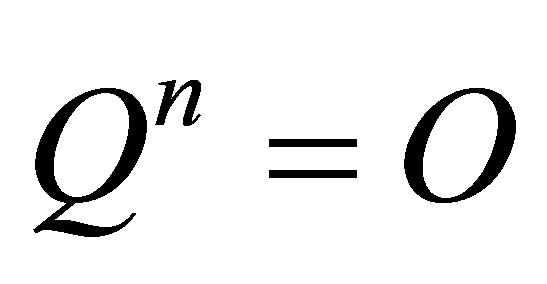 for some
for some , and nilpotent operators are quasinilpotent.
, and nilpotent operators are quasinilpotent.
Quasipolar operators are generalized invertible in the sense of Koliha: an operator 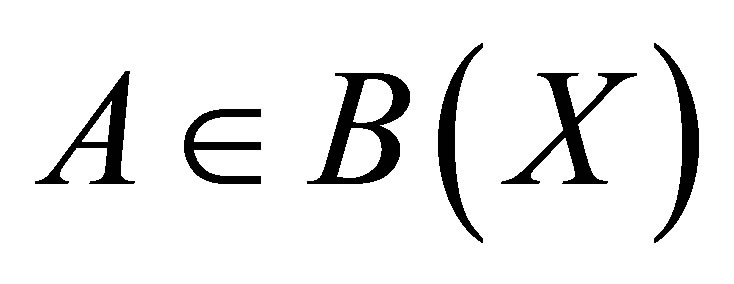 is Koliha-Drazin invertible if there exists
is Koliha-Drazin invertible if there exists 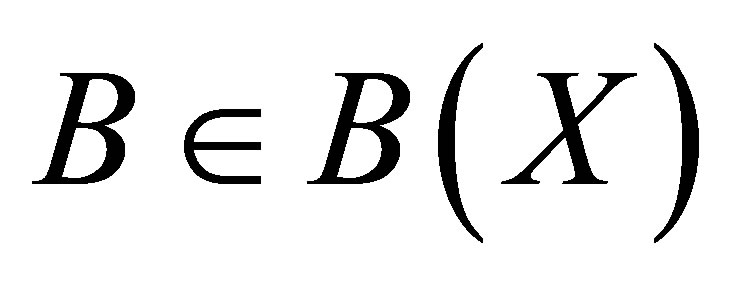 such that
such that 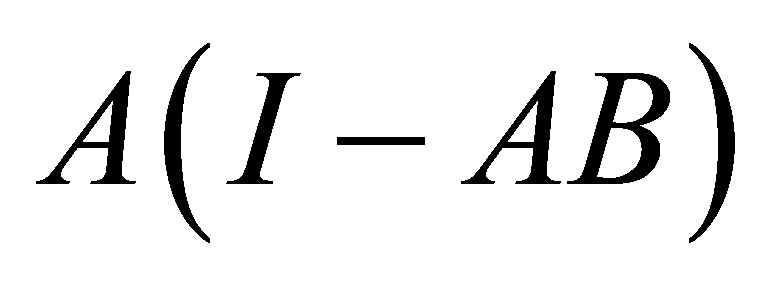 is quasinilpotent,
is quasinilpotent, 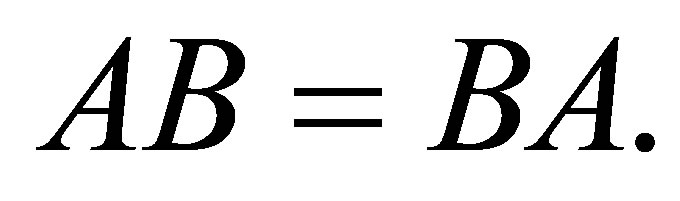
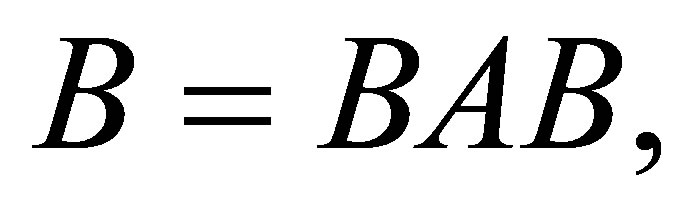
In this case, by Lemma 2.4 of [5], Koliha-Drazin inverse is unique and we write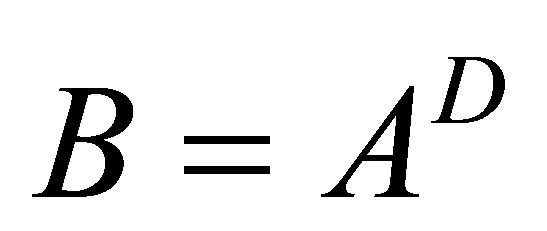 .
.
An operator  is Koliha-Drazin invertible if and only if 0 is an isolated point of
is Koliha-Drazin invertible if and only if 0 is an isolated point of . If
. If  is a pole of the resolvent of order
is a pole of the resolvent of order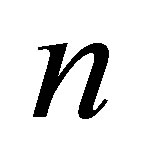 , then
, then  is Drazin invertible with Drazin index
is Drazin invertible with Drazin index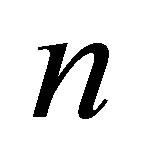 . If 0 is a simple pole then it is group invertible.
. If 0 is a simple pole then it is group invertible.
As noted above, the Koliha-Drazin is a particular case when we consider the spectral set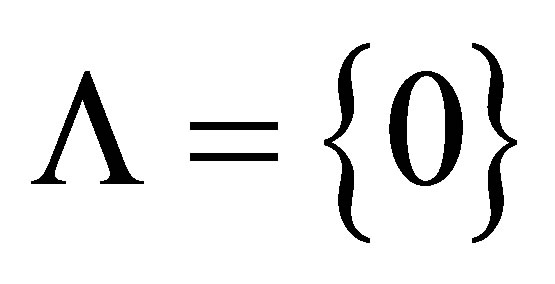 . For the general case when
. For the general case when  is a spectral set such that
is a spectral set such that , Dajić and Koliha have defined a generalized inverse and studied its properties ([3]).
, Dajić and Koliha have defined a generalized inverse and studied its properties ([3]).
Theorem 13. Let 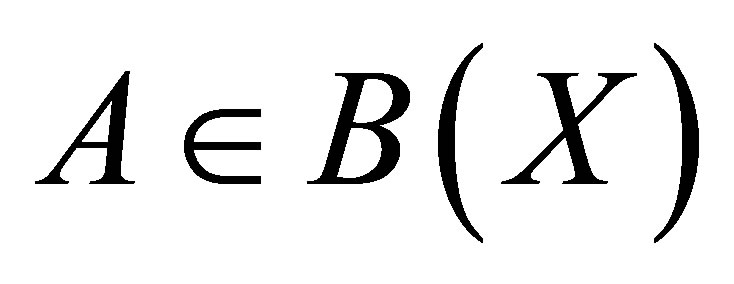 and
and  be a spectral set for
be a spectral set for . If
. If 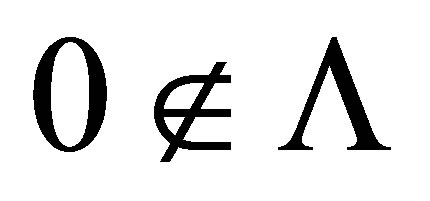 then
then  is invertible along
is invertible along .
.
Proof. Let . Then
. Then 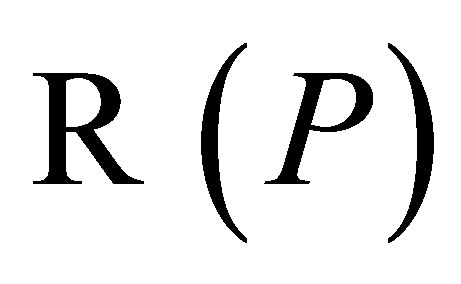 and
and  are closed and
are closed and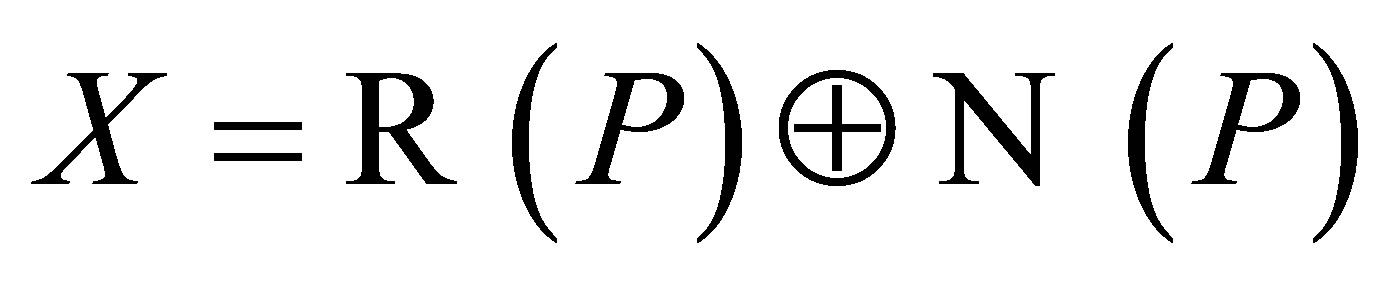 . Now, since
. Now, since 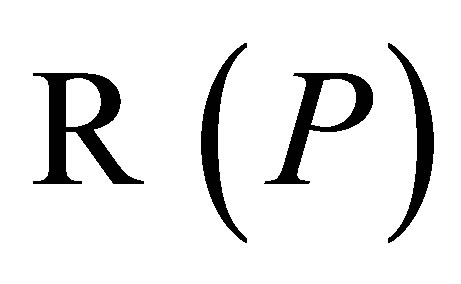
is  -invariant,
-invariant, 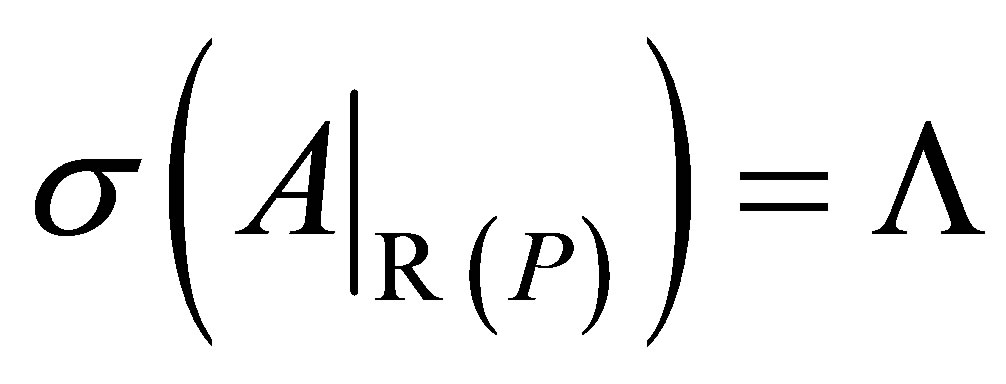 and
and  we have that
we have that 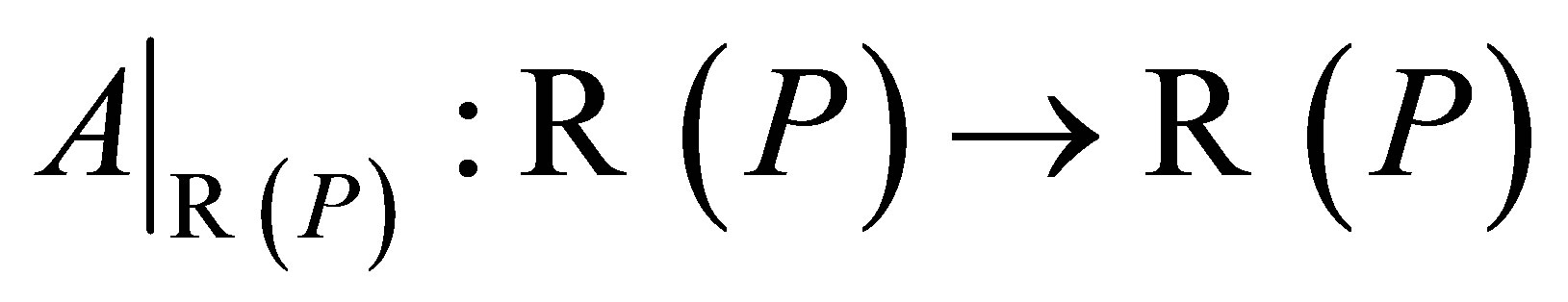 is invertible. Thus,
is invertible. Thus, 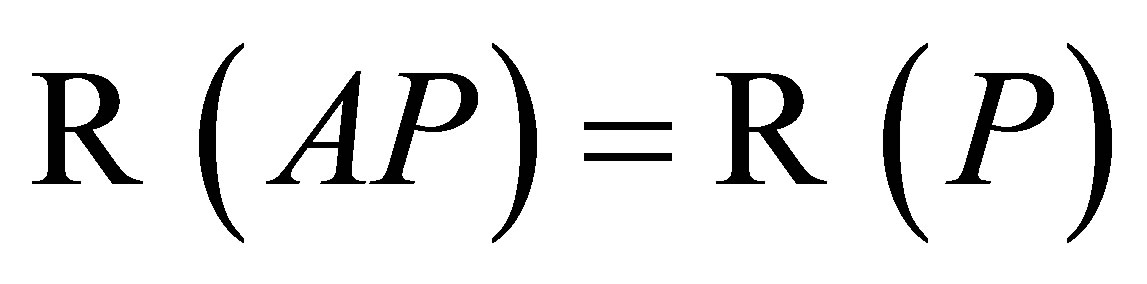 is closed,
is closed, 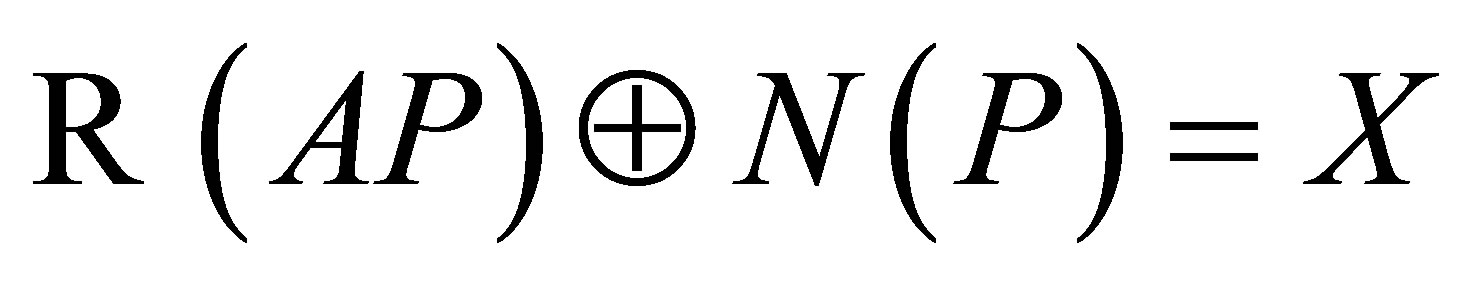 and
and 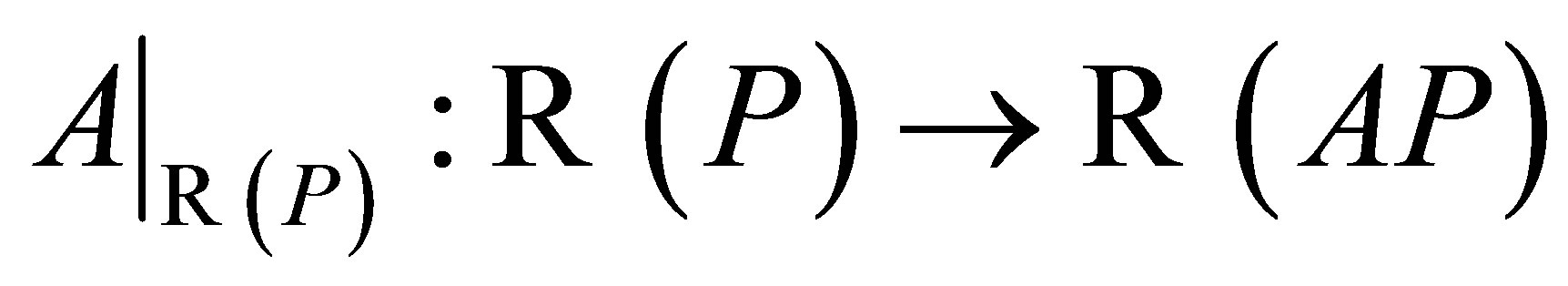 is invertible. Therefore, by Theorem 1
is invertible. Therefore, by Theorem 1  is invertible along
is invertible along .
.
Corollary 14. Let 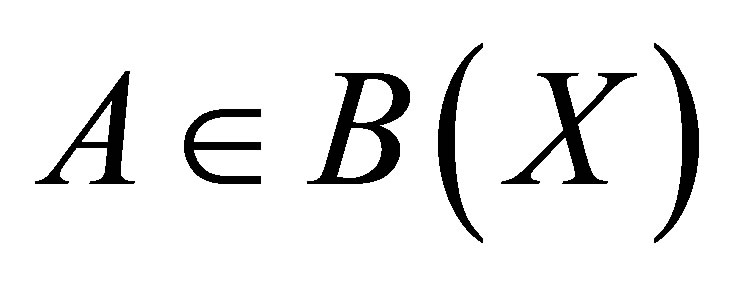 and
and  be a spectral set for
be a spectral set for . If
. If 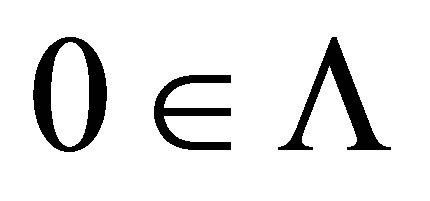 then
then  is invertible along
is invertible along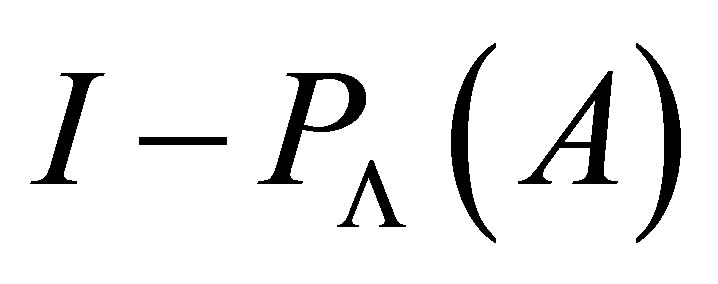 .
.
Proof. If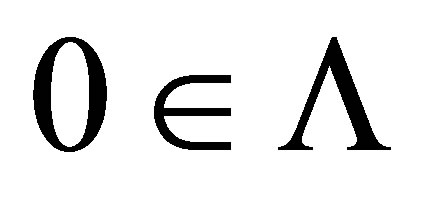 , then
, then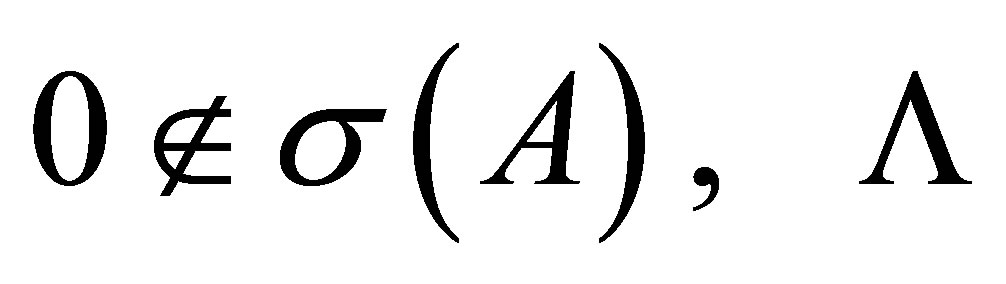 . From the theorem above,
. From the theorem above,  is invertible along
is invertible along 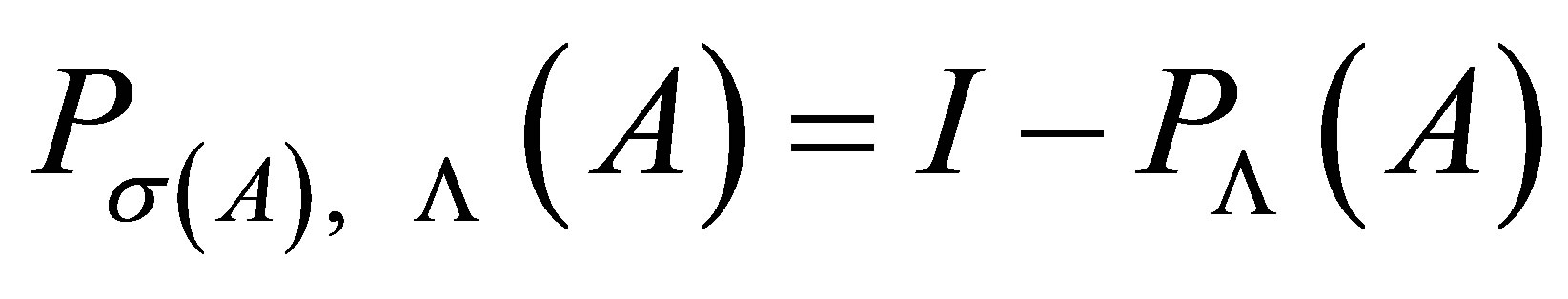 .
.
5. Acknowledgements
This research is partially supported by Grant-in-Aid Scientific Research No.24540195.
REFERENCES
- X. Mary, “On Generalized Inverses and Green’s Relations,” Linear Algebra Applications, Vol. 434, No. 8, 2011, pp. 1836-1844. http://dx.doi.org/10.1016/j.laa.2010.11.045
- G. Kantún-Montiel and S. V. Djordjević, “Invertibility along an Operator,” unpublished.
- A. Dajić and J. J. Koliha, “The Sigma-g-Drazin Inverse and the Generalized Mbekhta Decomposition,” Integral Equations and Operator Theory, Vol. 57, No. 3, 2007, pp. 309-326. http://dx.doi.org/10.1007/s00020-006-1454-0
- P. Aiena, “Fredholm and Local Spectral Theory, with Applications to Multipliers,” Kluwer Academic Publishers, Dordrecht-Boston-London, 2004.
- J. J. Koliha, “A Generalized Drazin Inverse,” Glasgow Mathematical Journal, Vol. 38, No. 3, 1996, pp. 367-381. http://dx.doi.org/10.1017/S0017089500031803

