Journal of Sustainable Bioenergy Systems
Vol.3 No.1(2013), Article ID:29094,4 pages
DOI:10.4236/jsbs.2013.31008
Global Optimization of Continuous Fermentation Involving Zymomonas mobilis
Chemical Engineering, University of Puerto Rico, San Juan, USA
Email: lakshmin.sridhar@upr.edu
Received January 26, 2013; revised February 28, 2013; accepted March 11, 2013
Keywords: Fermentation; Optimization; Bioreactor
ABSTRACT
Global steady-state optimization of Zymomonas mobilis fermentation process problems is performed to demonstrate the existence of multiple optimum solutions necessitating the use of a global optimization strategy. It is shown that the steady-state equations for the Zymomonas mobilis fermentation process can be reduced to a single equation which when used as a constraint results in yielding only one optimum solution, the global one.
1. Introduction
Production of ethanol from a variety of biomass feedstocks, solid and liquid waste resources is a national priority for a variety of reasons but most importantly for energy independence and sustainability. The biggest hurdle in the commercialization of any of the processes for making ethanol is the cost of production. Hence, it is important to develop strategies to produce clean ethanol with the least amount of expense. Ethanol can be produced by the fermentation of Zymomonas mobilis and it is important to ensure that that the process of fermentation operates in an optimal fashion.
A lot of work has been done in dealing with the nonlinearity of the Zymomonas Mibilis fermentation process [1-6]. The most comprehensive work that demonstrates the nonlinear behavior of the Zymomonas mobilis fermentation process is done by [7-9]. These articles show that the model presented by [7] is excellent not only in predicting the output concentrations but also the nonlinear behavior that results in multiple steady-states and oscillatory behavior.
While almost all of the computational work regarding the fermentation of Zymomonas mobilis involves demonstration of bifurcations and multiple steady-states, there has been little work concerning global optimization of these processes.
This paper deals with 1) a computational demonstration of the existence of multiple optimum solutions for the fermentation of Zymomonas mobilis requiring the use of a global optimum strategy to obtain the most optimum solution, and 2) using the process of elimination to reduce the steady-state equations for the Zymomonas mobilis fermentation process to a single equation and 2) demonstrating that if this equation is used instead of the original set of equations only one minimum (the global one) is obtained and not the unnecessary misleading local minima. This paper is organized as follows. First the model equations describing the steady-state fermentation process involving Zymomonas mobilis is described. In the next section a process of elimination is used to reduce these equations to a single equation. The optimization of the Zymomonas mobilis fermentation process using both these formulations are performed and compared. It is demonstrated that the original model optimization yields both local and global optimum solution, while the reduced model optimization yields only the global optimum.
2. Zymomobilis mobilis Fermentation
The steady-state equations governing the Zymomonas mobils fermentation process are given by [7] as
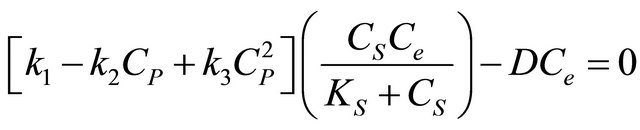 (1)
(1)
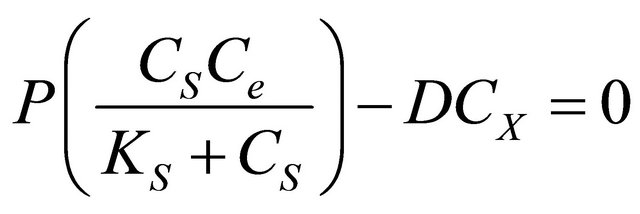 (2)
(2)
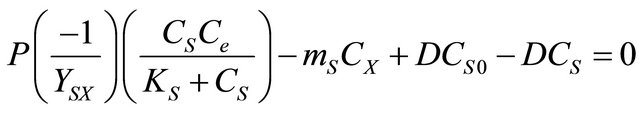 (3)
(3)
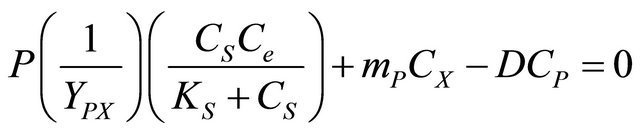 (4)
(4)
These equations can be succinctly represented as
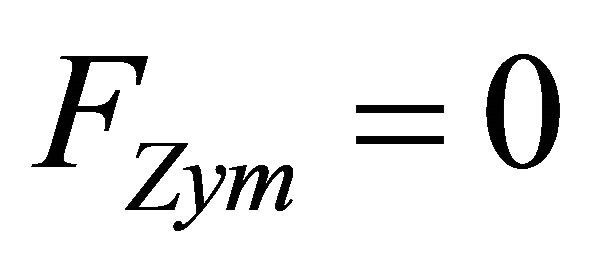 (5)
(5)
The variables are CX, Ce, CS & CP,
which are the concentrations of the biomass, key component, substrate and product.
Table 1 has the values of the parameters and constants.
The product concentration CP must be maximized which implies that the
optimization minimization objective function is
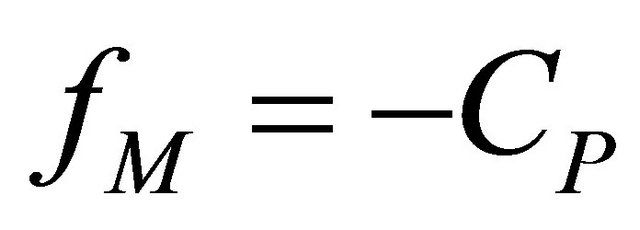 and the equality constraints are given by Equations (1)-(4). Hence the optimization
problem can be expressed as
and the equality constraints are given by Equations (1)-(4). Hence the optimization
problem can be expressed as
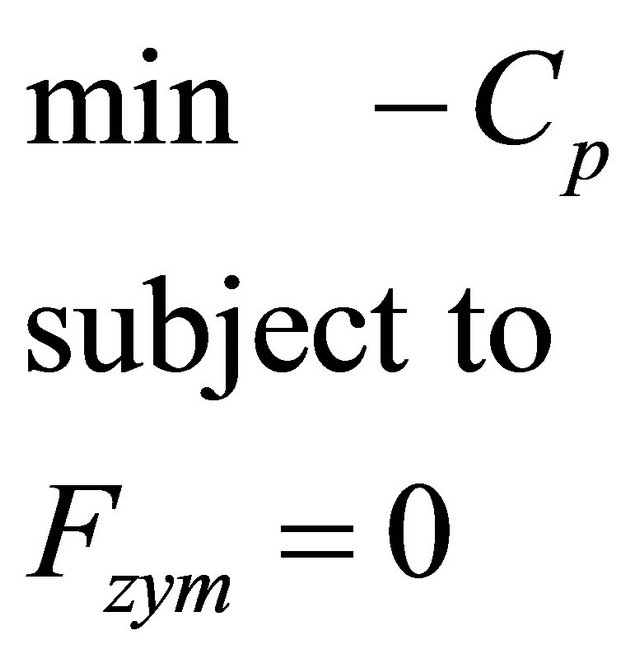 (6)
(6)
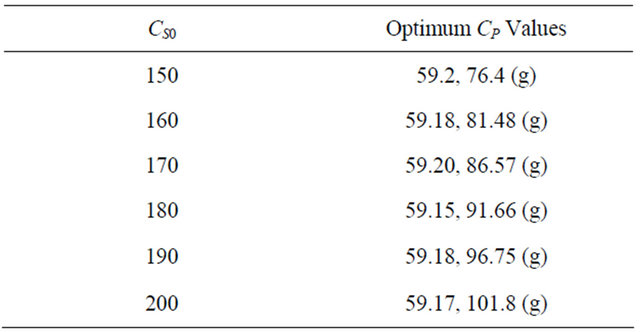
Garhyan and Elnshaie [7] studied the fermentation for CS0 values of 150.3 and 200 and performed a detailed bifurcation analysis for these two values of substrate concentrations. In this paper the MATLAB global optimization routines Global-Search and Multistart routines were used to determine all the optimum solutions satisfying Equation (6) for the CS0 values from 150 to 200. More than one minima were found for each of these CS0 values. This demonstrates that to obtain the optimum solution for the Zymomonas mobilis fermentation process, it is necessary to use a global strategy if the equations are used in the form given by (1)-(4). Table 2 gives the optimum values of CP for the various values of the substrate concentration CS0. The global optimum solution is indicated as “g”.
The entire range of CS0 values for which the Zymomonas mobilis fermentation process has been tested theoretically and experimentally [7,8] has been considered and two optimum solutions were found for the entire range when Equations (1)-(4) were used as constraints.
3. Reformulation of the Zymomonas mobilis Fermentation Steady-State Equations
Let
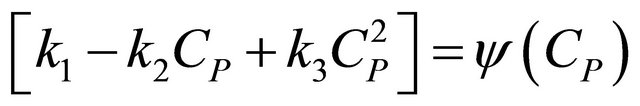
This implies that
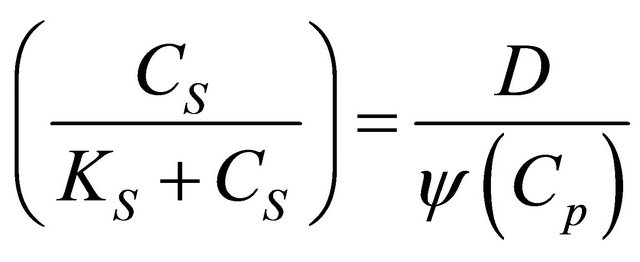 (7)
(7)
and
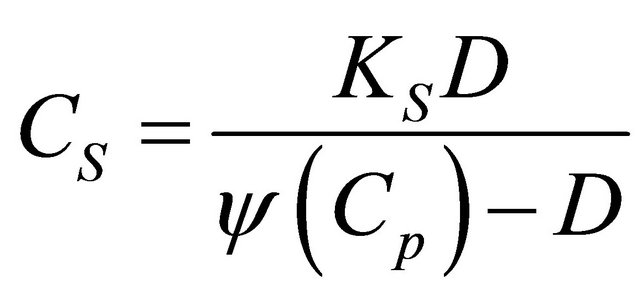 (8)
(8)
Substituting for
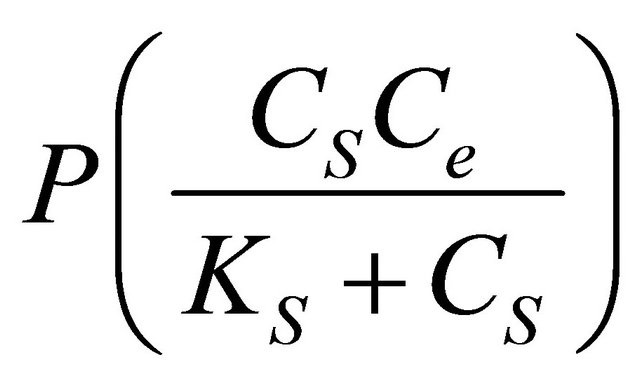 from Equation (2) into Equation (3) we take
from Equation (2) into Equation (3) we take
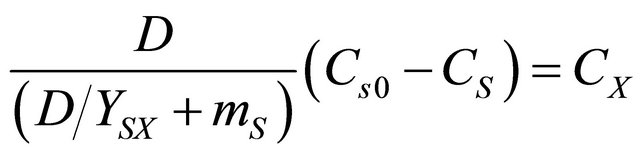 (9)
(9)
Table 1. Parameters used for the Zymomonas mobilis fermentation [7].
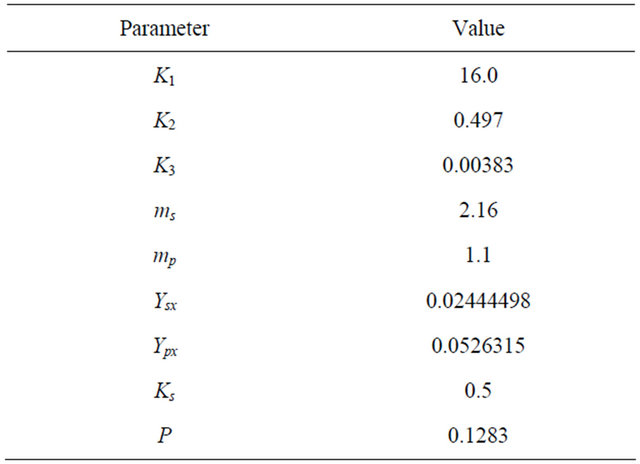
Table 2. Optimum CP Values for Zymomonas mobilis fermentation which are obtained by using the original model in [7]. Global optimum soution is marked g. With the refoirmulated model even with the starting point of the nonglobal optimum solution and using the local MATLAB optimization algorithm (fmincon) the non-global solution is not obtained (only the global solution is obtained).
and substituting for CS from Equation (6) yields
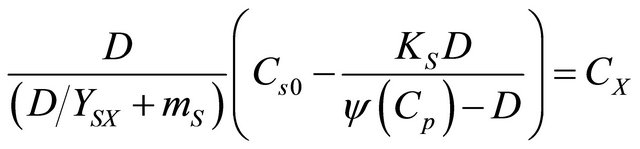 (10)
(10)
Similar substitution for
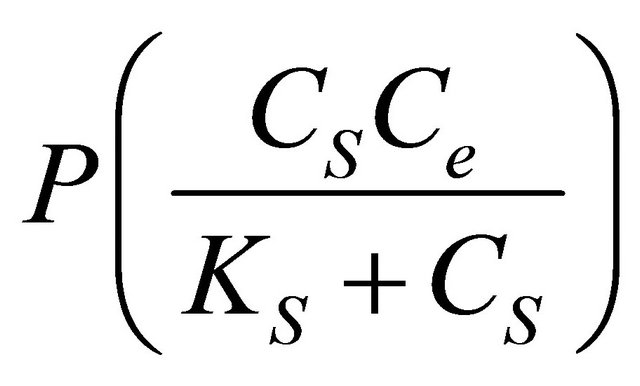 from Equation (2) into Equation (4) yields
from Equation (2) into Equation (4) yields
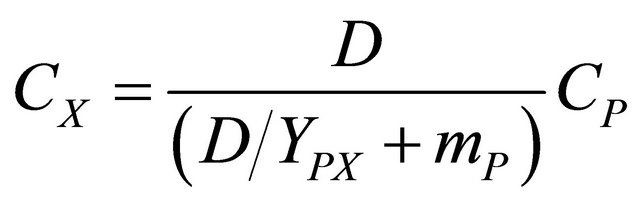 (11)
(11)
Equating (9) and (10) yields
 (12)
(12)
Simplification yields
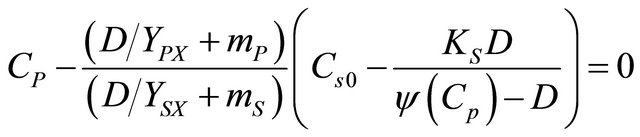 (13)
(13)
Defining
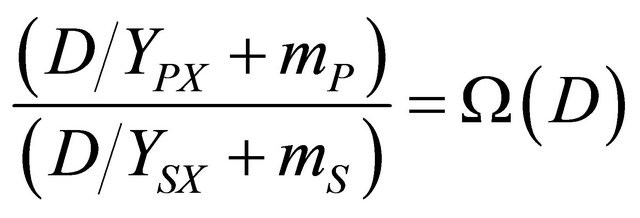 we get
we get
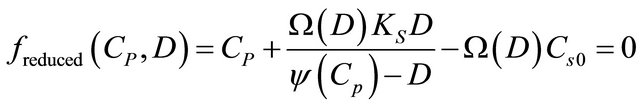 (14)
(14)
The optimization problem can be written as
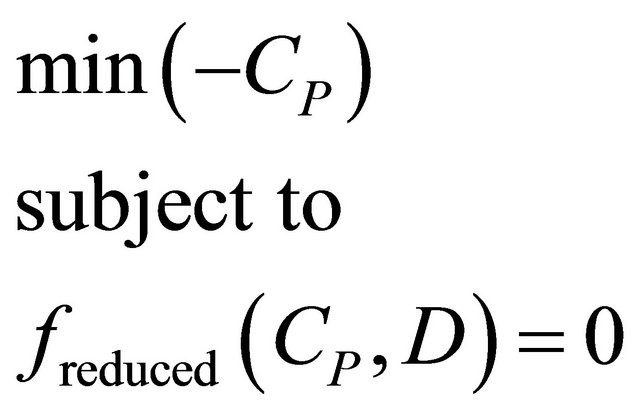 (15)
(15)
4. Global Optimization of the Zymomonas Fermentation Process
The global optimization of the Zymomonas mobilis fermentation process is performed using the global search and multistart routines in the global optimization MATLAB toolbox. Both these solvers use gradient based methods and start a local solver (fmincon) from multiple starting points to obtain local and global minima. The global search optimization uses a scatter search algorithm to generate multiple starting points while the multistart algorithm uses uniformly distributed starting points with predefined bounds. Both these solvers are used to ensure the correctness of the local and global optimum solutions. Table 2 provides the optimum values of the product concentration that were obtained for each of the input substrate concentrations. The whole range of input concentrations for which this model is theoretically studied and experimentally verified [7,8] is investigated for the existence of multiple optimum values of CP. It is shown that the original formulation given by Equation (6) yields 2 optimum values of CP. The global value is labeled (g). In all the cases when the formulation given by Equation (15) is used only the global value is obtained. Even when the local value is used as a starting point the MATLAB routine fmincon converges to the global value when the reduced formulation is used. This concludes that the reduced formulation (given by Equation (15)) yields only one optimum solution (the global one). This reduced formulation does not admit the unnecessary and misleading global solution that the original formulation admits.
5. Conclusions
The steady-state optimization of continuous fermentation processes involving both Zymomonas mobilis is shown to have multiple solutions satisfying the mathematical requirements for optimization. This makes it necessary to use global optimization strategies to obtain the most optimum solution for the optimization of the fermentation process. The steady-state equations for the Zymomonas mobilis fermentation process can be reduced to a single equation which when used as a constraint, yields only the required global optimum solution and if this new formulation is used, even a local optimization strategy will produce the most optimum solution.
REFERENCES
- K. J. Lee, D. E. Tribe and P. L. Rogers, “Ethanol Production by Zymomonas mobilis in Continuous Culture at High Glucose Concentrations,” Biotechnology Letters, Vol. 1, No. 10, 1979, pp. 421-426.
- K. J. Lee, M. L. Skotnicki, D. E. Tribe and P. L. Rogers, Kinetic Studies on a Highly Productive Strain of Zymomonas mobilis,” Biotechnology Letters, Vol. 2, No. 8, 1980, pp. 339-344. doi:10.1007/BF00138666
- I. M. L. Jobses, G. T. C. Egbertsa, K. C. A. M. Luyben and J. A. Roels, “Fermentation Kinetics of Zymomonas mobilis at High Ethanol Concentrations; Oscillations in Continuous Cultures,” Biotechnology and Bioengineering, Vol. 28, No. 6, 1986, pp. 868-877.
- C. Ghommidh, J. Vaija, S. Bolarinwa and J. M. Navarro, “Oscillatory Behavior of Zymomonas mobilis in Continuous Cultures, a Simple Stochastic Model,” Biotechnology Letters, Vol. 2, No. 9, 1989, p. 659.
- L. J. Bruce, D. B. Axford, B. Ciszek and J. A. Daugulis, “Extractive Fermentation by Zymomonas mobilis and the Control of Oscillatory Behavior,” Biotechnology Letters, Vol. 13, No. 4, 1991, pp. 291-296. doi:10.1007/BF01041487
- A. Mulchandani and B. Volesky, “Modelling of the Acetone-Butanol Fermentation with Cell Retention,” Canadian Journal of Chemical Engineering, Vol. 64, No. 4, 1986, pp. 625-631.
- P. Garhyan and S. Elnshaie, “Static/Dynamic Bifurcation and Chaotic Behavior of an Ethanol Fermentor,” Industrial & Engineering Chemistry Research, Vol. 43, No. 5, 2004, pp. 1260-1273
- P. Garhyan and S. Elnshaie, “Experimental Investigation and Confirmation of Static/Dynamic Bifurcation Behavior in a Continuous Ethanol Fermentor, Practical Relevance of Bifurcation and the Contribution of Harmon Ray,” Industrial & Engineering Chemistry Research, Vol. 44, No. 8, 2005, pp. 2525-2531.
- A. Mahecha-Botero, P. Garhyan and S. S. E. H. Elnnashie, “Nonlinear Characterestics of a Membrane Fermentor for Ethanol Production and Their Implications,” Nonlinear Analysis: Real World Applications, Vol. 7, No. 3, 2006, pp. 432-457. doi:10.1016/j.nonrwa.2005.03.010
Nomenclature
C Concentration D Dilution Rate V Volume E ethanol X cell mass concentration in K1, K2, K3 empirical constants P Permeability Y yield factor
Subscripts
e key component of biomas 0 input P product S substrate X biomass

