American Journal of Analytical Chemistry
Vol. 3 No. 3 (2012) , Article ID: 18271 , 7 pages DOI:10.4236/ajac.2012.33033
Influence of the Neutron Flux Characteristic Parameters in the Irradiation Channels of Reactor on NAA Results Using k0-Standardization Method
Research and Development Center for Radiation Technology, Hochiminh City, Vietnam
Email: tranhungkeiko@yahoo.com
Received November 28, 2011; revised January 5, 2012; accepted January 16, 2012
Keywords: k0-Standardization Technique; Error Propagation Function; Neutron Flux Characteristics; Dalat Reactor
ABSTRACT
An approximation method using to estimate the influence of the uncertainties of the neutron flux characteristic parameters in the irradiation positions on the NAA results using k0-standardization technique was presented. Those are the epithermal reactor neutron spectrum shape-factor a, the effective resonance energy  for a given nuclide and the thermal to epithermal neutron flux ratio f. The method is applied to estimate the effect of the uncertainties in the determination of a,
for a given nuclide and the thermal to epithermal neutron flux ratio f. The method is applied to estimate the effect of the uncertainties in the determination of a,  and f on final NAA results for some irradiation channels of the Dalat reactor. It also shows that presented method is suitable in practical use for the estimation of the errors due to the uncertainty of the neutron flux characteristic parameters at the irradiation position.
and f on final NAA results for some irradiation channels of the Dalat reactor. It also shows that presented method is suitable in practical use for the estimation of the errors due to the uncertainty of the neutron flux characteristic parameters at the irradiation position.
1. Introduction
Since the k0-standardization method was introduced in NAA [1], it has been broadly applied in the reactor in the world. The fundamental concept of k0-method was being elaborated previously in great detail [1-3]. The concentration of an element in the k0-method is calculated by:
 (1)
(1)
with k0 in Equation (1) defined as:
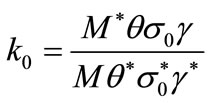 (2)
(2)
In Equations (1) and (2):
M—atomic mass;
q —isotopic abundance;
s0—2200 m∙s–1 (n, g) cross-section;
g —absolute gamma-intensity;
Np—peak area corrected for pulse losses;
W—sample weight in gram;
w*—comparator weight in microgram;
S = 1 – exp(–ltirr); tirr—irradiation time; l—decay constant;
D = exp (–ltd); td—decay time;
C = [1 – exp (–ltm)]/ltm; tm—measuring time;
f—thermal to epithermal neutron flux ratio;
Q0(a) = I0(a)/s0; I0(a)—resonance integral corrected for a non-ideal epithermal neutron flux distribution (assumed 1/E1+a);
εp—detector’s efficiency;
When the epithermal neutron flux distribution deviates from ideality, i.e. it does not follow the 1/E-law, Q0(a) of nuclide i can be written by:
 (3)
(3)
with a—neutron spectrum shape factor deviating from the 1/E-law, independent of neutron energy and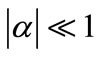 .
.
 —effective resonance energy of nuclide i.
—effective resonance energy of nuclide i.
The asterisks in Equations (1) and (2) refers to the comparator, which is suitable for coirradiation with the sample; in most case, Au is used as a comparator. The k0-factors to Au for interested isotopes in NAA were experimentally determined and tabulated in report [4] with an accuracy which better than 2% (average ~1%). The relevant nuclear data as Q0i and  can be found in a tabulated form or in a computer library. a, f and ep must be experimentally determined and they depend on specific irradiation channel and detector, which are used in practice. The detector’s efficiency (ep) can be determined with an uncertainty about 2%; but the uncertainty of a can be more than 10%, even bigger, depend on the irradiation channels in reactor. Since the term [f +
can be found in a tabulated form or in a computer library. a, f and ep must be experimentally determined and they depend on specific irradiation channel and detector, which are used in practice. The detector’s efficiency (ep) can be determined with an uncertainty about 2%; but the uncertainty of a can be more than 10%, even bigger, depend on the irradiation channels in reactor. Since the term [f + 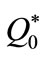 (a)]/ [f + Q0 (a)] in Equation (1), it is clear that an additional parameter,
(a)]/ [f + Q0 (a)] in Equation (1), it is clear that an additional parameter,  , should be considered, because the uncetainties of
, should be considered, because the uncetainties of 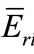 of some nuclides are about 20% [4,5].
of some nuclides are about 20% [4,5].
The accuracy and the applicability of the k0-standardization method were detailly presented in paper [5] by F. De CORTE et al. In paper [6], J. OP De BEEK evaluated the effect of errors of a and  on the results in terms of concentration, based on the 197Au comparator; in that Q0i(a) was approximated by :
on the results in terms of concentration, based on the 197Au comparator; in that Q0i(a) was approximated by :
 (4)
(4)
However, with this approximation, it led that some results in paper [6] have to be put to discussion (see below).
In this work, we carry out an approximation method to evaluate the effect of errors of a and 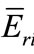 on the NAA results in the k0-standardization method. The obtained results showed that the approximate method in this work is acceptable with confident accuracy.
on the NAA results in the k0-standardization method. The obtained results showed that the approximate method in this work is acceptable with confident accuracy.
2. Base of Approximation
As we know, a value is smaller than unity in absolutte value. In practice, in irradiation channels of reactor, absolute value of a is less than 0.2 (in most cases, 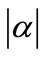 < 0.1 and this condition is satisfactory in reactor core). In the approximation of J. OP De BEEK, it is good for the nuclides having Q0i >1, but is not for the nuclides with Q0i <1. Due to
< 0.1 and this condition is satisfactory in reactor core). In the approximation of J. OP De BEEK, it is good for the nuclides having Q0i >1, but is not for the nuclides with Q0i <1. Due to , in paper [7,8], we suggest substituting
, in paper [7,8], we suggest substituting 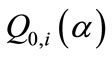 from Equation (3) by the following approximated formula:
from Equation (3) by the following approximated formula:
 (5)
(5)
where ai is constant for each nuclide and determined by fitting the values of Q0i(a), which are calculated from Equation (3) in range , then fitting according to function (5) (see reference [7,8]). Note that, ai of each nuclide depends on the sign of a. The values of ai for the interested nuclides in NAA are given in Table 1. Seeing the Equation (5), it differs to Equation (4) of J. OP De BEEK by a correctional coefficient ai. However, it can be used good for all nuclides with uncertainties of the calculated
, then fitting according to function (5) (see reference [7,8]). Note that, ai of each nuclide depends on the sign of a. The values of ai for the interested nuclides in NAA are given in Table 1. Seeing the Equation (5), it differs to Equation (4) of J. OP De BEEK by a correctional coefficient ai. However, it can be used good for all nuclides with uncertainties of the calculated 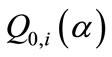 less than about 5% for the nuclides having Q0i < 1 and less than about 2% for Q0i > 1 with
less than about 5% for the nuclides having Q0i < 1 and less than about 2% for Q0i > 1 with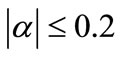 . Indeed, we carried out a survey of the ratios of Q0i(a) calculated from Equation (5) (in this work) and Equation (4) (of J. OP De BEEK) to Equation (3) (accurate expression) for Q0i from 0.44 (46Sc) to 248 (97Zr) with a = –0.1. The results are presented in Figure 1 and some results are presented in Table 2. Clearly, the approximated expression in this work is better than one of J. OP De BEEK. Moreover, the calculated Q0i(a) from three expression Equation (3), Equation (4) and Equation (5) for 45Sc(n, g)46Sc presented in Table 3. The another nuclides presented in papers [7,8] also confirm the above conclusion.
. Indeed, we carried out a survey of the ratios of Q0i(a) calculated from Equation (5) (in this work) and Equation (4) (of J. OP De BEEK) to Equation (3) (accurate expression) for Q0i from 0.44 (46Sc) to 248 (97Zr) with a = –0.1. The results are presented in Figure 1 and some results are presented in Table 2. Clearly, the approximated expression in this work is better than one of J. OP De BEEK. Moreover, the calculated Q0i(a) from three expression Equation (3), Equation (4) and Equation (5) for 45Sc(n, g)46Sc presented in Table 3. The another nuclides presented in papers [7,8] also confirm the above conclusion.

Figure 1. Survey of the ratios of Q0i(α) calculated from Equation (5) (in this work) and Equation (4) (of J. OP De BEEK) to Equation (3) (accurate expression) for different Q0i with α = –0.1.
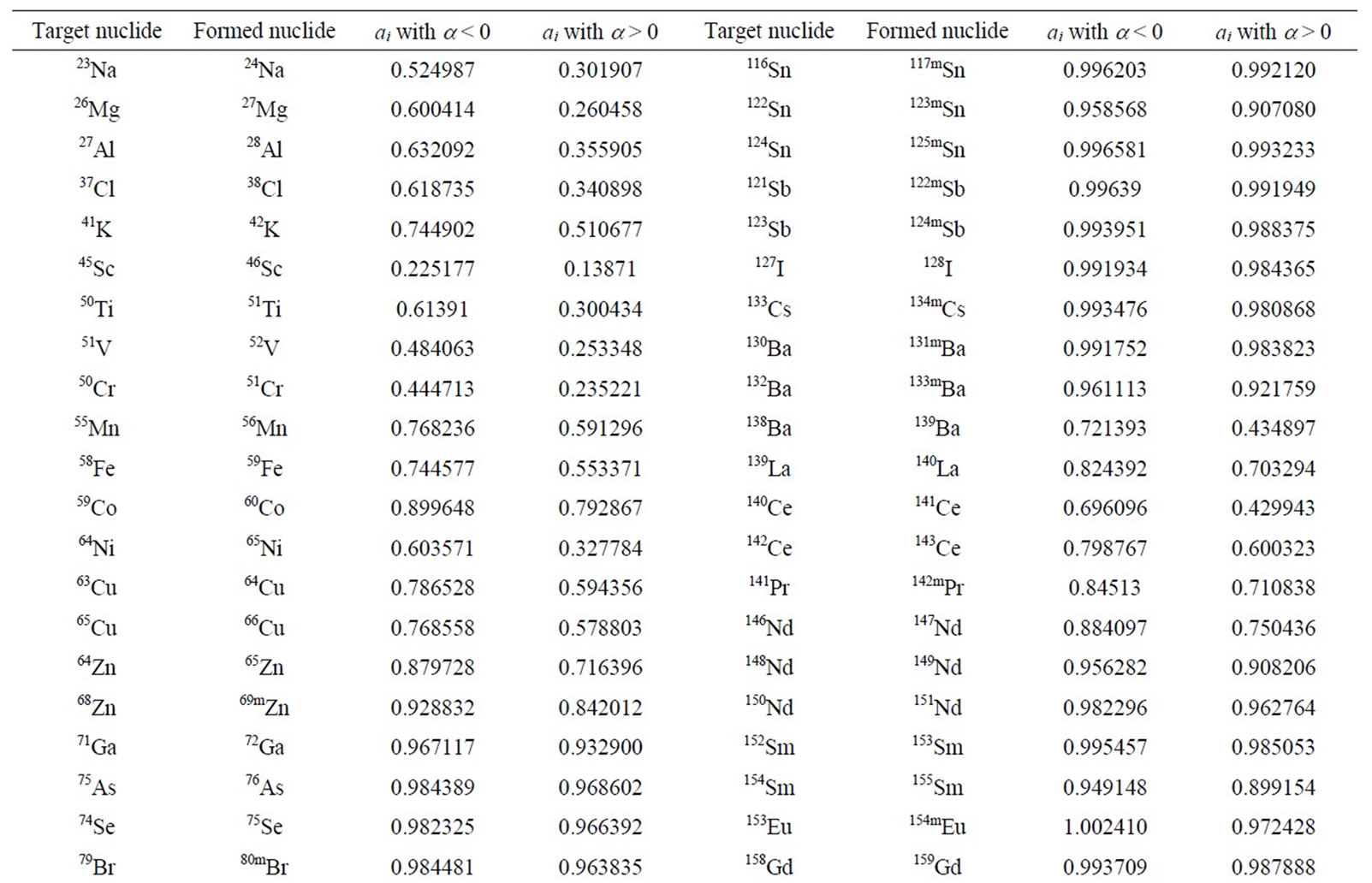

Table 1. The values of ai for the interesting nuclides in NAA.
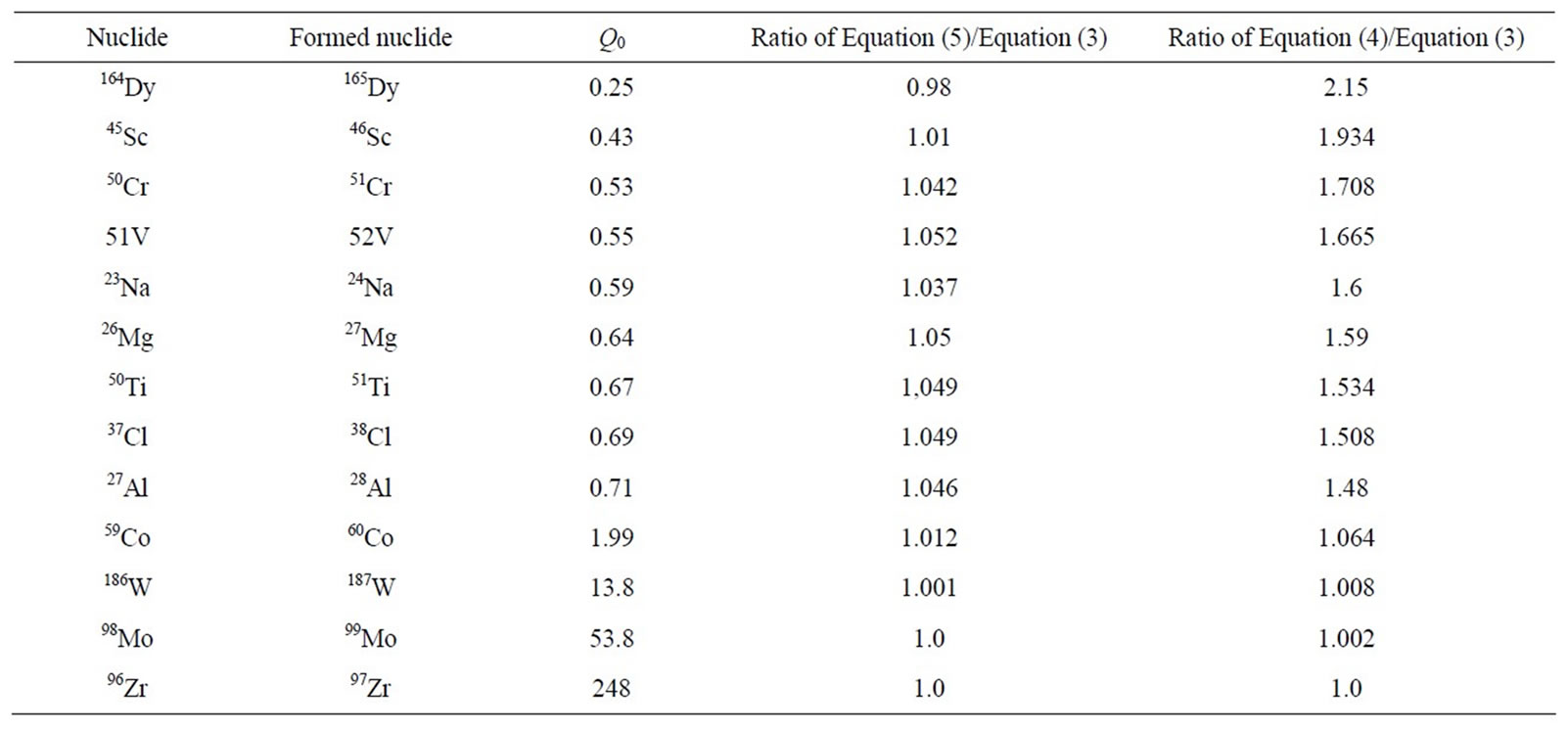
Table 2. Ratio of Q0(a) calculated by Equations (4) and (5) to Equation (3) of some nuclide in reaction (n, g) using in NAA.

Table 3. The results calculated Q0i(a) from three expression Equations (3)-(5) with a in interval [–0.2, 0.2] for 45Sc(n, g)46Sc.
From Table 1, it shows that coefficients ai of nuclides having Q0i > 1 are close to unity, but ai of the nuclides having Q0i < 1 differs more than unity. Therefore, the approximation of Equation (4) in paper [6] is only acceptable for the nuclides having Q0i > 1, but for the nuclides having Q0i < 1, it is not reliable.
In this work, we use the approximation expression; Equation (5), to evaluate influence of the uncertainties of a, f and 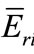 on the final element concentration in k0-method in the channels; 7 - 1, neutron trap of Dalat reactor (Vietnam) and channel 17 of THETIS reactor (Belgium) for the nuclides; 45Sc, 59Co, 94Zr, 186W, 197Au, 98Mo, 96Zr. We choose these nuclides, because they differ considerably in Q0i and
on the final element concentration in k0-method in the channels; 7 - 1, neutron trap of Dalat reactor (Vietnam) and channel 17 of THETIS reactor (Belgium) for the nuclides; 45Sc, 59Co, 94Zr, 186W, 197Au, 98Mo, 96Zr. We choose these nuclides, because they differ considerably in Q0i and 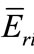 values. The numerical data of concerning isotopes and irradiation channels used in this work are summarized in Tables 4 and 5.
values. The numerical data of concerning isotopes and irradiation channels used in this work are summarized in Tables 4 and 5.
3. Results and Discussion
The absolute uncertainty in r can be calculated from the uncertainties of the variables (denoted xj) which determine r in Equation (1):
 (6)
(6)
where ∂a/∂xj are the corresponding partial derivatives.
According to the customary error propagation theory,

Table 4. Characteristics of isotopes used in the calculations of this work.

Table 5. Characteristics of irradiation channels considered: channles 17 of Thetis reactor, Belgium [9], 7 - 1 channel and neutron trap of Dalat reactor, Vietnam.
the error propagation functions can be written as:
 (7)
(7)
and relative error is:
 (8)
(8)
3.1. Influence of Uncertainty of 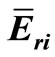 on NAA Results
on NAA Results
From Equation (8), the uncertainty of the concentration (r) in k0-method due to the uncertainties of the effective resonace energies can be written by:
 (9)
(9)
Using Equation (7) for the effective resonance energy of the nuclide i, we obtain:
 (10)
(10)
The values of calculated  for chosen nuclides are presented in Table 6. The effect of the effective resonance energy on NAA result include the uncertainties of the effective resonance energies of analytical and comparator nuclides. In this case, Au used as comparator with
for chosen nuclides are presented in Table 6. The effect of the effective resonance energy on NAA result include the uncertainties of the effective resonance energies of analytical and comparator nuclides. In this case, Au used as comparator with  of 5.65 eV and uncertainty of 7.1% from paper [5], the contribution of the uncertainty of
of 5.65 eV and uncertainty of 7.1% from paper [5], the contribution of the uncertainty of 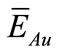 to the error of NAA result in channels 7 - 1, neutron trap of Dalat reactor and channel 17 of THETIS reactor is 0.17%, 0.077% and 0.13%, respectively. Clearly, the effect of the uncertainty of the effective resonance energy of Au is negligible and can be overlooked in the evaluation.
to the error of NAA result in channels 7 - 1, neutron trap of Dalat reactor and channel 17 of THETIS reactor is 0.17%, 0.077% and 0.13%, respectively. Clearly, the effect of the uncertainty of the effective resonance energy of Au is negligible and can be overlooked in the evaluation.
The analysis for 94 nuclides used in NAA showed that the uncertainties of their effective resonace energy are from 0 to 20%, except 75As (34%) [4]. In this measure, we are able to realize that the effect of them on NAA result is also negligible. For example, 45Sc ( = 5130 eV,
= 5130 eV, 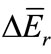 = 17%) and 95Zr (
= 17%) and 95Zr (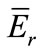 = 338 eV,
= 338 eV, 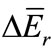 = 2.1%), the contribution of the uncertainty of the effective resonance energy to the error of NAA result in three above channels is less than 0.01% for 45Sc and 0.1% for 95Zr.
= 2.1%), the contribution of the uncertainty of the effective resonance energy to the error of NAA result in three above channels is less than 0.01% for 45Sc and 0.1% for 95Zr.
In epicadmium neutron activation analysis (ENAA), the f-term in Equation (10) should be omitted. The error propagation function of 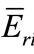 can be written:
can be written:
 (11)
(11)
The calculated results of 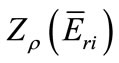 for the nuclides;
for the nuclides;
45Sc, 59Co, 94Zr, 186W, 197Au, 98Mo, 96Zr in ENAA are carried in Table 7. In this case, the error propagation function is higher than in the one of irradiation without cadmium. Generaly speaking, ai < 1 and if a  1, the contribution of
1, the contribution of  to the error of NAA result for almost analytical nuclides is less than 1% and can be omitted in the calculation.
to the error of NAA result for almost analytical nuclides is less than 1% and can be omitted in the calculation.
3.2. Influence of Uncertainty of ( on NAA Results
Also from Equation (8), the uncertainty of r due to the uncertainty of a can be written:
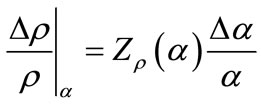 (12)
(12)
and error propagation function of a:
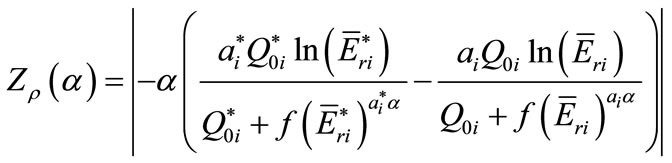 (13)
(13)
The values of the error propagation function of a in the channels; 7 - 1 and neutron trap of Dalat reactor (Vietnam) and channel 17 of THETIS reactor (Belgium) for the nuclides; 45Sc, 59Co, 94Zr, 186W, 197Au, 98Mo, 96Zr were shown in Table 8. From Table 8, for the nuclides having Q0 < Q0Au in three these channels, the contribution of the uncertainty of a to the error of NAA result is not significant, about less than 1%. But for nuclides having Q0  Q0Au, this effect is noticeable. For instance, in channel 7 - 1 of Dalat reactor (a = –0.044, Da = 12%
Q0Au, this effect is noticeable. For instance, in channel 7 - 1 of Dalat reactor (a = –0.044, Da = 12%

Table 6. Calculation results of 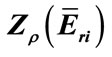 for chosen nuclides.
for chosen nuclides.
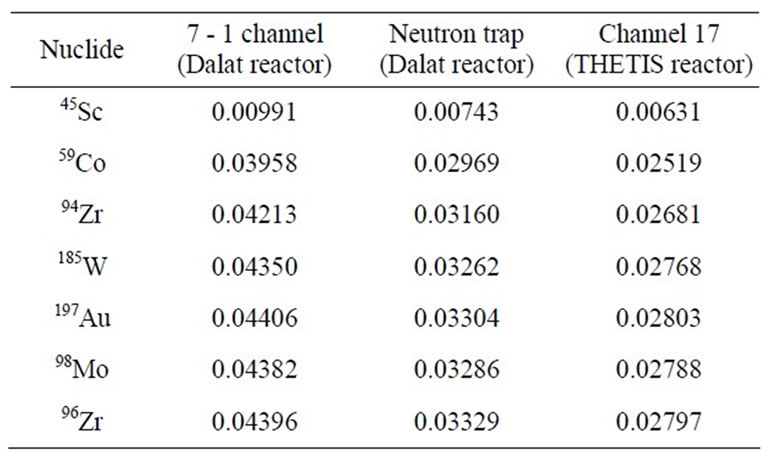
Table 7. Calculated results of 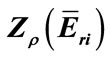 for the nuclides in ENAA.
for the nuclides in ENAA.
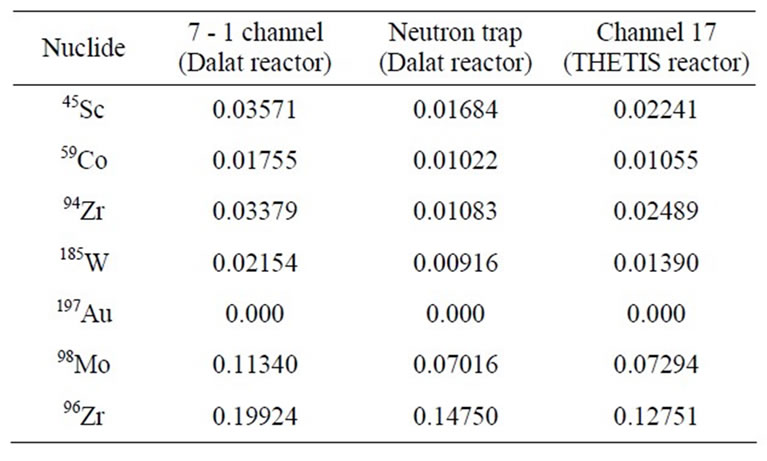
Table 8. Calculation results of Zr(a) for chosen nuclides.
[7,8]), the contribution of the uncertainty of a on the error of result of 45Sc (Q0 = 0.44) is 0.42%, but for 99Mo and 96Zr is 1.36% and 2.4%, respectively. As a comment, for RNAA using 197Au comparator, the systematic effect for a value up to 0.1 is practically negligible for all nuclides with a low enough Q0 value (e.g. 45Sc, 59Co, 58Fe, ect.). On the other hand, for nuclides with a relatively large Q0 value, a correction for the a effect becomes really necessary. To reduce the a effect, it is either to develop more accurate and precise techniques for a determination or to choose the irradiation channels with the a value low enough.
In the case of the epicadmium neutron activation, Equation (13) can be changed into:
 (14)
(14)
The values of the error propagation of a in this case were carried in Table 9. In this case, it clearly shows the inaccuracy of the approximation expression in [6] (Equation (4) in this report). Really, according to Equation (4), the error propagation function of a in the irradiation with cadmium can be written:
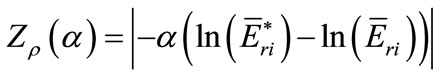 (15)
(15)
Equation (15) is different to Equation (14) by the correctional coefficients ai. However, the value of the error propagation function in channel 7 - 1 of Dalat reactor, for 45Sc is 0.0083 from Equation (14) and 0.2997 from Equation (15). If the uncertainty of a in experiment is 100%, the contribution of uncertainty of a on NAA result is 0.83% and 29.97%, respectively. It differs by a factor of 30 (!). Similarly, in channel 17 of Thetis reactor, the error propagation function for 45Sc is 0.0053 and 0.1907. The difference is huge. This comment is also correct for nuclides having Q0 < 1. It once more confirms that the approximation expression in paper [6] is not good for nuclides having Q0 < 1.
From Equation (13) or Equation (14), we easily estimate the influence of a on NAA results, if we know uncertainty of a in the irradiation channel. However, for ENAA (epicadmium neutron activation analysis) the situation is much more dramatic, especially for nuclides with low Q0 value.
3.3. Influence of Uncertainty of f on NAA Results
The error propagation function Zr(f) can be written:
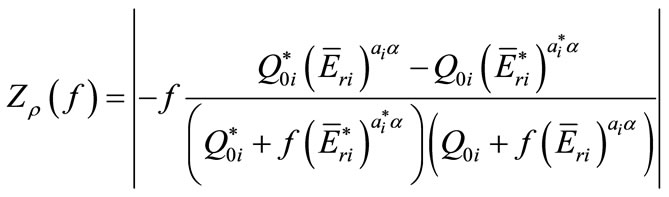 (16)
(16)
The values of the error propagation function of f in the channels; 7 - 1 and neutron trap of Dalat reactor and channel 17 of THETIS reactor for the nuclides; 45Sc, 59Co, 94Zr, 186W, 197Au, 98Mo, 96Zr were carried in Table 9. The uncertainty of f contributes on the error of NAA results is:
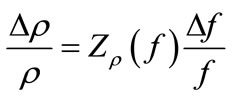 (17)
(17)
Generally seeing, the uncertainty of f in experiment is about less than 4%, therefore, from Table 10, the contribution of the uncertainty of f on the error of NAA result

Table 9. Calculation results of Zr(a) for the nuclides in ENAA.

Table 10. Calculation results of Zr(f) for chosen nuclides.
is about less than 2%.
3.4. Collective Influence of Uncertainties of (, 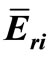 and f on NAA Results
and f on NAA Results
In view of the above, we can estimate the influence of the uncertainties of a, 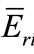 and f on final NAA results. The contribution of these parameters on the errors of the analysis results is written as:
and f on final NAA results. The contribution of these parameters on the errors of the analysis results is written as:
 (18)
(18)
However, as discussion above, the 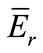 effect is negligible and can be omitted in Equation (18). Thus, the contribution on error of NAA results in this case is primarily due to the uncertainties of a and f. Finally, as well as estimation above, this overall contribution of a and f is about 2% on the error of NAA results. It was also confirmed by actual analysis.
effect is negligible and can be omitted in Equation (18). Thus, the contribution on error of NAA results in this case is primarily due to the uncertainties of a and f. Finally, as well as estimation above, this overall contribution of a and f is about 2% on the error of NAA results. It was also confirmed by actual analysis.
4. Conclusion
For a in the irradiation position relatively small ( ), Equation (5) is a good approximation to estimate influence of the neutron flux characteristics on NAA result using the k0 standardization method. From this approximative expression, the error propagation functions of the parameters were presented. They can be used for the estimation of the errors on NAA due to the uncertainty of the neutron flux characteristic parameters at the irradiation position. From the results of this report, it was also confirmed that the approximation in paper [6] is only acceptable for the nuclides having Q0i > 1, but not for the nuclides having Q0i < 1.
), Equation (5) is a good approximation to estimate influence of the neutron flux characteristics on NAA result using the k0 standardization method. From this approximative expression, the error propagation functions of the parameters were presented. They can be used for the estimation of the errors on NAA due to the uncertainty of the neutron flux characteristic parameters at the irradiation position. From the results of this report, it was also confirmed that the approximation in paper [6] is only acceptable for the nuclides having Q0i > 1, but not for the nuclides having Q0i < 1.
REFERENCES
- A. Simonits, F. De Corte and J. Hoste, “Single-Comparator Methods in Reactor Neutron Activation Analysis,” Journal of Radioanalytical and Nuclear Chemistry, Vol. 24, No. 1, 1975, pp. 31-46. doi:10.1007/BF02514380
- A. Simonits, L. Moens, F. De Corte, A. De Wispelaere, A. Elek and J. Hoste, “k0-Measurements and Related Nuclear Data Comilation for (n,g) Reactor Neutron Activation Analysis,” Journal of Radioanalytical and Nuclear Chemistry, Vol. 60, No. 2, 1980, pp. 461-516. doi:10.1007/BF02518906
- L. Moens, F. De Corte, A. De Wispelaere, J. Hoste, A. Simonits, A. Elek and J. Szabo, “k0-Measurements and Related Nuclear Data Comilation for (n, g) Reactor Neutron Activation Analysis,” Journal of Radioanalytical and Nuclear Chemistry, Vol. 82, No. 2, 1984, pp. 385-452. doi:10.1007/BF02037061
- F. De Corte, A. Simonits, F. De Wispelaere and J. Hoste, “A Compilation of k0-Factors and Related Nuclear Data for 94 Radionuclides of Interest in NAA,” INW/KFKI Interim Report, 1986.
- F. De Corte, A. Simonits, A. De Wispelaere and J. Hoste, “Accuracy and Applicability of the k0-Standardization Method,” Journal of Radioanalytical and Nuclear Chemistry, Vol. 113, No. 1, 1987, pp. 145-161. doi:10.1007/BF02036056
- J. Op De Beek, “Critical Evaluation of the Effective Resonance Energy Concept and the Epithemal Neutron Spectrum Shape-factor a for Reactor NAA Purposes,” Journal of Radioanalytical and Nuclear Chemistry, Vol. 89, No. 1, 1985, pp. 169-190.
- T. V. Hung, “Determination of a Factor of Epithemal Neutron Flux in Dalat Reactor, Vietnam, Based on Neutron Spectrum Calculated Using MCNP Code,” Journal of Radioanalytical and Nuclear Chemistry, Vol. 283, No. 2, 2010, pp. 707-711. doi:10.1007/s10967-010-0457-0
- T. V. Hung, “Modified Method of a Determination in the 1/E1+a Epithermal Neutron Spectrum of Reactor,” Journal of Radioanalytical and Nuclear Chemistry, Vol. 285, No. 2, 2010, pp. 331-336. doi:10.1007/s10967-010-0549-x
- F. De Corte, L. Moens, A. Simonits, K. Sordo-el Hammami, A. De Wispelaere and J. Hoste, “The Effect of the Epithermal Neutron Flux Distribution on the Accuracy of Absolue and Comparator Standardization Method in (n,g) Activation Analysis,” Journal of Radioanalytical and Nuclear Chemistry, Vol. 72, No. 1-2, 1982, pp. 275-286.

