Journal of High Energy Physics, Gravitation and Cosmology
Vol.02 No.01(2016), Article ID:62665,8 pages
10.4236/jhepgc.2016.21008
Gedanken Experiment Examining How Kinetic Energy Would Dominate Potential Energy, in Pre-Planckian Space-Time Physics, and Allow Us to Avoid the BICEP 2 Mistake
Andrew Walcott Beckwith
Physics Department, Chongqing University Huxi Campus, Chongqing, China

Copyright © 2016 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 20 October 2015; accepted 8 January 2016; published 12 January 2016
ABSTRACT
We use Padmabhan’s “Invitation to Astrophysics” formalism of a scalar field evolution of the early universe, from first principles, to show something which seems counter intuitive. How could, just before inflation, kinetic energy be larger than potential energy in pre-Planckian physics, and what physics mechanism is responsible for the Planckian physics result that Potential energy is far larger than kinetic energy. This document answers that question, as well as provides a mechanism for the dominance of kinetic energy in pre-Planckian space-time, as well as its reversal in the Planckian era of cosmology. The kinetic energy is proportional to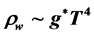 , with
, with  initial degrees of freedom, and T the initial temperature just before the onset of inflation. Our key assumption is the smallness of curvature, as given in the first equation, which permits adoption of the Potential energy and Kinetic energy formalism used, in the Planckian and pre-Planckian space-time physics. Interpretation of this result, if done correctly, will be able to allow a correct distinguishing of relic gravitational waves, as to avoid the BICEP 2 pickup of galactic dust as a false relic Gravitational wave signal, as well as serve as an investigative template as to if quantum gravity is embedded in a deterministic dissipative system, as cited in the conclusion.
initial degrees of freedom, and T the initial temperature just before the onset of inflation. Our key assumption is the smallness of curvature, as given in the first equation, which permits adoption of the Potential energy and Kinetic energy formalism used, in the Planckian and pre-Planckian space-time physics. Interpretation of this result, if done correctly, will be able to allow a correct distinguishing of relic gravitational waves, as to avoid the BICEP 2 pickup of galactic dust as a false relic Gravitational wave signal, as well as serve as an investigative template as to if quantum gravity is embedded in a deterministic dissipative system, as cited in the conclusion.
Keywords:
Geddanken Experiment, Kinetic Energy, Potential Energy

1. Introduction
We begin with a review from T. Padmanabhan [1] as to the foundations of a scalar field and a potential field, in terms of cosmological evolution. Following that, we are adding more detail as to a supposition by Handley et al. [2] . As to how one could invert the supposition of inflation, [1] , that the Kinetic energy would be much larger than the Potential energy [2] . Here, we offer a mechanism for how this may happen. This is in lieu as to C. VAN DEN BROECK in [3] namely that we need to distinguish between multiple early universe sources of gravitational wave, or the onset of inflation generated early gravitational waves, as seen in the below quotation
“Omni-directional gravitational wave background radiation could arise from fundamental processes in the early Universe, or from the superposition of a large number of signals with a point-like origin. Examples of the former include parametric amplification of gravitational vacuum fluctuations during the inflationary era”
In particular our approach is similar to the procedures outlined as to vacuum fluctuations in the (very early) inflationary era. And we will outline how we are avoiding multiple sources. Which would be done if there is a sharply focused peak frequency in magnitude and intensity, i.e. we wager that a sharply defined peak of GW amplitude and strain is about the only way to avoid the problems associated with Bicep 2, which was due to dust from galactic sources [3] - [5] .
Our gedanken experiment is a thought experiment, that kinetic energy dominates potential energy in the initial phase of cosmological evolution. As a second component of our thought experiment is then the smallness of curvature, so to a good first approximation so that then the formulation of near flatness in the beginning of space-time is a starting point for surprisingly traditional looking Friedman cosmological equations, due to the minimal influence of curvature, which would be a consequence of [6] .
Furthermore in our thought experiment is the supposition that the dominance of kinetic energy is in the regime of space-time before a Planck time interval has transpired. Implicit in this is the supposition that there is such a regime of space-time which the author has also worked out in [7] . If there is a regime of space-time just before Planck time, and this convention adheres to [2] that kinetic energy is, indeed greater than potential energy. In the pre-Planckian space time regime we will have, then a kinetic energy term with imaginary time, and that then the points just before Planck time will have a Potential energy as given by an imaginary time component as set by
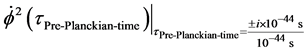 (1)
(1)
Here, what has done, is to scale real to imaginary time, and to normalize it by a division of 10−44 seconds, effectively having a “rescaled” pre-Planckian time which would be written as an imaginary number with
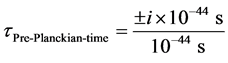 (2)
(2)
This means that in an interval just before the Planck time, that we are postulating a pre-Planckian space-time which is purely imaginary, i.e. operationally Equation (2) is, effectively in the regime of analysis of Kinetic energy dominance given by
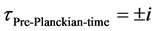 (3)
(3)
The change in time from imaginary to real time, is in line with a full evaluation of a transition from Equation (3) to the regime of space-time dominated by
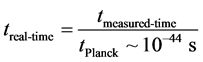 (4)
(4)
In particular what we are supposing is a transformation from the pre-Planckian to Planckian regime given by
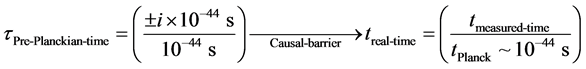 (5)
(5)
The right hand side would represent non imaginary time, whereas the regime where there is imaginary structure would represent sub divisions in causal structure of space-time, as alluded to by Dowker [5] [8] with what is represented in Equation (5) as a division from pre-Planckian to Planckian space-time, and a defacto Causal structure with the imaginary time component one which is “tunneled” through, to reach Planckian Space-time physics.
What is conserved between the transference from a prior universe, to present universe would be at the Planckian regime, a minimum stress energy Tensor, which by [3] is given as a term with has the label of 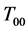 for transferred space-time energy, and then a measure of curvature of space-time as given in [6] as, if
for transferred space-time energy, and then a measure of curvature of space-time as given in [6] as, if
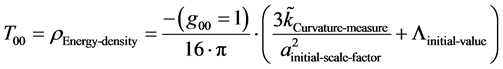 (6)
(6)
The 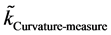 is defined in [6] and can be usually thought of as how gravity affects space-time geometry, as given in [9] which is part of the definition of a Riemann Scalar, for which as given in [6] we have that the Riemann scalar is given as
is defined in [6] and can be usually thought of as how gravity affects space-time geometry, as given in [9] which is part of the definition of a Riemann Scalar, for which as given in [6] we have that the Riemann scalar is given as
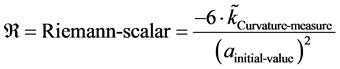 (7)
(7)
The term for a minimum scale factor is given in Equation (7) which is the smallest unit of evolving space-time which is accessible to analysis, which is akin to adopting the bounce definition of a non-singular starting point of a universe expansion as given in [7] [8] [10] [11] with a minimum initial scale value given in [3] [6] as
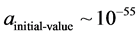 (8)
(8)
If so, then we find then that, if we are looking at a cosmological constant, as defined in [9] [10] [12] [13] with an initial value of this cosmological constant as written as 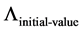 (leaving open the possibility that the cosmological constant could have changed over time, i.e. quintessence, as seen in [11] [14] ), that then, as given in part by [3] [6] , where
(leaving open the possibility that the cosmological constant could have changed over time, i.e. quintessence, as seen in [11] [14] ), that then, as given in part by [3] [6] , where  is three space volume, not including the time dimension,
is three space volume, not including the time dimension,
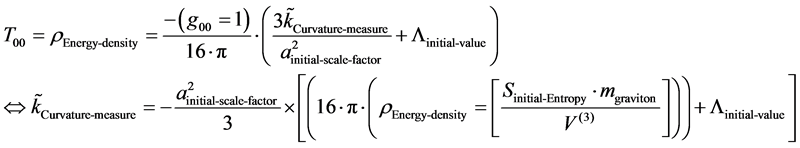 (9)
(9)
Here in part we are partaking of the idea of a massive graviton, of about 10−62 grams, as given by [12] [15] . and we also, to those whom object to the idea of a massive Graviton refer to Maggiore [13] [16]

Here, the T is the trace of the Einstein Stress energy Tensor, whereas h is the trace of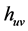



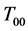
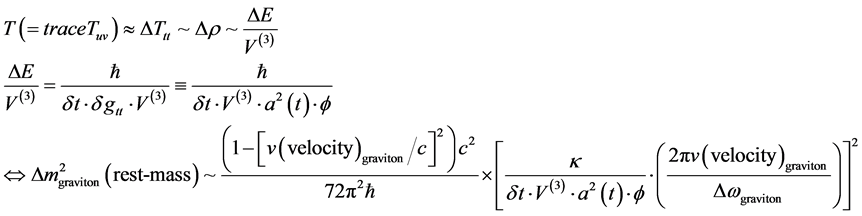
The term of the 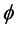
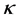
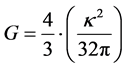
If the curvature measure, above is almost zero, then we can use from [1] , with 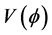
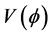
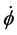
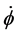

If so, then using the Potential energy and Kinetic energy values from [1] we can write the following: Keep in mind that in Equation (14) that the H referred to is defined by Equation (13) above, and so we write below explicit entries for the Potential energy, 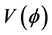
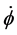
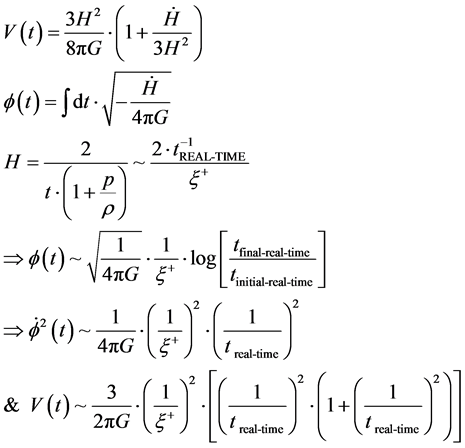
The term 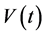
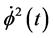
We will, for now on, to keep this real time non dimensional, make the following identification with, once again, Equation (4), which has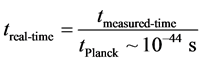
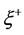
2. Re Examination of Equation (14) and Equation (4) in a Pre Universe Configuration
Our supposition is that Equation (2) to Equation (5) in the matter of pre-Planckian space time, say in a boundary of 2 times Planck time to buttress the repeating cyclical universe we are assuming as possibility given by Penrose [17] , is changed then to take into the quantum bounce analogy we think should be looked at [11] as given by C. Rovelli and F. Vidotto. So then we get from Planckian space time, a real time evaluation which shrinks to imaginary time, via the following rule
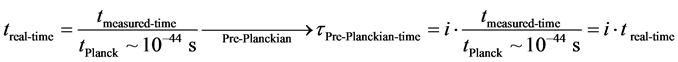
i.e. what we are saying is that, there is a retime in the pre-Planckian regime of space-time
In a boundary of 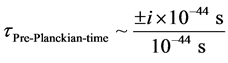
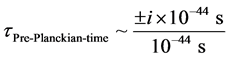
Pick the following point of evaluation, namely at the transit point between the plus to the minus regions of
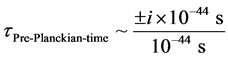

The fact we have a very large non zero 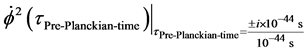
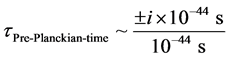
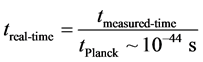
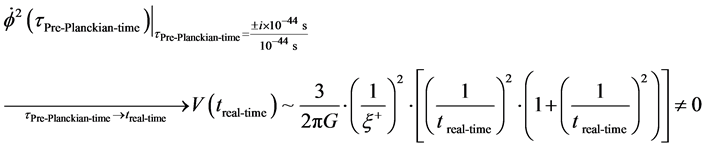
In making this evaluation, we are assuming that there could be use of the following for relic Gravitational waves., i.e. for Equation (17) to hold we will be looking at a time interval which may be specified by [18] [19]
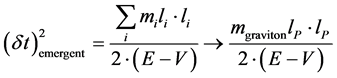
Initially, as postulated by Babour [18] [19] this set of masses, given in the emergent time structure could be for say the planetary masses of each contribution of the solar system. Our identification is to have an initial mass
value, at the start of creation, for an individual graviton. So If 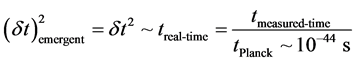
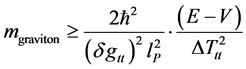
This would entail assuming relic gravitation generated by a massive graviton bounded below by
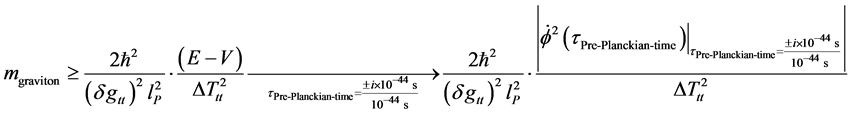
And the magnitude of K.E. as defined by
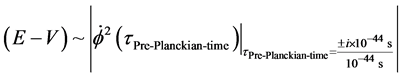
If so, then if we use Equation (16) and Equation (20) and Equation (21) so as to obtain

If so, then, we come to a conclusion, which uses a basic energy density result from Kolb and Turner [9] that the Kinetic energy, as defined in pre-Planckian physics, as defined in this document is decisively important, as given in the conclusion.
3. Re-Examining Relic Gravitational Wave Models as to What Relic Gravitational Waves Could Tell Us about the Origins of the Early Universe
It is very noticeable that in [21] we have that the following quote is particularly relevant to consider, in lieu of our results
“Thus, if advanced projects on the detection of GWs will improve their sensitivity allowing to perform a GWs astronomy (this is due because signals from GWs are quite weak) [16] , one will only have to look the interferometer response functions to understand if General Relativity is the definitive theory of gravity. In fact, if only the two response functions (2) and (19) will be present, we will conclude that General Relativity is definitive. If the response function (22) will be present too, we will conclude that massless Scalar-Tensor Gravity is the correct theory of gravitation. Finally, if a longitudinal response function will be present, i.e. Equation (25) for a wave propagating parallel to one interferometer arm, or its generalization to angular dependences, we will learn that the correct theory of gravity will be massive Scalar-Tensor Gravity which is equivalent to f(R) theories. In any case, such response functions will represent the definitive test for General Relativity. This is because General Relativity is the only gravity theory which admits only the two response functions (2) and (19) [21] . Such response functions correspond to the two “canonical” polarizations h+ and h×. Thus, if a third polarization will be present, a third response function will be detected by GWs interferometers and this fact will rule out General Relativity like the definitive theory of gravity”
We argue that a third polarization in Gravitational waves from the early universe may be detected, if there is proof positive that in the pre-Planckian regime that the Corda conjecture [20] as given below, namely if the following analysis is part of our take on relic gravitational waves, is supported by the kinetic energy being larger than the potential energy, namely what if
“The case of massless Scalar-Tensor Gravity has been discussed in [22] [23] with a “bouncing photons analysis” similar to the previous one. In this case, the line-element in the TT gauge can be extended with one more polarization, labelled with Φ(t + z), i.e. …”
i.e. the dominance of Kinetic energy over Potential energy, in pre-Planckian physics could serve as a template for verification for the existence of a third polarization along the lines brought up in [20] and its confirmation or falsification would yield foundational insight available nowhere else possible.
4. Conclusions
Our hypothesis, as to Equation (22), is equivalent to what is frequently postulated as an energy density as given by Kolb and Turner [12] . First of all the below is equivalent to
If so, then the lower bound to the graviton will be then as given by Equation (24) below, if we use Equation (23), then
i.e. if we have a comparatively low initial temperature, T, it will mean a large initial graviton mass. If the T is of the order of Planck temperature, say 1032 Kelvin, then the above will have a lower graviton mass value of about 10−66 grams. It goes up if there is what is called a (colder cosmology) about 1 order of magnitude lower initial temperature, leading to the mass of a graviton bounded below by 10−58 grams. Really cold initial temperatures far lower than 1032 degrees Kelvin for T would lead to maybe even 10−50 grams for the initial lower bound to the graviton mass.
For consistency with the 10−62 gram value as given by [15] we would probably be considering it desirable for 1032 degrees Kelvin for T. In all this we will be considering 
It is worth noting that Dr. Corda in [21] has extended the Maggiorie results [16] as given in the prior reference [21] section and that indeed Maggiore studied the detectability only for GWs having a wavelength very much longer than the interferometer’s arms, while Corda [21] extended the results to all the GWs wavelengths. The importance of this contribution is, if we find out if there is a third polarization as indicated above, possibly due to a dominance of kinetic energy, i.e. the dominance in a pre-Planckian mode of space time may allow for settling the question given in [21] , with an appropriately chosen magnitude, and frequency, and also allow for avoiding the mistake of Bicep 2, as given in references [21] [24] .
We also state unequivocally, that confirmation of this result would give reality to the suppositions given in references [16] - [20] , which would through analysis help toward falsifiable measurements which would allow us to determine if Quantum physics and quantum gravity are, indeed part of a larger non deterministic theory, as given in [25] .
Acknowledgements
This work is supported in part by National Nature Science Foundation of China grant No. 11375279.
Cite this paper
Andrew WalcottBeckwith, (2016) Gedanken Experiment Examining How Kinetic Energy Would Dominate Potential Energy, in Pre-Planckian Space-Time Physics, and Allow Us to Avoid the BICEP 2 Mistake. Journal of High Energy Physics, Gravitation and Cosmology,02,75-82. doi: 10.4236/jhepgc.2016.21008
References
- 1. Padmanabhan, T. (2006) An Invitation to Astrophysics. World Scientific Co., Pte. Ltd., Singapore.
- 2. Handley, W.J., Brechet, S.D., Lasenby, A.N. and Hobson, M.P. (2014) Kinetic Initial Conditions for Inflation. http://arxiv.org/pdf/1401.2253v2.pdf
- 3. Van Den Broeck, C., et al. (2015) Gravitational Wave Searches with Advanced LIGO and Advanced Virgo. http://arxiv.org/pdf/1505.04621v1.pdf
- 4. Cowen, R. (2015) Gravitational Waves Discovery Now Officially Dead; Combined Data from South Pole Experiment BICEP2 and Planck Probe Point to Galactic Dust as Confounding Signal. http://www.nature.com/news/gravitational-waves-discovery-now-officially-dead-1.16830
- 5. Cowen, R. (2014) Full-Galaxy Dust Map Muddles Search for Gravitational Waves. http://www.nature.com/news/full-galaxy-dust-map-muddles-search-for-gravitational-waves-1.15975
- 6. Beckwith, A. (in press) Geddankenexperiment for Degree of Flatness, or Lack Of, in Early Universe Conditions. Accepted for publication, JHEPGC. http://vixra.org/abs/1510.0108
- 7. Beckwith, A. (2016) “Gedanken Experiment for Fluctuation of Mass of a Graviton, Based on the Trace of a GR Stress Energy Tensor-Preplanckian Conditions Lead to Gaining of Graviton Mass, and Planckian Conditions Lead to Graviton Mass Shrinking to 10-62 Grams. Journal of High Energy Physics, Gravitation and Cosmology, 2, 19-24. http://vixra.org/abs/1510.0495
- 8. Dowker, F. (2005) Causal Sets and the Deep Structure of Space-Time. http://arxiv.org/abs/gr-qc/0508109
- 9. Katti, A. (2013) The Mathematical Theory of Special and General Relativity. Create Space Independent Publishing, North Charleston.
- 10. Haggard, H.M. and Rovelli, C. (2014) Black, Hole Fireworks: Quantum Gravity Effects Outside the Horizon Spark Black to White Hole Tunneling. http://arxiv.org/abs/1407.0989
- 11. Rovelli, C. and Vidotto, F. (2015) Covariant Loop Quantum Gravity: An Elementary Introduction to Quantum Gravity, and Spinfoam Theory. Cambridge University Press, Cambridge.
- 12. Kolb, E.W. and Turner, M.S. (1990) The Early Universe. The Advanced Book Program, Addison-Wesley Publishing Company, Redwood City.
- 13. Padmanabhan, T. (2010) Gravitation, Foundations and Frontiers. Cambridge University Press, Cambridge.
- 14. Ratra, P. and Peebles, L. (1988) Cosmological Consequences of a Rolling Homogeneous Scalar Field. Physical Review D, 37, 3406. http://dx.doi.org/10.1103/PhysRevD.37.3406
- 15. Goldhaber, A. and Nieto, M. (2010) Photon and Graviton Mass Limits. Reviews of Modern Physics, 82, 939-979. http://arxiv.org/abs/0809.1003 http://dx.doi.org/10.1103/RevModPhys.82.939
- 16. Maggiorie, M. (2008) Gravitational Waves, Volume 1: Theory and Experiments. Oxford University Press, Oxford.
- 17. Penrose, R. (2010) Cycles of Time: An Extraordinary New View of the Universe. The Bodley Head, London.
- 18. Barbour, J. (2009) The Nature of Time. http://arxiv.org/pdf/0903.3489.pdf
- 19. Barbour, J. (2010) Shape Dynamics: An Introduction. In: Finster, F., Muller, O., Nardmann, M., Tolksdorf, J. and Zeidler, E., Eds., Quantum Field Theory and Gravity, Conceptual and Mathematical Advances in the Search for a Unified Framework, Birkhauser, Springer-Verlag, London, 257-297.
- 20. Beckwith, A.W. (2015) Gedankenexperiment for Refining the Unruh Metric Tensor Uncertainty Principle via Schwartzshield Geometry and Planckian Space-Time with Initial Nonzero Entropy and Applying the Riemannian- Penrose Inequality and Initial Kinetic Energy for a Lower Bound to the Graviton. http://vixra.org/abs/1509.0173
- 21. Corda, C. (2009) Interferometric Detection of Gravitational Waves: The Definitive Test for General Relativity. International Journal of Modern Physics D, 18, 2275-2282. http://arxiv.org/abs/0905.2502 http://dx.doi.org/10.1142/S0218271809015904
- 22. Capozziello, S. and Corda, C. (2006) Scalar Gravitational Waves from Scalar-Tensor Gravity: Production and Response of Interferometers. International Journal of Modern Physics D, 15, 1119-1150. http://dx.doi.org/10.1142/S0218271806008814
- 23. Corda, C. (2007) The Virgo-Minigrail Cross Correlation for the Detection of Scalar Gravitational Waves. Modern Physics Letters A, 22, 1727-1735. http://dx.doi.org/10.1142/S0217732307024140
- 24. Das, S., Mukherje, S. and Souradeep, T. (2015) Revised Cosmological Parameters after BICEP 2 and BOSS. http://arxiv.org/abs/1406.0857
- 25. t’Hooft, G. (1999) Quantum Gravity as a Dissipative Deterministic System. http://arxiv.org/PS_cache/gr-qc/pdf/9903/9903084v3.pdf

