Journal of Geoscience and Environment Protection
Vol.04 No.12(2016), Article ID:72646,17 pages
10.4236/gep.2016.412008
Evaluation of GSMaP Daily Rainfall Satellite Data for Flood Monitoring: Case Study―Kyushu Japan
Martiwi Diah Setiawati1, Fusanori Miura2
1Integrated Research System for Sustainability Science (IR3S), The University of Tokyo, Bunkyo, Japan
2Graduate School of Science and Engineering, Yamaguchi University, Ube, Japan

Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: November 4, 2016; Accepted: December 5, 2016; Published: December 8, 2016
ABSTRACT
In this paper, the Global Satellite Mapping of Precipitation Moving Vector with Kalman filter (GSMaP_MVK) was evaluated and corrected at daily time scales with a spatial resolution of 0.1˚ latitude/longitude. The reference data came from thirty- four rain gauges on Kyushu Island, Japan. This study focused on the GSMaP_MVK’s ability to detect heavy rainfall patterns that may lead to flooding. Statistical analysis was used to evaluate the GSMaP_MVK data both quantitatively and qualitatively. The statistical analysis included the relative bias (B), the mean error (E), the Nash- Sutcliffe coefficient (CNS), the Root Mean Square Error (RMSE) and the correlation coefficient (r). In addition, Generalized Additive Models (GAMs) were used to conduct GSMaP_MVK data correction. The results of these analyses indicate that GSMaP_MVK data have lower values than observed data and may be significantly underestimated during heavy rainfall. By applying GAM to bias correction, GS- MaP_MVK’s ability to detect heavy rainfall was improved. In addition, GAM for bias correction could effectively be applied for significant underestimates of GSMaP_ MVK (i.e., bias of more than 55%). GAM is a new approach to predict rainfall amount for flood and landslide monitoring of satellite base precipitation, especially in areas where rain gauge data are limited.
Keywords:
Evaluation, GSMaP_MVK, Flood Monitoring, Kyushu

1. Introduction
Reliable global precipitation information and accurate temporal precipitation estimates are essential to manage freshwater resources and to predict high impact weather events such as hurricanes, typhoon, heavy rains which cause floods and landslides [1] . However, measuring precipitation is one of the most difficult observational challenges of meteorology because precipitation occurs intermittently and with pronounced geographic and temporal variability [2] . Conventional rain gauge networks provide relatively accurate point measurements of precipitation [3] [4] . However, the uneven distribution of gauges and their limited sampling area burden an important problem regarding to the effectiveness of spatial coverage [5] . Moreover, uninhabited and remote areas are not covered by rain gauge networks [3] [4] . Furthermore, continuous spatial and temporal distribution of rainfall are provided by radar, but the quantitative range of their measurements is generally limited to 150 km or less and produces incomplete coverage [3] [4] . On the other hand, satellite remote sensing technique became an interesting option for monitoring rainfall over a large area and high temporal resolution in near real time. In addition, satellite precipitation provides integrated spatial coverage of rainfall measurements even in remote land and ocean areas [3] [4] [6] . A combination of gauge data, radar data and satellite data is substantially needed to enhance space and time rainfall estimation [7] .
As satellite data, infrared and microwave satellite products, such as the Global Satellite Mapping of Precipitation (GSMaP) as a combination of multiple precipitation satellite data, could be used to derive estimates of large scale precipitation over a global area [8] . The GSMaP rain product is based on using four satellite microwave radiometers combined with Geo Infrared radiometer data to produce 0.1 degree spatial resolution [9] . There are several types of GSMaP rain product as explained in Section 2.3. In this paper, GSMaP_MVK (Moving Vector with Kalman Filter) Version 5 was employed due to its data which caused flooding in Kyushu Island.
Comprehensive details about the GSMaP_MVK ground validation program, algorithms and data processing were provided by Kubota et al. (2007) [10] . In addition, GSMaP_MVK was verified from January through December 2004 in Japan to determine whether monthly data, daily data and 3 hourly data matched rain gauge data [11] . The result showed that GSMaP_MVK of monthly, daily and 3 hourly data from May to October had high correlation and had the same trend as rain gauge data, but in some cases, GSMaP_MVK data still underestimate with the rain gauge data. For several years, other groups studied different locations to validate GSMaP_MVK data. According to their researches, the GSMaP_MVK data could detect a precipitation occurrence with the same trend as rain gauge data, but the precipitation amount generally underestimated in some cases [12] [13] [14] [15] and according to [16] GSMaP_MVK had serious underestimation of rainfall amount compared with other precipitation satellite. For these reasons, improving the GSMaP_MVK data verification result is important, especially when heavy rainfall occurs. In this study, first, we evaluated GSMaP_MVK data during rainy season in Japan, then we evaluated separately based on elevation, location, and heavy rainfall category.
The objectives of this study are to advance the quantitative and qualitative understanding of GSMaP_MVK product and to correct GSMaP_MVK product to achieve better agreement with rain gauge data for flood monitoring. In addition, Generalized Additive Model (GAM) was conducted to improve GSMaP_MVK ability. GAM is the statistical analysis which allows non-parametric distribution and extends the use of additive models to data sets hat have non-Gaussian distributions, such as binomial, Poisson and gamma distributions [17] . GAMs are rarely used to improve the accuracy of satellite precipitation data, but it was used to forecast daily precipitation data over the basin and to forecast the frequency of extreme daily precipitation [18] . We conducted this method due to non-parametric rain gauge data distribution and promising models for daily precipitation data [19] . By this method, we expected to improve the estimated rainfall amount by GSMaP_MVK data during heavy rainfall events in Kyushu Island, Japan.
2. Materials and Method
2.1. Study Area
2.1.1. Flood History in Kyushu, Japan
Japan is particularly vulnerable to flooding because of its steep geography and humid climate characterized by heavy rains and typhoons [20] . The number of floods, and, hence, the damage due to flooding, have increased since 2004 [20] . Several local heavy rainfalls have been recorded in Kyushu, Japan, in recent years (Miyazaki: 4-7 September 2005; Kumamoto: 3 July 2006; Kumamoto, Kagoshima, Miyazaki: 20-23 July 2006; Kagoshima, Miyazaki, Kumamoto: 11-17 July 2007). All of these heavy rainfalls created local floods and damage, leading to significant economic losses [21] .
2.1.2. Kyushu Geographic Landscape and Climate Pattern
Kyushu Island, the study area, was shown in Figure 1. This figure was constructed by overlaying topography (i.e., It was downloaded from Shuttle Radar Topography Mission (SRTM) of digital elevation model with spatial resolution 30 m) of the study area and rain gauge distribution. The study area is located in the south part of Japan and has an area of 35,640 km2 from latitude 31˚N to 34˚N and longitude 129˚30'E to 132˚E. It has a humid subtropical climate and has an elevation ranging from 0 m to 1791 m above the sea level. Kyushu Island is mountainous, with hills that run from north to south in the center of the island. Generally, the land use in this island is dominated by agriculture. Precipitation occurs throughout the year with the heaviest in the summer season, especially in rainy season (i.e., May, June, July). During the summer season the variability of temperature range is from 16˚C to 31˚C and the annual precipitation is about 1760 mm/year [22] .
2.2. Rain Gauge
Daily observed rainfall data from 34 rain gauges over Kyushu island were used as reference data to validate the GSMaP_MVK estimation. The rain gauge data were obtained from AMEDAS (Automated Meteorological Data Acquisition System) developed by the Japan Meteorological Agency (JMA) during 2005 to 2007 through the rainy season, from May to July. The distribution of the rainfall stations was shown in Figure 1. The total observation data were obtained by multiplying the total day (92 days × 3 years) and the number of rain gauge data (34 points). Due to some lack of in-situ data, the total of observational data was 9276. The data are available online at the JMA website (http://www.data.jma.go.jp).
Figure 1. The study area, Kyushu Island, and its topography (http://earthexplorer.usgs.gov/). Black triangle indicates the rain gauge locations.
2.3. GSMaP Data
GSMaP was initiated by the Japan Science and Technology Agency (JST) in 2002 and has been promoted by the Japan Aerospace Exploration Agency (JAXA) Precipitation Measuring Mission (PMM) science team since 2007 to produce a global precipitation product with high temporal and spatial resolution [23] . Moreover, the data set produced by GSMaP product can be downloaded from their website:
http://sharaku.eorc.jaxa.jp/GSMaP_crest/html/data.html. The standard version of the GSMaP data sets includes GSMaP_TMI (retrieved from TRMM/TMI algorithm), GSMaP_MWR (retrieved from six space borne microwave radiometers), GSMaP_ MWR+ (retrieved from six space borne microwave radiometers with AMSU-B product), GSMaP_MVK (retrieved from MWR GEO IR combined algorithm), GSMaP_ MVK+ (retrieved from MWR GEO IR combined algorithm with AMSU-B product) and other rainfall estimates from passive microwave radiometer [24] .
The GSMaP rainfall product used here for comparison with reference gauge data set is GSMaP_MVK product version 5. This product is the combination of low earth orbit multi satellite microwave radiometer data and infrared radiometer (IR) on geostationary (Geo) orbit. The available microwave sensors are SSM/I (Special Sensor Microwave/Imager), TMI (TRMM Microwave Imager), and AMSR-E (Advanced Microwave Scanning Radiometer for EOS). Whereas, the IR data sets used in the current version of the system are from the CPC (Climate Prediction Centre). The algorithm to regain surface precipitation rate based on the Aonashi, et al. (1996) was conducted in this product. The brightness temperature at microwave frequencies as the main input of GSMaP_MVK system was converted into precipitation data [23] . The combination technique to produce 0.1˚ in latitude and longitude and 1 hour resolution with the domain covering 60˚N to 60˚S was obtained using a morphing technique based on an infrared cloud moving vector and Kalman Filter technique (Ushio, et al., 2009). GSMaP_MVK version 5 is available from March 2000 until December 2010. Thus the history of rainfall data which caused flood in Kyushu Island can be obtained. The rain rate daily data of GSMaP_MVK from May to July in 2005 to 2007 were downloaded and then converted into accumulated daily rainfall of GSMaP_MVK. GSMaP_MVK was processed by using Open GRADS software and one-pixel average of precipitation data was calculated based on the rain gauge data position. Detail about GSMaP MVK was shown in Table 1.
2.4. Validation and Intercomparison
The data coverage of this study was three years (2005 to 2007) in the rainy seasons. It was selected based on the annual flood occurrence in the study area. The main validation was for daily satellite rainfall product. As shown in Figure 1, the validation region has very complex terrain. Thus validation data from the whole island may not give the whole picture. Therefore, validation of the daily satellite products was conducted separately for the elevation (highland and lowland part of Kyushu), location (west and east of Kyushu) and heavy rainfall to investigate the performance of the product over different climatic regimes. Lowland was defined where the elevation was under 500 m and highland was defined where the elevation was above 500 m [16] The west and east Kyushu were defined by dividing the prefectures according to the wind direction. In addition, heavy rain was defined as daily rainfall exceeding the 95th percentile (rain_P95) for all stations and all categories [25] . Point by point analysis and spatial average analysis were conducted to compare gauge data and satellite data. [26] and [27] also applied this method.
Table 1. Detail product [23] .
Standard validation statistics are used to evaluate the GSMaP_MVK product to the rain gauge data. Qualitative and quantitative validations were conducted as follows. Qualitative method is to measure the correspondence between the value of the estimates and the observations. To quantify the correspondence value, the following five statistical indices were used [28] , the relative bias (B), the mean error (E), the Nash- Sutcliffe (CNS), the Root Mean Square Error (RMSE) and the correlation coefficient (r). These indices are given by following Equations.
 (1)
(1)
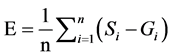 (2)
(2)
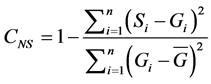 (3)
(3)
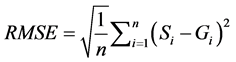 (4)
(4)
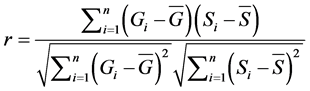 (5)
(5)
where, n is the total number of the rain gauge data or GSMaP data; Si is the satellite estimates and Gi is the rain gauge observation values.
The other validation statistics is the quantitative method which based on the contingency tables shown in Table 2. The rainfall threshold used for rain/non rain discrimination is 0 mm/day.
In Table 2, A, B, C, and D represent “hit”, “false alarm”, “miss” and “correct negative”. “Hit” represents correctly estimated rain events, “miss” describes when rain is not estimated but actual rain occurs, “false alarm” represents when rain is estimated but actually rain doesn’t occur, and “correct negative” represents correctly estimated no- rain events. Using the results shown in Table 2, Probability of Detection (POD), False Alarm Ratio (FAR), and Heidke Skill Score (HSS) statistics parameters are calculated by following Equations.
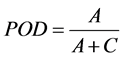 (6)
(6)
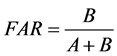 (7)
(7)
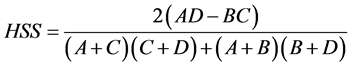 (8)
(8)
where, POD explains how good the GSMaP estimates are in detecting the occurrence of rainfall. FAR shows how often the GSMaP detects rainfall when rain gauge measurement is zero. Furthermore, HSS measures the rainfall detection accuracy of the satellite estimates relative to matches resulting from random chance.
Table 2. Contingency table of yes or no events/with rain or no rain.
2.5. Determining Bias Correction by Power Function
Comparison between GSMaP_MVK data with ground station measurement showed large differences during heavy rainfall as shown in the following sections. Therefore, the previous researchers obtained bias correction equations to achieve the best result. To accommodate for finding the relative bias varied with daily rainfall, a power function was applied to derive bias corrected rainfall (P*) [29] as follows:
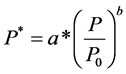 (9)
(9)
where P is GSMaP_MVK, P0 is the reference daily rainfall (1 mm/day), a (mm) is the constant and b is the power function. The linear regression analysis was previously applied to obtain the values of a (1.41 mm/day) and b (0.15) where all the data were transformed into logarithmic. This analysis is as a reference test for correction only for heavy rainfall section because this correction method has not been applied to the heavy rainfall case.
2.6. Determining Bias Correction by Generalized Additive Model
According to the previous research, GSMaP_MVK had underestimated the rain gauge data. Therefore, a bias correction equation was applied to achieve a closer fit between daily GSMaP_MVK and rain gauge data. GAM was applied because it has been widely adopted as an effective model and it has smoothing functions to analyze many complex time series data [17] . GAM have been widely employed in other disciplines to model the health impacts of air pollution or long term variability in biota spatial density, but rarely applied in hydrology [30] [31] .
GAM was created by R version 3.0.2 software, using the gam function of the mgcv package [17] , with the rain gauge data as response variables and GSMaP data as predictor variables. GAM model in the form of an Equation (10) was applied:
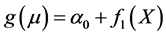 (10)
(10)
where g is the link function (identity link), µ is the expected value of the rain gauge data, α0 is the model constant and f1 is a smoothing function of the X (which corresponds to the daily GSMaP_MVK data) [17] . The α0 was calculated according to the total average of AMEDAS data (i.e., 12.4 mm/day). In addition, when the GSMaP_MVK value is zero, the expected value of rain gauge data is equal to 2.16 mm/day.
The Gaussian distribution is generally used in GAM, but we did not use the Gaussian distribution because the distribution of the rain gauge data was asymmetric. The rain gauge data could be predicted using the predict.gam function in the mgcv package using similar covariates as were used to build the model.
3. Results and Discussion
3.1. General Comparison of Daily Rain Gauges with GSMaP_MVK Data
This study first compared daily rain gauge data (AMEDAS) with GSMaP_MVK data. Figure 2 shows the scatter plot of AMEDAS data versus daily GSMaP_MVK data, the total data number and the mean values are also indicated in the plot. The validation statistics of GSMaP_MVK are listed in Table 3. In general, rainfall from GSMaP_MVK was lower than rainfall from rain gauge data: the average rainfall from rain gauge data was 12.39 mm/day, whereas the average rainfall from GSMaP_MVK was 6.59 mm/day. GSMaP_MVK data in the study area have a strong correspondence with rain gauge data
Figure 2. Scatter plot of daily rain gauge data versus GSMaP_MVK product during rainy season from 2005 to 2007.
Table 3. Validation statistics of daily GSMaP_MVK product during rainy season from 2005 to 2007.
(r = 0. 74), with the bias value was −46.78%. Moreover, the variance magnitude of individual errors can be described by calculating the values of E and RMSE (i.e., −5.8 mm/day and 22.82 mm/day, respectively). The greater difference between them, the greater the variance in the individual errors in the sample.
Furthermore, the consistency of GSMaP_MVK to measure the rainfall amount can be described through CNS index. The CNS index of the study area was 0.46 (46%), it means that GSMaP_MVK has the consistency to measure the rainfall amount about 46%. POD of GSMaP_MVK are close to 81% and FAR is generally small (18%). The HSS statistic shows that the GSMaP_MVK estimates have reasonably good skills in detecting the occurrence of rainfall (67%).
A comparison of long term means of daily rainfall measured by GSMaP_MVK and rain gauge data for a three-year period was shown in Figure 3. Figure 3 indicated that the pattern of daily means was similar and had a very strong correspondence to rain gauge data (r = 0.9), but GSMaP_MVK data were underestimated, with the bias, mean error and RMSE were −46.75%, −5.78 mm/day and 9.02 mm/day, respectively. In addition, GSMaP_MVK had high consistency with the CNs value of 0.53. In general, GS- MaP_MVK product had underestimated. This will be partly because the current algorithm of microwave radiometer did not include the topographical effect and the brightness temperature from microwave radiometer had directly underestimate relation with precipitation [23] . Consequently, GSMaP_MVK data correction was needed to reduce bias, error and RMSE and to increase CNs and correlation coefficient. In this study, GAM approach was applied for bias correction.
3.2. Validation and Correction of GSMaP_MVK in the Highland and Lowland
The main topographic feature of Kyushu is land is the large mountain ranges which located in the center of the island and the plain regions that cover the eastern and western
Figure 3. Long term mean of daily rainfall measured by AMEDAS and GSMaP_MVK for three years during rainy season. Daily rainfall is spatially averaged over 34 rain gauges.
part of the island. The elevation of mountainous region can exceed 1700 m while the eastern and western parts are below 500 m. In this study, we first divided the validation and correction based on the elevation because it has significant influence on the rainfall climatological pattern [16] . The eastern and western plain region receives about 2071 mm of annual rainfall while in the mountainous region receives about 3321 mm of annual rainfall. It is said that in the highland region rainfall amount is higher than in the lowland region. In addition, heavy rain is strongly influenced by topography [25] . In other words, heavy rainfall often occurs in the mountainous site.
To assess the orographic effects, the validation of GSMaP_MVK in the highland and lowland region was conducted in this section. Table 4 compares the validation and correction result of GSMaP_MVK in the highland and lowland regions. In the highland the bias, error, RMSE, and CNS were −56.18%, −8.69 mm/day, 29.5 mm/day and 0.4, while in the lowland they were −41.27%, −4.58 mm/day, 26.3 mm/day and 0.5, respectively. These results showed that the performance of satellite product was superior over the lowland, with lower bias, error and RMSE and better consistency measurement for rainfall estimates. In contrast, the performance of satellite product was seriously underestimated and had lower consistency measurement for rainfall estimates over the highland. This will be partly because the current algorithm of microwave radiometer does not include the topographical effect. This result should be noted that topography obviously influences the accuracy of the satellite product. Moreover, detection probability and HSS also gave the same result that is POD and HSS were higher in the lowland (82 % and 68 %) than in the highland (78% and 65%) while FAR was lower in the lowland (15%) than in the highland (19%) as shown in Table 4.
GSMaP_MVK data have underestimated both in the lowland and highland therefore, the correction was conducted. In this study, GAM was conducted for bias correction. The results showed that the bias, error and RMSE in the highland region decreased significantly and the CNS value increased. However, GAM did not give the significant impact for the lowland area. It should be noted that GAM only worked in the highland region. It was said that GAM tends to overestimate for forecasting [32] . As a result, GAM only be able to solve the underestimate value when the bias percentage is large. In addition, high bias percentage was found when the amount of rainfall was more than 100 mm/day as shown in Figure 4.
3.3. Validation and Correction of GSMaP_MVK in the Eastern Part and Western Part of Kyushu
As explained before, the mountain region of Kyushu island is located in the central of the island from north to south and it will affect the rainfall pattern over the region. Therefore, to assess the region effect, validation of GSMaP_MVK in the eastern part and the western part was conducted. The western part locates in the Kumamoto, Saga and Fukuoka Prefectures while the eastern part locates in Kagoshima and Miyazaki. Moreover, Kumamoto, Kagoshima and Miyazaki were hit by flash flood in July 2006 and 2007.
Table 4. Validation statistics over the highland and lowland before and after corrected by GAM.
Figure 4. Smoothing function of GSMaP_MVK.
Table 5 shows the validation and correction result of GSMaP_MVK in the eastern part and the western part of the region. In the eastern part the bias, error, RMSE, and CNS were −40.1%, −4.95 mm/day 21.37 mm/day and 0.52 while in the western part they were −55.07%, −7 mm/day, 24.73 mm/day and 0.4. These results indicated that the performance of satellite product was better over the eastern part, with lower bias, error and RMSE and better consistency measurement for rainfall estimates. It was strongly influenced by the location of the mountain area which affected local wind directions, then influenced the rainfall pattern. The wind direction in the study area moves from west to east. The water vapor as a main source of precipitation was not distributed perfectly in the region because the mountain is located in the central area as a barrier for cloud distribution. As a result, the rainfall pattern will be different.
Table 5. Validation statistics over the eastern part and western part before and after corrected by GAM.
However, the result showed that both in the western part and the eastern part of Kyushu, GSMaP_MVK data has underestimated. Thus, a correction was necessary. The results showed that the bias, error and RMSE in the western part of the region decreased significantly and the CNS value increased. However, GAM did not give the significant impact for the eastern part of the region. It should be noted that GAM only worked in the western part of the region. The same statement can be concluded that, GAM can greatly correct the GSMaP_MVK data if the bias percentage is large (i.e., more than 55%). In contrast, the correlation coefficient did not change significantly among eastern part, western part, before and after correction. Additionally, detection probability, FAR and HSS also did not give the different result between the eastern part (81%, 18% and 68%) and western part (81%, 18% and 67%).
3.4. Validation and Correction of GSMaP_MVK during Heavy Rainfall
Heavy rainfall is one of the important factors which trigger the occurrence of flash floods. Thus, predicting the amount of heavy rainfall by satellite precipitation, which close to rain gauge data is necessary. Here, heavy rain is defined as daily rainfall exceeding the 95th percentile (rain_P95) for all stations and all categories [25] . In addition, extreme rain is described as daily rainfall exceeding the 99th percentile (rain_P99) for all stations and all categories [25] . According to the definition, the heavy rains ranged equal and more than 66 mm/day (n = 465) and the extreme rainfalls ranged equal and more than 146 mm/day (n = 95). According to [16] and [11] stated that GSMaP_MVK had serious underestimation when heavy rainfall occurred. Thus, validation and correction of GSMaP_MVK during heavy rainfall is a challenge.
Table 6 describes the validation and correction result of GSMaP_MVK during heavy rainfall. During heavy rainfall, the bias, error, RMSE and CNS of uncorrected GSMaP_ MVK are −59.5%, −70.3 mm/day, 90.6 mm/day and −0.98. Validation of uncorrected GSMaP_MVK results showed that the performance of satellite products was a serious underestimate because the bias was the highest compare from other categories. This is probably because sudden increase in rain rate did not reflect the IR brightness temperature in this time scale (Ushio et al., 2009). In this section, GAM and power function [29] for bias correction were applied. We did both correction method and then compared. After GSMaP_MVK was corrected by power function, the bias, error, RMSE and CNS were −63.2%, −63.1 mm/day, 85.6 mm/day and −0.77 while by GAM the yare −8.8%, −10.44 mm/day, 55.44 mm/day and 0.26, respectively. After correction, the bias, error and RMSE values decreased dramatically and the CNS values increased of both correction methods. However, the GAM correction method gave the most significant result to reduce the error index. Moreover, when the values of CNS is positive, the correcting of GSMaP_MVK indicates that almost accurate (i.e. CNS = 0 means the models are accurate while CNS one means the models are perfectly accurate) [33] .
Because GAM approach gave the best result, Figure 5 only compare AMEDAS, GSMaP_MVK and corrected GSMaP_MVK by GAM. Figure 5(A) shows the heavy rainfall graphic from those components. It described that the underestimate of GSMaP_MVK could be reduced almost in all points. Figure 5(B) shows the extreme rainfalls, which caused flooding in the Miyazaki, Kagoshima and Kumamoto in 2006 and in Kumamoto in 2007. In the extreme rainfalls the bias of GSMaP_MVK is very large. On the other hand, the GAM can reduce the bias of GSMaP_MVK.
4. Conclusions
In this study, daily GSMaP_MVK rainfall estimates were compared with daily rain gauge measurements from AMEDAS. Data from 34 rain gauges in Kyushu Island, covering 3-year period (2005-2007), were used to evaluate daily rainfall pattern of GS- MaP_MVK data. Point-by-point and spatial average analysis compared the closeness of GSMaP_MVK and rain gauge data using bias, error, RMSE, CNS and correlation coefficients (r). In addition, GAM model has been applied to correct the GSMaP_MVK data.
Inter-comparison and correction were conducted between highland and lowland, between eastern part and western part and during heavy rainfall. From the analysis followings are obtained as results:
Daily rainfall data from GSMaP_MVK have a great performance in lowland and eastern part of the study area.
Table 6. Validation statistics during heavy rainfall.


Figure 5. (A) Heavy rainfall measurement by AMEDAS, GSMaP and corrected by GAM for three years. Heavy rainfall measurement by AMEDAS, GSMaP and corrected by GAM for three years; (B) Extreme rainfall, which caused flood in Miyazaki 2006 (a); Kagoshima 2006 (b); Kumamoto 2006 (c); Kumamoto 2007 (d).
Daily rainfall data from GSMaP_MVK have serious underestimate in the highland, western part of the study area and during heavy rainfall.
GAM correction only can be applied when the bias percentage was more than 55% of underestimate value. Therefore, it was well applied in the highland area, in the western part of Kyushu, and during heavy rainfall.
In addition, high bias was produced mostly due to heavy rainfall. This is probably due to topography effect. Consequently, to obtain better results, the quality of remote- sensing satellite data needs to be improved for better result in complex topography. The quality of the satellite rainfall measurements needs to be evaluated continuously and averaged over several years to accurately reveal climatological features. In general, the data from GSMaP_MVK are potentially usable to replace rain gauge data, especially with the data over lowland area, if the inconsistencies and errors are taken into account. Thus GAM is a promising way to predict the rainfall amount for flood and landslide monitoring, especially in the area where rain gauge data are limited.
Acknowledgements
We would like to thank the Japan Meteorological Agency (JMA) for providing rain gauge data, United States Geological Survey (USGS) for providing digital elevation map of SRTM data and Japan Aerospace Exploration Agency (JAXA) for proving GSMaP data.
Cite this paper
Setiawati, M.D. and Miura, F. (2016) Evaluation of GSMaP Daily Rainfall Satellite Data for Flood Monitoring: Case Study―Kyushu Japan. Journal of Geoscience and Environment Protection, 4, 101- 117. http://dx.doi.org/10.4236/gep.2016.412008
References
- 1. Hou, A.Y., Skofronick-Jackson, G., Kummerow, G. and Shepherd, M. (2008) Global Precipitation Measurement. In: Michaelides, S., Ed., Precipitation. Advances in Measurement, Estimation and Prediction, Springer-Verlag, Berlin, 131-170.
https://doi.org/10.1007/978-3-540-77655-0_6 - 2. National Research Council (US), Committee on the Future of the Tropical Rainfall M and Board on Atmospheric Sciences and Climate (2007) NOAA’s Role in Space-Based Global Precipitation Estimation and Application. National Academies Press, Washington DC.
- 3. Feidas, H., Kokolatos, G., Negri, A., Manyin, M., Chrysoulakis, N. and Kamarianakis, Y. (2009) Validation of an Infrared-Based Satellite Algorithm to Estimate Accumulated Rainfall over the Mediterranean Basin. Theoretical and Applied of Climatology, 95, 91-109.
https://doi.org/10.1007/s00704-007-0360-y - 4. Feidas, H. (2010) Validation of Satellite Rainfall Products over Greece. Theoretical and Applied Climatology, 99, 193-216.
https://doi.org/10.1007/s00704-009-0135-8 - 5. Xie, P. and Arkin, P.A. (1995) An Intercomparison of Gauge Observations and Satellite Estimates of Monthly Precipitation. Journal of Applied Meteorology, 34, 1143-1160.
https://doi.org/10.1175/1520-0450(1995)034<1143:AIOGOA>2.0.CO;2 - 6. Chokngamwong, R. and Chiu, L.S. (2006) TRMM and Thailand Daily Gauge Rainfall Comparison. Atlanta,.
- 7. Chiu, L.S., Liu, Z., Vongsaard, J., Morain, S., Budge, S., Neville, P. and Bales, C. (2006) Comparison of TRMM and Water District Rain Rate over New Mexico. Advance Atmospheric Science, 23, 1-13.
https://doi.org/10.1007/s00376-006-0001-x - 8. Okamoto, K., Iguchi, T., Takahashi, N., Iwanami, K. and Ushio, T. (2005) The Global Satellite Mapping of Precipitation (GSMaP) Project. 25th International Geoscience and Remote Sensing Symposium, Seoul, IEEE, 25-29 July 2005, 3414–3416
- 9. Aonashi, K., Awaka, J., Hirose, M., Kozu, T., Kubota, T., Liu, G., Shige, S., Siga, S., Seto, S., Takahashi, N. and Takayabu, Y.N. (2009) GSMaP Passive Microwave Precipitation Retrieval Algorithm: Algorithm Description and Validation. Journal of Applied Meteorology, 87A, 119-136.
- 10. Kubota, T., Shige, S., Hanshizume, H., Aonashi, K., Takahashi, N., Seto, S., Takayabu, Y.N., Ushio, T., Nakagawa, K., Iwanami, K., Kachi, M. and Okamoto, K. (2007) Global Precipitation Map Using Satellite-Borne Microwave Radiometers by the GSMaP Project: Production and Validation. IEEE Transactions Geoscience Remote Sensing, 45, 2259-2275.
https://doi.org/10.1109/TGRS.2007.895337 - 11. Kubota, T., Ushio, T., Shige, S., Kida, S., Kachi, M. and Okamoto, K. (2009) Verification of High Resolution Satellite-Based Rainfall Estimates around Japan Using a Gauge Calibrated Ground Radar Data Set. Journal of Meteorological Society of Japan, 87A, 203-222.
https://doi.org/10.2151/jmsj.87A.203 - 12. Seto, S. (2009) An Evaluation of Overland Rain Rate Estimates by the GSMaP and GPROF Algorithm: The Role of Lower Frequency Channels. Journal of Meteorological Society, 67, 183-202.
https://doi.org/10.2151/jmsj.87A.183 - 13. Fukami, K., Shirashi, Y., Inomata, H. and Ozawa, G. (2010) Development of Integrated Flood Analysis System (IFAS) Using Satellite-Based Rainfall Products with a Self-Correction Method. International Centre for Water Hazard and Risk Management under Auspices of UNESCO (ICHARM), Public Works Research Institute, Tsukuba.
- 14. Shrestha, M.S., Takara, K., Kubota, T. and Bajracharya, S.R. (2011) Verification of GSMaP Rainfall Estimates over the Central Himalayas. Journal of Japan Society of Civil Engineers, 67, I_37-I_42.
https://doi.org/10.2208/jscejhe.67.i_37 - 15. Setiawati, M.D., Miura, F. and Aryastana, P. (2013) Verification of Hourly GSMaP Rainfall Estimates during the Flood Events in Kumamoto Prefecture. Bali.
- 16. Dinku, T., Ruiz, F., Connor, S. and Ceccato, P. (2009) Validation and Intercomparison of Satellite Rainfall Estimates over Colombia. Journal of Applied Meteorology and Climatology, 49, 1004-1014.
https://doi.org/10.1175/2009JAMC2260.1 - 17. Wood, S.M. (2006) Generalized Additive Models: An Introduction with R. Chapman and Hall, London.
- 18. Jones, M.R., Blenkinsop, S., Fowler, H.J., Shephenson, D.B. and Kilsby, C.G. (2013) Generalized Additive Modelling of Daily Precipitation Extremes and Their Climatic Drivers. National Center for Atmospheric Research, Colorado.
- 19. Yang, C., Yan, Z. and Shao, Y. (2012) Probabilistic Precipitation Forecasting Based on Ensemble Output Using Generalized Additive Models and Bayesian Model Averaging. Acta Mechanica Sinica, 26, 1-12.
- 20. Kazama, S., Sato, A. and Kawagoe, S. (2009) Evaluating the Cost of Flood Damage Based on Changes in Extreme Rainfall in Japan. Sustainability Science, 4, 61-69.
https://doi.org/10.1007/s11625-008-0064-y - 21. Tezuka, S., Takiguchi, H., Sato, A., Kawagoe, S. and Sarukkalige, R. (2014) Estimation of the Effects of Climate Change on Flood-Triggered Economic Losses in Japan. International Journal of Disaster Risk Reduction, 9, 58-67.
https://doi.org/10.1016/j.ijdrr.2014.03.004 - 22. Japan Meteorological Agency (2016)
http://www.data.jma.go.jp/obd/stats/etrn/index.php - 23. Ushio, T., Sasashige, K., Kubota, T., Shige, S., Okamoto, K. and Aonashi, K. (2009) A Kalman Filter Approach to the Global Satellite Mapping of Precipitation (GSMaP) from Combined Passive Microwave and Infrared Radiometric Data. Journal of Meteorological Society of Japan, 87A, 137-151.
https://doi.org/10.2151/jmsj.87A.137 - 24. Liang, S., Li, X. and Wang, J. (2012) Advanced Remote Sensing: Terrestrial Information Extraction and Applications. Academic Press, Oxford.
- 25. Iwasaki, H. (2014) Increasing Trends in Heavy Rain during the Warm Season in Eastern Japan and Its Relation to Moisture Variation and Topographic Convergence. International Journal of Climatology, 35, 2154-2163.
https://doi.org/10.1002/joc.4115 - 26. As-Syakur, A.R., Tanaka, T., Prasetia, R., Swardika, I.K. and Kasa, I.W. (2011) Comparison of TRMM Multisatellite Precipitation Analysis (TMPA) Products and Daily-Monthly Gauge Data over Bali. International Journal of Remote Sensing, 32, 8969-8982.
https://doi.org/10.1080/01431161.2010.531784 - 27. Prasetia, R., As-Syakur, A.R. and Osawa, T. (2013) Validation of TRMM Precipitation Radar Satellite Data over Indonesian Region. Theoretical and Applied Climatology, 112, 575-587.
https://doi.org/10.1007/s00704-012-0756-1 - 28. Jiang, S., Ren, L., Yong, B., Yang, X. and Shi, L. (2010) Evaluation of High-Resolution Satellite Precipitation Products with Surface Rain Gauge Observations from Laohahe Basin in Northern China. Water Science Engineering, 3, 405-417.
- 29. Vernimmen, R.R., Hooijer, A., Aldrian, M.E. and Van Dijk, A.J. (2012) Evaluation and Bias Correction of Satellite Rainfall Data for Drought Monitoring in Indonesia. Hydrology and Earth System Sciences, 16, 133-146.
https://doi.org/10.5194/hess-16-133-2012 - 30. Morton, R. and Henderson, B.L. (2008) Estimation of Nonlinear Trends in Water Quality: An Improved Approach Using Generalized Additive Models. Water Resources Research, 44, W07420.
https://doi.org/10.1029/2007wr006191 - 31. Underwood, F.M. (2009) Describing Long-Term Trends in Precipitation Using Generalized Additive Models. Journal of Hydrology, 364, 285-297.
https://doi.org/10.1016/j.jhydrol.2008.11.003 - 32. He, S., Mazumdar, S. and Arena, V.C. (2006) A Comparative Study of the Use of GAM and GLM in Air Pollution Research. Environmetrics, 17, 81-93.
https://doi.org/10.1002/env.751 - 33. Krause, V., Boyle, D.P. and Base, F. (2005) Comparison of Different Efficiency Criteria for Hydrological Model Assessment. Advances in Geosciences, 5, 89-97.
https://doi.org/10.5194/adgeo-5-89-2005






