International Journal of Modern Nonlinear Theory and Application
Vol.1 No.3(2012), Article ID:23095,5 pages DOI:10.4236/ijmnta.2012.13015
The Global Attractor of Thermoelastic Coupled System*
Department of Mathematics, Taiyuan University of Technology, Taiyuan, China
Email: danxia.wang@163.com, #jianwen.z2008@163.com
Received July 12, 2012; revised August 12, 2012; accepted September 12, 2012
Keywords: The Mild Solution; Priori Estimates; Thermoelastic Coupled Rod; Global Attractor
ABSTRACT
In this paper, we consider a class of Sine-Gordon equations which arise from the model of the thermoelastic coupled rod. Firstly, by virtue of the classical semigroup theory, we prove the existence and uniqueness of the mild solution under certain initial-boundary value for above-mentioned equations. Secondly, we obtain the boundedness of solutions by the priori estimates. Lastly, we prove the existence of a global attractor.
1. Introduction
In this paper, we consider the following nonlinear thermoelastic coupled rod system
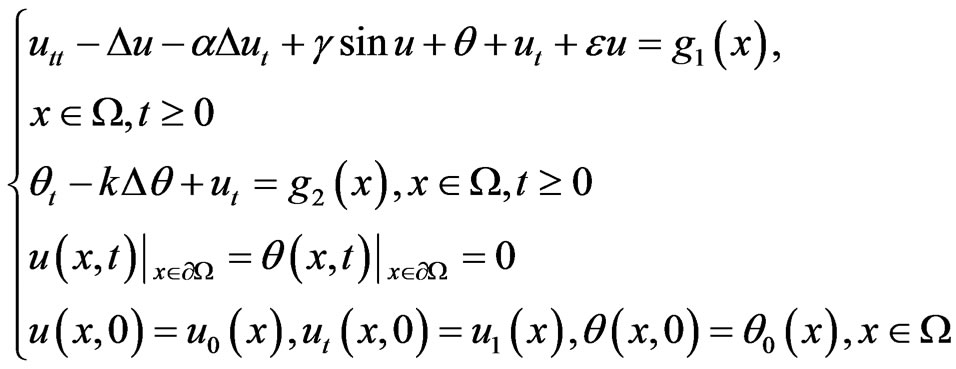 (1)
(1)
The above system describes the vibrations of an extensible thermoelastic rod model. Here u = u(x, t) and θ = θ(x, t) are all real-valued functions on Ω × [0, +∞], Ω = (0, 1) is an open bounded domain of R. The coefficient α, γ, ε, k are all positive constants, where α is called the strong damping coefficient of rod, ε is the small parameter. The sign Δ denotes
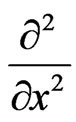 ,
,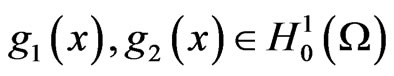 .
.
“Global solutions” and “global attractor” are two basic concepts in the study of long-time behavior of nonlinear dissipative evolution equations with various dissipation. If the coupled terms are equivalent to 0, Equations (1) will decouple to the Sine-Gordon equation
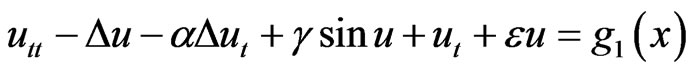 (2)
(2)
and the heat equation. The structure of global attractors for weakly damped nonlinear wave Equation (2) as α, ε = 0 is studied in Temam [1] and Zhu [2] and Wang [3] and the one for the strongly damped nonlinear wave equation is considered in Zhou [4]. Semion [5] shows the Frechet differentiability for a damped sine-Gordon equation with a variable diffusion coefficient. Han [6] proves the existence of Random attractors for stochastic Sine-Gordon lattice system. But have the global solution and the global attractor for the “thermoelastic coupled” rod system (1)? To our knowledge, nothing was known until now.
In this paper, we give the proof of the existence and uniqueness of the mild solution and the existence of a global attractor for system (1) in space 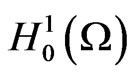 × L2(Ω) × L2(Ω).
× L2(Ω) × L2(Ω).
2. Existence and Uniqueness of Global Solutions
It is well known that operator A = –Δ:D(A) = 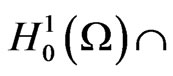 H2(Ω) → L2(Ω) is self-adjoint, positive and linear and its eigenvalues
H2(Ω) → L2(Ω) is self-adjoint, positive and linear and its eigenvalues 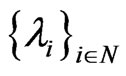 satisfy 0 < λ1 ≤ λ2 ≤ ··· ≤ λm ≤ ··· and λm → +∞ as m → +∞. Set L2(Ω),
satisfy 0 < λ1 ≤ λ2 ≤ ··· ≤ λm ≤ ··· and λm → +∞ as m → +∞. Set L2(Ω), 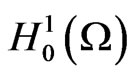 ,
, 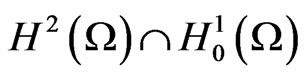 ,
, 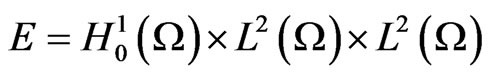 with the usual inner products and norms, respectively
with the usual inner products and norms, respectively
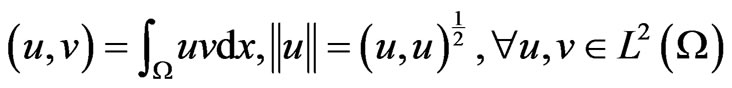 ,
,
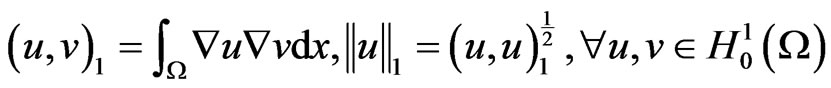
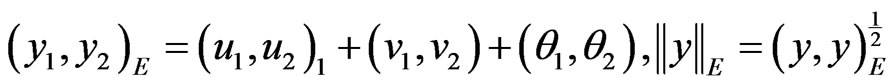
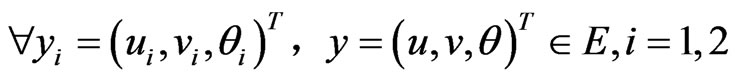
It is convenient to reduce (1) to an evolution equation of the first order in time, Let ut = v, then (1) are equivalent to the following initial value problem in E,
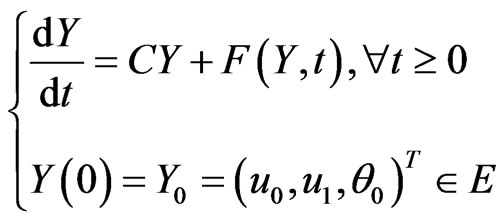 (3)
(3)
where Y = (u, v, θ)T,
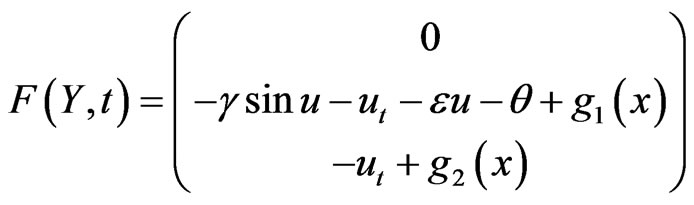
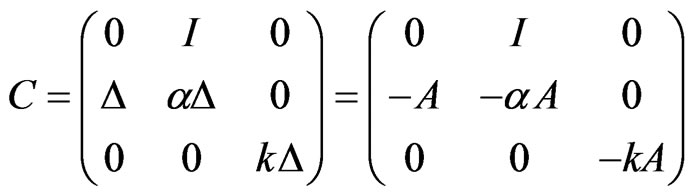
with D(C) = D(A) × D(A) × D(A), I is the identity operator L2(Ω),  and D(A). Set B = –C, then similar to [7], by making some slight modification and reasoning, we can prove that for any α, k > 0, B is a sectorial operator on E and generates an analytic semigroup
and D(A). Set B = –C, then similar to [7], by making some slight modification and reasoning, we can prove that for any α, k > 0, B is a sectorial operator on E and generates an analytic semigroup  on E for t > 0. By the assumptions g1(x),
on E for t > 0. By the assumptions g1(x),  , it is easy to check that the function F(Y, t):E → E is locally Lipschitz continuous with respect to Y, By the classical semigroup theory concerning the existence and uniqueness of the solution of evolution differential equations, we have Theorem 2.1. Assume that the assumptions g1(x),
, it is easy to check that the function F(Y, t):E → E is locally Lipschitz continuous with respect to Y, By the classical semigroup theory concerning the existence and uniqueness of the solution of evolution differential equations, we have Theorem 2.1. Assume that the assumptions g1(x), 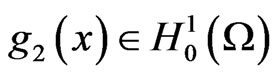 hold, then consider the initial value problem (3) in Hilbert space E. For any initial value
hold, then consider the initial value problem (3) in Hilbert space E. For any initial value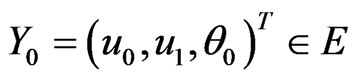 , there exists a unique continuous function Y(t) = Y(t, Y0) =
, there exists a unique continuous function Y(t) = Y(t, Y0) = 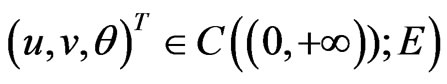 such that Y(t) = (u(t), v(t), θ(t))T satisfies the integral equation
such that Y(t) = (u(t), v(t), θ(t))T satisfies the integral equation
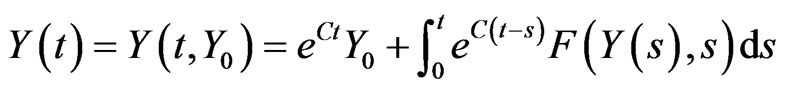 .
.
In this case, Y(t) is called a mild solution of the system (3) and Y(t) = Y(t, Y0) is jointly continuous in t and Y0, that is, the solution (u, ut, θ) of the system (1) satisfies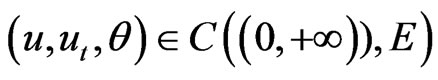 .
.
By Theorem 2.1, for any t > 0, we may introduce the map
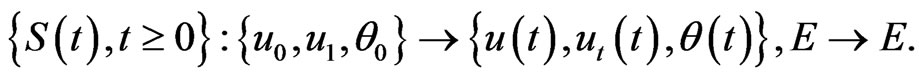
It maps E =  × L2(Ω) × L2(Ω) into itself and it enjoys the usual process properties as follows
× L2(Ω) × L2(Ω) into itself and it enjoys the usual process properties as follows
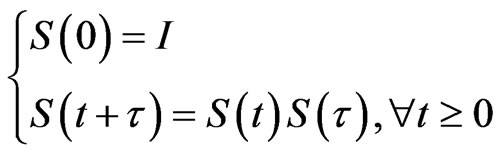
It is obviously that the map {S(t), t > 0},  is continuous in E. In the following, we will introduce the existence of the bounded absorbing set and the global attractor for map {S(t), t > 0} in E.
is continuous in E. In the following, we will introduce the existence of the bounded absorbing set and the global attractor for map {S(t), t > 0} in E.
3. The Existence of Bounded Absorbing Set
In this section, we will show boundedness of the solutions for system (3). For this purpose, we define a weighted inner product and norm in E = 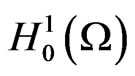 × L2(Ω) × L2(Ω) by
× L2(Ω) × L2(Ω) by
 (4)
(4)
for any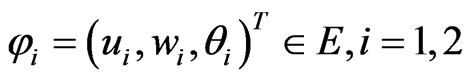 , where wi = uit + εi, i = 1, 2 and μ is chosen by
, where wi = uit + εi, i = 1, 2 and μ is chosen by
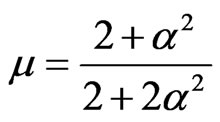 .
.
Obviously the norm  in (4) is equivalent to the usual norm in space E.
in (4) is equivalent to the usual norm in space E.
Let φ = (u, w, θ)T, w = ut + εu, where ε is chosen as
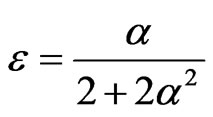 then the system (3) can be written as
then the system (3) can be written as
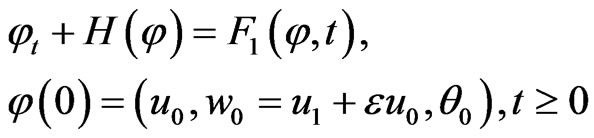 (5)
(5)
where 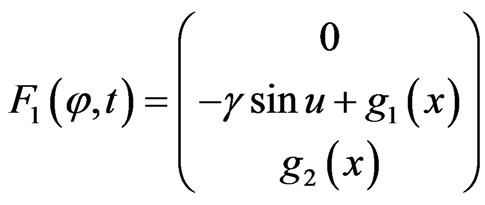
and 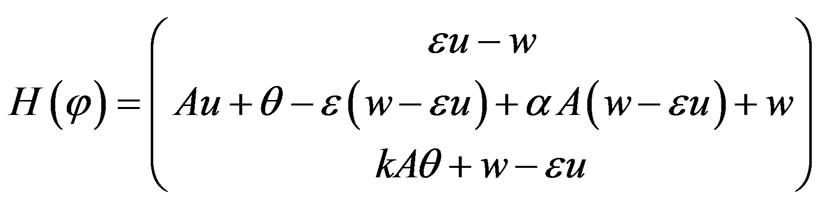
Obviously, the mapping
 (6)
(6)
has the relation with

where Rε{u, w, θ} →{u, w + εu, θ} is an isomorphism of E. So we only need consider the equivalent map (6).
For the boundedness of the solution of (5) in E, we firstly present an important lemma which plays an important role in this artical.
Lemma 3.1. For any 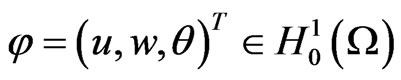 × L2(Ω) × L2(Ω). we have
× L2(Ω) × L2(Ω). we have
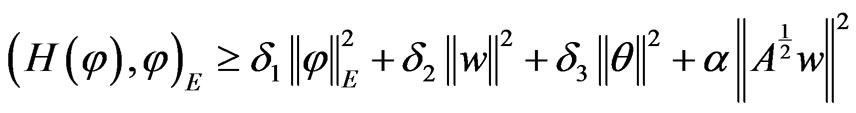 .
.
where
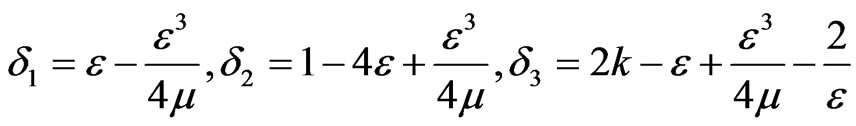
are all positive constants if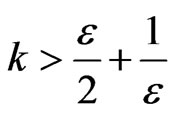 .
.
Proof.

with
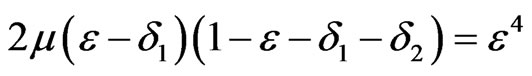
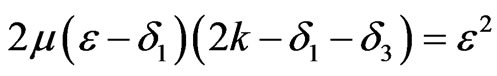

the Lemma is easily obtained.
Theorem 3.1. There exists a positive constant M > 0 such that for any bounded set B of E, then there exists T0(B) ≥ 0 such that the solution φ = (u(t), w(t), θ(t))T of (5) with 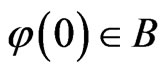 satisfies
satisfies
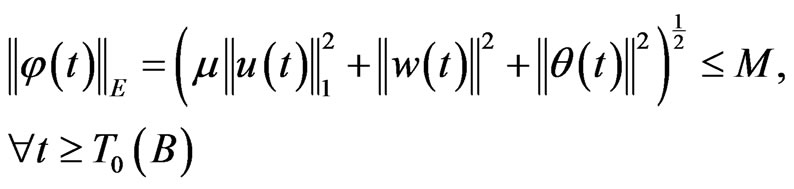
in which w = ut + εu.
Proof. Let φ = (u, w, θ)T, w = ut + εu be the solution of (5) with initial value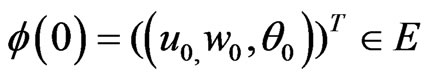 . Taking the inner product
. Taking the inner product 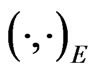 of (5) with φ = (u, w, θ)T and considering of Lemma 3.1, we have
of (5) with φ = (u, w, θ)T and considering of Lemma 3.1, we have
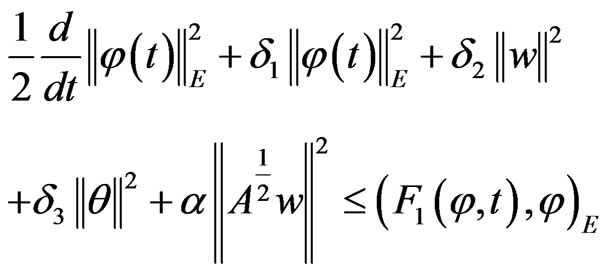
with
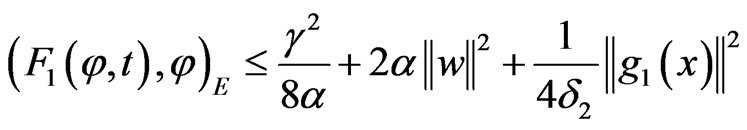
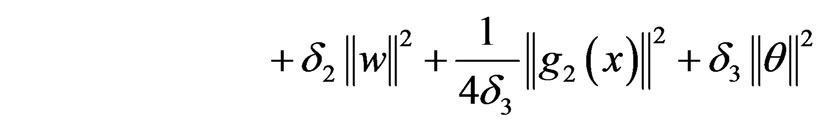 we have
we have

By Gronwall’s inequality we have
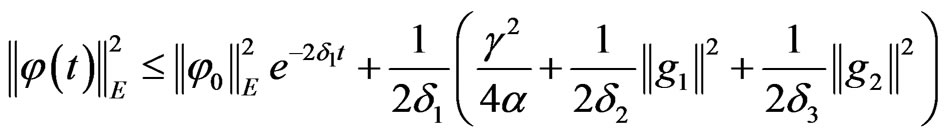
Set 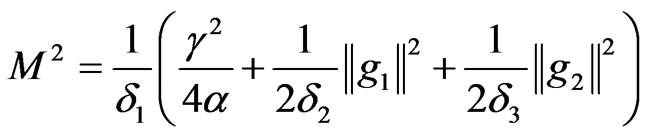
thus we complete the proof of the Theorem.
Corollary 3.1. Let B0 be a bounded closed ball of E centered at 0 of radius M. For any initial value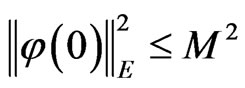 , there exists a constant M1 = M1(M) such that the solution of (5) φ(t) = (u(t), w(t), θ(t))T satisfies
, there exists a constant M1 = M1(M) such that the solution of (5) φ(t) = (u(t), w(t), θ(t))T satisfies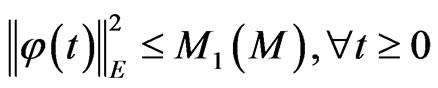 .
.
4. The Existence of a Global Attractor
Theorem 4.1. For any initial value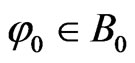 , the solution φ(t) = (u(t), w(t), θ(t))T of (5) can be decomposed into φ(t) = φ1(t) + φ2(t) where φi(t) = (ui(t), wi(t), θi(t))T, wi(t) = uit(t) + εui(t), i = 1, 2 satisfy, respectively(
, the solution φ(t) = (u(t), w(t), θ(t))T of (5) can be decomposed into φ(t) = φ1(t) + φ2(t) where φi(t) = (ui(t), wi(t), θi(t))T, wi(t) = uit(t) + εui(t), i = 1, 2 satisfy, respectively(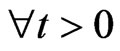 )
)
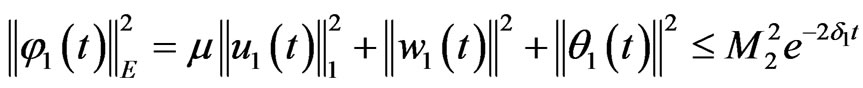 (7)
(7)
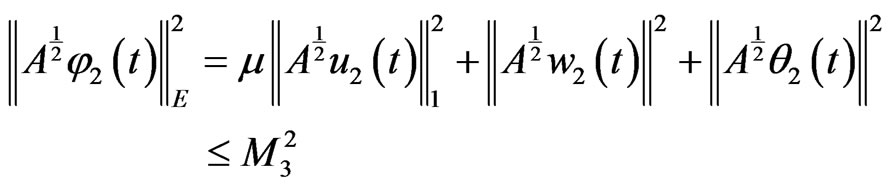 (8)
(8)
where 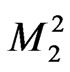 and
and 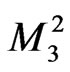 depend on M.
depend on M.
Proof. Let φ(t) = (u(t), w(t), θ(t))T, 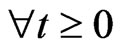 be a solution of (5) in space E with the initial value
be a solution of (5) in space E with the initial value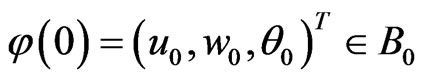 .
.
Let φ(t) =φ1(t) +φ2(t), where φi(t) = (ui(t), wi(t), θi(t))T, wi(t) = uit(t) + εui(t), i = 1, 2, satisfy, respectively
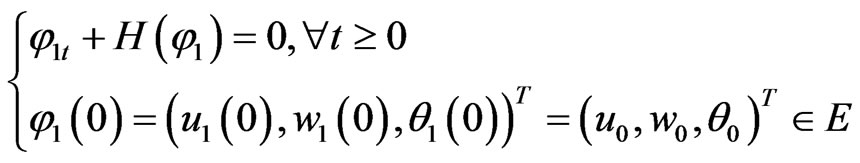 (9)
(9)
where
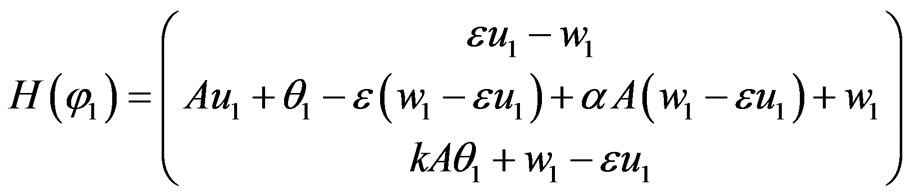
and
 (10)
(10)
where
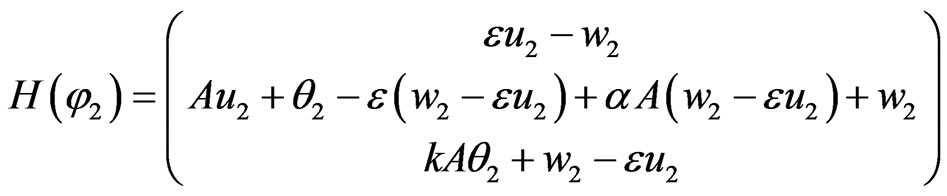
Taking the inner product of (9) with φ1(t) we have

 (11)
(11)
Similar to the proof of Lemma 3.1, we can obtain
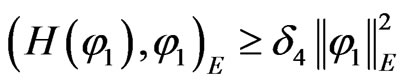 (12)
(12)
where 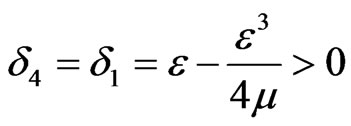 .
.
Thus by (12) and Gronwall’s inequality, (7) is easily obtained from (11).
By putting x = 0, 1 and t = 0 in (10) we get
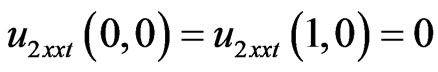 (13)
(13)
The operator 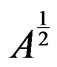 operates into (10) to get
operates into (10) to get
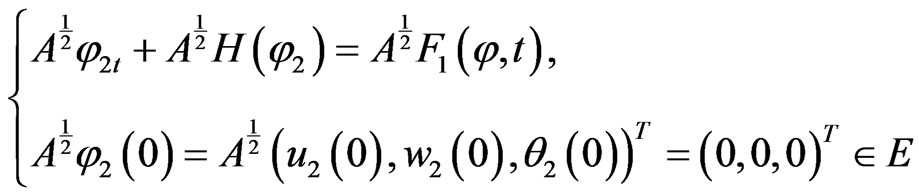 (14)
(14)
Taking the inner product of (14) with 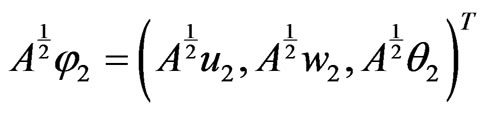
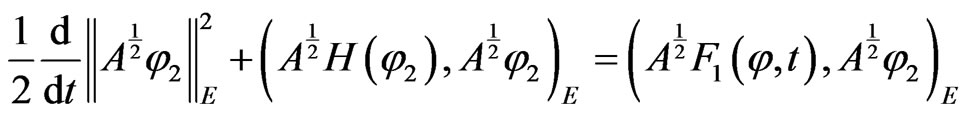 (15)
(15)
Considering to (13) we get that
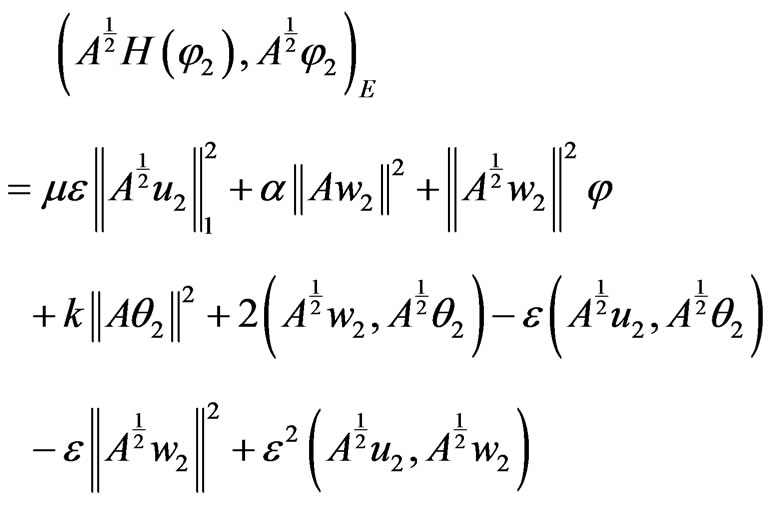
with
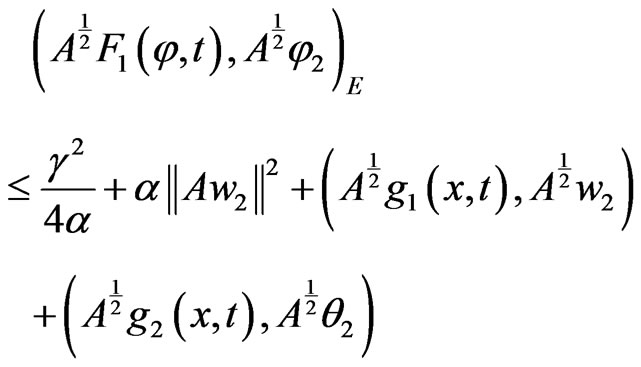
from (15) we have
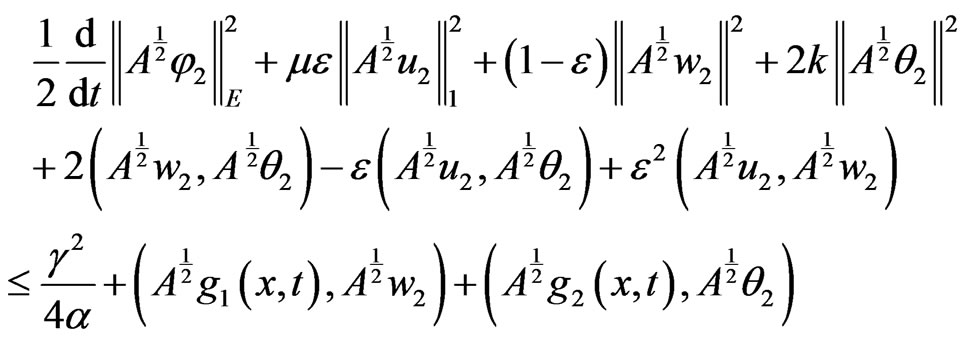 (16)
(16)
Similar to the proof of the Lemma 3.1, from (16) we get

By the Gronwall’s inequality, we have

Set
 .
.
Thus, the proof of Theorem 4.1 is complete.
REFERENCES
- R. Temam, “Infinite-Dimensional Dynamical Systems in Mechanics and Physics,” Applied Mathematical Sciences, Vol. 68, Springer-Verlag, New York, 1988.
- S. Zhu and S. F. Zhou, “Dimension of the Global Attractor for the Damped and Driven SINE-Gordon Equation,” Nonlinear Analysis, Vol. 37, 1999, pp. 389-399.
- G. X. Wang and S. Zhu, “Dimension of the Global Attractor for the Discretized Damped Sine-Gordon Equation,” Applied Mathematics and Computation, Vol. 117, No. 2-3, 2001, pp. 257-265. doi:10.1016/S0096-3003(99)00179-4
- S. F. Zhou, “Dimension of the Global Attractor for Strongly Damped Nonlinear Wave Equation,” Journal of Mathematical Analysis and Applications, Vol. 233, No. 1, 1999, pp. 102-115. doi:10.1006/jmaa.1999.6269
- G. Semion, “Frechet Differentiability for a Damped SineGordon Equation,” Journal of Mathematical Analysis and Applications, Vol. 360, No. 2, 2009, pp. 503-517. doi:10.1016/j.jmaa.2009.06.074
- X. Y. Han, “Randon Attractors for Stochastic Sine-Gordon Lattice Systems with Multiplicative White Noise,” Journal of Mathematical Analysis and Applications, Vol. 376, No. 2, 2011, pp. 481-493. doi:10.1016/j.jmaa.2010.11.032
- P. Massatt, “Limiting Behavior for Strongly Damped Nonlinear Wave Equations,” Journal of Differential Equations, Vol. 48, No. 3, 1983, pp. 334-349. doi:10.1016/0022-0396(83)90098-0
NOTES
*This work is supported by Natural Science Foundation of Shanxi Provice, and the Natural Science Foundation for Young Scientists of Shanxi Province (2010011008, 2011021002-2).
#Corresponding author.

