ABSTRACT

In this paper we investigate optimal control problems governed by a advection-diffusion-reaction equation. We present a method for deriving conditions in the form of Pontryagin’s principle. The main tools used are the Ekeland’s variational principle combined with penalization and spike variation techniques.

1. Introduction

Consider the following controlled advection convection diffusion equations:

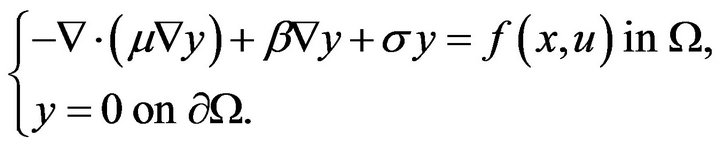(1.1)

where is a convex bounded domain with a smooth boundary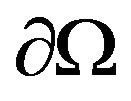, the diffusity 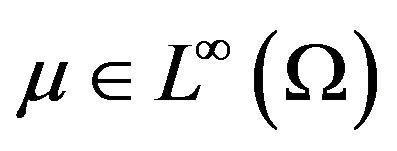with

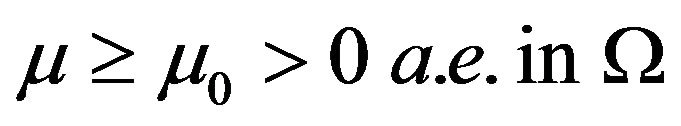, the reaction with

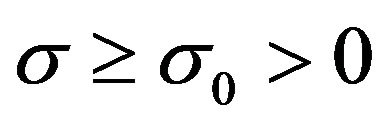, and the advective fieldwith 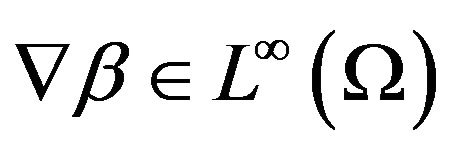and 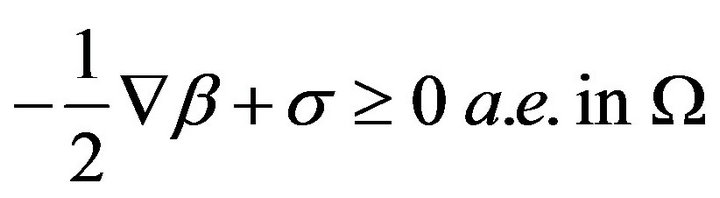are assigned functions. Here, with 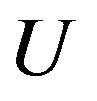being a separable metric space. Function, called a control, is taken from the set

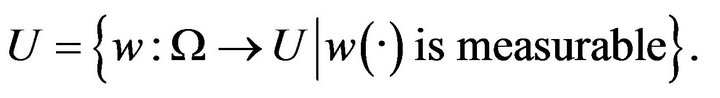
Under some mild conditions, for any, (1.1) admits a unique weak solution 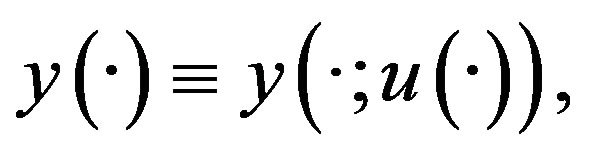which is called the state(corresponding to the control). The performance of the control is measured by the cost functional

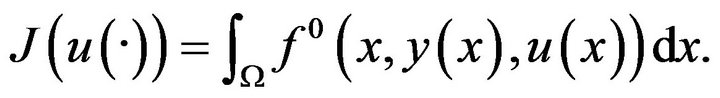(1.2)

for some given map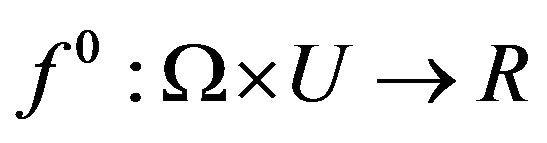. Our optimal control problem can be stated as follows.

Problem (C). Find a 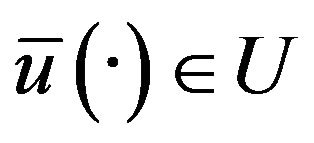such that

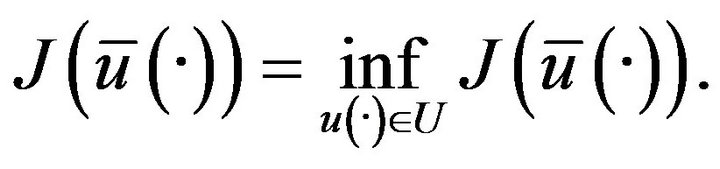(1.3)

And the state constraint of form:

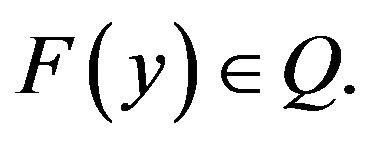(1.4)

In this paper, we make the following assumptions.

(H1) Set 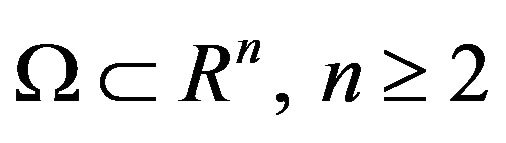is a convex bounded domain with a smooth boundary.

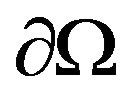(H2) Set 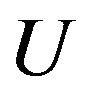is a separable metric space.

(H3) The function has the following properties: is measurable on, and continuous on and for any, a constant

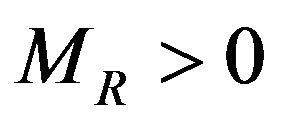, such that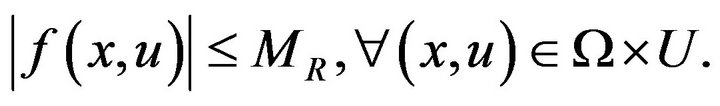

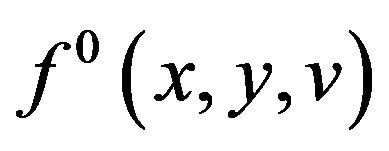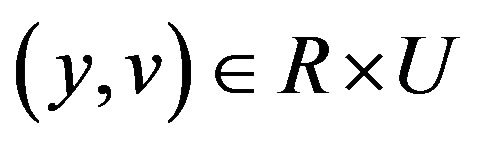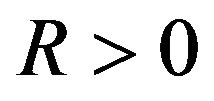(H4) Function is measurable in and continuous in for almost all. Moreover, for any, there exists a such that

(1.5)

(H5) 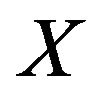is a Banach space with strictly convex dual, 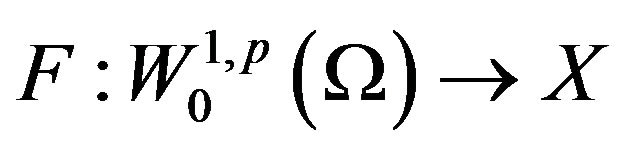is continuously Fréchet differentiable, and 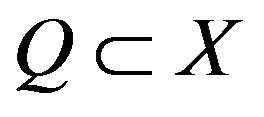is closed and convex set.

(H6) has finite condimensionality in for some, where.

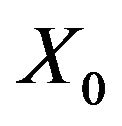Definition 1.1 (see [1]) Let is a Banach space and is a subspace of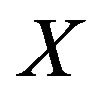. We say that 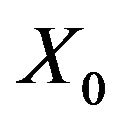is finite codimensional in if there exists such that

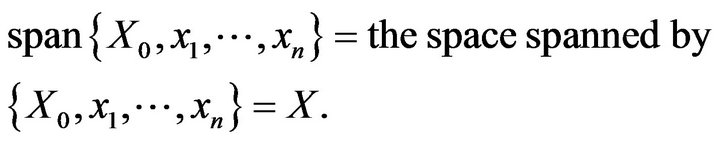
A subset of 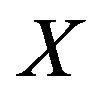is said to be finite codimensional in if for some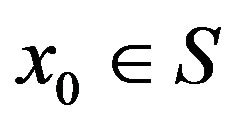, 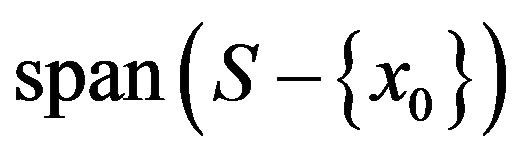the closed subspace spanned by 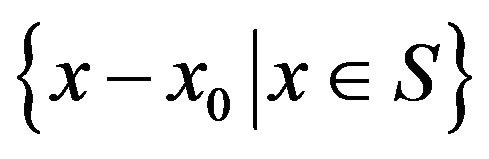is a finite codimensional subspace of and 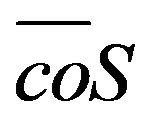the closed convex hull of 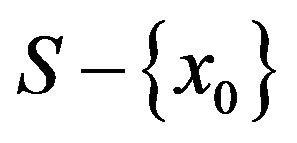has a nonempty interior in this subspace.

Lemma 1.2. Let (H1) - (H3) hold. Then, for any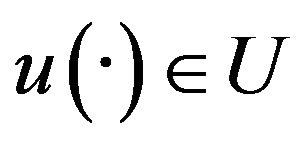, (1.1) admits a unique weak solution

.

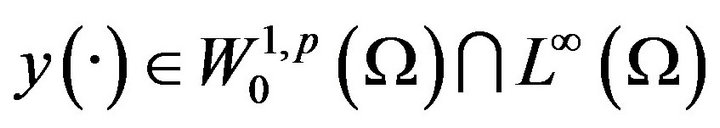Furthermore, there exists a constant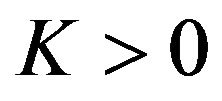, independent of

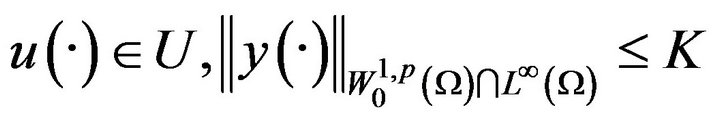(1.6)

The weak solution of the state Equation (1.1) is determined by

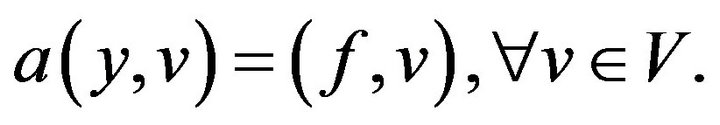
using the bilinear form 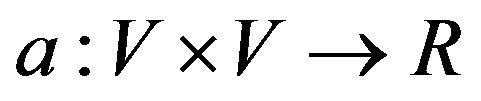given by

Existence and uniqueness of the solution to (1.1) follow from the above hypotheses on the problem data (see [2]). Let be the set of all pairs satisfying (1.1) and (1.4) is called an admissible set. Any is called an admissible pair. The pair

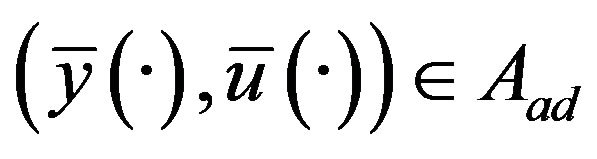, moveover satisfies

for all 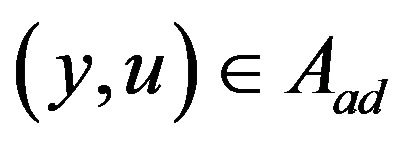is called an optimal pair. If it exists, refer to and as an optimal state and control, respectively.

Now, let be an optimal pair of Problem (C).

Let 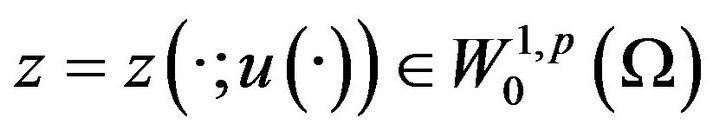be the unique solution of the following problem:

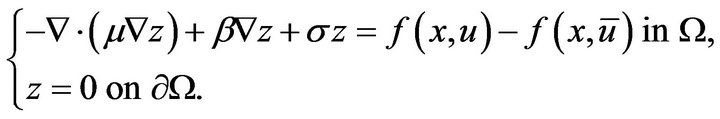(1.7)

And define the reachable set of variational system (1.7)

(1.8)

Now, let us state the first order necessary conditions of an optimal control to Problem (C) as follows.

Theorem 1.3. (Pontryagin’s maximum principle) Let (H1) - (H6) hold. Let 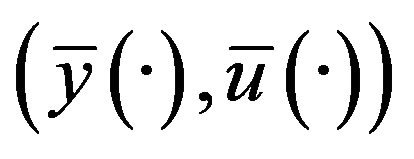be an optimal pair of Problem (C). Then there exists a triplet

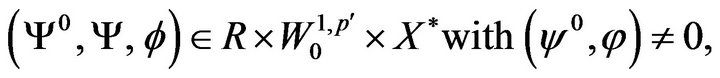
such that

(19)

(1.10)

(1.11)

where

(1.9), (1.10), and (1.11) are called the transversality condition, the adjoint system(along the given optimal pair), and the maximum condition, respectively.

Many authors (Dede [3], Yan [4], Becker [5], Stefano [6], Collis [7]) have already considered control problems for convection-diffusion equations from theoretical or numerical point of view. In the work mentioned above, the control set is convex. However, in many practical cases, the control set can not convex. This stimulates us to study Problem (C). To get Pontryagin’s Principle, we use a method based on penalization of state constraints, and Ekeland’s principle combined with diffuse perturbations [8].

In the next section, we will prove Pontryagin’s maximum principle of optimal control of Problem (C).

2. Proof of the Maximum Principle

This section is devoted to the proof of the maximum principle.

Proof of Theorem 1.3. Firstly, let

where is the Lebesgue measure of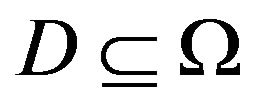. We can easily prove that 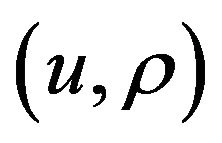is a complete metric space. Let 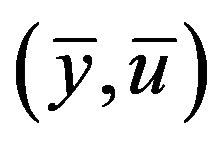be anoptimal pair of Problem (C). For any 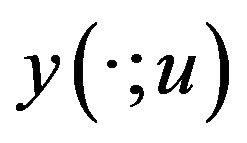be the corresponding state, emphasizing the dependence on the control. Without loss of generality, we may assume that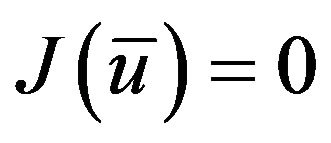. For any define

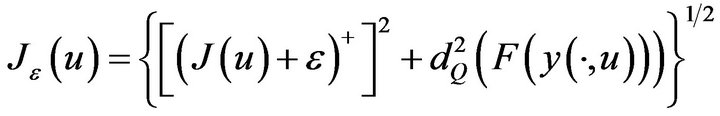(2.1)

where, and is an optimal control.

Clearly, this function is continuous on the (complete) metric space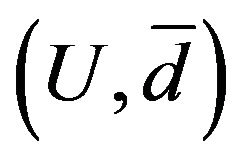. Also, we have

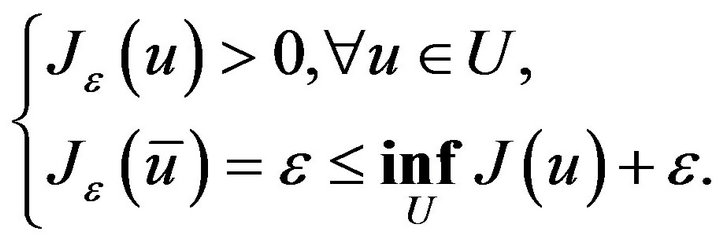(2.2)

Hence, by Ekeland’s variational principle, we can find a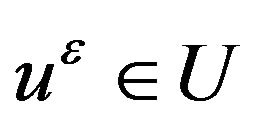, such that

(2.3)

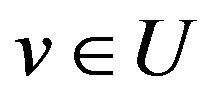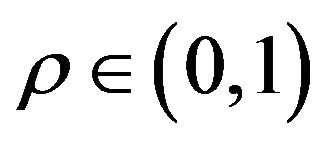Let and be fixed and let, we know that for any, there exists a measurable set 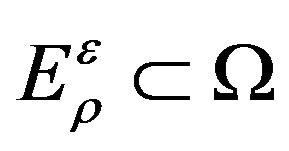with the property 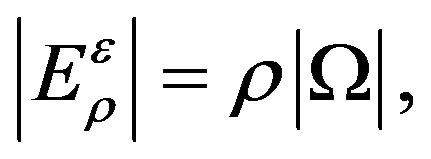such that if we define

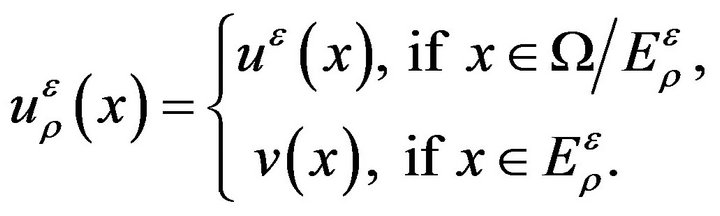
and let be the corresponding state, then

(2.4)

where 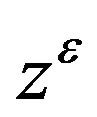and satisfying the following

(2.5)

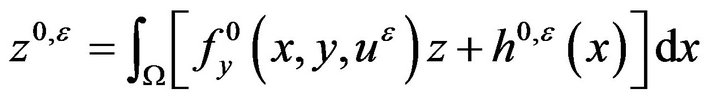(2.6)

with

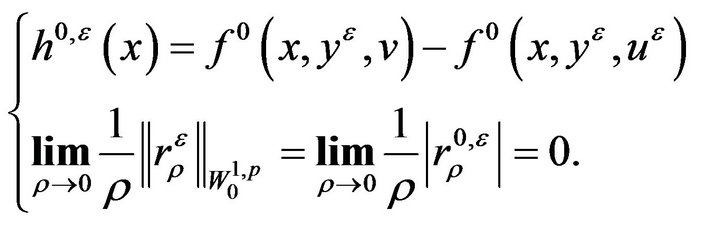(2.7)

We take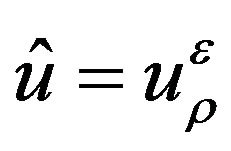. It follows that

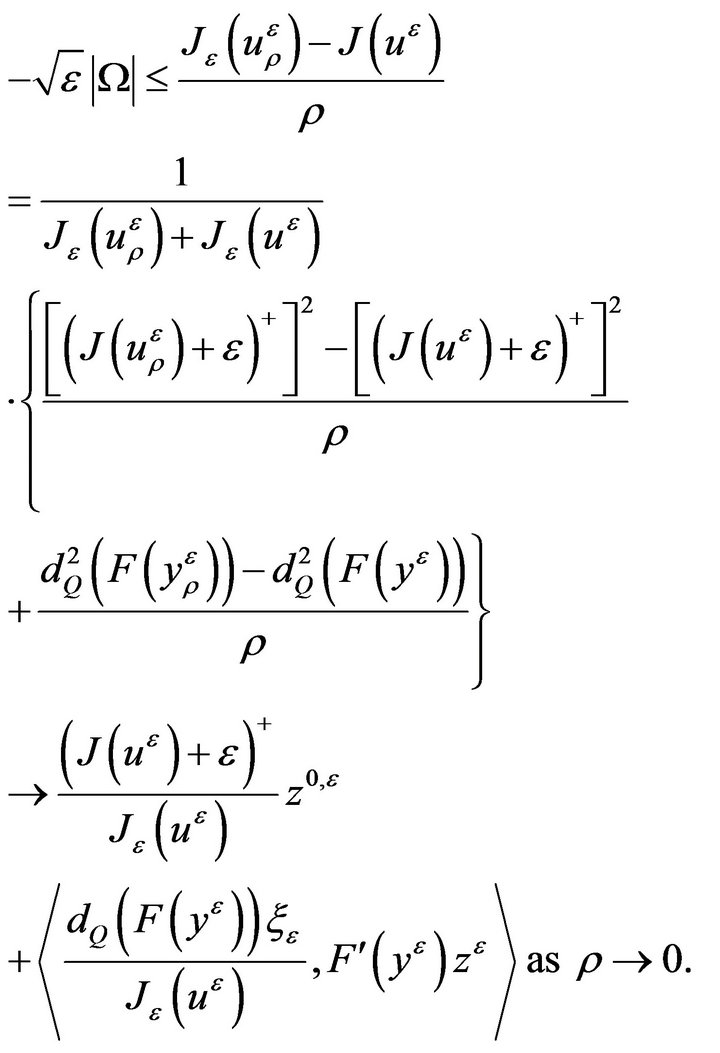(2.8)

where

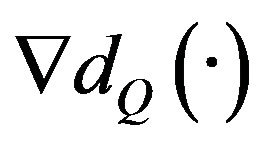denotes the subdifferential of.

Next, we define 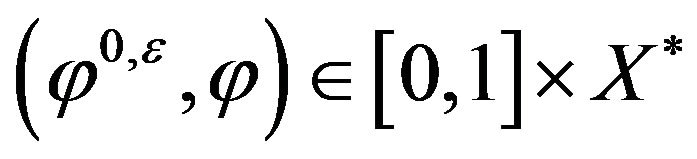as follows:

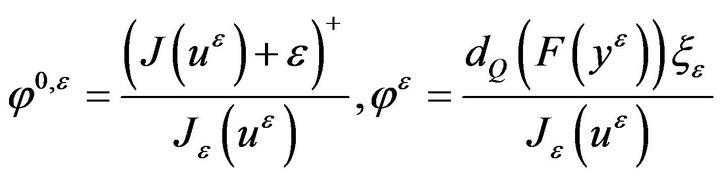(2.9)

By (2.1) and chapter 4 of [8], (2.8) becomes

(2.10)

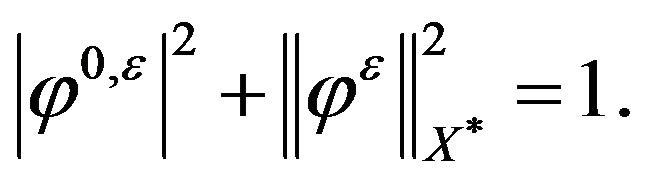(2.11)

On the other hand, by the definition of the subdifferential, we have

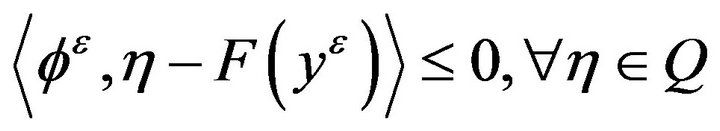(2.12)

Next, from the first relation in (2.3) and by some calculations, we have

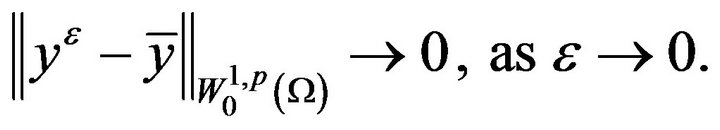(2.13)

Consequently,

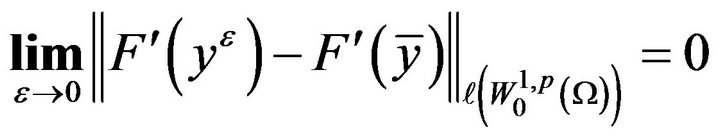(2.14)

From (2.5) and (2.6), we have

(2.15)

where is the solution of system (1.7) and

(2.16)

From (2.10), (2.12) and (2.15), we have

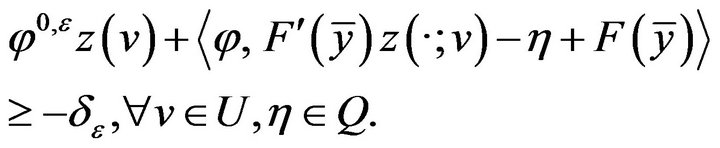(2.17)

with 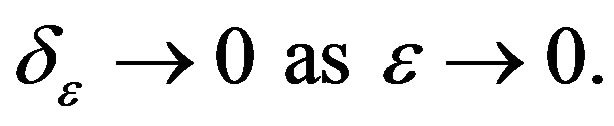Because 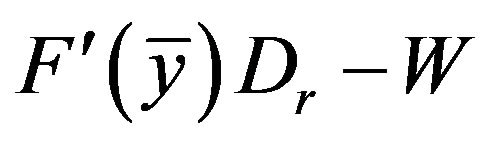has finite condimensionality in, we can extract some subsequence, still denoted by itself, such that

From (2.17), we have

(2.18)

Now, let

.

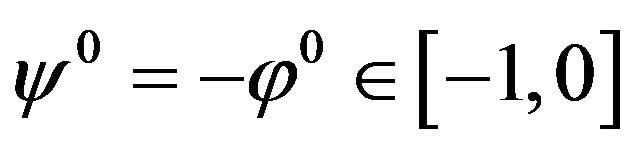Then

.

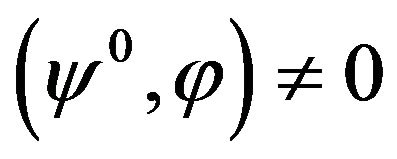Then we have

(2.19)

Take, we obtain (1.9).

Next, we let to get

(2.20)

Because, for the given, there exists a unique solution of the adjoint Equation (1.10). Then, from (1.6), (2.16), and (2.2), we have

(2.21)

There, (1.11) follows. Finally, by (1.10), if , then. Thus, in the case where

we must have, because.

3. Conclusion

We have already attained Pontryagin’s Maximum Principle for the advection-diffusion-reaction equation. It seems to us that this method can be used in treating many other relevant problems.

REFERENCES

NOTES

^*This work was partially supported by National Natural Science Foundation of China (Grant No. 11126170) and Hunan Provincial Natural Science Foundation of China (Grant No. 11JJ4006) and Ph.D startup Foundation of University of South China (Grant No 5-2011-XQD- 008).