Natural Resources
Vol.4 No.4(2013), Article ID:35634,7 pages DOI:10.4236/nr.2013.44044
A Bioeconomic Model for Sustainable Grazing of Old World Bluestem under Uncertainty
![]()
1Agricultural and Applied Economics, Texas Tech University, Lubbock, USA; 2Natural Resource Management, South Dakota State University, Brookings, USA.
Email: *aaron.benson@ttu.edu
Copyright © 2013 Aaron Benson, Cody Zilverberg. This is an open access article distributed under the Creative Commons Attribution License, which permits unrestricted use, distribution, and reproduction in any medium, provided the original work is properly cited.
Received January 11th, 2013; revised May 22nd, 2013; accepted June 14th, 2013
Keywords: Dryland Grazing; Sustainable Grazing; Profit Distribution
ABSTRACT
“WW B. Dahl”, a perennial old world bluestem (OWB) grass, has been promoted as a forage suitable for dryland grazing. Dryland grazing of OWB is however inherently risky economically and ecologically, may not be sustainable while remaining profitable. In this paper we develop a biological and economic single-season model of dryland grazing given production and price uncertainty, and identify a stocking rate that maximizes expected net revenue, subject to a sustainability constraint. We then simulate the distribution of net revenues, and find that probability of loss is greater than 35%, and median profit is roughly $30/ha.
1. Introduction
The Southern High Plains (SHP) of North America was covered by grasses and grazed by wild herbivores before European settlement converted much of the land to annual crops, and returning Southern High Plains land to perennial grasses is compatible with objectives of soil and water conservation [1]. The perennial grass, “WW B. Dahl”, an old world bluestem (OWB), has been used for this purpose [1], and is well-suited for dryland cultivation on the Southern High Plains [2]. As the Ogallala Aquifer, which provides much of the irrigation water on the SHP, reaches the end of its productive life, farmers and other agricultural producers who rely on Ogallala water need more complete information on dryland production alternatives. Since dryland production is less certain than irrigated production, knowledge of the biological and economic productivity and uncertainty associated with OWB is a critical factor in a private landowner’s decision to plant OWB. In this paper, we present a biological and economic model of OWB production. We then simulate optimal harvest under different weather conditions to estimate the distribution of profit for OWB ranchers. The model developed here can serve as a foundation for a stochastic-dynamic model of OWB grazing that prevents overgrazing and sustainably manages rangeland resources.
As described below, dryland grazing is risky not only because a producer may suffer a loss in a given year. Dryland grazing requires the producer to match the natural production of forage to cattle consumption. If the chosen consumption level is too high, the probability of permanent damage to the resource is much greater than on irrigated rangeland, either through overgrazing and damaging the productivity of the rangeland grasses themselves, or through degradation of the grasses and permitting invasive species to enter the resource and out-compete the damaged forage crop. In the model derived below, we attempt to determine a decision rule that mitigates this risk of impairing the long-term productivity of rangeland resources.
Philipp et al. [3,4] reported on productivity and quality of several old world bluestems, including “WW B. Dahl”, under irrigation treatments ranging from dryland to 100% replacement of evapotranspiration. These studies were replicated on small, ungrazed plots over the course of 3 years. In contrast, the studies by [5,6], and [2] were conducted on grazed pastures with little or no irrigation. Measurement of standing forage in these two types of study differed because grazed studies’ forage mass data were measurements of ungrazed residue, whereas Philipp et al. [4] measured total accumulated forage mass during the growing season. Neither type of study measured quantity of forage produced under grazing, although they do provide a basis for estimation. Since a grazed pasture is constantly being defoliated and producing regrowth, precise measurements of total forage growth under these conditions are impossible to obtain. Nevertheless, it is possible to create reasonable models of accumulated herbage mass under grazed conditions [7].
If forage is to be grazed rather than hayed, forage mass must be converted to animal weight gain. [5] and [6] measured average daily weight gain (ADG) of steers in their experiments, but they lack estimates of total forage production to allow conversion from forage production to animal weight gain. Since the marketable product from a grazed pasture is steer liveweight, it is critical that a simulation model create an accurate distribution of steer liveweight per unit of land (per hectare, in this study). For stochastic analysis, it is less important to accurately simulate forage production per hectare if a suitable relationship is developed between the variable of interest, liveweight gain per hectare, and the stochastic variable, which is growing season rainfall.
Dudensing [8] simulated OWB growth, quality and steer weight gain based on varying rates of irrigation and nitrogen fertilizer, while perfectly matching stocking rate to forage production; total steer weight gain was modeled as 345 kg/ha under no irrigation and 60 kg N/ha when initial steer size was 181 kg. However, perfectly matching stocking rate to forage production is impossible to do in practice because 1) adjustments to stocking rate are either reactive or predictive and therefore cannot be perfectly synchronized with forage growth, 2) actual forage growth is not perfectly known, and 3) variation in animals across individuals and time alter forage intake and growth. In addition, it is unrealistic to expect frequent changes in production settings due to the high transaction costs associated with such changes. Benson et al. [9] simulated profitability of an OWB system (which included a native grass) under production risk, but did not determine an optimal harvest rate, and also perfectly matched the stocking rate to forage production. They found mean steer gain to be 193 kg/ha and mean profitability to be $121/ha, with a 4% probability of loss. Benson et al. [9] also used low purchase and sale prices for steers, and assumed that the difference between purchase and sale prices differed little, despite the assumption that steers were sold at weights 278 kg/head heavier than when they were purchased. This assumption would most likely lead to unusually large estimates of profit.
Martin [10] simulated OWB and stocker steer production based on data from Allen et al. [1], but restricted her simulation to 10 years, somewhat limiting the resulting yield distributions. Mean stocker gain was 283 kg/ha. Martin [10] also assumed that 80% of the forage mass would be consumed, a very high proportion that could lead to overestimation of production.
While not an OWB study, Ritten et al. [11] determined optimal rangeland stocking decisions under production risk due to stochastic weather, but used a simplified biological component in their model, assuming a constant relationship between cattle weight gain and forage consumption, effectively assuming away some of the production uncertainty.
2. Methods
We develop our OWB grazing model by first assuming that producers wish to maximize profits subject to a conservation constraint that restricts grazing to a sustainable level. This is consistent with previous studies that have shown that profit maximization is often only one of multiple goals for ranchers and farmers (see, for example, [12-14]). Maintaining or improving the environment and maintaining familial ranch ownership are two such additional goals. In our model, we determine the profitability of an OWB grazing system assuming that the producer wishes to avoid overgrazing for unspecified reasons, and has a goal of maintaining the future potential of the site to produce forage. The “take half, leave half” concept is promoted by land mangers as a responsible conservation practice in which 50% of annual available forage is consumed. Others have proposed a rule in which a minimum level of biomass residue is left ungrazed at the end of the season [15]. In this model, we adopt the composite of the two, specifically restricting the choice of stocking rate and grazing period to leave the greater of 1000 kg/ha or 40% of total forage production of dry matter ungrazed at the end of the season. We choose the above composite restriction to better protect against the possibility of permanent damage to the rangeland, which, given the uncertain nature of forage growth from year to year, can be difficult to avoid.
The second important aspect of the model developed here is its stochastic nature. A dryland production model is inherently more risky than a model in which crops (or forage) are irrigated, and to be useful, the model must appropriately address that risk. In our model, we treat uncertainty in two parts of the process. In the first, we assume that uncertain rainfall produces an uncertain quantity of forage dry matter that itself is of uncertain quality. That is we assume DM = f(r, ε), where DM is quantity of forage dry matter (in kg), r is quantity of rainfall (in mm) and ε is a stochastic component; that FQ = 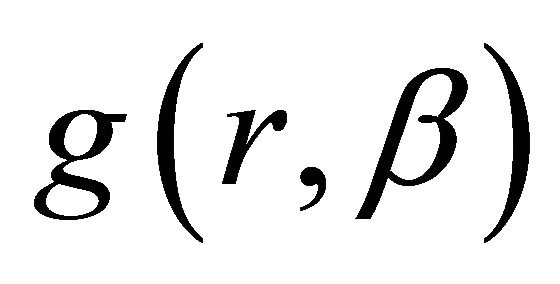 where FQ is forage quality (an index value between 0 and 1, where FQ = 1 would indicate that the maximum possible average daily weight gain is obtained) and β is another stochastic component, distributed independently of ε; and both β and ε are assumed to be distributed independently of r. The second component of the model to treat uncertainty is found in the purchase and sale prices of cattle, where we assume that the purchase price is random and the sale price is a function of the sale price; that is, SP = h(PP), where PP is purchase price and SP is sale price.
where FQ is forage quality (an index value between 0 and 1, where FQ = 1 would indicate that the maximum possible average daily weight gain is obtained) and β is another stochastic component, distributed independently of ε; and both β and ε are assumed to be distributed independently of r. The second component of the model to treat uncertainty is found in the purchase and sale prices of cattle, where we assume that the purchase price is random and the sale price is a function of the sale price; that is, SP = h(PP), where PP is purchase price and SP is sale price.
The uncertainty in a profit maximization model that incorporates these stochastic variables must be treated carefully for the model to be useful to potential producers. Therefore, we use a stochastic optimization method to determine the stocking rate that maximizes the expected profits of grazing OWB, given the uncertain nature of the process and the sustainability constraint described above.
2.1. Cattle Growth
Our model seeks to maximize the expected value of profits by choosing an optimal stocking rate at the beginning of the year, given uncertain production and prices. To accomplish this, it is not necessary to use a complex model of forage growth and animal weight gain in response to a multitude of climatic variables and forage quality measurements. Rather it is sufficient to create a realistic distribution of productivity based upon a few key parameters. That is the approach taken here.
The production of cattle, total weight gain, is determined by the average daily gain (ADG) of the steers and the length of the grazing period; that is,
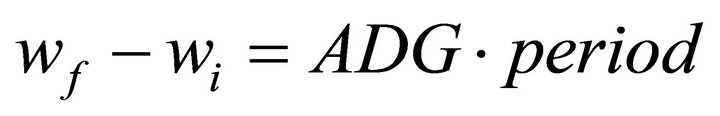 (1)
(1)
where, wf is final weight per steer (in kg), wi is initial weight (in kg), ADG is average daily gain (in kg/day) and period is number of days in the grazing period. ADG is influenced by forage quality. Forage quality is determined by environmental and management factors. Commonly measured aspects of quality include crude protein content, dry matter digestibility and fiber content [3], as well as antiquality factors such as lignin and tannins. However the ultimate measurement of quality is animal performance, which is ADG in this model. Complicated models exist to predict ADG based on forage quality parameters (such as the one employed by [8]), but the model presented here takes a simplified approach, with forage quality represented by a single variable, FQ, which is the percentage of potential ADG achieved. Forage quality is a function of rainfall, grazing pressure and a stochastic element, β. Grazing pressure is a function of stocking rate and forage availability [16]. Due to the conservation constraint, grazing pressure is restricted to moderate levels, and is therefore assumed to exert little influence on quality and can be safely ignored. We as- sume that forage quality is low for extremely low quantities of rainfall, reaches a maximum at moderate levels of rainfall and decreases gradually as rainfall exceeds the optimum. We calibrate a sine function so that, over the historical rainfall record, FQ ranges from 0.66 to 1.00, giving:
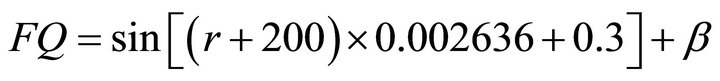 (2)
(2)
where r is rainfall and β is normally distributed with mean zero and standard deviation of 0.12. ADG in our model is given by
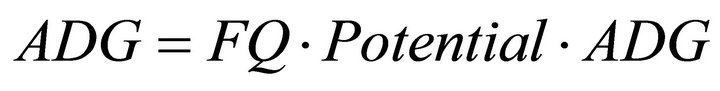 (3)
(3)
where potential ADG is a maximum potential value of ADG, which we set at 0.86 kg/day, slightly lower than the observed maximum season-long values for steers grazing OWB and small grains [17], since small grains are higher quality than OWB.
Grazing period is a function, in part, of available forage dry matter. Forage dry matter production is a function of rainfall, irrigation, fertilizer and residue from the previous period. Here, we assume that irrigation is constant at 0 mm/year and that fertilizer is held at 60 kg/ha. We also assume a constant residue quantity, which is held at a moderate level—typically only low or extremely high quantities of residue can negatively affect the following year’s production. Our forage dry matter production is therefore a function of rainfall and a stochastic component. We assume a logistic forage response to rainfall,
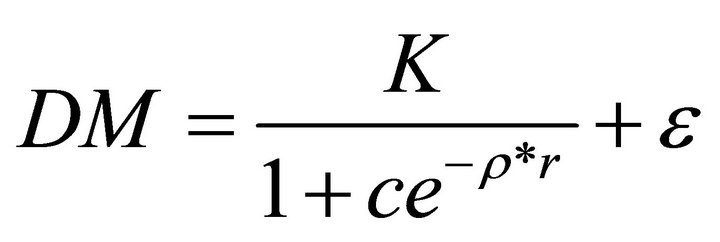 (4)
(4)
where DM is forage dry matter (in kg), r is rainfall (in mm), K, c and ρ are parameters to be estimated, and ε is normally distributed with mean zero and a standard deviation of 0.968. We fit Equation (4) using data from Philipp [18] and nonlinear least squares estimation, and estimate K = 12.78, c = 9.7, and ρ = 0.00537. The deterministic component of Equation (4) is graphed in Figure 1.
The producer selects an initial stocking rate before the quantity of available forage is known. We assume a constant stocking rate throughout the grazing season for modeling simplicity and to avoid the transaction costs associated with adding and subtracting cattle mid-season. The stocking rate is based on the amount of available forage a producer anticipates in a given year, before the growing season begins. We assume that the anticipated available forage is based on the producer’s (perfect) knowledge of past production, and that anticipated available forage is simply the forage produced by Equa- tion (4) with an average quantity of growing season rainfall (3900 kg and 285 mm, respectively). The producer observes the anticipated available forage and chooses a level of forage utilization intensity, int, which is a value greater than 0. For int = 1, the producer would choose a
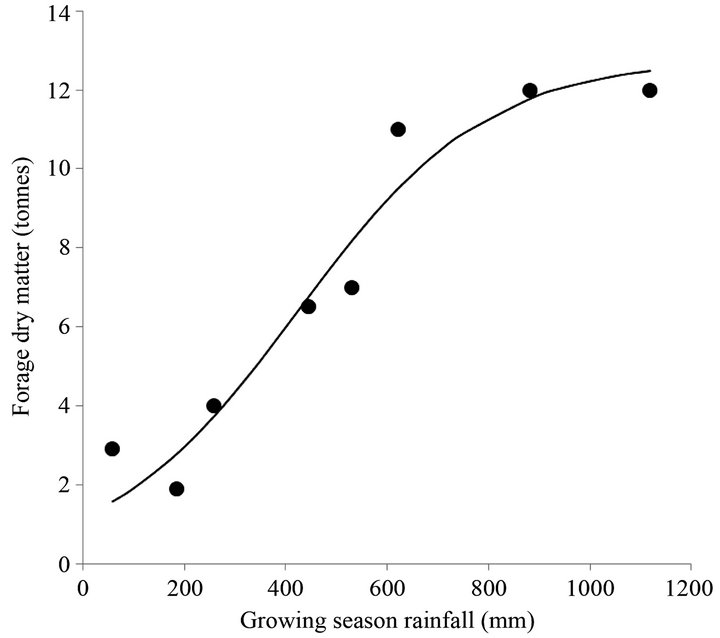
Figure 1. The deterministic component of forage dry matter. Logistic growth function is fit using data from Philipp [18].
stocking rate in which weight gain would be equal to that which would be expected in an average year. If int > 1 and an average or less than average rainfall occurs, then the grazing period will be cut short and the cattle sold early. However, if int ≤ 1 and a greater than average rainfall occurs, forage will go unconsumed and the producer will potentially lose revenue. Our equation for stocking rate (in head/ha) is
 (5)
(5)
where utilization is the targeted utilization of forage, set equal to 0.6, by the sustainability constraint; efficiency is grazing efficiency, or percentage of disappeared forage actually consumed by steers, set equal to 0.5 [16]; intake is daily forage consumption as a percentage of body weight (0.025); period, or grazing period, is determined primarily by stocking rate and forage, and is terminated when 40% of forage mass remains, 1000 kg/ha of forage remains or 170 days have passed, whichever comes first —we set expected period at 135 days; and weight is average weight of steers. Since total final weight gain is unknown at the beginning of the season, we use an expected average weight, based on the expected grazing period and ADG, of 282.35 kg. Together, Equation (5) becomes SR = 1.23 × int.
Finally, grazing period is determined by the chosen stocking rate and available forage. It is the period of time in which the chosen stocking rate consumes up to 60% of the available forage, and is restricted such that it cannot last more than 170 days nor can less than 1000 kg/ha of forage be left unconsumed at the end of the grazing period. Period solves the following equation (which sets consumed forage equal to available forage):
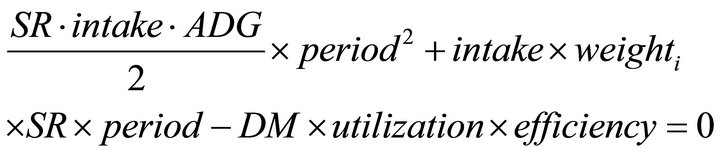
where weighti is initial weight of cattle at the beginning of the grazing season, and the other equations are defined as above. Using the parameter values from above and Equations (3)-(5), we solve the quadratic equation above for period to get:
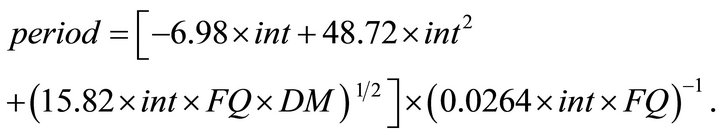
Equation (6) gives the number of days in which 60% of the available dry matter forage will be consumed. To further restrict period so that no less than 1000 kg/ha of dry matter is left at the end of the grazing period, we solve a similar quadratic equation and derive the following restriction:
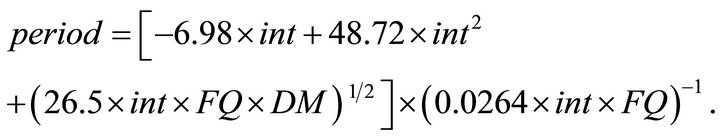 (7)
(7)
2.2. Expected Profit Maximization
Our producer seeks to maximize expected profits per acre by choosing forage utilization intensity, int, subject to our sustainability constraints (that the greater of 40% of initial dry matter forage or 1000 kg/ha remains at the end of the season) and subject to stochastic rainfall, forage growth, forage quality and prices. Mathematically, the producer solves
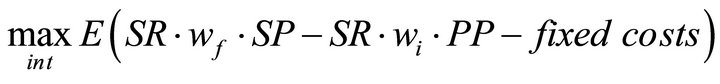
s.t.
Equations (1)-(7), and ;
;
where SR is stocking rate (in head/ha), wf is the weight per head at the end of the grazing season (in kg) and is equal to wi + ADG × period, PS is sale price (in $/kg), wi is weight per head at the beginning of grazing (in kg), PP is purchase price (in $/kg) and fixed costs are additional costs per ha.
Using 18 years of Amarillo stocker (purchase) and feeder (sale) prices, we estimate a base price of $2.58/kg with a standard deviation of 0.277. We assume that stocker prices are distributed normally, with the sample mean and standard deviation. We also determine an average ratio of feeder to stocker price for each day between May and November, and adjust feeder prices accordingly. Specifically, we have
 , (8)
, (8)
which results in sale prices being around 14% less than purchase prices, after a 170-day grazing season.
3. Results
To solve the expected maximization problem, we create discretized distributions of rainfall, purchase prices, forage quality and forage dry matter. For rainfall, we gather 101 seasonal (June-October) rainfall observations from Lubbock, Texas from 1911 through 2011, and create a discrete distribution of rainfall using the frequency distribution of the observations (Figure 2). For the other three variables, we create discrete distributions of their random components, all of which are assumed to be normally distributed.
We use the Maple modeling software package to calculate the expected value of profit by summing the profit function over each possible combination of occurrences of each random variable (where each discrete distribution has 10 outcomes), multiplied by their probabilities of occurring, and maintaining forage utilization intensity, int, as a variable. Given the complicated nature of the restrictions on the period function, the calculated expected profit function is many thousands of lines long. A plot of expected profit as a function of int is therefore shown in Figure 3. Expected profit achieves a maximum of $24/ha at a forage utilization intensity value of 1.42. This implies a stocking rate of 1.74 head/ha (or 0.7 head/acre).
Profit Simulation
To better inform potential producers of the uncertainty of dryland OWB grazing, we develop a simulation model to estimate a distribution of profits. To do so, we generate 20,000 simulated values of rainfall (by drawing uniformly randomly from the 101 collected observations), purchase sale prices (by simulating draws from a normal distribution with the sample average and standard deviation from the collected price data), and stochastic components of FQ and DM (by simulating draws from normal distributions as characterized above). For each simulated random variable, we calculate FQ, DM, period (with the restrictions as described above), and sale price, given the optimal intensity value, int = 1.42. Using these variables, we calculate simulated revenue, cost and profit values.
From our simulated data of profit, for which a sample CDF is graphed in Figure 4, we find that the producer has about a 39% probability of suffering a loss, and about a 25% probability of profit per hectare being greater than $100. The median profit is roughly $30/ha. Compared to previous studies of dryland grazing, this profit distribution is relatively low. [9] estimate only a 4% chance of loss and an average profit of over $120/ha, while OrtegaOchoa et al. [19], using two observations, estimate an average dryland profit of over $200/ha.
Given the low average profit and high probability of loss, we re-derive the above equations with a range of
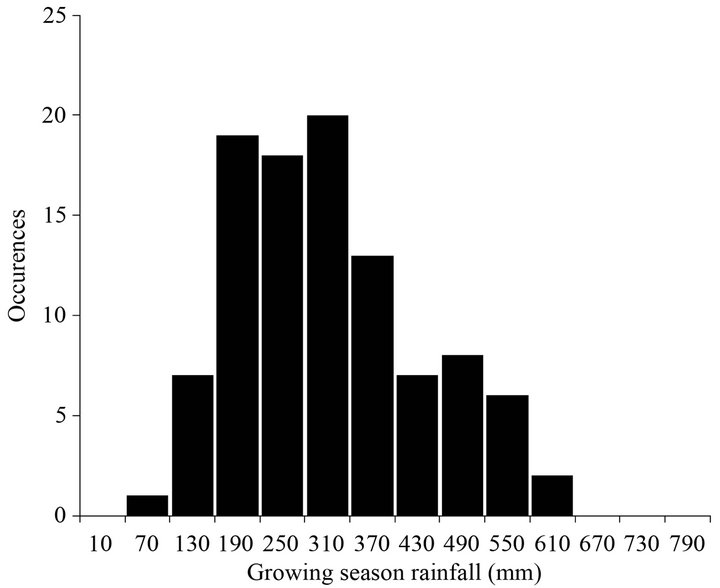
Figure 2. Frequency distribution of rainfall in Lubbock, TX.
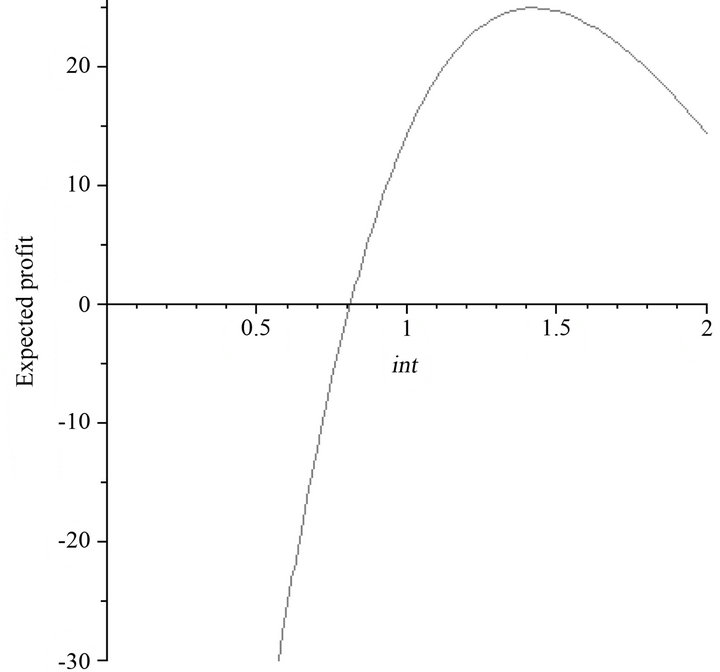
Figure 3. Expected profit as a function of forage utilization intensity, int.
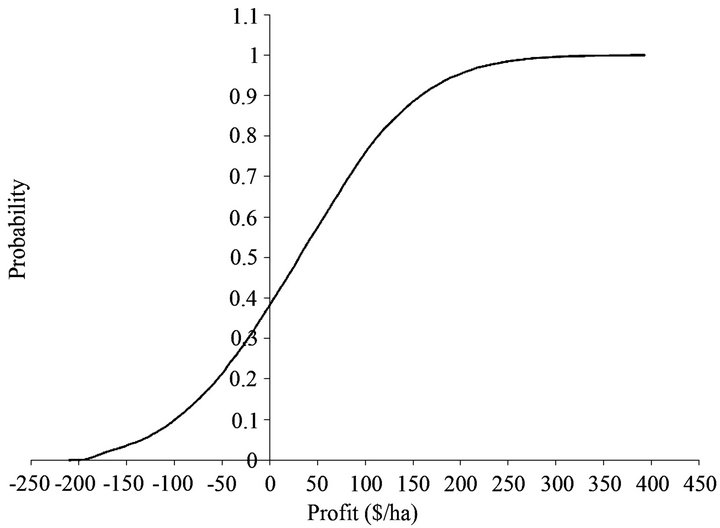
Figure 4. Sample CDF of simulated profits.
sustainability constraints, and re-ran the simulation described above. Specifically, we determine average annual net revenue and probability of loss for a rancher who grazes 60% or 70% of available forage and leaves 1000, 750 or 500 kg of forage ungrazed at the end of the season. The results of the simulations with the varying conservation constraints are reported in Table 1. Relaxing the residue constraint (while keeping quantity grazed at 60%) does not greatly affect the distribution of profit. Leaving less forage in low rainfall years, which is the effective response to decreasing the residue constraint, tends to decrease the probability of large losses. For example, the probability of net revenue being less than $100 decreases from 12% to about 9%. However, probability of net revenue less than zero and average and median annual net revenue are largely unchanged.
Increasing the percentage of forage grazed (or forage utilization), from 60% to 70%, does tend to increase average and median revenue and decrease the probability of loss, for all levels of the residue constraint. Also, changing the residue constraint has a more noticeable effect on net revenues with the higher forage utilization: average net revenue increases from $47/ha to $58/ha and probability of net revenue less than zero decreases from 33% to 30% when the residue constraint decreases from 1000 kg/ha to 500 kg/ha.
4. Discussion
In this paper we attempt to develop a more realistic estimate of the profitability of dryland OWB grazing. There are multiple sources of uncertainty in determining cattle weight gain, and many varying levels of complexity in which it can be modeled. Here, we opt for moderate complexity by assuming that some of the biomechanics are randomly given, assuming that the random variation in forage quality and forage growth can approximate natural variation that is driven by climate conditions beyond growing season rainfall.
In addition, we include varying constraints on forage grazing to guarantee future productivity (or at least to
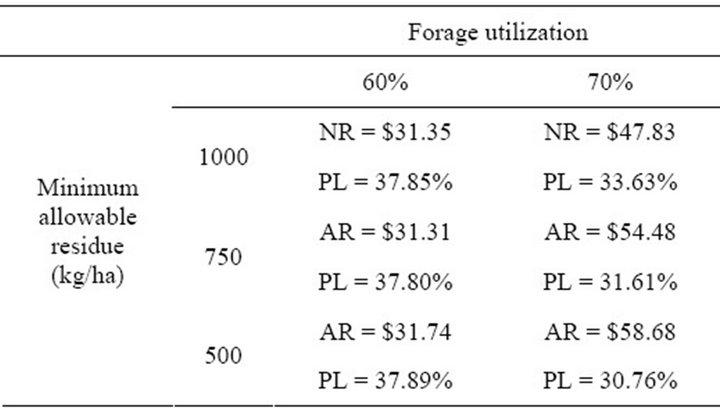
Table 1. Average net revenue (NR) and probability of loss (PL) for varying conservation constraints.
minimize the probability of harming future productivity). These constraints are difficult to specify optimally given the uncertainty that exists in the production of forage. The approach taken here could be similar to the application of decision analysis applied to natural resource harvest as described in Clark ([20], pp 279-282). Clark [20] suggests that, in resource harvest decision-making where uncertainty plays a large role in production and prices, it is necessary to identify the uncertainty, especially sources of uncertainty that have been overlooked; specify management objectives that recognize the uncertain nature of the resource; quantify the uncertainty; and model the resource system explicitly to capture the dynamics of the system and harvest. Finally, Clark [20] suggests that results be presented in terms of the uncertainty that underlies the process. In this manner, resource managers (in this case, ranchers), are able to understand the risk of the decisions that they make. Unfortunately, because of the lack of a fuller understanding of the OWB resource, specifically, the probability of causing irreparable damage to it by overgrazing, this study falls short of being a complete example of decision analysis.
Because of the introduced uncertainty and the sustainability constraints, our estimates of profitability are lower than previous studies of OWB grazing. We argue, however, that our results are more realistic as they better approximate the complexity of cattle production from grazing, and better model actual decision-making of ranchers who voluntarily constrain their profit to safeguard the possibility of future ranching for themselves and for their children.
For future work, a model of the rangeland over a period of years could be developed to capture the dynamics of forage growth given previous harvest, which will be a truer decision analysis as advocated by Clark [20] than the study presented here. To do so, however, we would require more research to be completed on rangeland systems. We would require data on the quantity of forage produced given the previous season’s residue, encroachment of invasive species given previous season’s residue, and forage growth in more varying climatic conditions. Currently, there are only a few observations of forage growth in controlled experiments, and are not ideal for determining realistic uncertainty of forage growth.
Additionally, there are low-irrigation grazing models currently being developed that require irrigation only occasionally (i.e. only in some years). These production models may be feasible on the Southern High Plains indefinitely given that the irrigation requirements, in some cases, may be low enough to match the natural recharge of the Ogallala aquifer. A dynamic (multi-year) grazing model of limited irrigation OWB would be necessary to determine whether, and to what extent, the risk-mitigation factor of irrigation water in low years can improve the profitability of the dryland system described here.
REFERENCES
- V. G. Allen, P. Brown, R. Kellison, E. Segarra, T. Wheeler, P. A. Dotray, J. C. Conkwright, C. J. Green and V. Acosta-Martinez, “Integrating Cotton and Beef Production to Reduce Water Withdrawal from the Ogallala Aquifer in the Southern High Plains Regions,” Agronomy Journal, Vol. 97, No. 2, 2005, pp. 556-567. doi:10.2134/agronj2005.0556
- C. Ortega-Ochoa, C. Villalobos, C. Britton, D. Wester, D. Ethridge and D. Wills, “A Profitability Analysis of a Beef Production on WW-B. Dahl Pasture under Different Combinations of Irrigation and Supplement Feeding,” The Texas Journal of Agriculture and Natural Resources, Vol. 20, No. 1, 2007, pp. 42-51.
- D. Philipp, V. G. Allen, R. J. Lascano, C. P. Brown and D. B. Wester, “Forage Nutritive Value and Morphology of Three Old World Bluestems under a Range of Irrigation Levels,” Crop Science, Vol. 45, No. 6, 2005, pp. 2258- 2268. doi:10.2135/cropsci2004.0669
- D. Philipp, V. G. Allen, R. B. Mitchell, C. P. Brown and D. B. Wester, “Production and Water Use Efficiency of Three Old World Bluestems,” Crop Science, Vol. 47, No. 2, 2007, pp. 787-794. doi:10.2135/cropsci06.05.0340
- J. C. Burns and D. S. Fisher, “Steer Performance and Pasture Productivity of Caucasian Bluestem at Three Forage Masses,” Agronomy Journal, Vol. 102, No. 3, 2010, pp. 834-842. doi:10.2134/agronj2009.0468
- C. Ortega-Ochoa, “Effect of Levels of Irrigation on Forage Standing Crop and Quality of WW-B. Dahl (Bothriochloa bladhii) Pasture under Summer Grazing,” PhD Dissertation, Texas Tech University, Lubbock, 2006.
- O. J. Chaco, “A Practical Equation for Pasture Growth under Grazing,” Grass and Forage Science, Vol. 48, No. 4, 1993, pp. 387-394. doi:10.1111/j.1365-2494.1993.tb01873.x
- J. D. Dudensing, “An Economic Analysis of Cattle Weight Gain Response to Nitrogen Fertilization and Irrigation on WW-B. Dahl Bluestem,” MS Thesis, Texas Tech University, Lubbock, 2005.
- A. Benson, P. Zhu, M. Farmer and C. Villalobos, “Profitability of a Dryland Grazing System Suitable for the Texas High Plains,” The Texas Journal of Agriculture and Natural Resources, Vol. 24, 2011, pp. 62-73.
- R. Martin, “Economic Evaluation of an Integrated Cropping System with Cotton,” MS Thesis, Texas Tech University, Lubbock, 2005.
- J. P. Ritten, W. M. Frasier, C. T. Bastian and S. T. Gray, “Optimal Rangeland Stocking Decisions under Stochastic and Climate-Impacted Weather,” American Journal of Agricultural Economics, Vol. 92, No. 4, 2010, pp. 1242- 1255. doi:10.1093/ajae/aaq052
- K. D. Young and C. R. Shumway, “Cow-Calf Producers’ Perceived Profit Maximization Objective: A Logit Analysis,” Southern Journal of Agricultural Economics, Vol. 23, No. 1, 1991, pp. 129-136.
- L. A. Torell, N. R. Rimbey, J. A. Tanaka and S. A. Bailey, “The Lack of a Profit Motive for Ranching: Implications for Policy Analysis,” Annual Meeting of the Society for Range Management, Kailua-Kona, 17-23 February 2001, pp. 1-12.
- L. A. Torell, N. R. Rimbey, O. A. Ramirez and D. W. McCollum, “Income Earning Potential versus Consumptive Amenities in Determining Ranchland Values,” Journal of Agricultural and Resource Economics, Vol. 30, No. 3, 2005, pp. 537-560.
- R. E. Sosebee, D. B. Wester, J. C. Villalobos, C. M. Britton, C. Wan and H. Nofal, “How Grasses Grow—How Plant Growth Relates to Grazing Management,” Proceedings of the 2nd National Conference on Grazing Lands, Nashville, 7-10 December 2003, pp. 117-125.
- A. J. Smart, J. D. Derner, J. R. Hendrickson, R. L. Gillen, B. H. Dunn, E. M Mousel, P. S. Johnson, R. N. Gates, K. K. Sedivec, K. R. Harmoney, J. D. Volesky and K. C. Olson, “Effects of Grazing Pressure on Efficiency of Grazing on North American Great Plains Rangelands,” Rangeland Ecology and Management, Vol. 63, No. 5, 2010, pp. 397-406. doi:10.2111/REM-D-09-00046.1
- V. G. Allen, P. Brown, R. Kellison, P. Green, C. J. Zilverberg, P. Johnson, J. Weinheimer, T. Wheeler, E. Segarra, V. Acosta-Martínez, T. Zobeck and J. C. Conkwright, “Integrating Cotton and Beef Production to Reduce Water Withdrawal from the Ogallala Aquifer in the Southern High Plains: I. Ten-Years of Effect on Water Use and Productivity,” Agronomy Journal, Vol. 104, No. 6, 2012, pp. 1625-1642. doi:10.2134/agronj2012.0121
- D. Philipp, “Influence of Varying Replacement of Potential Evapotranspiration on Water Use Efficiency and Nutritive Value of Three Old World Bluestems (Bothriochloa spp.),” PhD Dissertation, Texas Tech University, Lubbock, 2004.
- C. Ortega-Ochoa, M. Farmer and C. Villalobos, “A Pasture-Based Model for Extended Drought Management, Long-Term Sustainability, and Economic Viability in the Southern High Plains,” Forage and Grazinglands, 2007, in press. doi:10.1094/FG-2007-1108-01-MG
- C. W. Clark, “Mathematical Bioeconomics: The Mathematics of Conservation,” 3rd Edition, John Wiley & Sons, Inc., Hoboken, 2010.
NOTES
*Corresponding author.

