Journal of Power and Energy Engineering
Vol.04 No.04(2016), Article ID:66207,13 pages
10.4236/jpee.2016.44008
Performance Comparison of PI and Fuzzy Logic Based IPFC on Damping of Power System Oscillations
S. N. Dhurvey, V. K. Chandrakar
Dept. of Electrical Engg, G.H. Raisoni College of Engineering, Nagpur, India
Copyright © 2016 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 24 December 2015; accepted 26 April 2016; published 29 April 2016
ABSTRACT
This paper presents a new approach for determining the effective control signals for damping of oscillations by using fuzzy logic based Interline Power Flow Controller [IPFC]. The IPFC performance is tested with PI controllers in comparison with fuzzy logic based controller on Modified Phllips-Heffron Model of Single Machine Infinite Bus System to achieve improved damping performance by selecting effective control signals such as deviation in pulse width modulation index of voltage series converter 1 in line 1, pulse width modulation index of voltage series converter 2 in line 2, deviation in phase angle of the injected voltage of convertor 1, injected voltage phase angle deviation of convertor 2. Investigations reveal that coordinated tuning of Interline Power Flow Controller with Fuzzy Logic Controller provides the robust dynamic performance. The Fuzzy Logic Based Interline Power Flow Controller [IPFC] is designed with simple fuzzy rules to coordinate the additional damping signal. The proposed controllers for IPFC are able to achieve improved designed performance of the power system. Validity of effective control signals has been done by eigen value analysis.
Keywords:
FACTS, IPFC, FLC, Damping of Oscillations

1. Introduction
When a power system is subjected to a disturbance, the system variables undergo oscillations. Some low frequency electromechanical oscillations of small magnitude exist in the power system for long periods of time, and in some cases they may impose limitations on the transmission line functionality. With low damping, power system is subjected to prolonged large oscillations. Several devices and control methods have been developed to increase damping in power systems and improve power transfer limits. In particular, the application of multifunctional FACTS controllers based on back to back dc/ac voltage source converter has greatly met with power demand in the recent years. The high current semiconductor device based FACTS devices with proper control strategy can improve the power system stability of power system. Many researcher presented work on various nonlinear VSC based FACTS devices like STATCOM, SSSC [1] and UPFC for transient stability improvement of the power system under various system conditions. Amongst the other developed VSC based nonlinear FACTS devices, Interline Power Flow Controller (IPFC) is most versatile FACTS device, it consists of number of SSSC which are connected in each line which are connected via common dc bus, addresses the problem of compensating a number of transmission lines. The special feature of IPFC is not only to perform an independently controllable reactive series compensation of each individual line but also to deliver real power between the compensated lines. This capability of IPFC makes it possible to equalize both real and reactive power flow between the lines; hence avoid the burden of overloaded; making compensation for resistive line voltage drops and the associated reactive power demand and increasing the efficacy of the overall compensating system for dynamic disturbances [2] - [19] . Shan Jiang et al. [18] discuss the behavior of two FACTS devices; the combined series-series controller and the combined series-shunt controller in a benchmark system and prove that the IPFC has more series branches than the UPFC, it provides more opportunities for network segmentation and, hence, has the potential for greater damping improvement. Gopinath et al. [19] introduce the model of state estimation embedded with IPFC. A power injection model that shows the influence of IPFC on the power flow between the interconnected lines is presented. Segundo et al. [16] have examined the efficacy of VSC-based FACTS controllers in contributing to system-wide damping. The strategy is tested on a practical 45-machine Mexican system that includes number of static VAR compensators.
Fuzzy Logic Controller is robust and easily modified. It can use multiple input and output sources. Advantageous feature of fuzzy logic is to provide solution to the problem can be cast in terms that human operators can apply their experiences for the design of the controller to achieve maximum performance of the IPFC controller.
Dhurvey et al. [20] have examined the relative effectiveness of IPFC control signals on linearized power system model of single machine infinite bus system (SMIB) system for analyzing performance comparison of IPFC in coordination with Power Oscillation Damping Controller [POD] and Power System Stabilizer [PSS]. However, results have been not presented with the consideration of various damping factor D and Kp and Ki is not properly tuned. Hence, the aim of this paper is to present the modified version of reference [20] . Kazemi et al. [10] proved the effective damping control function of an IPFC installed in a power system. Parimi, et al. [5] implement the Fuzzy logic control for IPFC for damping low frequency oscillations. Alivelu M. Parimi [7] develop the nonlinear model of power system incorporated with Interline Power Flow Controller (IPFC). The oscillation modes with low damping ratio are obtained from the eigen value analysis of the linearized Phillips-Heffron model Parimi [12] has proved that IPFC control signal m2 is the most effective. M.R. Banaei et al. [14] has proved that signals m1, m2 based controllers have more effect on damping of oscillation and signal δ1, δ2 based controllers have less effect on damping of oscillation. Veeramalla, J. et al. [15] investigated the effectiveness of the IPFC based damping controller. Dynamic simulations results have emphasized that the damping controller which modulates the control signal m2 provides satisfactory dynamic performance under wide variations in loading condition and system parameters. However, they have not presented an approach for obtaining the simultaneous coordination of IPFC with each control signal and Fuzzy Logic Controller.
In view of the available work presented by the researchers, the main objective of this paper is to study effectiveness of various control signals [mi1, mi2, α1, α2] of IPFC for damping of power system oscillations. The comparative performance of PI based controller and fuzzy logic based IPFC for improved power system performance is demonstrated. The results are validated in MATLAB environment.
2. System Model
Single-Machine Infinite Bus Power System incorporated with Interline Power Flow Controller in one of the two transmission lines is considered for analysis which consists of an excitation transformer, a boosting transformer, a pair of voltage source converters and a DC link capacitor is shown in Figure 1. Δmi1 is the deviation in pulse width modulation index mi1 of voltage series converter 1 in line 1. By controlling mi1, the magnitude of series
Figure 1. A single machine infinite bus power system installed with an IPFC in one of the lines.
injected voltage in line 1 can be controlled. Δmi2 is the deviation in modulation index mi2 of series converter 2 in line 2. By controlling mi2, the magnitude of series injected voltage in line 2 can be controlled. Δα1 is the deviation in phase angle of the injected voltage Vse1. Δα2 is the deviation in phase angle of the injected voltage Vse2. The nominal loading condition and system parameters are given in Appendix A.
3. Interline Power Flow Controller
Interline Power Flow Controller (IPFC) is VSC based FACTS controller, consists of two voltage-sourced converters (VSCs) inserted in series with transmission lines, whose DC capacitors are linked such that active power can be transferred between the two VSCs. Each VSC provides series compensation for the selected transmission line and is capable of exchanging reactive power with its own transmission system. Basic function is to control power flow among transmission lines and damping of oscillations. A non-linear dynamic model of the system is derived by omitting the resistances of all the components of the system and the transients of the transmission lines and transformers of the IPFC.
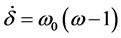 (1)
(1)
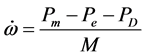 (2)
(2)
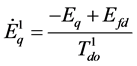 (3)
(3)
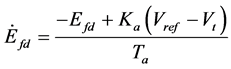 (4)
(4)
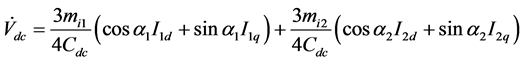 (5)
(5)
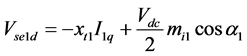 (6)
(6)
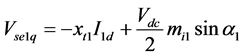 (7)
(7)
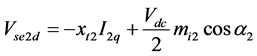 (8)
(8)
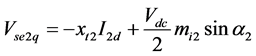 (9)
(9)
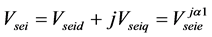 (10)
(10)
A linear dynamic model of IPFC is obtained by linearizing at operating point [14] .
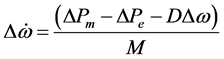 (11)
(11)
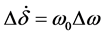 (12)
(12)
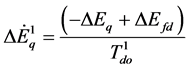 (13)
(13)
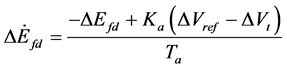 (14)
(14)

where,



Figure 2 shows the modified Phillips-Heffron model of the SMIB system with IPFC installed [4] . The constants of the modified Phillips-Heffron model are functions of the value of system parameters and the initial operating condition as shown in Appendix A. In terms of state-space representation, the power system can be modeled as


Figure 2. Phillips Heffron Model of IPFC.



4. Proportional Integral (PI) Based IPFC
In this section, PI Based IPFC [20] is suggested for damping of oscillations. The PI constants Kp and Ki are chosen by trial and error method. In Figure 3, additional damping signal Power Oscillation Damping Controller [POD] can be applied for improvement in PI controller performance. The POD controller [21] may be considered as comprising gain KDC, wash out block and lag-lead compensator. The values of parameters of the lead-lag compensator are chosen so as to obtain best damping performance. Optimum parameters for the damping controllers are given in Appendix A. The IPFC controllable signals (mi1, α1, mi2 and α2) can be modulated in order to produce a damping torque. Controllability indices for the different Interline Power Flow Controller controllable parameters are given in Appendix A. The washout circuit as shown in Figure 3 is provided to eliminate steady-state bias in the output of POD Controller. The Tω must be chosen in the range of 10 to 20.
5. Fuzzy Logic Based IPFC
Drawback of PI controller is the frequency deviation. It causes deterioration in performance during varying system conditions. Hence Fuzzy logic can be blended with conventional control techniques. Fuzzy logic is the art which makes machines more intelligent enabling them to reason in a fuzzy manner like humans. The mathematical concepts behind fuzzy reasoning are very simple. Hence fuzzy logic IPFC controller is proposed. Fuzzy logic is an innovative area of research as it does a good job of trading off between significance and precision. The main concept of fuzzy logic control (FLC) is to build a model of a human expert capable of controlling the plant without thinking in terms of a mathematical model. Figure 4 shows Fuzzy Logic Controller (FLC) in which the electrical power at IPFC location is feedback to the coordination of control signals are the inputs to the fuzzy
Figure 3. Structure of power oscillation damping [POD] controller.
Figure 4. Structure of fuzzy logic controller.
logic controller. The control strategy has been prepared based on rules. The fuzzy logic approach more accurately represents the operational constraints of power systems and fuzzified constraints are softer than conventional constraints. Fuzzy logic based IPFC controller consists of three major parts. (a) Fuzzification; (b) Inference; (c) Defuzzification units.
5.1. Fuzzification
In fuzzification the input and output are decomposed into one or more fuzzy sets. Here, the input variables are mapped onto fuzzy linguistic variables. The choice of membership functions influences the quality of a fuzzy logic controller. Membership function defined on the universe of discourse is the space where the fuzzy variables are defined. The membership functions designs the elements of the universe onto numerical values in the interval [0, 1]. Each fuzzified variable has certain membership function. The input (Pe) is fuzzified using three fuzzy sets: high, good and low. Many types of curves can be used, Out of all the curves available, triangular or trapezoidal shaped membership functions are the most popular. These shapes are easier to represent in embedded controllers. The shape of membership function is chosen by trial and error approach so that best performance of the fuzzy controller can be achieved. However, the shape of the membership function can vary the small deviations in output of fuzzy logic controller [22] [23] . The output membership function is fuzzified using three fuzzy sets: big, medium, small. Plot of membership function for input and output variable are as shown in Figure 5 and Figure 6 respectively.
The parameters of the membership function of the fuzzy logic controller, consisting of 

5.2. Inference
A relation between cause and effect, or a condition and a consequence is done by reasoning. For reasoning, logical inference is used, in order to draw a conclusion. The mechanism of the inference process is the search of input/output relationship to match the input conditions. The objective of control is to influence the behavior of a system by changing an input of that system according to a rule that model how the system operates. Therefore, an integral part of the inference process is the rule-base (a list of rules that relate the input values to the output values). Control decisions [24] are made on the basis of fuzzified linguistic variables. We usually follow rules of inference as shown in Table 2. The rules can be specified to include various operating conditions. In fuzzy logic control, in order to minimize the complexity of the controller, it is always desirable that number of rules in a working controller should be less which makes shorter controller execution time. Hence while designing FLC more stress has been given on effective input variable and minimum rule. FLC has one rule for one input variable. The min-max inference is applied to determine the degree of membership for the output variable. The main objective of the designed fuzzy inference system is for the improvement in damping of power system oscillations.
5.3. Defuzzification
After the process of fuzzy reasoning, linguistic output variable should be translated into a crisp value. Defuzzification is such inverse transformation which designs the output from the fuzzy domain back into the crisp domain. For IPFC control, the fuzzy inference system coordinates the linguistic input variables. The universe of
Figure 5. For input variable.
Figure 6. For output variable.
Table 1. Parameters of membership function for control signal mi1.
Table 2. Table for Input-output mapping.
discourse of the input variables decides the required scaling for correct per-unit operation. The fuzzy logic operations performed (Sup-Min inference) are decided by the decision making logic, and together with the knowledge base influences the outputs of each fuzzy IF-THEN rules. Those are combined and converted to crispy values with the defuzzification block. The fuzzy Controller uses the centroid method. The general function of the fuzzy Logic controller can be expressed as:

where, f denotes the mapping defined by the rule base and α, β is the appropriate scaling, which depends on the scale of the X-axis and Y-axis of input and output variables. The fuzzy output is given by equation:

6. Simulation Results
Digital Simulation has been carried out with Modified Phillips Heffron model in MATLAB environment. Independent damping signals and Fuzzy with IPFC has been demonstrated. In small signal analysis, the simulation result of the linearized model with four different input control signals under 10% of variation in mechanical power input is considered. The proposed PI and Fuzzy controllers performances are tested in Single Machine Infinite Bus system.
6.1. Dynamic Performance of the System with Control Signal mi1
Figure 7 depicts the comparative analysis of PI based IPFC, IPFC with POD as additional damping controller and fuzzy based IPFC. Simulation result depicts the performance of IPFC with POD as additional damping controller for control signal mi1, first peak of speed deviation is reduced from 0.018 rad/sec. to 0.014 rad/sec. and settling time is reduced upto 0.43 sec. However, Fuzzy based IPFC reduces first swing from 0.018 rad/sec to 0.012 rad/sec with settling time 0.4 sec. Hence fuzzy based IPFC with damping controller mi1 shows robust performance.
The eigen values as shown in Table 3 lying on negative half of the s-plane which indicates the stable system.
6.2. Dynamic Performance of the System with Control Signal mi2
Figure 8 demonstrates the satisfied performance of PI based IPFC, IPFC with POD as additional damping controller and fuzzy based IPFC for control signal mi2. Result indicates that fuzzy based IPFC reduces first peak of speed deviation from 0.025 to 0.01 rad/sec with settling time 0.25 sec. and improvement in steady state error. Also, system is more amenable with Fuzzy which suppress the oscillations well and hence gives the best result. Hence Fuzzy logic based IPFC significantly improves small signal stability of Single Machine Infinite Bus system.
Figure 7. Speed deviation response of linearized SMIB system for control signal mi1. a. Control signal mi1; b. Control signal mi1 with POD; c. Control signal mi1with Fuzzy Logic Controller.
Figure 8. Speed deviation response of linearized SMIB system for control signal mi2. a. Control signal mi2; b. Control signal mi2 with POD; c. Control signal mi2with Fuzzy Logic Controller.
Table 3. Comparison with POD controller and fuzzy logic controller for control signal mi1.
Time domain result has been verified by obtaining eigen value analysis of PI based IPFC, IPFC with POD as additional damping controller and Fuzzy based IPFC for control signal mi2 as shown in Table 4 in which the negative real part of eigen values proves that the system is stable.
6.3. Dynamic Performance of the System with Control Signal α1
The MATLAB result as shown in Figure 9 demonstrates the satisfactory performance of PI based IPFC, IPFC with POD as additional damping controller and Fuzzy based IPFC for control signal α1. Result indicates with fuzzy based IPFC, first peak of speed deviation is reduced from 0.017 to 0.012 rad/sec, settling time is reduced. Also, system is more suitable with Fuzzy based controller which suppress the oscillations well and hence give the best result.
Time domain result has been verified by obtaining eigen value analysis which are tabulated in Table 5 in which all the eigen values regarding PI based IPFC, IPFC with POD as additional damping controller and fuzzy based IPFC for control signal α1 respectively lies on negative part of real axis which ensures that the system is stable.
6.4. Dynamic Performance of the System with Control Signal α2
With coordinated action of IPFC and POD as additional damping controller, reduction in peak amplitude, settling time and steady error are delineated in Figure 10. However, fuzzy based IPFC shows the improvement in the response of the system for control signal α2 in which first peak of speed deviation is reduced from 0.016 to 0.013 rad/sec with settling time 0.4 sec. This again highlights the efficacy of the fuzzy based IPFC.
This inference has been checked by obtaining eigen value analysis of PI based IPFC, IPFC with POD as additional damping controller and Fuzzy based IPFC for control signal α2 as shown in Table 6. The negative real part of eigen value indicates that the system is stable.
Figure 9. Speed deviation response of linearized SMIB system for control signal α1. a. Control signal α1; b. Control signal α1 with POD; c. Control signal α1 with Fuzzy Logic Controller.
Figure 10. Speed deviation response of linearized SMIB system for control signal α2. a. Control signal α2; b. Control signal α2 with POD; c. Control signal α2 with Fuzzy Logic Controller.
Table 4. Comparison with POD controller and fuzzy logic controller for control signal mi2.
Table 5. Comparison with POD controller and fuzzy logic controller for control signal α1.
Table 6. Comparison with POD controller and fuzzy logic controller for control signal α2.
The comparative performance of Figures 7-10 justified that fuzzy based IPFC with pulse width modulation index of voltage series converter 1 and 2 (mi1 and mi2) are more effective in damping of power system oscillations. This inference has been checked by obtaining eigen value analysis which indicates that the system is stable.
7. Conclusion
In this paper, a systematic approach for determining relative effectiveness of Interline Power Flow Controller (IPFC) control signals (mi1, α1, mi2, α2) in damping low frequency oscillations has been presented. The linearized power system model of Single Machine Infinite Bus system for analyzing the performance of fuzzy based IPFC for variation in system parameters has been studied. These control signals show the significant improvement in damping of power system performance. Investigations have revealed that IPFC control signals mi1 and mi2 provide robust performance over other signals. The proposed Fuzzy Logic Controller performance is comparatively better than PI based controller. The fuzzy rules have been designed to minimize transients swing, improvement in damping of oscillations. The controllers in comparative performance in terms of small signal stability improvement and damping of oscillations are demonstrated. The fuzzy logic controller demonstrates the robust performance and is easy to coordinate with damping schemes. The simplicity of the design is the most attractive feature of fuzzy based control scheme. The proposed controller fulfills the main objective of this paper. Time domain analysis and eigen value analysis results validate the performance of various IPFC control strategy.
Cite this paper
S. N. Dhurvey,V. K. Chandrakar, (2016) Performance Comparison of PI and Fuzzy Logic Based IPFC on Damping of Power System Oscillations. Journal of Power and Energy Engineering,04,78-90. doi: 10.4236/jpee.2016.44008
References
- 1. Thakre, M.P., Kale, V.S., Dhenuvakonda, K.R., Umre, B.S. and Junghare, A.S. (2015) Study and Mitigation of Subsynchronous Oscillations with SSC Based SSSC. Journal of Power and Energy Engineering, 3, 33-43.
- 2. Kundur, P. (1994) Power System Stability and Control. Mc Graw-Hill, New York, 12.
- 3. Hingorami, N.G. and Gyugyi, L. (2001) Understanding FACTS: Concepts and Technology of Flexible AC Transmission System. IEEE Power Engineering Society, IEEE Press, Delhi.
- 4. Song and Johns, A.T. (1999) Flexible AC Transmission Systems. IEE Power and Energy Series 30, London.
- 5. Parimi, A.M., Elamvazuthi, I. and Saad, N. (2010) Fuzzy Logic Control for IPFC for Damping Low Frequency Oscillations. Intelligent and Advanced Systems (ICIAS): International Conference, 1-5.
- 6. Babu, A.V.N. and Sivanagaraju, S. (2010) Mathematical Modeling, Analysis and Effects of Interline Power Flow Controller (IPFC) Parameters in Power Flow Studies. India International Conference on Power Electronics (IICPE), 1-7.
- 7. Parimi, A.M., Sahoo, N.C., Elamvazuthi, I. and Saad, N. (2011) Transient Stability Enhancement and Power Flow Control in a Multi-Machine Power System Using Interline Power Flow Controller. International Conference on Energy, Automation, and Signal (ICEAS), 1-6.
- 8. Ramachandran, G.V. and Kumar, C.V. (2010) Simulation and State Estimation of Power System with Interline Power flow Controller. 45th International Universities Power Engineering Conference (UPEC), 1-6.
- 9. Moghadam, M.F., Gharehpetian, G.B. and Askarian Abyaneh, H(2010) Optimized Regulation of DC Voltage in Interline Power Flow Controller (IPFC) Using Genetic Algorithm. Power Engineering and Optimization Conference (PEOCO), 117-121.
- 10. Karimi, K. (2006) The Effect Interline Power Flow Controller (IPFC) on Damping Inter-Area Oscillations in the Interconnected Power Systems. IEEE International Symposium on Industrial Electronics, 3, 1911-1915.
- 11. Yuan, Z.H., de Haan, S.W.H. and Braham, F. (2008) A New Concept of Exchanging Active Power without Common DC Link for Interline Power Flow Controller (S-IPFC), Power and Energy Society General Meeting—Conversion and Delivery of Electrical Energy in the 21st Century. IEEE Conference, 1-7.
- 12. Parimi, A.M., Elamvazuthi, I. and Saad, N. (2008) Interline Power Flow Controller (IPFC) Based Damping Controllers for Damping Low Frequency Oscillations in a Power System. ICSET. IEEE International Conference on Sustainable Energy Technologies, 334-339.
- 13. Jiang, X., Fang, X.H., Chow, J.H., Edris, A. and Uzunovic, E. (2007) Regulation and Damping Control Design for Interline Power Flow Controllers. Power Engineering Society General Meeting, 1-8.
- 14. Banaei, M.R. and Kami, A. (2009) Interline Power Flow Controller Based Damping Controllers for Damping Low Frequency Oscillations. INTELEC 2009, 31st International Conference on Telecommunications Energy Conference, 1-6.
- 15. Veeramalla, J. and Sreerama Kumar, R. (2010) Application of Interline Power Flow Controller (IPFC) for Damping Low Frequency Oscillations in Power Systems. Proceedings of the International Symposium on Modern Electric Power Systems (MEPS), 1-6.
- 16. Segundo, F.R. and Messina, A.R.( 2009) Modeling and Simulation of Interline Power Flow Controllers: Application to Enhance System Damping. North American Power Symposium (NAPS), 1-6.
- 17. Jiang, X., Fang, X.H., Chow, J.H., Edris, A., Uzunovic, E., Parisi, M. and Hopkins, L. (2008) A Novel Approach for Modeling Voltage-Sourced Converter-Based FACTS Controllers. Power Delivery, IEEE Transactions, 23, 2591-2598.
- 18. Jiang, S., Gole, A.M., Annakkage, U.D. and Jacobson, D.A. (2011) Damping Performance Analysis of IPFC and UPFC Controllers Using Validated Small-Signal Models. IEEE Transactions on Power Delivery, 26, 446-454.
- 19. Gopinath, B., Suresh Kumar, S. and Ramya, M. (2013) Circuits, Power an Genetically Optimized IPFC for Improving Transient Stability Performance in Power System. International Conference on Computing Technologies (ICCPCT), 120-125.
- 20. Dhurvey, S.N. and Chandrakar, V.K. (2011) Performance Evaluation of IPFC by Using Fuzzy Logic Based Controller, IEEE 4th International Conference on Emerging Trends in Engineering & Technology, ICETET 2011, Mauritius, 16-18 November 2011, 168-173.
- 21. Dhurvey, S.N. and Chandrakar, V.K. (2008) Performance Comparison of UPFC in Coordination with Optimized POD and PSS on Damping of Power System Oscillations. International Journal of WSEAS Transaction on Power System, 3, 287-299.
- 22. Chandrakar, V.K. and Kothari, A.G. (2006) Fuzzy-Based Static Synchronous Compensator (STATCOM) for Improving Transient Stability Performance. International Journal Energy Technology and Policy, 5, 692-707.
- 23. Chandrakar, V.K. and Kothari, A.G. (2007) Comparison of RBFN and Fuzzy Based STATCOM Controllers for Transient Stability Improvement. IEEE Aegean Conference on Electric Machines Powers and Electromotion, Bodrum, 10-12 September 2007.
- 24. Chandrakar, V.K. and Kothari, A.G. (2006) Improvement of Transient Stability Using Fuzzy Logic Based Unified Power Flow Controller [UPFC]. International Journal Power and Energy Systems, 5, 1-18.
Appendix A
A.1. Generator
M = 2H = 0.1787, 
A.2. Excitation System
Ka = 50.0, Ta = 0.05
A.3. Constants
K1 = 0.3837, K2 = −0.1717, K3 = 3.6667, K4 = −0.7350, K5 = −0.0237, K6 = 1.0659, K7 = −0.0139, K8 = −0.6890, K9 = 0.0023
A.4. Interline Power Flow Controller Parameters
Kpα1 = 0.0376, Kqα1 = 0.0010, Kvα1 = −0.0029, Kcα1 = 0.0672
Kpα2 = −0.0045, Kqα2 = 0.0033, Kvα2 = −0.0021, Kcα2 = −0.01116
Kpmi1 = 0.0552, Kqmi1 = −0.0326, Kvmi1 = −0.0360, Kcmi1 = −0.000766
Kpmi2 = 0.2530, Kqmi2 = 0.0056, Kvmi2 = −0.0038, Kcmi2 = −0.0087, Kpp = 1, Kpi = 0.5












