Received 27 March 2015; accepted 21 May 2015; published 25 May 2015

ABSTRACT

One of the most important problems in the study of transient stability of power systems is the determination of perturbation’s maximum time of permanence without losing the synchronism of the generators that feed the network. The problem is generally solved by either the application of the equal-area criterion or through numerical integration methods. In the present work, the phase- plane is proposed as an alternative tool to solve the above-mentioned problem with greater efficiency.

Keywords:

Short Term Stability, Phase Plane, Swing Equation

1. Introduction

Transient stability is the power system ability to maintain synchronism after being subject to a severe perturbation, such as: line faults, generation losses or large load losses. When analyzing power systems, the short-term transient stability study is usually presented by using an array consisting on a generator connected to an infinite bus through a transmission network. The generator is modeled as an internal voltage source behind the transient reactance. Generally, in such studies, excitation and velocity control systems are not taken into account.

The equal-area criterion is used to examine the stability of a system composed by two machines or one machine connected to an infinite bus. By applying this criterion, there is no need to solve the so-called swing equation [1] .

Currently, numerical integration methods are mostly used to make simulations of the transient stability phenomenon in the time domain. The use of these methods implies the numerical integration of the differential equations describing this phenomenon [1] .

In this paper, we revisit an alternative technique that exploits the topology of the phase plane [2] . The previously mentioned technique is developed in references given in this work [3] -[7] . This reference does not provide direct comparisons among the proposed technique, the equal-area criterion, and numerical integration methods.

2. Conventional Calculation Methods

The rotational motion of a synchronous machine is governed by a second order, ordinary, non-lineal differential equation. This equation is the well-known swing equation. When damping is neglected, this equation has the following form:

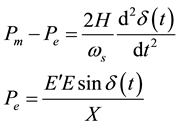(1)

where:

P_m = mechanical power input to the synchronous machine [pu].

P_e = electric power output from the synchronous machine [pu].

H = inertia constant [MWs/MVA].

d = rotor angle measured with respect to a reference axis that rotates at the synchronous velocity [electric radians].

w_s = synchronous angular velocity [rad/s].

t = time [s].

E' = voltage measures following the transient reactance [pu].

E = infinite bus voltage [pu].

X = reactance between E' and E [pu].

Solving the differential Equation (1), both the rotor angle time history, d(t), and the rotor generator deviation speed, with respect to the synchronous speed, Dw(t), can be obtained. The time histories of the variables d(t) and Dw(t) allow the study of the transient stability of a power system consisting on a generator connected to an infinite bus through a transmission network. In order to achieve that, it can be assumed that the system is initially working on a stable state. That is, the generator rotor angle keeps a constant value, indicated by d₀. If for a time t_f we apply a three-phase fault in any network node and immediately after, at t_f + Dt, the protection devices act eliminating the fault, then the curve d vs. t, shown in Figure 1 can be obtained.

Depending on the fault extent, in this case Dt, the following cases may occur:

Ÿ Stable case: the generator rotor oscillates around a new equilibrium position; this means that there is not synchronism loss.

Ÿ Unstable case: the generator rotor angle grows indefinitely; this means that the synchronism is lost.

The fault maximum extent without losing the generator synchronism is called critical time t_c. Such period of time is generally determined through trial and error procedures.

A similar methodology to be used to determine the transient stability is the one resulting from the application of the equal-area criterion. Using this method, there is no need to integrate the swing equation. As an alternative, the diagram shown in Figure 2 is built. In such diagram, the pre-fault and post-fault curves show the relation between the electric power output from the synchronous machine, P, and the rotor angle, d. In this method, the mechanical power input to the synchronous machine, P_m, is considered constant during the study. The angle d₀ represents the rotor position for the system in stable state. After the fault, the angle d increases to its d_c value, which represents the rotor angle when the protection devices eliminate the fault. Once the fault is eliminated, the angle d continues growing to its maximum value d_max. Taking this into consideration, the following cases may occur:

Ÿ Stable case: the angle d starts decreasing. Consequently, the generator rotor will oscillate around a new equilibrium position. That is, synchronism is maintained.

Ÿ Unstable case: the angle d exceeds its maximum value and grows indefinitely. Then, the generator synchronism is lost.

The objective of this method is to determine the critical time. This can be achieved by obtaining the maximum value of the angle d_c, which makes the areas A₁ and A₂ be equal.

3. Phase Plane

In order to develop the advantages of the phase plane topology, as a tool to study the solutions of the differential Equation (1), the transformation of the second-order differential equation into a pair of first-order differential equations is necessary. For this purpose, the state variable 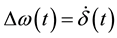is introduced. In terms of the state variables, the Equation (1) may be restated as follows:

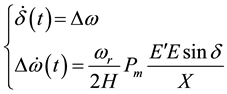(2)

The equilibrium points of the dynamical system governed by Equations (2) are determined by imposing the following conditions:

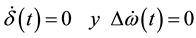(3)

which leads to:

(4)

where, the subscript e indicates an equilibrium state. The first equation in (4) shows that every possible equilibrium state correspond to null deviations of the generator rotor speed with respect to the synchronous speed. Graphically, this means that every equilibrium state will be located on the axis Dw = 0 of the phase plane. For

the determination of the d_e possible values, it is necessary to take into consideration the second equation in (4). This equation has infinite solutions and they are represented by:

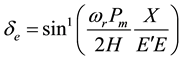(5)

From the infinite solutions of the Equation (5), only those included between 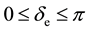have physical meaning. Then, by imposing this restriction to Equation (5), only 2 equilibrium points P₁ and P₂ can be obtained, as it can be seen in Figure 3. The point P₁ = (d₀, 0), corresponds to a Poincaré-stable center. On the other hand, P₂ is a hyperbolic-equilibrium point known as saddle point, which is inherently unstable.

In Figure 3, different trajectories of the phase plane corresponding to a determined configuration of the power system and for different initial conditions can be observed. The arrowheads in Figure 3 indicate the directions in which we must proceed along the phase paths for increasing time. In case A, non-perturbed case, the trajectory reduces to the point P₁. If a perturbation is introduced, producing a deviation of the angle d from its equilibrium point and therefore, a change in the initial values required to solve the swing equation, we may find different cases.

For example, in case B the angle value has been diminished in relation to its equilibrium value, whereas in case C this value has been increased. As it can be observed, in both cases the generator rotor stays indefinitely oscillating round its equilibrium position. In case D, the angle has been increased near the point P2 and the solution corresponds (in the phase plane) to a homoclinic trajectory [2] . For the case in which the angle deviation exceeds the point P₂, the trajectory shows the same aspect as case E, where the rotor angle and speed grow indefinitely. In case F, where the angle has been diminished to the intersection point between the homoclinic trajectory and the axis Dw = 0, the trajectory shows an oscillation tendency round the equilibrium point P₁ at the beginning. But, nearby the point P₂, the angle and speed start growing indefinitely. The analyzed cases show that for initial conditions given within the region of the phase plane bounded by the homoclinic orbit, the system is stable from a transient-stability point of view.

Supposing that such power system is initially in its stable-equilibrium position, which is d(t) = d₀ and Dw(t) = 0. Supposing also that the network configuration is ultimately changed through the application of a three-phase fault in some node, and that after a while the protection devices act eliminating it.

The superimposed phase planes corresponding to three different topologies of the network: pre-fault, fault and post-fault can be observed in Figure 4. Curve D' corresponds to the post-fault homoclinic trajectory and curve G corresponds to a fault trajectory. Point P₁ represents the above-mentioned initial condition. After the fault, the rotor angle and speed values increase, as it can be seen in the fault G trajectory. When the fault is not eliminated, the values d and Dw grow indefinitely and therefore the generator loses its synchronism. When the fault is eliminated, the power system configuration changes. Under these post-fault conditions, the equilibrium points are 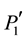and. 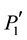As for point P₁, point represents a stable equilibrium point. Point 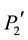represents the maximum angle (d_max) the rotor may adopt for not losing synchronism under a post-fault configuration. For fault elimination before the intersection of G and D' trajectories, the system is stable from a transient-stability point of view. This occurs because d and Dw values during fault removal represent the initial conditions needed to solve the equation system (2) under post-fault conditions. As it was mentioned before, the generator maintains its

synchronism as well as the initial values are kept within the region limited by the homoclinic trajectory. Therefore, the critical angle d_c is determined by the intersection of fault G and the homoclinic post-fault D' trajectories. The time necessary for the evolution of the system from (d, Dw) = (d₀, 0) state to (d, Dw) = (d_c, Dw_c) state is the critical time, t_c.

The developed method may be extended to multiple-generator systems. For these cases, a phase plane for each machine of the system should be built.

4. Numerical Results

As an application we analyze the example 13.1 of the book “Power System Stability and Control” [1] . In such example, the transient stability of a thermo-generation station consisting on four 555 MVA, 24 Kv, 60 Hz generators, supplying power to an infinite bus through two transmission circuit, is analyzed (Figure 5). For t_f = 0, a three-phase fault is applied at the end of one of the lines. After a while, the protection devices separate the perturbed line from the system. The objective of this method is to determine the fault permanence maximum value without losing synchronism.

The network reactance shown in Figure 5 is in p.u. on 2200 MVA and 24 Kv of base. The resistances are negligible.

The initial-operation conditions, expressed in p.u. on the previous base, are:

P = 0.9 [pu].

Q = 0.436 [pu] (overexcited).

H = 3.5 [MWs/MVA].

E_t = 1.0 ang 28,34˚.

E = 0.90081 [pu].

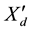= 0.3 [pu].

The X value for each state is:

Pre-fault:

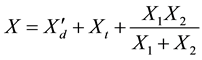= 0.7752 [pu]

Fault:

= 0.45 [pu]

Post-fault:

= 0.95 [pu]

The E' value is obtained as follows:

E' = 1.1626 Ð41.77˚

Considering these values and using the Equal-Area Criterion (Figure 6), the following results are obtained:

d₀ = 41.77˚

d_max = 125.27˚

d_c = 52.29˚

t_c = 0.0870 [s].

The following results are obtained by using the conventional numerical-integration method (Figure 7):

d₀ = 41.77˚

d_max = 125.27˚

d_c = 52.35˚

t_c = 0.0875 [s].

Using the phase plane (Figure 8), we obtain:

Therefore, the following values result:

d₀ = 41.77˚

d_max = 125.27˚

d_c = 52.52˚

t_c = 0.0879 [s].

5. Conclusions

A method that uses the phase plane to solve the problem of transient stability in a machine connected to an infinite bus through an interconnection network, has been presented. The proposed method combines the

strength of the conventional numerical-integration method and the simplicity and graphic representation of the equal-area criterion-based method. It also has additional properties in relation to both methods. For instance, it presents the following advantages associated to the equal-area criterion-based method:

Ÿ It offers the same integral vision of the problem. In addition, it shows the time-domain evolution of generator rotor speed variation.

Ÿ It allows extending the problem to multiple-generator electrical systems, with no need of reducing the network to an infinite bus.

On the other hand, it presents the following advantages in relation to conventional numerical-integration methods:

Ÿ It provides an integral vision of the problem.

Ÿ It allows the visualization in the same graphic of the angle variations and the rotor speed.

Ÿ It allows the direct determination of the critical time for fault elimination, avoiding thus the trial and error method.

References