Received 30 March 2015; accepted 30 May 2015; published 3 June 2015

ABSTRACT

Recently, space time block codes (STBCs) are proposed for multi-input and multi-output (MIMO) antenna systems. Designing an STBC with both low decoding complexity and non-vanishing property for the Long Term Evolution Advanced (LTE-A) remains an open issue. In this paper, first our previously proposed STBC’s non-vanishing property will be completely described. The proposed STBC scheme has some interesting properties: 1) the scheme can achieve full rate and full diversity; 2) its maximum likelihood (ML) decoding requires a joint detection of three real symbols; 3) the minimum determinant values (MDVs) do not vanish by increasing signal constellation sizes; 4) compatible with the single antenna transmission mode. The sentence has been dropped. Second, in order to improve BER performance, we propose a variant of proposed STBC. This scheme further decreases the detection complexity with a rate reduction of 33%; moreover, non-vanishing MDVs property is preserved. The simulation results show the second proposed STBC has better BER performance compared with other schemes.

Keywords:

Space Time Block Codes, Maximum Likelihood Decoding, Non-Vanishing Minimum Determinant Value

1. Introduction

Space-time block codes (STBCs) are known as well-suited techniques that provide an effective diversity method to mitigate the fading in wireless channels. In these codes, transmitted signals are repeated in different time slots by using two or more transmit antennas. In order to provide diversity gain, each replica of a signal must encounter independent fading. Thus, transmit (receive) antennas must be separated appropriately. Therefore, if each replica of transmitted signals encounters independent fading, the probability of occurring deep fading is very unlikely. Alamouti code is the most popular STBC scheme for two-transmit antennas systems [1] . It achieves code rate one and full diversity transmission using two-time slots for information symbols. Tarokh and et al. generalized Alamouti code for systems with an arbitrary number of transmit antennas which are called orthogonal codes [2] . Although, these codes provide full diversity for more than two transmit antennas with linear decoding complexity code rate is less than one. To increase code rate for more than two transmit antennas, Quasi-Orthogonal STBC (QSTBC) scheme is introduced in [3] and [4] . However, code rate is increased for QSTBC scheme decoding complexity is higher, but not exponentially, compared with orthogonal codes.

The Three Generation Partnership Project (3GPP) started the next generation wireless systems (4G) under the project Long Term Evolution Advanced (LTE-A) in 2008 [5] . In LTE-A, user equipment (UE) is imposed two transmit antennas. Therefore, STBC scheme can be the most popular candidate for the uplink diversity gain [6] . Alamouti STBC scheme sounds a suitable candidate in LTE-A systems. Unfortunately, in LTE frame structure is dedicated 3-time slots with Alamouti STBC scheme. This has brought up an interesting STBC design problem which is compatible with LTE frame structure. Hybrid STBC scheme as the first scheme has been proposed for 3-time slots and two transmit antennas systems [7] . Its encoding matrix includes two time slots Alamouti scheme followed by one time slot repetition transmission. Although, the Hybrid scheme achieves code rate one and its decoding complexity is linear at receiver does not achieve full diversity. To remove full diversity defect, a class of QSTBC scheme is proposed by Lie et al. in [8] [9] . The QSTBC scheme achieves code rate one and full diversity. But, there are two problems with this scheme. The first problem is highcomplexity of maximum likelihood (ML) decoding which requires a joint detection of two complex symbols (O(M²)), where M is size of the used symbol constellation. The second problem is that the minimum determinant values (MDVs) extremely vanish by increasing the symbol constellation size. Recently, Fast-Group-Decodable STBC (Fast-GSTBC) scheme has been proposed in [10] [11] . As generic construction method for odd-time slot, new GSTBC scheme has been designed for LTE-A that achieves code rate one and full diversity with symbol-wise decoding complexity (O(M¹)) [12] . GSTBC scheme achieves code rate one and full diversity with symbol-wise decoding complexity (O(M¹)). However, GSTBC scheme reduces decoding complexity for 3-time slots two transmit antennas its MVDs vanish. Also, this scheme is not compatible with single antenna.

In [13] , a novel 3-time slots STBC structure, based on trace criterion, has been designed. To the best our knowledge, this is the first 3-time slots two transmit antennas STBC scheme which has non-vanishing MDVs property. In this paper, by using this STBC structure, 1) a 3-time slots STBC scheme which can achieve code rate one and full diversity with decoding complexity of O(M^1.5) is proposed, 2) a 3-time slots code rate 2/3 STBC scheme which can achieve full diversity with symbol-wise decoding complexity is obtained. Also, we will show that both schemes have non-vanishing MDVs property. The simulation results show that our first scheme has the same bit error rate (BER) performance with the GSTBC scheme. However, BER for the second proposed scheme is improved about 0.3 dB compared with the first scheme.

The rest of the paper is organized as follows: Section 2 comprises two subsections: 2.1. Channel Model, 2.2. Code Design Criteria, and 2.3. Review of Three Time Slots Two Transmit Antennas STBC Schemes. In Section 3, the Non-Vanishing MDVs Code Rate One 3-Time Slots STBC is introduced. This section includes four subsections: 3.1. Encoding matrix, 3.2. Parameter k Optimization, 3.3. Decoding Complexity, and 3.4. Some Properties. In Section 4, Code Rate 2/3 3-time slot 2-antenna STBC is introduced. In Section 5, Simulation Results and Discussion is presented: 5.1. Performance Comparison in Rate One Scheme, and 5.2. Performance Comparison in Rate 2/3 Scheme. Conclusion is given in Section 6.

Notations: Hereafter, , small letters, bold letters and bold capital letters will designate scalars, vectors, and matrices, respectively. If A is a matrix A^H, A^T, and tr(A) denote the conjugate-transpose, transpose, and trace of A, respectively;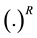, and 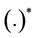denote the real part, the imaginary part and the complex conjugate, respectively.

2. Review of 3-Time Slots STBC for Two Transmit Antennas

2.1. Cannel Model

Consider a MIMO system with N_t (N_t = 2) transmit antennas and N_r receive antennas and with quasi-static flat fading of block length T (T = 3). It is assumed that the channel state information (CSI) to be known at the receiver but unknown at the transmitter. The input-output relation of this system can be written as

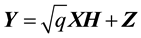(1)

where the normalization q 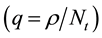is to ensure that the 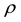(SNR at the receiver) is independent of the number of the transmit antennas (N_t). X is the complex matrix of the transmitted symbols that are drawn constellation. H is the 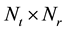complex matrix that contains all the channel coefficients with zero mean and unit variance. Z is the 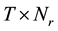complex noise matrix, and Y is the 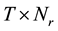complex matrix of the received signals. The entries of Z are assumed to be i.i.d. complex Gaussian random variables with the probability density function (pdf), where 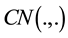stands for the complex Gaussian pdf and 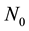for the noise variance.

2.2. Code Design Criteria

2.2.1. Rank and Determinant Criteria

Recently STBC schemes mainly rely on analysis of the pair wise error probability (PEP) 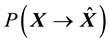which is

the probability that is detected while is transmitted. Chernoff bound Analysis of the PEP at high SNR values results in Rank criterion and Determinant criterion [14] . The STBC scheme has full diversity property if

the difference matrix is full rank for all codeword pairs. The diversity gain at high SNR values do-

minates the steepness of the Bit Error Rate (BER) curve. Thus, in STBC scheme design ensuring full diversity is important at high SNR values. Afterwards, coding gain should be maximized for given average transmit power that leads to a good determinant criterion. The maximum coding gain results in the minimum PEP. Besides maximizing coding gain, this value should be constant for any symbol constellation sizes. This property is called non-vanishing MDV and has been established for several popular STBC schemes [15] - [18] . The non-vanishing MDV can beexploited through the use of the adaptive constellation (adaptive rate) according to the wireless channel quality.

2.2.2. Trace Criterion

The trace criterion is less known but paramount for designing non-orthogonal STBC schemes [19] [20] . This criterion states: to optimize performance of the BER STBC scheme, say, should be designed so that the ei-

genvalues of the are as close as possible to each other and to,

and for which the row-wise sum of the absolute values of the elements off the main diagonal is as small as

possible. Moreover, the plays the role of the Euclidean distance between codewords.

2.3. Review of Three Time Slots Two Transmit Antennas STBC Schemes

In this section, the three time slots two transmit antennas STBC schemes has been reviewed. Also, advantageous and disadvantageous of the all schemes are included.

2.3.1. Hybrid STBC Scheme

The hybrid scheme, , is the first 3-time slot STBC scheme has been proposed [7] . Encoding matrix of this scheme is prescribed in (2). As can be seen in encoding matrix, Alamouti STBC is used at fist 2-time slots, and symbol is repeated at the last time slot over both antennas. Such STBC scheme has code rate one with linear decoding at receiver and symbols are encoded by standard modulation that has low hardware complexity. Because symbol is not transmitted in different time slot, full diversity does not achieve.

(2)

However, the scheme achieves code rate one and its decoding complexity is linear at receiver does not achieve full diversity.

2.3.2. QSTBC Scheme

Incapacitation of Hybrid STBC to achieve full diversity was good reason for author in [8] [9] to design a class of QSTBC scheme, , compatible with 3-time slots systems. The encoding matrix of such scheme has a general form of

(3)

where. By defining, A yields:

(4)

has code rate one, full diversity, and backward compatible with single antenna properties. Also, it is proven that ML decoding complexity of the is O(M²). There is two defects with. First defect is high decoding complexity, and second MDVs vanish by increasing symbol modulation orders (i.e. non-va- nishing MDV property does not preserve). Also, the rotation factors in matrix may cause encoder and decoder accommodate three different constellations our simulations show for 4-QAM modulation. MDV is 7.18 while for 16-QAM this value is 0.12. Therefore in order to reduce the decoding complexity, the code in subsection II.C.3. is proposed.

2.3.3. Group-Decodable STBC Scheme

Recently Fast-Group-Decodable STBC (Fast-GSTBC) scheme has been proposed in [10] [11] . As generic construction method for odd-time slot, new GSTBC scheme with arbitrary code dimension including odd time slot has been designed. Based on Fast-Group-Decodable STBC, in [12] a new STBC scheme for LTE-A system was designed as follows

(5)

achieves code rate one and full diversity with symbol-wise decoding complexity. Encoder/decoder only needs to accommodate one rotated constellation that reduces hardware complexity. However, similar to scheme in (4) cannot preserve non-vanishing MDVs property. For 4-QAM and 16-QAM, MDV is 16, but for 8-QAM the MVD is 6.18. Also, this scheme is not suitable for single antenna transmission.

So, design of 3-time slots two-transmit antennas STBC scheme with non-vanishing MDVs is required. In the next section a novel STBC structure with non-vanishing MDVs property that has been proposed in [13] will be presented.

3. Non-Vanishing MDVs Code Rate One 3-Time Slots STBC

In this section, initially the encoding matrix is presented. Then, parameter k is optimized to maximize the MDVs. Also, we will prove that our scheme achieves non-vanishing MDVs. Finally, the decoding complexity of the proposed STBC scheme with ML criterion is illustrated.

3.1. Encoding Matrix

In this subsection, the problem is formulated.

Figure 1 shows a schematic drawing of the proposed STBC scheme. Three data symbols are transmitted consecutively during three time slots. Therefore, full rate is achieved (an STBC rate is defined as the number of

transmitted symbols during time slots). The 1^st antenna transmits the three symbols x₁, x₂,and x₃ during three time slots. The 2^nd antenna transmits three symbols v₁, v₂, and v₃. Now, the three symbols transmitted by the 2^nd antenna will be defined. One possible way to define these symbols is to make vector v (v = [v₁v₂v₃]) orthogonal to vector s (s = [x₁ x₂ x₃]), i.e.. As will be shown in the next subsection this causes the decoding complexity reduces from joint three complex symbols detection to joint three real symbols; moreover results in suitable trace criteria [19] [20] . Then, improve BER performance at high SNR. To achieve this goal, three different STBC schemes are proposed as:

(6)

In all of the above schemes, the first row is orthogonal to the second one. However, zero entry in the second row reduces diversity order. The following solution overcomes to this deficiency:

(7)

where (i = 1, 2, 3) is the second row in matrix. Therefore, v yields as.

In order to achieve power balance, the symbols in the vector v are transmitted with power. Now, we can present the proposed encoding matrix as:

(8)

For full diversity, symbols x₁, x₂, and x₃ are selected from three different symbol constellations. Figure 2 represents these three symbol constellations. From the represented constellations x_i (i = 1, 2, 3) are obtained as [21] :

(9)

Power in and guarantees (i = 1, 2, 3), where is the excepted val-

ue of z. and are chosen from the standard QAM constellation. Parameter k is unknown and must be optimized to maximize the MDVs. In the subsection III.B the parameter k will be optimized. Note that despite the first row is orthogonal to the second one is neither orthogonal code nor quasi-orthogonal. Consider

orthogonal code, say, then, in which and is identity matrix.

3.2. Parameter K Optimization

In the previous subsection, the three different symbol constellations were represented. The parameter k norma-

lizes symbols and. In this subsection the parameter k is optimized.

(10)

Where and represent two different codewords and det(.) denotes determinant value of (.).

According to, it is easy to show that is full rank. Note that when, it is possible, although we consider in 3.1. This vouches that determinant is always nonzero. Then,

(11)

where (i = 1,2,3), and represents the possible error in symbol.

Lemma 1: has non-vanishing-MDV and for its value is 5.82.

Prove:

Consider M-ary QAM standard constellation, where the real and image components of a symbol can be viewed as M₁-ary standard PAM and M₂-ary standard PAM symbols, respectively (e.g. 8-ary QAM constellation can be considered as 4-ary PAM and 2-ary PAM for real and image components, respectively). Then, for real components, , , and, is the mini-

mum Euclidian distance between the PAM constellation points and here is considered as 1. (i = 1, 2, 3) is

an integer such that.

With the above assumptions, the optimized MDV for 4-QAM (for traceability constellation is assumed 4- QAM) in (11) is achieved for, observe that is compatible with any QAM constellation size. As mentioned before, when, the determinant in (11) is nonzero. To optimize MDV and show non-vanishing-MDV property, define expression D as follows:

(12)

where, , and. In fact, D is similar the expression in (11) that normalized by and for traceability is considered. Since the first term in (12) is always nonzero define. Now, suppose two following cases:

case1:, this case yields:

(13)

According to and and k, the minimum value is always obtained for and. Then, we define as follows

(14)

Note, both and cannot be zero at the same time.

case 2:, this case yields:

(15)

, is different from in (13). It is clear for, has minimum determinant value. Then, is defined as follows:

(16)

In order to maximize MDVs, equate and:

(17)

This equality yields and corresponding MDV is when therefore, the obtained is the maximum for all k.

Note that is assumed, this assumption is compatible with any constellation size.

3.3. Decoding

To illustrate the decoding complexity of the proposed STBC scheme with the ML criterion, the decision metric used for the ML decoder will be derived.

Consider a single antenna at receiver, the ML decoder metric is:

(18)

where X, h and y are represented in (1). The objection of the

ML decoder is to obtain optimal X between all of the possibilities which minimize (12). After some manipulations,

(19)

where

(20.1)

and

(20.2)

and

From (19), it is clear that is independent of, and and is independent of, and. The minimization of (19) is equivalent to minimize and independently. Therefore, the ML decoding requires a joint detection of three real symbols (O(M^1.5)). Compared with QSTBC scheme in [9] and GSTBC scheme in [12] , the proposed scheme for square symbol constellation has lower decoding complexity than QSTBC scheme and slightly higher decoding complexity than GSTBC scheme. But, for real constellations such as BPSK, the proposed scheme will have highest decoding complexity among the three time slots two transmit antennas schemes.

3.4. Some Properties

Simple but important properties of the proposed code are illustrated.

・ full rate and full diversity

It was mentioned that three information symbol are transmitted from two antennas during three time slots. This achieves full rate property. Also, when, the determinant of the difference matrix is always nonzero. This ensures full diversity property.

・ Non-vanishing MDVs

It was proved in lemma 1 always has nonzero determinant that guarantees achieves full diversity, and its MDVs do not vanish by increasing symbol constellation sizes. Non-vanishing MDVs property distinguishes our scheme from other schemes have been proposed for LTE-A systems.

・ Compatible with single transmit antenna

Our scheme has the property that first row is in (8), such property provide backward compatible for single antenna, which is desired in LTE-A. QSTBC encoding matrix in (3) is also compatible with single antenna system while has not such property.

4. Code Rate 2/3 3-time Slot 2-Antenna STBC

It was shown has non-vanishing-MDV property, but its decoding complexity slightly is high. To reduce detection complexity another STBC scheme, , is proposed. has these properties: 1) detection complexity reduces from order 1.5 to 1; 2) non-vanishing-MDV is preserved in; 3) code rate reduces from 1 to 2/3.

Encoding Matrix

The structure of is same. However, encoding of symbols is different from. Consider detection function in (19) again:

At the above expression, the last term is called symbol interference term. We can decrease interference by omitting one of the information symbols, say. In fact, instead of three symbols, two symbols, , , is transmitted. Note, the structure of the encoding matrix is preserved for, but encoding of symbols is changed as follows:

(21)

and

(22)

where and are chosen from the M-QAM standard constellation. Following lemma shows this scheme ensures non-vanishing MDVs property, too.

Lemma 2: has non-vanishing-MDV and its value is 32 when.

The determinant for is obtained:

(23)

Like lemma 1 Consider M-ary QAM standard constellation, where the real and image components of a symbol can be viewed as M₁-ary standard PAM and M₂-ary standard PAM symbols, respectively. shows Euclidian distance between the PAM constellation points and here is considered as 1. As regards the first term in (23)

is always greater than zero, we define. For traceability

Then, yields:

(24)

where and as mentioned before and are chosen from M-QAM standard constellation. Thus

(25)

where m_i (i = 1, 2) is an integer such that. Replace (24) by (25) and normalize by we obtain,

(26)

Assume following two cases:

Case 1: or

This case results in:

(27)

When or

Case 2:

This case results in:

(28)

is minimum when or and is minimum when Therefore,. This means expression in (23) is always nonzero for any symbol constellation sizes and has a minimum. According to (25), this minimum value is 32 when is considered. The minimum value 32 is non-vanishing and constant over all symbol constellation sizes.

・ Compared with Scheme

cannot ensure full rate property compared with. But, full diversity and non-vanishing properties preserve in scheme similar to scheme. Also, it has highest MDVs compared to the existing three time slots two transmit antennas STBCs [7] [9] [12] , and. It can be shown that ML decoding metric can be calculated as the sum where

(29.1)

and

(29.2)

since and is just function of and for respectively, the minimization of the ML metric is equivalent to minimizing the two metrics and independently. That implies has lower decoding complexity than and has the same decoding complexity compared to scheme for any symbol constellation sizes except for BPSK modulation.

In general, Table 1 summarizes various properties of all schemes and gives a detailed comparison.

5. Simulation Results and Discussion

In this section, the simulation results of the proposed schemes, and, are shown for 2 bits per channel use (2bpcu) and 4bpcu throughputs. It is assumed that the amplitudes of fading from each transmit antenna to the receive antenna are mutually uncorrelated Rayleigh-distributed and the receiver has perfect knowledge of the channel.

5.1. Performance Comparison in Rate One Scheme

We first give performance comparison between and other 3-time 2-antenna STBC schemes. Figure 3 shows the simulation results for the proposed STBC scheme for two transmit antennas and one receive antenna and compares BER performance with HSTBC in [7] , QSTBC in [8] [9] , and GSTBC in [12] scheme. Also, Alamouti scheme (two symbols are transmitted during three time slots) is considered. The transmitted symbols are 4-QAM modulated for all of the schemes except Alamouti scheme (8-QAM modulated), hence their spectral efficiencies are 2 bpcu. As can be observed from Figure 3 the proposed STBC, QSTBC, GSTBC, and Alamouti schemes have the same diversity order, but hybrid STBC scheme does not achieve full diversity. Also, from Figure 3 it is clear that even with lower decoding complexity, the proposed scheme outperforms the QSTBC scheme. However, the proposed scheme with higher decoding complexity than GSTBC scheme has same similar performance at high SNR. For 4-QAM modulation, Note that the MDVs for the proposed scheme, QSTBC, and GSTBC are 5.82, 7.18, and 16, respectively. Therefore, it is expected that the both QSTBC and GSTBC schemes to have better BER performance upon the which is in contrast with simulation results. But, beside rank (diversity) and determinant criteria, trace criterion must be considered, too. The trace criterion state:

In uncorrelated Rayleigh fading, the lowest expected value for the union bound to the pairwise error event is obtained when for all pairs (transmitted matrix) and (detected matrix) the matrix is diagonal with all diagonal elements equal. Alternatively, the best suboptimal codes are those for which the matrices are such that the main diagonal elements are as close as possible to each other, and the row-wise sum of the absolute values of the elements off the main diagonal is as small as possible for each row.

The matrix for the proposed scheme is diagonal with unequal main diagonal elements. However, both QSTBC and GSTBC schemes suffer from nonzero off the main diagonal elements that increases the absolute value of the off the main diagonal to main diagonal ratio. According to the trace criterion the proposed scheme has better BER performance upon QSTBC and GSTBC schemes with equal MVDs. In contrast, according to the

determinant criterion, the proposed scheme should have worse BER performance than QSTBC and GSTBC scheme. Therefore, there is a tradeoff between lower determinant criterion and good trace criterion. This tradeoff closes BER performance for all schemes at high SNR for 4-QAM modulation. Figure 3 shows BER performance of the proposed STBC scheme and the QSTBC scheme for 16-QAM modulation (4 bpcu).

It is clear that the QSTBC scheme because of nonzero values off the main diagonal and lower MDV (for 16- QAM its MDV is 0.12) has poor BER performance compared with other schemes, e.g. at BER 10⁻⁴ both the GSTBC and proposed scheme about 1.5 dB work better than the QSTBC scheme. The MDVs of the proposed scheme and GSTBC scheme for 16-QAM modulation are 16 and 5.82, respectively. Nevertheless, like 4-QAM modulation both schemes have same BER performance at high SNR.

5.2. Performance Comparison in Rate 2/3 Scheme

In this subsection, BER curve for with 4 bps throughput is presented and compared with other schemes in Figure 4. However, 64-QAM modulation is used for and 16-QAM modulation for other schemes simulation results show the second proposed scheme has lower BER than other schemes. Because the diagonal elements of the matrix in the second scheme are closer to each other can achieve trace criterion better than the first scheme. In other side, has higher coding gain than that result in good determinant criterion. Therefore, both trace and determinant criteria are dominant compared with other schemes. The profit of this can be seen in Figure 4 that our second proposed scheme outperforms 0.3 dB in power efficiency.

6. Conclusion

In this paper, a novel STBC structure for three time slots and two transmit antennas was proposed. Based on this structure, two STBC schemes were proposed. The first scheme achieves full rate and full diversity properties and has a joint three real symbols decoding complexity (O(M^1.5)). Also, the minimum determinant value is constant for different symbol constellation sizes. Then, the proposed scheme achieves non-vanishing-MDV property. Also, the proposed scheme has the property that first row is, such property provides backward compatible for single antenna, which is desired in LTE-A. However, the encoder (decoder) needs to accommodate 3 different constellations, which may increase the hardware complexity at the encoder (decoder). The second scheme cannot achieve full rate. But, full diversity and non-vanishing-MDV properties are preserved. Moreover, the second scheme reduces decoding complexity compared with the first one and is not compatible with single antenna transmission. Also, this scheme uses standard modulation in encoder (decoder) which is easily implementable. Simulation results show that our first scheme has better BER performance than QSTBC and similar BER performance with GSTBC at high SNR. Also, the second scheme has the best BER performance compared with other schemes.

References