Journal of Computer and Communications
Vol.02 No.14(2014), Article ID:52679,19 pages
10.4236/jcc.2014.214008
Architectural Model of a Biological Retina Using Cellular Automata
François Devillard, Bernard Heit
Université de Lorraine, CRAN, UMR CNRS 7039, Campus Sciences, BP 70239, Vandœuvre-lès-Nancy Cedex, 54506, France
Email: francois.devillard@univ-lorraine.fr, bernard.heit@univ-lorraine.fr
Copyright © 2014 by authors and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY).
http://creativecommons.org/licenses/by/4.0/



Received 10 October 2014; revised 5 November 2014; accepted 22 December 2014
ABSTRACT
Developments in neurophysiology focusing on foveal vision have characterized more and more precisely the spatiotemporal processing that is well adapted to the regularization of the visual information within the retina. The works described in this article focus on a simplified architec- tural model based on features and mechanisms of adaptation in the retina. Similarly to the bio- logical retina, which transforms luminance information into a series of encoded representations of image characteristics transmitted to the brain, our structural model allows us to reveal more information in the scene. Our modeling of the different functional pathways permits the mapping of important complementary information types at abstract levels of image analysis, and thereby allows a better exploitation of visual clues. Our model is based on a distributed cellular automata network and simulates the retinal processing of stimuli that are stationary or in motion. Thanks to its capacity for dynamic adaptation, our model can adapt itself to different scenes (e.g., bright and dim, stationary and moving, etc.) and can parallelize those processing steps that can be supported by parallel calculators.
Keywords:
Computer Vision, Cellular Automata, Retina Modeling, Video Processing

1. Introduction
The works presented in this article benefit from simultaneous information extraction mechanisms enabling the detection of spatial contrast and movement in the layers of the retina. This will allow flexibility in combining our model with other computational models of visual processing. Our model of the complexity of the retina is drawn from recent publications that highlight the interactions between the different layers. We modeled the extraction of information representing the observed scene [1] [2] . According to these publications, when the eye detects a structure, each element of that structure that is more or less extricable contributes to the consistent re- construction of a wider visual area.
Neurophysiology describes the functional architecture of the retina as a succession of layers of neurons form- ing three functional pathways, as shown in Figure 2 [3] . The study of retinal behavior highlights its very useful properties in accentuating the temporal and spatial characteristics before any subsequent analysis or interpreta- tion of the information. In this context, our works study this biological system up to a certain level of detail and from an architectural and functional point of view. We offer an alternative to the conventional modeling tech- niques, which are typically very specialized.
We chose a granular model that could evolve and that was governed deterministically by underlying mathe- matics. We are interested in solutions based on cellular automata [4] [5] . Cell-based automata networks share some features with biological neurons and can form a model with the appropriate rules. Like neurons, each cell has several inputs and only one output, which can be connected to many other controllers, just as the neuron output can be connected to several synaptic junctions that put it in touch with other layers of neurons. The structure and rules of the cellular automata network allow it to mimic the essential characteristics of the infor- mation exchange leading to the behavior dynamics of the different retinal layers.
In this article, Section 2 describes the mechanisms and the anatomical and functional structures that control the processing in the retina. This knowledge underpins our model description, which is given in Section 3. We present our model testing results on images and videos in Section 4. We end with a discussion of the likely fu- ture extensions and applications of these modeling techniques in Section 5.
2. Neurobiological Structure of the Retina
The vision mechanism starts with the processing of images ([6] [7] ) focused on the retina, as shown in Figure 1. The retina is more than a simple checkerboard of photoreceptors that converts light energy into electrical energy. It contains several layers of neuronsorganized to filter visual information. They perform an initial decomposition of the image into parallel information streams for processing. These information streams are analyzed separately before the transmission of signals to the brain via the optic nerve, which comprises retinalganglion cell axons [8] . This first analysis can be performed thanks to both the specific properties of the retinal cells and the organiza- tion of the receptive field.
The retina, which is the inner membrane [9] of the eye, is the only element of the eyeball presenting a neu- ronal origin. It consists in two types of photoreceptors that transform light energy to action potentials: rods, which implement achromatic and scotopic vision, and cones, which implement chromatic and photopic vision. Our model concerns the retinal fovea zone, essentially make up of cones, and it is limited to achromatic vision. Image luminance is sampled, then transmitted by a cone layer towards the downstream retinal and cortical layers.
Figure 1. The neuronal organization of the retina. R: rods; C: cones; BP: Bipolar; G: Ganglion cells.
2.1. Functional Architecture of the Vertebrate Retina
The retina is a complex neuronal structure shown Figure 1. It is organized into two functional layers: the Outer Plexiform Layer or OPL and the Inner Plexiform Layer or IPL [10] . This structured neuronal diversity imple- ments a very elaborate process. The neuronal activity is characterized by nonlinear processing [1] [2] . Through the biological retina, each layer is composed of a network of interconnected cells linked by more or less distant connections.
2.1.1. The Retinal Processors
In the visual system, we apply the concept of the receptive field [11] . The receptive field is the retinal field re- gion where luminous stimulation produces a response in the cell, e.g., to shape, color, or movement [12] . Thus, many receptive fields monitor the same area, each for different goals of perception.
The different receptive fields allow a variety of types of visual information to be processed in parallel. The cells of the different layers have different responses and work through a crossover game of excitatory effect, termed the “ON” effect, and of inhibitory effect, termed the “OFF” effect. The elementary receptive field is de- fined by its central disk, termed the center, and a ring, termed the surround. Thus, the bipolar ON center is sti- mulated when the receptive field center is exposed to light, and is inhibited when the surround is exposed to light [13] [14] .
This dual structure is common among the various retinal receptive fields, allowing us to predict the potential perception of spatial contrast.
2.1.2. The Retinal Mechanisms (Figure 2)
The OPL has already been well studied at the neurobiological level [15] . It forms the junction between the axons of the photoreceptors (rods and cones) and the horizontal and bipolar cells. Each junction is called a synaptic triad. The cone circuits, which are the object of our study, are responsible for high-resolution vision and are the origin of the trichromatic aspect of color vision. Only the monochrome aspect of vision will be addressed in this article. The cone signals that translate the luminance and the chrominance are conveyed to the bipolar cells, which provide connections to the ganglion cells. These in turn convert analog signals to all-or-nothing spikes [16] for transmission to the brain by the optic nerve.
The OPL begins with the processing of the light signal into an electric signal:
・ Cones, photoreceptors with nonlinear operation, are adapted to the conditions of photopic luminance [17] [18] .
・ The horizontal cells are interconnected and thus combine their activity in a larger surface that allows inter- connection between the cones [19] . These cells have an inhibitory effect on the bipolar cells.
・ The bipolar cells differentiate the responses of cones and horizontal cells which form the center and the surround of their receptive fields [20] [21] [22] .
The function of the horizontal cells is to provide the lateral inhibition that yields a reference baseline, which can then be compared to the cones’ input signals. Subtracting a local (spatiotemporal) average allows the eye to see details in both illuminated areas and dark areas in high-contrast scenes. The resulting signal from OPL processing must comply with the obligations of the three pathways from the IPL feature extraction.
In the IPL, we can generalize the concept of the receptive field. The biological cells involved in this layer are the amacrine and ganglion cells:
・ The amacrine cells [23] [24] work transversely in a similar manner to the horizontal cells of the OPL. They can be classified according to the size of their dendritic field into parasol type (large size) and dwarf type (small size).
・ The ganglion cells [25] [26] [27] carry the IPL’s output and present a great morphological diversity, which leads to the creation of specialized functional pathways. They differentiate the information coming directly from the OPL, and that modified by the amacrine cells. Different visual characteristics are extracted depending on the pathway taken: namely, luminance, movement contrast, and luminance contrast for the parvocellular (P), mag- nocellular (or M), and koniocellular (or K) pathways, respectively [28] .
There are three types of ganglion cells [29] :
・ The K cells are less understood and may estimate the luminance and contrast at lower resolutions.
・ The M cells are large, phasic (best sensitivity to temporal modulations), and fast. They transmit the percep-
Figure 2. Schema of the retina’s functional architecture.
tion of movement and scotopic information with little redundancy. These cells are sensitive to low spatial fre- quencies (coarse motifs or large objects) and to high temporal frequencies.
・ The P cells form the great majority. They are small, tonic (with lower sensitivity to temporal modulations), slow, and mostly located in the central retina. They are the headquarters of visual acuity and so encode the exact position of stimuli and their color. They are sensitive to high spatial frequencies (fine details or small objects) and low temporal frequencies.
This description of retinal processing highlights the fact that the retina filters input images to differentiate their spatial, temporal, and chromatic aspects and process these separately in parallel. Our study focuses on a model that reproduces the first two functions while preserving the biological architecture.
These three pathways convey the information from cones and form different layers in the primary visual areas.
2.2. Major Contribution of Our Works
In computer vision, many works lead separated developments in researching static or dynamic clues in images. This publication shows that existing knowledge in neurobiology makes an open realization possible, for an im- plementable and versatile architecture that can respond to problems of pattern recognition or motion in scenes.
Our works are based on simplified pathways M and P, to realize an architectural and functional modeling of the mammalian biological retina.
The choice of a distributed architecture based on cellular automata allowed us to introduce more capabilities of local adaptations to our algorithm.
3. Algorithmic Approach to the Retina
Our modeling is inspired by the many studies on biological retinas [9] [15] [30] and in particular the models presented by W.H. Beaudot [31] [32] . To capture the dynamic aspect of the information processing performed by the retina, our approach is based on the continuous filming of a scene.
3.1. Retinal Architecture
Our model architecture is a reasoned choice derived from the architecture of the biological system. For our study, cell densities and receptive fields are considered homogeneous, which means that we are actually considering local properties. We have implemented the P and M pathways. For the M pathway, we have followed the dia- gram described in paragraph 2.1.2. For the P pathway, we use as a reference the luminance of the horizontal cells of the M pathway. Thus, in terms of functionality:
・ Depending on the type of pathway, cells are set differently.
・ The just noticeable difference threshold (JND) or just noticeable differential threshold of Weber and Fech- ner’s works introduce discrimination of sensory systems capabilities.
・ The ON and OFF pathways are created [33] .
We have used cellular automata (CA) [4] [34] because they lean on discrete principles and thus avoid the complex equations that would otherwise be required to model the problem. Cellular automata are grids of cells [35] having common geometric properties. After initialization, all cells in the grid change or update their state (each cell may be in one of a finite number of possible discrete states) simultaneously according to fixed update rules for each cell type. They offer us a simple approach, from both the architectural and behavioral points of view, for modeling the local properties of the retinal layers [5] [36] . A cellular automaton is a dynamic spatial model allowing the contents of the cells to change according to local transition rules that apply to all cells in the same way at each time step. The new generation is created according to some fixed rule (generally, a mathematical function) that determines the new state of each cell in terms of its current state and the states of the cells in its neighbourhood.
In our algorithm, each cell is assigned the task of processing the luminance of one pixel of a grayscale image [37] . Each layer of the biological retina is modelled in our system by a mesh of square cells. There are three types of layers in our model: transduction (cones), regularization (horizontal and amacrine cells), and finally differentiation (bipolar and ganglion cells). They are implemented as follows:
・ The transduction layer is a spatiotemporal frequency filter with wide bandwidth. This filter is primarily a function of gain driven by the average value of the local luminance.
・ Adjustment layers behave as space-time low-pass filters.
・ The differentiation layers use difference operators.
Our model uses videos as stimuli for the CA operations. The video frame sampling sets the time step for data processing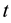 . The spatial scale is defined by the
. The spatial scale is defined by the 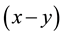 coordinates of the pixels in the frame.
coordinates of the pixels in the frame.
The retinal architecture consists of five cellular automata. For the OPL, it implements the cone layer and ho- rizontal cells, and for the IPL, it implements the amacrine and ganglion layers. At each new frame, the layers are processed sequentially from the cone layer toward the ganglionic output layer. The execution of each cellular automaton is iterative until a comprehensive stabilization is reached, when all cells are pending global synchro- nization. This global synchronization step is necessary because cells can be configured individually and their processing times may vary. For planning, controlling, and scheduling actions, a supervisor acts directly on the CA to set the cells.
3.2. Our Model Using Cellular Automata (Figure 3)
A cellular automaton is a system with elements called cells. Each cell has an activity that results in a single-state machine. The settings can be individualized to mimic, for example, the properties of cells depend on their envi- ronment (luminance, local contrast…) and the layer they belong to. The CA is a network of interconnected cells and the characteristics of this network are its topology. The mesh size of an image being square, our choice fell on a typology of eight neighbors, called the Moore neighborhood [35] and illustrated in Figure 4.
Transition rules define the nature of the interactions between cells and are by definition homogeneous and ap- plied throughout the cells of the CA. They determine the state to which a cell will evolve for the next iteration depending on its current state and the states of its neighbors. The cell 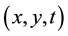 localized at line
localized at line , column
, column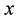 , and time
, and time 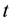 has:
has:
・ a state  that represents its processing status;
that represents its processing status;
・ a neighborhood 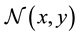 comprising spatially adjacent cells.
comprising spatially adjacent cells.
The 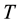 transition is applied to all the cells. It calculates the future state
transition is applied to all the cells. It calculates the future state , which depends on the initial state
, which depends on the initial state 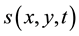 and the outputs of the eight cells in the neighborhood
and the outputs of the eight cells in the neighborhood .
.
3.2.1. Model of the Cells
Spatiotemporal filtering performed by the cells of the automaton consists in two cascaded processing steps:
・ The spatial filtering component uses morphological smoothing [38] .
・ The temporal component is a high-pass or low-pass filter, which is defined as a hybrid of morphological
Figure 3. Our modeling of the retinal pathways P and M.
Figure 4. The space support of the 2D CA is the discrete plan of an image. The resultant image is obtained by the application of local rules incorporated in each cell, corresponding to each image pixel.
and linear filtering [39] .
The first objective of these filters is to reduce noise in image sequences but they also permit the discrimina- tion of objects in the scene. The following two paragraphs illustrate the results obtained for two filtering algo- rithms. The filtering algorithms implemented in the CA network are detailed in paragraph 3.2.4.
3.2.2. Spatial Filtering
The spatial filter is an iterative midpoint filter [40] . It uses linear filtering properties and nonlinear properties of the morphological type. The kernel of the midpoint filter is applied in cascade 


The kernel midpoint (Equation (1)) calculates on each pixel 



3.2.3. Temporal Filtering
The temporal filter component is a hybrid IIR filter (both Infinite Impulse Response filter and temporal morphological midpoint). Figure 6 compares the contribution of the hybrid IIR with the response of the IIR filter given by Equation (2). These spatial and temporal cellular treatments are separable; we simplify the simulation to reflect only the influence of temporal filtering.
Figure 5. Spatial filtering: comparison of results of the midpoint filter with a pseudo-Gaussian FIR (binomial kernel) on line 450 of video frame 850 
Figure 6. Temporal filtering of cells: comparison between the methods IIR and hybrid IIR. The forgetting coefficient 
The hybrid IIR filter implemented in our cells gives a response close to the following filter response.

A difference in behavior appears during transitions in the input signal. Cells load or unload themselves very quickly during fast stimuli. This gives a better reactivity to events while maintaining the properties of temporal regularization of the signal.
In Equation (3), the coefficient included between 


This filter has the property of quickly revealing variations in high-amplitude signals while gradually reducing the oldest variations. The cell treatment parameterized with 



3.2.4. The Cellular Finite-State Machine
Each cell has an activity translated by its own finite-state machine (FSM). The settings are individualized to ad- just, for example, the properties of cells according to their environment (luminance, local contrast …).
The FSM shown in Figure 7 uses a sequence of five states to realize the cellular filtering:
・ State 0: Initial stage and acquisition of the input signal from the cell.
・ State 1: An iteration of spatial filtering.
・ State 2: Update of the intermediate result of the spatial filtering―Equation (1).
・ State 3: Temporal filtering and update of the final result―Equation (3).
・ State 4: Output of the final result, and waiting for global synchronization of the CA.
The conditions governing transitions between the states are given in Table 1.
Figure 7. Flowchart of the cellular FSM.
The parameters 

Step 3 of the algorithm (Table 3) above corresponds to the Equation (3) with a simplified notation. Thus 



3.3. Adaptation Mechanisms
The retina, in its first layers of cells, has mechanisms to adjust the response of the photoreceptors according to the level of illumination [41] .
3.3.1. Feedback between Horizontal Cells and Cones
The sensitivity adjustment (phototransduction) of the photoreceptors to the local luminance [42] is carried out
Table 1. FSM conditions.
Table 2. Data structure for each cell.
using a bio-inspired method that is used in various models ([43] [44] …), which in turn were inspired by the cell modeling of Naka and Rushton [45] . These methods model the response of cones using the Michaelis-Menten nonlinear function (Figure 8).
The cone transduction 






The compression factor 





Table 3. Operations associated with the states.
Figure 8. Dynamic pseudologarithmic range-compression transfer functions 
Figure 9. Temporal cell responses 



Equation 7 gives the calculation to obtain the local estimate of the luminance

A time-domain simulation in Figure 9 shows the results obtained on a temporal profile of the luminance of a pixel.
3.3.2. JND Threshold
The threshold JND of Figure 3 acts on the outputs of the bipolar P cells. These biologically inspired thresholds set the output to 0 when it is not significant according to some criterion. The psychophysical measurement linked to the ability of a subject to discriminate between two levels of stimulation is the JND [46] . There are many models for this threshold of perception. We have used Weber’s law as our criterion; it defines the contrast, for example 








4. Results
To illustrate the operation of our retina model, we applied our algorithms to sequences of real images and also to artificial sequences for a better demonstration of the system operation. Thus, we obtained results at different stages of processing and for different adaptations of mechanisms observed in the OPL.
The experimental conditions are detailed in the annexes.
4.1. OPL Output Results
Figure 10 shows the outputs of the OPL for a video frame (The ON - OFF bipolar pictures are signed and dis- played in 256 gray levels with a reference of 0 for level 128). The bipolar layers of the OPL give a signal hig- hlighting sharp contrasts. These visual indications highlight the objects observed in the scene. Thus in the processed video, we observe the contrasts that describe the forms of the objects in the scene, such as buildings, pedestrians, cars…
The bipolar layers at this level of perception highlight the shapes of the objects by zones of overcurrent. The following paragraph applies this visual processing step by simulating in our architecture the biological proper- ties of the retinal system, such as:
・ the variable density of cone photoreceptors on the surface of the retina;
・ the adaptive and nonlinear transduction of cones depending on the luminance.
These demonstrations illustrate the adaptability of our architecture.
4.1.1. Modeling of the Fovea
This section presents a model of the P OPL pathway, taking into account the variable density distribution of the cones on the retina as shown in [18] . Thanks to cellular automata, individualized settings of cells allow us to differentiate the local processing based on the pixel position in the image to which the cell corresponds. There- fore, the variable coefficients of the P cone 
We observe a concentration ratio of about 20 (from 7000 to approximately 140,000 cones per mm²) between the foveal and the parafoveal areas. To simulate this property, we have approximated the distribution by the size modulation of the cone field receptors with the variation of the parameter 


Figure 10. OPL P pathway results. Video at http://i21www.ira.uka.de/image_sequences/.
shown in Figure 11, as a function of

With




In Equation (10), 






Figure 12 shows the results. We observe at the output of the OPL an image divided into two areas:
・ a peripheral zone of low resolution simulating parafoveal vision;
・ a central zone reduced in size but with high resolution.
Figure 11. Density of receptors found in the human retina. Distribution of rods and cones along a line passing through the fovea and the blind spot of a human eye. Reproduced from Mustafi [18] ―distribution modeling of the cones and the adjustment of corresponding nc values.


Figure 12. Modeling of the fovea: the original web video and the OPL P pathway results. Video at {http://i21www.ira.uka.de/image_sequences
In a similar way to the biological retina, we obtain two complementary results. The first one has low resolu- tion in the periphery of the field of vision, and the second one has high resolution in the center (Figure 12 (b)).
4.1.2. Cone Phototransduction
The video frame in Figure 13 presents a scene under low lighting. The outputs of the various cells forming the OPL layer (The ON - OFF bipolar pictures are signed and displayed in 256 gray levels with a reference of 0 for level 128) are shown.
The P results are compared with and without the feedback loop of M horizontals for signal transduction of the cones. We notice a significant and automatic increase in contrast in the dark zones of the images. Figure 13(d) shows the estimation of the horizontal cells exploited by the feedback loop to induce the signal transduction of cones.
We note that the contrast in dark areas is increased compared with the one in bright areas. This property is found in the luminance perception of the biological retina.
4.2. IPL Output Results
The video frame in Figure 14 presents a scene with objects in motion. The layers of ganglion M cells deliver a signal that immediately highlights the events shown in the video. The events are of different nature, such as movement or the appearance or disappearance of objects. In the video, the tram and some pedestrians are mov-



Figure 13. OPL P pathway results with and without the feedback of the horizontals for signal transduction of the cones. Video of the film “North by northwest” by A. Hitchcock.
ing, and they are perfectly highlighted by areas of peaks of luminance (positive or negative―The ganglion pic- tures are signed and displayed in 256 gray levels with a reference of 0 at level 128) at the output of the M path- way.
Therefore, we obtain images exclusively highlighting objects in motion by the elimination of static objects. These results localize the events (displacement, appearance/disappearance) and indicate areas of interest. The following paragraph applies the same visual processing step to simple synthetic images for a behavioral analysis of M ganglion cells.
4.3. Dynamic Response
The dynamic properties of the retina are more understandable when the model is applied to a synthetic video. We have chosen two videos of 100 frames of 512 by 512 pixels. These results do not take into account the feed- back of horizontal cells to cones, which would accentuate the signals obtained.
This section presents the results from the M layer for the following cases:
・ The first relates to the movement of two objects in opposite directions at the same speed. This test is designed to show that the results obtained by our modeling approach the results already obtained by [47] .
・ The second focuses on events such as the appearance and disappearance of objects in a scene.
4.3.1. Object Movement
Figure 15 shows the results for two squares moving in opposite directions in the scene (object speed = 2 pixels/


Figure 14. IPL M pathway results. Video url: http://i21www.ira.uka.de/image_sequences

Figure 15. IPL M pathway results: responses to stimuli from moving objects.
frame).
The graph on the left shows the response profiles of the IPL for the square moving from the left to the right, and the graph on the right shows the results for the second square moving in the opposite direction. Our results agree with those obtained by Beaudot [32] . The cell temporal filtering shows artefacts in the form of a trail when objects move in the image. This effect contributes to the smoothing of the contrast.
The outputs of the M cells show that we can model the detection of movement by studying the zero crossings of the three ways. The following Table 4 gives passage configurations to zeroes in functions of the direction of the movement and the sign of the luminance variation.
The two channels ON and OFF contribute to the output of the ON - OFF channel and reflect the intensity re- lated to the direction of the displacement.
4.3.2. Appearance or Disappearance of Objects
The Figure 16 shows the results for two squares, one of which appears and then disappears in the scene. The bandwidth of the IPL is fixed by the coefficient
Table 4. Zero crossing appearances in M pathways in function of events.



Figure 16. IPL M pathway results: responses to stimuli from the appearance (a), (b), (c) and disappearance of an object.
the scene as well as the appearance or disappearance of immobile objects over time.
The Figure 16 introduces the phenomena of appearance and disappearance. The IPL instantly responds to the appearance or disappearance of an object, and then the response fades out gradually.
5. Conclusions
Our simulation architecture is derived from the architectural and functional modeling of biological vision sys- tems, and it offers an alternative to conventional modeling methods. We use operators whose properties aresi- milar to those of cells in biological models and which retain the temporal and spatial characteristics of those models.
Our retina imitates visual perception by discriminating among important details in a sequence of images. The cell modeling is a simple combination of morphological and linear filters. The spatiotemporal cellular operator is adaptive; this is demonstrated for the cone cells, which show transduction sensitive to lighting conditions.
Our architecture simultaneously isolates fixed and mobile objects in the same scene. The model allows the matching conservation of information during all stages of processing.
We have developed a versatile and robust temporal operator responsive to light conditions. This global oper- ator can detect the edges and movements of objects. It also highlights fixed and mobile areas of interest in a scene. It is very sensitive to the appearance and disappearance of objects in snapshots of a scene.
Our modular and distributed architecture based on cellular automata is being developed with the goal of im- plementing real-time parallel processors such as those in [48] . We have validated the approach to the architec- ture of the retina described in [49] , and other approaches would allow access to real-time processing through the use of routable logic circuits [50] .
These works are a first step toward the modeling of functional pathways (P and M). Therefore, as in reality, our goal is to simulate these pathways collaboration with the first cortical areas to locate and identify objects in a scene.
Our model adapts itself to many different scenes while relying on data acquired without a priori knowledge. It currently has a feedback loop between the horizontal cells and the signal transduction of the cone cells. This is a first step toward modeling adaptation phenomena within the OPL and IPL of the retina.
References
- Masland, R.H. (2001) Neuronal Diversity in the Retina. Current Opinion in Neurobiology, 11, 431-436. http://dx.doi.org/10.1016/S0959-4388(00)00230-0
- Masland, R.H. (2001) The Fundamental Plan of the Retina. Nature Neuroscience, 4, 877-886. http://dx.doi.org/10.1038/nn0901-877
- Frisby, J.P. and Stone, J.V. (2010) Seeing: The Computational Approach to Biological Vision. 2nd Edition. The MIT Press.
- Wolfram, S. (2002) A New Kind of Science. 1st Edition, Wolfram Media Inc., Champaign, 955.
- Beigzadeh, M., Golpayegani, S.M.R.H. and Gharibzadeh, S. (2013) Can Cellular Automata Be a Representative Model for Visual Perception Dynamics? Frontiers in Computational Neuroscience, 7, 1-2.
- Marr, D. (1982) Vision: A Computational Investigation into the Human Representation and Processing of Visual Information. W.H. Freeman and Company, San Francisco.
- Mead, C. (1989) Analog VLSI and Neural Systems. Addison-Wesley, Upper Saddle River. http://dx.doi.org/10.1007/978-1-4613-1639-8
- Masland, R.H. (2012) The Neuronal Organization of the Retina. Neuron, 76, 266-280. http://dx.doi.org/10.1016/j.neuron.2012.10.002
- Swaroop, A., Kim, D. and Forrest, D. (2010) Transcriptional Regulation of Photoreceptor Development and Homeostasis in the Mammalian Retina. Neuroscience, 11, 563-576.
- Rigaudière, F., Le Gargasson, J.F. and Delouvrier, E. (2010) IV-Les voies visuelles: Rappels anatomo-fonctionnels. Œil et physiologie de la vision, IV-Les voies visuelles, 209-262.
- Hartline, H.K. (1940) The Effects of Spatial Summation in the Retina on the Excitation of the Fibers of the Optic Nerve. American Journal of Physiology, 130, 700-711.
- Blythe, S.N. and Krantz, J.H. (2004) A Mathematical Model of Retinal Receptive Fields Capable of Form & Color Analysis. Impulse: The Premier Journal for Undergraduate Publications in the Neurosciences, 1, 38-50.
- Hashimoto, T., Katai, S., Saito, Y., Kobayashi, F. and Goto, T. (2012) ON and OFF Channels in Human Retinal Ganglion Cells. The Journal of Physiology, 591, 327-337.
- Protti, D.A., Di Marco, S., Huang, J.Y., Vonhoff, C.R., Nguyen, V. and Solomon, S.G. (2014) Inner Retinal Inhibition Shapes the Receptive Field of Retinal Ganglion Cells in Primate. Journal of Physiology, 592, 49-65.
- Dowling, J.E. (1987) The Retina: An Approach Part of the Brain. 2nd Edition, Belknap Press of Harvard University Press, Cambridge.
- Wohrer, A., Kornprobst, P. and Vieville, T. (2006) A Biologically-Inspired Model for a Spiking Retina. Technical Report 5848, INRIA.
- Muchungi, K. and Casey, M.C. (2012) Simulating Light Adaptation in the Retina with Rod-Cone Coupling. Proceedings of the 22nd International Conference on Artificial Neural Networks, Lausanne, 11-14 September 2012, 339-346. http://epubs.surrey.ac.uk/723403
- Mustafi, D., Engel, A.H. and Palczewski, K. (2009) Structure of Cone Photoreceptors. Progress in Retinal and Eye Research, 28, 289-302. http://dx.doi.org/10.1016/j.preteyeres.2009.05.003
- Van Hateren, J.H. (2007) A Model of Spatiotemporal Signal Processing by Primate Cones and Horizontal Cells. Journal of Vision, 7, 1-19. http://dx.doi.org/10.1167/7.4.1
- Dacey, D., Packer, O.S., Diller, L., Brainard, D., Peterson, B. and Lee, B. (2000) Center Surround Receptive Field Structure of Cone Bipolar Cells in Primate Retina. Vision Research, 40, 1801-1811. http://dx.doi.org/10.1016/S0042-6989(00)00039-0
- Demb, J.B., Haarsma, L., Freed, M.A. and Sterling, P. (1999) Functional Circuitry of the Retinal Ganglion Cell’s Nonlinear Receptive Field. The Journal of Neuroscience, 19, 9756-9767.
- Zhang, A.J. and Wu, S.M. (2009) Receptive Fields of Retinal Bipolar Cells Are Mediated by Heterogeneous Synaptic Circuitry. The Journal of Neuroscience, 29, 789-797. http://dx.doi.org/10.1523/JNEUROSCI.4984-08.2009
- MacNeil, M.A. and Masland, R.H. (1998) Extreme Diversity among Amacrine Cells: Implications for Function. Neuron, 20, 971-982. http://dx.doi.org/10.1016/S0896-6273(00)80478-X
- Hsueh, H.A., Molnar, A. and Werblin, F.S. (2008) Amacrine-to-Amacrine Cell Inhibition in the Rabbit Retina. Journal of Neurophysiology, 100, 2077-2088. http://dx.doi.org/10.1152/jn.90417.2008
- Brown, S., He, S. and Masland, R.H. (2000) Receptive Field Microstructure and Dendritic Geometry of Retinal Ganglion Cells. Neuron, 27, 71-383. http://dx.doi.org/10.1016/S0896-6273(00)00044-1
- Curcio, C.A. and Allen, K.A. (1990) Topography of Ganglion Cells in Human Retina. The Journal of Comparative Neurology, 300, 5-25. http://dx.doi.org/10.1002/cne.903000103
- Demb, J.B., Zaghloul, K., Haarsma, L. and Sterling, P. (2001) Bipolar Cells Contribute to Nonlinear Spatial Summation in the Brisk-Transient (Y) Ganglion Cell in Mammalian Retina. The Journal of Neuroscience, 21, 7447-7454.
- Geffen, M.N., de Vries, S.E. and Meister, M. (2007) Retinal Ganglion Cells Can Rapidly Change Polarity from Off to On. PLoS Biology, 5, e65.
- Li, Z.P. (1992) Different Retinal Ganglion Cells have Different Functional Goals. International Journal of Neural Systems, 3, 237-248.
- Wohrer, A. and Kornprobst, P. (2009) Virtual Retina: A Biological Retina Model and Simulator, with Contrast Gain Control. Journal of Computer Neuroscience, 26, 219-249. http://dx.doi.org/10.1007/s10827-008-0108-4
- Beaudot, W.H.A., Oliva, A. and Herault, J. (1995) Retinal Model of the Dynamics of X and Y Pathways: A Neural Basis for Early Coarse-to-Fine Perception. Proceedings of the European Conference on Visual Perception, Tuebingen, 21-25 August 1995, 93b.
- Beaudot, W.H.A. (1994) Le traitement neuronal de l’information dans la rétine des vertébrés―Un creuset d’idées pour la vision artificielle. Ph.D. Thesis, Institut National Polytechnique de Grenoble, Grenoble.
- Adelman, T.L., Bialek, W. and Olberg, R.M. (2003) The Information Content of Receptive Fields. Neuron, 40, 823- 833. http://dx.doi.org/10.1016/S0896-6273(03)00680-9
- Conway, J.H. (1970) Game of Life. Scientific American, 223, 120-123.
- Packard, N.H. and Wolfram, S. (1985) Two-Dimensional Cellular Automata. Journal of Statistical Physics, 38, 901- 946.
- Alber, M.S., et al. (2002) On Cellular Automaton Approaches to Modeling Biological Cells. In: Rosenthal, J. and Gilliam, D.S., Eds., IMA Mathematical Systems Theory in Biology, Communication and Finance, Springer-Verlag, Berlin.
- Chauhan, S. (2013) Survey Paper on Training of Cellular Automata for Image. International Journal of Engineering and Computer Science, 2, 980-985.
- Gonzalez, R.C. and Woods, R.E. (1989) Digital Image Processing. 3rd Edition, Prentice Hall, Englewood Cliff.
- Richefeu, J.C. and Manzanera, A. (2004) A New Hybrid Differential Filter for Motion Detection. Computer Vision and Graphics, 28, 727-732.
- Pitas, I. and Venetsanopoulos, A.N. (1992) Order Statistics in Digital Image Processing. Proceedings of the IEEE, 80, 1893-1921. http://dx.doi.org/10.1109/5.192071
- Lee, B.B., Dacey, D.M., Smith, V.C. and Pokorny, J. (1999) Horizontal Cells Reveal Cone Type-Specific Adaptation in Primate Retina. Proceedings of the National Academy of Sciences of United States of America, 96, 14611-14616.
- Shapley, R. and Enroth-Cugell, C. (1984) Visual Adaptation and Retinal Gain Controls. Progress in Retinal Research, 3, 263-346.
- Meylan, L., Alleysson, D. and Süsstrunk, S. (2007) A Model of Retinal Local Adaptation for the Tone Mapping of Color Filter Array Images. Journal of the Optical Society of America A, 24, 2807-2816.
- Benoit, A., Caplier, A., Durette, B. and Herault, J. (2010) Using Human Visual System Modeling for Bio-Inspired Low Level Image Processing. Computer Vision and Image Understanding, 114, 758-773.
- Naka, K.I. and Rushton, W.A.H. (1966) S-Potential from Luminosity Units in the Retina of Fish (Cyprinidae). Journal of Physiology, 185, 587-599.
- Buntain, C. (2012) Psychophysics and Just-Noticeable Difference CMSC828D Report 4. http://www.cs.umd.edu/class/fall2012/cmsc828d/\\reportfiles/buntain4.pdf
- Beaudot, W.H.A. (1993) The Vertebrate Retina: A Model of Spatiotemporal Image Filtering. In: GRETSI'93, XIVème GRETSI Conférence, Juan-les-Pins, 427-430.
- Kauffmann, C. and Piché, N. (2009) A Cellular Automaton Framework for Image Processing on GPU. Pattern Recogi- nition, 353-375.
- Gobron, S., Devillard, F. and Heit, B. (2006) Retina Simulation Using Cellular Automaton and GPU Programming. Machine Vision and Applications, 18, 331-342. http://dx.doi.org/10.1007/s00138-006-0065-8
- Khan, A.R. (2010) On Two Dimensional Cellular Automata and Its VLSI Applications. International Journal of Electrical & Computer Sciences, 10, 111-114.
Annexes
Simulations have been performed with the settings below. The modifications of parameters required to realize some of the tests have been described in the article itself.
Parvocellular pathway settings:
・ Cones-P:
・ Bipolars-P:
Magnocellular pathway settings:
・ Cones-M: 
・ Horizontals-M: 
・ Bipolars-M:
・ Ganglions-amacrines-M: 










































