Journal of Applied Mathematics and Physics
Vol.07 No.03(2019), Article ID:91262,12 pages
10.4236/jamp.2019.73040
Active Control of Chaotic Oscillations in Nonlinear Chemical Dynamics
Dagbégnon Luc Olabodé1*, Clément Hodévèwan Miwadinou1,2, Adjimon Vincent Monwanou1, Batablinlè Lamboni3, Jean Bio Chabi Orou1
1Laboratoire de Mécanique des Fluides, de la Dynamique Nonlinéaire et de la Modélisation des Systèmes Biologiques (LMFDNMSB); Institut de Mathématiques et de Sciences Physiques (IMSP), Porto-Novo, Bénin
2Département de Physique, ENS-Natitingou, UNSTIM, Abomey, Bénin
3Institut de Mathématiques et de Sciences Physiques (IMSP), Porto-Novo, Bénin

Copyright © 2019 by author(s) and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: February 15, 2019; Accepted: March 17, 2019; Published: March 20, 2019
ABSTRACT
Abstract: This work studies the active control of chemical oscillations governed by a forced modified Van der Pol-Duffing oscillator. We considered the dynamics of nonlinear chemical systems subjected to an external sinusoidal excitation. The approximative solution to the first order of the modified Van der Pol-Duffing oscillator is found using the Lindstedt’s perturbation method. The harmonic balance method is used to find the amplitudes of the oscillatory states of the system under control. The effects of the constraint parameter and the control parameter of the model on the amplitude of oscillations are presented. The effects of the active control on the behaviors of the model are analyzed and it appears that with the appropriate selection of the coupling parameter, the chaotic behavior of the model has given way to periodic movements. Numerical simulations are used to validate and complete the analytical results obtained.
Keywords:
Forced Modified Van der Pol-Duffing Oscillator, Chemical Dynamics, Active Control and Bifurcations

1. Introduction
Since the discovery of chaos in the 20th century, the chaos has been recognized as a very interesting behavior in nonlinear dynamical systems [1] [2] [3] [4] ; according to the domain, it is sometimes useful [5] or undesirable. The control from this chaos in nonlinear oscillations became a very important concern for scientists because of its multiple applications in various fields such as Physics, Chemistry, Biochemistry, Biology, etc. [6] - [11] . In nonlinear systems, several types of movement can be obtained, depending on the nature of the non-linearity, the choice of parameters and initial conditions considered. For potential applications, it has been found necessary to control or eliminate chaotic oscillations in some systems. In order to achieve this goal, several control techniques such as passive, active and semi-active controls are chosen and used according to the nature of the problem considered. An exhaustive review of the description and most important results of active control are given in Refs [9] [12] - [19] . In-depth study using passive control technique is done on nonlinear chemical systems and the most important results are given in Ref. [10] . The class of nonlinear chemicals reactions considered is that of Belousov-Zhabotinsky (BZ). The nonlinear oscillations of the chemical reactions of BZ can be modeled by a modified Van der Pol-Duffing oscillator [20] . Our goal in this work is to make active control of nonlinear oscillations of this class of chemical reactions of BZ by coupling the Forced modified Van der Pol-Duffing oscillator to a linear oscillator [13] which will be used as a control element. The organization of this paper is as follows: Section 2 presents the mathematical modeling of nonlinear chemical oscillations influenced by external sinusoidal excitation under an active control process. In Section 3, Lindstedt’s perturbation method and harmonic balance method are used to determine respectively the analytical solution of the modified Van der Pol-Duffing oscillator and the amplitude of the oscillatory states of the system under control. The effects of the constraint parameter β and the control parameter λ on the amplitude of oscillations are also presented. Section 4 discusses the effects of the active control process on the chaotic dynamic states of the system. The conclusion is presented in the last section.
2. Model and Equation of Oscillations
This work takes into account all nonlinear chemical systems as a kinetic example which can be described by the following equations [1] [21] [22]
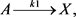 (1)
(1)
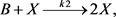 (2)
(2)
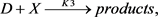 (3)
(3)
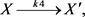 (4)
(4)
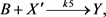 (5)
(5)
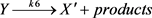 (6)
(6)
When we assume that the sink of the product is a first order reaction and we base ourselves that the laws of mass action and conservation, we get after some mathematical transformations that the self-oscillations in some nonlinear chemical systems can be modelised by the following single second order differential equation [10] - [20] :
 (7)
(7)
where 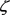 is proportional to the concentration of species X and represents the displacement.
is proportional to the concentration of species X and represents the displacement. 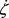 and
and 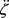 are the velocity and acceleration respectively. Parameters µ, α and γ respectively denote the damping coefficient, linear and cubic nonlinear restoring parameters. The nonlinear parameter β mark the difference between the oscillator equation Equation (7) and the equation of classical Van der Pol-Duffing oscillator. Many dynamic behaviors are obtained when the system is subject to an external sinusoidal excitation [20] and in this case the dynamics of the model is modeled by the following equation:
are the velocity and acceleration respectively. Parameters µ, α and γ respectively denote the damping coefficient, linear and cubic nonlinear restoring parameters. The nonlinear parameter β mark the difference between the oscillator equation Equation (7) and the equation of classical Van der Pol-Duffing oscillator. Many dynamic behaviors are obtained when the system is subject to an external sinusoidal excitation [20] and in this case the dynamics of the model is modeled by the following equation:
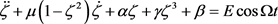 (8)
(8)
It has been noticed the presence of chaotic behaviors of this model [20] . Our main objective of the work is to limit the undesirable effects of external excitation by using the active control strategy. To achieve this goal of reduce the amplitude of the vibration and suppress nonperiodic movements in the model given by Equation (8), we use the following linear oscillator [13] for control element:
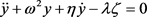 (9)
(9)
where y is the control force and λ the control gain parameters, ω the free frequency of the linear oscillator and η the damping coefficient. Accordingly, the equation of the nonlinear chemical system under such a control scheme becomes:

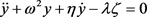 (10)
(10)
3. Effects of the Control on the Amplitude of Harmonic Oscillations
Without the external sinusoidal excitation force, Equation (7) is solved using the Lindstedt’s perturbation method [23] [24] [25] . We get that the solution of Equation (7) can be approached by:
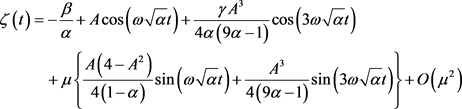 (11)
(11)
where the frequency ω is given by
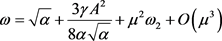 (12)
(12)
and
 (13)
(13)
With the external sinusoidal excitation force, assuming that the fundamental component of the solutions has the period of the external excitation, we express the solution ζ as follows:
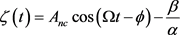 (14)
(14)
To determine the amplitude of the vibration of the chemical system under control, we use the harmonic balance method [25] . For this fact, we introduce the expression of ζ defined by Equation (14) in the second equation of the system of Equations (10) and we get the following:

with
Then, inserting the Equation (15) in the first equation of the system of Equations (10) gives us:

When we introduce the expression (14) in Equation (16) and equalize the coefficient of the terms in sinus and cosine, we obtain after a few algebraic manipulations the following differential equation satisfied by the amplitude Ac of the oscillatory states

It is noted that control is effective when amplitude Ac of vibration of the system under control is lower than amplitude Anc of oscillations of the uncontrolled system obtained for λ = 0. We determine the domain of the parameter of control λ for which control is effective by solving Equation (17) with the Newton-Raphson algorithm. The amplitude Ac obtained from this resolution is plotted on Figure 1 by varying the control parameter λ. It appears from this plot that the control is effective for 


Figure 1. Effects of the control on the amplitude of the oscillations for different values of β with the parameters µ = 0.0001; α = 1; γ = 0.5; E = 0.03; η = 0.2 and Ω = ω = 1.
Figure 2. Effects of the control parameter λ on the amplitude-response curve displaying jump in amplitude Ac(E) with the parameters µ = 0.045; α = 0.15; γ = 0.5; β = 0.008; η = 0.2; Ω = ω = 1.
Figure 3. Effects of the parameter β on the amplitude-response curve displaying jump in amplitude Ac(E) with the parameters λ = 0.25; η = 0.2; ω = 1 and the other parameters of the Figure 2.
4. Effects of the Control on the Chaotic Oscillations of Model
The conditions for suppressing chaotic oscillations or instabilities in the modified and forced Van der Pol-Duffing oscillator coupled to the considered linear oscillator are investigated by doing the numerical simulation of the Equation (10). Figure 4 and Figure 5 illustrate the effects of the coupling parameter λ on the bifurcation structure when E et β vary respectively. We notice the appearance of different structures of bifurcation on each of these figures when the coupling parameter varies. Figure 4 shows periodic, quasiperiodic and chaotic movements for

5. Conclusion
In this paper we have investigated the active control of chaotic oscillations in certain nonlinear chemical dynamics. We have considered chemical dynamics modeled by a modified Van der Pol-Duffing oscillator subjected to external periodic
Figure 4. Effects of the control on the bifurcation diagrams showing the variation of the variable ζ versus the amplitude E for (a) λ = 0; (b) λ = 0.15; (c) λ = 1.20; (d) λ = 1.705 with the parameters µ = 0.0001; α = 1; γ = 0.5; β = 0.008; η = 0.2 and Ω = ω= 1.
Figure 5. Effects of the control on the bifurcation diagrams showing the variation of the variable ζ versus the parameter β for (a) λ = 0; (b) λ = 0.20; (c) λ = 0.28; (d) λ = 0.40 with the parameters µ = 0.0001; α = 1; γ = 0.5; η = 0.2; E = 0.03 and Ω = ω = 1.
Figure 6. Effects of the parameter β on the bifurcation diagrams showing the variation of the variable ζ versus the control parameter λ for (a) β = 0.008; (b) β = 1.5; (c) β = 5 with the parameters µ = 0.0001; α = 1; γ = 0.5; η = 0.2; E = 0.03 and Ω = ω = 1.
Figure 7. Various phase portrait (left) and its corresponding times histories (right) for (a) (b) λ = 0; (c) (d) λ = 0.15; (e) (f) λ = 1.20; (g) (h) λ = 1.705 with the parametersµ = 0.0001; α = 1; γ = 0.5; β = 0.008; E = 24; η = 0.2; and Ω = ω = 1.
Figure 8. Various phase portrait (left) and its corresponding times histories (right) for (a) (b) λ = 0; (c) (d) λ = 0.20; (e) (f) λ = 0.28; (g) (h) λ = 0.40 with the parameters µ = 0.0001; α = 1; γ = 0.5; β = 0.5; E = 0.03; η = 0.2 and Ω = ω = 1.
Figure 9. Various phase portrait (left) and its corresponding times histories (right) for (a) (b) β = 0.008; (c) (d) β = 1.50; (e) (f) β = 5 with the parameters µ = 0.0001; α = 1; γ = 0.5; E = 0.03; η = 0.2; Ω = ω= 1 and λ = 0.75.
excitation. The model has been described and the corresponding equation presented. The Lindstedt’s perturbation method is used to find an analytic solution of the modified Van der Pol-Duffing oscillator. The amplitudes of the oscillatory states of the system under control have been found using the harmonic balance method. In the dynamics of the model under control, we noticed the appearance of the phenomena of hysteresis and jump amplitude, which is effectively controlled by the control parameter λ and the constraint parameter β. Active control is used to limit the presence of unwanted behaviors in the system. We have found the appropriate coupling parameter for which the linear oscillator effectively reduces the amplitude of the modified Van der Pol-Duffing oscillator. For a set of fixed values of the model parameters it was noted that the chaotic behavior of this oscillator has given way to periodic movements under the effect of active control.
Acknowledgements
The author thanks IMSP-UAC, DAAD for financial support and the anonymous referees whose useful criticisms, comments and suggestions have helped strengthen the content and the quality of the paper.
Conflicts of Interest
The authors declare no conflicts of interest regarding the publication of this paper.
Cite this paper
Olabodé, D.L., Miwadinou, C.H., Monwanou, A.V., Lamboni, B. and Orou, J.B.C. (2019) Active Control of Chaotic Oscillations in Nonlinear Chemical Dynamics. Journal of Applied Mathematics and Physics, 7, 547-558. https://doi.org/10.4236/jamp.2019.73040
References
- 1. Epstein, I.R. and Showalter, K. (1996) Nonlinear Chemical Dynamics: Oscillations, Patterns, and Chaos. Journal of Physical Chemistry, 100, 13132-13147. https://doi.org/10.1021/jp953547m
- 2. Enjieu Kadji, H.G., Chabi Orou, J.B. and Woafo, P. (2008) Regular and Chaotic Behaviors of Plasma Oscillations Modeled by a Modified Duffing Equation. Physica Scripta, 77, Article ID: 1025503. https://doi.org/10.1088/0031-8949/77/02/025503
- 3. Miwadinou, C.H., Monwanou, A.V., Hinvi, A.L., Koukpemedji, A.A., Ainamon, C., and Chabi Orou, J.B. (2016) Melnikov Chaos in a Modified Rayleigh-Duffing Oscillator with O6 Potential. International Journal of Bifurcation and Chaos, 26, Article ID: 1650085. https://doi.org/10.1142/S0218127416500851
- 4. Sprott, J.C. (2010) Elegant Chaos: Algebraically Simple Chaotic Flows. World Scientific, Singapore. https://doi.org/10.1142/7183
- 5. Yamapi, R., Filatrella, G., Aziz-Alaoui, M.A. and Enjieu Kadji, H.G. (2014) Modeling, Stability, Synchronization, and Chaos and Their Applications to Complex Systems. Abstract and Applied Analysis, 2, Article ID: 953813. https://doi.org/10.1155/2014/953813
- 6. Hayashi, C. (1964) Nonlinear Oscillations in Physical Systems. McGraw Hill, New York.
- 7. Nayfeh, A.H. (1981) Introduction to Perturbation Techniques. John Wiley and Sons, New York.
- 8. Strogatz, S.H. (1994) Nonlinear Dynamics and Chaos with Applications to Physics, Chemistry, and Engineering. Westview, Cambridge.
- 9. Soong, T.T. (1990) Active Structural Control Theory and Practice. John Wiley and Son, New York.
- 10. Olabodé, D.L., Miwadinou, C.H., Monwanou, A.V. and Chabi Orou, J.B. (2018) Horseshoes Chaos and Its Passive Control in Dissipative Nonlinear Chemical Dynamics. Physica Scripta, 93, Article ID: 085203. https://doi.org/10.1088/1402-4896/aacef0
- 11. Enjieu Kadji, H.G. and Nana Nbendjo, B.R. (2012) Passive Aerodynamics Control of Plasma Instabilities. Communications in Nonlinear Science and Numerical Simulation, 17, 1779-1794. https://doi.org/10.1016/j.cnsns.2011.09.017
- 12. Hackl, K., Yang, C.Y. and Cheng, A.H.D. (1993) Stability, Bifurcation and Chaos of Non-Linear Structures with Control I. Autonomous Case. International Journal of Non-Linear Mechanics, 28, 441-454. https://doi.org/10.1016/0020-7462(93)90018-G
- 13. Yamapi, R., Nana Nbendjo, B.R. and Enjieu Kadji, H.G. (2007) Dynamics and Active Control of a Motion of a Driven Multi-Lmit-Cycle Van der Pol Oscillator. International Journal of Bifurcation and Chaos, 17, 1343-1354. https://doi.org/10.1142/S0218127407017847
- 14. Tchoukuegno, R. and Woafo, P. (2002) Dynamics and Active Control of Motion of a Particle in a 6 Potential with a Parametric Forcing. Physica D, 167, 86. https://doi.org/10.1016/S0167-2789(02)00447-5
- 15. Tchoukuegno, R., Nana Nbendjo, B.R. and Woafo, P. (2003) Linear Feedback and Parametric Controls of Vibration and Chaotic Escape in a 6 Potential. International Journal of Non-Linear Mechanics, 38, 531-541. https://doi.org/10.1016/S0020-7462(01)00081-6
- 16. Nana Nbendjo, B.R. and Yamapi, R. (2007) Active Control of Extended Van der Pol Equation. Communications in Nonlinear Science and Numerical Simulation, 12, 1550-1559. https://doi.org/10.1016/j.cnsns.2006.01.016
- 17. Cheng, A.H.D., Yang, C.Y., Hackl, K. and Chajes, M.J. (1993) Stability, Bifurcation and Chaos of Non-Linear Structures with Control II, Non-Autonomous Case. International Journal of Non-Linear Mechanics, 28, 549-565. https://doi.org/10.1016/0020-7462(93)90047-O
- 18. Francescutto, A. and Contento, G. (1999) Bifurcations in Ship Rolling: Experimental Results and Parameter Identification Technique. Ocean Engineering, 26, 1095-1123. https://doi.org/10.1016/S0029-8018(98)00061-4
- 19. Nana Nbendjo, B.R., Salissou, Y. and Woafo, P. (2005) Active Control with Delay of Catastrophic Motion and Horseshoes Chaos in a Single Well Duffing Oscillator. Chaos, Solitons and Fractals, 23, 809-816. https://doi.org/10.1016/j.chaos.2004.05.041
- 20. Miwadinou, C.H., Monwanou, A.V., Yovogan, J., Hinvi, L.A., Nwagoum Tuwa, P.R. and Chabi Orou, J.B. (2018) Modeling Nonlinear Dissipative Chemical Dynamics by a Forced Modified Van der Pol-Duffing Oscillator with Asymmetric Potential: Chaotic Behaviors Predictions. Chinese Journal of Physics, 56, 1089-1104. https://doi.org/10.1016/j.cjph.2018.03.033
- 21. Boissonade, J. and De Kepper, P. (1980) Transitions from Bistability to Limit Cycle Oscillations. Theoretical Analysis and Experimental Evidence in an Open Chemical System. The Journal of Physical Chemistry, 84, 501-506. https://doi.org/10.1021/j100442a009
- 22. Bartuccelli, M., Gentile, G. and Wright, J.A. (2016) Stable Dynamics in Forced Systems with Sufficiently High/Low Forcing Frequency. Chaos, 26, Article ID: 083108. https://doi.org/10.1063/1.4960614
- 23. Lam, L. (1997) Introduction to Nonlinear Physics. Springer-Verlag Inc., New York. https://doi.org/10.1007/978-1-4612-2238-5
- 24. Rand, R.H. (2005) Lecture Notes on Nonlinear Vibrations. Version 52.
- 25. Nayfey, A.H. and Mook, D.T. (1979) Nonlinear Oscillations. John Wiley and Sons, New York.













