ABSTRACT

In this paper, we propose the multiple Stratonovich integral driven by G-Brownian motion under the G-expectation framework. Then based on G-Itô formula, we obtain the relationship between Hermite polynomials and multiple G-Stratonovich integrals by using mathematical induction method.

Keywords:

G-Stratonovich Integral, G-Brownian Motion, Mathematical Induction

1. Introduction

With the rapid development of the internet, computer science and data information technology, we are facing a real world with more and more dynamic characteristics, often dealing with a large number of high-dimensional random data, and the uncertainty is becoming more and more large. The Choquet expectation theory cannot satisfy the dynamic economic model in the risk study, such as financial risk with highly dynamic and complex characteristics. By introducing a backward stochastic differential equation (BSDE) in typical probability space, in 1997, Peng [1] constructs a new class of nonlinear expectations which are uniquely determined by the generating function g of BSDE, which is named g-expectation. In a sense, the discovery establishes the theoretical basis of dynamic nonlinear mathematical expectation. With more and more scholars studying, g-expectation has become a powerful tool for studying recursive utility theory and financial risk measurement [2] [3] [4] . The concept of g-expectation can be applied to handle a set 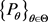of uncertain probabilities by reference probability P. However, especially for 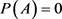and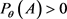, g-expectation is no longer applicable. Peng [5] introduced a new nonlinear mathematical expectation-G-expectation. Because the G-expectation constructive risk measure is a consistent risk measure, the theory has an important application in financial theory [6] [7] [8] [9] . In G-expectation theory, G-normal distribution theory is a sublinear expectation defined by Peng in the space of global continuous orbit. Next, there are concepts, which are introduced, such as a new stochastic process called G-Brownian motion, G-Itô integral and so on. Subsequently, the law of large numbers and central limit theorems under G-expectation are also proved [10] .

Now based on the multiple G-Itô integral, scholars get the relationship between Hermite polynomials and multiple G-Itô integrals. Stratonovish [11] introduced the Brown movement. The problems related to the Stratonovish integral are not easy to solve. In 2012, Yin [12] introduced one weight G-Stratonovish integral of Brownian motion.

In this paper, according to the definition of Stratonovish integral of Brownian motion in G-expectation space, we not only introduce the multiple G-Stratonovish integral of Brownian motion but also obtain the relationship between Hermite polynomials and multiple G-Stratonovish integrals.

The structure of this paper is as follows: in Section 2, we first introduce the basic theoretical framework of nonlinear expectation related to the main concepts. In Section 3, two related theorems which are the relationships between Hermite polynomials and multiple G-Stratonovish integrals are given by mathematical induction for the G-Stratonovish integral of Brownian motion.

2. Preliminaries and Notation

Let 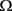be a given set and let 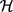be a linear space of real valued functions defined on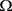. In this paper, we suppose that 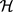satisfies 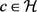for each constant c and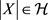. The space 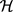can be considered as the space of random variables. Peng [13] gave the nonlinear G-mathematical expectation and G-normal distribution as follows.

Definition 1 [13] We define a functional sublinear expectation 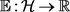by

1) Monotonicity: 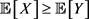if.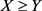

2) Constant preserving: 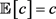for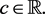

3) Sub-additivity: For each,.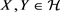

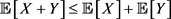4) Positive homogeneity: 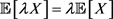for.

We call a sublinear expectation space, which is the triple. If 1) and 2) are satisfied, is called a nonlinear expectation and the triple is called a nonlinear expectation space.

Definition 2 [13] (G-normal distribution) A d-dimensional random vector on a sublinear expectation space is called (centralized) G-normal distributed if

where is an independent copy of X.

Now we give the definition of G-Brownian motion, G-quadratic variation process, and multi-dimensional G-Itô formula.

Definition 3 [13] A d-dimensional process on a sublinear expectation space is called a G-Brownian motion if the following properties are satisfied:

1);

2) For each, the increment is -distributed and is independent from, for each and.

Definition 4 [13] Let be a d-dimensional G-Brownian motion. For each fixed, is a 1-dimensional G_a-Brownian motion. We can define

where is called the quadratic variation process of.

Definition 5 [13] Let with satisfying polynomial growth condition for, and satisfying

where is the i-th of, and are the line i and column j elements of and respectively. And be bounded processes in. Then for each we have, in

Lemma 1 [13] In the G-expectation space, the following product rule is established:

The definition of G-Stratonovich integral for G-Brownnian motion is as below.

Definition 6 [13] Let is G-Itô process, then the G-Stratonovich integral of is

3. Main Result

In this section, in a multi-index the components that equal 0 refer to an integration with respect to time; the components that equal refer to an integration with respect to Stratonovich integral. We shall denote by and the sets of functions for which and, respectively, where is a d-dimensional Itô process which satisfies the Stratonovich stochastic differential equation.

Definition 7 Let and be two stopping times with w.p.1. Then for a multi-index and a function we define the multiple Stratonovich integral recursively by

(1)

There is a recursive relationship for multiple Stratonovich integrals analogous to that for multiple Itô integrals when the integrand is identically equal to 1. In order to state it succinctly we shall use the abbreviation

and as before, write for. Based on the above multiple Stratonovich integral, we would like to consider the following special cases.

Theorem 1 When, the multiple G-Stratonovich integral and Hermite polynomials have the following relations

(2)

where.

Proof 1 For, using Definition 7 and G-Itô formula we get

(3)

For, combining with formula (3), it’s easy to get

(4)

By G-Itô formula, we have Thus the first term of the right side of formula (4) can be represented as

(5)

We can derive

(6)

Assuming that when, we have

(7)

It is proved that when, we have the following equation

(8)

Actually, applying Definition 8 and formula (7), we can get

(9)

Applying G-Itô formula to and, we have

(10)

and

(11)

The formula (11) is equal to

(12)

Embedding formula (10) and formula (12) into formula (9), one has

(13)

The proof is completed.

The next Theorem, gives a clear indication of the same structure offered by multiple Stratonovich integrals when compared with its counterpart for multiple G-Itô integrals. Similarly, we will give the proof process.

Theorem 2 For different, the set being the all of the n level arrangement of, we have

such that

(14)

Proof 2 For, using Theorem 1 and Definition 7 we have

(15)

Suppose that when, one has

(16)

Now we prove that when,

(17)

In fact, we only need to prove that

(18)

where is gets rid of its last index element and gets the k-weight index. Using G-Itô formula and independence of G-Brownian motion on formula (18) we can get

(19)

Taking integral about the above equation, and combined with formula (18), the proof is completed.

Conflicts of Interest

The authors declare no conflicts of interest regarding the publication of this paper.

Cite this paper

Li, Z., Liu, F.Y. and Li, Y. (2018) Multiple G-Stratonovich Integral Driven by G-Brownian Motion. Journal of Applied Mathematics and Physics, 6, 2295-2301. https://doi.org/10.4236/jamp.2018.611190

References