ABSTRACT

Using subdivision potential approach and mean-field theory for a ferromagnetic cluster, we obtained nanothermodynamic properties for a ferromagnetic nanocluster in the presence and also the absence of the magnetic field. The subdivision potential and the magnetic field both makes Gibbs and Helmholtz free energies of the ferromagnetic nanocluster stand at a lower level compared to those of the ferromagnetic cluster. Our main conclusion is that the presence of the magnetic field leads to decrease in the amount of specific heat capacity for the ferromagnetic cluster. On the other hand, this effect leads to increase in the amount of specific heat capacity for the ferromagnetic nanocluster.

Keywords:

Subdivision Potential, Mean-Field Theory, Ferromagnetic, Nanocluster, Nanothermodynamic

1. Introduction

Science and technology at nanoscale are of great importance in the twenty-first century [1] , because the first level of organization of all structures, whether physical or living and intelligent organisms, namely physical nanostructures and bio-nanostructures is at nanoscale (one billionth of a meter). As a result, the rules governing their dynamics and growth are developed at this level [2] .

Nanostructural materials which their constitutive structural units’ size, are at a few nanometers scale, compared to ordinary materials have much advanced, preferable and completely different mechanical, thermal, electronic and optical properties. For example, electrical resistance of ferromagnetic materials such as iron and nickel consisting of nanostructural fine-graineds, is 55% and 35% higher than the corresponding values for the same materials but consisting of microstructural fine-graineds, respectively. The use of nanostructures in devices at nanoscale, requires a deep and comprehensive understanding of their stability and mechanical, electrical and thermal performance in interactive mode. Using the application of thermodynamics for big devices (classic thermodynamics), works have been done in the field of energy studies and thermal properties of these structures.

Given the close correlation between properties of nanostructures and their size, naturally one cannot expect that classic thermodynamics can offer a correct modeling for thermal properties of the nanostructures. For example, calculation of melting point in structures at nanoscale, has been encountered with some problems which in turn are caused by the application of classic thermodynamics relations developed for thermodynamic limit [3] . Thermodynamic limit for a physical device, consisting of N particles, means that when, then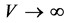, in such a way that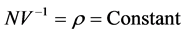, where 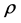is the density of particles [4] . For applicability of this limit, the device must have an infinite number of particles. In practice, for macroscopic devices that their number of particles is of order of 10²³, this condition is well satisfied. Basically at this limit, the intensive properties of the device become size independent [5] . If in a device, because of its small size, thermodynamic limit is not established, then one cannot expect the validity of common classical relations of thermodynamics in this device [6] .

For the first time in the early sixties, American chemist, Terrell Hill, through publishing a paper [7] and a book [8] introduced nanothermodynamics (first introduced in the sense mentioned above by his Colleague, Chamberlain, in an article in Nature Journal [9] ). The nanothermodynamic properties of a device are size dependent [10] .

Statistical standpoint of Evans fluctuation theory [11] predicts that for small devices consisting of the finite number of particles, the second law is reversible. However, by increasing the device size or prolonging its observation time, we enter the validity zone of the second law. This argument about nanothermodynamics has been evolved through entering energy fluctuations in paper [12] .

In this paper, using the partition function obtained from mean-field theory for ferromagnetic nanocluster and the application of nanothermodynamic relations, transition energy from classical thermodynamics to nanothermodynamics is calculated. Then, the effects of this energy on Helmholtz and Gibbs free energies, chemical potential and specific heat capacity are investigated in the presence and the absence of the magnetic field.

2. Theoretical Method

2.1. Nanothermodynamic and Subdivision Potential Approach

Nanothermodynamics can explain thermodynamic properties of small enough devices [13] . These devices are those in which the effects of small size in them are significant and they influence their physical properties. Generally, characteristics of these devices are as follows: first, the number of their particles is countable (finite) and second, their surface to volume ratio is significant (this is a very important property in small devices that are considerably used in nanotechnology).

In thermodynamics, a macroscopic device’s energy is given by following relations:

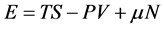
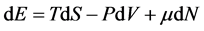
Generally, in classical thermodynamics, except internal energy, one can enumerate seven thermodynamic potentials that all of them are obtained through Legendre transform of E with respect to corresponding variables [14] . Two of these potentials that have been used until today are:

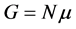
Generally, in nanothermodynamics, relations such as are not valid and in order to correct them, the effects due to the small size of device must be taken into account. Nowadays, these devices are called nanometric devices.

Terrell Hill approach, in investigation of thermodynamics of small devices, is called subdivision potential approach. In investigation of conductive thermodynamics of small devices, we only consider devices that satisfy two conditions: First, they are so small that macroscopic thermodynamics is not applicable on them. Second, they are so big that their properties can be assumed to be continuous.

In this approach, first as a principle, we accept that without any fundamental changes we can use common statistical mechanics for small devices. The basis of our work is as follows: we divide a macroscopic device into B independent subdevices. B represents the number of small subdevices resulting from subdividing a big device. If B is big, then we are sure that each subdevice is small enough and the effects of their size become important. Common thermodynamic relations are not valid on each individual small device, but we can take all of these small devices as a macroscopic device and therefore we can use classical thermodynamic relations [7] . Equation 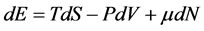can be rewritten for the entire subdivided macroscopic device as follows:

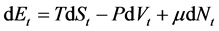(1)

where the index t represents the corresponding properties on all small devices.

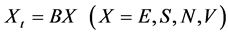(2)

N_t represents the number of all particles in the macroscopic device and B represents the number of particles in a small subdevice.

The energy of this particular macroscopic device also is a function of B; therefore, the correct form of Equation (1) is as follows [15] :

(3)

Using Equation (3), we have:

(4)

This means that the subdivision potential, 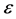, is equal to the energy variation of the big device consisting of a large number of small devices. Therefore, we can define as a type of a chemical potential that appears in transition from classical thermodynamics to nanothermodynamics [8] .

Since Equation (3) is written for a macroscopic device, then using Euler’s theorem [16] , we have:

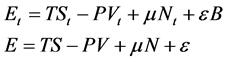(5)

One can obtain Helmholtz and Gibbs free energies for nanomaterials in nanother- modynamic state as:

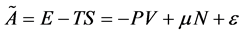(6)

(7)

Finally, if we define nanothermodynamic chemical potential as the common relation, the chemical potential variations in nanothermodynamic state become equal to [17] .

Through a series of calculations, we obtained subdivision potential in terms of Helm- holtz free energy as:

Given that and using Equation (6), one can obtain subdivision potential in terms of A as follows:

(8)

From Equation (8), one can obtain:

(9)

2.2. Mean-Field Theory of Ferromagnetism

Consider a physical device consisting of N clusters of particles. Each particle can be aligned in either of two directions. The mean energy for each particle in the mean-field in the presence of the magnetic field is approximated by [18] :

(10)

where, is the magnetic permeability of vacuum, is the magnetic moment of spin, H is the magnetic intensity, J is the magnitude of exchange interaction, C is the coordination number of the lattice and L is the number of particles in the up state. In macroscopic limit, , and in the absence of the magnetic field, Equation (10) is simplified to:

where, is the mean value of spin vector of particles [19] .

In this limit, thermodynamic potential is very big and we have

where:

(11)

If we take partition function as Equation (11), all thermodynamic properties are vanished above the critical temperature. Note that for this partition function, subdivision potential is always vanished. The critical temperature at macroscopic state is defined as

[20] .

In the case of a limited cluster, canonical partition function is obtained as [9] [21] :

(12)

3. Results and Discussions

3.1. Thermodynamic Properties of Ferromagnetic Cluster

For partition function mentioned above, one can obtain thermodynamic properties such as internal energy and entropy as follows:

(13)

(14)

The temperature dependence per particle of internal energy as well as the entropy for the ferromagnetic cluster is shown in Figure 1(a) and Figure 1(b), both in the presence and the absence of the magnetic field for N = 20, 50, 100.

In addition, in the presence of the magnetic field, there is a sharp decline in the level of internal energy. The presence of the magnetic field makes the spins to be polarized in the same direction and leads to decrease in the internal energy of the system.

Above the critical temperature, the entropy of the ferromagnetic cluster is vanished, but in the presence of the magnetic field for small N, the entropy is vanished just after a short time interval. Since degeneration depends on all up and down spin states, then we have

Also, chemical potential is:

(15)

where is the digamma function.

(Direct working with derivatives of the digamma function or the factorial function is inappropriate, but taking natural logarithm from the factorial and also from derivative of the factorial function is well-defined [22] ).

Gibbs and Helmholtz free energies and chemical potential for a ferromagnetic cluster are presented in Figure 2 and Figure 3.

As can be seen from Figure 2 and Figure 3, the presence of the magnetic field leads to decrease in chemical potential, Gibbs and Helmholtz free energies of the ferromagnetic cluster.

3.2. Nanothermodynamic Properties of Ferromagnetic Nanocluster

If we divide this ferromagnetic cluster into B independent subdevices, subdivision potential is obtained as:

(16)

This is the energy which is important in dividing a big device into small pieces. The temperature dependence per particle of this quantity is shown in Figure 4 for N = 20, 50, 100 for ferromagnetic nanocluster in the presence and also the absence of the magnetic field.

According to Figure 4, it is obvious that the subdivided potential is highly influenced by the magnetic field so that only for temperatures below the critical temperature, this

potential has a nonzero value. By using a large sample, i.e. by increasing the number of particles, this potential is vanished.

Finally, by using the Hill’s approach, the temperature dependence of nanothermo- dynamic properties such as chemical potential, Gibbs and Helmholtz free energies, per ferromagnetic nanocluster particle are shown in Figure 5 and Figure 6 for N = 20, 50, 100.

For more detailed analysis, we have found that the chemical potential variations compared to the initial state in the subdivided device (Figure 5(a)) shows fundamental changes in the properties of ferromagnetic clusters.

As shown in Figure 2(a), for a ferromagnetic cluster limited to, chemical potential undergoes a sharp decline. This behavior is also presented for a subdivided device (Figure 5(a)) and is more significant for small N. Comparing Figure 5(b) and Figure 2(b) and also Figure 3 and Figure 6, we see that the subdivision potential makes Gibbs and Helmholtz free energies of the ferromagnetic nanocluster stand at a lower level compared to those for the ferromagnetic cluster. The magnetic field in ferromagnetic and ferromagnetic nanoclusters always leads to decrease in Gibbs and Helmholtz free energies, but such variations for a ferromagnetic nanocluster state are different from those for a ferromagnetic cluster state. To see the effects of the subdivision potential, we study the specific heat capacity in both thermodynamic and nano- thermodynamic states. The specific heat capacity in nanothermodynamic state is:

(17)

The last term includes the size effects which is absent in the thermodynamic state (It exists only in the nanothermodynamic state). Temperature dependence of the specific heat capacity per particle in the case of N divided ferromagnetic nanoclusters is shown in Figure 7 for N = 20, 50 and is compared to that of the ferromagnetic state. Experimental data [23] [24] show that the specific heat capacity of ferromagnetic nanomaterials increases with respect to ferromagnetic ones which is in agreement with our results.

4. Conclusions

We study the properties of the ferromagnetic nanocluster by dividing a cluster of ferromagnetic materials into a set of small independent devices. When the size effects in each small device become important, a series of particular energies are generated in each small device. The diagram of this energy per particle for the ferromagnetic cluster in subdivision potential approach is shown in Figure 4. This energy is comparable to the internal energy of the device and even at some cases is equal to it. Therefore, when we are investigating the properties of the ferromagnetic nanocluster, we should take into account the energy. It is obvious that this energy is able to influence the properties of the ferromagnetic materials such as iron, nickel, etc. in small dimensions and especially at temperatures below the critical temperature. Therefore, for nanoscale materials, the classical thermodynamics is not applicable. With the enlargement of the device, the subdivision potential is vanished.

Using mean-field theory that provides us by the canonical partition function of the ferromagnetic cluster, we obtain the variations of Gibbs and Helmholtz free energies for the ferromagnetic cluster in terms of temperature. On the other hand, the size effects that are developed at nanostate, are not considered in mean-field theory. Therefore, it does not give us any information about the ferromagnetic cluster at nanoscale that is subdivided by taking into account the size effects.

Finally, we study the effect of the subdivision potential on the specific heat capacity of ferromagnetic and ferromagnetic nanoclusters. As shown in Figure 7, subdivision potential increases the specific heat capacity and in the presence of the magnetic field, makes shift into the maximum amount of the specific heat capacity. In other words, subdivision potential decreases the specific heat capacity for a ferromagnetic cluster and increases the specific heat capacity for a ferromagnetic nanocluster.

Cite this paper

Simiari, M., Mogaddam, R.R., Ghaebi, M., Farshid, E. and Zomorrodian, M.E. (2016) Assessment of Nanothermodynamic Properties of Ferromagnetic Nanocluster in Subdivision Potential Approach and Magnetic Field. Journal of Applied Mathematics and Physics, 4, 2233- 2246. http://dx.doi.org/10.4236/jamp.2016.412216

References