Journal of Applied Mathematics and Physics
Vol.04 No.11(2016), Article ID:72168,8 pages
10.4236/jamp.2016.411205
Integro-Differential Equations for a Jump-Diffusion Risk Process with Dependence between Claim Sizes and Claim Intervals
Heli Gao
Department of Mathematics, Binzhou University, Binzhou, China

Copyright © 2016 by author and Scientific Research Publishing Inc.
This work is licensed under the Creative Commons Attribution International License (CC BY 4.0).
http://creativecommons.org/licenses/by/4.0/



Received: October 30, 2016; Accepted: November 19, 2016; Published: November 22, 2016
ABSTRACT
The classical Poisson risk model in ruin theory assumed that the interarrival times between two successive claims are mutually independent, and the claim sizes and claim intervals are also mutually independent. In this paper, we modify the classical Poisson risk model to describe the surplus process of an insurance portfolio. We consider a jump-diffusion risk process compounded by a geometric Brownian motion, and assume that the claim sizes and claim intervals are dependent. Using the properties of conditional expectation, we establish integro-differential equations for the Gerber-Shiu function and the ultimate ruin probability.
Keywords:
Jump-Diffusion Risk Process, Diffusion, Geometric Brownian Motion, Gerber-Shiu Function

1. Introduction
Various papers in ruin theory modify the classical Poisson risk model to describe the surplus process of an insurance portfolio. An extension of the classical model is that the risk process perturbed by a diffusion was first introduced by Gerber [1] and has been further studied by many authors during the last few years, e.g. Dufresne and Gerber [2] , Gerber and Landry [3] , Wang and Wu [4] , Tsai and Willmot [5] [6] , Chiu and Yin [7] , and the references therein.
In the risk process that is perturbed by diffusion, the surplus process 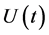 of an insurance portfolio is given by
of an insurance portfolio is given by
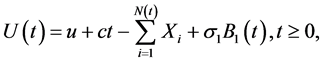 (1)
(1)
where 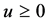 is the initial surplus,
is the initial surplus, 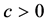 is the positive constant premium income
is the positive constant premium income
rate, 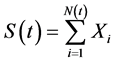 is the aggregate claims process, in which
is the aggregate claims process, in which

is the claim number process (denoting the number of claims up to time t), and the interarrival times 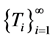 is a sequence of positive random variables.
is a sequence of positive random variables. 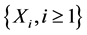 is a sequence of nonnegative independent identically distributed (i.i.d.) random variables with distribution function
is a sequence of nonnegative independent identically distributed (i.i.d.) random variables with distribution function 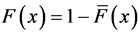 and density function
and density function ,
, 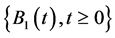 is a standard Brownian motion that is independent of the aggregate claims process
is a standard Brownian motion that is independent of the aggregate claims process ,
, 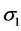 is a positive constant.
is a positive constant.
It is explicitly assumed in these papers that the interarrival times 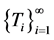 and the claim sizes
and the claim sizes 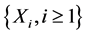 are mutually independent. However, this assumption is often too restrictive in practice, and there is a need for more general models where the independence assumptions can be relaxed. Recently, various results have been obtained concerning the asymptotic behavior of the probability of ruin for dependent claims, see [8] - [14] , as well as the references therein. Zhao [14] assumed that the distribution of the time between two claim occurrences depends on the previous claim size. Motivated by the results of Zhao [14] , the main aim of this paper is to modify the risk model (Equation (1)), and establish integro-differential equations for the Gerber-Shiu function and the ultimate ruin probability in the new risk model.
are mutually independent. However, this assumption is often too restrictive in practice, and there is a need for more general models where the independence assumptions can be relaxed. Recently, various results have been obtained concerning the asymptotic behavior of the probability of ruin for dependent claims, see [8] - [14] , as well as the references therein. Zhao [14] assumed that the distribution of the time between two claim occurrences depends on the previous claim size. Motivated by the results of Zhao [14] , the main aim of this paper is to modify the risk model (Equation (1)), and establish integro-differential equations for the Gerber-Shiu function and the ultimate ruin probability in the new risk model.
2. Improved Risk Model
In this paper, it is assumed that the claim occurrence process to be of the following type: If a claim 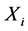 is larger than a random variable
is larger than a random variable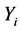 , then the time until the next claim
, then the time until the next claim 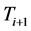 is exponentially distributed with rate
is exponentially distributed with rate




which is the net profit condition.
In the daily operation of insurance company, in addition to the premium income and claim to the operation of spending has a great influence on the outside, and there is also a factor that interest rates should not be neglected. As in [15] , this paper assume that the risk model Equation (1) is invested in a stochastic interest process which is assumed to be a geometric Brownian motion




Denote T to be the ruin time (the first time that the surplus becomes negative), i.e.,
and 

This article is interested in the expected discounted penalty (Gerber-Shiu) function:

where 




Furthermore, let 




For

such that

then,
3. Integro-Differential Equations for
In this section, a system of integro-differential equations with initial value conditions satisfied by the Gerber-Shiu function 
Define

Lemma 3.1 Let 





Proof 

acting on functions satisfying the reflecting boundary condition
If
and 

tingale. Using the separation variable technique, we find that
is a solution, where



Here

Using the initial condition 



Applying the Optional Stopping Theorem, it follows that

and thus

This ends the proof of Lemma 3.1.
Similarly, the following lemma can also be obtained.
Lemma 3.2 Let 





Theorem 3.1 Assuming that 



with the initial value conditions


Proof Let 




1) There are no claims in 


2) There is exactly one claim in 

a) The amount of the claim

b) The amount of the claim
c) The amount of the claim
3) There is more than one claim in 

Thus, considering the three cases above and noting that 

By Taylor expansion, we have

Then, by Itô’s formula we have

Therefore, by dividing t on both sides of Equation (12), letting
The condition 


For all



According to Lemma 3.1, it can be concluded that

Thus, 


And for all




This ends the proof of Theorem 3.1.
4. Differential Equations for
Let 



Obviously,

and

Suppose that


and 

Theorem 4.1 Assuming that 



with the initial value conditions
Proof According to Equation (9), it can be concluded that
By taking the derivative with respect to u on both sides of the above formula, and after some careful calculations, we obtain Equation (14). And similarly we can prove that Equation (15) holds. This ends the proof of Theorem 4.1.
5. Conclusion
In this paper, we consider a jump-diffusion risk process compounded by a geometric Brownian motion with dependence between claim sizes and claim intervals. We derive the integro-differential equations for the Gerber-Shiu functions and the ultimate ruin probability by using the martingale measure. Further studies are needed for the numerical solution of Equations (9), (10), (14) and (15). The results derived in this paper can be generalized to similar dependence ruin models.
Acknowledgements
This research was supported by the National Natural Science Foundation of China (No. 11601036), the Natural Science Foundation of Shandong (No. ZR2014GQ005) and the Natural Science Foundation of Binzhou University (No. 2016Y14).
Cite this paper
Gao, H.L. (2016) Integro-Differential Equations for a Jump- Diffusion Risk Process with Dependence between Claim Sizes and Claim Intervals. Journal of Applied Mathematics and Physics, 4, 2061-2068. http://dx.doi.org/10.4236/jamp.2016.411205
References
- 1. Gerber, H.U. (1970) An Extension of the Renewal Equation and Its Application in the Collective Theory of Risk. Skandinavisk Aktuarietidskrift, 1970, 205-210.
- 2. Dufresne, F. and Gerber, H.U. (1991) Risk Theory for the Compound Poisson Process That Is Perturbed by Diffusion. Insurance: Mathematics and Economics, 10, 51-59.
https://doi.org/10.1016/0167-6687(91)90023-Q - 3. Gerber, H.U. and Landry, B. (1998) On the Discounted Penalty at Ruin in a Jump-Diffusion and the Perpetual Put Option. Insurance: Mathematics and Economics, 22, 263-276.
https://doi.org/10.1016/s0167-6687(98)00014-6 - 4. Wang, G. and Wu, R. (2000) Some Distributions for the Classical Risk Process That Is Perturbed by Diffusion. Insurance: Mathematics and Economics, 26, 15-24.
https://doi.org/10.2307/253675 - 5. Tsai, C.C.L. and Willmot, G.E. (2002) A Generalized Defective Renewal Equation for the Surplus Process Perturbed by Diffusion. Insurance: Mathematics and Economics, 30, 51-66.
https://doi.org/10.1016/s0167-6687(01)00096-8 - 6. Tsai, C.C.L. and Willmot, G.E. (2002) On the Moments of the Surplus Process Perturbed by Diffusion. Insurance: Mathematics and Economics, 31, 327-350.
https://doi.org/10.1016/s0167-6687(02)00159-2 - 7. Chiu, S.N. and Yin, C.C. (2003) The Time of Ruin, the Surplus Prior to Ruin and the Deficit at Ruin for the Classical Risk Process Perturbed by Diffusion. Insurance: Mathematics and Economics, 33, 59-66.
https://doi.org/10.1016/s0167-6687(03)00143-4 - 8. Boudreault, M., Cossette, H., Landriault, D. and Marceau, E. (2006) On a Risk Model with Dependence between Interclaim Arrivals and Claim Sizes. Scandinavian Actuarial Journal, 5, 265-285.
https://doi.org/10.1080/03461230600992266 - 9. Bargès, M., Cossette, H., Loisel, S. and Marceau, E. (2011) On the Moments of the Aggregate Discounted Claims with Dependence Introduced by a FGM Copula. ASTIN Bulletin, 41, 215-238.
- 10. Li, J. (2012) Asymptotics in a Time-Dependent Renewal Risk Model with Stochastic Return. Journal of Mathematical Analysis and Applications, 387, 1009-1023.
https://doi.org/10.1016/j.jmaa.2011.10.012 - 11. Yong, W. and Xiang, H. (2012) Differential Equations for Ruin Probability in a Special Risk Model with FGM Copula for the Claim Size and the Inter-Claim Time. Journal of Inequalities and Applications, 2012, 156.
https://doi.org/10.1186/1029-242X-2012-156 - 12. Fu, K.A. and Ng, C.Y.A. (2014) Asymptotics for the Ruin Probability of a Time-Dependent Renewal Risk Model with Geometric Lévy Process Investment Returns and Dominatedly-Varying-Tailed Claims. Insurance Mathematics & Economics, 56, 80-87.
https://doi.org/10.1016/j.insmatheco.2014.04.001 - 13. Zhang, J. and Xiao, Q. (2015 ) Optimal Investment of a Time-Dependent Renewal Risk Model with Stochastic Return. Journal of Inequalities and Applications, 2015,181.
https://doi.org/10.1186/s13660-015-0707-3 - 14. Zhao, X.H. and Yin, C.C. (2009) A Jump-Diffusion Risk Model with Dependence between Claim Sizes and Claim Intervals. Acta Mathematica Scientia, 29A, 1657-1664.
- 15. Cai, J. and Xu, C. (2005) On the Decomposition of the Ruin Probability for a Jump-Diffusion Surplus Process Compounded by a Geometric Brownian Motion. North American Actuarial Journal, 10, 120-132.
https://doi.org/10.1080/10920277.2006.10596255










